1 Introduction

Polarization preserving optical fibers are vastly utilized in communication and sensing systems [1, 2]. In such systems, a high degree of polarization preservation can be achieved due to the presence of modal birefringence. Conventional mono-mode optical fibers used in communication system are having a perfect cylindrical core, with uniform diameter. Birefringent fibers can smartly handle high data rate transmission as well as long length communication. Optical fibers posses waveguide dispersion property giving rise to large bandwidth and hence increasing the data rate transmission capabilities [3,4,5]. In such class of fibers, the degenerate modes characterized as \( HE_{11}^{\text{e}} \) and \( HE_{11}^{\text{o}} \) can easily propagate. Birefringent fibers require non-circularity of core or asymmetrical length stress. The anisotropy in cross section yields large difference between the two polarized modes [6]. However, the state of polarization remains unaltered at the output when a polarized light is launched at the input of an off centered circular core fiber. Thus, modes intrinsic to off centered circular core fibers are non-degenerate in comparison to concentric circular optical fibers [7].

Various types of single-polarization single-mode (SPSM) fiber such as non-circular core [8,9,10], elliptical cladding [11, 12], isolated circular [13], PANDA fibers [14] were fabricated and experimented as well. In a bent optical fiber, lateral internal stress induces a birefringence [15]. Optical fibers operating at 1.5 µm have advantage over 1.3 µm owing to dispersion free characteristics [16]. The highly birefringent optical fibers have large impact on optical fiber sensors [17]. The value of fundamental cutoff frequency and fractional power for decaying fields for different order of eccentricity, wavelength and refractive index by conformal mapping technique were utilized in designing the structural parameters for off centered circular core fiber in long-distance absorption sensors [18, 19]. In case of PCF, the propagation of light takes place in air due to large band gap with respect to surrounding material and hence principle of propagation of light is opposite to that of conventional fiber [20]. Losses in case of PCF are low, and birefringence is one order higher than the conventional SMF [21,22,23]. A simple hexagonal PCF achieves ultra-high birefringence, large non-linear coefficient and two zero-dispersion wavelengths as studied by using FEM technique [24]. PCF operates in tetra hertz region, which has limited practical implementation ability because of bulky size and its dependence on free space propagation. In case of free space propagation, number of undesirable losses takes place such as coupling with other component, transporting and management of tetra hertz beam, etc.

Mono-mode polarization maintaining highly birefringent (HB) optical fibers has become a topic of major interest due to the importance of their potential applications in fiber-optic sensing devices. Our approach can be extended to multi-mode fiber, but major difficulty lies in the fact that they suffer from intermodal dispersion causing pulse to spread out at the output. However, it can be reduced with the use of graded-index fiber [5]. The other way of minimizing intermodal dispersion is by controlling the helix pitch angle [25] to a desired level, which effectively reduces the number of guided modes, there by fulfilling the requirement for long-distance transmission.

In this article, we present the computational results of modal birefringence for mono-mode polarization maintaining optical fiber with off centered core by using FEM technique. The approach is based on the solution of scalar wave equation with appropriate boundary conditions at the interfaces. The work embodied in this article is as follows: In Sect. 2, we present formulation of the problem. In Sect. 3, we present the description of numerical results and discussion. Sect. 3.1 deals with physical structure and electromagnetic wave confinement aspect. In Sect. 3.2, we present modal birefringence analysis. In Sect. 3.3, we present effective index analysis, while Sect. 3.4, we present bending loss analysis. Finally in Sect. 4, we describe the outcome of our contribution.

2 Formulation of the problem

Refractive index profile of step index fiber is given by

$$ n_{\text{cl}} = n_{\text{co}} \left( {1 - \Delta } \right) $$
(1)

where

$$ \begin{aligned} n_{\text{cl}} & = {\text{R}} . {\text{I}}\;{\text{of}}\;{\text{cladding}} \\ n_{\text{co}} & = {\text{R}} . {\text{I}}\;{\text{of}}\;{\text{core}} \\ \Delta & = {\text{core}} - {\text{cladding}}\;{\text{index}}\;{\text{difference}}. \\ \end{aligned} $$

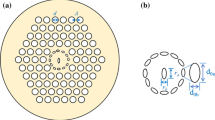
Figure 1 shows a long cylindrical dielectric optical waveguide with circular cross section and off centered circular core. The electric and magnetic field equations are expressed in the cylindrical coordinate systems. The electric and magnetic field components satisfy the scalar wave equation, and the equations for region I, II and III are expressed as

$$ \left[ {\nabla_{t}^{2} + \alpha_{i}^{2} } \right]\left\{ \begin{aligned} E_{z} \hfill \\ H_{z} \hfill \\ \end{aligned} \right\} = 0 $$
(2)

where

$$ \alpha_{i}^{2} = \omega^{2} \mu_{i} \varepsilon_{i} - \beta^{2} $$
(3)

here \( i = 1,2,3 \) for the region I, II and III and \( \alpha_{i}^{2} \) is positive for the region I and negative for the region II and III with \( \nabla_{t}^{2} \) as the Laplacian operator.

Fig. 1
figure 1

Geometrical configuration for an off centered circular core of a cylindrical optical fiber

Full size image

Once these equations are solved, other perpendicular components of the electromagnetic fields are derived from \( E_{z} \) and \( H_{z} \), using Maxwell’s equations. We have intentionally not included ‘z’ and ‘t’ dependence in the solution which is in the form \( \exp \left[ {i\left( {\beta z - \omega t} \right)} \right] \), where \( \omega \) is the angular frequency and \( \beta \) is the axial propagation constant determined by the interface boundary conditions.

The hybrid electromagnetic fields are expanded in terms of linear combinations of Bessel functions. The fields in the direction of propagation in region I are expressed as

$$ E_{z1} = \sum\limits_{m = 0}^{\infty } {A_{m}^{1} J_{m\,} \left( {\alpha_{1} r} \right)\cos \left( {m\theta + \theta_{\text{o}} } \right)} $$
(4)
$$ H_{z1} = \sum\limits_{m = 0}^{\infty } {B_{m}^{1} J_{m\,} \left( {\alpha_{1} r} \right)\sin \left( {m\theta + \theta_{\text{o}} } \right)} $$
(5)

The even and odd modes are given by Eqs. (4) and (5) with \( \theta_{\text{o}} = 0 \) and \( \theta_{\text{o}} = \frac{\pi }{2} \), respectively. \( \theta_{\text{o}} \) is the phase constant.

The field components in the direction of propagation in region II are

$$ E_{z2} = \sum\limits_{m = 0}^{\infty } {\left[ {A_{m}^{2} I_{m\,} \left( {\alpha_{2} r} \right) + C_{m}^{2} K_{m} \left( {\alpha_{2} r} \right)} \right]\cos \left( {m\theta + \theta_{\text{o}} } \right)} $$
(6)
$$ H_{z2} = \sum\limits_{m = 0}^{\infty } {\left[ {B_{m}^{2} I_{m\,} \left( {\alpha_{2} r} \right) + D_{m}^{2} K_{m} \left( {\alpha_{2} r} \right)} \right]\sin \left( {m\theta + \theta_{\text{o}} } \right)} $$
(7)

In this analysis, we have considered the region III as medium of air and the fields are given by

$$ E_{z3} \, = \,\sum\limits_{m = 0}^{\infty } {C_{m}^{3} \,K_{m\,} \left( {\alpha_{3} \,r} \right)\cos \left( {m\,\theta \, + \,\theta_{\text{o}} } \right)} $$
(8)
$$ H_{z3} \, = \,\sum\limits_{m = 0}^{\infty } {D_{m}^{3} \,K_{m\,} \left( {\alpha_{3} \,r} \right)\sin \left( {m\,\theta \, + \,\theta_{\text{o}} } \right)} $$
(9)

The perpendicular field components are obtained with the use of following equations

$$ E_{r} = \left( {\frac{i}{{\alpha^{2} }}} \right)\left[ {\beta \frac{{\partial E_{z} }}{\partial r} + \left( {\frac{\omega \mu }{r}} \right)\frac{{\partial H_{z} }}{\partial \theta }} \right] $$
(10)
$$ H_{r} = \left( {\frac{i}{{\alpha^{2} }}} \right)\left[ {\beta \frac{{\partial H_{z} }}{\partial r} - \left( {\frac{\omega \varepsilon }{r}} \right)\frac{{\partial E_{z} }}{\partial \theta }} \right] $$
(11)
$$ E_{\theta } = \left( {\frac{i}{{\alpha^{2} }}} \right)\,\left[ {\left( {\frac{\beta }{r}} \right)\frac{{\partial E_{z} }}{\partial \theta } - \omega \mu \frac{{\partial H_{z} }}{\partial r}} \right] $$
(12)
$$ H_{\theta } = \left( {\frac{i}{{\alpha^{2} }}} \right)\left[ {\left( {\frac{\beta }{r}} \right)\frac{{\partial H_{z} }}{\partial \theta } + \omega \varepsilon \frac{{\partial E_{z} }}{\partial r}} \right] $$
(13)

The boundary condition can be conveniently applied if \( E_{z}^{{{\prime }s}} \) and \( H_{z}^{{{\prime }s}} \) are expressed explicitly in terms of \( r^{{\prime }} \) and \( \theta^{\prime } \), and it has been achieved by the use of the Graf’s addition theorem [26, 27]. Applying the continuity of the tangential field components at the region I–II interface and the region II–III interface, the equations so obtained are expressed in terms of constants \( C_{m}^{2} \, \) and \( D_{m}^{2} \, \) after doing required mathematical manipulations and simplifications. The two equations are as follows

$$ \sum\limits_{m = 0}^{\infty } {\left[ {P_{mn} C_{m}^{2} + Q_{mn} D_{m}^{2} } \right] = 0} $$
(14)

and

$$ \sum\limits_{m = 0}^{\infty } {\left[ {R_{mn} C_{m}^{2} + S_{mn} D_{m}^{2} } \right] = 0} $$
(15)

The above two equations are characteristics equations for HE and EH modes. The cutoff conditions are expressed in the form

$$ \det \left| {\begin{array}{*{20}c} {\tilde{P}_{mm} } & {\tilde{Q}_{mm} } \\ {\tilde{R}_{mm} } & {\tilde{S}_{mm} } \\ \end{array} } \right| = 0 $$
(16)

here tilde sign represents the transpose of the corresponding matrix. The elements are in closed analytical form, and matrix elements involve combination of Bessel’s functions of first kind \( J_{m\,} \left( x \right) \) and also the modified Bessel’s functions of first kind \( I_{m\,} \left( x \right) \) and second kind \( K_{m\,} \left( x \right) \) along with optical fiber parameters such as permittivity, permeability, core cladding radius and eccentricity. Above equation is same as obtained by authors [6]. The elements also involve eccentricity factor after the use of Graf’s addition theorem and play very important role in determining the modal characteristics of optical fiber. Solutions of dual core optical fiber can be obtained by other methods [28].

The propagation constant is the eigenvalues obtained by determinantal equation. The odd and even mode matrix equations are constructed separately from the coefficients of the matrix and by setting the determinant equal to zero, \( \beta_{\text{e}} \) and \( \beta_{\text{o}} \) are obtained. The difference between the propagation constants of two orthogonal modes \( \Delta \beta \, = \,\beta_{\text{e}} \, - \,\beta_{\text{o}} \) is called modal birefringence, and the normalized quantity is called normalized birefringence and is given by

$$ B\, = \,\frac{\Delta \beta }{k}\, = \,\frac{2\pi }{\lambda }\,\left( {\beta_{\text{e}} \, - \,\beta_{\text{o}} } \right) $$
(17)

where \( \lambda \) is the optical wavelength. The birefringence results from geometrical deformation. We have also calculated the effect of microbending radius on the effective index of the fiber. Due to the total internal reflection mechanism, a mode will propagate in the core region if it travels with a propagation constant \( \beta \) such that effective index \( n_{\text{eff}} \) is larger than \( n_{\text{cl}} \). The bending of the fiber was taken into account by transforming the index profile \( n\left( r \right) \) to \( n_{\text{bend}} \left( r \right) \) [29, 30] and is expressed as

$$ n_{\text{eff}} \left( r \right) = n\left( r \right)\left[ {1 + 2\frac{x}{\xi }\,\frac{1}{{R_{\text{bend}} }}} \right] $$
(18)

where \( \xi \) accounts for bend-induced stress in the fiber and its value is nearly one.

3 Numerical results and discussion

3.1 Physical structure and electromagnetic wave confinement

Figures 2, 3, 4, 5 and 6 show the order of eccentricity in steps of 5 µm up to a maximum of 20 µm in an off centered circular core mono-mode birefringent fiber.

Fig. 2
figure 2

Order of eccentricity (e = 0 µm)

Full size image
Fig. 3
figure 3

Order of eccentricity (e = 5 µm)

Full size image
Fig. 4
figure 4

Order of eccentricity (e = 10 µm)

Full size image
Fig. 5
figure 5

Order of eccentricity (e = 15 µm)

Full size image
Fig. 6
figure 6

Order of eccentricity (e = 20 µm)

Full size image

The values of fiber parameters are practical with \( \Delta = 0.2\% \) and cladding to core radius ratio as 14. The electromagnetic energy or electric field is mainly confined in the fiber core region irrespective of order of the eccentricity, and evanescent field may leak into cladding region as shown in Figs. 7, 8 and 9.

Fig. 7
figure 7

Variation of electric field with eccentricity when e = 0 µm

Full size image
Fig. 8
figure 8

Variation of electric field with eccentricity when e = 10 µm

Full size image
Fig. 9
figure 9

Variation of electric field with eccentricity when e = 20 µm

Full size image

Figures 10, 11 and 12 show the propagation of electromagnetic waves in an off centered circular core fiber with order of eccentricity 0 µm, 10 µm and 20 µm. It is mostly seen that electromagnetic waves propagate along the axis of the off centered circular core of the fiber.

Fig. 10
figure 10

Propagation of electromagnetic waves when e = 0 µm

Full size image
Fig. 11
figure 11

Propagation of electromagnetic waves when e = 10 µm

Full size image
Fig. 12
figure 12

Propagation of electromagnetic waves when e = 20 µm

Full size image

3.2 Modal birefringence analysis

In this subsection, we present the birefringence characteristics of a mono-mode birefringent off centered circular core fiber. The physical quantities are as follows: The refractive index of the region I \( \left( {n_{\text{co}} } \right) \) is 1.447 and that of the region II \( \left( {n_{\text{cl}} } \right) \) is 1.444. The core and cladding radius are being 4.5 µm and 62.5 µm with input signal wavelength \( \lambda = 1.55\,\mu m \).

The modal birefringence was computed for various wavelengths ranging from 1.40 to 1.60 µm using FEM numerical technique. The results of modal birefringence so obtained with respect to operating wavelength are shown in Fig. 13.

Fig. 13
figure 13

Variation of birefringence with wavelength

Full size image

The result obtained by FEM technique proposed in this article for different order of eccentricity say e = 5 µm, e = 10 µm and e = 20 µm is shown in the graph. The values of birefringence are found to vary from \( 1.2880 \times 10^{ - 4} \) to \( 1.2960 \times 10^{ - 4} \) when the operating wavelength is varied from \( 1.40 \) to \( 1.60 \) µm. We observed that as the eccentricity increases, the value of modal birefringence also increases, which clearly explains that the separation between two orthogonal polarized modes also increases and the orthogonal modes become significantly birefringent.

The value of modal birefringence calculated by us is one order of magnitude higher than the values obtained by Alphones and Sanyal [1].

3.3 Effective index analysis

In this subsection, we present the computation of fundamental mode effective index \( \left( {n_{eff} } \right) \) which is a mode-related property and its variation with the bending radius of the optical fiber at an operating wavelength of \( 1.55 \) µm using numerically efficient technique. The calculated values suggest that \( n_{eff} \) lies between \( n_{co} \) and \( n_{cl} \), when the bending radius is varied from 80 to 260 mm for an order of eccentricity ranging from 5 to 20 µm as shown in Fig. 14. For \( e = 5 \) µm, there is slow variation in the value of effective index for the considered value of bending radius. Further, the effective index increases with eccentricity and decreases with increasing bending radius. The \( n_{eff} \) value is 1.44523 at \( e = 20 \) µm, while \( n_{eff} = 1.44508 \) at \( e = 10 \) µm for a bending radius of 100 mm. Thus, we notice that \( n_{eff} \) value at \( e = 20 \) µm is very close to \( n_{co} \) value, and hence the fundamental mode is more tightly bound to the core than at \( e = 10 \) µm and therefore bending loss will be minimum. However, if the bending radius is further increased, the modes no more remain tightly bound to the core as \( n_{eff} \) value approaches toward \( n_{cl} \) leading to bending loss more pronounced. Thus, one can say that the fundamental mode remains confined to the core at e = 20 µm at \( \lambda = 1.55 \) µm, at bending radius of 100 mm, and hence loss is minimum.

Fig. 14
figure 14

Variation of effective index with bending radius

Full size image

Bending loss in microbending region at a wave length of \( \lambda = 1.55 \) µm is found to be minimum [31]. Loss can further be minimized by creating a spatial shift between the fiber and the source and then coupling it with microlens.

It has been observed experimentally that loss on account of bending is sensitive to the direction of bending. From experiment, it has been observed that + X direction (neutral axis direction) orientation of optical fiber yields less bending losses in comparison to + Y direction orientation (perpendicular to neutral axis direction) at the same operating wavelength and bending radius [32, 33].

3.4 Bending loss analysis

Microbending loss is due to microscopic fiber deformation at the core cladding interface usually caused by poor cable design and fabrication. Non-uniform lateral stresses during the cabling and the deployment of the fiber in the ground induce microbending [34].

For a single-mode fiber with length ‘\( \ell \)’ bending loss ‘\( L_{\alpha } \)’ is obtained by

$$ L_{\alpha } = 10\log_{10} \left[ {\exp \left( {2\alpha \ell } \right)} \right] $$
(19)

Here \( \alpha \, \) is the bending loss coefficient and is function of radius, operating wavelength, optical structure and material of the fiber [35].

The bending loss calculation shows that loss per km due to bending is minimum at around 100 mm bending radius as shown in Fig. 15, which supports our results of effective index versus bending radius. This happens because of the confinement of the electromagnetic wave to the core is maximum and the loss is minimum. There is a role of eccentricity on the bending loss, and it is observed that as eccentricity increases the bending loss also increases. We can thus conclude that the bending radius and the eccentricity contribute to bending loss, and it clearly relates to the confinement of electromagnetic wave to the core. Furthermore, the losses at 1.55 µm wavelength are found to be minimum in single-mode fiber.

Fig. 15
figure 15

Variation of bending loss with bending radius

Full size image

The losses can further be minimized by adhering to the following:

  • By taking high quality cables.

  • By choosing qualified connectors.

  • Splicing should be done by following environment requirements.

4 Conclusion

We have discussed the polarization preservation for an off centered core fiber, and the analysis has been made by a numerically efficient FEM technique. It gives large modal birefringence of the order of \( 1.2960 \times 10^{ - 4} \) at \( \lambda = 1.55 \) µm, at \( e = 20 \) µm, and therefore two polarized modes get widely separated. Further, the value of \( n_{\text{eff}} \) is found to be 1.44523 at \( e = 20 \) µm, and hence mode remains tightly confined to the core. Further, bending loss is very small and is of the order of 0.05 dB/km for a fiber of bending radius from 100 to 400 mm for different order of eccentricity. This class of fiber is cheap, practical and promising as well.