1 Introduction

Ferrofluids are a new class of heat transfer fluids that can be prepared by dispersing super-paramagnetic nanoparticles with a typical diameter of less than 20 nm in base fluids such as water, oil, ethylene glycol. Ferrofluids exhibit both the fluid and magnetic properties [1,2,3]. Ferrofluids have remarkable potential for heat transfer applications. In recent year, ferrofluids have found several applications in heat transfer processes such as thermosyphons controlled by magnetic field and improved cooling systems of high-power electric transformers [4,5,6,7,8,9]. Using ferrofluids in the presence of an external magnetic field can be considered as an appropriate solution for enhancing forced-convection heat transfer and fluid mixing [10, 11]. In an experimental work, Goharkhah et al. [12] studied the effects of constant and alternating magnetic field on the laminar forced-convection heat transfer of water-based ferrofluids in a uniformly heated tube using four electromagnets as the magnetic field source. According to their results, as the magnetic field is turned off, using the base fluid with a 2% particle concentrations of nanoparticles improves the average heat transfer rate by 13.5% compared to the base fluid. This enhancement could be increased to 18.9% and 31.4% by applying constant and alternating magnetic fields with magnetic field. Laminar forced-convection heat transfer of \( {\text{Fe}}_{3} {\text{O}}_{4} \) magnetic nanofluid in an isothermal minichannel in the presence of constant and alternating magnetic field was numerically studied by Ghasemian et al. [13] using the two-phase mixture approach. Their obtained results indicate that the heat transfer enhancement becomes more significant when the magnetic field source is located in the fully developed region. A maximum value of 16.48% for the heat transfer enhancement was reported using a constant magnetic field. This value could be increased to 27.72% using an alternating magnetic field with the same intensity. Ellahi et al. [14] instigated theoretical study on ferrofluid under the influence of low oscillating magnetic field over disk. They found 7.86% heat transfer enhancement in the absence of a magnetic field and found 8.73% heat transfer enhancement in the presence of a magnetic field. A numerical study on the heat transfer of ferrofluids in microchannels was conducted by Xuan et al. [15]. They finally concluded that heat transfer rate could increase if the directions of magnetic field gradient and fluid flow are the same. It is remarkable that there are still only relatively few such publications. To apply the ferrofluid to practical heat transfer processes, more studies on its flow and heat transfer feature are needed.

Furthermore, except for enhancing the convection heat transfer as much as possible, it is also of significant importance to reduce the entropy generation to the greatest extent. Entropy generation determines the level of irreversibility accumulation during the flow and heat transfer process. Consequently, entropy generation is usually used for evaluating the performance of engineering devices. Reducing the generated entropy will result in more efficient designs of energy systems. In 1996, Bejan [16] presented a method named Entropy Generation Minimization (EGM) to measure and optimize the disorder or disorganization generated during a process specifically in the fields of refrigeration (cryogenics), heat transfer, storage and solar thermal power conversion. Minimization of the total entropy generation for two typical heat transfer enhancement problems related to the variation of heat transfer area and the variation of temperature difference was studied by Perez Blanco [17]. Jery et al. [18] studied the effects of magnetic field, Prandtl number and Grashof number on entropy generation in natural convection. They found that the magnetic field decreases the convection currents, the heat transfer and entropy generation inside the enclosure. Yazdi et al. [19] investigated the entropy generation numbers as well as the Bejan number in magnetohydrodynamics (MHD) fluid flow in open parallel microchannels. They showed that entropy generation reduces in the presence of magnetic field.

The presented literature survey shows that the heat transfer and entropy generation in ferrofluid under the influence of low oscillating magnetic field over stretching rotating disk have not yet been addressed. In the present study, magnetic force into the fundamental hydrodynamic equations is introduced and their effects along with particles concentration on physical properties, entropy generation, convection heat transfer coefficient and thermal resistance are discussed. To achieve this goal, the present work is organized in the following way. The basic governing equations and models of effective physical properties are discussed in mathematical modeling section. In the next section, homotopy analysis method-based Bvph2 package is applied to solve the nonlinear coupled equations and write the results up to first iteration of package. The impacts of parameters on thermal and fluid friction irreversibilities, local and average entropy generation as well as average convection heat transfer coefficient along with thermal resistance are examined and discussed in Results and discussion section. The achievements of the study are concluded and give a way to minimize the entropy and enhance the convective heat transfer during fluid flow in last section.

2 Formulation of the problem

2.1 Flow modeling

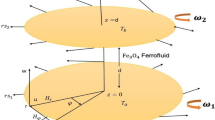
Consider the axially symmetric laminar and non-conducting flow of an incompressible nano-ferrofluid past a stretchable rotating disk that has an angular velocity varying with time \( \left( {\varOmega_{v} /1 - \beta_{v} t} \right) \). The coordinate system and geometry of the problem are shown in Fig. 1. We consider that the disk rotation speed has a form of \( \varOmega_{v} r/1 - \beta_{v} t \) and the disk stretching velocity is \( \alpha_{v} \varOmega_{v} r/1 - \beta_{v} t \), which is proportional to the radius \( r \).

Fig. 1
figure 1

Geometry of the problem

Full size image

The basic governing equations containing the continuity, momentum, energy, magnetization and rotational motion equations in vector form are as follows [14]:

$$ {\mathbf{\nabla }} \cdot {\mathbf{V}} = 0, $$
(1)
$$ \rho_{\text{nf}} \frac{{{\text{d}}{\mathbf{V}}}}{{{\text{d}}t}} = - {\mathbf{\nabla }}p + \mu_{\text{nf}} \nabla^{2} {\mathbf{V}} + \mu_{0} \left( {{\mathbf{M}} \cdot {\mathbf{\nabla }}} \right){\mathbf{H}} + \frac{1}{{2\tau_{\text{s}} }}{\mathbf{\nabla }} \times \left( {{\varvec{\upomega}}_{{\mathbf{p}}} - {\varvec{\Omega}}} \right), $$
(2)
$$ \left( {\rho C_{p} } \right)_{\text{nf}} \frac{{{\text{d}}T}}{{{\text{d}}t}} = k_{\text{nf}} \nabla^{2} T, $$
(3)
$$ \frac{{{\text{d}}{\mathbf{M}}}}{{{\text{d}}t}} = {\varvec{\upomega}}_{{\mathbf{p}}} \times {\mathbf{M}} - \frac{1}{{\tau_{\text{B}} }}\left( {{\mathbf{M}} - {\mathbf{M}}_{o} } \right), $$
(4)
$$ {\mathbf{I}}\frac{{{\text{d}}{\varvec{\upomega}}_{{\mathbf{p}}} }}{{{\text{d}}t}} = {\mathbf{M}} \times {\mathbf{H}} - \frac{1}{{\tau_{\text{s}} }}\left( {{\varvec{\upomega}}_{{\mathbf{p}}} - {\varvec{\Omega}}} \right). $$
(5)

In the above, \( {\mathbf{V = }}\left( {v_{r} ,v_{\theta } ,v_{z} } \right) \) is the velocity, \( T \) is the temperature, \( {\mathbf{M}} \) is the magnetization of the fluid, \( {\mathbf{H}} \) is the strength magnetic field, \( {\mathbf{M}}_{o} \) is the instantaneous magnetization, \( \tau_{\text{s}} \) is the relaxation time parameter, \( \tau_{\text{B}} \) is the Brownian relaxation time, \( \mu_{0} \) is the permeability of free space, \( {\mathbf{I}} \) is the sum of moments of inertia of the particles per unit volume, \( {\varvec{\upomega}}_{{\mathbf{p}}} \) is the internal angular momentum due to the self-rotation of particles and \( {\varvec{\Omega}} \) is the vorticity of the flow.

Since \( \tau_{\text{s}} \) is small, the inertial term is negligible in comparison with relaxation term, i.e., \( {\mathbf{I}}\frac{{{\text{d}}{\varvec{\upomega}}_{{\mathbf{p}}} }}{{{\text{d}}t}} \ll {\mathbf{I}}\frac{{{\varvec{\upomega}}_{{\mathbf{p}}} }}{{\tau_{\text{s}} }} \); therefore, Eq. (5) can be written by way of

$$ {\varvec{\upomega}}_{{\mathbf{p}}} = {\varvec{\Omega}} + \frac{{\tau_{\text{s}} }}{{\mathbf{I}}}\left( {{\mathbf{M}} \times {\mathbf{H}}} \right). $$
(6)

Now, Eqs. (2) and (4) in view of Eq. (6) can be written as

$$ \rho_{\text{nf}} \frac{{{\text{d}}{\mathbf{V}}}}{{{\text{d}}t}} = - {\mathbf{\nabla }}p + \left( {{\mathbf{M}} \cdot {\mathbf{\nabla }}} \right){\mathbf{H}} + \mu_{\text{nf}} {\mathbf{\nabla }}^{2} {\mathbf{V}} + \frac{1}{2}{\mathbf{\nabla }} \times \left( {{\mathbf{M}} \times {\mathbf{H}}} \right), $$
(7)
$$ \frac{{{\text{d}}{\mathbf{M}}}}{{{\text{d}}t}} = {\varvec{\Omega}} \times {\mathbf{M}} - \frac{1}{{\tau_{\text{B}} }}\left( {{\mathbf{M}} - {\mathbf{M}}_{o} } \right) + \frac{{\tau_{\text{s}} }}{I}{\mathbf{M}} \times \left( {{\mathbf{M}} \times {\mathbf{H}}} \right). $$
(8)

The magnetic torque \( {\mathbf{M}} \times {\mathbf{H}} \) and the viscous torque \( \left( {{\varvec{\Omega}} - {\varvec{\upomega}}_{{\mathbf{p}}} } \right) \) are acting on the particles and equilibrium of both torques, which leads to the hindrance of the particle rotation, can thus be written from Eq. (6) as

$$ {\mathbf{M}} \times {\mathbf{H}} = - 6\mu_{\text{nf}} \phi \left( {{\varvec{\Omega}} - {\varvec{\upomega}}_{{\mathbf{p}}} } \right) . $$
(9)

In the existence of low oscillating magnetic field, Eq. (8) can be written as [14]

$$ \tau_{\text{B}} \frac{{{\text{d}}R\left( {\varvec{\xi}_{e} } \right)}}{{{\text{d}}t}} = \left( {1 - \frac{1}{2}\left( {\frac{1}{{L_{e} }} - \frac{1}{{\varvec{\xi}_{e} }}} \right)\varvec{\xi}_{o} R\left( {\varvec{\xi}_{e} } \right)\cos \omega_{0} t} \right). $$
(10)

Above, the parameters \( \omega_{o} \) and \( \xi_{o} \) are frequency and amplitude of the real magnetic field, whereas the effective Lange in function is donated by \( L_{e} \).

By Eqs. (9) and (10), the expression for mean magnetic torque becomes

$$ \overline{{{\mathbf{M}} \times {\mathbf{H}}}} = - 6\mu \phi {\varvec{\Omega}}g,\quad g = \frac{1}{2}\varvec{\xi}_{0} \overline{{\cos \omega_{0} t\varvec{L}\left( {\varvec{\xi}_{e} } \right)R\left( {\varvec{\xi}_{e} } \right)}} . $$
(11)

Here, \( g(\xi_{0} ,\omega_{0} \tau_{\text{B}} ) \) is the effective magnetization parameter.

$$ \frac{1}{2}{\mathbf{\nabla }} \times \overline{{{\mathbf{M}} \times {\mathbf{H}}}} = \frac{1}{2}{\mathbf{\nabla }} \times - 6\mu_{\text{f}} \phi g{\varvec{\Omega}} = - \frac{3}{2}\mu_{\text{f}} \phi g{\mathbf{\nabla }}\left( {{\mathbf{\nabla }} \cdot {\mathbf{V}}} \right) = \frac{3}{2}\mu_{\text{f}} \phi g\nabla^{2} {\mathbf{V}}\text{.} $$
(12)

Now Eq. (7) with the help of Eq. (12) can be written as

$$ \rho_{\text{nf}} \frac{{{\text{d}}{\mathbf{V}}}}{{{\text{d}}t}} = - {\mathbf{\nabla }}p + \left( {{\mathbf{M}} \cdot {\mathbf{\nabla }}} \right){\mathbf{H}} + \left( {\mu_{\text{nf}} + \frac{3}{2}\mu_{\text{f}} \phi g} \right)\nabla^{2} {\mathbf{V}}, $$
(13)
$$ \rho \frac{{{\text{d}}{\mathbf{V}}}}{{{\text{d}}t}} = - {\mathbf{\nabla }}\tilde{p} + \left( {\mu_{\text{nf}} + \frac{3}{2}\mu_{\text{f}} \phi g} \right)\nabla^{2} {\mathbf{V}}\text{.} $$
(14)

As \( - {\mathbf{\nabla }}\tilde{p} = - {\mathbf{\nabla }}p + \left( {{\mathbf{M}} \cdot {\mathbf{\nabla }}} \right){\mathbf{H}} \) i.e., is reduced pressure. The equations of continuity, momentum and energy can be written in the cylindrical form after boundary layer approximation as

$$ \frac{{\partial v_{r} }}{\partial r} + \frac{{v_{r} }}{r} + \frac{{\partial v_{z} }}{\partial z} = 0, $$
(15)
$$ \begin{aligned} & - \frac{{\partial \tilde{p}}}{\partial r} + \left( {\mu_{\text{nf}} + \frac{3}{2}\mu_{\text{f}} \phi g} \right)\left[ {\frac{{\partial^{2} v_{r} }}{{\partial r^{2} }} + \frac{\partial }{\partial r}\left( {\frac{{v_{r} }}{r}} \right) + \frac{{\partial^{2} v_{r} }}{{\partial z^{2} }}} \right] \\ & \quad = \rho_{\text{nf}} \left[ {\frac{{\partial v_{r} }}{\partial t} + v_{r} \frac{{\partial v_{r} }}{\partial r} + v_{z} \frac{{\partial v_{r} }}{\partial z} - \frac{{v_{{_{\theta } }}^{2} }}{r}} \right], \\ \end{aligned} $$
(16)
$$ \begin{aligned} & \left( {\mu_{\text{nf}} + \frac{3}{2}\mu_{\text{f}} \phi g} \right)\left[ {\frac{{\partial^{2} v_{\theta } }}{{\partial r^{2} }} + \frac{\partial }{\partial r}\left( {\frac{{v_{\theta } }}{r}} \right) + \frac{{\partial^{2} v_{\theta } }}{{\partial z^{2} }}} \right] \\ & \quad = \rho_{\text{nf}} \left[ {\frac{{\partial v_{{_{\theta } }} }}{\partial t} + v_{r} \frac{{\partial v_{\theta } }}{\partial r} + v_{z} \frac{{\partial v_{\theta } }}{\partial z} + \frac{{v_{r} v_{\theta } }}{r}} \right], \\ \end{aligned} $$
(17)
$$ \begin{aligned} & - \frac{{\partial \tilde{p}}}{\partial z} + \left( {\mu_{\text{nf}} + \frac{3}{2}\mu_{\text{f}} \phi g} \right)\left[ {\frac{{\partial^{2} v_{z} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial v_{z} }}{\partial r} + \frac{{\partial^{2} v_{z} }}{{\partial z^{2} }}} \right] \\ & \quad = \rho_{\text{nf}} \left[ {\frac{{\partial v_{z} }}{\partial t} + v_{r} \frac{{\partial v_{z} }}{\partial r} + v_{z} \frac{{\partial v_{z} }}{\partial z}} \right], \\ \end{aligned} $$
(18)
$$ \left( {\rho C_{p} } \right)_{\text{nf}} \left[ {\frac{\partial T}{\partial t} + v_{r} \frac{\partial T}{\partial r} + v_{z} \frac{\partial T}{\partial z}} \right] = k_{\text{nf}} \left[ {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{\partial r} + \frac{{\partial^{2} T}}{{\partial z^{2} }}} \right] $$
(19)

along the following boundary conditions:

$$ \left. {\begin{array}{*{20}l} {{\text{at}}\;z = 0;\quad v_{r} = \frac{{\alpha_{v} \varOmega_{v} r}}{{1 - \beta_{v} t}},\quad v_{\theta } = \frac{{\varOmega_{v} r}}{{1 - \beta_{v} t}},\quad v_{z} = 0,\quad T\left( {r,\theta ,z} \right) = T_{w} } \hfill \\ {{\text{at}}\;z = \infty ;\quad v_{r} = 0,\quad v_{\theta } = 0,\quad T\left( {r,\theta ,z} \right) = T_{\infty } } \hfill \\ \end{array} } \right\}. $$
(20)

Now, introduce the following similarity transformation:

$$ \left. {\begin{array}{*{20}l} {\eta = \sqrt {\frac{{\varOmega_{v} }}{{\nu_{f} }}} \frac{z}{{\sqrt {1 - \beta_{v} t} }},\quad v_{r} \left( {r,z,t} \right) = \frac{{\varOmega_{v} r}}{{1 - \beta_{v} t}}F\left( \eta \right),\quad v_{\theta } \left( {r,z,t} \right) = \frac{{\varOmega_{v} r}}{{1 - \beta_{v} t}}G\left( \eta \right),} \hfill \\ {v_{z} \left( {r,z,t} \right) = \sqrt {\frac{{\varOmega_{v} \nu_{\text{f}} }}{{1 - \beta_{v} t}}} E\left( \eta \right),\quad \theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }},\quad \tilde{p} = - \frac{{\varOmega_{v} \mu_{\text{f}} }}{{1 - \beta_{v} t}}P\left( \eta \right)} \hfill \\ \end{array} } \right\} $$
(21)

By using Eq. (21) into Eqs. (15)–(19), the dimensionless nonlinear system of ordinary differential equations is

$$ 2F + E^{\prime} = 0, $$
(22)
$$ \frac{{\rho_{\text{nf}} }}{{\rho_{\text{f}} }}\left[ {F^{2} - G^{2} + EF^{\prime} + S\left( {F + \frac{\eta }{2}F^{\prime}} \right)} \right] = \left( {\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }} + \frac{3}{2}\phi g} \right)F^{\prime\prime}, $$
(23)
$$ \frac{{\rho_{\text{nf}} }}{{\rho_{\text{f}} }}\left[ {EG^{\prime} + 2FG + S\left( {G + \frac{\eta }{2}G^{\prime}} \right)} \right] = \left( {\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }} + \frac{3}{2}\phi g} \right)G^{\prime\prime}, $$
(24)
$$ \frac{{\rho_{\text{nf}} }}{{\rho_{\text{f}} }}\left[ {EE^{\prime} + \frac{S}{2}\left( {E + \eta E^{\prime}} \right)} \right] = - \frac{{{\text{d}}P}}{{{\text{d}}\eta }} + \left( {\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }} + \frac{3}{2}\phi g} \right)E^{\prime\prime}, $$
(25)
$$ \frac{{\left( {\rho C_{p} } \right)_{\text{nf}} }}{{\left( {\rho C_{p} } \right)_{\text{f}} }}\Pr \left[ {E\theta^{\prime} + S\frac{\eta }{2}\theta^{\prime}} \right] = \frac{{k_{\text{nf}} }}{{k_{\text{f}} }}\theta^{\prime\prime} $$
(26)

and the corresponding boundary conditions are

$$ \left. {\begin{array}{*{20}l} {F\left( 0 \right) = \alpha_{v} ,\quad G\left( 0 \right) = 1,\quad E\left( 0 \right) = 0,\quad \theta \left( 0 \right) = 1,} \hfill \\ {F\left( \infty \right) = 0,\quad G\left( \infty \right) = 0,\quad \theta \left( \infty \right) = 0} \hfill \\ \end{array} } \right\}. $$
(27)

where \( \Pr = \frac{{\mu_{\text{f}} (C_{p} )_{\text{f}} }}{{k_{\text{f}} }} \) is the Prandtl number and \( S = \frac{\beta }{{\varOmega_{v} }} \) is the unsteadiness parameter.

2.2 Thermodynamics properties

In Eqs. (23)–(26), models for physical properties like the effective density \( \rho_{\text{nf}} , \) heat capacitance \( \left( {C_{p} } \right)_{\text{nf}} \), viscosity \( \mu_{\text{nf}} \) and thermal conductive \( k_{\text{nf}} \) for nano-ferrofluid are defined as

$$ \rho_{\text{nf}} = \left( {1 - \phi_{\text{a}} } \right)\rho_{\text{f}} + \phi \rho_{\text{a}} , $$
(28)
$$ \left( {\rho C_{p} } \right)_{\text{nf}} = \left( {1 - \phi_{\text{a}} } \right)\left( {\rho C_{p} } \right)_{\text{f}} + \phi_{\text{a}} \left( {\rho C_{p} } \right)_{\text{a}} , $$
(29)
$$ k_{\text{nf}} = \frac{{k_{\text{a}} + 2k_{\text{f}} + 2\phi_{\text{a}} \left( {k_{\text{a}} - k_{\text{f}} } \right)}}{{k_{\text{a}} + 2k_{\text{f}} - \phi_{\text{a}} \left( {k_{\text{a}} - k_{\text{f}} } \right)}}k_{\text{f}} , $$
(30)
$$ \mu_{\text{nf}} = \mu_{\text{f}} \mathop {\left( {1 - \frac{{\phi_{\text{a}} }}{{\phi_{\hbox{max} } }}} \right)}\nolimits^{{ - 2.5\phi_{\hbox{max} } }} . $$
(31)

Here, subscripts \( {\text{a}} \) and f are illustrated to aggregate and base fluid water, respectively. Further, the thermal properties of particle aggregation are given as

$$ \rho_{\text{a}} = \left( {1 - \phi_{\text{int}} } \right)\rho_{\text{f}} + \phi_{\text{int}} \rho_{\text{s}} , $$
(32)
$$ \left( {C_{p} } \right)_{\text{a}} = \left( {1 - \phi_{\text{int}} } \right)\left( {C_{p} } \right)_{\text{f}} + \phi_{\text{int}} \left( {C_{p} } \right)_{\text{s}} . $$
(33)

The above subscript s is used for solid single particles. The \( \phi_{\text{int}} \) is donated for the nanoparticles volume fraction in cluster or in aggregate and \( \phi = \phi_{\text{int}} \phi_{\text{a}} \). With the influence of magnetics, particles become lineup in the direction of the field that makes a chain which is called backbone and other free particles are called dead-end particles. In this situation, thermal conductivity is the combination of backbone and dead-end particles thermal conductivities. The effective thermal conductivity of dead-end particles is given as

$$ {{\left( {1 - \phi_{\text{nc}} } \right)\left( {k_{\text{f}} - k_{\text{nc}} } \right)} \mathord{\left/ {\vphantom {{\left( {1 - \phi_{\text{nc}} } \right)\left( {k_{\text{f}} - k_{\text{nc}} } \right)} {{{\left( {k_{\text{f}} + 2k_{m} } \right) + \phi_{\text{nc}} \left( {k_{\text{s}} - k_{\text{nc}} } \right)} \mathord{\left/ {\vphantom {{\left( {k_{\text{f}} + 2k_{m} } \right) + \phi_{\text{nc}} \left( {k_{\text{s}} - k_{\text{nc}} } \right)} {\left( {k_{\text{s}} + 2k_{\text{nc}} } \right)}}} \right. \kern-0pt} {\left( {k_{\text{s}} + 2k_{\text{nc}} } \right)}}}}} \right. \kern-0pt} {{{\left( {k_{\text{f}} + 2k_{m} } \right) + \phi_{\text{nc}} \left( {k_{\text{s}} - k_{\text{nc}} } \right)} \mathord{\left/ {\vphantom {{\left( {k_{\text{f}} + 2k_{m} } \right) + \phi_{\text{nc}} \left( {k_{\text{s}} - k_{\text{nc}} } \right)} {\left( {k_{\text{s}} + 2k_{\text{nc}} } \right)}}} \right. \kern-0pt} {\left( {k_{\text{s}} + 2k_{\text{nc}} } \right)}}}} = 0. $$
(34)

The thermal conductivity of aggregate \( k_{\text{a}} \) is determined by using composite theory for misprinted ellipsoidal particles for the backbone, and the following equations are used

$$ k_{\text{a}} = k_{\text{nc}} \frac{{3 + \phi_{\text{c}} \left[ {2\beta_{11} \left( {1 - L_{11} } \right) + \beta_{33} \left( {1 - L_{33} } \right)} \right]}}{{3 - \phi_{\text{c}} \left[ {2\beta_{11} L_{11} + \beta_{33} L_{33} } \right]}}, $$
(35)

where

$$ \left. {\begin{array}{*{20}l} {L_{11} = {{0.5p^{2} } \mathord{\left/ {\vphantom {{0.5p^{2} } {{{\left( {p^{2} - 1} \right) - 0.5p\cosh^{ - 1} p} \mathord{\left/ {\vphantom {{\left( {p^{2} - 1} \right) - 0.5p\cosh^{ - 1} p} {\left( {p^{2} - 1} \right)^{1.5} }}} \right. \kern-0pt} {\left( {p^{2} - 1} \right)^{1.5} }}}}} \right. \kern-0pt} {{{\left( {p^{2} - 1} \right) - 0.5p\cosh^{ - 1} p} \mathord{\left/ {\vphantom {{\left( {p^{2} - 1} \right) - 0.5p\cosh^{ - 1} p} {\left( {p^{2} - 1} \right)^{1.5} }}} \right. \kern-0pt} {\left( {p^{2} - 1} \right)^{1.5} }}}},} \hfill \\ {L_{33} = 1 - 2L_{11} ,} \hfill \\ {\beta_{ii} = {{\left( {k_{ii}^{c} - k_{\text{nc}} } \right)} \mathord{\left/ {\vphantom {{\left( {k_{ii}^{c} - k_{\text{nc}} } \right)} {\left[ {k_{\text{nc}} - L_{ii} \left( {k_{ii}^{c} - k_{\text{nc}} } \right)} \right]}}} \right. \kern-0pt} {\left[ {k_{\text{nc}} - L_{ii} \left( {k_{ii}^{c} - k_{\text{nc}} } \right)} \right]}}} \hfill \\ \end{array} } \right\}. $$
(36)

Interfacial resistance is accounted for in the term

$$ k_{ii}^{c} = {{k_{\text{s}} } \mathord{\left/ {\vphantom {{k_{\text{s}} } {\left( {1 + {{\gamma L_{ii} k_{\text{s}} } \mathord{\left/ {\vphantom {{\gamma L_{ii} k_{\text{s}} } {k_{\text{f}} }}} \right. \kern-0pt} {k_{\text{f}} }}} \right)}}} \right. \kern-0pt} {\left( {1 + {{\gamma L_{ii} k_{\text{s}} } \mathord{\left/ {\vphantom {{\gamma L_{ii} k_{\text{s}} } {k_{\text{f}} }}} \right. \kern-0pt} {k_{\text{f}} }}} \right)}}. $$
(37)

Here, \( \gamma = (2 + {1 \mathord{\left/ {\vphantom {1 p}} \right. \kern-0pt} p})\alpha ,\,\,\alpha = {{A_{k} } \mathord{\left/ {\vphantom {{A_{k} } {a_{1} }}} \right. \kern-0pt} {a_{1} }} \), \( A_{\text{k}} \) is the Kapitza radius and \( p = R_{\text{g}} a_{1} \). The number of particles in aggregation and belonging to the backbone is calculated through

$$ N_{\text{int}} = \mathop {\left( {{{R_{\text{g}} } \mathord{\left/ {\vphantom {{R_{\text{g}} } {a_{1} }}} \right. \kern-0pt} {a_{1} }}} \right)}\nolimits^{{d_{\text{f}} }} , $$
(38)
$$ N_{\text{c}} = \left( {{{R_{\text{g}} } \mathord{\left/ {\vphantom {{R_{\text{g}} } {a_{1} }}} \right. \kern-0pt} {a_{1} }}} \right)^{{d_{l} }} , $$
(39)

where \( a_{1} \) is the radius of the primary particle,\( R_{\text{g}} \) is the average radius of gyration, \( d_{\text{f}} \) is the fractal dimension and \( d_{l} \) is the chemical dimension.

The volume fraction of backbone particles \( \phi_{\text{c}} \) and particles belonging to dead ends \( \phi_{\text{nc}} \) is given by

$$ \phi_{\text{c}} = \left( {{{R_{\text{g}} } \mathord{\left/ {\vphantom {{R_{\text{g}} } {a_{1} }}} \right. \kern-0pt} {a_{1} }}} \right)^{{d_{l} - 3}} , $$
(40)
$$ \phi_{\text{nc}} = \phi_{\text{int}} - \phi_{\text{c}} , $$
(41)

where \( \phi_{\text{int}} = \mathop {(R_{\text{g}} /a_{1} )}\nolimits^{{{1 \mathord{\left/ {\vphantom {1 {d_{\text{f}} - 3}}} \right. \kern-0pt} {d_{\text{f}} - 3}}}} \).

2.3 Entropy generation

Generally, the local volumetric entropy generation rate is defined as

$$ S^{\prime\prime\prime}_{\text{gen}} = \frac{{k_{\text{nf}} }}{{T_{w}^{2} }}\left[ {\nabla T} \right]^{2} + \frac{{\mu_{\text{nf}} }}{{T_{w} }}\varPhi , $$
(42)

where

$$ \left[ {\nabla T} \right]^{2} = \left[ {\left( {\frac{\partial T}{\partial r}} \right)^{2} + \left( {\frac{1}{r}\frac{\partial T}{\partial \varphi }} \right)^{2} + \left( {\frac{\partial T}{\partial z}} \right)^{2} } \right]^{2} $$
(43)

and

$$ \varPhi = 2\left[ {\left( {\frac{\partial u}{\partial r}} \right)^{2} + \frac{1}{{r^{2} }}\left( {\frac{\partial v}{\partial \varphi } + u} \right)^{2} + \left( {\frac{\partial w}{\partial z}} \right)^{2} } \right] + \left( {\frac{\partial v}{\partial z} + \frac{1}{r}\frac{\partial w}{\partial \varphi }} \right)^{2} + \left( {\frac{\partial w}{\partial r} + \frac{\partial u}{\partial z}} \right)^{2} + \left[ {\frac{1}{r}\frac{\partial u}{\partial \varphi } + r\frac{\partial }{\partial r}\left( {\frac{v}{r}} \right)} \right]. $$
(44)

Thus, the entropy generation rate Eq. (42) is reduced in this form

$$ S^{\prime\prime\prime}_{\text{gen}} = \underbrace {{\frac{{k_{\text{nf}} }}{{T_{w}^{2} }}\left( {\frac{\partial T}{\partial z}} \right)^{2} }}_{{{\text{Thermal}}\;{\text{irreversibility}}}} + \underbrace {{\frac{{\mu_{\text{nf}} }}{{T_{w} }}\left\{ {2\left[ {\left( {\frac{\partial u}{\partial r}} \right)^{2} + \frac{1}{{r^{2} }}u^{2} + \left( {\frac{\partial w}{\partial z}} \right)^{2} } \right] + \left( {\frac{\partial v}{\partial z}} \right)^{2} + \left( {\frac{\partial u}{\partial z}} \right)^{2} + \left[ {r\frac{\partial }{\partial r}\left( {\frac{v}{r}} \right)} \right]^{2} } \right\}}}_{{{\text{Fluid}}\;{\text{friction}}\;{\text{irreversibility}}}}. $$
(45)

Equation (45) reveals that the entropy is generated due to two factors. Firstly, the entropy is generated by reason of heat transfer irreversibility \( \left( {N_{\text{HTI}} } \right) \) and secondly due to fluid friction irreversibility \( \left( {N_{\text{FFI}} } \right) \). The similarity transformation parameters of Eq. (21) are employed to dimensionalize the local entropy generation given in Eq. (45),

$$ N_{G} = \frac{{k_{\text{nf}} }}{{k_{\text{f}} }}\varepsilon \theta^{\prime}\left( \eta \right) + \frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }}{\text{Br}}\left[ {\frac{3}{\text{Re}}H^{\prime}\left( \eta \right)^{2} + F^{\prime}\left( \eta \right)^{2} + G^{\prime}\left( \eta \right)^{2} } \right]. $$
(46)

Here, dimensionless temperature difference is \( \varepsilon = \Delta T/T_{w} \), \( {\text{Br}} = \mu_{\text{f}} \varOmega^{2} r^{2} /\left( {1 - \beta t} \right)^{2} k_{\text{f}} \Delta T \) is the rotational Brinkman number and \( N_{G} = S^{\prime\prime\prime}_{\text{gen}} /\left( {k_{\text{f}} \varOmega \Delta T/\left( {1 - \beta t} \right)\nu_{\text{f}} T_{w} } \right) \) is the dimensionless entropy generation rate. The averaged entropy generation number can be evaluated using the following formula:

$$ N_{{G,{\text{av}}}} = \frac{1}{\forall }\int\limits_{0}^{m} {\int\limits_{0}^{1} {2\pi \bar{r}N_{G} {\text{d}}\bar{r}{\text{d}}\eta } } , $$
(47)

where \( \forall \) is the volume of fluid. In order to consider both the velocity and thermal boundary layers, we calculate the volumetric entropy generation in a large finite domain. Thus, integrations shown in Eq. (47) are obtained in the domain \( 0 \le r \le 1 \) and \( 0 \le \eta \le m \), where \( m \) is a sufficiently large number. From the above equation, it is possible to evaluate the contributions of heat transfer and fluid friction in the averaged entropy generation.

2.4 Heat transfer coefficient

To understand the convection boundary layers, it is necessary to understand convective heat transfer between a surface and a fluid flowing past it. The heat transfer rate can then be written as

$$ Q_{z} = hA\left( {T_{w} - T_{\infty } } \right), $$
(48)

where \( A \) is the area of plate and \( h \) is the convection heat transfer coefficient of the flow. The heat transfer at the surface by conduction is

$$ Q_{z} = - k_{\text{nf}} A\left. {\frac{{\partial \left( {T_{w} - T_{\infty } } \right)}}{\partial y}} \right|_{z = 0} . $$
(49)

These two terms are equal, thus

$$ hA\left( {T_{w} - T_{\infty } } \right) = - k_{\text{nf}} A\left. {\frac{{\partial \left( {T_{w} - T_{\infty } } \right)}}{\partial y}} \right|_{z = 0} . $$
(50)

Rearranging

$$ h = \frac{{ - k_{\text{nf}} \left. {\frac{{\partial \left( {T - T_{\infty } } \right)}}{\partial y}} \right|_{z = 0} }}{{\left( {T_{w} - T_{\infty } } \right)}}. $$
(51)

The average convection heat transfer coefficient is calculated as

$$ h_{\text{av}} = \frac{1}{\forall }\int_{0}^{1} {2\pi \bar{r}h{\text{d}}\bar{r}} , $$
(52)

The resistance to heat transfer via convection is calculated by the following equation:

$$ {\text{Thermal}}\;{\text{resistance}} = \frac{1}{{h_{\text{av}} }}. $$
(53)

3 Solution of the problem

Due to the nonlinear nature of Eqs. (22)–(26), an exact solution is not possible. Now, we opted to go for analytic solution. The analytic solutions of differential equations are obtained by many different methods in the literature [20,21,22,23,24]. In this study, we use the homotopy analysis method. For this, the Mathematica package BVPh2.0 which is based on the homotopy analysis method is employed for solving nonlinear ordinary differential equation. In this package, it is needed to put appropriate initial guess of solutions and auxiliary linear operators to find the desired solution. Thus, we take the auxiliary linear operators corresponding to Eqs. (22)–(24) and (26) as

$$ \left. {\begin{array}{*{20}l} {\pounds_{E} \left( H \right) = \frac{{{\text{d}}E}}{{{\text{d}}\eta }},\quad \pounds_{F} (F) = \frac{{{\text{d}}F}}{{{\text{d}}\eta }} + \frac{{{\text{d}}^{2} F}}{{{\text{d}}\eta^{2} }},} \hfill \\ {\pounds_{G} (G) = \frac{{{\text{d}}G}}{{{\text{d}}\eta }} + \frac{{{\text{d}}^{2} G}}{{{\text{d}}\eta^{2} }},\quad \pounds_{\theta } (\theta ) = 2\frac{{{\text{d}}\theta }}{{{\text{d}}\eta }} + \frac{{{\text{d}}^{2} \theta }}{{{\text{d}}\eta^{2} }},} \hfill \\ \end{array} } \right\} $$
(54)

By taking the boundary conditions in Eq. (27), we, respectively, selected the following initial guess as

$$ \left. {\begin{array}{*{20}l} {E_{o} = 0,\quad F_{o} \left( \eta \right) = \alpha e^{ - \eta } ,} \hfill \\ {G_{o} \left( \eta \right) = e^{ - \eta } ,\quad \theta_{o} \left( \eta \right) = e^{ - 2\eta } } \hfill \\ \end{array} } \right\}, $$
(55)

Taking the linear auxiliary operators in Eq. (55) and the initial guess in Eq. (56), the coupled nonlinear Eqs. (22) and (26) subject to Eq. (27) can be solved directly by using package BVPh2.0. Finally, the solutions of velocity and temperature profiles can be exposed explicitly by means of an infinite series of the following form:

$$ \left. {\begin{array}{*{20}c} {E\left( \eta \right) = \mathop {\mathop {\mathop \sum \limits }\limits_{m = 0} }\limits^{\infty } E_{m} \left( \eta \right),\quad F\left( \eta \right) = \mathop {\mathop {\mathop \sum \limits }\limits_{m = 0} }\limits^{\infty } F_{m} \left( \eta \right),} \\ {G\left( \eta \right) = \mathop {\mathop {\mathop \sum \limits }\limits_{m = 0} }\limits^{\infty } G_{m} \left( \eta \right),\quad \theta \left( \eta \right) = \mathop {\mathop {\mathop \sum \limits }\limits_{m = 0} }\limits^{\infty } \theta_{m} \left( \eta \right)} \\ \end{array} } \right\}, $$
(56)

where \( E_{m} \left( \eta \right),F_{m} \left( \eta \right),G_{m} \left( \eta \right) \) and \( \theta_{m} \left( \eta \right) \) are governed by high-order deformation equations. The results for \( E_{m} \left( \eta \right),F_{m} \left( \eta \right),G_{m} \left( \eta \right) \) and \( \theta_{m} \left( \eta \right) \) are calculated up to 30th order of approximation.

It should be emphasized that \( E\left( \eta \right),F\left( \eta \right),G\left( \eta \right) \) and \( \theta \left( \eta \right) \) given by BVPh2.0 contain four unknown convergence control parameters \( c_{E} \), \( c_{F} \), \( c_{G} \) and \( c_{\theta } \) which are used to guarantee the convergence of the series solutions. The optimal values of the convergence control parameters are obtained by minimizing the total squared residual error at k-th order of approximation. The squared residual error at k-th order is

$$ \varepsilon_{H} \left( {c_{H} ,c_{F} ,c_{G} ,c_{\theta } } \right) = \frac{1}{N + 1}\sum\limits_{j = 0}^{N} {\left[ {\aleph_{E} \left. {\left( {\sum\limits_{i = 0}^{k} {E_{i} } ,\sum\limits_{i = 0}^{k} {F_{i} } } \right)} \right|_{\eta = j\delta \eta } } \right]}^{2} , $$
(57)
$$ \varepsilon_{F} \left( {c_{H} ,c_{F} ,c_{G} ,c_{\theta } } \right) = \frac{1}{N + 1}\sum\limits_{j = 0}^{N} {\left[ {\aleph_{F} \left. {\left( {\sum\limits_{i = 0}^{k} {E_{i} } ,\sum\limits_{i = 0}^{k} {F_{i} } ,\sum\limits_{i = 0}^{k} {G_{i} } } \right)} \right|_{\eta = j\delta \eta } } \right]}^{2} , $$
(58)
$$ \varepsilon_{G} \left( {c_{H} ,c_{F} ,c_{G} ,c_{\theta } } \right) = \frac{1}{N + 1}\sum\limits_{j = 0}^{N} {\left[ {\aleph_{G} \left. {\left( {\sum\limits_{i = 0}^{k} {E_{i} } ,\sum\limits_{i = 0}^{k} {F_{i} } ,\sum\limits_{i = 0}^{k} {G_{i} ,\sum\limits_{i = 0}^{k} {\theta_{i} } } } \right)} \right|_{\eta = j\delta \eta } } \right]}^{2} , $$
(59)
$$ \varepsilon_{\theta } \left( {c_{H} ,c_{F} ,c_{G} ,c_{\theta } } \right) = \frac{1}{N + 1}\sum\limits_{j = 0}^{N} {\left[ {\aleph_{\theta } \left. {\left( {\sum\limits_{i = 0}^{k} {E_{i} } ,\sum\limits_{i = 0}^{k} {\theta_{i} } } \right)} \right|_{\eta = j\delta \eta } } \right]}^{2} , $$
(60)

where nonlinear operators are

$$ \aleph_{E} \left( {F,E} \right) = 2F + E^{\prime} = 0 $$
(61)
$$ \aleph_{F} \left( {E,F,G} \right) = \frac{{\rho_{\text{nf}} }}{{\rho_{\text{f}} }}\left[ {F^{2} - G^{2} + EF^{\prime} + S\left( {F + \frac{\eta }{2}F^{\prime}} \right)} \right] - \left( {\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }} + \frac{3}{2}\phi g} \right)F^{\prime\prime} = 0, $$
(62)
$$ \aleph_{G} \left( {E,F,G} \right) = \frac{{\rho_{\text{nf}} }}{{\rho_{\text{f}} }}\left[ {EG^{\prime} + 2FG + S\left( {G + \frac{\eta }{2}G^{\prime}} \right)} \right] - \left( {\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }} + \frac{3}{2}\phi g} \right)G^{\prime\prime} = 0, $$
(63)
$$ \aleph_{\theta } \left( {E,\theta } \right) = \frac{{\left( {\rho C_{p} } \right)_{\text{nf}} }}{{\left( {\rho C_{p} } \right)_{\text{f}} }}\Pr \left[ {E\theta^{\prime} + S\frac{\eta }{2}\theta^{\prime}} \right] - \frac{{k_{\text{nf}} }}{{k_{\text{f}} }}\theta^{\prime\prime} = 0 $$
(64)

and the total error at k-th order of approximation is defined as

$$ \varepsilon_{\text{Total}} = \varepsilon_{E} \left( {c_{H} ,c_{F} ,c_{G} ,c_{\theta } } \right) + \varepsilon_{F} \left( {c_{H} ,c_{F} ,c_{G} ,c_{\theta } } \right) + \varepsilon_{G} \left( {c_{H} ,c_{F} ,c_{G} ,c_{\theta } } \right) + \varepsilon_{\theta } \left( {c_{H} ,c_{F} ,c_{G} ,c_{\theta } } \right) $$
(65)

To check the accuracy of this method, values of \( F^{\prime}\left( 0 \right) \) and \( G^{\prime}\left( 0 \right) \) are compared with the results obtained by Rashidi et al. [25] and an excellent agreement were found with these results as shown in Table 1.

Table 1 Comparison of the obtained results with the ones from the open literature against when \( \phi = 0\% \) and \( \alpha_{v} = 2 \)
Full size table

Further, the results for velocity components and temperature up to first iteration are as follows:

$$ E = e^{ - 2\eta } \left( { - \frac{73}{100} + \frac{73}{100}} \right), $$
$$ \begin{aligned} F & = \left( \begin{aligned} \frac{1}{2} + \frac{83}{400}\left( {\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }} + \frac{3}{2}\phi g} \right) + \frac{83}{800}\left( {\frac{{\rho_{\text{nf}} }}{{\rho_{\text{f}} }}} \right) - \hfill \\ \frac{83S}{1600}\left( {\frac{{\rho_{\text{nf}} }}{{\rho_{\text{f}} }}} \right) - \frac{249}{800}\left( {\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }} + \frac{3}{2}\phi g} \right) \hfill \\ \end{aligned} \right)e^{ - \eta } \\ & \quad + \left( \begin{aligned} \frac{ - 83}{400}\left( {\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }}} \right) + \frac{83S}{1600}\left( {\frac{{\rho_{\text{nf}} }}{{\rho_{\text{f}} }}} \right) - \hfill \\ \frac{83S}{800}\left( {\frac{{\rho_{\text{nf}} }}{{\rho_{\text{f}} }}} \right)z - \frac{249}{800}\left( {\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }} + \frac{3}{2}\phi g} \right) \hfill \\ \end{aligned} \right)e^{ - 2\eta } \, - \left( {\frac{83}{800}\left( {\frac{{\rho_{\text{nf}} }}{{\rho_{\text{f}} }}} \right)} \right)e^{ - 3\eta } , \\ \end{aligned} $$
(66)
$$ \begin{aligned} G & = \left( \begin{aligned} 1 + \frac{43}{200}\left( {\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }}} \right) - \frac{43}{600}\left( {\frac{{\rho_{\text{nf}} }}{{\rho_{\text{f}} }}} \right) - \hfill \\ \frac{43S}{800}\left( {\frac{{\rho_{\text{nf}} }}{{\rho_{\text{f}} }}} \right) + \frac{192}{400}\left( {\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }} + \frac{3}{2}\phi g} \right) \hfill \\ \end{aligned} \right)e^{ - \eta } \\ & \quad + \left( \begin{aligned} - \frac{43}{200}\left( {\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }}} \right) + \frac{43S}{800}\left( {\frac{{\rho_{\text{nf}} }}{{\rho_{\text{f}} }}} \right) - \hfill \\ \frac{43S}{400}\left( {\frac{{\rho_{\text{nf}} }}{{\rho_{\text{f}} }}} \right)z - \frac{192}{400}\left( {\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }} + \frac{3}{2}\phi g} \right) \hfill \\ \end{aligned} \right)e^{ - 2\eta } - \left( {\frac{43}{600}\left( {\frac{{\rho_{\text{nf}} }}{{\rho_{\text{f}} }}} \right)} \right)e^{ - 3\eta } , \\ \end{aligned} $$
(67)
$$ E = e^{ - 2\eta } \left( { - \frac{73}{100} + \frac{73}{100}} \right), $$
(68)
$$ \begin{aligned} T & = \left( { - \frac{53}{75}\left( {\frac{{k_{\text{nf}} }}{{k_{\text{f}} }}} \right) - \frac{53}{225}\Pr S - \frac{53}{300}\Pr S\left( {\frac{{\left( {\rho C_{p} } \right)_{\text{nf}} }}{{\left( {\rho C_{p} } \right)_{\text{f}} }}} \right)z} \right)e^{ - 3\eta } , \\ & \quad + \left( {1 + \frac{53}{75}\left( {\frac{{k_{\text{nf}} }}{{k_{\text{f}} }}} \right) + \frac{53}{225}\Pr S\left( {\frac{{\left( {\rho C_{p} } \right)_{\text{nf}} }}{{\left( {\rho C_{p} } \right)_{\text{f}} }}} \right)} \right)e^{ - 2\eta } . \\ \end{aligned} $$
(69)

4 Results and discussion

The impact of low isolating magnetic field and different particle concentrations on heat transfer characteristics as well as thermal and fluid friction irreversibilities fluid flow is demonstrated in graphical, pie charts and tabular form. To prepare these results, some assumptions are taken to account. Consider particles made the aggregations due to magnetic field and its average radius of gyration is 200 nm. In single aggregation, the total particles are 200 in which 50 particles belong to backbone. To observe the behavior of particles concentration and magnetization, other parameters are taken to be fixed such as stretching parameter \( \alpha_{v} = 0.5 \), unsteadiness parameter \( S = 0.5 \), rotational Brinkman number \( {\text{Br}} = 0.001 \), temperature ratio \( \varepsilon = 0.01 \) and rotational Reynolds number \( \text{Re} = 700 \).

The impacts of particle concentrations and magnetic parameter on irreversibilities due to fluid flow friction are shown in Figs. 2 and 3. In these figures, it is seen that fluid friction irreversibilities with both parameters are increased, but noticeable impact is happened by particle concentrations as compared to magnetization. It is noticed that when the nanoparticle concentration is enhanced, resistance between adjacent layers of moving fluid is enhanced which leads to enhancement in viscosity of fluid that is main cause of irreversibility enhancement in system. On the other hand, when angular velocity of particle is decreased as compared to vorticity of flow, the value of magnetization parameter is increased. In enhancement of magnetization parameter, viscosity is enlarged. Therefore, irreversibility in system is enhanced by magnetization parameter. The influences of particle concentration and magnetization parameter on irreversibility due to heat transfer are shown in Figs. 4 and 5. It is perceived that irreversibilities due to heat flow are rapidly reduced near to wall by nanoparticles distribution but this behavior is not continued when moving far from wall. On the other hand, irreversibilities by heat transfer are enhanced throughout in flow region when magnetization parameters’ effect is increased. Figures 6 and 7 show the total contribution of thermal and fluid friction irreversibilities in the form of local entropy generation in axial direction. From above figures, it is noted that maximum contribution in irreversibilities is processed by heat transfer as compared to fluid friction. So, Figs. 6 and 7 have similar behavior as shown in Figs. 4 and 5.

Fig. 2
figure 2

Effect of nanoparticle concentrations on fluid flow friction irreversibilities

Full size image
Fig. 3
figure 3

Effect of magnetization parameter on fluid flow friction irreversibilities

Full size image
Fig. 4
figure 4

Effect of nanoparticle concentrations on heat transfer irreversibilities

Full size image
Fig. 5
figure 5

Effect of magnetization parameter on heat transfer irreversibilities

Full size image
Fig. 6
figure 6

Effect of nanoparticle concentrations on local entropy generation

Full size image
Fig. 7
figure 7

Effect of magnetization parameter on local entropy generation

Full size image

The numerical sets of values show the results for average entropy generation as displayed in Figs. 8 and 9 under the impact of particle concentration and magnetic parameter. In Fig. 8, it is found the values of average entropy generation are increased by increasing particle concentration. In enhancement of entropy generation, maximum contribution is due to heat transfer irreversibilities as compared to fluid friction. This is due to rapid enhancement in thermal conductivity by dispersion of nanoparticle concentration. On the hand, when magnetization effect is increased, the values of average entropy generation are increased with maximum contribution of irreversibilities due to fluid flow friction. This is due to increase of fluid viscosity.

Fig. 8
figure 8

Contributions of average heat transfer and fluid friction irreversibilities in the total average entropy generation at different particles volume fraction

Full size image
Fig. 9
figure 9

Contributions of average heat transfer and fluid friction irreversibilities in the total average entropy generation at different values of magnetization parameter

Full size image

For applications of heat transfer enhancement in renewable energy systems and industrial thermal management, the value of convection heat transfer coefficient and thermal resistance is found at different particle concentrations and various values of magnetic field in Table 2. It is seen that when particle concentration is increased, the values of convection heat transfer coefficient are increased and thermal resistance is reduced. On the other hand, due to magnetization effect, the values of convection heat transfer coefficient are increased but not as increased by nanoparticle concentration.

Table 2 Results of average convection heat transfer coefficient and average thermal resistance under influence of particle concentration and magnetization parameter
Full size table

5 Concluding remarks

In this paper, theoretical study is done on analysis of entropy generation in ferrofluid flow under the influence of low oscillating magnetic field over rotating disk. Outcome of the analysis shows that irreversibilities due to heat transfer are increased by dispersion of nanoparticles which enhances the total entropy. These irreversibilities are minimized by magnetic influences. On the other side, fluid flows’ irreversibilities are increased by influences of this parameter.