Thermal analysis of MHD electro-osmotic peristaltic pumping of Casson fluid through a rotating asymmetric micro-channel

Abstract

In this paper, we investigate the combined effects of wall slip, viscous dissipation, and Joule heating on MHD electro-osmotic peristaltic motion of Casson fluid with heat transfer through a rotating asymmetric micro-channel. Using long wavelength and small Reynolds number assumptions, the governing equations of momentum and energy balance are obtained and tackled analytically. The effects of various embedding parameters on the stream function, velocity, temperature, skin friction, Nusselt number and trapping phenomenon are displayed graphically and discussed. It is found that Casson fluid velocity, temperature, and heat transfer rate are enhanced with a boost in electro-osmotic force.

1 Introduction

Many fluids of industrial and physiological importance such as salt solutions, molten polymers, ketchup, custard, toothpaste, starch suspensions, paints, blood, shampoo, etc., are non-Newtonian due to the nonlinearity behavior between their stress and the rate of strain. In this situation, non-Newtonian fluid models are very important because of their applications in polymer processing industries, petroleum drilling and biofluids dynamics and many others. Meanwhile, it is difficult to express all the properties of non-Newtonian fluids in a single constitutive equation, the Navier–Stokes theory is also inadequate for such type of fluids. The most popular subclass of these non-Newtonian fluids is Casson fluid [1] which displays yield stress impact. This fluid can be considered as a shear thinning liquid which is supposed to have an infinite viscosity at zero rates of shear, a yield stress below which no flow exists and a zero viscosity at an infinite rate of shear. In other words, this type of fluids acts like a solid, when a shear stress lower than the yield stress is applied to it, while it starts to move when a shear stress more than the yield stress is applied. The constitutive equation of Casson fluid is nonlinear in nature and has been defined to describe properly the flow curves of suspensions of pigments in lithographic varnishes utilized for preparing printing inks and silicon suspension [2]. Eld-abe and Salwa [3] discussed the effects of MHD and heat transfer analysis in non-Newtonian Casson fluid flow between two rotating cylinders. Dash et al. [4] investigated the analysis of a Casson fluid in a pipe filled with a homogeneous porous medium by considering the Brinkman model. Ullah et al. [5] investigated the hydromagnetic Falkner-Skan flow of reactive Casson nanofluid over a flat surface.

Recent advancements in micro-fabrication and miniaturization take into consideration many applications spanning from biological to cooling of microelectronics applications [6,7,8,9,10,11,12]. The operational state of many micro-instruments deals with fluid flow in microscale channels (micro-channel is the channel that its smallest dimension is between 10 and 200 μm). Microfluidic devices offer many advantages such as a significant reduction in the consumption of required materials, ability to perform in vitro experiments on the continuous flow in a manner similar to the real situation in a living biological system, being portable and vibration free. Electro-osmotic flow is commonly used in microfluidic devices, soil analysis and processing, and chemical analysis, all of which routinely involve systems with highly charged surfaces, often of oxides. One example is capillary electrophoresis, in which electric fields are used to separate chemicals according to their electrophoretic mobility by applying an electric field to a narrow capillary, usually made of silica. The heat transfer analysis of electro-osmotic flow in a slowly varying asymmetric micro-channel was reported by Mondal and Shit [13]. Hadian et al. [14] presented a theoretical study of temperature distribution patterns in electro-osmotic flow through a slit micro-channel. The microscale thermo-fluidic transport in two immiscible liquid layers subject to combined electro-osmotic and pressure-driven transport was investigated by Garai and Chakraborty [15]. Shit et al. [16] analyzed the two-layer electro-osmotic flow and heat transfer in a hydrophobic micro-channel with fluid–solid interfacial slip and zeta potential difference.

Peristalsis is a well-known mechanism for fluid transport in physiology. In this mechanism, the fluid flows through contraction and expansion of the tubes/channel walls. Among the latest investigations, the peristaltic phenomenon is entirely influential due to its extensive applications in engineering, physics, applied mathematics and the physiological world. Transport of food via esophagus, movement of chyme in intestines, bile transport in the bile duct, locomotion of worms and blood circulation are the application of peristalsis in biological/medical processes. Engineers have selected such technique in view of its benefit for industrial devices including the design of the heart–lung machine, roller pump, finger and hand pumps. Different types of hose pump also work under the principle of peristalsis. Many theoretical investigations related to physiology and industries are described due to such immense development of peristalsis. Several theoretical and experimental attempts have been made to examine the peristaltic flows in view of their obvious importance since the seminal researchers of Latham [17] and Shapiro et al. [18]. Such investigations have been presented under various assumptions of long wavelength, low Reynolds number, small wave number, small amplitude ratio, etc. The peristaltic flows of viscous and non-Newtonian fluids have been discussed by many authors recently in the studies [19,20,21,22,23].

The phenomenon of rotation has its numerous applications in cosmic and geophysical flows. The occurrence of rotation also helps in better understanding the behavior of ocean circulation and galaxies formation. In particular, the peristalsis of MHD fluid in presence of rotation is relevant with regard to certain flow cases involving the movement of physiological fluids, for example, the blood and saline water. Obviously, the magnetic field and rotation are useful for biofluid transport in the intestines, ureters and arterioles. Abd-Alla et al. [24] studied the effects of rotation and magnetic field on nonlinear peristaltic motion of second-order fluid in an asymmetric channel through a porous medium. Ali et al. [25] numerically investigated the impact of the rotation on Couette flow and heat transfer of nanofluid. The influence of the rotation and magnetic field on Couette flow with Hall current was numerically investigated by Seth et al. [26].

The studies of heat transfer have significant applications in industry and medicine. Especially heat transfer in the human body is an important area of research. The Bioheat transfer in tissues has attracted the attention of biomedical engineers in view of thermotherapy and the human thermoregulation system. The heat transfer in humans takes place as conduction in tissues, perfusion of the arterial—venous blood through the pores of the tissue, metabolic heat generation etc. The other applications are the destruction of undesirable cancer tissues, dilution technique in examining blood flow and vasodilation. In addition mass transfer also occurs when nutrients diffusion out from the blood to neighboring tissues, membrane separation process, reverse osmosis, distillation process, combustion process and diffusion of chemical impurities. The combined heat and mass transfer effects can be seen in processes like drying, evaporation, thermodynamics at the surface of a water body and oxygenation etc. With this viewpoint, the recent researchers have made efforts for peristalsis with the combined effect of heat and mass transfer [27,28,29,30]. Very recently, Makinde et al. [31] analyzed the effects of thermal radiation on MHD peristaltic motion of Walters-B Fluid with a heat source and slip conditions.

Existing flow literature survey reveals that the combined effects of magnetic field, viscous dissipation, wall slip and Joule heating on electro-osmotic peristaltic motion of a conducting Casson fluid in a rotating asymmetric micro-channel with the heat transfer is not yet studied. Our main objective is to carry out this analysis in this paper. The analytical solutions for the problem have obtained a base on long wavelength and small Reynolds number assumptions. Effects of sundry embedded parameters on the stream function, velocity, temperature, shear stress, trapping phenomenon and Nusselt number are presented graphically and quantitatively discussed.

2 Mathematical Formulation

We consider the electro-osmotic peristaltic flow of an electrically conducting incompressible Casson fluid and heat transfers through a rotating asymmetric micro-channel with charged walls under the influence of an imposed the magnetic field. The flow is assumed to be asymmetric about $x^{{\prime }}$ and the liquid is flowing in the $x^{{\prime }}$-direction. The hydrophobic micro-channel is bounded by slowly varying walls at $y^{{\prime }} = h_{1} \left( {x^{{\prime }} } \right)$ and $y^{{\prime }} = h_{2} \left( {x^{{\prime }} } \right)$ respectively, in which the length of the channel $\left( L \right)$ is assumed to be much larger than the height, i.e.,$L > > \left( {h_{1} + h_{2} } \right)$. Figure 1 below depicts the schematic diagram of the problem under current study.

Fig. 1

Physical model for peristaltic wave propagation induced by electro-osmotic flow

The geometrical expression of the wavy channels are given by

$$h_{1}^{\prime } \left( {x^{\prime } } \right) = d_{1}^{\prime } + a_{1}^{\prime } \cos \left( {\frac{{2\pi x^{\prime } }}{L}} \right),$$

(1)

$$h_{2}^{\prime } \left( {x^{\prime } } \right) = - d_{2}^{\prime } - a_{2}^{\prime } \cos \left( {\frac{{2\pi x^{\prime } }}{L} + \phi } \right),$$

(2)

2.1 Electrical Potential Distribution

The basic theory of electrostatics is related to the local net electric charge density $\rho_{e}$ in the diffuse layer of EDL and charge density is coupled with the potential distribution $\psi^{\prime }$ through the Poisson-Boltzmann equation for the symmetric electrolyte [15, 16], given by

$$\frac{{d^{2} \psi^{\prime } \left( {y^{{\prime }} } \right)}}{{dy^{{{\prime }^{2} }} }} = \frac{{2n_{0} ez_{v} }}{\varepsilon }\sinh \left( {\frac{{ez_{v} \psi^{\prime } \left( {y^{{\prime }} } \right)}}{{k_{B} T_{av} }}} \right)$$

(3)

where $\eta_{o}$ represents the concentration of ions at the bulk, $\varepsilon$ is the charge of a proton, $z_{v}$ is the valence of ions, $e$ is the permittivity of the medium, $k_{B}$ is the Boltzmann constant and $T_{av}$ is the boundary conditions for potential function are taken as

$$\begin{aligned} \psi^{\prime } \left( {y^{{\prime }} } \right) = \psi_{1}^{\prime } \quad {\text{at}}\quad y^{{\prime }} = h_{1}^{\prime } (x^{{\prime }} ), \hfill \\ \psi^{\prime } \left( {y^{{\prime }} } \right) = \psi_{2}^{\prime } \quad {\text{at}}\quad y^{{\prime }} = h_{2}^{\prime } (x^{{\prime }} ), \hfill \\ \end{aligned}$$

(4)

where $\psi_{1}^{\prime }$ and $\psi_{2}^{\prime }$ are the electric potential at the upper and lower wall respectively.

Let us now introduce the following non-dimensional variables,

$$\left[ {\psi_{0} ,\psi_{1} ,\psi_{2} } \right] = \frac{{ez_{v} }}{{k_{B} T_{av} }}\left[ {\psi^{\prime } ,\psi_{1}^{\prime } ,\psi_{2}^{\prime } } \right],y = \frac{{y^{{\prime }} }}{{d_{1}^{\prime } }}\;{\text{and}}\;x = \frac{{x^{{\prime }} }}{L}$$

(5)

The dimensionless form of Eqs. (1), (2) and the Poisson–Boltzmann equation defined in (3) take in the following form,

$$h_{1} \left( x \right) = \frac{{h_{1}^{{\prime }} }}{{d_{1}^{{\prime }} }} = 1 + a\cos \left( {2\pi x} \right),$$

(6)

$$h_{2} \left( x \right) = \frac{{h_{2}^{{\prime }} }}{{d_{1}^{\prime } }} = - d - b\cos \left( {2\pi x + \phi } \right),$$

(7)

and

$$\frac{{d^{2} \psi_{0} }}{{dy^{2} }} = k^{2} \sinh \left( {\psi_{0} ,} \right)$$

(8)

where $a = \frac{{a_{1}^{\prime } }}{{d_{1}^{{\prime }} }}$, $b = \frac{{a_{2}^{{\prime }} }}{{d_{1}^{{\prime }} }}$, $d = \frac{{d_{2}^{{\prime }} }}{{d_{1}^{{\prime }} }}$ and $k = \frac{{d_{1}^{{\prime }} }}{\lambda }$ is defined as the electro-osmotic parameter, $\lambda_{2}$ is the reciprocal of the EDL thickness and is defined by $\frac{1}{\lambda } = \left( {\frac{{2n_{o} e^{2} z_{\nu }^{2} }}{{\varepsilon k_{B} T_{a\nu } }}} \right)^{{\frac{1}{2}}}$. Thus the electro-osmotic parameter is inversely proportional to EDL thickness $\lambda$. The dimensionless form of boundary conditions defined in (4) using the dimensionless variables (5) reduce to

$$\psi_{0} \left( y \right) = \psi_{1} \quad {\text{at}}\quad y = h_{1} \left( x \right),$$

$$\psi_{0} \left( y \right) = \psi_{2} \quad {\text{at}}\quad y = h_{2} \left( x \right).$$

(9)

We assumed that the electric potential is much smaller than the thermal potential for which the Debye-Hiickel linearization principle can be approximated as $\sinh \left( x \right) \approx x$. On the basis of this assumption, the solution of Poisson-Boltzmann Eq. (8) takes in the form

$$\frac{{d^{2} \psi_{0} }}{{dy^{2} }} = k^{2} \psi_{0} .$$

(10)

Finally, by employing the boundary conditions (9), the closed form solution of the Eq. (10) is given as

$$\psi_{0} \left( y \right) = F_{1} \cosh \left( {ky} \right) + F_{2} \sinh \left( {ky} \right).$$

(11)

2.2 Model Formulation

The rheological equation of state for anisotropic flow of a Casson fluid can be expressed as

$$\tau_{ij} = \left\{ {\begin{array}{*{20}c} {\left( {\mu_{B} + \frac{{P_{y} }}{{\sqrt {2\pi } }}} \right)2e_{ij} ,\quad \pi > \pi_{c} } \\ {\left( {\mu_{B} + \frac{{P_{y} }}{{\sqrt {2\pi_{c} } }}} \right)2e_{ij} ,\quad \pi < \pi_{c} } \\ \end{array} } \right.$$

(12)

In the above equation P_y = e_ije_ij and e_ij denotes the (i, j)th component of the deformation rate, π be the product of the component of deformation rate with itself, π_c be a critical value of this product based on the non-Newtonian model, μ_B be the plastic dynamic viscosity of the non-Newtonian fluid and P_y be the yield stress of the fluid. From Eq. (1) we obtain (for π < π_c),

$$\tau_{ij} = \mu_{B} \left( {1 + \frac{1}{\beta }} \right)2e_{ij} ,$$

(13)

where $\beta = \mu \sqrt {2\pi_{c} } /P_{y}$ is the Casson fluid parameter. The governing equations for this investigation are obtained from the balance of linear momentum and energy equations as

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$

(14)

$$\rho \left[ {\frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} - 2\varOmega v} \right] = - \frac{\partial P}{\partial x} + \upsilon \left( {1 + \frac{1}{\beta }} \right)\left( {\frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{{\partial^{2} u}}{{\partial x^{2} }}} \right) - \sigma B_{0}^{2} u + \rho_{e} E,$$

(15)

$$\rho \left[ {\frac{\partial v}{\partial t} + u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} + 2\varOmega u} \right] = - \frac{\partial P}{\partial y} + \upsilon \left( {1 + \frac{1}{\beta }} \right)\left( {\frac{{\partial^{2} v}}{{\partial y^{2} }} + \frac{{\partial^{2} v}}{{\partial x^{2} }}} \right) ,$$

(16)

$$\rho c_{p} \left[ {\frac{\partial T}{\partial t} + u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y}} \right] = K\left( {\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{\partial^{2} T}}{{\partial x^{2} }}} \right) + \left( {1 + \frac{1}{\beta }} \right)\mu \left[ {2\left( {\frac{\partial u}{\partial x}} \right)^{2} + 2\left( {\frac{\partial v}{\partial y}} \right)^{2} + \left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}} \right)^{2} } \right] + \sigma B_{0}^{2} u^{2} + \sigma E^{2} ,$$

(17)

The velocity slip conditions (Navier-Slip) at the fluid–solid interface are given by

$$u + b_{1} \left( {1 + \frac{1}{\beta }} \right)\frac{du}{dy} = 0,\quad {\text{at}}\quad y = h_{1}^{{\prime }} \left( x \right)$$

(18)

$$u - b_{2} \left( {1 + \frac{1}{\beta }} \right)\frac{du}{dy} = 0,\quad {\text{at}}\quad y = h_{2}^{{\prime }} \left( x \right)$$

(19)

where $b_{1}$ and $b_{2}$ are the lengths of the channel walls $y = h_{1}^{{\prime }}$ and $y = h_{2}^{{\prime }}$ respectively. Let us $\bar{u} = \frac{u}{{U_{HS} }}$, with $U_{HS} = - \frac{{\varepsilon E_{o} KT_{a\nu } }}{{ez_{\nu } \mu }}$ the classical electro-osmotic flow velocity of micro-channel in the absence of slip velocity, $k$ is the thermal conductivity, $u$ and $v$ are the velocity components in the $x$ and $y$-directions, respectively; $\sigma$ is the electric conductivity, $\vec{\varOmega } = \varOmega \vec{k},$$\vec{k}$ is the unit vector, $\vec{\varOmega } = \left( {0,0,\varOmega } \right)$ is the rotation vector, $\bar{R}$ is given by $\bar{R}^{2} = x^{2} + y^{2}$, $\bar{P}$ is the modified pressure. The equation of motion in the rotating frame has two additional terms i.e. $\rho \,\vec{\varOmega } \wedge \left( {\vec{\varOmega } \wedge \vec{R}} \right)$ the centrifugal force and $2\rho \,\left( {\vec{\varOmega } \wedge \vec{v}} \right)$ the Coriolis force. The flow is inherently unsteady in the laboratory frame $\left( {x,y} \right)$, $\vec{R} = \left( {u,v,0} \right)$. However, the flow becomes steady in a wave frame $\left( {\bar{x},\bar{y}} \right)$ moving away from the laboratory frame with speed $c$ in the direction of propagation of the wave. Taking $u$ and $v$ the velocity component in $x$ and y-directions, the transformation from the laboratory frame to the wave frame is given by

$$\bar{x} = x - ct,\bar{y} = y,\bar{u} = u - c,\bar{v} = v,\bar{p}\left( {\bar{x}} \right) = \bar{P}\left( {x,t} \right).$$

(20)

where, $\bar{u}$ and $\bar{v}$ are the velocity components in the wave frame $\left( {\bar{x},\bar{y}} \right)$, $\bar{p}\,\,$ and $\bar{P}$ are pressured in wave and fixed frame of references, respectively. The appropriate non-dimensional variables for the flow defined as

$$\begin{aligned} u = \frac{{\bar{u}}}{c},v = \frac{{\bar{v}}}{c\delta },\delta = \frac{{2\pi d_{1}^{{\prime }} }}{\beta },p = \frac{{2\pi d_{1}^{{{\prime }^{2} }} \bar{p}}}{\mu c\beta },t = \frac{{2\pi c\bar{t}}}{\beta },h_{1} = \frac{{h_{1}^{{\prime }} }}{{d_{1}^{{\prime }} }},h_{2} = \frac{{h_{2}^{{\prime }} }}{{d_{1}^{{\prime }} }}, \hfill \\ d = \frac{{d_{2}^{{\prime }} }}{{d_{1}^{{\prime }} }},M = \sqrt {\frac{\sigma }{\mu }} B_{0} d,a = \frac{{a_{1}^{{\prime }} }}{{d_{1}^{{\prime }} }},b = \frac{{a_{2}^{{\prime }} }}{{d_{1}^{{\prime }} }},d = \frac{{d_{2}^{{\prime }} }}{{d_{1}^{{\prime }} }}\,R = \frac{{\bar{\varOmega }}}{\mu }a_{1}^{2} ,\text{Re} = \frac{{cd^{\prime}_{1} }}{\nu },\theta = \frac{{T - T_{0} }}{{T_{1} - T_{0} }}, \hfill \\ Ec = \frac{{c^{2} }}{{c_{p} \left( {T_{1} - T_{0} } \right)}},\Pr = \frac{{\rho \nu \,c_{p} }}{K},\beta_{1} = \frac{{b_{1} }}{{d_{1}^{{\prime }} }},\beta_{2} = \frac{{b_{2} }}{{d_{1}^{{\prime }} }},C_{o} = \frac{{\left( { - \frac{{d\bar{p}}}{dx}} \right)d_{1}^{{{\prime }^{2} }} }}{{\mu U_{HS} }},\lambda_{1} = \frac{{\sigma \bar{E}^{2} d_{1}^{{{\prime }^{2} }} }}{{\rho \upsilon c_{p} (T_{1} - T_{0} )}} \hfill \\ \end{aligned}$$

(21)

Introducing the dimensionless stream function $\psi \left( {x,y} \right)$ such that

$$u = \frac{\partial \psi }{\partial y},v = - \delta \frac{\partial \psi }{\partial x}.$$

(22)

By using (20)–(22) and under the assumptions of long wavelength $\left( {\delta < < 1} \right)$ and low Reynolds number, the Eqs. (14)–(17) are reduced to

$$\left( {1 + \frac{1}{\beta }} \right)\frac{{\partial^{4} \psi }}{{\partial y^{4} }} + \left( {R - M^{2} } \right)\frac{{\partial^{2} \psi }}{{\partial y^{2} }} + \frac{{d^{3} \psi_{0} }}{{dy^{3} }} = 0,$$

(23)

$$\frac{1}{\Pr }\frac{{\partial^{2} \theta }}{{\partial y^{2} }} + Ec\left( {1 + \frac{1}{\beta }} \right)\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)^{2} + M^{2} \left( {\frac{\partial \psi }{\partial y}} \right)^{2} + \lambda_{1} = 0.$$

(24)

The corresponding boundary conditions for the stream function and temperature in the wave frame are given by

$$\psi = \frac{q}{2},\frac{\partial \psi }{\partial y} + \beta_{1} \left( {1 + \frac{1}{\beta }} \right)\frac{{\partial^{2} \psi }}{{\partial y^{2} }} = 0,\frac{{\partial^{2} \psi }}{{\partial y^{2} }} = - 1,\quad {\text{at}}\quad {\text{h}}_{ 1} (x) = 1 + a\cos (x),$$

(25)

$$\psi = - \frac{q}{2},\frac{\partial \psi }{\partial y} - \beta_{2} \left( {1 + \frac{1}{\beta }} \right)\frac{{\partial^{2} \psi }}{{\partial y^{2} }} = 0,\frac{{\partial^{2} \psi }}{{\partial y^{2} }} = - 1,\quad {\text{at}}\quad {\text{h}}_{ 2} (x) = - d - b\cos (2\pi x + \varphi ),$$

(26)

$$\theta = 0\quad {\text{at}}\quad {\text{h}}_{ 1} (x) = 1 + a\cos (x),$$

(27)

$$\theta = 1\quad {\text{at}}\quad {\text{h}}_{ 2} (x) = - d - b\cos (2\pi x + \varphi ),$$

(28)

where $M$ is the Hartmann number, $\Pr$ is the Prandtl number, $Ec$ is the Eckert number,$\lambda_{1}$ is the Joule heating parameter, $R$ is the rotation parameter, $\phi$ is phase difference, $\beta_{1}$ and $\beta_{2}$ are the slip parameters, $\beta$ is the Casson fluid parameter and $q$ is the flux in the wave frame.

3 Analytical Solution

The solution of the Eq. (23) subject to the boundary conditions (25)–(26) is given by

$$\psi = C_{1} + C_{2} y + C_{3} \cosh \left( {Ny} \right) + C_{4} \sinh \left( {Ny} \right) + F_{3} y^{2} + F_{4} \cosh \left( {ky} \right) + F_{5} \sinh \left( {ky} \right).$$

(29)

The expression of the axial velocity is given by

$$u = \frac{\partial \psi }{\partial y} = C_{2} + C_{3} N\sinh \left( {Ny} \right) + C_{4} N\cosh \left( {Ny} \right) + 2F_{3} y + F_{4} k\sinh \left( {ky} \right) + F_{5} k\cosh \left( {ky} \right).$$

(30)

The solution of non-dimensional temperature Eq. (24) using Eq. (30) subject to the boundary conditions (27)–(28) is given by

$$\theta = C_{5} + C_{6} y + G_{50} + G_{51} + G_{52} .$$

(31)

The dimensionless shear stress is defined as

$$s_{xy} = \left( {1 + \frac{1}{\beta }} \right)\mu_{B} \frac{{\partial^{2} \psi }}{{\partial y^{2} }},$$

(32)

thus,

$$s_{xy} = \left( {1 + \frac{1}{\beta }} \right)G_{56} .$$

(33)

The rate of heat transfer is given in the form of Nusselt number as

$$Nu = - \left. {\frac{\partial \theta }{\partial y}} \right|_{{y = h_{1} ,h_{2} }} .$$

(34)

The Nusselt number at the upper wall $\left( {h_{1} } \right)$ is obtained from (34), which is given by

$$Nu = - \left( {G_{53} + G_{54} + G_{55} } \right),$$

(35)

where the involved constants in Eqs. (10)–(35) are given in “Appendix”

4 Results and Discussion

In order to gain some insight into the complex hydromagnetic electro-osmotic peristaltic flow of Casson fluid and thermal structures in asymmetric micro-channel, the numerical results of the obtained analytical solutions are presented graphically in Figs. 2, 3, 4, 5, 6, 7, 8, 9 and 10 for the stream function, velocity, temperature, skin friction, Nusselt number and the trapping phenomenon. The following parameter values are utilized in the computation: a = 0.4, b = 0.9, ϕ = π/3, d = 1.0, β = 1.5, R = 3.5, Q = 2.0, β₁ = 0.03, β₂ = 0.02, ψ₁ = 0.3, ψ₂ = 0.3, k = 1, Pr = 0.71, Ec = 1, λ₁ = 1.5. These values are kept in common in the entire study except the variations in respective figures.

Fig. 2

Effect of $M$ on velocity profile

Fig. 3

Effect of $k$ on velocity profile

Fig. 4

Effect of $\beta$ on velocity profile

Fig. 5

Effect of $\lambda_{1}$ on temperature profile

Fig. 6

Effect of $\beta$ on temperature profile

Fig. 7

Effect of $k$ on Nusselt number

Fig. 8

Effect of $\beta$ on shear stress

Fig. 9

Effect of $\beta$ on stream lines for $\beta = 1.5$

Fig. 10

Effect of $\beta$ on stream lines for $\beta = 1.7$

4.1 Velocity profile

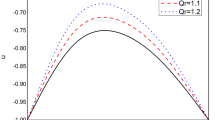
Figures 2, 3, 4, 5, 6, 7, 8, 9 and 10 illustrate the effects of various embedded parameters on the axial velocity profiles (u). A decrease in the velocity profile within the channel core region is observed with a rise in the magnetic field intensity (i.e. Hartmann number M increases) as shown in Fig. 2. This can be attributed to the flow resistance caused by the opposing Lorenz force due to the presence of magnetic field. In Fig. 3, the axial velocity rises within the channel core region due to an enhanced electro-osmotic force (k). Since electro-osmotic parameter k is the reciprocal of EDL, it indicates that an increase in the height of the micro-channel as well as a decrease in the Debye thickness of the micro-channel causes a rise in axial velocity. For thick EDLs, the effect of large zeta potential at the shear plane implicitly ensures the transport of a large extent of mobile ions in the micro-channel EDL. Figure 4 shows the impact of Casson parameter $\beta$ on velocity profiles. As β increases, the fluid velocity within the channel core region increases. It is noteworthy that the fluid tends to behave as a Newtonian fluid at extremely large values of Casson parameter.

4.2 Temperature profile

In this section, using the obtained analytical formulas, the temperature distribution is simulated. The effects of Joule heating parameter $\lambda_{1}$ and Casson parameter $\beta$ on temperature distribution are displayed in Figs. 5, 6. It is observed that the fluid temperature is enhanced with a rise in Casson parameter and Joule heating within the micro-channel. This may be attributed to additional internal heat generated within the fluid due to flow resistance caused by Lorenz force in the magnetic field.

4.3 Nusselt Number

Figure 7 depicts the impact of electro-osmotic parameter k on the magnitude of heat transfer coefficient at the upper wall of an asymmetric micro-channel. Generally, the Nusselt number is oscillatory in nature due to peristaltic motion of the walls. An increase in k enhances the peak value of heat transfer rate across the channel.

4.4 Shear stress

The shear stress distribution (S_xy) on the upper wall of an asymmetric micro-channel for different values of Casson fluid parameter $\left( \beta \right)$ is presented in Fig. 8. The shear stress shows oscillatory behavior due to peristalsis and decreases with a rise in the Casson fluid parameter as shown in Fig. 8.

4.5 Trapping Phenomenon

An intriguing phenomenon in the transport of fluid is trapping and is presented by sketching streamlines in the Figs. 9, 10. A bolus is enclosed by splitting of a streamline under certain conditions and it is carried along with the wave in the wave frame. This process is called trapping. The trapped bolus is found to expand by increasing $\beta$ from Figs. 9, 10.

5 Conclusions

Motivated by novel developments in electro-osmotic micro-pumps, the hydromagnetic peristaltic flow and heat transfer characteristics of Casson fluid in a rotating asymmetric micro-channel driven by the combined action of electro-osmotic force and the pressure gradient is theoretically examined. The important findings of the present study are summarized as follows:

• Electro-osmotic motion shows strong dependent on Debye length.

• An increase in Casson parameter enhances fluid velocity, temperature, and trapping phenomenon.

• An increase in Hartman number decreases the fluid velocity but increases the fluid temperature

• The temperature rises with increasing values of PDF and EOF.

• The Nusselt number increases with EOF and Joule heating but decreases with PDF.

• The shear stress shows oscillatory behavior.

Appendix

$$\begin{aligned} F_{1} & = \frac{{\psi_{1} - \psi_{2} \sinh \left( {kh_{1} } \right)}}{{\cosh \left( {kh_{1} } \right)}},F_{2} = \frac{{\psi_{1} \cosh \left( {kh_{2} } \right) - \psi_{2} \cosh \left( {kh_{1} } \right)}}{{\sinh \left( {kh_{1} } \right)\cosh \left( {kh_{2} } \right) - \sinh \left( {kh_{1} } \right)\cosh \left( {kh_{2} } \right)}},N_{1} = \frac{\beta }{\beta + 1} \\ F_{3} & = \frac{{\left( {1 + \lambda_{1} } \right)C_{o} }}{{2N^{2} }},N_{2} = 1 + \frac{1}{\beta },F_{4} = \frac{{ - F_{1} N_{1} }}{{k^{2} - N^{2} }},F_{5} = \frac{{ - F_{2} N_{1} }}{{k^{2} - N^{2} }} \\ F_{6} & = N\sinh \left( {Nh_{1} } \right) + \beta_{1} N_{2} N^{2} \cosh \left( {Nh_{1} } \right),F_{7} = N\cosh \left( {Nh_{1} } \right) + \beta_{1} N_{2} N^{2} \sinh \left( {Nh_{1} } \right) \\ F_{9} & = N\sinh \left( {Nh_{2} } \right) - \beta_{2} N_{2} N^{2} \cosh \left( {Nh_{2} } \right),F_{10} = N\cosh \left( {Nh_{2} } \right) - \beta_{2} N_{2} N^{2} \sinh \left( {Nh_{2} } \right) \\ F_{12} & = h_{1} - h_{2} ,F_{13} = \cosh \left( {Nh_{1} } \right) - \cosh \left( {Nh_{2} } \right),F_{14} = \sinh \left( {Nh_{1} } \right) - \sinh \left( {Nh_{2} } \right) \\ F_{8} & = 2F_{3} h_{1} + F_{4} k\sinh \left( {kh_{1} } \right) + F_{5} k\cosh \left( {kh_{1} } \right) + \beta_{1} N_{2} \left( {2F_{3} + F_{4} k^{2} \cosh \left( {kh_{1} } \right) + F_{5} k^{2} \sinh \left( {kh_{1} } \right)} \right) + 1, \\ F_{11} & = 2F_{3} h_{2} + F_{4} k\sinh \left( {kh_{2} } \right) + F_{5} k\cosh \left( {kh_{2} } \right) - \beta_{2} N_{2} \left( {2F_{3} + F_{4} k^{2} \cosh \left( {kh_{2} } \right) + F_{5} k^{2} \sinh \left( {kh_{2} } \right)} \right) + 1,F_{16} = \frac{{F_{13} }}{{F_{12} }},F_{17} = \frac{{F_{14} }}{{F_{12} }},F_{18} = \frac{{F_{15} }}{{F_{12} }}, \\ F_{15} & = F_{3} \left( {h_{1}^{2} - h_{2}^{2} } \right) + F_{4} \left( {\cosh \left( {kh_{1} } \right) - \cosh \left( {kh_{2} } \right)} \right) + F_{5} \left( {\sinh \left( {kh_{1} } \right) - \sinh \left( {kh_{2} } \right)} \right) - q,F_{19} = F_{6} - F_{16} ,F_{20} = F_{7} - F_{17} ,F_{21} = F_{8} - F_{18} \\ F_{22} & = F_{9} - F_{16} ,F_{23} = F_{10} - F_{17} ,F_{25} = F_{11} - F_{18} ,c_{4} = \frac{{F_{25} F_{19} - F_{21} F_{22} }}{{F_{20} F_{22} - F_{23} F_{19} }},c_{3} = - \frac{{F_{21} + F_{20} c_{4} }}{{F_{19} }} \\ \end{aligned}$$

$$\begin{aligned} G_{1} & = - BrN_{2} ,G_{2} = - M^{2} \Pr ,G_{3} = G_{1} c_{3}^{2} N^{4} + G_{2} c_{4}^{2} N^{2} ,G_{4} = G_{1} c_{4}^{2} N^{4} + G_{2} c_{3}^{2} N^{2} , \\ G_{5} & = G_{1} F_{4}^{2} k^{4} + G_{2} F_{5}^{2} k^{2} ,G_{6} = G_{1} F_{5}^{2} k^{4} + G_{2} F_{4}^{2} k^{2} , \\ G_{7} & = 2C_{2} G_{2} C_{3} N + 4C_{4} G_{1} F_{3} N^{2} ,G_{8} = 2C_{2} G_{2} F_{4} k + 4F_{3} G_{1} F_{5} k^{2} ,G_{9} = 2C_{2} G_{2} F_{4} k + 4F_{3} G_{1} F_{5} k^{2} , \\ G_{10} & = 2C_{2} G_{2} F_{5} k + 4F_{3} G_{1} F_{4} k^{2} ,G_{11} = C_{3} G_{2} C_{4} N^{2} + C_{3} G_{1} C_{4} N^{4} ,G_{12} = 4C_{3} G_{2} F_{3} N, \\ G_{13} & = 2C_{3} G_{2} F_{4} kN + 2C_{4} G_{1} F_{5} k^{2} N^{2} ,G_{14} = 2C_{3} G_{2} F_{5} kN + 2C_{4} G_{1} F_{4} k^{2} N^{2} , \\ G_{15} & = 2C_{4} G_{2} F_{4} kN + 2C_{3} G_{1} F_{5} k^{2} N^{2} ,G_{16} = 2C_{4} G_{2} F_{5} Nk + 2C_{3} G_{1} F_{4} N^{2} k^{2} , \\ G_{17} & = F_{4} F_{5} G_{2} k^{2} + F_{4} F_{5} G_{1} k^{4} ,G_{18} = 4F_{3}^{2} G_{2} ,G_{19} = 2C_{2} G_{2} F_{3} ,G_{20} = 4C_{4} G_{2} F_{3} N,G_{21} = 4F_{3} G_{2} F_{4} k, \\ G_{22} & = 4F_{3} G_{2} F_{5} k,G_{23} = 4F_{3}^{2} G_{2} + G_{2} C_{2}^{2} - \lambda \Pr ,G_{24} = \frac{{G_{3} }}{{8N^{2} }} + \frac{{G_{4} }}{{8N^{2} }},G_{25} = \frac{{G_{5} }}{{8k^{2} }} + \frac{{G_{6} }}{{8k^{2} }}, \\ G_{26} & = \frac{{G_{7} }}{{N^{2} }} + \frac{{\left( {2G_{20} } \right)}}{N},G_{27} = \frac{{G_{8} }}{{N^{2} }} + \frac{{\left( {2G_{12} } \right)}}{N},G_{28} = \frac{{G_{9} }}{{k^{2} }} + \frac{{\left( {2G_{22} } \right)}}{k},G_{29} = \frac{{G_{10} }}{{k^{2} }} + \frac{{\left( {2G_{21} } \right)}}{k},G_{30} = \frac{{G_{11} }}{{4N^{2} }}, \\ G_{31} & = \frac{{G_{12} }}{{N^{2} }},G_{32} = \frac{{G_{13} }}{{N^{2} }} + \frac{1}{{k^{2} }} + \frac{{2G_{16} }}{kN},G_{33} = \frac{{G_{16} }}{{N^{2} }} + \frac{1}{{k^{2} }} + \frac{{2G_{13} }}{kN},G_{34} = \frac{{G_{14} }}{{N^{2} }} + \frac{1}{{k^{2} }} + \frac{{2G_{15} }}{kN}, \\ G_{35} & = \frac{{G_{15} }}{{N^{2} }} + \frac{1}{{k^{2} }} + \frac{{2G_{14} }}{kN},G_{36} = \frac{{G_{17} }}{{4k^{2} }},G_{37} = \frac{{G_{20} }}{{N^{2} }},G_{38} = \frac{{G_{21} }}{{k^{2} }},G_{39} = \frac{{G_{22} }}{{k^{2} }},G_{42} = \frac{{G_{18} }}{12},G_{41} = \frac{{G_{19} }}{6}, \\ G_{40} & = \frac{{G_{3} }}{4} - \frac{{G_{4} }}{4} + \frac{{G_{5} }}{4} - \frac{{G_{6} }}{4} + \frac{{G_{23} }}{2}, \\ \end{aligned}$$

$$\begin{aligned} G_{43} & = G_{24} \left( {\cosh \left( {2Nh_{1} } \right) - \cosh \left( {2Nh_{2} } \right)} \right) + G_{25} \left( {\cosh \left( {2kh_{1} } \right) - \cosh \left( {2kh_{2} } \right)} \right) + G_{26} \left( {\sinh \left( {Nh_{1} } \right) - \sinh \left( {Nh_{2} } \right)} \right) \\ & \quad + G_{27} \left( {\cosh \left( {Nh_{1} } \right) - \cosh \left( {Nh_{2} } \right)} \right) + G_{28} \left( {\sinh \left( {kh_{1} } \right) - \sinh \left( {kh_{2} } \right)} \right) \\ G_{44} & = G_{29} \left( {\cosh \left( {kh_{1} } \right) - \cosh \left( {kh_{2} } \right)} \right) + G_{30} \left( {\sinh \left( {2Nh_{1} } \right) - \sinh \left( {2Nh_{2} } \right)} \right) + G_{31} \left( {h_{1} \sinh \left( {Nh_{1} } \right) - h_{2} \sinh \left( {Nh_{2} } \right)} \right) \\ & \quad + G_{32} \left( {\sinh \left( {Nh_{1} } \right)\sinh \left( {kh_{1} } \right) - \sinh \left( {Nh_{2} } \right)\sinh \left( {kh_{2} } \right)} \right) \\ G_{45} & = G_{33} \left( {\cosh \left( {Nh_{1} } \right)\cosh \left( {kh_{1} } \right) - \cosh \left( {Nh_{2} } \right)\cosh \left( {kh_{2} } \right)} \right) \\ & \quad + G_{34} \left( {\sinh \left( {Nh_{1} } \right)\cosh \left( {kh_{1} } \right) - \sinh \left( {Nh_{2} } \right)\cosh \left( {kh_{2} } \right)} \right) \\ & \quad + G_{35} \left( {\cosh \left( {Nh_{1} } \right)\sinh \left( {kh_{1} } \right) - \cosh \left( {Nh_{2} } \right)\sinh \left( {kh_{2} } \right)} \right), \\ G_{46} & = G_{36} \left( {\sinh \left( {2kh_{1} } \right) - \sinh \left( {2kh_{2} } \right)} \right) + G_{37} \left( {h_{1} \cosh \left( {Nh_{1} } \right) - h_{2} \cosh \left( {Nh_{2} } \right)} \right) \\ & \quad G_{38} \left( {h_{1} \sinh \left( {kh_{1} } \right) - h_{2} \sinh \left( {kh_{2} } \right)} \right) + G_{39} \left( {h_{1} \cosh \left( {kh_{1} } \right) - h_{2} \cosh \left( {kh_{2} } \right)} \right) + G_{40} \left( {h_{1}^{2} - h_{2}^{2} } \right) \\ & \quad + G_{41} \left( {h_{1}^{3} - h_{2}^{3} } \right) + G_{42} \left( {h_{1}^{4} - h_{2}^{4} } \right), \\ C_{6} & = \frac{1}{{h_{2} - h_{1} }}\left( {1 + G_{43} + G_{44} + G_{45} + G_{46} } \right), \\ G_{47} & = C_{6} h_{1} + G_{24} \cosh \left( {2Nh_{1} } \right) + G_{25} \cosh \left( {2kh_{1} } \right) + G_{26} \sinh \left( {Nh_{1} } \right) \\ & \quad + G_{27} \cosh \left( {Nh_{1} } \right) + G_{28} \sinh \left( {kh_{1} } \right) + G_{29} \cosh \left( {kh_{1} } \right) + G_{30} \sinh \left( {2Nh_{1} } \right) + G_{31} h_{1} \sinh \left( {Nh_{1} } \right), \\ G_{48} & = G_{32} \sinh \left( {Nh_{1} } \right)\sinh \left( {kh_{1} } \right) + G_{33} \cosh \left( {Nh_{1} } \right)\cosh \left( {kh_{1} } \right) \\ & \quad G_{34} \sinh \left( {Nh_{1} } \right)\cosh \left( {kh_{1} } \right) + G_{35} \cosh \left( {Nh_{1} } \right)\sinh \left( {kh_{1} } \right) \\ & \quad + G_{36} \sinh \left( {2kh_{1} } \right) + G_{37} h_{1} \cosh \left( {Nh_{1} } \right), \\ G_{49} & = G_{38} h_{1} \sinh \left( {kh_{1} } \right) + G_{39} h_{1} \cosh \left( {kh_{1} } \right) + G_{40} h_{1}^{2} + G_{41} h_{1}^{3} + G_{42} h_{1}^{4} , \\ G_{50} & = G_{24} \cosh \left( {2Ny} \right) + G_{25} \cosh \left( {2ky} \right) + G_{26} \sinh \left( {Ny} \right) + G_{27} \cosh \left( {Ny} \right) \\ & \quad + G_{28} \sinh \left( {ky} \right) + G_{29} \cosh \left( {ky} \right) + G_{30} \sinh \left( {2Ny} \right) + G_{31} y\sinh \left( {Ny} \right), \\ G_{51} & = G_{32} \sinh \left( {Ny} \right)\sinh \left( {ky} \right) + G_{33} \cosh \left( {Ny} \right)\cosh \left( {ky} \right) + G_{34} \sinh \left( {Ny} \right)\cosh \left( {ky} \right) \\ & \quad + G_{35} \cosh \left( {Ny} \right)\sinh \left( {ky} \right) + G_{36} \sinh \left( {2ky} \right) + G_{37} y\cosh \left( {Ny} \right), \\ G_{52} & = G_{38} y\sinh \left( {ky} \right) + G_{39} y\cosh \left( {ky} \right) + G_{40} y^{2} + G_{41} y^{3} + G_{42} y^{4} , \\ G_{53} & = C_{6} + 2G_{24} N\sinh \left( {2Nh_{2} } \right) + 2G_{25} k\sinh \left( {2kh_{2} } \right) + G_{26} N\cosh \left( {Nh_{2} } \right) + G_{27} N\sinh \left( {Nh_{2} } \right) + G_{28} k\cosh \left( {kh_{2} } \right) \\ & \quad + G_{29} k\sinh \left( {kh_{2} } \right) + 2G_{30} N\cosh \left( {2Nh_{2} } \right) + G_{31} \left( {Nh_{1} \cosh \left( {Nh_{2} } \right) + \sinh \left( {Nh_{2} } \right)} \right) \\ G_{54} & = G_{32} \left( {N\cosh \left( {Nh_{2} } \right)\sinh \left( {kh_{2} } \right) + k\sinh \left( {Nh_{2} } \right)\cosh \left( {kh_{2} } \right)} \right) \\ & \quad + G_{33} \left( {N\sinh \left( {Nh_{2} } \right)\cosh \left( {kh_{2} } \right) + k\cosh \left( {Nh_{2} } \right)\sinh \left( {kh_{2} } \right)} \right) \\ & \quad + G_{34} \left( {k\sinh \left( {Nh_{2} } \right)\sinh \left( {kh_{2} } \right) + N\cosh \left( {Nh_{2} } \right)\cosh \left( {kh_{2} } \right)} \right), \\ G_{55} & = G_{35} \left( {N\sinh \left( {Nh_{2} } \right)\sinh \left( {kh_{2} } \right) + k\cosh \left( {Nh_{2} } \right)\cosh \left( {kh_{2} } \right) + 2kG_{36} \cosh \left( {2kh_{2} } \right)} \right) \\ & \quad + G_{37} \left( {Nh_{2} \sinh \left( {Nh_{2} } \right) + \cosh \left( {Nh_{2} } \right)} \right) \\ & \quad + G_{38} \left( {kh_{2} \cosh \left( {kh_{2} } \right) + \sinh \left( {kh_{2} } \right)} \right) + G_{39} \left( {kh_{2} \sinh \left( {kh_{2} } \right) + \cosh \left( {kh_{2} } \right)} \right) + 2G_{40} h_{2} \\ & \quad + 3G_{41} h_{2}^{2} + 4G_{42} h_{2}^{3} \\ G_{56} & = C_{3} N^{2} \cosh \left( {Ny} \right) + C_{4} N^{2} \sinh \left( {Ny} \right) + 2F_{3} + F_{4} k^{2} \cosh \left( {ky} \right) + F_{5} k^{2} \sinh \left( {ky} \right) \\ \end{aligned}$$