1 Introduction

‘Hardness’ is one of the fundamental mechanical properties of materials and is defined as the property that enables the material to resist being scratched by another. Designing a supplementary hard/superhard material that is harder than diamond and c-BN is still under research. The combined effect of large coordination number, higher covalency between atoms and shorter bond length are the peculiar properties of conventional superhard materials. These materials find excellent technological applications in polishing tools, abrasives, cutting tools and wear-resistant/protective coating [1–3]. Historically III-V semiconductors especially, boron based compounds viz., BN, BP and BAs [4–16] are familiar for their excellent mechanical properties due to their smaller atomic radii and stronger polar directional bonding. Investigation of BP, BAs, BSb, BBi, c-BN, h-BN, B2CN, BCN, B2O, B4C, BC3 and BC5 compounds shows that they have promising mechanical thermal, electrical properties, excellent thermal conductivity and a high thermoelectric power [4–16]. Further, comparative electronic and structural properties of BN, BP, BAs and BSb are reported by Zaoui et al. [17] in the year 2001; Bagci et al. [18] have reported the electronic and phonon properties of BP, BAs and BSb compounds. In parallel, many researchers have worked on boron based ternary materials by doping. Guemou et al. [19] have reported the structural and optical properties of ternary BNxAs1−x alloys. Origin of gap bowing in BNxP1−x, BNxAs1−x and BPxAs1−x alloy combinations are reported by El Haj Hassan et al. [20] in the year 2005. Bouhemadou et al. [21] have reported the elastic properties in zinc-blende III-P compounds under pressure effects in the year 2009. Further, Abdiche et al. [22] have discussed the structural and electronic properties of cubic quaternary BxGa1−xAs1−yNy alloys using the first principles calculation.

For the ternary alloys under present study namely B(P,As)1−xNx (x = 0.25, 0.5, 0.75), only some of the optical properties are reported whereas their mechanical and thermal properties are not yet been discussed earlier in the literature. Hence, in the present study, we report on (i) mechanical, optical and thermal properties of B(P,As)1−xNx (x = 0.25, 0.5, 0.75) alloy combinations (ii) hardness behavior of BP and BAs under compression by using Full Potential-Linear Augmented Plane Wave method for the first time.

2 Computational details

The present computations on B(P,As)1−xNx (x = 0, 0.25, 0.5, 0.75, 1) materials are carried out by means of FP-LAPW method as implemented in the Wien2k code [23] based on density functional theory [24] as in our previous work [25]. In the present study, exchange and correlation effect treated with local density approximation (LDA) [26] and with generalized gradient approximation (GGA) [27] has been applied. The plane wave cut-off of RMTKMax = 7 has been chosen, where RMT is the smallest muffin tin sphere radius and kmax is being the largest k vector in the plane wave expansion. The RMT of ‘B’, ‘P’, ‘As’ and ‘N’ are 1.3, 1.61, 1.7 and 1.5 a.u. respectively. Boron Phosphide and Boron Arsenide crystallize in the zinc-blende structure of the space group 216_F-43m. The position of ‘B’ atom is (0, 0, 0) and ‘P’, ‘As’ atom is (0.25, 0.25, 0.25). k-sampling has been done to identify the consistency in total energy and 10 × 10 × 10 k—points has been chosen in the present calculation. The chosen RMT is used to minimize the charge leakage and energy. The self-consistent calculations have been carried out until the difference in the total energy and charge did not exceed 0.0001 mRy and 0.001 e respectively. Volume optimization is done for the compound both BP and BAs where the initial structure file is generated with experimental lattice parameter as reported in the literature [9, 15, 16]. Then, a supercell of size 2 × 2 × 2 is generated for BP (BAs) and in this super cell there will be eight boron and eight phosphorus atoms. When two phosphorus (arsenic) atoms are replaced with two nitrogen atoms, we get B(P/As).75N.25 combination; similarly replacement of four and six phosphorus (arsenic) atoms with the respective number of nitrogen atoms, one will get B(P/As).5N.5 and B(P/As).25N.75 combinations. Volume optimization and fitting in Birch–Murnaghan [28] equation of states gives the optimized lattice parameters for each of B(P,As)1−xNx alloys (where x = 0.25, 0.5, 0.75). The crystal structures are drawn using xCrysden [29]. Elast package contributed by Thomas Charpin and Mortaza Jamal [30] as implemented in the Wien 2 k code has been applied to each of B(P,As)1−xNx combination in order to find the respective stiffness coefficients namely C11, C12 and C44. The computations are repeated on both BP and BAs in order to generate the structural file under each compression namely at V/V0 = 1, 0.95, 0.9, 0.85, 0.8, 0.7 and 0.6 with the respective optimized lattice constant and the corresponding elastic constants are computed.

3 Results and discussion

3.1 Structural properties of B(P,As)1−xNx (x = 0, 0.25, 0.5, 0.75, 1) alloys

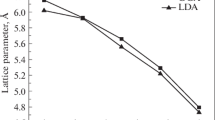
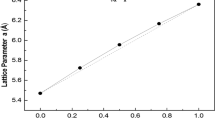
The obtained optimized structural parameters such as lattice parameters (aopt), space group and density of each of B(P,As)1−xNx (x = 0, 0.25, 0.5, 0.75, 1) alloy combinations by GGA and LDA schemes are given in Table 1. The analysis of Table 1 shows that there is a good agreement in the optimized lattice parameter values with the existing literature values. As the concentration of nitrogen increases in B(P,As)1−xNx (x = 0, 0.25, 0.5, 0.75, 1) alloy combinations, (i) it is found that the ‘aopt’ value decreases and this may be due to the replacement of larger atom namely ‘P/As’ by ‘N’. (ii) Density of B(P)1−xNx alloy combination increases whereas the density of B(As)1−xNx alloy combination decreases. For combinations of x = 0, 0.5, 1 the material behaves as Face Centered Cubic (space group 216) and for the remaining combinations such as x = 0.25, 0.75 the system exists as Simple Cubic (space Group 215). The volume optimization curve for each of B(P,As)1−xNx (x = 0.25, 0.5, 0.75) alloy combination that is drawn between total energy versus V/V0 is shown in Fig. 1. Electronic, mechanical, thermal and optical properties of these B(P,As)1−xNx (x = 0.25, 0.5, 0.75) alloy combination are shown in Tables 2, 3, 5 and 6 respectively. Comparison of mechanical properties of BP.25N.75 and BAs.25N.75 alloys with c-BN and Diamond is shown in Table 4.

Table 1 Structural parameters of each of B(P,As)1−xNx; (x = 0, 0.25, 0.5, 0.75, 1) alloy combinations by GGA and LDA schemes
Full size table
Fig. 1
figure 1

Volume optimization curve for each of B(P,As)1−xNx; (x = 0.25, 0.5, 0.75) alloy combinations

Full size image
Table 2 Electronic properties of B(P,As)1−xNx; (x = 0, 0.25, 0.5, 0.75, 1) alloy combinations by GGA schemes
Full size table
Table 3 Ductile–Brittle nature and hardness of each of B(P,As)1−xNx; (x = 0, 0.25, 0.5, 0.75, 1) alloy combinations by Jamal elastic package
Full size table
Table 4 Comparison of B(P,As)1−xNx; (x = 0, 0.25, 0.5, 0.75, 1) alloy combinations
Full size table
Table 5 Thermal properties such as elastic wave velocity, Debye’s temperature (θD) and melting point (Tm) for each of B(P,As)1−xNx; (x = 0, 0.25, 0.5, 0.75 and 1) alloy combinations
Full size table
Table 6 Optical properties such as real and imaginary dielectric constants, refractive index (n), extinction coefficient (k) and reflectivity (R) for each of B(P,As)1−xNx; (x = 0, 0.25, 0.5, 0.75, 1) alloy combinations
Full size table

3.2 Electronic properties of B(P,As)1−xNx (x = 0, 0.25, 0.5, 0.75, 1) alloys

The electronic parameters such as energy gap and Fermi energy of B(P,As)1−xNx (x = 0.25, 0.5, 0.75) alloys are listed in Table 2. From the Table 2, it is observed that the band gap (Eg) at ‘Г’ decreases from 1.2 eV (BP) to 0.06 eV (BP.75N.25) and then it gradually increases to 1.4 eV (BP.5N.5), 2 eV (BP.25N.75), 4.5 eV (BN). The same trend is observed in the case of BAs compound. The band structure of B(P,As).75N.25, B(P,As).5N.5 and B(P,As).25N.75 ternary alloys are plotted and are shown in Fig. 2. In B(P,As).5N.5 and B(P,As).25N.75 alloys, the bands are not crossing the Fermi Energy level and therefore it confirms their semiconducting/insulating behaviour; whereas in the case of B(P,As).75N.25, the valence and conduction bands overlap slightly at the Fermi level. Hence it may be stated that there is a possibility of B(P,As).75N.25 alloys to exist as semimetals. Density of states (DOS) histograms and charge density plots are drawn for B(P,As)1−xNx (x = 0.25, 0.5, 0.75) alloys and are shown in Figs. 3 and 4. From the analysis of DOS histograms, ‘N’-2p states contribute towards the total DOS and the covalent nature of B(P,As).25N.75 alloy is revealed in their respective charge density plots (Fig. 4) as there are uniformly distributed directional charge density contours that encloses P–N–B in ‘BP.25N.75’ and As–N–B in ‘BAs.25N.75’ alloy.

Fig. 2
figure 2

Band structure of each of B(P,As)xN1−x; (x = 0.25, 0.5, 0.75) alloy combinations

Full size image
Fig. 3
figure 3

Density of states histogram for each of B(P,As)1−xNx; (x = 0.25, 0.5, 0.75) alloy combinations

Full size image
Fig. 4
figure 4

Charge density plot for each of B(P,As)1−xNx; (x = 0.25, 0.5, 0.75) alloy combinations along (001) plane

Full size image

3.3 Mechanical properties of B(P,As)1−xNx (x = 0, 0.25, 0.5, 0.75, 1) alloys

The linear variation of Voigt elastic coefficients with the concentration of ‘N’ in the present alloys are obtained both by GGA and LDA scheme and are shown in Fig. 5. Bulk modulus (B), shear modulus (GH), and Young’s modulus (Y) of B(P,As)1−xNx (x = 0, 0.25, 0.5, 0.75, 1) alloys are depicted in Fig. 6. Zener anisotropy factor (A), Kleinmann Parameter (ξ), Cauchy (Ca) ratio, Born (Bo) ratio and plasticity (B/C44) of B(P,As)1−xNx (x = 0, 0.25, 0.5, 0.75, 1) alloys are shown in Fig. 7. Poisson’s ratio (σ), Pugh’s ratio (G/B), Cauchy pressure (C12–C44), Vicker’s micro hardness (HV) of B(P,As)1−xNx (x = 0, 0.25, 0.5, 0.75, 1) alloys are listed in Table 3 and are verified with existing literature of the parent compounds.

Fig. 5
figure 5

Elastic stiffness coefficients of each of B(P,As)1−xNx; (x = 0, 0.25, 0.5, 0.75, 1) alloy combinations

Full size image
Fig. 6
figure 6

Elastic modulus of each of B(P,As)1−xNx; (x = 0, 0.25, 0.5, 0.75, 1) alloy combinations

Full size image
Fig. 7
figure 7

Other elastic constants such as Ca, Bo, A, B/C44 and ξ for each of B(P,As)1−xNx; (x = 0, 0.25, 0.5, 0.75, 1) alloy combinations

Full size image

3.3.1 Elastic stiffness coefficients and various moduli

For the present ternary alloy combinations namely B(P,As)1−xNx (x = 0, 0.25, 0.5, 0.75, 1), the analysis of Voigt elastic coefficients (Fig. 5), shows that they satisfy the stability criteria, namely C11 > 0, C44 > 0, (C11 − C12) > 0, (C11 + 2C12) > 0 and C12 < B < C11 [43–45]. From Fig. 5, it is inferred that the curve drawn between concentration of N versus C12 is steeper than that is drawn with C11 and C44. The Voigt elastic constants obtained by LDA are found to be higher than that of GGA.

From Fig. 6, one can observe that in each of B(P,As)1−xNx (x = 0, 0.25, 0.5, 0.75, 1) alloy combination, the profile of each modulus with ‘concentration of nitrogen’ is observed to be similar. Further one can state that the bulk modulus value increases as one move from BP—BP.75N.25—BP.5N.5—BP.25N.75—BN and also from BAs—BAs.75N.25—BAs.5N.5—BAs.25N.75—BN. The maximum bulk modulus value is obtained for BP.25N.75 (267 GPa) combination and its lattice constant is the smallest among the other alloys (Table 1). The Young’s modulus and shear modulus values in Fig. 6 reveals that the stiffness and hardness increases as one move from BP—BP.75N.25—BP.5N.5—BP.25N.75—BN alloy and from BAs—BAs.75N.25—BAs.5N.5—BAs.25N.75—BN. Further, it is observed that in each of B(P,As)1−xNx (x = 0, 0.25, 0.5, 0.75, 1) alloy combination, the shear and bulk modulus values are almost the same value. It is inferred that if B = G, then one will get the Poisson’s ratio will be of the order of 0.1 [46] and they exhibit covalent nature. The lower Poisson’s values suggest [46] that a large volume change is associated with its deformation.

3.3.2 Ductile–brittle nature

The variation in Poisson’s ratio, Cauchy pressure and G/B ratio with the concentration of N in both BP and BAs is shown in Table 3. For the present B(P,As)1−xNx (x = 0, 0.25, 0.5, 0.75, 1) alloys,

  1. (i)

    Cauchy’s pressure values are negative and hence they are of brittle nature. Of all the alloy combinations, B(P,As).25N.75 material is more brittle.

  2. (ii)

    G/B ratio ranges from 0.93 to 0.98; hence they are of brittle nature.

  3. (iii)

    σ value ranges from 0.13 to 0.15. Hence the proposed ternary alloys are of brittle nature.

From the above study, one can confirm that all six ternary compounds namely BP.75N.25, BP.5N.5, BP.25N.75 and BAs.75N.25, BAs.5N.5, BAs.25N.75 are of brittle nature, of which B(P,As).25N.75 materials are more brittle than the other.

3.3.3 Measure of plasticity, Zener anisotropy factor (A), Kleinman parameter (ξ), Cauchy (Ca) and Born (Bo) ratio

The ratio of the bulk modulus and C44 predict the measure of plasticity [47]. Larger values of this ratio indicates the excellent lubricating property offered by that material [44]. For an example, Graphite [48] is found to have ‘the measure of plasticity’ as 56.1 and it is identified as a good lubricant. Hence, the present ternary alloy system may not serve as good lubricants as the above ratio ranges from 0.83 to 0.89 (Fig. 7).

The Zener anisotropy factor for the cubic crystals is calculated using the formula [49],

$${\text{A}} = \frac{{2C_{44} }}{{C_{11} - C_{12} }}$$
(1)

If A < 1, the crystal is stiffest along 〈100〉 cube axes and when A > 1, it is stiffest along the 〈111〉 body diagonals. If A = 1, the crystal is elastically isotropic and is uniformly deformable along all the directions of the body [50]. For the present B(P,As)1−xNx (x = 0.25, 0.5, 0.75) alloys, the Zener anisotropy factor values range from 1.43 to 1.57 which clearly indicates that these ternary alloys are of anisotropic nature and the degree of stiffness will vary along the 〈111〉 body diagonals.

The bulk modulus values can also be correlated to the anisotropic nature of the given material. If the anisotropy value is closer to unity for a given material then the corresponding bulk modulus value is found be larger. In the present work, the anisotropy values (Fig. 7) of ternary alloys namely B(P,As)1−xNx (x = 0, 0.25, 0.5, 0.75, 1) decrease towards unity as the nitrogen concentration increases. Here one can witness from the same figure that the bulk modulus value is maximum only for BP.25N.75 (A = 1.434).

The condition of minimum energy [50–52] is characterised by the Kleinman parameter and it is calculated by the relation,

$$\upxi \, = \frac{{C_{11} + 8C_{12} }}{{7 C_{11} + 2C_{12} }}$$
(2)

Here ξ = 0 indicates no internal displacement and ξ = 1 indicates the existence of internal displacement alone [53]. For the present ternary alloy combinations B(P,As)1−xNx (x = 0.25, 0.5, 0.75), the Kleiman parameter values (Fig. 7) range from 0.39 to 0.41.

The elastic stiffness constants are related by the Cauchy (Ca) and Born (Bo) ratio for the cubic crystals by the following relation [54],

$${\text{C}}_{\text{a}} = \frac{{C_{11} }}{{C_{44} }}$$
(3)
$${\text{B}}_{\text{o}} = \frac{{\left( {C_{11} + C_{12} } \right)^{2} }}{{4C_{11} \left( {C_{11} - C_{44} } \right)}}$$
(4)

From Fig. 7, one can find that the Cauchy ratio increases from B(P/As).75N0.25—B(P/As)..5N.5—B(P/As).25N.75 ternary alloys where as Born ratio decreases in the same order.

3.3.4 Hardness

Hardness of a given material can be calculated by using various experimental and theoretical available methods [55]. Here, the Vicker’s micro hardness is calculated by using Chen’s formula [38, 56] given by,

$${\text{H}}_{\text{V}} = 0.92\;{\text{K}}^{1.137} {\text{G}}^{0.708} ,\quad {\text{where}}\quad {\text{K}} = {\text{G/B}}.$$
(5)

The calculated microhardness by both GGA and LDA are presented and compared with available experimental and theoretical microhardness. The variation in microhardness for B(P,As)1−xNx (x = 0, 0.25, 0.5, 0.75, 1) alloy combination with ‘concentration of nitrogen’ is shown in Table 3 and it is found that the microhardness value increases with increase in ‘concentration of nitrogen’. The microhardness value ranges from 29 to 45 GPa for the ternary alloys under present study and is found to be greater than 40 GPa for BP.25N.75 and BAs.25N.75 alloys. Hence BP.25N.75 and BAs.25N.75 alloys could serve as superhard materials. The calculated hardness values are consistent in both GGA and LDA method. The enhancement of hardness, reduction of lattice constants, enhancement of directional bonding, least value of Poisson’s ratio (<0.25) in B(P,As)1−xNx (x = 0, 0.25, 0.5, 0.75, 1) alloy combinations suggest the possibility of these materials to be [53] indexed as conventional hard materials. In this present work, the maximum hardness is about 43 GPa in the case of BP1−xNx (x = 0.75) alloy.

3.4 Structural and hardness properties of compounds BP and BAs under compression

Calculations are further extended to study the hardness of BP and BAs at ambient condition and under compressions namely V/V0 = 0.95, 0.9, 0.85, 0.8 & 0.7. The curve that is drawn between the pressure values and the corresponding calculated lattice parameter values of BP and BAs are shown in Fig. 8. From Fig. 8, one can state that as the lattice parameter value decreases as the pressure increases.

Fig. 8
figure 8

Pressure versus calculated lattice parameter acal (Å) of BP and BAs compounds

Full size image

The study of hardness for BP and BAs is analyzed for the pressure range from ambient condition to 125 GPa and is shown in Fig. 9. The hardness of BP and BAs increases as the pressure increases. The hardness of BP reaches 40 GPa at pressure 20 GPa and reaches a maximum of 47 GPa at 112 GPa. As such getting hardness of more than 40 GPa under very high pressure is of no practical use. But it gives an important clue to the experimentalists for synthesizing the hard phase of BP/BAs. The same pressure effect can be realized by doping with a suitable element in such a way that one could synthesize a material of reduced lattice parameter that matches with that of high pressure; mimicking high pressure is possible.

Fig. 9
figure 9

Hardness versus pressure of BP and BAs under compression

Full size image

3.5 Thermal properties of B(P,As)1−xNx (x = 0, 0.25, 0.5, 0.75, 1) alloys

The lattice vibrations are responsible for the characteristic properties of matter such as specific heat, thermal conductivity, electrical conductivity, optical and dielectric properties, diffusion mechanism, phase change phenomena etc. [57]. Anisotropic materials are directional dependent on all properties including thermal properties. Longitudinal (νl) and transverse (νt) wave velocities are the two types of sound elastic waves exist in the solids. We can calculate the average elastic wave velocity (νm) from νl and νt, if we know the crystal density (ρ) and the elastic stiffness coefficients (Cij) [58]. They are calculated using the following relations,

$$\upnu_{\text{l}} = \left( {\frac{3B + 4G}{3\rho }} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}$$
(6)
$$\upnu_{\text{t}} = \left( {\frac{G}{\rho }} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}$$
(7)
$$\upnu_{\text{m}} = \left[ {\frac{1}{3}\left( {\frac{2}{{\upsilon_{t}^{3} }} + \frac{1}{{\upsilon_{l}^{3} }}} \right)} \right]^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}}$$
(8)

The calculated Longitudinal (νl), transverse (νt), average elastic wave velocity (νm) and Debye temperature (θD) of the present work are tabulated in Table 5. There seems excellent accordance with the available literature. In both the cases of BP and BAs, addition of nitrogen increases the longitudinal and transverse velocities and maximum can be seen for BP.25N.75 and BAs.25N.75 ternary alloys.

Many of the physical properties of the solid such as specific heat, elastic stiffness constants (Cij), bond strength, melting temperature (TM), thermal expansion and thermal conductivity are closely related to the Debye temperature (θD) of the given material [59]. It is the temperature above which the crystal behaves classically, because the thermal vibrations become more important than the quantum effects. At low temperature, the lattice vibrational excitations arise solely from acoustic modes, i.e., when θD is associated with lattice vibrations.

The Debye temperature is obtained through well-established empirical or semi-empirical formulas. One of the semi-empirical formulas [59] can be used to estimate the values of Debye temperature through the averaged elastic wave velocity vm

$$\uptheta_{\text{D}} = \frac{h}{{k_{B} }}\left( {\frac{3}{{4\pi V_{a} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} {\text{v}}_{\text{m}}$$
(9)

where h is Planck’s constant, kB is Boltzmann’s constant, Va is atomic volume and vm is average sound wave velocity.

From the Table 5 one can notice that the θD values increase as the nitrogen concentration increases in the case of both BP and BAs compound. θD value reaches maximum for BP.25N.75 (1283 K)and BAs.25N.75 (1203 K) ternary alloys. This shows that the thermal conductivities of these alloys are more than that of other ternary alloys in the present work.

Also the melting temperature increases as the θD value increases and is maximum of 1480 ± 300 K for BP.25N.75 alloys.

3.6 Optical properties of B(P,As)1−xNx (x = 0, 0.25, 0.5, 0.75, 1) alloys

The optical properties are key tool to study energy band structure of solid which is directly related to complex dielectric function and ε(ω) is determined mainly by the transition between the valence and conduction bands. The imaginary part is obtained directly from the electronic structure calculations. From the result, the real part is determined using the Kramers–Kronig dispersion relation. According to the perturbation theory and Kramers–Kronig relation [17], the real and imaginary part of dielectric function i.e. ε1(ω) and ε2(ω) are expressed as,

$$\upvarepsilon_{2} \left(\upomega \right) \, = \frac{{e^{2} h}}{{\pi m^{2} \omega^{2} }}\mathop \sum \limits_{\upsilon , c} \mathop \int \limits_{BZ} \left| {M_{c\upsilon } \left( k \right)} \right|^{2} \delta \left[ {\omega_{c\nu } \left( k \right) - \omega } \right]d^{3} k,$$
(10)
$$\upvarepsilon_{1} \left(\upomega \right) \, = 1 + \frac{2}{\pi }P\mathop \int \limits_{0}^{\infty } \frac{{\omega^{\prime } \varepsilon_{2} \left( {\omega^{\prime } } \right)}}{{\omega^{\prime 2} - \omega^{2} }}d\omega^{\prime } ,$$
(11)

where m, e are the mass and electrical charge of the electron, respectively. The integral is taken over the first Brillouin zone. The momentum dipole elements: Mcv(k) =  〈uck|δ∇|uvk〉, where δ is the potential vector defining the electric field, are matrix elements for direct transitions between valence—uvk(r) and conduction-band uck(r) states, and the energy ħωcv(k) = Eck − Evk is the corresponding transition energy. P implies the principal value of the integral.

The optical dispersion and absorption spectra i.e. real and imaginary parts of the complex dielectric function versus the photon energy for the present B(P,As)1−xNx (x = 0.25, 0.5 and 0.75) alloys are presented in Fig. 10(a)–10(c). The complex dielectric function can be written as ε(ω) = ε1(ω) + iε2(ω) and is one of the best tool for analyzing band structure and energy gap of the crystalline materials. The static dielectric constant i.e. real part of dielectric function in the zero frequency limit ε1(0) is the most important quantity and the values for present alloys are given in Table 6. The results are verified with the literature available and there is a good accordance with the previous results. The value of ε1(0) decreases in BP1−xNx (x = 0.25, 0.5 and 0.75) alloys from 8.8(BP.75N.25)–7.5(BP.5N.5)–5.8(BP.25N.75) and in BAs1−xNx (x = 0.25, 0.5 and 0.75) alloys from 9.0(BAs.75N.25)–7.8(BAs.5N.5)–5.8(BAs.25N.75). It is clearly implies that ε1(0) decreases by increasing the concentration of nitrogen with BP and BAs. The main peaks in the real part of the dielectric spectrum has appeared in low frequency side for the present alloy system at 4.41 eV (BP.75N.25), 4.50 eV (BP.5N.5), 6.44 eV (BP.25N.75), 3.89 eV (BAs.75N.25), 4.42 eV (BAs.5N.5) and 6.33 eV (BAs.25N.75) respectively.

Fig. 10
figure 10

Real and imaginary part of dielectric function and refractive index of each of B(P,As)1−xNx; (x = 0, 0.25, 0.5, 0.75, 1) alloy combinations

Full size image

ε2(ω) is some way responsible for optical absorption in materials due to various inter-band transitions and for the present ternary alloys the values are almost zero which shows negligible absorption in the zero frequency limit. The analysis of ε2(ω) spectrum in our present work show that the first critical point i.e. absorption threshold occur at 2.39 eV (BP.75N.25), 3.12 eV (BP.5N.5), 4.49 eV (BP.25N.75), 2.41 eV (BAs.75N.25), 3.26 eV (BAs.5N.5) and 4.41 eV (BAs.25N.75). Optical transitions between top of the valence band maximum and bottom of the conduction band at the Γ point (ΓV–ΓC) are responsible for these critical points. The addition of nitrogen increases the direct band gap and hence increases the first critical point energies towards higher energies. Other than critical points there are some main peaks exist in the absorption spectra. For the present alloy system, there are three peaks appear at 0.33 eV, 5.15 eV & 6.69 eV for BP.75N.25 alloy. As BP.75N.25 alloy is semimetal and its band gap is so small, the first peak at 0.33 eV occurs due to direct band transitions at ΓV–ΓC. In the case BP.5N.5 alloy the main peaks are found at 5.84, 6.56 and 7.75 eV and for BP.25N.75 alloy found at 6.99, 7.8 and 10.24 eV. In the case of BAs, the main peaks are appear at 0.41, 4.71 and 6.55 eV for BAs.75N.25 alloy, six peaks at 4.97, 5.5, 5.89, 6.30, 6.82 and 7.31 eV for BAs.5N.5 alloy and five peaks at 7.2, 7.53, 8.03, 9.7 and 10.49 eV for BAs.25N.75 alloy. These peaks occur because of inter-band transitions of top of the valance band to conduction band at different k point.

The other important optical constants known as refractive index (n), reflectivity (R) and the local maxima of the extinction coefficient (k) are obtained using both real and imaginary parts of the dielectric function by the following formulae [11, 60–62],

$${\text{n}} = \left[ {\frac{{\sqrt {\varepsilon_{1}^{2} + \varepsilon_{2}^{2} } + \varepsilon_{1} }}{2}} \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}$$
(12)
$${\text{k}} = \left[ {\frac{{\sqrt {\varepsilon_{1}^{2} + \varepsilon_{2}^{2} } - \varepsilon_{1} }}{2}} \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}$$
(13)
$${\text{R}} = \frac{{\left( {n - 1} \right)^{2} + k^{2} }}{{\left( {n + 1} \right)^{2} + k^{2} }}$$
(14)

Semiconductors especially III–V semiconductors are well known for their optoelectronic applications. When light passes through the different substances its velocity decreases by increasing of the refractive index of these substances [63, 64]. The refractive index and band gap are the two fundamental properties that decide the optical and electronic properties of semiconductors. From the Table 6, it is observed that the energy band gap and refractive index of B(P,As)1−xNx (x = 0, 0.25, 0.5, 0.75, 1) alloys are inversely proportional to each other. One can also found from the same Table that all ε1(0), n & R values decrease as the concentration of nitrogen increases in BP and BAs.

4 Conclusion

Structural, electronic, mechanical, thermal and optical properties of B(P,As)1−xNx (x = 0, 0.25, 0.5, 0.75, 1) compounds at ambient condition using the first principle calculations by both GGA and LDA schemes are studied. Charge density plots show all B(P,As)1−xNx (x = 0, 0.25, 0.5, 0.75, 1) alloy combinations have highly directional bonding. Band structure and DOS show that B(P,As)1−xNx (x = 0.5 and 0.75) alloys are semiconductors and they have direct band gap while B(P,As)1−xNx (x = 0.25) alloys are observed to be semimetals. The bulk, shear and Young’s modulus is found to be comparatively more for BP.25N.75 (/BAs.25N.75)alloy than that of respective B(P)1−xNx (x = 0.25 and 0.5) (/B(As)1−xNx (x = 0.25, 0.5 and 0.75) alloys). Hardness of BP.25N.75 alloy and BAs.25N.75 alloy is computed to be 44 and 40 GPa respectively which makes these alloys to be superhard materials. Since all B(P,As)1−xNx (x = 0, 0.25, 0.5, 0.75, 1) alloy combinations have highly directional bonding, they exhibit brittle nature. The study of hardness for BP and BAs under compression gives an important clue and impetus to the experimentalists about the possibility of deriving materials of hardness value more than 40 GPa and it could be obtained by doping with a suitable element in such a way that one could synthesize material of reduced lattice parameter that matches with that of high pressure. In both the cases i.e. BP and BAs, addition of nitrogen increases the longitudinal and transverse velocities and maximum can be seen for BP.25N.75 and BAs.25N.75 ternary alloys. θD values increases as the nitrogen concentration increases and reaches maximum for BP.25N.75 (1283 K) and BAs.25N.75 (1203 K) ternary alloys. The effect of nitrogen addition decreases the refractive index values in both BP and BAs cases.