1 Introduction

The pre-big-bang cosmology (see for a review [1] and references therein) has been initiated with the advent of the application of stringy duality (see for a review [2] and references therein) to cosmology. According to the pre-big-bang cosmology, the universe is initially in the state of string perturbative vacuum which evolves to high curvature regime. The crucial technical point is the invariance of the action under duality symmetry. This duality is called a scale factor duality (SFD) [3] due to the following property: inversion of the scale factor \(a(t)\rightarrow a(t)^{-1}\) with simultaneous shift of \(\phi (t)\rightarrow \phi (t)-6a(t)\) where a(t) and \(\phi (t)\) are scale factor and dilaton, respectively.

In string theory, there is a chance for string to wrap a compact space because of its extension in spatial direction. In this case the theory reveals additional symmetry due to the property of physical invariance under the duality \(R\rightarrow 1/R\) where R is a radius of compact space. It is called T-duality in string theory or equivalently O(d, d) symmetry [4]. The scale factor duality is very reminiscent of its T-duality because it can be embedded into O(d, d) symmetry of string theory.

Because of the SFD in addition to the time reversal symmetry there may exist two more branches leading to four branches in spacetime. The interesting branch is accelerating and contracting one. The accelerating phase in \(t<0\) is related to contracting phase in \(t>0\) while the contracting phase in \(t<0\) is related to accelerating phase in \(t>0\). They are disconnected by cosmological big-bang singularity.

The graceful exit problem [5] arises when the accelerating (pre-big-bang) phase (inflating) does not stop and does not turn to decelerating (post-big-bang) phase. Within the low energy effective action the smooth connection of two branches, accelerating and contracting phases, is problematic and is a major concern here. In two dimensions the contribution of quantum back reaction smoothly connects these two branches [6]. In four dimensions the conformal field theoretic consideration for the full stringy correction would smoothly connect the two branches [7].

Instead of connecting the two branches we try to find the possibility of quantum mechanical transition between the two branches. We apply Wheeler–De Witt equation [8] for this job. The Wheeler–De Witt equation is considered as a transition from pre- to post-big-bang or as an anti-tunneling [9–11] in string theory effective action (for a review see[12]). The Wheeler–De Witt equation to the Brans–Dicke type scalar–tensor theory with cosmological constant is considered in [13]: \(S=\int d^4 x \sqrt{-g}e^{-\phi }(R-\omega (\partial \phi )^2-\Lambda )\). The parameter \(\omega \) is equal to \(-1\) for low energy string effective action. In [14], when \(\Lambda =0\) and specific matter is included, the tunneling probability is obtained. In [15], the tunneling probability is calculated for specific matter coupled and non-zero \(\omega \). In this work, we consider the string effective action with a perfect fluid type matter, i.e., the pressure and the energy density have a relation such as \(p =\gamma \rho \).

2 Classical solution: the behavior of the cosmological model

In this section we study the scalar–tensor theory coming from low energy string effective action. Besides gravity and dilaton, the only contribution to the action comes from a perfect fluid type matter. The extra contributions to the action are supposed to be melted in the matter term.

The one of the general extension of Einstein general relativity is Brans–Dicke theory. In Jordan frame the action reads

$$\begin{aligned} S=\int d^4 x \sqrt{-g} \left( \Phi R-\omega {{(\nabla \Phi )^2} \over \Phi }\right) , \end{aligned}$$
(1)

where \(\Phi \) is a Brans–Dicke scalar field and g is determinant of the metric \(g_{\mu \nu }\). By redefining \(\Phi \) as \(e^{-\phi }\), this action turns out to be an action more familiar to string theorists:

$$\begin{aligned} S=\int d^4 x \sqrt{-g} e^{-\phi } \left( R-\omega (\nabla \phi )^2\right) . \end{aligned}$$
(2)

As a reference, in [16], the similar action called p-brane frame action is obtained for \(\omega =-[(D-1)(p-1)-(p+1)^2]/[(D-2)(p-1)-(p+1)^2]\) where D is a spatial dimension and p is a dimension of brane, respectively. This action can be identified with the so called the low energy effective string action with gravity \(g_{\mu \nu }\) and dilaton field \(\phi \) only when \(\omega =-1\) (\(p=1\) or one-brane). Now let us consider the case that includes matter contribution. We may regard its contribution as that of coming from all other fields. As an example, in string theory there are branes which are sources of various tensor fields. As stated these branes will be treated as matter. We denote the matter term as \(S_m\). Therefore the final action of our main concern is given by

$$\begin{aligned} S=\int d^4 x \sqrt{-g} e^{-\phi } \left( R-\omega (\nabla \phi )^2\right) +S_m. \end{aligned}$$
(3)

In [17], it is shown that the matter can be identified with D-brane [18].

2.1 Isotropic case

In this subsection, we consider the spacetime as being homogeneous and isotropic such that the metric reads

$$\begin{aligned} ds^2=-dt^2+e^{2\alpha (t)}dx_i dx^i, \quad (i=1,2,3). \end{aligned}$$
(4)

The matter is assumed to be a perfect fluid type satisfying \(p=\gamma \rho \) where p is a pressure and \(\rho \) is an energy density, respectively.

Suppose all fields are time dependent only, and from the results of [19], the action can be written as

$$\begin{aligned} S=\int dt e^{3\alpha -\phi } \left( -6\dot{\alpha }^2+6\dot{\alpha }\dot{\phi }- \dot{\phi }^2 -\rho _0 e^{-3(1+\gamma )\alpha +\phi }\right) , \end{aligned}$$
(5)

where we have set \(\omega \) to \(-1\) and a dot (\(\cdot \)) means the derivative with respect to time t. Interestingly, this action is invariant under the change of \(\alpha \), \(\phi \) and \(\gamma \) such as

$$\begin{aligned} \alpha \rightarrow -\alpha ,\;\phi \rightarrow \phi -6\alpha ,\;\gamma \rightarrow -\gamma . \end{aligned}$$
(6)

When there is no matter (\(\rho =0\) and \(\gamma =0\)), this is originally called the SFD. Note that the possible extension of the SFD to nonvanishing \(\gamma \) was already discussed in Ref. [3]. (The authors thank an anonymous reviewer for pointing out this.) In that case the matter is identified with classical string sources. By applying the above changes we see that the scale factor \(e^\alpha \) is replaced by \(e^{-\alpha }\). As we have seen above, by flipping the sign of \(\gamma \), SFD is still applicable to the \(\gamma \ne 0\) case, namely the case of the existence of matter. We will discuss more detail about this case later on. From this invariant property of the action we can generate other solutions from one solution. One of the striking point of SFD is the appearance of two branches, super inflating (or accelerating) and deflating one, respectively. Even though they are disconnected classically, it seems quite natural phenomena to a pre-big-bang cosmology.

Now let us try to find out the classical solution to study the behavior of scale factor and dilaton. If we introduce \(\tau \) such that

$$\begin{aligned} d\tau e^{3\alpha -\phi }=dt, \end{aligned}$$
(7)

we get the following action:

$$\begin{aligned} S=\int d\tau \left( -6\alpha '^2+6\alpha '\phi '-\phi '^2-\rho _0e^{3(1-\gamma )\alpha -\phi } \right) , \end{aligned}$$
(8)

where the prime (\('\)) means the derivative with respect to \(\tau \). In order to simplify the action further, we introduce new variables, X and Y such that

$$\begin{aligned} X= & {} -{1\over 2} \left( 3(1-\gamma )\alpha -\phi \right) , \nonumber \\ Y\,=\, & {} \alpha +{2\gamma \over {1-3\gamma ^2}}X. \end{aligned}$$
(9)

Then, we have the simplified action:

$$\begin{aligned} S=\int d\tau \left( 3(1-3\gamma ^2)Y'^2 -{4\over {1-3\gamma ^2}}X'^2 -\rho _0 e^{-2X}\right) . \end{aligned}$$
(10)

Here, it is easy to see that Y is free of interaction while X is interacting with the potential term. Recalling the SFD, we see X and Y transform under the duality like transformation:

$$\begin{aligned} X\rightarrow X, \quad Y\rightarrow -Y. \end{aligned}$$
(11)

By varying the action we get the following equations of motion:

$$\begin{aligned}&X'' +{\rho _0 (1-3\gamma ^2)\over 4}e^{-2X}=0,\nonumber \\&Y''=0. \end{aligned}$$
(12)

Then the solutions are given by

$$\begin{aligned} X= & {} \log \left[ \sqrt{(1-3\gamma ^2)\rho _0\over {4c}}\sinh (\sqrt{c}\tau +d)\right] ,\nonumber \\ Y\,=\,& {} A\tau , \end{aligned}$$
(13)

where A, c and d are integration constants. By solving a constraint equation

$$\begin{aligned} 3(1-3\gamma ^2)Y'^2 -{4\over {1-3\gamma ^2}}X'^2 +\rho _0 e^{-2X}=0, \end{aligned}$$
(14)

A is determined to be as follows:

$$\begin{aligned} A=\pm \sqrt{4c \over {3(1-3\gamma ^2)^2}}\rightarrow {2\sqrt{c}\over {\sqrt{3}(1-3\gamma ^2)}}. \end{aligned}$$
(15)

We choose \(+\) sign here. For A to be a non-singular value \(\gamma \) should satisfy \(\gamma \ne \pm 1/\sqrt{3}\).

This completes solving the equations of motion. We have found \(\alpha \) and \(\phi \) as a function of \(\tau \). Explicitly, \(\alpha (\tau )\) and \(\phi (\tau )\) are given by

$$\begin{aligned} \alpha (\tau )= & {} {2\sqrt{c} \over {\sqrt{3} (1-3\gamma ^2)}}\tau -{2\gamma \over {1-3\gamma ^2}}\log \left[ \sqrt{(1-3\gamma ^2)\rho _0 \over {4c}}\sinh (\sqrt{c}\tau +d)\right] ,\nonumber \\ \phi (\tau )= & {} 3(1-\gamma )\sqrt{4c \over {3(1-3\gamma ^2)}}\tau +{2(1-3\gamma )\over {1-3\gamma ^2}}\log \left[ \sqrt{(1-3\gamma ^2)\rho _0 \over {4c}}\sinh (\sqrt{c}\tau +d)\right] . \end{aligned}$$
(16)

Since the time t and a new variable \(\tau \) are related by \(dt=e^{3\alpha -\phi } d\tau \), we obtain the following relation by using Eq. (16)

$$\begin{aligned} \int dt =\int d\tau \left( {(1-3\gamma ^2)\rho _0 \over {4c}}\right) ^{ -{1\over {1-3\gamma ^2}}} e^{ {2\sqrt{3c}\gamma \over {1-3\gamma ^2}}\tau } \left( \sinh (\sqrt{c}\tau +d)\right) ^{ -{2\over {1-3\gamma ^2}}}. \end{aligned}$$
(17)

To analyse \(\alpha (\tau )\) as a function of t, let us look at the asymptotic limits of the scale factor and time with respect to \(\tau \). In the limit \(\tau \rightarrow \infty \), we have

$$\begin{aligned} t\sim & {} \left( {4c\over {(1-3\gamma ^2)\rho _0}}\right) ^{ {1\over {1-3\gamma ^2}}}\left( {2\gamma \sqrt{3c}\over {1-3\gamma ^2}}-{2\sqrt{c}\over {1-3\gamma ^2}}\right) ^{-1} e^{ {2(\gamma \sqrt{3}-1)\sqrt{c}\over {1-3\gamma ^2}}\tau }\nonumber \\= & {} \left( {4c\over {(1-3\gamma ^2)\rho _0}}\right) ^{ {1\over {1-3\gamma ^2}}}\left( -{2\sqrt{c}\over {1+\sqrt{3}\gamma }}\right) e^{-{2\sqrt{c} \over {1+\sqrt{3}\gamma }}\tau }, \nonumber \\ e^{\alpha }\sim & {} \left( {4c\over {(1-3\gamma ^2)\rho _0}}\right) ^{ {1\over {1-3\gamma ^2}}} e^{ {2(1-\sqrt{3}\gamma )\sqrt{c}\over {\sqrt{3}(1-3\gamma ^2)}}\tau }=\left( {4c\over {(1-3\gamma ^2)\rho _0}}\right) ^{ {1\over {1-3\gamma ^2}}} e^{{2\sqrt{c}\over {\sqrt{3}(1+\sqrt{3}\gamma )}}\tau }. \end{aligned}$$
(18)

We already have the condition \(\gamma \ne \pm 1/\sqrt{3}\) and \({2\gamma \sqrt{3c}\over {1-3\gamma ^2}}-{2\sqrt{c}\over {1-3\gamma ^2}}=-1/(1+\sqrt{3}\gamma )\) is negative for \(\gamma >-1/\sqrt{3}\) while positive for \(\gamma <-1/\sqrt{3}\). Therefore, since \(\sqrt{c}\) is positive, we see that \(t\rightarrow 0\) as \(\tau \rightarrow \infty \) for \(\gamma >-1/\sqrt{3}\) while \(t\rightarrow \infty \) as \(\tau \rightarrow \infty \) for \(\gamma <-1/\sqrt{3}\), respectively. Using the relations in Eq. (18) the scale factor \(e^\alpha \) can be written as

$$\begin{aligned} e^\alpha\sim & {} \left( {4c\over {(1-3\gamma ^2)\rho _0}}\right) ^{ {1\over {1-3\gamma ^2}}} \left( \left( {4c\over {(1-3\gamma ^2)\rho _0}}\right) ^{ -{1\over {1-3\gamma ^2}}} \left( {2\gamma \sqrt{3c}\over {1-3\gamma ^2}}-{2\sqrt{c}\over {1-3\gamma ^2}} \right) t \right) ^{-1\over {\sqrt{3}}}\nonumber \\= & {} \left( {4c \over {(1-3\gamma ^2)\rho _0}}\right) ^{{1+\sqrt{3} \over {\sqrt{3}(1-3\gamma ^2)}}}\left( -{2\sqrt{c} \over {1+\sqrt{3}\gamma }}\right) ^{-{1\over \sqrt{3}}}t^{-{1\over \sqrt{3}}}. \end{aligned}$$
(19)

As a function of t we see that the scale factor \(e^\alpha \) behaves \(e^\alpha \rightarrow t^{-1/\sqrt{3}}\). Likewise as \(\tau \rightarrow 0\), we have the ralation

$$\begin{aligned} t\sim & {} \left( {4c\over {(1-3\gamma ^2)\rho _0}}\right) ^{ {1\over {1-3\gamma ^2}}} (2\sqrt{c})^{-{2\over {1-3\gamma ^2}}}\left( {1\over \tau }\right) ^{2\over {1-3\gamma ^2}},\nonumber \\ e^\alpha\sim & {} \left( {4c\over {(1-3\gamma ^2)\rho _0}}\right) ^{ {1\over {1-3\gamma ^2}}} (2\sqrt{c})^{-{2\gamma \over {1-3\gamma ^2}}}\left( {1\over \tau }\right) ^{2\gamma \over {1-3\gamma ^2}}. \end{aligned}$$
(20)

Hence, we have \(t\rightarrow \infty \) when \(-1/\sqrt{3}<\gamma <1/\sqrt{3}\) while \(t\rightarrow 0\) when \(\gamma >1/\sqrt{3}\) or \(\gamma < -1/\sqrt{3}\) as \(\tau \rightarrow 0\) . As a function of time t, the scale factor is given by

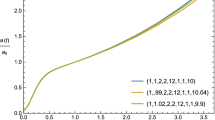
$$\begin{aligned} e^\alpha\sim & {} \left( {4c\over {(1-3\gamma ^2)\rho _0}}\right) ^{ {1\over {1-3\gamma ^2}}} (2\sqrt{c})^{-{2\gamma \over {1-3\gamma ^2}}}\left( \left( {4c\over {(1-3\gamma ^2)\rho _0}} \right) ^{-{1\over {1-3\gamma ^2}}}(2\sqrt{c})^{2\over {1-3\gamma ^2}} t\right) ^\gamma \nonumber \\= & {} \left( {4c \over { (1-3\gamma ^2)\rho _0}}\right) ^{{1-\gamma \over {(1-3\gamma ^2)\rho _0}}}t^\gamma . \end{aligned}$$
(21)

Therefore, we have the scale factor \(e^\alpha \sim t^\gamma \). We summarize that for \(-1/\sqrt{3}<\gamma <1/\sqrt{3}\), the behavior of time t is that \(t\rightarrow 0 (\tau \rightarrow \infty )\) and \(t\rightarrow \infty (\tau \rightarrow 0)\). The scale factor behaves \(e^\alpha \sim t^{-{1/\sqrt{3}}} \) and \(e^\alpha \sim t^\gamma \), respectively. According to the study in [20], this solution has a curvature singularity. From our t and \(\tau \) relation, the singularity might have originated in the behavior of finite running of t for full range of \(\tau \).

2.2 Anisotropic case

In this subsection, the anisotropic spacetime is considered. Even though the present spacetime is observed as homogeneous and isotropic, near the big bang or in the very early universe we can assume different spacetime. We will consider the most simple anisotropic spacetime. The metric of this spacetime is the following:

$$\begin{aligned} ds^2=-dt^2+e^{2\alpha -2\beta }dx^2+e^{2\alpha }dy^2+e^{2\alpha +2\beta }dz^2. \end{aligned}$$
(22)

Here \(\beta \) plays the role of breaking the isotropic property of the spacetime. In this case the action can be written as

$$\begin{aligned} S=\int dt e^{3\alpha -\phi }\left( -6\dot{\alpha }^2+6\dot{\alpha }\dot{\phi }+2\dot{\beta }^2-\dot{\phi }^2-\rho _0 e^{-3(1+\gamma )\alpha +\phi }\right) . \end{aligned}$$
(23)

The above action respects the following symmetry which is an analogue of SFD to the anisotropic spacetime:

$$\begin{aligned} \alpha \rightarrow -\alpha ,\quad \beta \rightarrow -\beta ,\quad \phi \rightarrow \phi -6\alpha ,\quad \mathrm{with}\; \gamma \rightarrow -\gamma . \end{aligned}$$
(24)

Following the same procedure taken in the isotropic case we simplify the action with the new introduction of variables, V and W:

$$\begin{aligned} S=\int d\tau \left( 3(1-3\gamma ^2)V'^2+6\beta '^2-{4\over {1-3\gamma ^2}}W'^2-\rho _0 e^{-2W}\right) , \end{aligned}$$
(25)

where

$$\begin{aligned} V=\alpha +{2\gamma \over {1-3\gamma ^2}}W,\quad -2W=3(1-\gamma )\alpha -\phi . \end{aligned}$$
(26)

The equations of motions for these variables are given by

$$\begin{aligned}&V''=0,\quad \beta ''=0,\nonumber \\&W''+{\rho _0 (1-3\gamma ^2)\over 4}e^{-2W}=0. \end{aligned}$$
(27)

Suppose that \(\rho _0>0\) and \(-1/\sqrt{3}<\gamma < 1/\sqrt{3}\), then the solutions for the above equations of motions are the following:

$$\begin{aligned}&V=A\tau ,\quad \beta =B\tau ,\nonumber \\&W=\log \left[ \sqrt{{\rho _0(1-3\gamma ^2)\over {4c}}}\sinh \sqrt{c}\tau \right] . \end{aligned}$$
(28)

The constraint equation eliminates one of the constants. We find the relation between them as

$$\begin{aligned} A=\sqrt{{4c\over {3(1-3\gamma ^2)^2}}-{2B^2\over {1-3\gamma ^2}}}. \end{aligned}$$
(29)

To be a real value the sign inside the square root is required to be a positive and B should satisfy

$$\begin{aligned} B^2<{2c\over {3(1-3\gamma ^2)}}. \end{aligned}$$
(30)

Hence by rearranging the variables we get

$$\begin{aligned}&\alpha =-{2\gamma \over {1-3\gamma ^2}}\log \left[ \sqrt{{(1-3\gamma ^2)\rho _0 }\over {4c} }\sinh \sqrt{c}\tau \right] ,\nonumber \\&\phi =-{4\over {1-3\gamma ^2}}\log \left[ \sqrt{{(1-3\gamma ^2)\rho _0}\over {4c}}\sinh \sqrt{c}\tau \right] +3(1-\gamma )\sqrt{{4c\over {3(1-3\gamma ^2)}}-{2B^2\over {1-3\gamma ^2}}}\tau ,\nonumber \\&3\alpha -\phi =-{2\over {1-3\gamma ^2}}\log \left[ \sqrt{{(1-3\gamma ^2)\rho _0}\over {4c}}\sinh \sqrt{c}\tau \right] +3\gamma \sqrt{{4c\over {3(1-3\gamma ^2)^2}}-{2B^2\over {1-3\gamma ^2}}}\tau . \end{aligned}$$
(31)

Now the interpretations for the solutions are the following. First let us consider the limit \(\tau \rightarrow \infty \). In this limit, we find

$$\begin{aligned}&t-t_0\sim e^{{-2\sqrt{c} \over {1-3\gamma ^2}}\tau +3\gamma \sqrt{{4c\over {3(1-3\gamma ^2)^2}}-{2B^2\over {1-3\gamma ^2}}}\tau },\nonumber \\&e^{\alpha \pm \beta }\sim e^{{-2\gamma \over {1-3\gamma ^2}}\tau +\sqrt{{4c\over {3(1-3\gamma ^2)^2}}-{2B^2\over {1-3\gamma ^2}}}\tau \pm B\tau }\sim (t-t_0)^{{{ -{2\gamma \over {1-3\gamma ^2}}+\sqrt{{4c\over {3(1-3\gamma ^2)^2}}-{2B^2\over {1-3\gamma ^2}}}\pm B}\over {-{2\sqrt{c}\over {1-3\gamma ^2}}+3\gamma \sqrt{ {4c\over {3(1-3\gamma ^2)^2}}-{2B^2\over {1-3\gamma ^2}} } }}},\nonumber \\&e^\alpha \sim e^{-{2\gamma \over {1-3\gamma ^2}}\tau +\sqrt{{4c\over {3(1-3\gamma ^2)}}-{2B^2\over {1-3\gamma ^2}}}\tau }\sim (t-t_0)^{{{ -{2\gamma \over {1-3\gamma ^2}}+\sqrt{{4c\over {3(1-3\gamma ^2)^2}}-{2B^2\over {1-3\gamma ^2}}}}\over {-{2\sqrt{c}\over {1-3\gamma ^2}}+3\gamma \sqrt{ {4c\over {3(1-3\gamma ^2)^2}}-{2B^2\over {1-3\gamma ^2}} } }}}. \end{aligned}$$
(32)

If we consider B and c with \(-1/\sqrt{3}<\gamma <1\sqrt{3}\) such that

$$\begin{aligned} -2\sqrt{c}/(1-3\gamma ^2)+3\gamma \sqrt{4c/(3(1-3\gamma ^2))-2B^2/(1-3\gamma ^2) }<0, \end{aligned}$$
(33)

the limit \(\tau \rightarrow \infty \) corresponds to the finite time \(t\rightarrow t_0\). Since the time t runs in finite range for a given parameter \(\tau \) ranging \(-\infty<\tau <\infty \) the spacetime might have a curvature singularity. Moreover as time approaches that point \(t_0\) (this time would indicate a big bang) the scale factors \(e^{\alpha \pm \beta }\) and \(e^\alpha \) behave differently showing the anisotropic spacetime.

In the limit \(\tau \rightarrow 0\), we have the following relations

$$\begin{aligned}&t-t_0\sim \tau ^{-2{\gamma \over {1-3\gamma ^2}}},\nonumber \\&e^{\alpha \pm \beta }\sim \tau ^{-2{\gamma \over {1-3\gamma ^2}}}\sim (t-t_0)^{\gamma },\nonumber \\&e^\alpha \sim \tau ^{-2{\gamma \over {1-3\gamma ^2}}}\sim (t-t_0)^{\gamma }. \end{aligned}$$
(34)

So we have \(t\rightarrow \infty \) as \(\tau \rightarrow 0\). We see that the scale factors \(e^{\alpha \pm \beta }\) and \(e^\alpha \) behave the same way corresponding to the isotropic spacetime.

In the limit \(\tau \rightarrow -\infty \), we have the following relations

$$\begin{aligned}&t-t_0\sim e^{{2\sqrt{c} \over {1-3\gamma ^2}}\tau +3\gamma \sqrt{{4c\over {3(1-3\gamma ^2)^2}}-{2B^2\over {1-3\gamma ^2}}}\tau },\nonumber \\&e^{\alpha \pm \beta }\sim e^{{2\gamma \over {1-3\gamma ^2}}\tau +\sqrt{{4c\over {3(1-3\gamma ^2)^2}}-{2B^2\over {1-3\gamma ^2}}}\tau \pm B\tau }\sim (t-t_0)^{{{ {2\gamma \over {1-3\gamma ^2}}+\sqrt{{4c\over {3(1-3\gamma ^2)^2}}-{2B^2\over {1-3\gamma ^2}}}\pm B}\over {{2\sqrt{c}\over {1-3\gamma ^2}}+3\gamma \sqrt{ {4c\over {3(1-3\gamma ^2)^2}}-{2B^2\over {1-3\gamma ^2}} } }}},\nonumber \\&e^\alpha \sim e^{{2\gamma \over {1-3\gamma ^2}}\tau +\sqrt{{4c\over {3(1-3\gamma ^2)}}-{2B^2\over {1-3\gamma ^2}}}\tau }\sim (t-t_0)^{{{ {2\gamma \over {1-3\gamma ^2}}+\sqrt{{4c\over {3(1-3\gamma ^2)^2}}-{2B^2\over {1-3\gamma ^2}}}}\over {{2\sqrt{c}\over {1-3\gamma ^2}}+3\gamma \sqrt{ {4c\over {3(1-3\gamma ^2)^2}}-{2B^2\over {1-3\gamma ^2}}}}}}. \end{aligned}$$
(35)

In summary, we see that in the limit \(\tau \rightarrow \pm \infty \), t goes to \(t_0\) and the scale factors \(e^{\alpha \pm \beta }\) and \(e^\alpha \) behave differently which represents anisotropic universe while the scale factors \(e^{\alpha \pm \beta }\) and \(e^\alpha \) become \(t^\gamma \) for \(\tau \rightarrow 0\) (\(t\rightarrow \infty \)) which represents isotropic universe. This model is consistent in the sense that the current universe is isotropic. In the later section we find that the quantum mechanical analysis helps pick out \(\gamma \).

3 Wheeler–De Witt equation

In this section we study the canonical quantization. We construct the Wheeler–De Witt equation [8] based on the action above as a way of quantization. The wave function as a solution makes it possible to interpret the universe as quantum mechanically: the wave function of the universe. In this way, we finally calculate the probability of the universe. In fact, here, we calculate the transition rate between the two branches: pre- and post-big-bang universe [9–11] (for a review see [12]).

First, from the Sect. 2, the Lagrangian for the action can be read:

$$\begin{aligned} L=3(1-3\gamma ^2)Y'^2-{4\over {1-3\gamma ^2}}X'^2-\rho _0e^{-2X}=0. \end{aligned}$$
(36)

The canonical momenta for each X and Y are obtained by applying \(p_q=\partial L /\partial \dot{q}\). They are given by

$$\begin{aligned} p_X=-{8\over {1-3\gamma ^2}}X',\quad p_Y=6(1-3\gamma ^2)Y'. \end{aligned}$$
(37)

Under the SFD, \(p_X\) is invariant while \(p_Y\) changes it sign. With the inclusion of solutions X and Y, the two conjugate momenta read

$$\begin{aligned} p_X= & {} -{8\over {1-3\gamma ^2}}X'=-{8\sqrt{c}\over {1-3\gamma ^2}}{\cosh (\sqrt{c}\tau +d)\over \sinh (\sqrt{c}\tau +d)},\nonumber \\ p_Y= & {} 6(1-3\gamma ^2)Y'=12{\sqrt{c\over 3}}=4\sqrt{3c}. \end{aligned}$$
(38)

The Hamiltonian is thus obtained by the relation \(H=p_q \dot{q} -L\) and then the result is given by

$$\begin{aligned} H={1\over {12(1-3\gamma ^2)}}p_Y^2-{(1-3\gamma ^2)\over 16}p_X^2+\rho _0 e^{-2X}. \end{aligned}$$
(39)

The quantization is implemented through the introduction of operators for each conjugate momentum \(p_X\) and \(p_Y\) such as \(p_X=i\partial _X\) and \(p_Y=i\partial _Y\). By putting these operators in the Hamiltonian we get the Wheeler–De Witt equation

$$\begin{aligned} \left( -{1\over {12(1-3\gamma ^2)}}\partial _Y^2+{(1-3\gamma ^2)\over 16} \partial _X^2+\rho _0 e^{-2X}\right) \Psi (X,Y)=0. \end{aligned}$$
(40)

By dividing by \((1-3\gamma ^2)/16\) and in order to apply the separation of variables we put \(\Psi (X,Y)\) as

$$\begin{aligned} \Psi (X,Y)=\Psi (X) e^{i {\sqrt{3}(1-3\gamma ^2)\over 2} kY}=e^{i k'Y}, ~~\mathrm{where}\,k'={\sqrt{3}(1-3\gamma ^2)\over 2}k. \end{aligned}$$
(41)

Then, we simplify the equation further and obtain the following equation:

$$\begin{aligned} \left( k^2+\partial _X^2+{16\rho _0\over {1-3\gamma ^2}}e^{-2X}\right) \Psi (X)=0. \end{aligned}$$
(42)

This is a well known Bessel equation. The solution is \(\Psi (X)=Z_{\pm ik}(4\sqrt{1/(1-3\gamma ^2)}e^{-X})\) where \(Z_{\pm k}\) is a linear combination of Bessel functions of order \(\pm ik\). In the limit \(z\rightarrow 0\) for Bessel function \(J_\nu (z)\), we see \(J_\nu (z)\rightarrow z^\nu \). So we choose \(\nu =-ik\). The solution for the pre-big-bang branch near singularity is given by

$$\begin{aligned} \Psi (X,Y)=J_{-ik}\left( 4\sqrt{{\rho _0\over {1-3\gamma ^2} }} e^{-X}\right) e^{i{\sqrt{3}\over 2}(1-3\gamma ^2)k Y}. \end{aligned}$$
(43)

The momentum conjugate is given by

$$\begin{aligned} p_Y\Psi =i {\partial \Psi \over {\partial Y}}=-k'\Psi =- {\sqrt{3}\over 2}(1-3\gamma ^2)k\Psi . \end{aligned}$$
(44)

When \(X\rightarrow \infty \) (near singularity) the potential term, \(\rho _0e^{-X}\), becomes negligible, so it is a free wave. For this case the wave solution looks like \(\Psi _{+\infty }^{(\pm )}\sim e^{-ik(Y'\mp X)}=e^{-ik({\sqrt{3}\over 2}(1-3\gamma ^2)Y\mp X)}\). The eigenvalue of \(p_X\) is given by \(\lim _{X\rightarrow \infty }p_X\Psi _{+\infty }^{(\pm )}=i\partial _X \Psi _{+\infty }^{(\pm )}=\mp k \Psi _{+\infty }^{(\pm )} \). Hence, the wave functions \(\Psi ^{(+)}_{+\infty }\) and \(\Psi ^{(-)}_{+\infty }\) represent that of the pre- and post-big-bang branches, respectively. Here Y is timelike and the minisuperspace metric is \(-dY^2+dX^2\). When \(X\rightarrow -\infty \) we get the following:

$$\begin{aligned} \lim _{X\rightarrow -\infty }\Psi =\Psi ^{(+)}_{-\infty }+\Psi ^{(-)}_{-\infty }, \end{aligned}$$
(45)

where

$$\begin{aligned} \Psi ^{(\pm )}_{-\infty }=\left( 8\pi \sqrt{ {\rho _0\over {1-3\gamma ^2}}}e^{-X}\right) ^{-{1\over 2}} e^{-i k {\sqrt{3}\over 2}(1-3\gamma ^2)Y \pm i 4 \sqrt{\rho _0\over {1-3\gamma ^2}}e^{-X}\pm i {\pi \over 4}\pm {\pi \over 2}k}. \end{aligned}$$
(46)

The transition rate R between the two branches is then given by

$$\begin{aligned} R={|\Psi ^-|^2\over |\Psi ^+|^2}=e^{-2\pi k}=e^{-2\pi {2\over {\sqrt{3}(1-3\gamma ^2)}}k'}. \end{aligned}$$
(47)

If we insert the value \(k'\) with the help of the following relation

$$\begin{aligned} p_Y=6(1-3\gamma ^2)Y'=- k' =6(1-3\gamma ^2)2\sqrt{c\over 3}{1\over {1-3\gamma ^2}}=4\sqrt{3}c, \end{aligned}$$
(48)

we see that the tunneling rate becomes divergent when \(\gamma \rightarrow 1/\sqrt{3}\). As an interpretation this means that after the transition the universe is dominantly made up of a perfect type matter with \(\gamma \) close to the value \(1/\sqrt{3}\). In this case the scale factor behaves like \(t^\gamma \sim t^{{1\over \sqrt{3}}+\epsilon }\) where \(\epsilon<<1\).

We now discuss the Wheeler–De Witt equation for the anisotropic case. Since the action is given by

$$\begin{aligned} S=\int d\tau \left( 3(1-3\gamma ^2)Y'^2+6\beta '^2-{4\over {1-3\gamma ^2}}X'^2-e^{-2X}\right) , \end{aligned}$$
(49)

the corresponding conjugate momenta are then read

$$\begin{aligned} P_Y=6(1-3\gamma ^2)Y', \quad P_\beta =12\beta ',\quad P_X=-{8\over {1-3\gamma ^2}}X'. \end{aligned}$$
(50)

The Hamiltonian becomes

$$\begin{aligned} H={P_Y^2\over {12(1-3\gamma ^2)}}+{P_\beta ^2\over 24}-{{1-3\gamma ^2}\over 16}P_X^2+\rho _0e^{-2X}. \end{aligned}$$
(51)

By introducing \(P_X=-i\partial _X\), \(P_\beta =-i\beta \), and \(P_Y=-i\partial _Y\), the Wheeler–De Witt equation \(H\Psi (X,Y,\beta )=0\) becomes

$$\begin{aligned} \left( {k_Y^2\over {12(1-3\gamma ^2)}}+{k_\beta ^2 \over 24}+{{1-3\gamma ^2}\over 16}\partial _X^2+\rho _0e^{-2X}\right) \Psi (X)=0, \end{aligned}$$
(52)

where we put \(\Psi (X,Y,\beta )=\Psi (X)e^{ik_Y+ik_\beta }\). By introducing K such that \(K^2={4k_Y^2\over {3(1-3\gamma ^2)}}+{2k_\beta ^2\over {3(1-3\gamma ^2)}}\) we have

$$\begin{aligned} \left( \partial _X^2+{16\rho _0\over {1-3\gamma ^2}}e^{-2X}\right) \Psi (X)=0 \end{aligned}$$
(53)

and the solution is \(\Psi (X,Y,\beta )=Z_{\pm iK}(z)e^{-ik_Y-ik_\beta }\) where \(z=4\sqrt{{\rho _0\over {1-3\gamma ^2}}}e^{-X}\). We can proceed the same steps as was taken above and calculate the probability for this case and we see that the anisotropic effect is not effective in our transition rate between pre- and post-big bang. As was seen above the probability becomes maximum when \(\gamma \) approaches to \(1/\sqrt{3}\).

4 Results and discussion

The cosmological behavior has been obtained for general \(\gamma \) for both isotropic and anisotropic spacetime. The solution of scale factor has a curvature singularity and the pre- and post-big-bang branches are disconnected by the singularity. They can not be smoothly connected classically. As a way to solve this, so called graceful problem, the quantum approach is introduced. In this work the canonical quantization has been proceeded using the Wheeler–De Witt equation. By solving the Wheeler–De Wit equation the wave function of the universe is obtained. We identify each corresponding wave function as the two branches: pre- and post-big-bang branch, respectively. The probability of tunneling between the two branches has been studied and it diverges as \(\gamma \) approaches the boundary value: \(\gamma =1/\sqrt{3}\). This turns out to suggest that the most probable universe being created/observed is dominated by this specific matter. It would be interesting to consider the third quantization and Hartle-Hawking’s boundary condition [21] instead of Vilenkin’s one [22] studied in our work.

5 Conclusions

In this work we have considered scalar–tensor theory coming from low energy string action with matter. The action can be considered as a truncated low energy string theory action. In some sense it is Brans–Dicke theory with the parameter \(\omega \) fixed: \(\omega =-1\). The matter is treated as a perfect fluid type satisfying the relation \(p=\gamma \rho \), where p and \(\rho \) are pressure and energy density, respectively. When \(\gamma \) is replaced by \(-\gamma \), we have seen that the scale factor is still applicable.

We have discussed the somewhat general cosmological model of isotropic as well as anisotropic spacetime. It is open to consider further the anisotropic spacetime such as Taub–NUT, for example.