Abstract
A Picture fuzzy set (PFS) is a set used to quantify uncertainty with the condition that the sum of degrees of the membership, the neutral membership, and the non-membership is equal to or less than one. Utilizing PFS and decision makers’ degrees of familiarity with the decision making problem in terms of confidence level, the paper proposes some novel aggregating operators such as confidence Picture fuzzy weighted averaging, confidence Picture fuzzy ordered weighted averaging, confidence Picture fuzzy hybrid averaging, confidence Picture fuzzy weighted geometric, confidence Picture fuzzy ordered weighted geometric and confidence Picture fuzzy hybrid geometric. Some desirable properties are also discussed. Finally, a multi criteria group decision making method has been presented by utilizing the proposed aggregating operators and applying it to solve a green supplier selection problem. Sensitivity analysis has been conducted to examine the effect of different combinations of decision makers’ confidence levels on the aggregated values, while comparative analysis has also been conducted to validate the consistency of the proposed aggregation operators over some other existing operators. Results are computed, tabulated, and plotted graphically. Some concluding remarks are also provided.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Decision making is the cognitive process generally used in upstream of both industries and academia resulting in the selection of a course of action among a set of alternative scenario. In other words, decision making is the study of identifying and choosing alternatives based on the values and preferences of the decision maker. Analysis of individual decision is concerned with the logic of decision making (or reasoning) which can be rational or irrational on the basis of explicit assumptions. Logical decision making is an important part of all science based professions, where specialists apply their knowledge in a given area to make informed decisions. However, it has been proved that the decision made collectively tend to be more effective than decision made by an individual. Therefore group decision making is a collective decision making process in which individuals’ decisions are grouped together to solve a particular problem. But sometimes, when individuals make decisions as part of a group, there may be a tendency to exhibit biasness towards discussing shared information, as opposed to unshared information. To overcome such kind of error in decision making process, highly experience, dynamic and brilliant experts or practitioners are indeed required to participate and they should have much knowledge in the concerned area of judgment. Moreover, decision making is a nonlinear and recursive process because most of decisions are made by moving back and forth between the choice of criteria and the identification of alternatives. Every decision is made within a decision environment, which is defined as the collection of information, alternatives, values, and preferences available at the time of the decision. Since both information and alternatives are constrained because the time and effort to gain information or identify alternatives are limited. In fact decisions must be made within this constrained environment. Today, the major challenge of decision making is uncertainty, and a major goal of decision analysis is to reduce uncertainty. Recent robust decision efforts have formally integrated uncertainty and criterion subjectivity into the decision making process. Due to such kind of uncertainty and subjectivity involved in evaluative criterion, fuzziness has come into the picture. The area of decision making has attracted the interest of many researchers and management practitioners, is still highly debated as there are many multi criteria decision making (MCDM) methods which may yield different results when they are applied on exactly the same data. This leads to a decision making inconsistency. A detailed literature survey for the applicability of picture fuzzy set (PFS) in MCDM has been provided in the next section.
1.1 Literature survey
In decision science, MCDM is a very useful research topic, which can be defined as the solution of best alternatives according to criteria. Due to imprecise data, there are various difficulties and uncertainty in MCDM problems. Therefore, to control it, Zadeh [33] introduced the definition of a fuzzy set (FS) which contains elements with their membership values ranging in the closed interval [0, 1]. Following its invention, it is now widely used in a variety of fields such as linguistics, decision making, image processing, cluster analysis, and so on. Unfortunately, a FS does not include the non-membership degree of any element from the set under consideration. So, by including membership degree along with non-membership degree, [1] defined a novel FS named the “intuitionstic fuzzy set (IFS)” with the condition that the sum of these two degrees not exceed one. IFS is important as it has applications in different areas such as pattern recognition, image segmentation, decision making, etc. After that, researchers showed interest in IFS, and it has become a more popular technique to deal with impreciseness and vagueness in the data. Consequently, Atanassov studied some operations having interaction, union, compliment, algebraic sum, algebraic product, geometric sum, geometric product, score, and accuracy functions [30, 31]. Researchers utilised IFS very efficiently, but it has been observed that in some real-life problems whose answers are required in the form of yes, no, abstain, and refusal, they cannot be handled by IFS. To handle such problems, the concept of Picture fuzzy set (PFS) was introduced by Cuong [3], which includes membership, non-membership, and neutral degrees with the condition that the sum of these three degrees does not exceed one. PFS is becoming a more popular research topic by incorporating multi-techniques for different operators, operational laws, similarity measures, distance measures, score and accuracy functions [4, 22, 26]. Wei [27] studied the averaging and geometric aggregation operators under the PFS environment. As an application of PFS, Singh [19] explored the correlation coefficients, Son [20] and Thoung and Son [21] analysed clustering algorithms, while Wei [25] evaluated the cross-entropy of decision making problems. Later on, Garg [7] studied some Picture fuzzy aggregation operators. Zhang et al. [34] proposed a MCGDM method for solving a green supplier selection problem. Many authors have developed different aggregation operators for solving a variety of decision-making problems under the PFS environment [2, 5, 6, 9, 11,12,13, 15, 17, 18, 23, 24, 28, 29].
1.1.1 Motivation of this study
From literature survey, it has been observed that the decision makers give their suggestions based on the performance of alternatives after their aggregation process through a suitable aggregating operator on different criteria, which is called the familiarity degree or confidence levels of experts with the evaluation objects. From the above mentioned literature, it is clearly seen that the noticed aggregating operators do not consider familiarity degree in terms of confidence level under a PFS environment. However, Yu [32] incorporated the idea of confidence level and developed novel aggregation operators under IFS environment. Then, Garg [8] used the concept of confidence level under PyFS environment to solve any MCGDM problem. Afterthat, Joshi and Gegov [10] integrated the concept of confidence level under q-rung orthopair fuzzy set (q-ROFS) environment. Apart from these, some of the researchers incorporate confidence levels under different fuzzy environments [14, 16]. Their contributions represent significant advancements in the field and offer promising avenues for further research in decision-making and aggregation methodologies within complex and uncertain contexts.
1.1.2 Main contribution of this study
From above motivation and findings from the literature survey, it becomes evident that, to the best of our knowledge, there exists a notable gap in research related to the development of aggregation operators specifically modified for the PFS environment while considering confidence levels. No prior investigation has addressed this specific context. In light of this observed shortcoming, the primary objective of this paper is to fill this by introducing a set of innovative aggregation operators within the PFS framework that are explicitly designed to incorporate confidence levels. This represents the core idea of the study. The central contribution of this paper lies in the creation and thorough exploration of a series of aggregation operators collectively referred to as “confidence Picture fuzzy aggregating operators”. These operators are denoted as CPFWA, CPFOWA, CPFHA, CPFWG, CPFOWG, and CPFHG. The paper not only defines and formulates these operators but also precisely investigates their essential properties, providing a comprehensive understanding of their behavior and capabilities. Additionally, the paper explores specific scenarios and special cases where these operators can be effectively applied, further enhancing their practical utility. Moreover, recognizing the broader need for practical decision-making tools in the context of MCGDM, this paper introduces a dedicated MCGDM method. This method leverages the newly developed aggregation operators to address complex group decision-making problems, extending the applicability of these operators to real-world decision scenarios. In summary, this paper not only addresses a notable research gap by introducing aggregation operators modified to the PFS environment with a focus on confidence levels but also goes the extra mile by thoroughly examining their properties and applicability, making a valuable contribution to the field of decision science. The introduction of the MCGDM method further enhances the practical significance of the proposed operators in the realm of group decision-making.
The remaining part of the presented paper is as follows: In Sect. 2, some basic definitions are provided such as Picture fuzzy set, operational laws, score and accuracy functions. Section 3, develops CPFWA, CPFOWA, CPFHA, CPFWG, CPFOWG and CPFHG operators with some of their essential properties. In Sect. 4, we discussed a MCGDM method. After that, to exemplify the proposed MCGDM approach, an illustrative example for selecting green supplier has been discussed in Sect. 5. To show the stability and consistency, section also provides sensitivity and comparative analyses with some existing aggregation operators. Finally, paper ends with some concluding remarks and possible future extensions of this work.
2 Basic concepts
This section briefly recalls some basic concepts about Picture fuzzy set (PFS), score and accuracy functions for Picture fuzzy values (PFVs) and arithmetic operational laws for Picture fuzzy numbers (PFNs).
2.1 Picture fuzzy set (PFS)
Definition 1
(Cuong [3]) Let X be a universal set, then the PFS on X is defined as:
where \(\mu _{P}(x), \eta _{P}(x), \nu _{P}(x) \in [0,1]\) are called as the degrees of positive, neutral and negative memberships of x in P, respectively with condition \(0\le \mu _{P}(x)+\eta _{P}(x)+\nu _{P}(x)\le 1\), \(\forall x\in X\). The degree of refusal membership of x in P is then defined as \(\pi _{P}(x)=1-(\mu _{P}(x)+\eta _{P}(x)+\nu _{P}(x)),~~\forall x\in X\). For sake of convenience, \(p=(\mu _p,\eta _p,\nu _p)\) is called as Picture fuzzy number (PFN).
2.2 Score and accuracy functions for PFVs
Definition 2
(Wei [27]) Let \(p=(\mu ,\eta ,\nu )\) be a PFN then (S(p)) and (H(p)) are called the score and accuracy functions of p, respectively and defined as \(S(p)=\mu -\eta -\nu \), and \(H(p)=\mu +\eta +\nu \). Let \(p_1\) and \(p_2\) be two PFNs then using score and accuracy functions, the ranking of these numbers can be done using following criterion.
-
(a)
if \(S(p_1)>S(p_2)\), then \(p_1\succ p_2\)
-
(b)
if \(S(p_1)=S(p_2)\), then
-
(i)
if \(H(p_1)>H(p_2)\), then \(p_1\succ p_2\),
-
(ii)
if \(H(p_1)<H(p_2)\), then \(p_1\prec p_2\),
-
(iii)
if \(H(p_1)=H(p_2)\), then \(p_1=p_2\).
-
(i)
2.3 Arithmetic operational laws for PFNs
Definition 3
(Wei [27]) Let \(p=(\mu ,\eta ,\nu )\), \(p_1=(\mu _1,\eta _1,\nu _1)\) and \( p_2=(\mu _2,\eta _2,\nu _2)\) be three PFNs, and let \(\lambda \) be a positive real number. Then,
-
(i)
\( p_1\oplus p_2=(\mu _1+\mu _2-\mu _1\mu _2, \eta _1\eta _2, \nu _1\nu _2),\)
-
(ii)
\( p_1\otimes p_2=(\mu _1\mu _2, \eta _1+\eta _2-\eta _1\eta _2, \nu _1+\nu _2-\nu _1\nu _2),\)
-
(iii)
\({\lambda }p\)=\((1-(1-\mu )^{\lambda }, \eta ^{\lambda }, \nu ^{\lambda })\),
-
(iv)
\(p^{\lambda }\)=\((\mu ^{\lambda }, 1-(1-\eta )^{\lambda }, 1-(1-\nu )^{\lambda })\).
Using these basic operations, Picture fuzzy weighted averaging (PFWA) and Picture fuzzy weighted geometric (PFWG) aggregation operators for a collection of PFNs \( p_j (1\le j\le n)\) are defined as follows(Wei [27]):
where \(\omega = (\omega _1,\omega _2,\ldots ,\omega _n)^T\) is the associated normalized weight vector.
3 Novel Picture fuzzy aggregation operator with confidence levels
In this section, we proposed series of weighted averaging and geometric aggregation operators using arithmetic operational laws under confidence levels in the PFS environment.
3.1 CPFWA operator
Definition 4
Let \(p_j=(\mu _{p_j},\eta _{p_j},\nu _{p_j})(j=1,2,\ldots ,n)\) be a collection of n PFNs and \(l_j\) be the associated confidence levels of PFNs \(p_j\) such that \(0\le l_j\le 1\), then the CPFWA operator is defined as:
where \(\omega =(\omega _1, \omega _2,\ldots ,\omega _n)^T\) be the weight vector of PFNs \((p_1, p_2,\ldots ,p_n)\) such that \(\omega _j\in [0,1]\) and \(\displaystyle \sum _{j=1}^{n} \omega _j=1\).
Remark 1
The CPFWA operator is simplified to the PFWA operator if \(l_1=l_2=\cdots =l_n=1\), then
Theorem 1
Let \(p_j=(\mu _j,\eta _j,\nu _j),\) \((j=1,2,\ldots ,n)\) be n PFNs and \(l_j\) be the associated confidence levels of \(p_j\) then the aggregated value by CPFWA operator is also a PFN and
Proof
To prove this theorem, mathematical induction is used.
For \(n=2\):
Then,
which is true.
Now suppose that Eq. (4) holds for \(n=k\), that is
then, we will prove Eq. (4) for \(n=k+1\). By the operational laws, for \(n=k+1\) we have
i.e. Eq. (4) holds for \(n=k+1\) and as a result, Eq. (4) is true for all n. Then,
Now, it will be proved that the aggregated value by CPFWA operator is a PFN.
As \(p_j=(\mu _j,\eta _j,\nu _j)\) for all j is PFN, thus \(0\le {\mu _j,\eta _j,\nu _j}\le 1\) and \(\mu _j+\eta _j+\nu _j\le 1\).
Therefore,
\(0\le (1-\mu _j)\le 1\) which implies that \(0\le \displaystyle \prod _{j=1}^{n}(1-\mu _j)^{l_j\omega _j}\le 1\) and hence \(0\le 1-\displaystyle \prod _{j=1}^{n}(1-\mu _j)^{l_j\omega _j}\le 1\); \(0\le \displaystyle \prod _{j=1}^{n}\eta _j^{l_j\omega _j}\le 1\) and \(0\le \displaystyle \prod _{j=1}^{n}\nu _j^{l_j\omega _j}\le 1\).
Again,
Thus, the aggregated value by CPFWA operator is a PFN and this completes the proof. \(\square \)
In the following, an example is provided to illustrate the calculation process.
Example 1
Let \(p_1=\langle 0.70,(0.56,0.12,0.20)\rangle \), \(p_2=\langle 0.90,(0.62,0.14,0.23)\rangle \) and \(p_3=\langle 0.80,(0.47,0.33,0.10)\rangle \) be three PFNs with associated confidence levels and the weights vector that corresponds to them is \(\omega =(0.25,0.40,0.35)^T\), then
By Eq. (4),
Some essential properties followed by CPFWA operator are proved hereafter.
Property 1
(Idempotency) If \(\langle l_j,p_j\rangle =\langle l_0,p_0\rangle =\langle l_0,(\mu _0,\eta _0,\nu _0)\rangle \) for all j i.e. \(\mu _j=\mu _0,\eta _j=\eta _0,\nu _j=\nu _0\) and \(l_j=l_0\) then
Proof
Given that \(\langle l_j,p_j\rangle =\langle l_0,p_0\rangle =\langle l_0,(\mu _0,\eta _0,\nu _0)\rangle \) for all j and \(\displaystyle \sum _{j=1}^{n} \omega _j=1\), then by Theorem 1,
This completes the proof. \(\square \)
Example 2
If \(\langle l_j,p_j\rangle =\langle 0.70,(0.56,0.12,0.20)\rangle \) for all \(j=1,2,3\) i.e. \(\mu _j=0.56,\eta _j=0.12,\nu _j=0.20\) and \(l_j=0.70\) then
Proof
Given that \(\langle l_j,p_j\rangle =\langle 0.70,(0.56,0.12,0.20)\rangle \) for all \(j=1,2,3\) and \(\displaystyle \sum _{j=1}^{3} \omega _j=1\), then by property 1,
\(\square \)
Property 2
(Boundedness) Let \(p^- = (\text {min}_j{\{l_j\mu _j\}},\text {max}_j{\{l_j\eta _j\}},\text {max}_j{\{l_j\nu _j\}})\) and \(p^+=(\text {max}_j{\{l_j\mu _j\}},\text {min}_j{\{l_j\eta _j\}},\text {min}_j{\{l_j\nu _j\}})\) then
Proof
As \(\text {min}_j{\mu _j}\le \mu _j\le \text {max}_j{\mu _j},~~\forall j=1,2,\ldots ,n\), then
Further more,
\(\text {min}_j{\{\eta _j\}}\le {\{\eta _j\}}\le \text {max}_j{\{\eta _j\}},~~\forall j=1,2,\ldots ,n\) this implies that,
Similarly,
Then we have,
Therefore, by definition of score function, we can conclude
This completes the proof. \(\square \)
Example 3
Let \(\langle l_1,p_1\rangle =\langle 0.70,(0.56,0.12,0.20)\rangle \), \(\langle l_2,p_2\rangle =\langle 0.90,(0.62,0.14,0.23)\rangle \) and \(\langle l_3,p_3\rangle =\langle 0.80,(0.47,0.33,0.10)\rangle \) be three PFNs and the weights vector that corresponds to them is \(\omega =(0.25,0.40,0.35)^T\).
Proof
Here,
By using Definition 2, \(S(p^-)=0.376-0.264-0.207=-0.095.\) Similarly,
By using Definition 2, \(S(p^+)=0.558-0.084-0.08=0.394.\)
By using Definition 2,
Thus, by ranking results provided in Definition 2, we get
\(\square \)
Property 3
(Monotonicity) If \(p_j\) and \(p'_j\) are two distinct sets of PFNs such that \(p_j\le p'_j,~~\forall j\) then
Proof
Since \(p_j\le p'_j,~~\forall j\),
\(\Rightarrow \mu _p\le \mu _p'; \eta _p\ge \eta _p'; \nu _p\ge \nu _p', ~~\forall j\). Then
Furthemore,
Similarly,
Following this way, we have
This completes the proof. \(\square \)
Example 4
Let \(p=\{\langle 0.70,(0.56,0.12,0.20)\rangle , \langle 0.90,(0.62,0.14,0.23)\rangle \), \(\langle 0.80,(0.47,0.33,0.10)\rangle \}\), \(p'=\{\langle 0.70,(0.60,0.10,0.18)\rangle , \langle 0.90,(0.64,0.12,0.20)\rangle \), \(\langle 0.80,(0.49,0.29,0.09)\rangle \}\) are two distinct sets of PFNs and the weights vector that corresponds to them is \(\omega =(0.25,0.40,0.35)^T\).
Then,
Proof
For the first collection of PFNs,
Similarly, for the second collection of PFNs,
The score value of first and second collection are 0.0056 and 0.0799, respectively. Therefore, by ranking results provided in definition 2, we get
\(\square \)
3.2 CPFOWA operator
Definition 5
Let \(p_j=(\mu _{p_j},\eta _{p_j},\nu _{p_j})(j=1,2,\ldots ,n)\) be a collection of n PFNs and \(l_j\) be the associated confidence levels of PFNs \(p_j\) such that \(0\le l_j\le 1\). Then CPFOWA operator can be defined as:
where, \(w=(w_1,w_2,\ldots ,w_n)^T\) be the weights vector of CPFOWA operator such that \(w_j\in [0,1]\), \(\displaystyle \sum _{j=1}^{n}w_j=1\) and \((\delta {(1)},\delta {(2)},\ldots ,\delta {(n)})\) is a permutation of \((1,2,\ldots ,n)\) such that \(p_{\delta {(j-1)}}\ge p_{\delta {(j)}}\) for any j.
Remark 2
The CPFOWA operator is simplified to the Picture fuzzy ordered weighted averaging (PFOWA) operator if \(l_1=l_2=\cdots =l_n=1\), then
Theorem 2
Let \(p_j=(\mu _j,\eta _j,\nu _j), j=1,2,\ldots ,n\) be n PFNs and \(l_j\) be the associated confidence levels then the aggregated value by CPFOWA operator is also a PFN and
Proof
The proof of Theorem 2 is same as that of Theorem 1. \(\square \)
In the following, an example is provided to illustrate the calculation process.
Example 5
Let \(p_1=\langle 0.70,(0.56,0.12,0.20)\rangle \), \(p_2=\langle 0.90,(0.62,0.14,0.23)\rangle \) and \(p_3=\langle 0.80,(0.47,0.33,0.10)\rangle \) be three PFNs with associated confidence levels and the weights vector that corresponds to them is \(w=(0.25,0.40,0.35)^T\). Then the score values of each PFN is \(S(p_1)=0.56-0.12-0.20=0.24\), \(S(p_2)=0.62-0.14-0.23=0.25\) and \(S(p_3)=0.47-0.33-0.10=0.04\).
Thus \(p_2>p_1>p_3\) and therefore \(p_{\delta (1)}=\langle 0.90,(0.62,0.14,0.23)\rangle \), \(p_{\delta (2)}=\langle 0.70,(0.56,0.12,0.20)\rangle \) and \(p_{\delta (3)}=\langle 0.80,(0.47,0.33,0.10)\rangle \).
Now,
Then by Eq. (10),
3.3 CPFHA operator
Definition 6
Let \(p_j=(\mu _{p_j},\eta _{p_j},\nu _{p_j})(j=1,2,\ldots ,n)\) be a collection of n PFNs and \(l_j\) be the associated confidence levels of PFNs \(p_j\) such that \(0\le l_j\le 1\). Then CPFHA operator can be defined as:
where \({\dot{p}}_{\delta {(j)}}\) is the \(j^{th}\) largest weighted PFVs \({\dot{p}}_j({\dot{p}}_j=n\omega _jp_j,j=1,2,\ldots ,n)\), \(w=(w_1,w_2,\ldots ,w_n)^T\) is the weighted vector of the CPFHA operator, such that \(w_j\in [0,1]\), \(\displaystyle \sum _{j=1}^{n}w_j=1\). \(\omega =(\omega _1, \omega _2,\ldots ,\omega _n)^T\) be the weights vector of these PFNs such that \(\omega _j\in [0,1]\), \(\sum _{j=1}^{n} \omega _j=1\) and n is called the balancing coefficient using it a balance between numbers is maintained.
Remark 3
The CPFHA operator is simplified to the Picture fuzzy hybrid averaging (PFHA) operator if \(l_1=l_2=\cdots =l_n=1\), then
Theorem 3
Let \(p_j=(\mu _j,\eta _j,\nu _j), j=1,2,\ldots ,n\) be n PFNs and \(l_j\) be the associated confidence levels then the aggregated value by CPFHA operator is also a PFN and
Proof
The proof of Theorem 3 is same as that of Theorem 1. \(\square \)
Example 6
Let \(p_1=\langle 0.70,(0.56,0.12,0.20)\rangle \), \(p_2=\langle 0.90,(0.62,0.14,0.23)\rangle \) and \(p_3=\langle 0.80,(0.47,0.33,0.10)\rangle \) be three PFNs with associated confidence levels and the weights vector that corresponds to them is \(w=(0.25,0.40,0.35)^T\). Then, \({\dot{p}}_1=(0.4598,0.2039,0.2991)\), \({\dot{p}}_2=(0.6869,0.0945,0.1714)\) and \({\dot{p}}_3=(0.4866,0.3122,0.0891)\).
By calculating score values of each PFN, we have \(S({\dot{p}}_1)=-0.0432\), \(S({\dot{p}}_2)=0.4210\) and \(S({\dot{p}}_3)=0.0852\).
Thus, \(p_2>p_3>p_1\) and therefore \(p_{\delta (1)}=\langle 0.90,(0.62,0.14,0.23)\rangle \), \(p_{\delta (2)}=\langle 0.80,(0.47,0.33,0.10)\rangle \) and \(p_{\delta (3)}=\langle 0.70,(0.56,0.12,0.20)\rangle \).
Now, we have
Then by Eq. (13), we have
3.4 CPFWG operator
Definition 7
Let \(p_j=(\mu _{p_j},\eta _{p_j},\nu _{p_j})(j=1,2,\ldots ,n)\) be a collection of n PFNs and \(l_j\) be the associated confidence levels of PFNs \(p_j\) such that \(0\le l_j\le 1\). Then CPFWG operator is defined as:
where \(\omega =(\omega _1, \omega _2,\ldots ,\omega _n)^T\) be the weight vector of PFNs \(p_j\) such that \(\omega _j\in [0,1]\) and \(\displaystyle \sum _{j=1}^{n} \omega _j=1\).
Remark 4
The CPFWG operator is simplified to the Picture fuzzy weighted geometric (PFWG)operator if \(l_1=l_2=\cdots =l_n=1\), then
Theorem 4
Let \(p_j=(\mu _j,\eta _j,\nu _j), j=1,2,\ldots ,n\) be n PFNs and \(l_j\) be the associated confidence levels of PFNs \(p_j\) then the aggregated value by applying CPFWG operator is a PFN and
where \(\omega _j\) is the weights vector associate with \(p_j\) such that \(\omega _j \in [0,1]\) and \(\displaystyle \sum _{j=1}^{n}\omega _j=1\).
Proof
Theorem is proved with the help of mathematical induction.
-
(1)
First, the conclusion is proved for \(n=2\). Since
$$\begin{aligned} (p_1)^{l_1\omega _1}= & {} ({\mu _1}^{l_1\omega _1},1-({1-\eta _1})^{l_1\omega _1},1-({1-\nu _1})^{l_1\omega _1})\\ (p_2)^{l_2\omega _2}= & {} ({\mu _2}^{l_2\omega _2},1-({1-\eta _2})^{l_2\omega _2},1-({1-\nu _2})^{l_2\omega _2}) \end{aligned}$$then we have,
$$\begin{aligned}{} & {} CPFWG(\langle l_1,p_1\rangle ,\langle l_2,p_2\rangle )=(p_1)^{l_1\omega _1}\otimes (p_2)^{l_2\omega _2}\\{} & {} \quad =\big ((\mu _1)^{l_1\omega _1}(\mu _2)^{l_2\omega _2},1-({1-\eta _1})^{l_1\omega _1}({1-\eta _2})^{l_2\omega _2},1-({1-\nu _1})^{l_1\omega _1}({1-\nu _2})^{l_2\omega _2}\big ) \end{aligned}$$So, conclusion is true for \(n=2\).
-
(2)
Now, suppose Eq. (16) holds for \(n=k\), i.e.
$$\begin{aligned}{} & {} CPFWG(\langle l_1,p_1\rangle ,\langle l_2,p_2\rangle ,\ldots ,\langle l_k,p_k\rangle )\\{} & {} \quad =(p_1)^{l_1\omega _1}\otimes (p_2)^{l_2\omega _2}\otimes \cdots \otimes (p_k)^{l_k\omega _k}\\{} & {} \quad =\Bigg (\displaystyle \prod _{j=1}^{k}\mu _j^{l_j\omega _j}, 1-\prod _{j=1}^{k}(1-\eta _j)^{l_j \omega _j}, 1-\prod _{j=1}^{k}(1-\nu _j)^{l_j \omega _j}\Bigg ) \end{aligned}$$
then, we will prove that Eq. (16) also holds for \(n=k+1\). By the operational laws, we have
i.e. for \(n=k+1\), Eq. (16) holds universally. As a result, Eq. (16) is true for all n. Then,
In the following, an example is provided to illustrate the calculation process. \(\square \)
Example 7
Let \(p_1=\langle 0.70,(0.56,0.12,0.20)\rangle \), \(p_2=\langle 0.90,(0.62,0.14,0.23)\rangle \) and \(p_3=\langle 0.80,(0.47,0.33,0.10)\rangle \) be three PFNs with associated confidence levels and the weights vector that corresponds to them is \(\omega =(0.25,0.40,0.35)^T\) then
Then by Eq. (16), we have
Property 4
- (1) (Idempotency):
-
If \(p_j=p_0=\langle l_0,(\mu _0,\eta _0,\nu _0\rangle \) for all j i.e. \(\mu _j=\mu _0,\eta _j=\eta _0,\nu _j=\nu _0\) and \(l_j=l_0\) then
$$\begin{aligned} CPFWG(\langle l_1, p_1\rangle ,\langle l_2, p_2\rangle ,\ldots ,\langle l_n,p_n\rangle )={p_0}^{l_0} \end{aligned}$$(17) - (2) (Boundedness):
-
Let \(p^-=(\text {min}_j{\{l_j,\mu _j\}},\text {max}_j{\{l_j,\eta _j\}},\text {max}_j{\{l_j,\nu _j\}})\) and \(p^+=(\text {max}_j{\{l_j,\mu _j\}},\text {min}_j{\{l_j,\eta _j\}},\text {min}_j{\{l_j,\nu _j\}})\) then
$$\begin{aligned} p^-\le CPFWG(\langle l_1, p_1\rangle ,\langle l_2, p_2\rangle ,\ldots ,\langle l_n,p_n\rangle )\le p^+ \end{aligned}$$(18) - (3) (Monotonicity):
-
If \(p_j\) and \(p'_j\) are two distinct sets of PFNs such that \(p_j\le p'_j\) for all j then
$$\begin{aligned} CPFWG(\langle l_1, p_1\rangle ,\langle l_2, p_2\rangle ,\ldots ,\langle l_n,p_n\rangle )\le CPFWG(\langle l_1, p'_1\rangle ,\langle l_2, p'_2\rangle ,\ldots ,\langle l_n,p'_n\rangle ) \end{aligned}$$(19)
3.5 CPFOWG operator
Definition 8
Let \(p_j=(\mu _{p_j},\eta _{p_j},\nu _{p_j})\),\((j=1,2,\ldots ,n)\) be a collection of n PFNs and \(l_j\) be the associated confidence levels of PFNs \(p_j\) such that \(0\le l_j\le 1\). Then CPFOWG operator is defined as:
where \(w=(w_1,w_2,\ldots ,w_n)^T\) is the weights vector of CPFOWG operator such that \(w_j\in [0,1]\), \(\displaystyle \sum _{j=1}^{n}w_j=1\) and \((\delta {(1)},\delta {(2)},\ldots ,\delta {(n)})\) is a permutation of \((1,2,\ldots ,n)\) such that \(p_{\delta {(j-1)}}\ge p_{\delta {(j)}}\) for any j.
Remark 5
The CPFOWG operator is simplified to the Picture fuzzy ordered weighted geometric(PFOWG) operator if \(l_1=l_2=\cdots =l_n=1\), then
Theorem 5
Let \(p_j=( \mu _j,\eta _j,\nu _j), j=1,2,\ldots ,n\) be n PFNs and \(l_j\) be the associated confidence levels then the aggregated value by applying CPFOWG operator is a PFN and
Proof
The proof of Theorem 5 is the same as that of Theorem 4. \(\square \)
In the following, an example is provided to illustrate the calculation process.
Example 8
Let \(p_1=\langle 0.70,(0.56,0.12,0.20)\rangle \), \(p_2=\langle 0.90,(0.62,0.14,0.23)\rangle \) and \(p_3=\langle 0.80,(0.47,0.33,0.10)\rangle \) be three PFNs with associated confidence levels and the weights vector that corresponds to them is \(w=(0.25,0.40,0.35)^T\). Then the score values of each PFN is \(S(p_1)=0.56-0.12-0.20=0.24\), \(S(p_2)=0.62-0.14-0.23=0.25\) and \(S(p_3)=0.47-0.33-0.10=0.04\).
Thus \(p_2>p_1>p_3\) and therefore \(p_{\delta (1)}=\langle 0.90,(0.62,0.14,0.23)\rangle \), \(p_{\delta (2)}=\langle 0.70,(0.56,0.12,0.20)\rangle \) and \(p_{\delta (3)}=\langle 0.80,(0.47,0.33,0.10)\rangle \).
Now, we have
Then by Eq. (22), we have
3.6 CPFHG operator
Definition 9
Let \(p_j=(\mu _{p_j},\eta _{p_j},\nu _{p_j})(j=1,2,\ldots ,n)\) be a set of n PFNs and \(l_j\) be the associated confidence levels of PFNs \(p_j\) such that \(0\le l_j\le 1\). Then CPFHG operator is defined as:
where, \({\dot{p}}_{\delta {(j)}}\) is the \(j^{th}\) largest of the weighted Picture fuzzy values \({\dot{p}}_j({\dot{p}}_j=(p_j)^{n\omega _j},j=1,2,\ldots ,n)\), \(w=(w_1,w_2,\ldots ,w_n)^T\) is the weighted vector of the CPFHG operator such that \(w_j\in [0,1]\), \(\displaystyle \sum _{j=1}^{n}w_j=1\). \(\omega =(\omega _1, \omega _2,\ldots ,\omega _n)^T\) be the weights vector of these PFNs such that \(\omega _j\in [0,1]\), \(\displaystyle \sum _{j=1}^{n} \omega _j=1\) and n is the balancing coefficient, which plays a role of balance.
Remark 6
The CPFHG operator is simplified to the Picture fuzzy weighted geometric (PFHG) operator if \(l_1=l_2=\cdots =l_n=1\), then
Theorem 6
Let \(p_j=(\mu _j,\eta _j,\nu _j)\), \(j=1,2,\ldots ,n\) be a set of n PFNs and \(l_j\) be the associated confidence levels then the aggregated value by applying CPFHG operator is also a PFN and
Proof
The proof of Theorem 6 is same as that of Theorem 4. \(\square \)
In the following, an example is provided to illustrate the calculation process.
Example 9
Let \(p_1=\langle 0.70,(0.56,0.12,0.20)\rangle \), \(p_2=\langle 0.90,(0.62,0.14,0.23)\rangle \) and \(p_3=\langle 0.80,(0.47,0.33,0.10)\rangle \) be three PFNs with associated confidence levels and the weights vector that corresponds to them is \(w=(0.25,0.40,0.35)^T\). Then \({\dot{p}}_1=(0.4598,0.2039,0.2991)\), \({\dot{p}}_2=(0.6869,0.0945,0.1714)\) and \({\dot{p}}_3=(0.4866,0.3122,0.0891).\)
By calculating score values of each PFN, we have \(S({\dot{p}}_1)=-0.0432\), \(S({\dot{p}}_2)=0.4210\) and \(S({\dot{p}}_3)=0.0852\).
Thus \(p_2>p_3>p_1\) and therefore \(p_{\delta (1)}=\langle 0.90,(0.62,0.14,0.23)\rangle \), \(p_{\delta (2)}=\langle 0.80,(0.47,0.33,0.10)\rangle \) and \(p_{\delta (3)}=\langle 0.70,(0.56,0.12,0.20)\rangle \).
Now, we have
Then by Eq. (25), we have
4 MCGDM approach with confidence levels
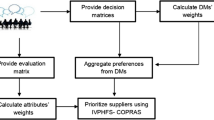
Let us consider a MCGDM problem having a collection of n distinct alternatives \(B=\{B_1,B_2,\ldots ,B_n\}\) and m criteria \(D=\{D_1,D_2,\ldots ,D_m\}\) with weights vector \(\omega =(\omega _1,\omega _2,\ldots ,\omega _m)^T\) satisfying the condition \(\omega _j\in [0,1]\) and \(\displaystyle \sum _{j=1}^{m}\omega _j=1\). Assume that there are r set of decision makers denoted by \(A=\{A_1,A_2,\ldots ,A_r\}\), whose weight vector is \(\tau =(\tau _1,\tau _2,\ldots ,\tau _r)^T\) satisfying \(\tau _s>0,~s=1,2,\ldots ,r\) and \(\displaystyle \sum _{s=1}^{r}\tau _s=1\) which are evaluating each alternative \(B_i\) with respect to the criteria \(D_j\) in the form of PFNs. The following steps are executed to implement proposed MCGDM method for evaluating the best alternative.
Step 1. For each decision maker \(A_r\), collect the information about each alternative \(B_i\) under the criteria \(D_j\) and represent it in the form of PFNs \(C^s=\langle l_{ij}^s,(\mu _{ij}^s,\eta _{ij}^s,\nu _{ij}^s)\rangle _{n\times m}\) for \(i=1,2,\ldots ,n;~j=1,2,\ldots ,m\) and \(s=1,2,\ldots ,r\) as
where \(l_{ij}^s\), \((0\le l_{ij}^s\le 1)\) denotes the decision makers’ level of confidence that they are familiar with the subject under discussion.
Step 2. The following transformation is used to normalized distinct types of criteria.
Step 3. Aggregate all the r Picture fuzzy decision matrices \(C^s,~~s=1,2,\ldots r\) as provided by r decision makers into a collective Picture fuzzy decision matrix by employing proposed CPFWA operator
or the CPFWG operator
Step 4. Calculate \({\dot{p}}_{ij}=n\omega _jp_{ij}\) for PFHA operator or \({\dot{p}}_{ij}=(p_{ij})^{n\omega _j}\) for PFHG operator.
Step 5. Calculate the values of score \(S(p_{ij})\) and accuracy \(H(p_{ij})\) for each \({\dot{p}}_{ij}\) \((i=1,2,\ldots ,n;~j=1,2,\ldots ,m)\).
Step 6. Aggregate PFNs \(p_{ij}\) by using PFHA operator
or the PFHG operator
Step 7. Calculate the values of score \(S(p_i)\) and accuracy \(H(p_i)\) for each alternative \(B_i(i=1,2,\ldots ,n)\).
Step 8. Finally, all the alternatives are ranked based on the score and accuracy values, and best alternative is then select.
The steps of proposed MCGDM problem is depicted in Fig. 1.
5 Illustrative example
To illustrate the proposed method, a green supplier selection problem is adapted from Zhang et al. [34]) and analysed by using developed novel aggregating operators. In this problem, there are five alternatives \(B_i(i=1,2,3,4,5)\). Three experts \(C^s(s=1,2,3)\) are working as decision makers, whose weights vector is \(\tau =(0.35,0.2,0.45)^T\). There are mainly four criteria \(D_j,(j=1,2,3,4)\) is considered with weights vector \(\omega =(0.25,0.18,0.35,0.22)^T\) to assess these green suppliers having following details:
-
1.
Price factor \(D_1\),
-
2.
Delivery factor \(D_2\),
-
3.
Environmental factors \(D_3\) and
-
4.
Product quality factor \(D_4\).
5.1 Procedural steps for group decision making
5.1.1 CPFWA operator
Step 1. The experts provide information in the form of PFN matrices \(Q^s=\langle l_{ij}^s,(\mu _{ij}^s,\eta _{ij}^s,\nu _{ij}^s)\rangle \) \((s=1,2,3)\), with weights vector \(\tau =(0.35,0.2,0.45)^T\). The provided information is presented in Tables 1, 2 and 3.
Step 2. All the criteria are benefit type, so normalization step is not required.
Step 3. Aggregate all the three Picture fuzzy decision matrices \(C^s(s=1,2,3)\) into the single comprehensive Picture decision matrix C by employing proposed CPFWA operator, where \(\tau =(0.35,0.2,0.45)^T\). The computed values are shown in Table 4.
Step 4. Calculate \({\dot{p}}_{ij}=n\omega _jp_{ij}\), where \(\omega =(0.25,0.18,0.35,0.22)^T\), then we have
Step 5. Calculate the score values:
Thus,
Step 6. Utilize PFHA operator to aggregate all preference values, where \(w=(0.25,0.18,0.35,0.22)^T\). The computed values are shown in Table 5.
Step 7. Since \(S(B_1)=-0.0586\), \(S(B_2)=0.1888\), \(S(B_3)=-0.0387\), \(S(B_4)=-0.2318\) and \(S(B_5)=0.1560\).
Step 8. Hence, \(S(B_2)>S(B_5)>S(B_3)>S(B_1)>S(B_4)\). Thus, \(B_2\) is best alternative.
5.1.2 CPFWG operator
Step 1 and Step 2 are similar to Sect. 5.1.1.
Step 3. Aggregate all the Picture fuzzy decision matrices \(C^s(s=1,2,3)\) into the single comprehensive Picture decision matrix \(C'\) by employing proposed CPFWG operator, where \(\tau =(0.35,0.2,0.45)^T\). The computed values are shown in Table 6.
Step 4. Calculate \({\dot{p}}_{ij}=(p_{ij})^{n\omega _j}\), where \(\omega =(0.25,0.18,0.35,0.22)^T\), then we have
Step 5. Calculate the score values:
Thus,
Step 6. Utilize PFHG aggregation operator to aggregate all preference values, where \(w=(0.25,0.18,0.35,0.22)^T\). The computed values are shown in Table 7.
Step 7. Since \(S(B_1)=0.3027\), \(S(B_2)=0.2223\), \(S(B_3)=0.2419\), \(S(B_4)=0.0676\) and \(S(B_5)=0.1859\).
Step 8. Hence, \(S(B_1)>S(B_3)>S(B_2)>S(B_5)>S(B_4)\). Thus, \(B_1\) is best alternative.
5.2 Sensitivity analysis
In this section, sensitivity analysis has been conducted to examine the effect of different combination of three decision makers’ confidence levels \(l=(l_{ij}^1,l_{ij}^2,l_{ij}^3),~~i=1,2,3,4; j=1,2,3\) on the final decision making when CPFWA and CPFWG operators are used to solve current MCGDM problem. The computed results are tabulated in Tables 8 and 9 and plotted in Figs. 2 and 3 for CPFWA and CPFWG operators respectively by taking all the considered combinations. From Tables 8 and 9 and Figs. 2 and 3, it is observed that alternatives have different score values for different combinations of l. From all the selected combinations, the best alternatives are always \(B_2\) and \(B_1\) for CPFWA and CPFWG operators, respectively, while \(B_4\) is the worst alternative for the both the operators. Thus, we can conclude that both operators are consistent and provide stable results for varying confidence levels.
5.3 Comparative analysis
To investigate the stability of the proposed aggregating operators, a comparative analysis has been done in this section. To compare the results, calculation is done for PFWA, PFOWA, PFHA, PFWG, PFOWG and PFHG operators [27]. The computed results are shown in Table 10 and plotted in Fig. 4.
From the comparative analysis, following observations have been noticed.
-
(i)
All the existing methods under PFS environment have been developed in the assumptions that all the experts are 100% familiar with the evaluated objects. But these types of limitations are not fully met in dealing with real life problems. In other side, proposed approach considered the situation where the experts are not fully familiar with evaluated objects.
-
(ii)
The ranking order obtained from different operators depends upon the type of the aggregation operator and the algebraic operations applied. From Table 10, it is observed that, the ranking results obtained from existing operators are differ from the proposed method. Because, these existing operators for PFN does not consider confidence level of decision maker, which reflects the familiarity of the decision maker with the problem under consideration. Whereas, the proposed operators incorporated the idea of confidence level in decision making.
-
(iii)
Fig. 4 represents the score values of each alternative for different operators, and here the scale of grid is \(-1\) to 1. In this figure, the alternatives \(B_1\), \(B_2\), \(B_3\), \(B_4\) and \(B_5\) are represented by the green, red, purple, yellow and blue lines, respectively. Here ranking of alternatives is done, according to the occurrence of score values of each alternative, from center to circumference in the particular direction of the operators applied. As an example, if we move center to circumference in the direction of PFWA operator, then first we will reach in order to yellow, green, purple, red and blue lines, and hence the ranking order of alternatives will be \(B_5>B_2>B_3>B_1>B_4\). Similar observations can be done for other operators.
-
(iv)
When the confidence level \(l=1\) is applied to the proposed CPFWA, CPFOWA, CPFHA, CPFWG, CPFOWG, and CPFHG operators, they undergo a transformation, effectively becoming the existing PFWA, PFOWA, PFHA, PFWG, PFOWG, and PFHG operators, respectively. This transition occurs because, at a confidence level of 1, the two sets of operators become equivalent, thereby simplifying the choice between them. Consequently, this equivalence provides a streamlined approach in decision-making and aggregation, making the decision process more straightforward and consistent.
Thus, it has been observed that the proposed aggregating operators are more general, flexible, stable and consistent in comparison to some existing aggregating operators and provide more realistic results to handle MCGDM problems under PFS environment.
6 Conclusions
The paper investigated a MCGDM problem in a PFS environment by involving the familiarity degree of an expert through a confidence level and utilising arithmetic operational laws. The paper developed some novel aggregating operators such as CPFWA, CPFOWA, CPFHA, CPFWG, CPFOWG, and CPFHG. The proposed aggregation operators not only take into account the evaluation information of the decision makers in terms of PFNs but also consider the degrees to which they are familiar with the problem under consideration in terms of confidence level. In addition, some desirable properties and special cases for the proposed aggregating operators are also discussed. Then, a MCGDM problem of green supplier selection based on novel aggregating operators was examined. Finally, to examine the validity and effectiveness of the proposed aggregation operators, sensitivity and comparative analyses have also been conducted. The main notice points for the considered problem and proposed aggregation operators are as follows:
-
(a)
All the novel and existing aggregating operators provide the same conclusion, i.e., the alternative \(B_4\) is the worst.
-
(b)
The proposed novel aggregating operators are more general, flexible, stable, and consistent, and they provide more realistic results by incorporating decision makers’ familiarity degree with the problem in terms of confidence levels.
Due to the broader acceptance of PFS, we will make an effort in the future to apply the concept of PFS to solve real-life problems such as fuzzy cluster analysis, uncertain programming, pattern recognition, and so on. In addition, we will also focus on developing some new operational laws and aggregation operators for PFS.
References
Atanassov, K.T.: Intuitionstic fuzzy set. Fuzzy Sets. Syst. 2, 89–96 (1986)
Ates, F., Akay, D.: Some Picture fuzzy Bonferroni mean operators with their application to multicriteria decision making. Int. J. Intell. Syst. (2020). https://doi.org/10.1002/int.22220
Cuong, B.C.: Picture fuzzy sets. J. Comput. Sci. Cybern. 30, 409–420 (2014)
Dutta, P.: Medical diagnosis based on distance measures between Picture fuzzy sets. Int. J. Fuzzy Syst. 7(4), 15–36 (2018)
Feng, M., Geng, Y.: Some Novel Picture 2-tuple linguistic Macluarin symmetric mean operators and their application to multi attribute decision making. Symmetry (2019). https://doi.org/10.3390/sym11070943
Ganie, A.H., Singh, S.: A Picture fuzzy similarity measure based on direct operations and novel multi-attribute decision-making. Neural Comput. Appl. 33, 9199–9219 (2021)
Garg, H.: Some Picture fuzzy aggregation operators and their application to multi criteria decision making. Arab. J. Sci. Eng. 42(12), 5275–5290 (2017)
Garg, H.: Confidence levels based Pythagorean fuzzy aggregation operators and theirs application to application to decision-making process. Comput. Math. Organ. Theory (2017). https://doi.org/10.1007/s10588-017-9242-8
Jana, C., Senapati, T., Pal, M., Yager, R.-R.: Picture fuzzy dombi aggregation operators: application to MADM process. Appl. Soft Comput. (2018). https://doi.org/10.1016/j.asoc.2018.10.021
Joshi, B.P., Gegov, A.: Confidence levels q-rung orthopair fuzzy aggregation operators and its applications to MCDM problems. Int. J. Intell. Syst. (2019). https://doi.org/10.1002/int.22203
Khalil, A.M., Li, S.G., Garg, H., Li, H., Ma, S.: New operators on interval valued Picture fuzzy set. Interval-valued Picture fuzzy soft sets and their applications. IEEE Access 7(1), 51236–51253 (2019)
Khan, S., Abdullah, S., Ashraf, S.: Picture fuzzy aggregation information based on Einstein operations and their applications in decision making. Math. Sci. 13, 213–229 (2019)
Khan, S., Abdullah, A., Abdullah, L., Ashraf, S.: Logrithmic aggregation operators of picture fuzzy numbers for multi-attribute decision making problems. Mathematics (2019). https://doi.org/10.3390/math7070608
Liu, P., Ali, Z., Mahmood, T.: Archimedean aggregation operators based on complex pythagorean fuzzy sets using confidence levels and their application in decision making. Int. J. Fuzzy Syst. 25, 42–58 (2023)
Luo, S., Xing, L.: Picture fuzzy interaction partitioned heronian aggregation operators for Hotel selection. Mathematics (2020). https://doi.org/10.3390/math8010003
Qiyas, M., Naeem, M., Khan, N.: Confidence levels complex q-Rung orthopair fuzzy aggregation operators and its application in decision making problem. Symmetry 14(12), 2638 (2022)
Seikh, M.R., Mandal, U.: Some Picture fuzzy aggregation operators based on frank \(t\)-norm and \(t\)-conorm: application to MADM process. Informatica 45, 447–461 (2021)
Si, A., Das, S., Kar, S.: Picture fuzzy set-based decision-making approach using Dempster–Shafer theory of evidence and grey relation analysis and its application in COVID-19 medicine selection. Soft Comput. (2021). https://doi.org/10.1007/s00500-021-05909-9
Singh, P.: Correlation coefficients for Picture fuzzy sets. J. Intell. Fuzzy Syst. 27, 2857–2868 (2014)
Son, L.H.: DPFCM: a novel distributed Picture fuzzy clustering method on Picture fuzzy sets. Expert Syst. Appl. 2, 51–66 (2015)
Thong, N.T., Son, L.H.: HIFCF: an effective hybrid model between Picture fuzzy clustring and intuationstic fuzzy recommender systems for medical diagnosis. Expert Syst. Appl. 42, 3682–3701 (2015)
Wang, C., Zhou, X., Tu, H., Tao, S.: Some geometric aggregation operators based on Picture fuzzy sets and their applications in multiple attribute decision making. Ital. J. Pure Appl. Math. 37, 477–492 (2017)
Wang, R., Li, Y.: Picture hesitant fuzzy set and its application to multi criteria decision-making. Symmetry (2018). https://doi.org/10.3390/sym10070295
Wang, R., Wang, J., Gao, H., Wei, G.: Methods for MADM with Picture fuzzy Muirhead Mean operators and their application for evaluating the financial investment risk. Symmetry (2018). https://doi.org/10.3390/sym11010006
Wei, G.W.: Picture fuzzy cross-entropy for multiple attribute decision making problems. J. Bus. Econ. Manag. 17(4), 491–502 (2016)
Wei, G.: Picture fuzzy aggregation operators and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 33, 713–724 (2017)
Wei, G.: Some cosine similarity measure for Picture fuzzy sets and their applications to strategic decision making. Informatics 28(3), 547–564 (2017)
Wei, G.: Picture fuzzy Hamacher aggregation operators and their applications to multi attribute decision making. Fandamenta Inform. 157, 271–320 (2018)
Wei, G., Lu, M., Gao, H.: Picture fuzzy heronian mean aggregation operators in multiple attribute decision making. Int. J. Knowl. Based Intell. Syst. 22, 167–175 (2018)
Xu, Z.S., Yager, R.R.: Some geometric aggregation operators based on intuitionstic fuzzy sets. Int. J. Gen. Syst. 35, 417–433 (2006)
Xu, Z.: Intuitionistic fuzzy aggregation operators. IEEE Trans. Fuzzy Syst. 14(6), 1176–1189 (2008)
Yu, D.: Intuitionstic fuzzy information aggregation under confidence levels. Appl. Soft Comput. 19, 147–160 (2014)
Zadeh, L.A.: Fuzzy set. Inf. Contr. 8, 338–353 (1965)
Zhang, S., Wei, G., Gao, H., Wei, C., Wei, Y.: Edas method for multiple criteria group decision making with Picture fuzzy information and its application to green supplier selections. Technol. Econ. 25(6), 1123–1128 (2019)
Acknowledgements
The authors are thankful to the anonymous referees for providing their valuable comments and suggestions to improve the quality of the paper.
Funding
During this research no funding was received.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Ethical approval
This article does not contain any studies with human participants or animals preformed by any of the authors.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Punetha, T., Komal Confidence Picture fuzzy hybrid aggregation operators and its application in multi criteria group decision making. OPSEARCH 61, 1404–1440 (2024). https://doi.org/10.1007/s12597-023-00720-6
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12597-023-00720-6