Introduction

Thermal lensing is a major issue affecting the performance, stability, and efficiency of solid-state lasers. The thermal lens is a consequence of thermal gradients that occur in the laser medium during the absorption of light and its subsequent relaxation [1,2,3,4,5]. Minimizing and quantifying the thermal lens effect is critical to improving the stability and reliability of DPSSLs, which were used in several technological applications [6,7,8,9,10]. To mitigate the thermal lens effect, different strategies have been suggested. One of them involves the use of double-end pumping geometry, which has a great deal of potential for reducing the thermal effects because it increases the stability range of the laser resonator and reduces thermal loading by distributing the pump source among the ends of the laser crystal [1, 11, 12]. Another approach involves utilizing a pump beam with an annular-shaped intensity profile to produce a more uniform temperature distribution within the pump region, as well as a particular constant temperature distribution within the inner ring of the pump beam with an intensity null [13]. Annular beams may expand the applications of laser technology, particularly at the nanoscale, enhancing lithography accuracy, extending laser materials processing techniques, and generating novel structures in materials. Additionally, the annular profile is essential in laser heat treatment and laser hardening processes at which temperature is the leading factor [14]. The dynamical thermal effects have not yet been specified; therefore, several studies have been conducted on the thermal effects associated with solid-state lasers.

Several previous studies have discussed analytical and numerical methods for thermal lensing in solid crystals under single-end pumping with different pump beam intensity profiles [15,16,17,18,19]. Utilizing the double-end pump geometry, several studies have been conducted to reduce the thermal effects in the laser medium [20,21,22,23,24,25,26]. Another method for reducing thermal effects is to use an annular-shaped pump profile. Utilizing the annular-shaped pump profile, a simple analytical expression for the temperature distribution and thermal lens focal length in the laser medium was derived [27]. The use of an annular-shaped pump beam in conjunction with an aperture was demonstrated to achieve the TEM00 mode in an end-pumped Nd:YVO4 laser with high efficiency [13]. Analytical solutions to the thermoelastic and heat equations were obtained for materials with low optical absorption. This system of equations demonstrated profiles that described the temperature distribution, surface displacement, stresses, and optical path within a sample excited by an annular-shaped laser beam distribution with a thick-disk geometry [28].

For the heat conduction process in the laser rod, most of the analysis methods are designed to solve the steady-state heat conduction process utilizing single-end-pumped configuration. In this work, and based on our previous results [29], a model was proposed to simulate a lens-like effect as a major challenge associated with annular-shaped beam end-pumped configurations for solid-state lasers. The temperature-independent thermal conductivity case (m = 0) was assumed to derive the expression of thermal lensing for solid-state laser rods in double-end pump cavity. The calculated results provide an enhancement as compared with the results reported in the works of literature [30].

Mathematical model

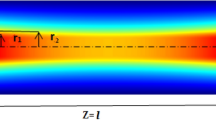
Based on our previous work [29], the temperature difference between the edge of a solid-state laser rod pumped by a laser diode in a double-end pumping geometry by a beam with an annular-shaped profile and a generic point (r,z) as illustrated in Fig. 1 is determined as follows:

$$\begin{aligned} \Delta T\left( {r,z} \right) & = \left\{ {\frac{{\eta _{h} \alpha T_{0}^{m} \left( {m + 1} \right)}}{{4\pi k_{0} }}\left( {P_{{inL}} e^{{ - \alpha z}} + P_{{inR}} e^{{ - \alpha \left( {l - z} \right)}} } \right)A + \left[ {T_{c} + \frac{{\eta _{h} \alpha }}{{2\pi r_{0} h}}\left( {P_{{inL}} e^{{ - \alpha z}} + P_{{inR}} e^{{ - \alpha \left( {l - z} \right)}} } \right)} \right]^{{m + 1}} } \right\}^{{\frac{1}{{m + 1}}}} \\ & \quad - \left\{ {T_{c} + \frac{{\eta _{h} \alpha }}{{2\pi r_{0} h}}\left( {P_{{inL}} e^{{ - \alpha z}} + P_{{inR}} e^{{ - \alpha \left( {l - z} \right)}} } \right)} \right\} \\ \end{aligned}$$
(1)

where

$$A = \left\{ {\begin{array}{*{20}l} {\frac{{r_{2}^{2} - r_{1}^{2} + r_{2}^{2} \ln \left( {\frac{{r_{0}^{2} }}{{r_{2}^{2} }}} \right) - r_{1}^{2} \ln \left( {\frac{{r_{0}^{2} }}{{r_{1}^{2} }}} \right)}}{{r_{2}^{2} - r_{1}^{2} }}} \hfill & {0 \le r \le r_{1} } \hfill \\ {\frac{{r_{2}^{2} - r^{2} + r_{2}^{2} \ln \left( {\frac{{r_{0}^{2} }}{{r_{2}^{2} }}} \right) - r_{1}^{2} \ln \left( {\frac{{r_{0}^{2} }}{{r^{2} }}} \right)}}{{\left( {r_{2}^{2} - r_{1}^{2} } \right)}}} \hfill & {r_{1} < r \le r_{2} } \hfill \\ {\ln \left( {\frac{{r_{0}^{2} }}{{r^{2} }}} \right)} \hfill & {r_{2} < r \le r_{0} } \hfill \\ \end{array} } \right.$$
(2)

\(m\), \({ }T_{0}\), and \(k_{0} = k\left( {T_{0} } \right)\) offer the best fit of the data, \(\eta_{h}\) is the fractional thermal load,\(P_{inL}\) and \(P_{inR}\) are the incident pump powers on the left and right end faces of the laser rod, respectively, \(h\) is the heat transfer coefficient at the rod edge, and \(T_{c}\) is the temperature that surrounds it. \(r_{1}\) and \(r_{2}\) are the inner and outer radii of the pump beam, respectively, while \(r_{0}\) is the rod radius.

Fig. 1
figure 1

Pump profile representation along the laser rod axis

Full size image

The formation of a thermal lens in solid-state lasers is influenced by several factors, including temperature- and birefringence-related changes in the refractive index, as well as the thermal expansion that affects the length of the laser rod [23], considering the refractive index impact in the thermal lens induced by the temperature gradient rather than the change in the optical path length caused by thermal expansion or crystal stress [27]. Thermal-induced focal length can be evaluated from

$$f_{th} \left( r \right) = \frac{2\pi r}{{\lambda \left( {{\raise0.7ex\hbox{${d\Delta \emptyset }$} \!\mathord{\left/ {\vphantom {{d\Delta \emptyset } {dr}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${dr}$}}} \right)}}$$
(3)

where \({\uplambda }\) is the wavelength of the signal, and because of the temperature-dependent refractive index, there will be a phase difference which is denoted as [\({\Delta }\emptyset = \emptyset \left( 0 \right) - \emptyset \left( {\text{r}} \right)\)] and can be evaluated from [27]

$$\Delta \emptyset = \frac{2\pi }{\lambda }\mathop \int \limits_{0}^{l} \Delta T\left( {r,z} \right)\frac{dn}{{dT}}dz$$
(4)

In the case of temperature-independent thermal conductivity (i.e., m = 0), Eq. (1) can be rewritten as

$$\Delta T\left( {r,z} \right) = \frac{{\eta_{h} \alpha }}{4\pi k}\left( {P_{inL} e^{ - \alpha z} + P_{inL} e^{{ - \alpha \left( {L - z} \right)}} } \right)\left\{ {\begin{array}{*{20}l} {\frac{{r_{2}^{2} - r_{1}^{2} + r_{2}^{2} \ln \left( {\frac{{r_{0}^{2} }}{{r_{2}^{2} }}} \right) - r_{1}^{2} \ln \left( {\frac{{r_{0}^{2} }}{{r_{1}^{2} }}} \right)}}{{r_{2}^{2} - r_{1}^{2} }}} \hfill & {0 \le r \le r_{1} } \hfill \\ {\frac{{r_{2}^{2} - r^{2} + r_{2}^{2} \ln \left( {\frac{{r_{0}^{2} }}{{r_{2}^{2} }}} \right) - r_{1}^{2} \ln \left( {\frac{{r_{0}^{2} }}{{r^{2} }}} \right)}}{{\left( {r_{2}^{2} - r_{1}^{2} } \right)}}} \hfill & {r_{1} < r \le r_{2} } \hfill \\ {\ln \left( {\frac{{r_{0}^{2} }}{{r^{2} }}} \right)} \hfill & {r_{2} < r \le 0,} \hfill \\ \end{array} } \right.$$
(5)

By integrating Eq. (5) and substituting in Eq. (5), the phase difference equation can be found.

$$\Delta \emptyset = \frac{2\pi }{\lambda }\frac{dn}{{dT}}\frac{1}{4\pi k}A\left( {P_{hL} + P_{hR} } \right)$$
(6)

where the absorption efficiency is given by \(\left( {\eta_{abs} = 1 - e^{ - \alpha l} } \right)\), and the total heat load at the left and right ends is denoted by \(P_{hR}\) and \(P_{hL}\), respectively, and is given by \(P_{h} = \eta_{abs} \eta_{h} P_{in}\).

Substituting Eq. (6) into Eq. (4) and solving for each region separately, the thermal lensing focal length can be obtained as follows:

$$f_{th} = \left\{ {\begin{array}{*{20}l} \infty \hfill & {0 \le r \le r_{1} } \hfill \\ {\frac{{2\pi kr^{2} }}{{\left( {{\raise0.7ex\hbox{{dn}} \!\mathord{\left/ {\vphantom {{dn} {dT}}}\right.\kern-0pt} \!\lower0.7ex\hbox{{dT}}}} \right)\left( {P_{h1} + P_{h2} } \right)}}\left( {\frac{{\left( {r^{2} - r_{1}^{2} } \right)}}{{\left( {r_{2}^{2} - r_{1}^{2} } \right)}}} \right)} \hfill & {r_{1} \le r \le r_{2} } \hfill \\ {\frac{{2\pi kr^{2} }}{{\left( {{\raise0.7ex\hbox{{dn}} \!\mathord{\left/ {\vphantom {{dn} {dT}}}\right.\kern-0pt} \!\lower0.7ex\hbox{{dT}}}} \right)\left( {P_{h1} + P_{h2} } \right)}}} \hfill & {r_{2} \le r \le 0} \hfill \\ \end{array} } \right.$$
(7)

where \(\left(\raisebox{1ex}{dn}\!\left/ \!\raisebox{-1ex}{dT}\right.\right)\) is the thermal dispersion.

For single-ended pumping (i.e., \({P}_{h2}=0\)), Eq. (7) becomes the known expression for the thermally induced focal length, given by [27].

Comparison and results

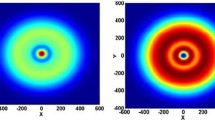
The thermal lens analytical expression was applied to 1% atm. Nd:YAG laser rod with a diameter of 2.5 mm and a length of 5 mm to obtain the simulation results using MATLAB. The laser rod was assumed to be pumped by a diode laser at a wavelength of 808 nm in a double-cavity design. It was assumed also that the rod was pumped by a total pump power of 50 W (distributed evenly on each face of the rod) with an annular-shaped beam with inner radius of 0.225 mm and outer radius of 0.375 mm, respectively, and all the used physical and thermal parameters of the laser rod utilized in the simulation are listed in Table 1.

Table 1 Nd:YAG laser parameters [16, 29]
Full size table

The temperature of the laser rod rises due to heat generated during pumping; Fig. 2 illustrates the dependence of the thermal conductivity on temperature impacts on the temperature distribution along the rod radius.

Fig. 2
figure 2

Radial temperature difference in the case of temperature-dependent and independent thermal conductivity

Full size image

Additionally, Fig. 2 illustrates a clear distinction between a temperature-independent thermal conductivity and a temperature-dependent thermal conductivity. Considering a temperature-dependent thermal conductivity results in a difference of ∼ 69.22 K between the two scenarios.

The normalized dioptric power along the radial axis for the annular and top-hat intensity profiles is shown in Fig. 3a,b. As shown in this figure, the dioptric power for the top-hat pump profile maintained a constant value for the pumped region where (\(0\le r\le {r}_{2}\)), whereas for the annular profile, the dioptric power decreased to zero in the inner unpumped region (\(0\le r\le {r}_{1}\)) owing to the infinite focal length. For the pumped region (\({r}_{1}\le r\le {r}_{2}\)), the lens power increased rapidly to the value of the top-hat profile at point (\(r={r}_{2}\)). After the pumping region (\({r}_{2}\le r\le 0\),), the dioptric power behaves similarly for both types of pumping. Consequently, a lower average thermal lens power is required for pumping with an annular beam profile.

Fig. 3
figure 3

Normalized dioptric power along a radial axis for: a annular intensity profile, b top-hat intensity profile

Full size image

Figure 4 shows a comparison of the thermal lens dioptric power between the annular and top-hat pump profiles in the pump region. It is clear from this figure that the dioptric power of the annular pump profile increases linearly from 0.5 m−1 to 4.4 m−1 when the pump power was increased from 10 to 50 W with a slope of (0.09 m−1/W). For the top-hat pumping, the thermal lens dioptric power increases linearly from 0.5 m−1 to 3.5 m−1 when the pump power was increased from 10 to 50 W with a slope of (0.07 m−1/W). The results show that, with top-hat pumping, the thermal lens dioptric power is approximately 20% weaker than that with annular pumping.

Fig. 4
figure 4

Thermal lens dioptric power as a function of total pump power for both annular and top-hat intensity profile

Full size image

Figure 5 shows the dioptric power of the thermal lens as a function of the total pump power in the pumped region. According to this figure, the dioptric power of the thermal lens increased approximately in line with the total pump power. However, owing to the infinite focal length, the dioptric power falls to zero in the inner unpumped region, leading to a lower average thermal lens power.

Fig. 5
figure 5

Thermal lens dioptric power as a function of total pump power

Full size image

A thermal lens dioptric power comparison between single- and double-end-pumped geometries is depicted in Fig. 6. Utilizing the double-end-pumped geometry significantly reduced the dioptric power compared with the single-end-pumped geometry, which can be obtained by adjusting one of the input powers to zero.

Fig. 6
figure 6

Thermal lens dioptric power comparison between single- and double-end-pumped geometry

Full size image

Figure 7 shows the thermal lens dioptric power as a function of the total pump power in the pumped region for different annular radii. Clearly, the dioptric power decreased significantly as the inner and outer radii of the annular beam increased at a constant ratio (r1/r2). The thermal lens dioptric power increased in line with the total pump power, so the slopes were found to be (0.09 m−1/W, 0.05 m−1/W, 0.03 m−1/W, and 0.02 m−1/W) for the inner and outer radii of (0.225, 0.375, 0.3, 0.5; 0.375,0.625 and 0.45,0.75) mm, respectively. The slope of the dioptric power line decreases as the inner and outer radii increase.

Fig. 7
figure 7

Thermal lens dioptric power versus total pump power for different annular radii

Full size image

In summary, Table 2 lists a comparison between the calculated results of our proposed model and the experimental work in the literature [30].

Table 2 Comparison with experimental work in the literature
Full size table

By implementing the double-end-pumping configuration, the results confirm that the annular-shaped pump beam can significantly reduce detrimental thermal effects, including thermal lensing, which is beneficial for high-power laser operation.

Conclusions

In conclusion, the annular-shaped pump configuration offers several advantages for solid-state lasers. However, the thermal lensing effect can pose a significant performance challenge. By implementing effective mitigation techniques, it is possible to overcome this challenge and improve overall laser performance. The results show that there is no thermal lensing in the inner region and a much longer focal length in the pumped region compared with the top-hat pump beam. In other words, the overall thermal lensing was considerably reduced for the annular-shaped pump beam. These results confirm that the annular-shaped pump beam can significantly reduce detrimental thermal effects, including thermal lensing, which is beneficial for high-power laser operations.