Introduction

In recent years, the study of optical solitons in nonlinear partial differential equation (NLPDE) [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25] has become a hot topic in the field of nonlinear science. The construction of optical soliton solutions of NLPDE can further explain scientific problems from the fields of physics, nonlinear optics and engineering technology. Therefore, many experts and scholars [26,27,28,29,30,31,32,33,34,35,36] have devoted themselves to the study of optical solitons in NLPDE. However, in the fields of natural science and engineering technology, the occurrence of random phenomena is inevitable [37, 38]. Therefore, the problem of considering the solution of NLPDE with random noise is a very difficult problem that has puzzled mathematicians and physicists [39,40,41,42,43,44,45,46,47,48,49,50,51]. Therefore, the main purpose of this paper is to construct optical soliton solutions for a class of stochastic NLPDE.

In this article, we consider the following the stochastic Schrödinger–Hirota equation in birefringent fibers with spatiotemporal dispersion and parabolic law nonlinearity [52]

$$\begin{aligned} {\left\{ \begin{array}{ll} i\psi _{t}+a_{1}\psi _{xx}+b_{1}\psi _{xt}+(c_{1}|\psi |^{2}+d_{1}|\phi |^{2})\psi +(e_{1}|\psi |^{4}+f_{1}|\psi |^{2}|\phi |^{2}+g_{1}|\phi |^{4})\psi +i[\alpha _{1}\psi _{x}+\lambda _{1}(|\psi |^{2}\phi )_{x}\\ +v_{1}(|\psi |^{2})_{x}\psi +\theta _{1}|\psi |^{2}\psi _{x}+\gamma _{1}\psi _{xxx}]+\sigma _{1}(\psi -ib_{1}\psi _{x})\frac{d\omega _{1}(t)}{dt}=0,\\ i\phi _{t}+a_{2}\phi _{xx}+b_{2}\phi _{xt}+(c_{2}|\phi |^{2}+d_{2}|\phi |^{2})\phi +(e_{2}|\phi |^{4}+f_{2}|\phi |^{2}|\psi |^{2}+g_{2}|\psi |^{4})\phi +i[\alpha _{2}\phi _{x}+\lambda _{2}(|\phi |^{2}\phi )_{x}\\ +v_{2}(|\phi |^{2})_{x}\phi +\theta _{2}|\phi |^{2}\phi _{x} +\gamma _{2}\phi _{xxx}]+\sigma _{2}(\phi -ib_{2}\phi _{x})\frac{d\omega _{2}(t)}{dt}=0, \end{array}\right. } \end{aligned}$$
(1.1)

where \(\psi (t,x)\) and \(\phi (t,x)\) represent the soliton profiles. \(a_{j}\) and \(b_{j}\)(\(j=1,2\)) stand for the coefficients of chromatic dispersions terms and spatio-temporal dispersion terms, respectively. \(c_{j}\) and \(d_{j}\)(\(j=1,2\))represent the coefficients of self-phase modulation and cross-phase modulation terms, respectively. \(f_{j}\), \(e_{j}\) and \(g_{j}\) (\(j=1,2\)) stand for nonlinear terms. \(\alpha _{j}\) and \(\lambda _{j}\)(\(j=1,2\)) are the self-steepening terms. \(v_{j}\) and \(\theta _{j}\)(\(j=1,2\)) represent the nonlinear dispersion terms. \(\frac{d\omega _{j}(t)}{dt}\)(\(j=1,2\)) are the white noises. \(\omega _{j}(t)\)(\(j=1,2\)) represents the standard Wiener processes. \(\sigma _{j}\)(\(j=1,2\)) stands for the noises strength. In [52], Elsayed et al. obtained the optical soliton solutions of Eq. (1.1) using the Jacobi-elliptic expansion approach and the extended auxiliary equation algorithm, respectively. The main purpose of this article is to construct optical soliton solutions for equation Eq. (1.1) using the complete discriminant system method.

The rest of this article is organized as follows: In Sect. 2, Eq. (1.1) is transformed into the ODEs using traveling wave transformation. Moreover, the optical soliton solutions of stochastic Schrödinger–Hirota equation are obtained. In Sect. 3, a brief summary is presented.

Optical soliton solutions of Eq. (1.1)

Mathematical analysis

Firstly, let’s consider the following transformation

$$\begin{aligned} \begin{aligned}&\psi (t,x)=\Psi (\xi ){\textbf{e}}^{i[\eta _{1}(t,x)+\sigma _{1}\omega _{1}(t)-\sigma _{1}^{2}t]},\\&\phi (t,x)=\Phi (\xi ){\textbf{e}}^{i[\eta _{2}(t,x)+\sigma _{2}\omega _{2}(t)-\sigma _{2}^{2}t]},\\&\xi =x-vt,\ \ \eta _{l}(t,x)=-k_{l}x+\Omega _{l}t+\theta _{l}, l=1,2, \end{aligned} \end{aligned}$$
(2.1)

where \(\Psi\) and \(\Phi\) represent the amplitude portions of the solitons. \(\eta _{j}(t,x)\), \(k_{j}\), \(\Omega _{j }\) and \(\theta _{j}\) (\(j=1,2\)) stand for the phase amplitude format, the frequencies of the solitons, the wave numbers and phase constants, respectively. v represents the soliton velocity. So, substituting Eq. (2.1) into Eq. (1.1) yields the real parts:

$$\begin{aligned} \begin{aligned}&(a_{1}-b_{1}v+3k_{1}\gamma _{1})\Psi ^{\prime\prime}(\xi )-[a_{1}k_{1}^{2}-k_{1}\alpha _{1}+\gamma _{1}k_{1}^{3}\\&\quad +(\Omega _{1}-\sigma _{1}^{2})(1-b_{1}k_{1})]\Psi (\xi ) +d_{1}\Psi (\xi )\Phi ^{2}(\xi )+(c_{1}+k_{1}\lambda _{1}\\&\quad +k_{1}\theta _{1})\Psi ^{3}(\xi ) +e_{1}\Psi ^{5}(\xi )+f_{1}\Psi ^{3}(\xi )\Phi ^{2}(\xi )\\&\quad +g_{1}\Psi (\xi )\Phi ^{4}(\xi )=0,\\&(a_{2}-b_{2}v+3k_{2}\gamma _{2})\Phi ^{\prime\prime}(\xi )-[a_{2}k_{2}^{2}-k_{2}\alpha _{2}+\gamma _{2}k_{2}^{3}\\&\quad +(\Omega _{2}-\sigma _{2}^{2})(1-b_{2}k_{2})]\Phi (\xi ) +d_{2}\Phi (\xi )\Psi ^{2}(\xi )+(c_{2}+k_{2}\lambda _{2}\\&\quad +k_{2}\theta _{2})\Phi ^{3}(\xi ) +e_{2}\Phi ^{5}(\xi )+f_{2}\Phi ^{3}(\xi )\Psi ^{2}(\xi )\\&\quad +g_{2}\Phi (\xi )\Psi ^{4}(\xi )=0, \end{aligned} \end{aligned}$$
(2.2)

and the imaginary parts:

$$\begin{aligned} \begin{aligned}&\gamma _{1}\Psi ^{\prime\prime\prime}(\xi )-[2a_{1}k_{1}-b_{1}(\Omega _{1}-\sigma _{1}^{2})-\alpha _{1}+3\gamma _{1}k_{1}^{2}\\&\quad +(1-b_{1}k_{1})v]\Psi ^{\prime}(\xi ) +(3\lambda _{1}+2\mu _{1}+\theta _{1})\Psi ^{2}(\xi )\Psi ^{\prime}(\xi )=0,\\&\gamma _{2}\Phi ^{\prime\prime\prime}(\xi )-[2a_{2}k_{2}-b_{2}(\Omega _{2}-\sigma _{2}^{2})-\alpha _{2}+3\gamma _{2}k_{2}^{2}\\&\quad +(1-b_{2}k_{2})v]\Phi ^{\prime}(\xi ) +(3\lambda _{2}+2\mu _{2}+\theta _{2})\Phi ^{2}(\xi )\Phi ^{\prime}(\xi )=0. \end{aligned} \end{aligned}$$
(2.3)

Next, let be the transformation \(\Phi (\xi )=A\Psi (\xi )\), where A is a nonzero constant. Thus, Eqs. (2.2) and (2.3) can be convert into

$$\begin{aligned} \begin{aligned}&(a_{1}-b_{1}v+3k_{1}\gamma _{1})\Psi ^{\prime\prime}(\xi )-[a_{1}k_{1}^{2}-k_{1}\alpha _{1}+\gamma _{1}k_{1}^{3}\\&\quad +(\Omega _{1}-\sigma _{1}^{2})(1-b_{1}k_{1})]\Psi (\xi ) +(A^{2}d_{1}+c_{1}+k_{1}\lambda _{1}\\&\quad+k_{1}\theta _{1})\Psi ^{3}(\xi ) +(e_{1}+A^{2}f_{1}+A^{4}g_{1})\Psi ^{5}(\xi )=0,\\&(a_{2}-b_{2}v+3k_{2}\gamma _{2})\Psi ^{\prime\prime}(\xi )-[a_{2}k_{2}^{2}-k_{2}\alpha _{2}+\gamma _{2}k_{2}^{3}\\&\quad +(\Omega _{2}-\sigma _{2}^{2})(1-b_{2}k_{2})]\Psi (\xi ) +[d_{2}+A^{2}(c_{2}+k_{2}\lambda _{2}\\&\quad +k_{2}\theta _{2})]\Psi ^{3}(\xi ) +(e_{2}A^{4}+f_{2}A^{2}+g_{2})\Psi ^{5}(\xi )=0, \end{aligned} \end{aligned}$$
(2.4)

and

$$\begin{aligned} \begin{aligned}&\gamma _{1}\Psi ^{\prime\prime\prime}(\xi )-[2a_{1}k_{1}-b_{1}(\Omega _{1}-\sigma _{1}^{2})-\alpha _{1}+3\gamma _{1}k_{1}^{2}\\&\quad +(1-b_{1}k_{1})v]\Psi ^{\prime}(\xi ) +(3\lambda _{1}+2\mu _{1}+\theta _{1})\Psi ^{2}(\xi )\Psi ^{\prime}(\xi )=0,\\&\gamma _{2}\Psi ^{\prime\prime\prime}(\xi )-[2a_{2}k_{2}-b_{2}(\Omega _{2}-\sigma _{2}^{2})-\alpha _{2}+3\gamma _{2}k_{2}^{2}\\&\quad +(1-b_{2}k_{2})v]\Phi ^{\prime}(\xi ) +A^{2}(3\lambda _{2}+2\mu _{2}+\theta _{2})\Psi ^{2}(\xi )\Psi ^{\prime}(\xi )=0. \end{aligned} \end{aligned}$$
(2.5)

Integrating Eq. (2.5) and assuming an integral constant of zero, we obtain

$$\begin{aligned} \begin{aligned}&\gamma _{1}\Psi ^{\prime\prime}(\xi )-[2a_{1}k_{1}-b_{1}(\Omega _{1}-\sigma _{1}^{2})-\alpha _{1}+3\gamma _{1}k_{1}^{2}\\&\quad +(1-b_{1}k_{1})v]\Psi (\xi ) +\frac{1}{3}(3\lambda _{1}+2\mu _{1}+\theta _{1})\Psi ^{3}(\xi )=0,\\&\gamma _{2}\Psi ^{\prime\prime}(\xi )-[2a_{2}k_{2}-b_{2}(\Omega _{2}-\sigma _{2}^{2})-\alpha _{2}+3\gamma _{2}k_{2}^{2}\\&\quad +(1-b_{2}k_{2})v]\Psi (\xi ) +\frac{1}{3}A^{2}(3\lambda _{2}+2\mu _{2}+\theta _{2})\Psi ^{3}(\xi )=0. \end{aligned} \end{aligned}$$
(2.6)

By the linearly independent principle on Eq. (2.6) yields

$$\begin{aligned}{} & {} \gamma _{1}=\gamma _{2}=0,\quad \alpha _{l}=2a_{l}k_{l}-b_{l}(\Omega _{l}-\sigma _{l}^{2})+(1-k_{l}b_{l})v,\nonumber \\{} & {} \quad 3\lambda _{l}+2\mu _{l}+\theta _{l}=0,\ \ l=1,2. \end{aligned}$$
(2.7)

Therefore, Eq. (2.3) are equivalent under following conditions

$$\begin{aligned}{} & {} \frac{a_{1}-b_{1}v}{a_{2}-b_{2}v}=\frac{a_{1}k_{1}^{2}-k_{1}\alpha _{1}+\gamma _{1}k_{1}^{3}+(\Omega _{1}-\sigma _{1}^{2})(1-b_{1}k_{1})}{a_{2}k_{2}^{2}-k_{2}\alpha _{2}+\gamma _{2}k_{2}^{3}+(\Omega _{2}-\sigma _{2}^{2})(1-b_{2}k_{2})}\nonumber \\{} & {} \quad =\frac{A^{2}d_{1}+c_{1}+k_{1}\lambda _{1} +k_{1}\theta _{1}}{d_{2}+A^{2}(c_{2}+k_{2}\lambda _{2} +k_{2}\theta _{2})} =\frac{e_{1}+A^{2}f_{1}+A^{4}g_{1}}{e_{2}A^{4}+f_{2}A^{2}+g_{2}}. \end{aligned}$$
(2.8)

Consequently, the velocity of the soliton can be obtained from Eq. (2.8)

$$\begin{aligned} v=\frac{a_{2}[a_{1}k_{1}^{2}-k_{1}\alpha _{1}+(\Omega _{1}-\sigma _{1}^{2})(1-b_{1}k_{1})]-a_{1}[a_{2}k_{2}^{2}-k_{2}\alpha _{2}+(\Omega _{2}-\sigma _{2}^{2})(1-b_{2}k_{2})]}{b_{2}[a_{1}k_{1}^{2}-k_{1}\alpha _{1}+(\Omega _{1}-\sigma _{1}^{2})(1-b_{1}k_{1})]-b_{1}[a_{2}k_{2}^{2}-k_{2}\alpha _{2}+(\Omega _{2}-\sigma _{2}^{2})(1-b_{2}k_{2})]}, \end{aligned}$$
(2.9)

and

$$\begin{aligned} \begin{aligned}&A=[\frac{(a_{2}-b_{2}v)(c_{1}+k_{1}\lambda _{1}+k_{1}\theta _{1})-(a_{1}-b_{1}v)d_{2}}{(a_{1}-b_{1}v)(c_{2}+k_{2}\lambda _{2}+k_{2}\theta _{2})-(a_{2}-b_{2}v)d_{1}}]^{\frac{1}{2}},\\&e_{1}=\frac{(a_{1}-b_{1}v)(A^{4}e_{2}+A^{2}f_{2}+g_{2})-A^{2}(a_{2}-b_{2}v)(f_{1}+A^{2}g_{1})}{a_{2}-b_{2}v}, \end{aligned} \end{aligned}$$
(2.10)

satisfying \((a_{1}-b_{1}v)(c_{2}+k_{2}\lambda _{2}+k_{2}\theta _{2})\ne (a_{2}-b_{2}v)d_{1}\) and \((a_{2}-b_{2}v)(c_{1}+k_{1}\lambda _{1}+k_{1}\theta _{1})\ne (a_{1}-b_{1}v)d_{2}\).

Thus, the first equation of Eq. (2.4) can be rewritten as

$$\begin{aligned} \Psi ^{\prime\prime}(\xi )-\Theta _{1}\Psi ^{5}(\xi )-\Theta _{2}\Psi ^{3}(\xi )-\Theta _{3}\Psi (\xi )=0, \end{aligned}$$
(2.11)

where \(\Theta _{1}=\frac{e_{1}+A^{2}f_{1}+A^{4}g_{1}}{a_{1}-b_{1}v}\), \(\Theta _{2}=-\frac{A^{2}d_{1}+c_{1}+k_{1}\lambda _{1}+k_{1}\theta _{1}}{a_{1}-b_{1}v}\) and \(\Theta _{3}=-\frac{a_{1}k_{1}^{2}-k_{1}\alpha _{1}+(\Omega _{1}-\sigma _{1}^{2})(1-b_{1}k_{1})}{a_{1}-b_{1}v}\) satisfying \(a_{1}\ne b_{1}v\).

Multiplying both sides of Eq. (2.11) by \(\Phi (\xi )\) and integrating once with respect to \(\xi\), we have

$$\begin{aligned} (\Psi ^{\prime}(\xi ))^{2}=\frac{\Theta _{1}}{3}\Psi ^{6}(\xi )+\frac{\Theta _{2}}{2}\Psi ^{4}(\xi )+\Theta _{3}\Psi ^{2}(\xi )+2c, \end{aligned}$$
(2.12)

where c is integral constant.

Setting \(\Xi (\xi )=\Psi ^{2}(\xi )\), then the integral expression of Eq. (2.12) is

$$\begin{aligned} \pm 2\sqrt{\varepsilon \frac{\Theta _{3}}{3}}(\xi -\xi _{0})=\int \frac{d\Xi }{\sqrt{\varepsilon \Xi (\Xi ^{3}+P\Xi ^{2}+Q\Xi +D)}}, \end{aligned}$$
(2.13)

where \(P=\frac{3\Theta _{2}}{2\Theta _{1}}\), \(Q=\frac{2\Theta _{3}}{\Theta _{2}}\) and \(D=\frac{6c}{\Theta _{1}}\) satisfying \(\Theta _{1}\ne 0\).

Optical soliton solutions of Eq. (1.1)

Assume that \(F(\Xi )=\Xi ^{3}+P\Xi ^{2}+Q\Xi +D\), \(\Delta =-27(\frac{2P^{3}}{27}+D-\frac{PQ}{3})^{2}-4(Q-\frac{P^{2}}{3})^{3}\) and \(\Gamma =Q-\frac{P^{2}}{3}\). Here, when \(\Theta _{3}>0\), we take \(\varepsilon =1\). Conversely, when \(\Theta _{3}<0\), we take \(\varepsilon =-1\). Therefore, according to the complete discriminant system of third-order polynomials, we can obtain the optical soliton solution of Eq. (1.1).

  1. (i)

    \(\Delta =0, \Gamma <0, \varepsilon =1\). Suppose that \(F(\Xi )=\Xi ^{3}+P\Xi ^{2}+Q\Xi +D=(\Xi -\alpha )^{2}(\Xi -\beta )\), where \(\alpha\) and \(\beta\) are the real constants satisfying \(\alpha \ne \beta\). When \(\alpha >\beta\) and \(\Xi >\beta\), or when \(\alpha <0\) and \(\Xi <0\), we can obtain the solution of Eq. (1.1) from Eq. (2.13)

    $$\begin{aligned}{} & {} \pm 2\sqrt{\frac{\Theta _{3}}{3}}(\xi -\xi _{0})\nonumber \\{} & {} \quad =\frac{1}{\alpha (\alpha -\beta )}\ln \frac{(\sqrt{\alpha (\Xi -\beta )}-\sqrt{\Xi (\alpha -\beta )})^{2}}{|\Xi -\alpha |}. \end{aligned}$$
    (2.14)

    When \(\alpha >\beta\) and \(\Xi <0\), or when \(\alpha <\Xi\) and \(\Xi <\beta\), we can obtain the solution of Eq. (1.1) from Eq. (2.13)

    $$\begin{aligned}{} & {} \pm 2\sqrt{\frac{\Theta _{3}}{3}}(\xi -\xi _{0})\nonumber \\{} & {} \quad =\frac{1}{\alpha (\alpha -\beta )}\ln \frac{(\sqrt{-\alpha (\Xi -\beta )}-\sqrt{\Xi (\beta -\alpha )})^{2}}{|\Xi -\alpha |}. \end{aligned}$$
    (2.15)

    When \(\beta>\alpha >0\), we can obtain the solution of Eq. (1.1) from Eq. (2.13)

    $$\begin{aligned}{} & {} \pm 2\sqrt{\frac{\Theta _{3}}{3}}(\xi -\xi _{0})\nonumber \\{} & {} \quad =\frac{1}{\alpha (\beta -\alpha )}\arcsin \frac{\alpha (\Xi -\beta )+\Xi (\alpha -\beta )}{\beta |\Xi -\alpha |}. \end{aligned}$$
    (2.16)
  2. (ii)

    \(\varepsilon =-1\)

When \(\alpha >\beta\) and \(\Xi >\beta\), or when \(\alpha <0\) and \(\Xi <0\), we can obtain the solution of Eq. (1.1) from Eq. (2.13)

$$\begin{aligned}{} & {} \pm 2\sqrt{-\frac{\Theta _{3}}{3}}(\xi -\xi _{0})\nonumber \\{} & {} \quad =\frac{1}{\alpha (\beta -\alpha )}\ln \frac{(\sqrt{\alpha (-\Xi +\beta )}-\sqrt{\Xi (\beta -\alpha )})^{2}}{|\Xi -\alpha |}. \end{aligned}$$
(2.17)

When \(\alpha >\beta\) and \(\Xi <0\), or when \(\alpha <0\) and \(\Xi <\beta\), we can obtain the solution of Eq. (1.1) from Eq. (2.13)

$$\begin{aligned}{} & {} \pm 2\sqrt{-\frac{\Theta _{3}}{3}}(\xi -\xi _{0})\nonumber \\{} & {} \quad =\frac{1}{\alpha (\beta -\alpha )}\ln \frac{(\sqrt{-\alpha (-\Xi +\beta )}-\sqrt{\Xi (\alpha -\beta )})^{2}}{|\Xi -\alpha |}. \end{aligned}$$
(2.18)

When \(\beta>\alpha >0\), we can obtain the solution of Eq. (1.1) from Eq. (2.13)

$$\begin{aligned}{} & {} \pm 2\sqrt{-\frac{\Theta _{3}}{3}}(\xi -\xi _{0})\nonumber \\{} & {} \quad =\frac{1}{\alpha (\alpha -\beta )}\arcsin \frac{(-\Xi +\beta )(\alpha -\gamma )+\Xi (\beta -\alpha )}{|\beta (\Xi -\alpha )|}. \end{aligned}$$
(2.19)

Case II. If \(\Delta =0\), \(\Gamma =0\), then \(F(\Xi )=(\Xi -\rho )^{3}\), where \(\rho\) is the real number.

  1. (i)

    \(\varepsilon =1\) If \(\Xi >\rho\) and \(\Xi >0\), or if \(\Xi <\rho\) and \(\Xi <0\), we can obtain the solution of Eq. (1.1) from Eq. (2.13)

    $$\begin{aligned}{} & {} \psi _{1}(t,x)=\;\pm \;[\frac{3\rho }{\rho ^{2}\Theta _{1}(x-vt-\xi _{0})^{2}-3}\nonumber \\{} & {} \quad +\rho ]^{\frac{1}{2}}{\textbf{e}}^{i[\eta _{1}(t,x) +\sigma _{1}\omega _{1}(t)-\sigma _{1}^{2}t]}. \end{aligned}$$
    (2.20)
  2. (ii)

    \(\varepsilon =-1\) If \(\Xi >\rho\) and \(\Xi <0\), or if \(\Xi <\rho\) and \(\Xi >0\), we can obtain the solution of Eq. (1.1) from Eq. (2.13)

    $$\begin{aligned}{} & {} \psi _{2}(t,x)=\;\pm\; [\frac{3\rho }{-\rho ^{2}\Theta _{1}(x-vt-\xi _{0})^{2}-3}\nonumber \\{} & {} \quad +\rho ]^{\frac{1}{2}}{\textbf{e}}^{i[\eta _{1}(t,x)+\sigma _{1}\omega _{1}(t)-\sigma _{1}^{2}t]}. \end{aligned}$$
    (2.21)

Case III. If \(\Delta >0\), \(\Gamma <0\), \(F(\Xi )=\;(\Xi -\theta _{1})(\Xi -\theta _{2})(\Xi -\theta _{3})\), where \(\theta _{1}\), \(\theta _{2}\) and \(\theta _{3}\) are real numbers satisfying \(0<\theta _{1}<\theta _{2}<\theta _{3}\).

  1. (i)

    \(\varepsilon =1\) When \(\Xi >0\) and \(\Xi <\theta _{3}\), we can obtain the solution of Eq. (1.1) from Eq. (2.13)

    $$\begin{aligned} \psi _{3}(t,x)= & {} \pm \sqrt{\frac{-\theta _{1}\theta _{3}{{\textbf{s}}}{{\textbf{n}}}^{2}(\sqrt{-\theta _{2}(\theta _{1}-\theta _{3})}\sqrt{\frac{\Xi _{1}}{3}}(x-vt-\xi _{0}),m)}{-\theta _{3}{{\textbf{s}}}{{\textbf{n}}}^{2}(\sqrt{-\theta _{2}(\theta _{1}-\theta _{3})}\sqrt{\frac{\Theta _{1}}{3}}(x-vt-\xi _{0}),m)-(\theta _{1}-\theta _{3})}}{\textbf{e}}^{i[\eta _{1}(t,x)+\sigma _{1}\omega _{1}(t)-\sigma _{1}^{2}t]}, \end{aligned}$$
    (2.22)
    $$\begin{aligned} \psi _{4}(t,x)= & {} \pm \sqrt{\frac{\theta _{3}(\theta _{1}-\theta _{2}){{\textbf{s}}}{{\textbf{n}}}^{2}(\sqrt{-\theta _{2}(\theta _{1}-\theta _{3})}\sqrt{\frac{\Theta _{1}}{3}}( x-vt-\xi _{0}),m)-\theta _{2}(\theta _{1}-\theta _{3})}{(\theta _{1}-\theta _{2}){{\textbf{s}}}{{\textbf{n}}}^{2}(\sqrt{-\theta _{2}(\theta _{1}-\theta _{3})}\sqrt{\frac{\Theta _{1}}{3}}(x-vt-\xi _{0}),m)-(\theta _{1}-\theta _{3})}}{\textbf{e}}^{i[\eta _{1}(t,x)+\sigma _{1}\omega _{1}(t)-\sigma _{1}^{2}t]}, \end{aligned}$$
    (2.23)

    where \(m^{2}=\frac{\theta _{3}(\theta _{1}-\theta _{2})}{\theta _{2}(\theta _{1}-\theta _{3})}\).

  2. (ii)

    \(\varepsilon =-1\)When \(\theta _{3}<\Xi <\theta _{2}\), we can obtain the solution of Eq. (1.1) from Eq. (2.13)

    $$\begin{aligned} \psi _{5}(t,x)= & {} \pm \sqrt{\frac{-\theta _{1}\theta _{2}{{\textbf{s}}}{{\textbf{n}}}^{2}(\sqrt{-\theta _{2}(\theta _{1}-\theta _{3})}\sqrt{\frac{\Theta _{1}}{3}}(x-vt-\xi _{0}),m)+\theta _{1}\theta _{2}}{-\theta _{1}{{\textbf{s}}}{{\textbf{n}}}^{2}(\sqrt{-\theta _{2}(\theta _{1}-\theta _{3})}\sqrt{\frac{\Theta _{1}}{3}}(x-vt-\xi _{0}),m)+\theta _{3}}}{\textbf{e}}^{i[\eta _{1}(t,x)+\sigma _{1}\omega _{1}(t)-\sigma _{1}^{2}t]}, \end{aligned}$$
    (2.24)
    $$\begin{aligned} \psi _{6}(t,x)= & {} \pm \sqrt{\frac{-\theta _{2}\theta _{3}}{(\theta _{2}-\theta _{3}){{\textbf{s}}}{{\textbf{n}}}^{2}(\sqrt{-\theta _{2}(\theta _{1}-\theta _{3})}\sqrt{\frac{\Theta _{1}}{3}}(x-vt-\xi _{0}),m)-\theta _{2}}}{\textbf{e}}^{i[\eta _{1}(t,x)+\sigma _{1}\omega _{1}(t)-\sigma _{1}^{2}t]}, \end{aligned}$$
    (2.25)

    where \(m^{2}=\frac{\theta _{1}(\theta _{2}-\theta _{3})}{\theta _{2}(\theta _{1}-\theta _{3})}\).

Case IV. If \(\Delta <0\), \(F(\Xi )=(\Xi -\vartheta _{1})[(\Xi -\vartheta _{2})^{2}+\vartheta _{3}^{2}]\), where \(\vartheta _{1}\), \(\vartheta _{2}\) and \(\vartheta _{3}\) are real numbers, and \(\vartheta _{1}>0\), \(\theta _{2}>0,\theta _{3}>0\). So, we can obtain the solution of Eq. (1.1) from Eq. (2.13), where the positive sign corresponds to \(\varepsilon = 1\) and the symbol corresponds to \(\varepsilon = -1\).

$$\begin{aligned} \psi _{7}(t,x)=\pm \sqrt{\frac{d_{1}{{\textbf{c}}}{{\textbf{n}}}^{2}(\frac{\sqrt{\mp 6\vartheta _{3}m_{1}\vartheta _{1}c_{1}}}{3mm_{1}}(x-vt-\xi _{0}),m)+d_{2}}{d_{3}{{\textbf{c}}}{{\textbf{n}}}^{2}(\frac{\sqrt{\mp 6\vartheta _{3}m_{1}\vartheta _{1}c_{1}}}{3mm_{1}}(x-vt-\xi _{0}),m)+d_{4}}}{\textbf{e}}^{i[\eta _{1}(t,x)+\sigma _{1}\omega _{1}(t)-\sigma _{1}^{2}t]}, \end{aligned}$$
(2.26)

where \(d_{1}=\frac{1}{2}\vartheta _{1}(d_{3}-d_{4})\), \(d_{2}=\frac{1}{2}\vartheta _{1}(\vartheta _{4}-d_{3})\), \(d_{3}=\vartheta _{1}-\vartheta _{2}-\frac{\vartheta _{3}}{m_{1}}\), \(d_{4}=\vartheta _{1}-\vartheta _{2}-\vartheta _{3}m_{1}\), \(E=\frac{\vartheta _{3}^{2}-\vartheta _{2}(\vartheta _{1}-\vartheta _{2})}{\vartheta _{1}\vartheta _{3}}\), \(m_{1}=E\pm \sqrt{E^{2}+1}\) and \(m^{2}=\frac{1}{1+m_{1}^{2}}\).

Numerical simulation

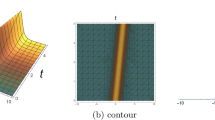
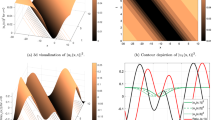
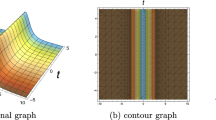
When \(\Theta _{1}=-1,\Theta _{2}=2,\Theta _{3}=3,\xi _{0}=0,v=1,c=\frac{1}{6}\), we can plot three-dimensional diagram, two-dimensional diagram and contour plot of optical soliton solution \(|\psi _{1}(t,x)|\) as shown in Fig. 1. When \(\Theta _{1}=1,\Theta _{2}=-4,\Theta _{3}=\frac{11}{2},\xi _{0}=0,v=1,c=-1\), we can plot three-dimensional diagram, two-dimensional diagram and contour plot of optical soliton solution \(|\psi _{3}(t,x)|\)as shown in Fig. 2.

Fig. 1
figure 1

The graph of optical soliton solution \(|\psi _{1}(t,x)|\) at \(\Theta _{1}=-1,\Theta _{2}=2,\Theta _{3}=3,\xi _{0}=0,v=1,c=\frac{1}{6}\)

Full size image
Fig. 2
figure 2

The graph of optical soliton solution \(|\psi _{3}(t,x)|\) at \(\Theta _{1}=1,\Theta _{2}=-4,\Theta _{3}=\frac{11}{2},\xi _{0}=0,v=1,c=-1\)

Full size image

Conclusion

In the paper, the optical soliton solutions of stochastic Schrödinger–Hirota equation with spatiotemporal dispersion and parabolic law nonlinearity are investigated by using the complete discriminant system method. Moreover, we obtained seven sets of solutions and implicit function solutions, and we also draw three-dimensional diagram, two-dimensional diagram and contour plot of the solitons \(|\psi _{1}(t,x)|\) and \(|\psi _{3}(t,x)|\), which are meaningful for us to further understand the propagation of optical solitons. Compared with reference [52], our obtained solutions are more abundant.