Introduction

Optic-fiber optical tweezers (OFOTs), as a prominent manipulation approach, enable optofluidic technology to address micro- and nanoparticles of interest in the fields, such as separation, purification, transport, and analysis in recent years [1, 2]. The waveguide of optical fiber not only migrates the majority of particles moving toward desired position [3], but stably traps smaller particles using a low light intensity other than objective lens with high numeric aperture value [4]. Hence, both precise manipulation and strong trapping can be further exploited to understand both the characterization and classification of single cell with free label in life science [5]. Meanwhile, Chen et al. [6, 7] have reported dual-beam optic-fibers with transverse offset realizing the rotational motion of polystyrene bead or cell, which could be used to assist the prediction and diagnosis of disease. In this case, the structure of misalignment related to dual-beam optic-fibers, generating spin and orbital rotation, is more convenient than special optical field, for example circularly polarized light [8, 9], Hermite–Gaussian [10], and Bessel beam [11]. Afterward, Pei and Chen [12] continued to utilize this approach in the measurement of viscosity coefficient. In addition, Li et al. [13] pointed out that different optic-fiber misalignment, optical power, and optic-fiber separation could exhibit three dynamic behaviors. The existence of both optical tweezers and gravity leads to an “8-shaped” trajectory for such a borosilicate particle suspending in air.

In addition, an array of optic-fiber, providing multi-path light source, has already been used in point-of-care diagnostic platform for medical endoscopes and measurement [14, 15]. To best of our knowledge, it is seldom that optic-fiber array is used to trap and manipulate microparticles. Therefore, we attempt to research on optic-fiber array leading to particle rotation or enrichment through optical radiation pressure. Moreover, this approach based on dynamic simulation offers a detailed theoretical perspective supporting experimental configuration and observation [7, 12, 16]. In this way, the numerical model has been built to study the optic-fiber array with a certain offset distance. Making this quad-beam misalignment, the adjustment referred to both axial and radial distance has been studied to generate various motion behaviors. This provides a technical feasibility serving the characteristic identification of different biological cell due to much more rotational optical fields.

Theory and model

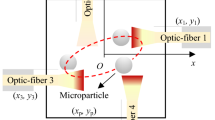
In our research, quad-beam consists of four same optic-fibers, and then two pairs are brought face to face in array form. A particle suspending in the solution is exerted by optical pressure from these four optic-fibers, as shown in Fig. 1a. Compared to only one dual beam, quad-beams would be more flexible due to more controllable parameters. In this case, the position of these four optic-fibers can be illustrated in Fig. 1b. To simplify the research work, the numerical model is proposed to study the dynamic behavior of microparticle in two-dimensional zx plane. The coordinate (zi, xi) in zx plane corresponds directly to the focal spot position of individual optic-fiber, in which the subscript i stands for the corresponding optic-fiber label. The coordinate of a particle should be noted (zp, xp). The variable S0 is a simulated width in square area.

Fig. 1
figure 1

Schematic structure of quad-beam: a Microparticle experienced by optical force from four optic-fibers, b Coordinate system for both quad-beam optic-fibers and microparticle in zx plane

Full size image

Optical radiation pressure, so-called optical tweezers, is attributed to the interaction between dielectric particle and light to produce an observable dynamic behavior. Owing to wave-particle duality of light, a particle suspending in media acts by optical radiation pressure interpreted with either ray optics (RO) [17, 18] or electromagnetic (EM) [11] model. In comparison between particle size and light wavelength, it is thought as Mie regime in RO approximation to predict optical trapping force if the particle diameter is far greater than wavelength [19]. In contrast, electromagnetic approximation based on Maxwell equation attempted to acquire the strength of the force relying on Maxwell stress tensor or volume-integration method. The calculation of optical radiation pressure relevant to optic-fiber has been described by Sidick and co-workers [20]. Since then, many research groups have carried out outstanding work with optic-fiber for particle manipulation by means of their presented theoretical model. Assuming that light with fixed polarization orientation is orthogonal to light propagated from other optic-fiber. Without regard to interference effect, the optical force generated by ith optic-fiber can be divided into x- and z-axial components, as expressed in Eqs. (1) and (2).

$$ \begin{aligned} F_{{{\text{zi}}}} (z_{{\text{p}}} ,x_{{\text{p}}} ) = & \frac{{n_{1} P_{0} }}{c}\frac{{2r_{0}^{2} }}{\pi }\int\limits_{0}^{\pi } {d\varphi } \int\limits_{0}^{{\theta_{\max } }} {d\theta \sin 2\theta \frac{{\exp \left( { - {{2r^{2} } \mathord{\left/ {\vphantom {{2r^{2} } {\omega^{2} }}} \right. \kern-\nulldelimiterspace} {\omega^{2} }}} \right)}}{{\omega^{2} R_{{\text{c}}} }}} \\ & \times \left\{ {q_{{\text{s}}} R_{z} + \frac{{q_{{\text{g}}} }}{\tan \gamma }\left[ {R_{{\text{z}}} - R_{{\text{c}}} \frac{{R_{{\text{z}}} + r_{0} \cos \theta }}{a\cos \gamma }} \right]} \right\} \\ \end{aligned} $$
(1)
$$ \begin{aligned} F_{{{\text{xi}}}} (z_{{\text{p}}} ,x_{{\text{p}}} ) = & \frac{{n_{1} P_{0} }}{c}\frac{{2r_{0}^{2} }}{\pi }\int\limits_{0}^{\pi } {{\text{d}}\varphi } \int\limits_{0}^{{\theta_{\max } }} {{\text{d}}\theta \sin 2\theta \frac{{\exp \left( { - {{2r^{2} } \mathord{\left/ {\vphantom {{2r^{2} } {\omega^{2} }}} \right. \kern-\nulldelimiterspace} {\omega^{2} }}} \right)}}{{\omega^{2} R_{{\text{c}}} }}} \\ & \times \left\{ {q_{s} (r_{0} \sin \theta \cos \varphi - d_{{{\text{ip}}}} ) + \frac{{q_{{\text{g}}} }}{\tan \gamma }} \right. \\ & \times \left. {\left[ {r_{0} \sin \theta \cos \varphi - d_{{{\text{ip}}}} (1 - \frac{{R_{{\text{c}}} }}{a\cos \gamma })} \right]} \right\} \\ \end{aligned} $$
(2)

where n1 refractive index of medium, c light velocity in vacuum, P0 power of incident light source, r0 radius of microparticle, dip the transverse distance between the particle and the optical axis of ith optic-fiber. The integral form is assigned to spherical coordinate. Thus, the variables φ and θ are azimuthal and colatitude angle, respectively. The parameters qs and qg are related to the fractions of the momentum transferred to the microparticle, as expressed in Eqs. (3) and (4) [19].

$$ q_{{\text{s}}} = 1 + R\cos 2\alpha_{{\text{i}}} - T^{2} \frac{{\cos \left( {2\alpha_{{\text{i}}} - 2\alpha_{{\text{t}}} } \right) + R\cos 2\alpha_{{\text{i}}} }}{{1 + R^{2} + 2R\cos 2\alpha_{{\text{t}}} }} $$
(3)
$$ q_{{\text{g}}} = - R\sin 2\alpha_{{\text{i}}} + T^{2} \frac{{\sin \left( {2\alpha_{{\text{i}}} - 2\alpha_{{\text{t}}} } \right) + R\sin 2\alpha_{{\text{i}}} }}{{1 + R^{2} + 2R\cos 2\alpha_{{\text{t}}} }} $$
(4)

Herein, these intermediate parameters in Eqs. (1) ~ (4) could be calculated by Eq. (5). The detailed reduction of these formulas was cited in Ref. [20]. The sign of Rz is determined by Rc.

$$ \begin{array}{*{20}l} {R = \frac{1}{2}\left[ {\frac{{\sin^{2} \left( {\alpha_{{\text{i}}} - \alpha_{{\text{t}}} } \right)}}{{\sin^{2} (\alpha_{{\text{i}}} + \alpha_{{\text{t}}} )}} + \frac{{\tan^{2} \left( {\alpha_{i} - \alpha_{{\text{t}}} } \right)}}{{\tan^{2} \left( {\alpha_{{\text{i}}} + \alpha_{{\text{t}}} } \right)}}} \right],} \hfill & {T = 1 - R} \hfill \\ {R_{{\text{c}}} = z_{{\text{p}}} \left[ {1 + \left( {\frac{{\pi n_{1} \omega_{0}^{2} }}{{\lambda_{0} z_{{\text{p}}} }}} \right)} \right],} \hfill & {R_{{\text{z}}} = \pm \sqrt {R_{{\text{c}}}^{2} - r^{2} } } \hfill \\ {\gamma = \cos^{ - 1} \left( {\frac{{R_{{\text{c}}}^{2} + a^{2} - r_{0}^{2} }}{{2aR_{{\text{c}}} }}} \right),} \hfill & {a = \sqrt {d_{{{\text{ip}}}}^{2} + \left( {R_{{\text{z}}} + r_{0} \cos \theta } \right)^{2} } } \hfill \\ {\alpha_{{\text{i}}} = \cos^{ - 1} \left[ {\frac{{d_{{{\text{ip}}}}^{2} + \left( {R_{{\text{z}}} + r_{0} \cos \theta } \right)^{2} - r_{0}^{2} - R_{{\text{c}}}^{2} }}{{2r_{0} R_{{\text{c}}} }}} \right],} \hfill & {n_{1} \sin \alpha_{{\text{i}}} = n_{2} \sin \alpha_{{\text{t}}} } \hfill \\ {r = \sqrt {d_{{{\text{ip}}}}^{2} + \left( {r_{0} \sin \theta } \right)^{2} - 2d_{{{\text{ip}}}} r_{0} \sin \theta \cos \varphi } ,} \hfill & {\omega = \omega_{0} \sqrt {1 + \left( {\frac{{\lambda_{0} z_{{\text{p}}} }}{{\pi n_{1} \omega_{0}^{2} }}} \right)} } \hfill \\ \end{array} $$
(5)

Noting that value θmax can be obtained by solution for θ in dip2 + (Rz + r0cosθ)2 − r02 − Rc2 = 0. Apart from optical radiation pressure, Stokes drag force Fs is used as friction term in Eq. (6).

$$ F_{{\text{s}}} = - 6\pi r_{0} \eta v $$
(6)

where η is viscosity of medium and v is velocity of particle. However, inertial forces are by orders of magnitude smaller than viscous friction effects at microscales and below. Neglecting Brownian stochastic force, Newton’s dynamics can be used to calculate the particle behavior in Eq. (7),

$$ \begin{array}{*{20}c} {m\dot{v}(t) = F_{{\text{s}}} + \hat{x}F_{{{\text{x}}i}} + \hat{z}F_{{{\text{z}}i}} } & {\left( {i = 1, \ldots ,4} \right)} \\ \end{array} $$
(7)

where m is mass of particle. In our simulation, the differential equation in Eq. (7) could be studied by using Runge–Kutta method in a small temporal discretization.

Results and discussion

Considered the medium containing microparticle, its refractive index n1 is 1.33, and the viscosity η is 1 mPa·s. The refractive index n2 for microparticle is 1.59, and its radius r0 is 5.5 μm. As for incident light source, light wavelength 980 nm with power P0 equal to 100mW is coupled into the four optic-fibers; beam waist radius ω0 is 3 μm. Herein, the offset distance of these optic-fibers could be studied to simulate the motion behaviors of particles as follows.

Same axial distance

Firstly, the same radial distance (zi = zj, i, j = 1,.., 4) regarding four optic-fibers is studied, which have two offset distances at x-axial direction. In addition, the radial distance z of such optic-fibers is 85 μm concerning original point. Beyond the misalignment at vertical level, the field of optical pressure force can be plotted in Fig. 2a. There are two trapping positions pointed to ± 10 μm at x-axial direction. Relying on dynamic simulation, six particles at different random position could be calculated to describe their own trajectories, as shown in Fig. 2b. These particles below the horizontal level move toward the bottom trapping location, and vice versa.

Fig. 2
figure 2

Simulation without misalignment of four optic-fibers at symmetric structure: a Optical trapping force for particle with radius of 5.5 μm. Four red arrows on the both sides imply the vertical position of optic-fibers. Meanwhile, the colors and directions of arrows represent the magnitudes and directions of optical trapping forces, respectively. Equipotential curve describes strength of optical force. b These motion trajectories of six particles

Full size image

When the misalignment of four optic-fiber is assumed, there are two vortex fields to induce these particle to perform an orbital rotation within their nearby regions. The position of optic-fibers is (− 85 μm, 15 μm), (− 85 μm, -6 μm), (85 μm, − 15 μm), (85 μm, 6 μm), respectively. Analyzing one of vortex field, the gradient forces from bottom and top optic-fibers always trap particles moving toward the center position in z-axial direction. Due to the misalignment structure of optic-fiber, the scattering forces from the bottom and top optic-fibers alternately repel the particle away from optic-fiber facet. Thus, the orbital rotation of particle can occur in the dual beam with offset distance, as shown in Fig. 3. It is illustrated that one optic-fiber array or more could form more vortexes to cause particle orbital rotation. This have benefited the generation of so many vortical effects to expand the dynamic observation and contributed to compare different types of cell with its rotary velocity, which identifies the biophysical characteristics of biological cells. Furthermore, both the offset distance and the optic-fiber setout can discretionarily be adjusted to form special vortex pattern. Decreasing the distance between four optic-fibers, two vortexes have merged together. Finally, only one vortex leads to the orbital motion for these nearby particles, as shown in Fig. 4. In comparison with the structure in Fig. 3, the distance of left-hand optic-fibers can be lower than the right-hand side. As a result, the top and bottom spins have clockwise and counterclockwise direction, as shown in Fig. 5. The top particles are clockwise motion, but the bottom particles exhibit counterclockwise. Especially, this adjustable function could be expected to utilize in the control of molecular gear-driven motion with co-rotation or anti-rotation [21].

Fig. 3
figure 3

Simulation with offset distance regarding optic-fibers: a Field of optical trapping force existed in two vortexes, b These motion trajectories of four particles at different position

Full size image
Fig. 4
figure 4

Coordinate of optic-fibers is (− 85 μm, 12.5 μm), (− 85 μm, − 4 μm), (85 μm, − 12.5 μm), (85 μm, 4 μm), respectively: a Only one steady vortex field, b Particles sustain same circular motion closing to original point

Full size image
Fig. 5
figure 5

Coordinate of optic-fibers is (− 85 μm, 6 μm), (− 85 μm, − 6 μm), (85 μm, − 15 μm), (85 μm, 15 μm), respectively: a Two vortex fields with different spin direction, b Particles move in either clockwise or anticlockwise motion

Full size image

In Chen’s work, particle behaviors regarding four different types have been identified including capture, spiral motion, orbital rotation, and escape. As far as their final position is concerned, both orbital rotation and capture are of great importance which are in favor of study on momentum and rotational inertia. Moreover, the offset distances have been decreased so that vortex field can be restrained. These particles attempt to move toward the region with minimum optical radiation area, as shown in Figs. 6 and 7. Different from Fig. 2, these particles maintain the motion with tortuous forms instead of straights due to the effect of vortex field. Similar to the position of orbital rotation, the trapping region can occur in the original point, as shown in Fig. 7. This assembly of optic-fiber array is better to capture the particle to satisfy the demand of particle enrichment.

Fig. 6
figure 6

Coordinate of optic-fibers is (− 85 μm, 12 μm), (− 85 μm, -6 μm), (85 μm, − 12 μm), (85 μm, 6 μm), respectively: a Weak vortex field disables the orbital rotation, b Each of particles move toward the vortex center

Full size image
Fig. 7
figure 7

Coordinate of optic-fibers is (− 85 μm, 12 μm), (− 85 μm, − 3 μm), (85 μm, − 12 μm), (85 μm, 3 μm), respectively: a There is an irregular vortex field due to the superposition of three vortex fields, b Particles could only move toward the original point

Full size image

Different axial distance

Apart from changing the offset distance relevant to x-axial direction, the axial distance in z-axial direction can be considered in our numerical model. Due to various possibility for the radial distance of four optic-fiber in z-direction, we mainly consider two situations which refer to two combinations, namely fibers 1 and 4, as well as fibers 2 and 3. When the radial distance zi (i = 1, 4) reduces to 71 μm, but the fibers 2 and 3 are still 85 μm, the vortex field in the asymmetry is inevitable to cause the different particle behaviors on the top and bottom. In Fig. 8a, the vortex field turns to non-axisymmetric spiral. In the horizontal position, the vortex field in the top and bottom is rather different from Fig. 4a. Compared with each other, the top vortex has a bulge closing to left. It implies that two particles are inclined to move to left-hand side on the top level. Conversely, the bottom particles are close to the right-hand side. According to dynamic simulation, the particle motion can be plotted in Fig. 8b, which have demonstrated the abovementioned speculation. However, the top particles simultaneously move in an approximated ellipsoid. The bottom particles no experienced by strong torques become spiral motion into the trap center. Thus, we also speculate that the radial distance for fibers 1 and 4 can be controlled to change the rotational radius on the top and bottom region. Cooperating with the adjustment in vertical offset distance, one larger vortex field on the top region than the bottom region can be generated, as shown in Fig. 9a. Therefore, it is obvious to find that the rotational area regarding the top particles is larger than the bottom particles, as shown in Fig. 9b. In Fig. 9b, the position of four particles is similar to Fig. 8b.

Fig. 8
figure 8

Coordinate of optic-fibers is (− 79 μm, 12 μm), (− 85 μm, − 4 μm), (85 μm, − 12 μm), (79 μm, 4 μm), respectively: a Asymmetric vortex field, b The top particles move in approximated ellipsoid, whereas the bottom particles become spiral motion

Full size image
Fig. 9
figure 9

Coordinate of optic-fibers is (− 79 μm, 14 μm), (− 85 μm, − 5 μm), (85 μm, − 14 μm), (79 μm, 5 μm), respectively: a The top vortex field is different from the bottom, b The top and bottom particles simultaneously move in periodic movement, but the rotational area on the top is larger than the bottom

Full size image

Considered the particle enrichment on the center, the misalignment distance can be decreased to play against the top and bottom vortex having a relative balance field. Actually, the quasi-balance position is closed to right-hand side compared to Fig. 7a. In this case, these particles would move toward the horizontal area closing to right-hand side, as shown in Fig. 10. According to this simulated results, this manipulation can be used in the particle microscale migration without the aid of motorized stages by changing the optic-fiber radial distance.

Fig. 10
figure 10

Coordinate of optic-fibers is (− 91 μm, 13 μm), (− 85 μm, − 4 μm), (85 μm, − 13 μm), (91 μm, 4 μm), respectively: a Decentered weak vortex field, b These particles are closed to right-hand side related to original point

Full size image

Conversely, the middle of two optic-fibers, namely fiber 2 and 3, has been adjusted for their radial distance zi. Keeping these particles on same position, the same offset distance illustrates different motion. In Fig. 11, the patterns of the top and bottom vortex occur to exchange so that the rotational radius with respect to the bottom particles could be greater than the top particles. This verifies that changing the radial distance could realize two different motion results in optic-fiber array. Compared to the change of optic-fibers 1 and 4, the particles are inclined to move toward the left-handed side, as shown in Fig. 12. Decreasing the radial distance between two optic-fibers, the force in the z-axial direction becomes weak, which results in failure to the horizontal motion. Finally, these particles exerted on vertical force only stop on the weakest optical trapping area.

Fig. 11
figure 11

Coordinate of optic-fibers is (− 85 μm, 14 μm), (− 79 μm, − 5 μm), (79 μm, − 14 μm), (85 μm, 5 μm), respectively: The top vortex field is different from the bottom, b The top and bottom particles simultaneously move in periodic movement, but the rotational area on the bottom is larger than the top

Full size image
Fig. 12
figure 12

Coordinate of optic-fibers is (− 85 μm, 13 μm), (− 91 μm, − 4 μm), (91 μm, − 13 μm), (85 μm, 4 μm), respectively: a Decentered weak vortex field, b These particles are closed to left-hand side related to original point

Full size image

Researching on particle rotational period, the particle A with respect to two kinds of different radial distance, reflecting optic-fibers 1–4 and 2–3, could be compared and plotted in Fig. 13. By applying method for seeking peak, the period in z-axial direction is 0.30 s and 0.26 s for particle A in Figs. 9 and 11, respectively. Considered in x-axial direction, the period 0.29 s in Fig. 9 is quite close to 0.27 s in Fig. 11. This implies that shorter major axis of ellipse is higher rotational frequency when particle moves in elliptic orbit. Meanwhile, the movement rule of these bottom particles is consistent with the above result. A particle motion with controllable period behavior based on quad-beam is expected to continue in our future work.

Fig. 13
figure 13

The displacement of particle A changes with time in Figs. 9 and 11: a Displacement of z-axial direction, b Displacement of x-axial direction

Full size image

Conclusion

Attempt to manipulate the motion of microparticle is fascinating work by using optic-fiber tweezers. The particle trapping and rotation behaviors have opened up exciting possibilities for analyzing particle property, size, shape in biomedical application. Thus, an array of optic-fibers having quad-beam has been presented to generate two kinds of effect on the particle motion. In same axial distance, this symmetric structure of optical field could realize two same vortex fields inducing neighboring particle in rotational motion with elliptic orbit. As soon as the offset distance of four optic-fibers change, the trapping location could be either original point or the center of a pair of two optic-fibers. In addition, the axial distance of two different individual optic-fiber could change the top and bottom vortex range, which has benefits for realizing particle motion in different rotational radius. In this end, this quad-beam by using four same optic-fibers, compared to dual beam, could offer an opportunity to generate more vortex or trapping field to manipulate particle motion, which is expected to explore the biophysical properties of various single cells synchronously.