Introduction

In the research of modern terahertz (THz) optoelectronics, monochromatic THz sources play an important role in high-resolution THz applications, such as environmental gas monitoring, high-density and high-speed wireless communications [1,2,3,4]. Difference frequency generation (DFG) with two closely spaced laser frequencies \( \omega_{1} \) and \( \omega_{2} \) in second-order nonlinear optics crystals is one of the promising processes for efficient monochromatic THz wave output in the wide frequency tuning range and room temperature operation [5, 6]. THz wave generation based on DFG has been intensively researched [7,8,9]. Unfortunately, the maximum frequencies generated by these optics processes are limited to 7 THz [10]. Moreover, the output power of THz wave with high frequency is extremely low. Such limitations on output frequencies and power are caused by the dramatically increased absorption of the nonlinear materials in the vicinity of polariton resonance region (PRR). However, at the same time, polariton resonances can induce giant second-order nonlinearities. The giant second-order nonlinearities in the vicinity of PRR can be exploited to extend the output frequencies and enhance the output power of THz wave [11]. In the vicinity of PRR for THz wave generation, the crucial point for efficient THz wave generation is to minimize the path of THz wave in the crystal. A transverse pumping geometry can overcome this problem [12,13,14]. The optical beams propagate close to crystal lateral surface, and THz wave radiates from the crystal surface and propagates perpendicular to the direction of the optical beams. The absorption loss is minimized because the THz wave is generated from the crystal surface.

A frequently employed material for DFG is the nonlinear optical crystal MgO:LiNbO3, because of its relatively large second-order nonlinear optical coefficient (d33 = 25.0 pm/V at 1064 nm) and its wide transparency range [15]. However, DFG from zinc-blende-type semiconductors, such as GaP, GaAs and CdTe, is advantageous in obtaining an intense THz wave since their second-order nonlinear optical coefficients are several times larger than that of MgO:LiNbO3. d36 of GaAs, GaP and CdTe is 170 pm/V, 70.6 pm/V and 109 pm/V at 1064 nm, respectively [16, 17]. In addition, their absorption coefficients in the THz frequency region are about ten times smaller than that of MgO:LiNbO3 [18].

In this paper, we explore THz wave generation from zinc-blende crystals, such as GaAs, InP, ZnTe and CdTe with a transverse pumping geometry. Parametric gain coefficient in the low-loss limit of THz wave during DFG process in the vicinity of PRR is analyzed. We investigate the frequency tuning characteristics of THz wave via varying wavelength of optical waves and poling period of periodically inverted crystal.

Theoretical model

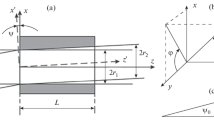
The schematic drawing of a surface-emitted DFG from zinc-blende crystal waveguide with a transverse pumping geometry is presented in Fig. 1. Two input optical waves \( \lambda_{1} \) and \( \lambda_{2} \) at the frequencies of \( \omega_{1} \) and \( \omega_{2} \) in the infrared (IR) domain are propagating collinear along the x-axis in a zinc-blende crystal waveguide. The waveguide is achieved by periodically switching the orientation between \( \left[ {111} \right] \) and \( \left[ {\bar{1}\bar{1}\bar{1}} \right] \), achievable through the epitaxial growth of zinc-blende crystals on an orientation-patterned substrate [19, 20]. A THz wave is emitted due to the oscillating nonlinear polarization at the difference frequency between the two input waves. The radiation angle \( \theta \) between directions of the optical and THz wave propagation is determined by the refractive index of optical waves and THz wave in the crystal, and the poling period of periodically inverted crystal,

$$ \cos \theta = \frac{{K_{{\text{IR}}} }}{{K_{{\text{THz}}} }}, $$
(1)

where \( K_{{\text{THz}}} = {{\omega_{{\text{THz}}} n_{{\text{THz}}} } \mathord{\left/ {\vphantom {{\omega_{{\text{THz}}} n_{{\text{THz}}} } c}} \right. \kern-0pt} c} \) is the wave vector of THz wave, \( n_{{\text{THz}}} \) is the refractive index at \( \omega_{{\text{THz}}} \) frequency; \( K_{{\text{IR}}} = {{n_{1} \omega_{1} } \mathord{\left/ {\vphantom {{n_{1} \omega_{1} } c}} \right. \kern-0pt} c} - {{n_{2} \omega_{2} } \mathord{\left/ {\vphantom {{n_{2} \omega_{2} } c}} \right. \kern-0pt} c} - {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \varLambda }} \right. \kern-0pt} \varLambda }, \)where \( \varLambda \) is the poling period of periodically inverted crystal, \( n_{1} \) and \( n_{2} \) are the refractive indices at optical wavelengths \( \lambda_{1} \) and \( \lambda_{2} \) at \( \omega_{1} \) and \( \omega_{2} \) frequencies, respectively. THz wave can be generated in a direction perpendicular to the optical wave propagations if \( K_{{\text{IR}}} \) equals to zero.

Fig. 1
figure 1

Schematic diagram of a surface-emitted DFG from zinc-blende crystal waveguide with a transverse pumping geometry

Full size image

The parametric gain coefficient \( g_{0} \) in the low-loss limit during DFG processes in cgs units can be determined by the following expression [21]:

$$ g_{0}^{2} = \frac{{\pi \omega_{{\text{THz}}} \omega_{2} }}{{2c^{3} n_{1} n_{2} n_{{\text{THz}}} }}I_{\lambda 1} \left( {d_{E}^{{\prime }} + \frac{{S\omega_{0}^{2} d_{Q}^{{\prime }} }}{{\omega_{0}^{2} - \omega_{{\text{THz}}}^{2} }}} \right)^{2} $$
(2)
$$ \alpha_{{\text{THz}}} = 2\frac{{\omega_{{\text{THz}}} }}{c}\text{Im} \left( {\varepsilon_{\infty } + \frac{{S\omega_{0}^{2} }}{{\omega_{0}^{2} - \omega_{{\text{THz}}}^{2} - i\omega_{{\text{THz}}} \varGamma }}} \right)^{{\frac{1}{2}}} $$
(3)

where \( \alpha_{{\text{THz}}} \) is absorption coefficient in THz region, and \( \omega_{0} \), S and \( \varGamma \) denote eigen frequency, oscillator strength of the polariton mode and the bandwidth of the phonon mode in the zinc-blende crystal, respectively. \( I_{\lambda 1} \) is the power density of the optical wave with wavelength \( \lambda_{1} \). \( d_{E}^{{\prime }} \) and \( d_{Q}^{{\prime }} \) are nonlinear coefficients related to pure parametric (second order) and Raman (third order) scattering processes, respectively. The relationship between \( d_{E}^{{\prime }} \) and \( d_{Q}^{{\prime }} \) is [21].

$$ d_{E}^{{\prime }} + Sd_{Q}^{{\prime }} = rn_{1}^{4} $$
(4)

where r is the electro-optic coefficient. In this paper, the data for GaAs, InP, ZnTe and CdTe are taken from references [16, 22, 23].

Parametric gain characteristics

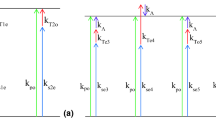
GaAs, InP, ZnTe and CdTe have infrared- and Raman-active transverse optical (TO) phonon modes at the frequencies of 269 cm−1, 304 cm−1, 179 cm−1 and 141 cm−1, respectively. The TO phonon modes are useful for efficient THz wave generation because of the largest parametric gain in the vicinity of PRR, as shown in Fig. 2. From the figure, we find that the central frequencies of PRR are 4.23 THz, 5.37 THz, 8.07 THz and 9.12 THz, corresponding to CdTe, ZnTe, GaAs and InP, respectively. As THz wave frequencies approach PRR, the parametric gain coefficient \( g_{0} \) sharply reaches a maximum value (> 105 cm−1) and the absorption coefficient \( \alpha_{{\text{THz}}} \) intensively increases to 104 cm−1. Such dramatic enhancements of parametric gain coefficients can be exploited for improving the output powers and extending the frequency bands of THz waves if using a transverse pumping geometry to minimize the propagation path of THz wave within the crystal. As discussed above, output frequencies of THz wave from 4.23 THz to 9.12 THz can be efficiently realized in the vicinity of PRR by using CdTe, ZnTe, GaAs and InP with a transverse pumping geometry.

Fig. 2
figure 2

Parametric gain coefficient in the low-loss limit \( g_{0} \) and absorption coefficient \( \alpha_{{\text{THz}}} \) versus THz wave frequency at room temperature. \( \lambda_{1} { = 1} . 0 6 4\;\upmu{\text{m}} \), \( I_{\lambda 1} = 100\;{\text{MW}}/{\text{cm}}^{2} \). a GaAs, b InP, c ZnTe, d CdTe

Full size image

Frequency tuning characteristics

According to Eq. (1), the frequencies of the THz wave can be tuned by varying poling period \( \varLambda \) and wavelength of optical waves \( \lambda_{1} \) and \( \lambda_{2} \). Figure 3 shows the tuning characteristics as a function of optical wavelength \( \lambda_{1} \) ranging from 0.75 to 2.5 μm. From the figure, we find that the frequencies of THz wave are rapidly and smoothly increased with the increase in wavelength \( \lambda_{1} \). In Fig. 3a, THz wave with frequencies ranging from 5.65 to 8.88 THz can be obtained from GaAs crystal as \( \varLambda = 10\;\upmu{\text{m}} \). The central frequency of PRR corresponds to \( \lambda_{1} = 1.22\;\upmu{\text{m}} \). Similarly, THz wave with frequencies ranging from 8.25 to 9.62 THz, from 4.71 to 5.76 THz and from 3.22 to 7.29 THz can be obtained from InP, ZnTe and CdTe crystals as \( \varLambda = 10\;\upmu{\text{m}} \), \( \varLambda = 20\;\upmu{\text{m}} \) and \( \varLambda = 15\;\upmu{\text{m}} \), respectively. The central frequency of PRR corresponds to \( \lambda_{1} = 1.08\;\upmu{\text{m}} \), \( \lambda_{1} = 1.13\;\upmu{\text{m}} \) and \( \lambda_{1} = 0.8\;\upmu{\text{m}} \), respectively. THz wave generated from PRR can be realized by tuning the wavelength \( \lambda_{1} \).

Fig. 3
figure 3

THz wave frequencies versus the wavelength of optical wave \( \lambda_{1} \). a GaAs, \( \varLambda = 10\;\upmu{\text{m}} \), b InP, \( \varLambda = 10\;\upmu{\text{m}} \), c ZnTe, \( \varLambda = 20\;\upmu{\text{m}} \), d CdTe, \( \varLambda = 15\;\upmu{\text{m}} \)

Full size image

The frequencies of THz wave as a function of poling period \( \Lambda \) as \( \lambda_{1} { = 1} . 0 6 4\;\upmu{\text{m}} \) are depicted in Fig. 4. From the figure, we find that widely tunable THz wave can be obtained by varying poling period \( \Lambda \). From the figure, we find that the frequencies of THz wave are rapidly and smoothly decreased with the increase in poling period \( \Lambda \). As shown in Fig. 4a, b, THz wave with frequencies ranging from 9.5 to 1.6 THz and from 11.3 to 1.9 THz can be obtained from GaAs and InP crystals as \( \varLambda \) changes from 8 to 48 μm, respectively. The central frequencies of PRR correspond to \( \varLambda = 9.4\;\upmu{\text{m}} \) and \( \varLambda = 9.9\;\upmu{\text{m}} \), respectively. As shown in Fig. 4c, d, THz wave with frequencies ranging from 10.5 to 2.1 THz and from 9.4 to 1.88 THz can be obtained from ZnTe and CdTe crystals as \( \varLambda \) changes from 10 to 50 μm, respectively. The central frequencies of PRR correspond to \( \varLambda = 19.7\;\upmu{\text{m}} \) and \( \varLambda = 22.1\;\upmu{\text{m}} \), respectively. THz wave generated from PRR can realized by tuning the poling period \( \Lambda \).

Fig. 4
figure 4

THz wave frequencies versus the poling period \( \varLambda \), \( \lambda_{1} { = 1} . 0 6 4\;\upmu{\text{m}} \). a GaAs, b InP, c ZnTe, d CdTe

Full size image

Compared with other works in which THz wave generations are far from PRR to avoid intensive absorption, the theoretical model proposed in this letter can exploit dramatic enhancement of parametric gain in the vicinity of PRR with a transverse pumping geometry. The theoretical model proposed in this work is useful to other materials with crystal birefringence properties, such as LiNbO3, LiTaO3 and KTA, in which polaritons are both infrared active and Raman active. The theoretical model is also useful to semiconductor optical waveguide with modal birefringence properties. By utilizing modal birefringence of fundamental TE and TM modes in planar waveguide, the absorption at PRR can be efficiently reduced [24].

Conclusion

We explore THz wave generation at PRR of zinc-blende crystal waveguide by DFG with a transverse pumping geometry. It is shown that by using grating vector of periodically inverted crystal, THz wave can be efficiently generated by DFG in the vicinity of PRR. Dramatic enhancement of parametric gain coefficients in the vicinity of PRR can be exploited for improving the output power and extending the frequency bands of THz wave by using a transverse pumping geometry to minimize the propagation path of THz wave within the crystal. THz wave generated from PRR can be realized by tuning the wavelength \( \lambda_{1} \) and poling period \( \Lambda \).