Introduction

During the past decades, photonic crystals (PCs) have inspired great interest of researchers due to their novel electromagnetic (EM) properties and potential application in several scientific and technical areas such as filters, optical switches, cavities and design of more efficient lasers. [1,2,3]. The conventional PCs are artificial materials, in which the different dielectrics are periodically arranged in one- two-, or three dimensions of space. The key motivation behind the proposal of PCs is the possibility of modifying the propagation of EM wave by creating a frequency region where EM waves cannot propagate through the structure, named photonic band gap (PBG) [4]. Two-dimensional (2D) PCs are important because they can be fabricated fairly easily and result in devices, such as waveguides and channel drop filters, which can be part of an all-optical chip [5,6,7]. It is well known that the EM wave can be decomposed into the E-polarization (TM-mode) and H-polarization (TE-mode) modes for 2D structures. A full PBG exists for a 2D PC only when the PBG for both polarization modes is presented and overlaps with each other [8]. Many potential applications of PCs rely on their photonic band gaps. So, it is of great interest to design PCs with a full band gap as large as possible. So many attempts like symmetry reduction [9, 10] and anisotropy in dielectricity [11,12,13] have been made to enlarge the PBG in 2D PCs.

However, the PBGs of conventional PCs suffer from being highly sensitive to the lattice. It means that the PBGs cannot be changed as the dielectrics and topology of PCs are certain. To overcome these drawbacks, the metamaterials, which are frequency-dependent dielectrics, have been introduced into PCs to achieve tunable PBGs [14, 15]. The typical metamaterials in the nature are plasma [16], superconductors [17], semiconductors [18] metals [19], and so on. In 2004, the Japanese researchers Hojo and Mase proposed plasma PCs (PPCs) for the first time [20]. Similar to conventional PCs, PPCs are artificial periodic arrangements composed of alternating the plasma and dielectric. Photonic band structure of PPCs has been investigated for both H-polarization and E-polarization many times, separately [21,22,23,24,25,26,27,28,29]. In 2015, Shiveshwari and Awasthi [30] have been introduced plasma-based PCs in which full PBGs are observable. In the following, Fathollahi Khalkhali et al. [31, 32] studied the possibility of creation full PBG in PPCs consist of plasma rod in anisotropic tellurium (Te) back ground with square and triangular lattice and triangular lattice of Te rods in plasma background. Their investigation shows that the mentioned structures represent wide full band gaps.

Thus, in this work we study the band gap properties of 2D PPCs consisting of periodic arrays of infinitely long parallel anisotropic dielectric cylinder with different geometrical-shaped cross section in a plasma background in square lattice. So we discuss the modification of the full band gap as a function of dielectric rods size, the orientation of non-circular ones and variation effect of the plasma frequency of the plasma medium on the band structure.

Structures and computational methods

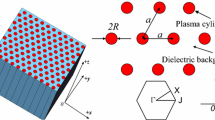
In the present study, we have considered square lattice created by circular, hexagonal and square Te rods in the plasma background. Figure 1 shows the schematic diagram of the structures under consideration. In all structures, the parameter \(a\) is the lattice constant. We assume that the periodicity of the PPCs is in the X–Y plane. The orientation of the non-circular Te rods relative to the lattice axes is defined by the angle \(\theta\). For instance, the rotation angle, \(\theta\), of square rods in square lattice is depicted in Fig. 2, which is defined as the angle between axes of the square cross section and the lattice axes. We have chosen Te as the anisotropic material, which has a positive uniaxial crystal with two different principle refractive indices as ordinary-refractive index \(n_{o}^{\text{Te}} = 4.8\) and extraordinary-refractive index \(n_{\text{e}}^{\text{Te}} = 6.2\) over the wavelength range of \(4.50 - 6.25\,\,\upmu{\text{m}}\) [33, 34], in which the extraordinary one is parallel to the Z axis. When we chose different refractive index constants for E- and H-polarization modes, we can match the relative position of band gaps for two modes; thus, this will enable the optimal overlapping of band gaps, and the largest full band gap can be obtained.

Fig. 1
figure 1

Schematic diagrams of studied structures: square lattice of a circular b hexagonal c square Te rods in plasma background

Full size image
Fig. 2
figure 2

Rotated square rods in a square lattice with angle \(\theta\), which is defined as the angle between axis of the square rods cross section and the lattice axis

Full size image

It is well known that the non-magnetized plasma is a kind of frequency-dependent dielectrics, the dielectric constant \(\varepsilon_{\text{p}}\) that meets the Drude model, which is written as the following [35]:

$$\varepsilon_{\text{p}} (\omega ) = 1 - \frac{{\omega_{\text{p}}^{2} }}{{\omega^{2} - j(\nu_{c} \omega )}}$$
(1)

where \(\omega_{\text{p}} ,\,\nu_{\text{c}} \,\,{\text{and}}\,\,\omega\) are the plasma frequency, the plasma collision frequency and EM wave frequency, respectively. Plasma frequency is defined as \(\omega_{\text{p}} = (e^{2} n_{\text{e}} /\varepsilon_{0} m)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}\) in which \(e,\,\,m,\,\,n_{\text{e}} \,\,{\text{and}}\,\,\,\varepsilon_{0}\) are electron charge, electron mass, plasma density and dielectric constant in the vacuum, respectively.

One of the most common computational tools in classical electromagnetism is the finite-difference time-domain (FDTD) algorithm. The FDTD method is a general method for numerically solving the time-dependent Maxwell equations in media that is structured on the scale of the wavelength. It is therefore, particularly, well suited to simulate light field dynamics and propagation in finite PC structures. This method is implemented perfectly in MIT EM Equation Propagation (Meep) package [36], and we have used this software in our simulations. In our calculations, each unit cell is divided into 30 × 30 grid points. At the boundaries of unit cells, we impose Bloch periodic boundary conditions. The structures are excited by a temporal Gaussian pulse source spanning the frequencies of interest, which is located in a non-symmetric point of the unit cell. The electric and magnetic fields of the source for TM and TE modes are polarized along the Te rods direction (Z-direction), respectively. It should be noted that in our simulations all frequencies are normalized as \(\omega a/2\pi c\), in which a and c are lattice constant and speed of light, respectively.

Results and discussions

In this section, we study the mentioned structures (Fig. 1a–c) and all the calculations were performed using FDTD method. Our main goal here is to investigate the modification of the full band gap spectrum by adjusting the geometrical parameters of the mentioned PPCs and changing the plasma frequency. We know that for plasma to exist ionization is necessary. The term plasma frequency by itself usually refers to the plasma and electron density, that is, the number of free electrons per unit volume. The degree of ionization of a plasma is the proportion of atoms that have lost or gained electrons and is controlled mostly by the temperature. Thus, by changing the temperature it is possible to vary the plasma frequency. In our calculations for simplification, the frequency region is normalized by \(\omega a/2\pi c\), and the collision frequency is defined as \(\nu_{\text{p}} = 0.02\omega_{{{\text{p}}_{0} }}\). It is noticed that \(\omega_{{{\text{p}}_{0} }}\) is a constant, which is equal to \(2\pi c/a\). The variation of full PBG of these structures for each kind of rod shapes will be separately analyzed in the next there subsections.

Circular rods

In this subsection, the results for the square lattice are presented. We begin our discussion with square lattice of circular Te rods in the plasma background. In this case the radii of Te rods and plasma frequency are our adjustable parameter. Thus, the photonic band spectrum of the structure investigated for all possible value of \(r\) (radius of Te rods) for different values of plasma frequency. The photonic band spectrum of the structure has been investigated for all possible value of \(r\) (radius of rods) when plasma frequency is equal to zero; then, we slightly increase the value of \(\omega_{\text{p}}\). Therefore, the photonic band structure is studied for all possible values of \(r\), \(\omega_{\text{p}}\) and the effect of the plasma frequency changes is studied completely. The obtained results demonstrate that for \(\omega_{\text{p}} = 0\), when \(r\) ranges from 0.18a to 0.42a relatively wide full PBG is observable and by increasing the plasma frequency from zero to \(\omega_{\text{p}} = 0.20(2\pi c/a)\), especially at \(r\) around 0.34, the width of the full band gap smoothly increases and for plasma frequency larger than \(0.20(2\pi c/a)\) the band width is reduced. The variation of full PBG and gap–midgap ratio \(\omega_{r}\) (ratio between band gap width and midgap frequency) as a function of \(r\) and \(\omega_{\text{p}}\) are shown in Fig. 3a, b. Furthermore, the full photonic gap structure at \(\,\,r = 0.34a\) for \(\omega_{\text{p}} = 0\) and \(\omega_{\text{p}} = 0.10(2\pi c/a)\) with normalized width of \(\Delta \omega = 0.0\,386(2\pi c/a)\) and \(\Delta \omega = 0.0\,495(2\pi c/a)\) is shown in Fig. 3c, d, respectively. These full PBG is produced by an overlap of the TM3-4 and TE1-2 band gaps.

Fig. 3
figure 3

Variation of a gap width and b gap–midgap ratio as a function of parameters \(r\,\,{\text{and}}\,\,\omega_{\text{p}}\) and dispersion relation of E-polarization (red dashed) and H-polarization (blue dashed) at c \(\omega_{\text{p}} = 0\) and d \(\omega_{\text{p}} = 0.10(2\pi c/a)\) at \(r = 0.34a\), for square lattice of plasma photonic crystals made of circular Te rods in plasma background (color figure online)

Full size image

Hexagonal rods

At next step, we study the band gap spectrum properties of PPCs with hexagonal Te rods in the plasma background. In this case, the side length \((r)\) and orientation (\(\theta\)) of hexagonal Te rods are effective parameters in the creation of PBG. In this case, at \(\omega_{\text{p}} = 0\) and for a reasonable given value of \(r\,\,\,\,\) the band structure studied as a function of \(\theta\) and this procedure is repeated for other values of \(r\,\); therefore, the photonic band spectrum is calculated for all possible values of \(r,\,\theta \,\,{\text{at}}\,\,\omega_{\text{p}} \, = \,0\). Our comprehensive calculations reveal that when \(r\) is in the range of \(0.22a\,\, - \,\,42a\) at \(\theta = 30^{ \circ }\), the width of full PBGs is noticeable. It should be noted that the maximum band gaps in the structure are obtained for \(r\) around \(0.38\) in which variation of the band gap versus \(\theta\) is smooth and negligible. Now we consider the case in which the plasma frequency is increased as a result of temperature variations. Figure 4a, b represents the modification of full PBG of the structure at \(\theta = 30^{ \circ }\) as a function of \(r\,\,{\text{and}}\,\,\omega_{\text{p}}\). It can be found that when \(r\) is in the area of \(0.45a - 0.51a\) and at \(\theta = 30^{ \circ }\), when \(\omega_{\text{p}}\) changes from \(0.00(2\pi c/a)\,\,\,\,to\,\,\,0.30(2\pi c/a)\), the width of band gaps so slightly and smoothly grows and by increasing normalized plasma frequency \((\omega_{\text{p}} > 0.30(2\pi c/a))\), the band gap completely disappears.

Fig. 4
figure 4

Variation of a gap width and b gap–midgap ratio as a function of parameters \(r\,\,{\text{and}}\,\,\omega_{\text{p}}\) at \(\theta = 30^{ \circ }\) for square lattice of hexagonal Te rods in plasma background (color figure online)

Full size image

Square rods

Finally, we have simulated band structure of PPCs of square Te rods in the plasma background (Fig. 1c). Our main goal here is to investigate the variation of the band gap structure and the full band gap width by adjusting the two geometrical parameters: \(r\,\) (half side length of square rods) and \(\theta\) (orientation of square rods with respect to the lattice axis) for different values of plasma frequency. At first we studied the evolution of PBG versus \(r\,\) by fixing \(\theta = 0^{ \circ }\), and this process has been repeated for other values of \(\theta\) at \(\omega_{p} = 0.\) Our calculations reveal that this structure represents full PBG for \(r\) in the range of 0.20a–0.28a at \(\theta = 0^{ \circ }\). The simulations show that the full band gap in the structure is sensitive to \(\theta\), so that by increasing \(\theta\), the full gaps disappears. The results show that by increasing the plasma frequency from \(0.00(2\pi c/a)\,\,{\text{to}}\,\,0.30(2\pi c/a)\), the size of PBGs is maintained constant for optimum value of geometrical parameter and for plasma frequency greater than \(\,0.30(2\pi c/a)\), the band gaps become narrower. Figure 5a, b shows the variations of full PBG of the structure at \(\theta = 0^{ \circ }\) as a function of \(r\,\,{\text{and}}\,\,\omega_{\text{p}}\).

Fig. 5
figure 5

Variation of a gap width and b gap–midgap ratio as a function of parameters \(r\,\,{\text{and}}\,\,\omega_{\text{p}}\) at \(\theta = 0^{ \circ }\) for square lattice of square Te rods in plasma background (color figure online)

Full size image

At the end, it should be noted that in convectional PCs, when each scatterer has the same geometric symmetry as the lattice for a given lattice symmetry, the largest gaps are obtained. While our proposed structure consists of plasma materials, the mentioned rule does not always hold in PPCs and the width of obtained band gaps is larger than previously studied square lattices which consist of dielectric materials in plasma background.

Conclusion

In summary, we have performed a detailed numerical analysis on photonic band properties of square lattice of PPCs created by Te rods with different geometrical shapes in the plasma background, using the FDTD method. Extensive calculations reveal that all of these structures represent full PBG with noticeable width and gap–midgap ratio for optimum values of structural parameters, and we can tune the band gap by varying plasma frequency. These results can be helpful in designing waveguide, reflector, all-optical convertor and splitter based on PPCs.