Dynamics of CoVid-19 Disease in Semarang, Indonesia: Stability, Optimal Control, and Model-Fitting

Abstract

The dynamics of CoVid-19 disease becomes a concern in this paper. Initially, the positivity and boundedness are established to ensure that the number of susceptible, infected, quarantined, and recovered individuals are always positive in the population and the population numbers are always bounded. The equilibrium points of disease-free and endemic are then determined for uncontrolled dynamical system. Based on the equilibrium points, we can provide the basic reproduction number to ensure that infectious disease can transmit or not in the population. The infection has ability to transmit in the population if $\mathcal {R}_0>1$ and vice versa. The local stability is established through the Jacobian matrix at the disease-free and endemic equilibrium points. The appropriate Lyapunov function is initially introduced to provide the global stability of dynamical system. Moreover, the sensitivity analysis is used to determine the dominant parameters for each state variable (most positive or negative). The least square technique is used to compare the numerical results using the fourth-order Runge–Kutta and actual data of CoVid-19 disease in Semarang, Indonesia. Moreover, Continuous Time Markov Chain (CTMC) gives the same patterns between the deterministic and stochastic results. Because vaccination and social distancing have a significant impact on the profile of susceptible, infected, quarantined, and recovered classes, then we introduce a mathematical model of CoVid-19 with two time-dependent controls $(u_1,u_2)(t)$. It follows from the results obtained, the implementation of control gives the number of infected, quarantined, and recovered individuals decreased, and the number of susceptible individuals increased. The neural network approach also gives the significant estimations based on the root mean square error by using the training function of Levenberg-Marquadt.

Introduction

Covid-19 originated from a coronavirus that has been endemic since 2019. Coronaviruses can spread through the air and can cause fever and shortness of breath. In Indonesia, Covid-19 spread for the first time on March 2, 2020 [25]. The Covid-19 epidemic has not yet ended. In data sourced from covid.19.go.id there are 14,657 active cases of covid-19 in Indonesia. The Ministry of Health has appealed to the public to actively use masks again to prevent a potential spike in Covid-19 cases. The increase in Covid-19 was due to a new variant of Covid-19 that entered Indonesia, namely the Arcturus variant. This variant causes fever, cough, muscle aches, and also conjunctivitis. In January 2023, the Arcturus variant was discovered for the first time in India. To form Arcturus, two or more sublineages underwent homologous recombination [34]. Sourced from the Ministry of Health, cases of the Arcturus variant of Covid-19 increased in mid-April 2023 in Indonesia. Predicting the spread of disease outbreaks can be studied through applied mathematics. The SI (Susceptible-Infection) simple mathematical model is applied to Covid-19’s spread. The SI model involves the Bernoulli Verhulst model to derive an identification parameter approach [24]. Predicting the number of population requiring medical treatment can use the SIR model with Susceptible-Infection-Recovered during Covid-19’s spread pandemic [3]. By combining the Lyapunov method and the LaSalle invariant principle, the Covid-19 model with SIR considers the effect of room availability at the hospital and reduces the spread of Covid-19 [7]. Using the classic Kermack-McKendrick model, this study examines the spread of Covid-19. Additionally, the SIR model was applied to the first wave of Covid-19 spreading in Malaysia. This study shows that control in the form of awareness of cleanliness and social distancing can reduce the transmission of Covid-19 [9]. With appropriate restrictions and strong policies, the SIR model of Covid-19’s spread can be controlled in all communities based on the data recorded and the data from the modeling approach [23]. The SIR model for individuals I and R depends on the parameters of the level of interaction and the intensity of the patient’s recovery [33]. The Convex event rate at SIR was solved numerically using the Non-Standard Finite Difference (NSFD) method [45]. In a short-term comparison of the Covid-19 spread model to the SIR, Verhulst, and Gompertz models, the SIR is found to be more useful [26]. The spread of Covid-19 in the SIR model based on the influence of the health system shows local stability when the reproductive number is less than one [4].

A model for predicting Covid-19’s spread in the short and long-term was based on four compartments, namely SIRD (susceptible-infection-recovered-decreased) [12]. The SIRD model is a nonlinear differential equation used to predict Covid-19 infection in the short term [36]. A model called SIRD (susceptible-infection-recover-dead) was implemented in Indonesia to estimate the Covid-19’s spread in the long term [37]. When the SIRD is used to predict Covid-19’s spread with sex and age filters, it shows that the younger population is more likely to infect the older population [13]. Covid-19 is an epidemic that can occur in any country, according to the SIRD model, with a reproduction number ranging from 1.0011 to 2.7936 [6]. In the case of Covid-19, there are exposed individuals, namely individuals who are not necessarily positive but experience symptoms of Covid-19. The addition of the exposed subpopulation to the SEIR model shows the need for control to reduce the impact of Covid-19 [30]. The SEIR considering vaccination and isolation for the Covid-19 case shows an increase in the recovered population in Indonesia [8]. The Adaptive SIRV Model ($A-SIRV$) is time-dependent for estimating the spread of the Covid-19 outbreak using the Variational Imbedding method [35]. Vaccination against Covid-19 is not only done once. Research on mathematical models with the first and second vaccinations was conducted by Sepulveda et al. The study describes the behavior of Covid-19 after the initial vaccination [43]. The SVIR (susceptible-vaccine-infection-removed) mathematical model assumes that susceptible individuals will be vaccinated. This study uses the ordinary least squares in the SVIR model [40]. Vaccine allocation based on the highest spread of Covid-19 can increase the benefits of the vaccination program in Indonesia [28]. Even though they have implemented vaccinations, it is undeniable that susceptible individuals can be re-exposed to Covid-19. One of the efforts to prevent the spread is to implement quarantine for individuals exposed to Covid-19. A SIQR model is a Covid-19 model that consists of four compartments: susceptible, infection, quarantine, and recovery [38]. The SIQR model is suitable for areas that have implemented quarantine rules. According to research on the SIQR model, large noise can cause the disease to disappear exponentially, establishing sufficient conditions for a unique stationary distribution to exist [15]. The SIQR model with the Atangana-Beleanu-Caputo (ABC) fractional fractal derivative was applied in the spread of Covid-19 conducted by Adnan et al. This research shows that quarantine is able to control the spread of Covid-19 [1]. The nonstandard finite difference (NSFD) numerical solution applied to the SIQR model of the spread of Covid-19 provides a positive and convergent solution towards stability [2]. With the new Arcturus Covid-19 variant entering Indonesia, it is necessary to provide preventive measures in the form of quarantine. It is of interest to researchers to see how Covid-19 spreads concerning quarantine, which reduces the risk of individuals contracting the infection. In this study, a model of Covid-19 spread is presented with strategic control of social restrictions, observing both local and global stability of disease-free and endemic areas. The other studies of the latest progress in this research field can be referred to [10, 11, 17,18,19,20, 31, 39, 44].

Other parts of this paper are organized as follows. Section 1 provides the introduction of this study. The model formulation and also the theorems of positivity, boundedness, existence, and uniqueness are given in Section 2. Section 3 presents equilibria points, basic reproduction number, local stability, and global stability at the equilibria points. Due to the effectiveness of control for our dynamical system, the optimal control is introduced in Section 4. Section 5 gives the numerical results and discussion consisting of sensitivity analysis, simulation of SIQR model, best fit parameters using least square technique, comparison results between deterministic and stochastic SIQR models using continuous time markov chain, simulation of SIQR model with optimal control, and also the estimation results by using neural network, where the training function of Levenberg-Marquardt and activation function of Tangent Sigmoid are employed for the best model of neural network. Finally, the conclusions of this study are established in Section 6.

Mathematical Model

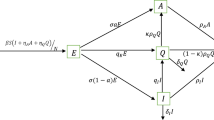
We firstly consider the following SIQR model on CoVid-19 disease without a control strategy

$$\begin{aligned} \begin{aligned}&\frac{dS}{dt}=\Lambda -\beta \delta SI-\mu S,\\&\frac{dI}{dt}=\beta \delta SI-(r+\epsilon +\mu +d)I,\\&\frac{dQ}{dt}=\epsilon I-(\varphi +d+\mu )Q,\\&\frac{dR}{dt}=rI+\varphi Q-\mu R, \end{aligned} \end{aligned}$$

(2.1)

where the notations and values in system (2.1) are shown in Table 1 and the state variables S, I, Q, R respectively represent the susceptible, infected, quarantined, and recovered sub populations. The dynamical system (2.1) is a modification of mathematical model introduced by Crokidakis [21, 22], by introducing the lockdown $\delta$ and isolation rate $\epsilon$. Moreover, we validate our system (2.1) by comparing the numerical results using fourth-order Runge–Kutta and actual data of CoVid-19 in Semarang, Indonesia. Due to the effectiveness of control implementation for our model of dynamical system, then we also introduce two controls including the vaccination and social distancing.

Remark 1

In epidemiology, the main concern is to reduce the number of infected individuals. Based on the previous studies in [21, 22], then our contributions of this paper are to introduce the lockdown $\delta$ ($\delta \in (0,1]$, there is no lockdown when $\delta =1$, and full lockdown is when $\delta =0$) and isolation rate $\epsilon$, where these two strategies are effective enough to reduce the transmission number of CoVid-19. Moreover, the time-dependent optimal controls of vaccination $u_1$ and social distancing $u_2$ are also provided to degrade the CoVid-19 transmission in the population.

Theorem 1

Let the initial conditions of system (2.1) (S, I, Q, R)(0) be positive, then the solutions (S, I, Q, R)(t) of system (2.1) are also positive for every $t>0$.

Proof

For first state variable of (2.1), one has

$$\begin{aligned} \begin{aligned} \frac{dS}{dt}=\Lambda -H(t)S(t), \end{aligned} \end{aligned}$$

(2.2)

where $H(t)=\beta \delta I(t)+\mu$. Multiplying the above result by the term

$$\begin{aligned} \begin{aligned} \exp \left( \int _{0}^{t}H(\xi )d\xi \right) . \end{aligned} \end{aligned}$$

Then one can obtain

$$\begin{aligned} \begin{aligned} \frac{dS}{dt}\cdot \exp \left( \int _{0}^{t}H(\xi )d\xi \right) =\left( \Lambda -H(t)S(t) \right) \cdot \exp \left( \int _{0}^{t}H(\xi )d\xi \right) , \end{aligned} \end{aligned}$$

implying that

$$\begin{aligned} \begin{aligned} \frac{d}{dt}\left( S(t)\cdot \exp \left( \int _{0}^{t}H(\xi )d\xi \right) \right) =\Lambda \cdot \exp \left( \int _{0}^{t}H(\xi )d\xi \right) . \end{aligned} \end{aligned}$$

By taking the integration with respect to t, one has

$$\begin{aligned} \begin{aligned} S(t)=\left( S(0)+\int \Lambda \cdot \exp \left( \int _{0}^{t}H(\xi )d\xi \right) \;dz \right) \cdot \exp \left( -\int _{0}^{t}H(\xi )d\xi \right) \ge 0, \end{aligned} \end{aligned}$$

(2.3)

where $S(0)\ge 0$ for all $t>0$.

The other state variables are solved by the similar ways for $(I,Q,R)(0)\ge 0$. Therefore, the solutions of system (2.1) are $(I,Q,R)(t)>0$ for every $t>0$. $\square$

Theorem 2

Let (S, I, Q, R) be the solution of system (2.1) with the initial conditions (S, I, Q, R)(0). Then, (S, I, Q, R)(t) are bounded in a region $\Omega$.

Proof

Let N(t) be total population of system (2.1) stated as $N(t)=(S+I+Q+R)(t)$. Then, derivative in t, one has

$$\begin{aligned} \begin{aligned} \frac{dN}{dt}&=\frac{d(S+I+Q+R)}{dt}\\&=\Lambda -\mu (S+I+Q+R)(t)-d(I+Q). \end{aligned} \end{aligned}$$

At disease-free $d(I+Q)=0$

$$\begin{aligned} \begin{aligned} \frac{dN}{dt}=\Lambda -\mu (S+I+Q+R)(t).\\ \end{aligned} \end{aligned}$$

(2.4)

Due to $S+I+Q+R=N,$

$$\begin{aligned} \begin{aligned} \frac{dN}{dt}\le \Lambda -\mu N(t),\\ \end{aligned} \end{aligned}$$

Applying the integration for both sides, then one has

$$\begin{aligned} \begin{aligned}&\int _{N(0)}^{N(t)}\frac{dN}{\Lambda -\mu N}\le \int ^t_0 dt, \\&N(t)\le N(0)e^{-\mu t}+\frac{\Lambda }{\mu }\left( 1-e^{-\mu t} \right) \end{aligned} \end{aligned}$$

Hence

$$\begin{aligned} \begin{aligned} \lim _{t\rightarrow \infty }\sup N(t)\le \frac{\Lambda }{\mu }. \end{aligned} \end{aligned}$$

Therefore, the bounded region of system (2.1) where it has biological and epidemiological meaningful can be stated as follows

$$\begin{aligned} \begin{aligned} \Omega =\left\{ (S,I,Q,R)(t)\in {\mathbb {R}}: 0\le N(t)\le \frac{\Lambda }{\mu } \right\} . \end{aligned} \end{aligned}$$

$\square$

The existence and uniqueness of the solution of system (2.1) can be provided through the maximality condition which is stated in the following theorem.

Theorem 3

Let ${\mathcal {C}}_j, {\mathcal {C}}^*_j$ be the constant for $j=1,2,3,4$ such that

$$\begin{aligned} \begin{aligned}&|{\mathcal {F}}_j(M_j,t)-{\mathcal {F}}_j (M^*_j,t)|^2\le {\mathcal {C}}_j|M_j-M_j^*|^2,\\&|{\mathcal {F}}_j(M_j,t)|^2\le {\mathcal {C}}_j^*(1+|M_j|^2),\;\text {or}\; |{\mathcal {F}}_j(M_j,t)|^2\le {\mathcal {C}}_j^*|M_j|^2, \end{aligned} \end{aligned}$$

(2.5)

for all $(M,t)\in {\mathbb {R}}\times (0,T)$.

Proof

We firstly give the notation of ${\mathcal {F}}_j, M_j$, and $M_j^*$ for all state variables S, I, Q, R as follows

$$\begin{aligned} \begin{aligned}&{\mathcal {F}}_1(S,I,Q,R,t):=\frac{dS}{dt}=\Lambda -\beta \delta SI-\mu S,\\&{\mathcal {F}}_2(S,I,Q,R,t):=\frac{dI}{dt}=\beta \delta SI-(r+\epsilon +\mu +d)I,\\&{\mathcal {F}}_3(S,I,Q,R,t):=\frac{dQ}{dt}=\epsilon I-(\varphi +d+\mu )Q,\\&{\mathcal {F}}_4(S,I,Q,R,t):=\frac{dR}{dt}=rI+\varphi Q-\mu R,\\&(M_1,M_2,M_3,M_4):=(S,I,Q,R),\\&(M_1^*,M_2^*,M_3^*,M_4^*):=(S^*,I^*,Q^*,R^*). \end{aligned} \end{aligned}$$

(2.6)

It follows from (2.6) and first inequality of (2.5) for first state variable, one has

$$\begin{aligned} \begin{aligned} |{\mathcal {F}}_1(S,t)-{\mathcal {F}}_1 (S^*,t)|^2&=|-\beta \delta (S-S^*)I-\mu (S-S^*)|^2\\&\le 2\left| \beta \delta I+\mu \right| ^2|S-S^*|^2\\&\le 2\left( \beta ^2\delta ^2 \sup _{0\le t\le \tau } |I|^2 + \mu ^2 \right) |S-S^*|^2\\&\le {\mathcal {C}}_1|S-S^*|^2, \end{aligned} \end{aligned}$$

(2.7)

where ${\mathcal {C}}_1=2\left( \beta ^2\delta ^2 \left\| I \right\| ^2_\infty +\mu ^2\right)$. Similarly for $|{\mathcal {F}}_2(I,t)-{\mathcal {F}}_2 (I^*,t)|^2\le {\mathcal {C}}_2|I-I^*|^2$, $|{\mathcal {F}}_3(Q,t)-{\mathcal {F}}_3 (Q^*,t)|^2\le {\mathcal {C}}_3|Q-Q^*|^2$, $|{\mathcal {F}}_4(R,t)-{\mathcal {F}}_4 (R^*,t)|^2\le {\mathcal {C}}_4|R-R^*|^2$, then one has

$$\begin{aligned}{} & {} \begin{aligned} |{\mathcal {F}}_2(I,t)-{\mathcal {F}}_2 (I^*,t)|^2&=|\beta \delta S-(r+\epsilon +\mu +d)(I-I^*)|^2\\&\le 2\left| \beta \delta S-(r+\epsilon +\mu +d) \right| ^2|I-I^*|^2\\&\le 2\left( \beta ^2\delta ^2 \sup _{0\le t\le \tau } |S|^2 + (r^2+\epsilon ^2+\mu ^2+d^2) \right) |I-I^*|^2\\&\le {\mathcal {C}}_2|I-I^*|^2, \end{aligned} \end{aligned}$$

(2.8)

$$\begin{aligned}{} & {} \begin{aligned} |{\mathcal {F}}_3(Q,t)-{\mathcal {F}}_3 (Q^*,t)|^2&=|-(\varphi +d+\mu )(Q-Q^*)|^2\\&\le 2(\varphi ^2+d^2+\mu ^2)|Q-Q^*|^2\\&\le {\mathcal {C}}_3|I-I^*|^2, \end{aligned} \end{aligned}$$

(2.9)

$$\begin{aligned}{} & {} \begin{aligned} |{\mathcal {F}}_4(R,t)-{\mathcal {F}}_4 (R^*,t)|^2&=|-\mu (R-R^*)|^2\\&\le 2\mu ^2|R-R^*|^2\\&\le {\mathcal {C}}_4|R-R^*|^2, \end{aligned} \end{aligned}$$

(2.10)

where ${\mathcal {C}}_2=2\left( \beta ^2\delta ^2 \left\| S \right\| ^2_\infty +(r^2+\epsilon ^2+\mu ^2+d^2)\right)$, ${\mathcal {C}}_3=2(\varphi ^2+d^2+\mu ^2)$, and ${\mathcal {C}}_4=2\mu ^2$. Based on the results of (2.7)–(2.10), one proves the first inequality of (2.5). To prove the second inequality of (2.5), one has first state variable as follows

$$\begin{aligned} \begin{aligned} |{\mathcal {F}}_1(S,t)|^2&=|\Lambda -\beta \delta SI-\mu S|^2\\&\le 2\Lambda ^2+2\left( \beta ^2\delta ^2 \sup _{0\le t\le \tau } |I|^2 + \mu ^2 \right) |S|^2\\&\le 2\Lambda ^2+2\left( \beta ^2\delta ^2 \left\| I \right\| ^2_\infty + \mu ^2 \right) |S|^2\\&\le {\mathcal {C}}_1^*(1+|S|^2), \end{aligned} \end{aligned}$$

(2.11)

which implies $\frac{\beta ^2\delta ^2 \left\| I \right\| ^2_\infty + \mu ^2}{\Lambda ^2}<1$, where ${\mathcal {C}}_1^*=\Lambda ^2$. Similarly, for second state variable, we have

$$\begin{aligned} \begin{aligned} |{\mathcal {F}}_2(I,t)|^2&=|\beta \delta SI-(r+\epsilon +\mu +d)I|^2\\&\le 2\left( \beta ^2\delta ^2 \sup _{0\le t\le \tau } |S|^2 + (r^2+\epsilon ^2+\mu ^2+d^2) \right) |I|^2\\&\le {\mathcal {C}}_2^*|I|^2, \end{aligned} \end{aligned}$$

(2.12)

where ${\mathcal {C}}_2^*=\beta ^2\delta ^2 \left\| S \right\| ^2_\infty + (r^2+\epsilon ^2+\mu ^2+d^2)$. For third state variables, one provides

$$\begin{aligned} \begin{aligned} |{\mathcal {F}}_3(Q,t)|^2&=|\epsilon I-(\varphi +d+\mu )Q|^2\\&\le 2\epsilon ^2\sup _{0\le t\le \tau } |I|^2+ 2(\varphi ^2+d^2+\mu ^2)|Q|^2\\&\le 2\left\| I \right\| ^2_\infty + 2(\varphi ^2+d^2+\mu ^2)|Q|^2\\&\le {\mathcal {C}}_3^*(1+|Q|^2), \end{aligned} \end{aligned}$$

(2.13)

which implies $\frac{\varphi ^2+d^2+\mu ^2}{\epsilon ^2\left\| I \right\| ^2_\infty }<1$, where ${\mathcal {C}}_3^*=\epsilon ^2\left\| I \right\| ^2_\infty$. Finally, the fourth state variable gives

$$\begin{aligned} \begin{aligned} |{\mathcal {F}}_4(R,t)|^2&=|rI+\varphi Q-\mu R|^2\\&\le 2r^2\sup _{0\le t\le \tau } |I|^2+2\varphi ^2\sup _{0\le t\le \tau } |Q|^2+ 2\mu ^2|R|^2\\&\le 2r^2\left\| I \right\| ^2_\infty +2\varphi ^2\left\| Q \right\| ^2_\infty + 2\mu ^2|R|^2\\&\le {\mathcal {C}}_4^*(1+|R|^2), \end{aligned} \end{aligned}$$

(2.14)

which implies $\frac{\mu ^2}{r^2\left\| I \right\| ^2_\infty +\varphi ^2\left\| Q \right\| ^2_\infty }<1$, where ${\mathcal {C}}_4^*=r^2\left\| I \right\| ^2_\infty +\varphi ^2\left\| Q \right\| ^2_\infty$. Employing the following maximality condition

$$\begin{aligned} \begin{aligned} Max\left\{ \frac{\beta ^2\delta ^2 \left\| I \right\| ^2_\infty + \mu ^2}{\Lambda ^2}, \frac{\varphi ^2+d^2+\mu ^2}{\epsilon ^2\left\| I \right\| ^2_\infty }, \frac{\mu ^2}{r^2\left\| I \right\| ^2_\infty +\varphi ^2\left\| Q \right\| ^2_\infty } \right\} <1. \end{aligned} \end{aligned}$$

Then the second conditions of (2.5) can be provided. $\square$

Stability Analysis

Equilibria and the Basic Reproduction Number

This section provides the equilibria points and reproduction number ${\mathcal {R}}_0$. In epidemiology, the basic reproduction number ${\mathcal {R}}_0$ of an infection can be thought of as the number of cases produced by one case, on average during its infectious period, in an uninfected population [27]. This basic reproduction number is helpful to ensure that infectious disease can transmit or not in the population. If ${\mathcal {R}}_0<1$ the infection will stop in the long term. Moreover, if ${\mathcal {R}}_0>1$ the infection has the ability to transmit in the population. In general, if the ${\mathcal {R}}_0$ value is greater, then the control of epidemic is more difficult.

Theorem 4

In system (2.1), there is a disease-free equilibrium when the basic reproduction number ${\mathcal {R}}_0<1$, i.e.,

$$\begin{aligned} \begin{aligned} E^0=(S^0,I^0,Q^0,R^0)=\left( \frac{\Lambda }{\mu },0,0,0 \right) . \end{aligned} \end{aligned}$$

(3.1)

Moreover, there is an endemic disease equilibrium when the basic reproduction number ${\mathcal {R}}_0>1$, i.e.,

$$\begin{aligned} \begin{aligned} E^*=(S^*,I^*,Q^*,R^*), \end{aligned} \end{aligned}$$

(3.2)

where

$$\begin{aligned} \begin{aligned}&S^*=\frac{r+\epsilon +\mu +d}{\beta \delta },\;I^*=\frac{\Lambda }{r+\epsilon +\mu +d}-\frac{\mu }{\beta \delta },\\&Q^*=\frac{\epsilon }{\varphi +d+\mu }I^*,\;R^*=\frac{r}{\mu }I^*+\frac{\varphi }{\mu }Q^*. \end{aligned} \end{aligned}$$

Proof

By considering the derivatives in the left-hand side of system (2.1) equal to zero and $I=0$, then one has a disease-free equilibrium $E^0$. Moreover, applying $I\ne 0$, we can get an endemic disease equilibrium $E^*$. $\square$

The next generation matrix is then used to get the basic reproduction number $R_0$ of (2.1). By linearizing around the disease-free equilibrium ($E^0$), one has

$$\begin{aligned} \begin{aligned} \begin{pmatrix}I\\ Q\end{pmatrix}_t&=\begin{pmatrix}\beta \delta SI-(r+\epsilon +\mu +d)I\\ \epsilon I-(\varphi +d+\mu )Q\end{pmatrix}\\&=\left[ \begin{pmatrix}\beta \delta S &{}0\\ 0&{} 0\end{pmatrix}-\begin{pmatrix}r+\epsilon +\mu +d &{}0\\ epsilon&{} \varphi +d+\mu \end{pmatrix} \right] \begin{pmatrix}I\\ Q\end{pmatrix}\\&=({\mathcal {F}}-{\mathcal {V}})\begin{pmatrix}I\\ Q\end{pmatrix}, \end{aligned} \end{aligned}$$

where ${\mathcal {F}}$ is the transmission matrix of new infected individuals, and ${\mathcal {V}}$ is the transition matrix of individual displacements between groups of individuals. Then, the next generation matrix can be expressed as

$$\begin{aligned} \begin{aligned} {\mathcal {F}}{\mathcal {V}}^{-1}=\begin{pmatrix} \frac{\Lambda \beta \delta }{\mu (r+\epsilon +\mu +d)} &{} 0 \\ 0 &{} 0 \end{pmatrix} \end{aligned} \end{aligned}$$

Therefore, based on the dominant eigenvalues of next generation matrix, one has the basic reproduction number

$$\begin{aligned} \begin{aligned} {\mathcal {R}}_0=\frac{\Lambda \beta \delta }{\mu (r+\epsilon +\mu +d)}. \end{aligned} \end{aligned}$$

(3.3)

Local Stability of the Disease-Free Equilibrium

Theorem 5

The disease-free equilibrium $E^0$ is local asymptotically stable if ${\mathcal {R}}_0<1$.

Proof

We firstly provide the Jacobian matrix of system (2.1) at the disease-free equilibrium $E^0$ as follows

$$\begin{aligned} \begin{aligned} J(E^0)=\begin{pmatrix} -\mu &{} -\frac{\Lambda \beta \delta }{\mu } &{} 0 &{} 0 \\ 0 &{} \frac{\Lambda \beta \delta }{\mu }-(r+\epsilon +\mu +d) &{} 0 &{} 0 \\ 0 &{} \epsilon &{} -(\varphi +d+\mu ) &{} 0 \\ 0 &{} r &{} \varphi &{} -\mu \end{pmatrix}. \end{aligned} \end{aligned}$$

(3.4)

The eigenvalues of (3.4) are easy to obtain by solving the characteristic equation $|J(E^0)-\lambda I_d|=0$, then one has

$$\begin{aligned} \begin{aligned}&\lambda _1=-\mu<0,\;\lambda _2=-(\varphi +d+\mu )<0,\\&\lambda _3=\frac{-\left( \frac{\Lambda \beta \delta }{\mu }-(r+\epsilon +\mu +d) \right) -\sqrt{{\mathcal {D}}}}{2}\\&\lambda _4=\frac{-\left( \frac{\Lambda \beta \delta }{\mu }-(r+\epsilon +\mu +d) \right) +\sqrt{{\mathcal {D}}}}{2}, \end{aligned} \end{aligned}$$

(3.5)

where

$$\begin{aligned} \begin{aligned} {\mathcal {D}}=\left( \frac{\Lambda \beta \delta }{\mu }-(r+\epsilon +\mu +d) \right) ^2-4\mu (r+\epsilon +\mu +d)+4\Lambda \beta \delta >0. \end{aligned} \end{aligned}$$

Therefore, $\lambda _3$ is negative. If $R_0<1$, then one has $\Lambda \beta \delta <\mu (r+\epsilon +\mu +d)$, implying that

$$\begin{aligned} \begin{aligned} {\mathcal {D}}<\left( \frac{\Lambda \beta \delta }{\mu }-(r+\epsilon +\mu +d) \right) ^2. \end{aligned} \end{aligned}$$

Then

$$\begin{aligned} \begin{aligned} \lambda _4<\frac{-\left( \frac{\Lambda \beta \delta }{\mu }-(r+\epsilon +\mu +d) \right) +\sqrt{\left( \frac{\Lambda \beta \delta }{\mu }-(r+\epsilon +\mu +d) \right) ^2}}{2}=0. \end{aligned} \end{aligned}$$

Because all eigenvalues $\lambda _i<0$ for $i=1,2,3,4$, we can conclude that the equilibrium $E^0$ is local asymptotically stable. $\square$

Fig. 1

Tendency of $R_0$ with infection rate $\beta$ and isolation rate $\epsilon$

Figure 1 shows the function of $R_0$ with the independent variables $\beta$ and $\epsilon$. It is clear that $R_0$ increases as infection rate $\beta$ increases and $R_0$ decreases as isolation rate $\epsilon$ increases. The most effective to control the CoVid-19 spread is to control reproduction number $R_0$ less than one. Based on this principle, the strategy of isolation should be advocated, so the viruses spread will be decreased.

Local Stability of the Endemic Disease Equilibrium

Theorem 6

The endemic disease equilibrium $E^*$ is local asymptotically stable if ${\mathcal {R}}_0>1$.

Proof

Similarly, we firstly provide the Jacobian matrix of system (2.1) at the endemic disease equilibrium $E^*$ as follows

$$\begin{aligned} \begin{aligned} J(E^*)=\begin{pmatrix} -\beta \delta I^*-\mu &{} -\beta \delta S^* &{} 0 &{} 0 \\ \beta \delta I^* &{} \beta \delta S^*-(r+\epsilon +\mu +d) &{} 0 &{} 0 \\ 0 &{} \epsilon &{} -(\varphi +d+\mu ) &{} 0 \\ 0 &{} r &{} \varphi &{} -\mu \end{pmatrix}. \end{aligned} \end{aligned}$$

(3.6)

The eigenvalues of (3.4) are similar ways as in Theorem 5 to obtain by solving the characteristic equation $|J(E^*)-\lambda I_d|=0$. We determine the minor values of $J(E^*)$ to get the cofactor expansion, then the eigenvalues satisfy the following equation

$$\begin{aligned} \begin{aligned} (-\mu -\lambda )(-(\varphi +d+\mu )-\lambda )\det (A)=0, \end{aligned} \end{aligned}$$

(3.7)

where

$$\begin{aligned} \begin{aligned} A=\begin{pmatrix} -\beta \delta I^*-\mu &{} -\beta \delta S^* \\ \beta \delta I^* &{} \beta \delta S^*-(r+\epsilon +\mu +d) \end{pmatrix}. \end{aligned} \end{aligned}$$

(3.8)

Obviously, $\lambda _1=-\mu <0$, $\lambda _2=-(\varphi +d+\mu )<0$. Moreover, the eigenvalues $\lambda _{3,4}$ provide the stability criterion. All eigenvalues of the matrix A will be real and negative if

$$\begin{aligned} \begin{aligned} Tr(A)=\lambda _3+\lambda _4<0,\;Det(A)=\lambda _3\cdot \lambda _4>0. \end{aligned} \end{aligned}$$

Using the matrix A, one has

$$\begin{aligned} \begin{aligned}&Tr(A)=-\frac{\Lambda \beta \delta }{r+\epsilon +\mu +d}<0\\&Det(A)=\mu ({\mathcal {R}}_0-1)(r+\epsilon +\mu +d). \end{aligned} \end{aligned}$$

Based on the above results, all eigenvalues of matrix (3.8) are negative real part if $R_0>1$. Thus, the equilibrium $E^*$ is local asymptotically stable. $\square$

Global Stability of the Disease-Free Equilibrium

To establish the global stability at the disease-free equilibrium $E_0$, there are two conditions that must be satisfied [16]. Initially, the Eq. (2.1) is divided into two systems as follows

$$\begin{aligned} \begin{aligned}&\frac{dY_1}{dt}=F_1(Y_1,Y_2),\\&\frac{dY_2}{dt}=F_2(Y_1,Y_2),\;F_2(Y_1,0)=0, \end{aligned} \end{aligned}$$

(3.9)

where $Y_1=(S,R)$ provides the number of uninfected individuals and $Y_2=(I,Q)$ provides the number of infected individuals. Moreover, ${\mathcal {P}}_0=(Y_1^0,0)$ denotes the disease-free equilibrium of the Eq. (3.9). It follows from Eq. (3.1) and Eq. (3.9), one has ${\mathcal {P}}_0=(Y_1^0,0)=(S^0,0)$. Then, the following two conditions must be satisfied to guarantee the global asymptotically stability.

$$\begin{aligned} \begin{aligned}&\text {(H1) If}\;\frac{dY_1}{dt}=F_1(Y_1,0),\;\text {then}\; Y_1^0\;\text {is global asymptotically stable},\\&\text {(H2) If}\;(Y_1,Y_2)\in \Omega ,\;\text {then}\; F_2(Y_1,Y_2)={\mathcal {M}}Y_2-{\mathcal {K}}(Y_1,Y_2)\;\text {for}\;{\mathcal {K}}(Y_1,Y_2)\ge 0, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} {\mathcal {M}}=\frac{dF_2}{dY_2}(Y_1^0,0). \end{aligned} \end{aligned}$$

Theorem 7

Let ${\mathcal {P}}_0=(Y_1^*,0)$ be disease-free equilibrium of Eq. (3.9). Then the fixed point ${\mathcal {P}}_0$ is global asymptotically stable in the interior $\Omega$ if ${\mathcal {R}}_0<1$ and the conditions (H1) and (H2) are satisfied.

Proof

Since $\frac{dY_1}{dt}=F_1(Y_1,0)$ gives

$$\begin{aligned} \begin{aligned}&\frac{dS}{dt}=\Lambda -\mu S,\\&\frac{dR}{dt}=-\mu R.\\ \end{aligned} \end{aligned}$$

Then, by conducting the limit $t\rightarrow +\infty$, one has

$$\begin{aligned} \begin{aligned} (S,R)\rightarrow \left( \frac{\Lambda }{\mu },0 \right) =(Y_1^0,0), \end{aligned} \end{aligned}$$

implying that $(S,R)\rightarrow (S^0,0)$ and $Y_1^0$ is global asymptotically stable. Since $Y_1=(S,R)$, $Y_2=(I,Q)$ and the assumption $S\sim N$ at the early phase of epidemic, then one can establish

$$\begin{aligned} \begin{aligned}&F_1(Y_1,0)= \left( \frac{\Lambda }{\mu },0 \right) ,\\&{\mathcal {M}}=\begin{pmatrix} \beta \delta N-(r+\epsilon +\mu +d) &{} 0 \\ \epsilon &{} -(\varphi +d+\mu ) \end{pmatrix},\\&{\mathcal {K}}(Y_1,Y_2)=\begin{pmatrix} \beta \delta I(N-S) \\ 0 \end{pmatrix}. \end{aligned} \end{aligned}$$

It follows from Eq. (2.6) and $N=S+I+Q+R$ then one has $0\le S\le N$, implying that ${\mathcal {K}}(Y_1,Y_2)\ge 0$. If the matrix ${\mathcal {M}}$ is irreducible and ${\mathcal {K}}(Y_1,Y_2)\ge 0$ then the theorem becomes true for ${\mathcal {R}}_0<1$. Hence, the fixed point ${\mathcal {P}}_0=(Y_1^*,0)$ is global asymptotically stable in the interior $\Omega$. $\square$

Global Stability of the Endemic Disease Equilibrium

Theorem 8

The endemic disease equilibrium $E^*$ is global asymptotically stable on the interior $\Omega$ if ${\mathcal {R}}_0>1$.

Proof

Let the Lyapunov function ${\mathcal {L}}$ be defined as

$$\begin{aligned} \begin{aligned} {\mathcal {L}}(x_i)=\sum _{i=1}^{N}\frac{1}{2}(x_i-x^*_i)^2, \end{aligned} \end{aligned}$$

(3.10)

where

$$\begin{aligned} \begin{aligned}&N =\text {number of state variables}\;(S,I,Q,R),\\&x_i = i^{th}\;\text {state variable},\\&x_i^* = i^{th}\;\text {state variable for endemic disease equilibrium}. \end{aligned} \end{aligned}$$

Applying (3.10) into the system of (2.1), then one has

$$\begin{aligned} \begin{aligned} {\mathcal {L}}(S,I,Q,R)=\frac{1}{2}[(S-S^*)+(I-I^*)+(Q-Q^*)+(R-R^*)]^2. \end{aligned} \end{aligned}$$

Differentiating the above results with respect to t, one further has

$$\begin{aligned} \begin{aligned} \frac{d{\mathcal {L}}}{dt}=[(S-S^*)+(I-I^*)+(Q-Q^*)+(R-R^*)]\frac{d}{dt}(S+I+Q+R). \end{aligned} \end{aligned}$$

(3.11)

Based on (2.4), one gets

$$\begin{aligned} \begin{aligned} N^*=(S^*+I^*+Q^*+R^*)=\frac{\Lambda }{\mu }. \end{aligned} \end{aligned}$$

(3.12)

Substituting (2.4) and (3.12) into (3.11) gives

$$\begin{aligned} \begin{aligned} \frac{d{\mathcal {L}}}{dt}&=\left[ N-\frac{\Lambda }{\mu } \right] \left[ \Lambda -N\mu \right] \\&=\left[ 2N\Lambda -N^2\mu -\frac{\Lambda ^2}{\mu } \right] \\&=-\frac{1}{\mu }\left[ \Lambda ^2-2N\Lambda \mu +N^2\mu ^2 \right] \\&=-\frac{1}{\mu }\left[ \Lambda -N\mu \right] ^2<0. \end{aligned} \end{aligned}$$

(3.13)

Then $\frac{d{\mathcal {L}}}{dt}$ is a Lyapunov function as stated in (3.13), which concludes that the endemic disease equilibrium $E^*$ is global asymptotically stable. $\square$

Optimal Control

In this section, the mathematical model of CoVid-19 with the control of vaccination and social distancing is formulated. Based on the sensitivity index of lockdown $(\delta )$, this paremeter gives the significant impact for the basic reproduction number with the sensitivity index $\Gamma ^{{\mathcal {R}}_0}_{\delta }=100\%$. The significant impact of lockdown becomes a reason to consider the optimal control of this parameter. Moreover, the control of the transmission rate will give a good impact of reducing the spread of CoVid-19 in the community. Therefore, we provide the control of social distancing $(u_2)$ and vaccination $(u_1)$ to degrade the CoVid-19 transmission in the population. The mathematical model of CoVid-19 with the presence of control can be stated as follows

$$\begin{aligned} \begin{aligned}&\frac{dS}{dt}=(1-u_1)\Lambda -(1-u_2)\beta \delta SI-\mu S,\\&\frac{dI}{dt}=(1-u_2)\beta \delta SI-(r+\epsilon +\mu +d)I,\\&\frac{dQ}{dt}=\epsilon I-(\varphi +d+\mu )Q,\\&\frac{dR}{dt}=u_1\Lambda +rI+\varphi Q-\mu R. \end{aligned} \end{aligned}$$

(4.1)

The aim of the objective function is to minimize the CoVid-19 transmission by introducing two controls of vaccination $(u_1)$ and social distancing $(u_2)$, and also to minimize the control costs. Therefore, the objective function of system (4.1) is given below

$$\begin{aligned} \begin{aligned} {\mathcal {J}}(u_1,u_2):=\min \int ^{T}_{0}\left[ I(t)+\frac{A_1}{2}u_1^2(t)+\frac{A_2}{2}u_2^2(t) \right] dt, \end{aligned} \end{aligned}$$

(4.2)

where $A_1$ and $A_2$ are the cost factors with respect to controls $u_1$ and $u_2$, and T is final time of control implementations.

Pontryagin’s maximum principle establishes the necessary conditions that the quadratic objective function must satisfy. This principle has the role to convert the system (4.1) and the objective functional ${\mathcal {J}}$ (4.2) into the minimizing pointwise problem known as the Hamiltonian ${\mathcal {H}}$ with respect to controls $(u_1,u_2)(t)$ for all $t\in [0,T]$. The Hamiltonian referring to the system (4.1) and quadratic objective functional (4.2) can be formulated as follows

$$\begin{aligned} \begin{aligned} {\mathcal {H}}&=I+\frac{A_1}{2}u_1^2(t)+\frac{A_2}{2}u_2^2(t)+\psi _1 \left[ (1-u_1)\Lambda -(1-u_2)\beta \delta SI-\mu \right] \\&\quad +\psi _2 \left[ (1-u_2)\beta \delta SI-(r+\epsilon +\mu +d)I \right] +\psi _3 \left[ \epsilon I-(\varphi +d+\mu )Q \right] \\&\quad +\psi _4 \left[ u_1\Lambda +\varphi Q-\mu R \right] , \end{aligned} \end{aligned}$$

(4.3)

where $\psi _i$ for $i=1,2,3,4$ are the adjoint variables for each state variable S, I, Q, R respectively. Let ${\mathcal {U}}$ be a non-empty control set stated as follows

$$\begin{aligned} \begin{aligned} {\mathcal {U}}:=\left\{ (u_1,u_2): u_i\;\text {is Lebesgue measurable}, u_i\in [0,1]\;\text {for}\; i=1,2, t\in [0,T] \right\} . \end{aligned} \end{aligned}$$

(4.4)

Then, the optimal control $u^*=(u_1^*,u_2^*)$ is defined as follows

$$\begin{aligned} \begin{aligned} {\mathcal {J}}(u^*):=\min \left\{ {\mathcal {J}}(u_1,u_2): u_1, u_2\in {\mathcal {U}} \right\} . \end{aligned} \end{aligned}$$

(4.5)

Theorem 9

Let $u^*=(u_i^*)$ for $i=1,2$ be an optimal control and $S^*,I^*,Q^*,R^*$ be the solutions of system (4.1) minimizing ${\mathcal {J}}(u^*)$ over the control set ${\mathcal {U}}$ defined in (4.4), then there exists adjoint variables $\psi _i$ for $i=1,2,3,4$ satisfying

$$\begin{aligned} \begin{aligned}&\frac{d\psi _1}{dt}=\mu \psi _1+(1-u_2)\beta \delta I^*,\\&\frac{d\psi _2}{dt}=(1-u_2)(\psi _1-\psi _2)\beta \delta S+(r+\epsilon +\mu +d)\psi _2-\epsilon \psi _3-r\psi _4,\\&\frac{d\psi _3}{dt}=\psi _3(\varphi +d+\mu )-\psi _4\varphi ,\\&\frac{d\psi _4}{dt}=\psi _4\mu . \end{aligned} \end{aligned}$$

(4.6)

with transversality conditions $\psi _i(T)=0$, for $i=1,2,3,4$, and

$$\begin{aligned} \begin{aligned} u^*=\left\{ \begin{matrix} u_1^*(t)=\min \left\{ \max \left\{ 0,\frac{\Lambda (\psi _1-\psi _4)}{A_1} \right\} , u_{1_{\max }} \right\} ,\\ u_2^*(t)=\min \left\{ \max \left\{ 0,\frac{\beta \delta SI(\psi _2-\psi _1)}{A_2} \right\} , u_{2_{\max }} \right\} . \end{matrix}\right. \end{aligned} \end{aligned}$$

(4.7)

Proof

Pontryagin et al. [41] provides the adjoint system and transversality conditions with respect to this optimal control. For this purpose, we establish the derivative of Hamiltonian function (4.3) with respect to S, I, Q, R as stated as follows

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{l} \frac{d\psi _1}{dt}=-\frac{\partial {\mathcal {H}}}{\partial S},\;\; \psi _1(T)=0,\\ \frac{d\psi _2}{dt}=-\frac{\partial {\mathcal {H}}}{\partial I},\;\; \psi _2(T)=0,\\ \frac{d\psi _3}{dt}=-\frac{\partial {\mathcal {H}}}{\partial Q},\;\; \psi _3(T)=0,\\ \frac{d\psi _4}{dt}=-\frac{\partial {\mathcal {H}}}{\partial R},\;\; \psi _4(T)=0. \end{array}\right. \end{aligned} \end{aligned}$$

Meanwhile, the optimal control can be provided by finding the optimal solution of

$$\begin{aligned} \begin{aligned} \frac{\partial {\mathcal {H}}}{\partial u_i}=0,\;\text {for}\; u^*_i\;\text {where}\; i=1,2. \end{aligned} \end{aligned}$$

We further apply the standard ways of bounds on the optimal control as written as follows

$$\begin{aligned} \begin{aligned} u^*_i=\left\{ \begin{matrix} 0\;\;\text {if}\;\;\phi _i^*\le 0,\\ \phi _i^*\;\;\text {if}\;\;0\le \phi _i^*\le u_{i_{\max }},\\ u_{i_{\max }}\;\;\text {if}\;\;\phi _i^*\ge u_{i_{\max }}, \end{matrix}\right. \end{aligned} \end{aligned}$$

where $i=1,2$ and

$$\begin{aligned} \begin{aligned} \phi _1^*&=\frac{\Lambda (\psi _1-\psi _4)}{A_1},\\ \phi _2^*&=\frac{\beta \delta SI(\psi _2-\psi _1)}{A_2}. \end{aligned} \end{aligned}$$

$\square$

Numerical Results and Discussion

The first-order derivative differential equations of system (2.1) is solved numerically using the fourth order Runge-Kutta method. The sensitivity analysis of $R_0$ is then provided by applying the Partial Rank Correlation Coefficient (PRCC) method. The MATLAB codes are available in GitHub through this link: https://github.com/mghaniunair/SIQR-Model-on-CoVid-19.

Sensitivity Analysis

The effect of each parameters on the endemic treshold is provided in the sensitivity analysis. This essential method of sensitivity analysis shows the strength of each parameters of SIQR model [14]. Moreover, the parameter values are all assumed and presented in Table 1. Meanwhile, the sensitivity index of ${\mathcal {R}}_0$ depending differentiably on a parameter $\pi$ can be stated as

$$\begin{aligned} \begin{aligned} \Gamma ^{{\mathcal {R}}_0}_{\pi }=\frac{\partial {\mathcal {R}}_0}{\partial \pi }\times \frac{\pi }{{\mathcal {R}}_0}. \end{aligned} \end{aligned}$$

(5.1)

From (5.1), the sensitivity indices are calculated and provided in Table 1.

The parameters of birth rate $\Lambda$, transmission rate $\beta$, and lockdown $\delta$ achieve the most positive sensitivity index with the basic reproduction number $\Gamma ^{{\mathcal {R}}_0}_{\Lambda }=\Gamma ^{{\mathcal {R}}_0}_{\beta }=\Gamma ^{{\mathcal {R}}_0}_{\delta }=1$, which means that the greater the numbers of births, transmission, and lockdown in a susceptible population, the greater the chance of the number of infected individuals if there is direct contact. Moreover, the most negative sensitivity index is achieved by the natural death rate $\mu$ with the basic reproduction number $\Gamma ^{{\mathcal {R}}_0}_{\mu }=-1$, which means that $100\%$ of natural death rate plays an important role to reduce the transmission of disease. The transmission rate $\beta$ and lockdown $\delta$ have the positive impact $100\%$ for the basic reproduction number. This means that the lockdown have a significant impact on basic reproduction number. Moreover the isolation rate $\epsilon$ and cure rate related to infected r give the same impact of $44.10\%$ to reduce (due to the negative sign as in Table 1) the number of disease transmission. Figure 2 provides the sensitivity analysis for 7 parameters of basic reproduction number ${\mathcal {R}}_0$. By referring to Eq. (3.3), there is no parameter of cure rate related to isolation $\varphi$ for the basic reproduction number, which means that there is no significant impact for sensitivity index.

Simulation of SIQR Model

The numerical simulation of our dynamical system (2.1) is provided in Fig. 3, which gives the descriptions that the susceptible class decreases due to the lockdown and at a time increases to reach the equilibrium point as the susceptible individuals move to the infected class and other individuals die naturally. Moreover, the infected class decreases as the individuals move from susceptible class to infected class, this may be caused by the isolation rate increasing the cure rate related to infected individuals and other impact is caused by the natural death. The quarantined class increases from the infected class and at a time decreases due to the individuals moving to recovered class to achieve the equilibrium point. The recovered class increases from susceptible, infected, and quarantined individuals due to the isolation rate, lockdown, and other individuals die naturally. The variables S, I, Q, R vary with time (t).

In the susceptible class as in Fig. 4, the decaying rate increases when the variation of transmission rate $\beta$ increases. The susceptible individuals then move to the infected class, where this class provides the decreased decaying rate while the transmission rate increases (it also indicates the contact rate between susceptible and infected individuals). The infected class increases when the transmission rate increases and decreases by the individuals moving to quarantined class and isolation rate increases as in Fig. 4a, b. As shown in Fig. 4c, d, the quarantined class gives the similar results of decaying rate as in infected class which decrease when the transmission rate increases. The quarantined class will be increased when the transmission rate increases and will be decreased due to the individuals moving to recovered class and transmission rate decreasing. In this case, the number of recovered class will be increased because of individuals movement from quarantined class.

Figure 5a provides that the decaying rate decreases when the variation of isolation rate increases. The susceptible individuals then move to the infected class. This infected class provides the increased decaying rate while the isolation rate increases as in Fig. 5b. The quarantined class will be decreased when the isolation rate increases and the individuals move to the quarantined class. Meanwhile, Fig. 5c shows the decreased decaying rate when the isolation rate increases which means that the quarantined individuals will be increased when isolation rate increases and will be decreased when the individuals move to the recovered class and die naturally. The individuals movement from quarantined class can affect the recovered individuals increased. For more detailed visualization of infected class, Fig. 8 gives the indication that the higher the isolation rate is the smaller the number of infection is and otherwise (from the contour, the red color indicates the higher number of infection than the other regions).

Table 1 Parameter values and sensitivity index

Fig. 2

PRCC results for ${\mathcal {R}}_0$

Fig. 3

Simulation of SIQR model

Fig. 4

Variation of $\beta$ and deterministic versus stochastic in (S, I, Q, R)(t)

Fig. 5

Variation of $\epsilon$ and deterministic versus stochastic in (S, I, Q, R)(t)

The simulation of (S, I, Q, R)(t) model with optimal control $(u_1,u_2)(t)$ is based on the Eqs. (4.1), (4.6) and (4.7) by using the iterative method of fourth order Runge-Kutta with the assumptions of cost factors $A_1=A_2=1$. As in Fig. 6a–d and Fig. 7a–d, there is a profile change for state variable (S, I, Q, R)(t) without or with control $(u_1,u_2)(t)$ or only $u_2(t)$. The susceptible class with control ($(u_1,u_2)(t)$ or only $u_2(t)$) gives the higher values than without control which means that the controls of only social distancing or the combinations between social distancing and vaccination provide the number of susceptible individuals increased. Meanwhile, the infected and quarantined classes are more decreased with control ($(u_1,u_2)(t)$ or only $u_2(t)$) than without control. The results of infected class give the impact on the quarantined class, which means that if the infected individuals are decreased then automatically the quarantined individuals are also decreased. Moreover, the recovered class is more decreased with control ($(u_1,u_2)(t)$ or only $u_2(t)$) than without control. This indicates that the vaccination and social distancing employed earlier in susceptible class (subject to Eq. (4.1)) give the significant impact for the susceptible, and infected classes, which means that the controls of vaccination and social distancing are not effective in recovered class. The profiles of two controls $(u_1,u_2)(t)$ and of (S, I, Q, R)(t) with $(u_1,u_2)(t)$ or only $u_2(t)$ are provided in Fig. 6e and Fig. 7e respectively. As in Fig. 7e, it gives the results that there are significant difference between $(u_1,u_2)(t)$ and only $u_2(t)$ for each state variable (S, I, Q, R)(t). The profile of recovered class with the combination of two controls $(u_1,u_2)$ is greater than the profile of recovered class only with one control $u_2$. The profiles of infected and quarantined class provide the same results, those two classes with the combination of two controls $(u_1,u_2)$ are smaller than the ones only with one control $u_2$. Based on these results of infected, quarantined, and recovered classes, the susceptible class with the combination of two controls $(u_1,u_2)$ are smaller than the ones only with one control $u_2$.

Fig. 6

Simulation of SIQR(t) model with only optimal control $u_2(t)$, and profile of control $u_1(t)$ and $u_2(t)$

Fig. 7

Simulation of SIQR(t) model with two optimal control $u_1(t)$ and $u_2(t)$

Best Fit Parameters of SIQR Model

Now, we validate our dynamical system with the actual data by conducting the classical formula of least square technique written as

$$\begin{aligned} \begin{aligned} RMSE({\mathcal {N}}) = \sum ^{M}_{k=1}({\mathcal {Y}}_{pred}(k)-{\mathcal {Y}}_{data}(k)), \end{aligned} \end{aligned}$$

(5.2)

where M is the number of actual data, ${\mathcal {Y}}_{pred}$ is the numerical result of our dyamical system, ${\mathcal {Y}}_{data}$ is the actual data of CoVid-19 in Semarang, Indonesia, taken from 09 Apr 2020 until to 16 May 2022, and ${\mathcal {N}}$ is the unknown parameters of our dynamical system in (2.1). Initially, the general form of our dynamical system (2.1) is represented as follows

$$\begin{aligned} \begin{aligned} \frac{d{\mathcal {Y}}(t)}{d t}={\mathcal {F}}(t,{\mathcal {Y}},{\mathcal {N}}), \end{aligned} \end{aligned}$$

(5.3)

where Eq. (5.3) is approximated by the iterative method, fourth order Runge–Kutta. Moreover, our goal is to minimize the objective function

$$\begin{aligned} \begin{aligned}&\min _{{\mathcal {N}}}\;RMSE({\mathcal {N}}),\\&\text {subject to}\;\text {Eq.}\;(5.3). \end{aligned} \end{aligned}$$

(5.4)

The more detailed algorithm of parameter estimation can be addressed in [42] and the algorithm of optimization is in [32]. We divide the actual data into five parts: (a) Part 1 in Fig. 9a, (b) Part 2 in Fig. 9b, (c) Part 3 in Fig. 9c, (d) Part 4 in Fig. 9d, and (e) Part 5 in Fig. 9e, where each part has the peak values for number of infection. Moreover, Table 2 represents the best fit estimation values of parameters between SIQR model and actual data of CoVid-19 in Semarang, Indonesia, where the smallest RMSE (6.17%) is achieved in Fig. 9a, and the highest RMSE (28.68%) is provided in Fig. 9c as shown in Table 3 indicating the difference for each state (S, I, Q, R) between ODE45 results (based on the fitted parameters) and actual data. Moreover, Figs. 10, 11 and 12 provide the distribution of fitted parameters with actual data, where the highest number of outlier is shown in Fig. 11b for the parameter of $\lambda$. The parameters of $\mu , \epsilon , \delta , \mu$ do not provide the outlier and the obtained box-plots are mostly asymmetrical for each range.

Fig. 8

Tendency of number of infection with infection rate $\beta$ and isolation rate $\epsilon$

Fig. 9

Parameter fitting results of our SIQR model on CoVid-19 disease in Semarang, Indonesia (https://siagacorona.semarangkota.go.id/halaman/covid19pertahun/2020)

Fig. 10

Box-plot for all parameters ($\lambda ,\beta ,\delta ,\mu ,r,\epsilon ,d,\varphi$) with the range (09 Apr to 05 Sept 2020) and (06 Sept 2020 to 01 Feb 2021)

Fig. 11

Box-plot for all parameters ($\lambda ,\beta ,\delta ,\mu ,r,\epsilon ,d,\varphi$) with the range (02 Feb to 01 Sept 2021) and (02 Sept to 29 Nov 2021)

Fig. 12

Box-plot for all parameters ($\lambda ,\beta ,\delta ,\mu ,r,\epsilon ,d,\varphi$) with the range (30 Nov 2021 to 16 May 2022)

Table 2 Best fit estimation of parameters for SIQR model and actual data CoVid-19

Table 3 Dynamics of infected profiles for time 0, 50, 100, and 150

Moreover, Fig. 4e, f and Fig. 5e, f provide the deterministic and stochastic of SIQR model of (2.1). The stochastic process are employed to describe the dynamical system for each event [5]. Initially, the dynamical system (2.1) is written as follows

$$\begin{aligned} \begin{aligned} \frac{d}{dt}X(\tau ,x_0)=F(X(\tau ,x_0)), \end{aligned} \end{aligned}$$

(5.5)

where F is Lipschitz continuous, and X is state space, for $X=(S,I,Q,R)$, and $X(0,x_0)=X_0$. By employing the limit $N\rightarrow +\infty$, the sequence of state space $X_N(0,x_0)=X_0$ and for every $\delta >0$ the stochastic process is closed to the deterministic process as shown as follows

$$\begin{aligned} \begin{aligned} Pr\left( \sup _{t\le \tau }|X_N(t)-X(t,x_0)|>\varepsilon \right) \rightarrow 0,\;\text {as}\;N\rightarrow +\infty ,\;\text {for every}\;t\ge 0,\;\text {and}\;\varepsilon >0, \end{aligned} \end{aligned}$$

implying that the sequence of state space $(X_N(t),\;t\ge 0)$ can be approximated by the first order ordinary differential equations in Eq. (5.5). We notice that the function F is summation of a continuous function f(X, L), where $f(X,L):{\mathbb {R}}^4\times {\mathbb {Z}}^4\rightarrow {\mathbb {R}}$ and it is called as the process jumps for each event L. It follows from system (2.1), the process jumps are given below

$$\begin{aligned} \begin{aligned} f(X,L)=\left\{ \begin{matrix} \beta \delta SI,\;\;\;\;\;\;\;\; L=(-1,1,0,0),\\ rI,\;\;\;\;\;\;\;\;\;\;\;\; L=(0,-1,0,1),\\ \epsilon I,\;\;\;\;\;\;\;\;\;\;\;\; L=(0,-1,1,0),\\ \varphi Q,\;\;\;\;\;\;\;\;\;\; L=(0,0,-1,1),\\ \mu S,\;\;\;\;\;\;\;\;\;\; L=(-1,0,0,0). \end{matrix}\right. \end{aligned}\;\; \begin{aligned} f(X,L)=\left\{ \begin{matrix} (\mu +d)I,\;\; L=(0,-1,0,0),\\ (\mu +d)Q,\;\; L=(0,0,-1,0),\\ \mu R,\;\;\;\;\;\;\;\;\; L=(0,0,0,-1),\\ \Lambda ,\;\;\;\;\;\;\;\;\; L=(1,0,0,0).\\ \end{matrix}\right. \end{aligned} \end{aligned}$$

As in Figs. 4e, f and 5e, f, we can conclude that the deterministic and stochastic results give the same patterns for the profiles of susceptible, infected, quarantined, and recovered individuals. By referring to Fig. 13, we provide the control profiles for the estimation results with the actual data of infected individuals only in range (09 Apr to 05 Sept 2020) as the representation of five possible ranges as shown in Fig. 9. It can be seen that after applying the controls (only control of social distancing and after that using two controls of vaccination and social distancing), the infected profiles are more sloping than before applying the controls. If we compare for both figures (Fig. 13a, b), we can conclude that applying two controls (vaccination and social distancing) at once is more sloping than only applying one control (social distancing). It indicates that applying two controls can effectively reduce the number of infected individuals for CoVid-19 disease in Semarang, Indonesia.

Fig. 13

Controls for estimation results with the actual data of infected individuals in range 09 Apr to 05 Sept 2020 (it refers to Fig. 9a)

Fig. 14

a, b Estimation of neural network, c, d Performance, and e, f Regression for actual data as in Fig. 9a (LHS) and in Fig. 9e (RHS)

Fig. 15

Architecture of neural network consisting of 2 hidden layers, 50 neurons, training function of Levenberg-Marquardt, and activation function of Tangent Sigmoid

Applying the same strategy as in [29] and based on the results of Fig. 9a, e, we propose the neural network to estimate the infected profile of CoVid-19 in Semarang Indonesia and the results are respectively obtained for the S, I, Q, R profiles, performance and regression as shown in Fig. 14. The left hand side (LHS) needs 732 epochs and the right hand side (RHS) needs 921 epochs to achieve the optimal conditions. Moreover, the regression results for both RHS and LHS provide the distribution data which is still on the track (for the correlations between training and testing). To achieve these all optimal results, the architecture of neural network proposes two hidden layers consisting of 50 neurons for each hidden layer. Moreover, we employ Levenberg-Marquadt and Tangent Sigmoid as the training and activation functions respectively as in Fig. 15. According to the root mean square error for the profile of S, I, Q, R (between least square and neural network), one can conclude that the estimation results by using neural network are very significant as shown in Table 4.

The correlation between two parameters (based on the actual data of Covid-19 in Semarang, Indonesia from 09 Apr 2020 to 16 May 2022) is represented as the matrix correlation as shown in Fig. 16. Positive correlations are displayed in blue and negative correlations in red color. Color intensity and the size of the circle are proportional to the correlation coefficients. In the right side of the correlogram, the legend color shows the correlation coefficients and the corresponding colors. Based on the matrix correlation, the smallest correlation size is the correlation between (d and $\lambda$ indicating the small circle) for the range (09 Apr to 05 Sept 2020). Meanwhile, two ranges of (06 Sept 2020 to 01 Feb 2021) and (02 Feb to 01 Sept 2021) provide the same size circle (indicating the correlation size) for almost all correlations among the parameters. If we compare these two matrix correlations with the box-plot as in Fig. 12, there is no outlier for two ranges of (06 Sept 2020 to 01 Feb 2021) and (02 Feb to 01 Sept 2021), where all numerical values of Fig. 16 are shown in Table 5 and the performance analytics are in Fig. 17. The distribution of each parameter is shown on the diagonal. On the bottom of the diagonal, the bivariate scatter plots with a fitted line are displayed. On the top of the diagonal, the value of the correlation plus the significance level as stars Each significance level is associated to a symbol, i.e., p-values(0.001, 0.01, 0.05, 0.1, 1) refer to symbols(“***”, “**”, “*”, “.”, “ ”).

Table 4 The root mean square error between least square and neural network for the range of actual data from (09 Apr to 05 Sept 2020) and (30 Nov 2021 to 16 May 2022) for time 10, 20, 30, 40, 50, 60, 70, 80, 90, and 100

Fig. 16

Correlation matrix between two parameters

Table 5 Numerical values of correlation matrix between two parameters X and Y (Corr(X, Y))

Fig. 17

Performance analytics between two parameters

Conclusion

The mathematical model of CoVid-19 with optimal control of vaccination and social distancing becomes our concern in this paper. The aim of control implementation is to reduce the number of infected individuals. Based on the results obtained in the numerical simulation, those two controls give a significant effect on a dynamical system for each variable state. The local stability is established by analyzing the stability characteristic through the Jacobian matrix at the disease-free and endemic disease equilibrium points. Moreover, the global stability issue is from the appropriate Lyapunov function. The least-square technique is employed to provide the validation of our dynamical system by comparing the numerical results using fourth-order Runge Kutta and actual data of CoVid-19 disease in Semarang, Indonesia. As in the results obtained, our model of a dynamical system is good enough for the estimation based on the RMSE values. By employing the Continuous Time Markov Chain (CTMC), we have the same patterns for the profiles of susceptible, infected, quarantined, and recovered individuals between the deterministic and stochastic results. Applying two controls (vaccination and social distancing) at once is more effective than only applying one control (social distancing) to reduce the number of infected individuals for CoVid-19 in Semarang, Indonesia. According to the discussions, it can be seen that the infected profile of two controls at once (vaccination and social distancing) is more sloping than the infected profile of only one control (social distancing). The neural network technique also gives the significant estimations based on the root mean square error by using the training function of Levenberg-Marquadt and activation function of Tangent Sigmoid consisting of two hidden layers and 50 neurons for each hidden layer.

Appendix: Source Code of Continuous Time Markov Chain