B-Class Solitary Waves and Their Persistence Under Kuramoto–Sivashinsky Perturbation

Abstract

In this paper, we study the b-class shallow water equation. We take different bifurcation parameters to consider solitary wave solutions as well as their persistence under singular Kuramoto–Sivashinsky perturbation. We apply phase portrait analysis and the method of geometric singular perturbation theory.

Introduction

In this paper, we study the following nonlinear partial differential equation

$$\begin{aligned} m_t+2ku_x+bmu_x+um_x=0,\quad x\in \mathbb {R}, \; t>0, \end{aligned}$$

(1)

where b and k are arbitrary real constants with momentum density $m=u-u_{xx}$. This equation was derived by Degasperis, Holm and Hone [7, 8] , called the b-class equation. Among all cases, $b=2$ and $b=3$ are two special ones. When $b=2$, (1) was reduced to the familiar Camassa-Holm (CH) shallow-water equation [2]

$$\begin{aligned} m_t+2ku_x+2mu_x+um_x=0,\quad m=u-u_{xx}. \end{aligned}$$

(2)

When $b=3$, (1) was reduced to the Degasperis-Procesi(DP) shallow-water equation [9]

$$\begin{aligned} m_t+2ku_x+3mu_x+um_x=0,\quad m=u-u_{xx}. \end{aligned}$$

(3)

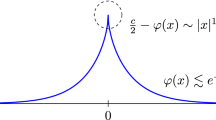
The above two cases exhaust the integrable candidates for b-equation (1), which was shown in [7]. The CH equation was first derived as an abstract bi-Hamiltonian equation with infinitely many conservation laws, and later re-derived by Camassa and Holm in [2] from physical principles. It admits solutions that exist indefinitely in time [5]. Also [3], it has peakon(peaked soliton) of the form $u(x,t)=ce^{-|x-ct|}$ when $k\rightarrow 0$. The DP equation, like the CH equation, has a Lax pair, a bi-Hamiltonian structure, and an infinite number of conservation laws [7, 22]. While it was discovered solely for its mathematical properties, later has been rigorously derived as a model for the propagation of shallow water waves. It also owns asymptotic accuracy as the CH equation [6, 9]. The DP and CH equations feature strong nonlinear effects, making them better suited to model nonlinear phenomena like wave breaking and solutions with singularities.

With respect to equation (1), Holm and Staley [13] studied the numerical solutions for different b. Guo and Liu [1] studied the periodic cuspons and the single soliton of this equation. Escher and Seiler [17] explored the relationships between equation (1) and Euler equations. Vitanov et al. [24] found some traveling wave solutions to this equation.

In this paper, we will focus on the fundmental bifurcation phenomena of b-equation (1) when the constant b and k are taken as the bifurcation parameters seperately. In the 1990s, Zhengrong Liu and Jibin Li [15, 19, 20] applied the qualitative theory of differential equations and the bifurcation theory of dynamical systems to the study of nonlinear waves. The core idea of this method is to transform the differential equation into a plane Hamiltonian system by traveling wave transformation, and then use the relevant knowledge of qualitative theory to get the bifurcation phase diagram of this Hamiltonian system, and finally calculate the corresponding traveling wave solutions. According to the bifurcation phase diagram, it can also visually see the limit form of the traveling wave solutions and the gradual change process.

During the process of studying the above articles, I realized an interesting phenomenon, which led to the following thoughts. As is known [4], the KdV-KS equation is derived as a model for wave motions, which involves a balance between dispersion, dissipation and nonlinearity for long waves. When $\varepsilon$ is small, KdV pulse and cnoidal wave solutions persist [23]. It happens that there is a similar case, according to Du’s work [10, 14]: when $b=2$, there is a homoclinic orbit persists under singular Kuramoto–Sivashinsky perturbation. We will therefore discuss whether this fact still holds for other bs in the b-family equation (1) with methods of the geometric singular perturbation theory.

The paper is structured as follows: in “The Discussion of Bifurcation Parameter b” section, I will discuss the bifurcation phenomena when the constant b is taken as a bifurcation parameter; in “The Discussion of Bifurcation Parameter k” section, then discuss the bifurcation phenomena about k parameter and additionally the $H_1$ norm convergence among those solitons. In “Geometric Theory of Singular Pertubation” section, I will provide the introduction about geometric singular perturbation theory; and in “Persistence of Solitary Wave Under Kuramoto–Sivashinsky Perturbation” section, I will study the existence of solitary wave solutions for b-equation when there exists small KS perturbation.

Bifurcation of B-Equation

At first, let’s introduce some definitions and lemmas.

Definition 2.1

A traveling wave solution $u(t,x)=\phi (x-ct)=:\phi (\xi )$ of the equation(1) is called a solitary wave if $\lim \limits _{\xi \rightarrow \pm \infty }\phi (\xi )=0$. Here $c>0$ is the wave speed.

Definition 2.2

The profile of a wave function is called pulse if its derivatives are continuous. Usually, such pulses are above the water surface. If they lie below the water surface, they will be called anti-pulses.

Definition 2.3

[12] Usually, the profile of a wave function is called peakon if there is a continuous point whose left and right derivatives are finite and have different signs.

Definition 2.4

[21] The so called “pseudo-peakon” means that the wave profile looks like peakon, but the solution still has continuous first order derivative.

Definition 2.5

[21] If the left and right derivatives of the profile of a wave function are positive and negative infinities, then the wave profile is called cuspon.

Lemma 2.1

(The rapid-jump property of the derivative near the singular straight line) [16] Suppose that in a left (or right) neighborhood of a singular straight line there exists a family of periodic orbits. Then, along a segment of every orbit near the straight line, the derivative of the wave function jumps down rapidly on a very short time interval.

Lemma 2.2

(Existence of finite time interval of solution with respect to wave variable in the positive or negative direction) [16] For a singular nonlinear traveling wave system of the first class with possible change of the wave variable, if an orbit transversely intersects with a singular straight line at a point or it approaches a singular straight line, but the derivative tends to infinity, then it only takes a finite time interval to make moved point of the orbit arrive on the singular straight line.

The Discussion of Bifurcation Parameter b

In this section, we treat the constant b of b-equation(1) as a bifurcation parameter. Assume that $c>0$ and $k>0$ first. The aim of this part is to investigate the classification of solitary waves vanishing at infinity of the b-equation(1) under different parametric ranges of b.

Changing the (x, t) coordinates into the traveling frame $(\xi ,t)$, where $\xi =x-ct$, the equation(1) under traveling frame admits the following steady state equation:

$$\begin{aligned} (2k-c)\phi '+(1+b)\phi \phi '-b\phi '\phi ''+c\phi '''-\phi \phi '''=0, \end{aligned}$$

(4)

where $'=\frac{d}{d\xi }$. Integrate once,

$$\begin{aligned} (2k-c)\phi +\frac{(1+b)}{2}\phi ^2-\frac{b-1}{2}\phi '^2+c\phi ''-\phi \phi ''=0, \end{aligned}$$

(5)

where the integration constant is taken to be 0 such that $\phi , \phi '$ and $\phi ''$ vanish at $\xi \rightarrow \pm \infty$. The above is equivalent to the following system of first-order equations

$$\begin{aligned} \left\{ \begin{aligned} \phi '&=\psi ,\\ (c-\phi )\psi '&=(c-2k)\phi -\frac{1+b}{2}\phi ^2-\frac{1-b}{2}\psi ^2.\\ \end{aligned} \right. \end{aligned}$$

(6)

This system is degenerate at the vertical line $\phi =c$: the orbits of this system can only touch the line at most at two points $B_{1,2} = (c,\pm \sqrt{\frac{4kc-2c^2+(1+b)c^2}{b-1}})$ (which fail when $b=1$).Then study the following (partially equivalent) system by a simple transformation:

$$\begin{aligned} \left\{ \begin{aligned} \dot{\phi }&=(c-\phi )\psi ,\\ \dot{\psi }&=(c-2k)\phi -\frac{1+b}{2}\phi ^2-\frac{1-b}{2}\psi ^2,\\ \end{aligned} \right. \end{aligned}$$

(7)

where $\dot{\ }=\frac{d}{(c-\phi )d\xi }$. It is easy to find that systems (6) and (7) have same orbits on the left side of the vertical line ${\phi = c}$ with the same direction, and have same orbits on the right side of the line with opposite directions. By caculation, the integral factor for the b-equation (1) is $(c-\phi )^{b-2}$ and the system(7) can be transformed into the following equality

$$\begin{aligned} \left( (c-2k)\phi -\frac{1+b}{2}\phi ^2-\frac{1-b}{2}\psi ^2\right) (c-\phi )^{b-2}d\phi =(c-\phi )^{b-1}\psi d\psi . \end{aligned}$$

(8)

Now, figure out the first integrals for different bs as

$$\begin{aligned} H_b(\phi , \psi ) = \left\{ \begin{aligned}&2k\ln |c-\phi |+\left( -\frac{1}{2}c^2+2ck+\frac{1}{2}\psi ^2+\frac{1}{2}c\phi -\frac{1}{2}\phi ^2\right) (c-\phi )^{-1},&b=0\\&\frac{1}{2}\left( -\phi ^2-4k\phi -4ck\ln |c-\phi |+\psi ^2-c^2\right) ,&b=1\\&\left( (2k-c)\phi -ck+\frac{1}{2}c^2+\frac{1}{2}\psi ^2\right) (c-\phi )^{-2},&b=-1\\&\left( -\frac{1}{2}\phi ^2-\frac{2k}{b}\phi -\frac{2ck}{b(b-1)}+\frac{1}{2}\psi ^2\right) (c-\phi )^{b-1},&b\ne -1,0,1\\ \end{aligned} \right. \end{aligned}$$

(9)

whose total differential $dH_b(\phi ,\psi )=0$, which indicates that any orbit of system (7) lies on some level curve of function $H_b(\phi ,\psi )$. Moreover, we have known $(\phi ,\psi )\rightarrow (0,0)$ as $\xi \rightarrow \pm \infty$. Therefore, we only consider the level curve of function $H_b(\phi ,\psi )$ which passes the point O(0, 0).

Also, from the above representations, we can easily find that there are three special points $b=-1,0,1.$ This inspired the following classifications:

• b > 1

In this case,

$$\begin{aligned} H_b(\phi ,\psi )=\left( -\frac{1}{2}\phi ^2-\frac{2k}{b}\phi -\frac{2ck}{b(b-1)}+\frac{1}{2}\psi ^2\right) (c-\phi )^{b-1}, \end{aligned}$$

(10)

and the system possesses two equilibrium points O(0, 0) and $A(\frac{2c-4k}{1+b},0)$ at the left side of the line $\phi =c$, whose eigenvalues are decided by the equalities $\lambda ^2=(c-2k)c$ and $\lambda ^2=\frac{(c-2k)(c-4k-bc)}{1+b}$ separately. When $c>2k>0$, the equilibrium point O(0, 0) is a saddle point and the point $A (\frac{2c-4k}{1+b},0)$, which lies at the right side of O(0, 0) and the left side of $\phi =c$, is a center point, these provide the possibility of the existence of the solitary waves. When $0<c<2k$, inversely, the equilibrium point O(0, 0) is a center point while $A(\frac{2c-4k}{1+b},0)$ is a saddle point and lies at the left side of O(0, 0), which makes the existence of the homoclinic orbit to O(0, 0) impossible. Therefore, we will add hypothesis $c>2k>0$ in the following to make the paper more concise.

Then, we set $H_b(\phi ,\psi )=H_b(0,0)=\frac{-2kc^b}{b(b-1)}$, i.e.,

$$\begin{aligned} \psi ^2=\frac{-4kc^b}{b(b-1)}(c-\phi )^{1-b}+\phi ^2+\frac{4k}{b}\phi +\frac{4ck}{b(b-1)}. \end{aligned}$$

(11)

In order to figure out what (11) looks like, we let

$$\begin{aligned} f(\phi )\triangleq \frac{-4kc^b}{b(b-1)}(c-\phi )^{1-b}+\phi ^2+\frac{4k}{b}\phi +\frac{4ck}{b(b-1)}. \end{aligned}$$

(12)

Because of the inequality $H_b(c,\cdot )\ne H_b(0,0)$, we only need to analyze $\phi <c$. Then we get

$$\begin{aligned} \begin{aligned} f'(\phi )&=\frac{-4kc^b}{b}(c-\phi )^{-b}+2\phi +\frac{4k}{b},\\ f''(\phi )&=-4kc^b(c-\phi )^{-b-1}+2,\\ f'''(\phi )&=-4(b+1)kc^b(c-\phi )^{-b-2}, \end{aligned} \end{aligned}$$

(13)

where $f'''(\phi )<0$. Thus, $f''(\phi )$ is a monotonically decreasing function. By calculation, $f''(\phi )|_{\phi =0}=-\frac{4k}{c}+2>0$, $f''(\phi )|_{\phi \rightarrow c^-}\rightarrow -\infty$. Thus, $f'(\phi )$ is a function that increases first and then decreases, with the turning point between 0 and c. Again, we calculate $f'(\phi )|_{\phi =0}=0$ and $f'(\phi )|_{\phi \rightarrow c^-}\rightarrow -\infty$. Thus, $f(\phi )$ is a function that decreases first and then increases and then decreases again, the turning points are 0 and some value which is between 0 and c. At last, I figure out $f(\phi )|_{\phi =0}=0$ and $f(\phi )|_{\phi \rightarrow c^-}\rightarrow -\infty$. Hence, the figure of $f(\phi )$ is clear, which can be seen in Fig. 1(a). Then, I come to the conclusion, when $c>2k>0$, there exists the unique pulse $\Gamma _b$, which lies on the left side of the vertical line $\phi =c$ and to the right of the orgin. See Fig. 1(b).

Fig. 1

$b>1$

• b = 1

At this time,

$$\begin{aligned} H_1(\phi ,\psi )=\frac{1}{2}(-\phi ^2-4k\phi -4ck\ln |c-\phi |+\psi ^2-c^2). \end{aligned}$$

(14)

Just like the first case, the system possesses two equilibrium points O(0, 0) (saddle) and $A(c-2k,0)$ (center) at the left side of the line $\phi =c$ when $c>2k>0$. We can similarly detect the existence of the unique pulse $\Gamma _1$ from the relationship $H_1(\phi ,\psi )=H_1(0,0)=-\frac{1}{2}c^2-2ck\ln {c}$.

$\bullet \ 0<b<1$

Something different happens. At this time, the point O(0, 0) is still a saddle point and the eigenvalue of $A(\frac{2c-4k}{1+b},0)$ is still decided by the equality $\lambda ^2=\frac{(c-2k)(c-4k-bc)}{1+b}$. When $b>1-\frac{4k}{c}$, we still have $\lambda ^2<0$. While when $b\le 1-\frac{4k}{c}$, we can find that $\lambda ^2\ge 0$, which shows that the point A is a center point. More than that, along with the type of eigenvalue changes, the location of the point A moves from the left side of the line $\phi =c$ to its right side.

Hence, when $b\in (0,1)\cap (1-\frac{4k}{c},+\infty )$, just like what we do before, we can detect the existence of the homoclinic orbit $\Gamma _b$ by setting $H_b(\phi ,\psi )=H_b(0,0)=\frac{-2kc^b}{b(b-1)}$. However, when $b\in (0,1)\cap (-\infty ,1-\frac{4k}{c}]$, we calculate

$$\begin{aligned} H_b(0,0)=\frac{-2kc^b}{b(b-1)},\ H_b\left( c,\pm \sqrt{c^2+\frac{4ck}{b-1}}\right) =0,\ H_b(c,\cdot ) =\infty , \end{aligned}$$

along with

$$\begin{aligned} f\left( \phi \right) |_{\phi =0}=0,\ f\left( \phi \right) |_{\phi \rightarrow c^-}\rightarrow c^2+\frac{4ck}{b-1}>0,\ f^\prime \left( \phi \right) |_{\phi \rightarrow c^-}\rightarrow -\infty . \end{aligned}$$

It is easy to find that the figure starts from O(0, 0) will never touch the line $\phi =c$, according to Definition 2.4 and Lemma 2.2, we can claim that the system possesses a pseudo-peakon at the left side of the line $\phi =c$ and at this time there exists no pulse. See Fig. 2.

Fig. 2

$b\in (0,1)\cap (-\infty ,1-\frac{4k}{c})$

• b = 0

In this case,

$$\begin{aligned} H_0(\phi ,\psi )=2k\ln |c-\phi |+(-\frac{1}{2}c^2+2ck+\frac{1}{2}\psi ^2+\frac{1}{2}c\phi -\frac{1}{2}\phi ^2)(c-\phi )^{-1}. \end{aligned}$$

(15)

The equilibrium point O(0, 0) is still a saddle point, but $A(2c-4k,0)$ has two possibilities. When $2k<c<4k$, A stays at the left side of the line $\phi =c$, it is still a center point and thus similarly surrounded by a homoclinic orbit. When $c>4k$, A lies at the right side of the line $\phi =c$, we can detect the existence of the pseudo-peakon $\Gamma _0$ by the same method.

$\bullet \ -1<b<0$

Just like the third case, $b=1-\frac{4k}{c}$ is the only special point. When $b\in (1-\frac{4k}{c},+\infty )\cap (-1,0)$, the system possesses a unique pulse; when $b\in (-\infty ,1-\frac{4k}{c}]\cap (-1,0)$, the system possesses a pseudo-peakon at the left side of the line $\phi =c$.

• b = − 1

At this time,

$$\begin{aligned} H_{-1}(\phi ,\psi )=((2k-c)\phi -ck+\frac{1}{2}c^2+\frac{1}{2}\psi ^2)(c-\phi )^{-2}. \end{aligned}$$

(16)

The system possesses only one equilibrium point O(0, 0) , which is a saddle point. Similarly, we set

$$\begin{aligned} H_{-1}(\phi ,\psi )= H_{-1}(0,0)=\frac{1}{2}-\frac{k}{c}, \end{aligned}$$

(17)

then we have

$$\begin{aligned} \psi ^2=\frac{c-2k}{c}\phi ^2. \end{aligned}$$

(18)

Obviously, according to Definition 2.3 and Lemma 2.2, there exists a peakon $\Gamma _{-1}$. See Fig. 3.

Fig. 3

$b=-1$

• b < − 1

At this time, this system possesses two equilibrium points O(0, 0) (saddle) and $A(\frac{2c-4k}{1+b},0)$ (center). However, the point $A(\frac{2c-4k}{1+b},0)$ moves to the left side of the origin, slightly different from the first case. By the analysis of $f(\phi )$ and it’s derivations, we find that $f(\phi )$ is a function that increases first and then decreases and then increases again, the turning points are 0 and some value which is smaller than 0. Moreover,

$$\begin{aligned} f(\phi )|_{\phi =0}=0,\ f(\phi )|_{\phi =c}=c^2+\frac{4ck}{b-1}>0,\ f(\phi )|_{\phi \rightarrow -\infty }\rightarrow -\infty , \end{aligned}$$

and

$$\begin{aligned} f'(\phi )|_{\phi =c}=2c+\frac{4k}{b}>0. \end{aligned}$$

Hence, the figure of $f(\phi )$ can be seen in Fig. 4(a). At this time, there exists an anti-pulse $\Gamma _b$ at the left side of origin.

Fig. 4

$b<-1$

We summarize as the following theorem

Theorem 2.1

When $c>2k>0$, there exist two bifurcation points $b=1-\frac{4k}{c}$ and $b=-1$ for b-equation (1). For $b>1-\frac{4k}{c}$, the orbit $\Gamma _b$ which passes through the origin is a pulse; for $-1< b\le 1-\frac{4k}{c}$, the orbit $\Gamma _b$ breaks to be a pseudo-peakon; for $b=-1$, the orbit $\Gamma _0$ is a peakon; for $b<-1$, the orbit $\Gamma _b$ contains an anti-pulse. When $0<c<2k$, there exists no solitary wave solution.

For the sake of visual representation, we take $k=0.2$, $c=1$ as an example. See Fig. 5.

Fig. 5

Numerical simulations of $\Gamma _b$(blue line) which goes through O(0, 0) and orbits(red line) around $\Gamma _b$ when $k=0.2$, $c=1$

The Discussion of Bifurcation Parameter k

In this section, we treat the constant k of b-equation (1) as a bifurcation parameter. According to Theorem 2.1, we assume $c>2k$, $b>1-\frac{4k}{c}$ and we assume $c>0$ still.

Under these assumptions, the equilibrium point O(0, 0) is always a saddle point. From (9), there are

$$\begin{aligned}&H_b(O)=H_b(0,0) = \frac{-2kc^b}{b(b-1)},\ b\ne -1,0,1 \end{aligned}$$

(19)

$$\begin{aligned}&H_b(B_{1,2})=H_b\left( c,\pm \sqrt{\frac{4kc-2c^2+(1+b)c^2}{b-1}}\right) =0,b\ne -1,0,1. \end{aligned}$$

(20)

When $b\ne -1,0,1$, the values of the above two expressions are equal at $k=0$. Moreover,

$$\begin{aligned} H_b(B_{1,2})|_{k=0}=H_b(c,\pm c)=H_b(\phi ,\pm \phi )|_{k=0}=0=H_b(0,0)|_{k=0}. \end{aligned}$$

(21)

According to Definition 2.3 and Lemma 2.2, the system (7) possesses a peaked soliton.

For the remaining b: When $b=-1$, the system (7) possesses a peaked soliton by Theorem 2.1; When $b=0$, similarly, we get

$$\begin{aligned} H_0(B_{1,2})|_{k=0}=H_0(c,\pm c)=H_0(\phi ,\pm \phi )|_{k=0}=0=H_0(0,0)|_{k=0}, \end{aligned}$$

so the orbit $\Gamma _b$ is a peakon; When $b=1$, there exist no equilibrium points $B_{1,2}$, but we still have

$$\begin{aligned} H_1(\phi ,\pm \phi )|_{k=0}=-\frac{1}{2}c^2=H_1(0,0)|_{k=0}, \end{aligned}$$

(22)

it also indicates the existence of the peakon.

Summarize these, we come to the conclusion:

When $k=0$, $\forall b>1-\frac{4k}{c}$, there exists a peakon for equation (1). When $k\ne 0$: if the value of k is positive, it is the situation which we have discussed in Chapter 2.1; when the value of k is negative, by similar analysis as in Chapter 2.1, we find that $f(\phi )$ is a function that decreases first and then increases, whose turning point is 0. Moreover,

$$\begin{aligned} f(\phi )|_{\phi =0}=0,\ f(\phi )|_{\phi \rightarrow c^-}\rightarrow +\infty ,\ f(\phi )|_{\phi \rightarrow -\infty }\rightarrow +\infty ,\ f'(\phi )|_{\phi \rightarrow c^-}\rightarrow +\infty . \end{aligned}$$

(23)

According to Definition 2.5 and Lemma 2.2, there exists a cuspon for equation (1).

So, we get the following theorem:

Theorem 2.2

When $c>0$, $c>2k$, $b>1-\frac{4k}{c}$, there exists one bifurcation point $k=0$ for b-equation(1). When k is positive, $\Gamma _b$ is a pulse; when $k=0$, $\Gamma _b$ is a peakon; when k is negative, $\Gamma _b$ contains a cuspon.

Fig. 6

Solutions when $c>2k$, $c>0$, $b>1-\frac{4k}{c}$

The corresponding situations can be seen in Fig. 6. For the sake of visual representation, we take $b=2,3$ as the representative examples, which are depicted in Figs. 7 and 8.

Fig. 7

$b=2$

Fig. 8

$b=3$

Actually, the corresponding soliton converges to the peakon in $H_1$ norm when $k\rightarrow 0$. To see it, first, we review (11)

$$\begin{aligned} \psi ^2=\frac{-4kc^b}{b(b-1)}(c-\phi )^{1-b}+\phi ^2+\frac{4k}{b}\phi +\frac{4ck}{b(b-1)}. \end{aligned}$$

Then, because of the property of $\Gamma _b$, we get rid of the positive situation to have

$$\begin{aligned} \psi =-\sqrt{\frac{-4kc^b}{b(b-1)}(c-\phi )^{1-b}\phi ^{-2}+1+\frac{4k}{b}\phi ^{-1}+\frac{4ck}{b(b-1)}\phi ^{-2}}\phi . \end{aligned}$$

(24)

When $k=0$, the corresponding ODE is $\phi '=-\phi$ and the corresponding peaked soliton is $\hat{\phi }=Ce^{-|x-ct|}$. When $k\ne 0$, we come back to the original system(7)

$$\begin{aligned} \left\{ \begin{aligned} \phi '&=(c-\phi )\psi ,\\ \psi '&=(c-2k)\phi -\frac{1+b}{2}\phi ^2-\frac{1-b}{2}\psi ^2,\\ \end{aligned} \right. \end{aligned}$$

which can be transformed into the first order equation

$$\begin{aligned} \frac{d\psi }{d\phi }=\frac{\left( c-2k\right) \phi -\frac{1+b}{2}\phi ^2-\frac{1-b}{2}\psi ^2}{\left( c-\phi \right) \psi }. \end{aligned}$$

(25)

Let

$$\begin{aligned} g(\phi ,\psi ,k)\triangleq \frac{\left( c-2k\right) \phi -\frac{1+b}{2}\phi ^2-\frac{1-b}{2}\psi ^2}{\left( c-\phi \right) \psi }, \end{aligned}$$

(26)

then we can find by observation that when $(\phi ,\psi ,k)\in (0,c)\times \mathbb {R}\setminus \{0\}\times \mathbb {R}$, $g(\phi ,\psi ,k)$ is continuous and satisfies local Lipschitz conditions about $\psi$ uniformly. Hence, according to the continuity theorem of solution on parameters, we get

$$\begin{aligned} |\psi (\phi ;\,c,k,b)-\psi (\phi ;\,c,0,b)|<\epsilon ,\ k\rightarrow 0, \end{aligned}$$

i.e.,

$$\begin{aligned} \left| \phi ^\prime -{\hat{\phi }}^\prime \right| <\epsilon ,\ k\rightarrow 0. \end{aligned}$$

Put (24) into (25), we have

$$\begin{aligned} \frac{d\phi }{d\xi }=-\sqrt{\frac{-4kc^b}{b\left( b-1\right) }\left( c-\phi \right) ^{1-b}\phi ^{-2}+1+\frac{4k}{b}\phi ^{-1}+\frac{4ck}{b\left( b-1\right) }\phi ^{-2}}\phi . \end{aligned}$$

(27)

Similarly, according to the continuity theorem of solution on parameters, we get

$$\begin{aligned} \left| \phi \left( \xi \right) -\hat{\phi }\left( \xi \right) \right| <\epsilon ,\ k\rightarrow 0,\ (\phi ,\xi )\in (0,c)\times \mathbb {R} \end{aligned}$$

Combine with the results we have already known, it is apparently $0<\phi <c$, so we just need to figure out what it looks like when $\phi =0$. Now, $\left( \phi ,\psi \right) =\left( 0,0\right)$ is a saddle point of the system (7), we can depict the property of solutions at (0, 0) by linearizations at (0, 0)

$$\begin{aligned} \left\{ \begin{aligned} \phi '&=c\psi ,\\ \psi '&=(c-2k)\phi .\\ \end{aligned} \right. \end{aligned}$$

(28)

This system (28) has solutions

$$\begin{aligned} \phi \left( \xi \right) =C_1\left( c,k\right) e^{\sqrt{c^2-2ck}\xi }+C_2\left( c,k\right) e^{-\sqrt{c^2-2ck}\xi }, \end{aligned}$$

(29)

where $C_{1,2}\left( c,k\right)$ are functions about c and k. Review our initial conditions, $C_{1,2}$ need to satisfy

$$\begin{aligned} \begin{aligned} |C_1(c,k)e^{\sqrt{c^2-2ck}\xi }|<\varepsilon ,\ \xi \rightarrow +\infty ,\\ |C_2(c,k)e^{-\sqrt{c^2-2ck}\xi }|<\varepsilon ,\ \xi \rightarrow -\infty .\\ \end{aligned} \end{aligned}$$

Hence, $\forall c,k$ satisfy Theorem 2.2,

$$\begin{aligned}&\exists M_1>0,\ \forall \xi >M_1,\ C_1(c,k)e^{\sqrt{c^2-2ck}\xi }\rightarrow 0;\\&\exists M_2<0,\ \forall \xi <M_2,\ C_2(c,k)e^{-\sqrt{c^2-2ck}\xi }\rightarrow 0. \end{aligned}$$

In conclusion,

$$\begin{aligned} \begin{aligned} \lim \limits _{k\rightarrow 0}\Vert \phi -\hat{\phi }\Vert _{H^1}&=\lim \limits _{k\rightarrow 0}\int _{-\infty }^{+\infty }|\phi -\hat{\phi }|^2+|D(\phi -\hat{\phi })|^2d\xi \\&=\lim \limits _{k\rightarrow 0}\int _{-\infty }^{M_2}|\phi -\hat{\phi }|^2+|D(\phi -\hat{\phi })|^2d\xi +\lim \limits _{k\rightarrow 0}\int _{M_2}^{M_1}|\phi -\hat{\phi }|^2+|D(\phi -\hat{\phi })|^2d\xi \\&\ \ \ \ +\lim \limits _{k\rightarrow 0}\int _{M_1}^{+\infty }|\phi -\hat{\phi }|^2+|D(\phi -\hat{\phi })|^2d\xi \\&=0. \end{aligned} \end{aligned}$$

(30)

So, we claim

Corollary 2.1

For $b>1-\frac{4k}{c}$ fixed, the solitons of equation(1) converge to the peakons in $H_1$ norm when $k\rightarrow 0$.

The Existence of Solitary Wave Solutions for B-Class Kuramoto–Sivashinsky Equation

In this section, we discuss the persistence of solitary wave solutions for b-class equation under Kuramoto–Sivashinsky perturbation. First, we recall some basic theories of geometric singular perturbation, which serve as our main tool to study the persistence of solitary wave solutions.

Geometric Theory of Singular Pertubation

Consider the system

$$\begin{aligned} \left\{ \begin{aligned} \phi '&=f(\phi ,\psi ,\nu ,\varepsilon ),\\ \psi '&=g(\phi ,\psi ,\nu ,\varepsilon ),\\ \nu '&=\varepsilon h(\phi ,\psi ,\nu ,\varepsilon ),\\ \end{aligned} \right. \end{aligned}$$

(31)

where $'=\frac{d}{dt}$, $\phi \in R^l$, $\psi \in R^m$, $\nu \in R^n$ and $\varepsilon$ is a real parameter, f, g, h are $C^\infty$ on the set $V\times I$ where $V\in R^{l+m+n}$ and I is an open interval, containing 0.

System (31) can be reformulated with a change of time-scale as

$$\begin{aligned} \left\{ \begin{aligned} \varepsilon \dot{\phi }&=f(\phi ,\psi ,\nu ,\varepsilon ),\\ \varepsilon \dot{\psi }&=g(\phi ,\psi ,\nu ,\varepsilon ),\\ \dot{\nu }&=h(\phi ,\psi ,\nu ,\varepsilon ),\\ \end{aligned} \right. \end{aligned}$$

(32)

where $\dot{ }=\frac{d}{d\tau }$ and $\tau =\varepsilon t$. The time scale given by $\tau$ is said to be slow whereas that for t is fast. Thus we call (31) the fast system and (32) the slow system. As long as $\varepsilon \ne 0$, the two systems are equivalent. Each of the scalings is naturally associated with a limit as $\varepsilon \rightarrow 0$. These two limits are respectively given by

$$\begin{aligned} \left\{ \begin{aligned} \phi '&=f(\phi ,\psi ,\nu ,0),\\ \psi '&=g(\phi ,\psi ,\nu ,0),\\ \nu '&=0,\\ \end{aligned} \right. \end{aligned}$$

(33)

and

$$\begin{aligned} \left\{ \begin{aligned} 0&=f(\phi ,\psi ,\nu ,0),\\ 0&=g(\phi ,\psi ,\nu ,0),\\ \dot{\nu }&=h(\phi ,\psi ,\nu ,0).\\ \end{aligned} \right. \end{aligned}$$

(34)

The former is called the layer problem and the letter is called the reduced system.

Definition 3.1

[11] A manifold $M_0$ on which $f(\phi ,\psi ,\nu ,0)=0$ , $g(\phi ,\psi ,\nu ,0)=0$ is called a critical manifold. A critical manifold $M_0$ is said to be normally hyperbolic if the linearization of the system (33) at each point in $M_0$ has exactly n eigenvalues on the imaginary axis $R(\lambda )=0$.

Definition 3.2

[11] A set of M is locally invariant under the flow of (31) if it has neighborhood V so that no trajectory can leave M without also leaving V. In other words, it is locally invariant if for all $(\phi ,\psi )\in M$, $(\phi ,\psi )\cdot [0,t]\subset M$, and similarly with [0, t] replaced by [t, 0] when $t<0$, where $(\phi ,\psi )\cdot t$ denotes the application of a flow after time t to the initial condition $(\phi ,\psi )$.

Fenichel [11] established the following geometric theory of singular perturbation.

Lemma 3.1

Let $M_0$ be a compact, normally hyperbolic critical manifold, then for sufficiently small positive $\varepsilon$ and any $0<r<+\infty$.

$\bullet$ there exists a manifold $M_\varepsilon$, which is locally invariant under the flow of (31) and $C^r$ in $\phi ,\psi ,\nu ,\varepsilon$.

$\bullet$ $M_\varepsilon$ possesses locally invariant stable and unstable manifold $W^s(M_\varepsilon )$ and $W^u(M_\varepsilon )$ lying within $O(\varepsilon )$ and being $C^r$ diffeomorphic to the stable and unstable manifold $W^s(M_0)$ and $W^u(M_0)$ of the critical manifold $M_0$.

$\bullet$ the dynamics on $M_\varepsilon$ is a regular perturbation of that generated by system (34).

Persistence of Solitary Wave Under Kuramoto–Sivashinsky Perturbation

It is proved recently in [14] that for Camassa-Holm equation ($b=2$), there is a unique persistent solitary wave under singular Kuramoto–Sivashinsky perturbation. We want to see whether this fact still remains true for other bs in the b-class equation.

To figure out, first, we consider the following equation with $k>0$:

$$\begin{aligned} u_t-u_{xxt}+2ku_x+(b+1)uu_x+\epsilon (u_{xx}+u_{xxxx})=bu_xu_{xx}+uu_{xxx}. \end{aligned}$$

(35)

By the same method used in Chapter 2, we get the corresponding solitary wave ODE

$$\begin{aligned} c\phi '''-(c-2k)\phi '+(b+1)\phi '\phi -b\phi '\phi ''-\phi \phi '''+\epsilon (\phi ''+\phi ^{(4)})=0. \end{aligned}$$

(36)

Integrate once to yield

$$\begin{aligned} (c-\phi )\phi ''+(2k-c)\phi +\frac{1+b}{2}\phi ^2-\frac{b-1}{2}\phi '^2+\epsilon (\phi '+\phi ''')=0, \end{aligned}$$

(37)

which is equivalent to the following slow system of first-order equations

$$\begin{aligned} \left\{ \begin{aligned} \phi '&=\psi ,\\ \psi '&=\nu ,\\ \epsilon \nu '&=-(c-\phi )\nu +(c-2k)\phi -\frac{1+b}{2}\phi ^2+\frac{b-1}{2}\psi ^2-\epsilon \psi . \end{aligned} \right. \end{aligned}$$

(38)

With $s=\frac{\xi }{\epsilon }$ and $\dot{ }=\frac{d}{ds}$, the corresponding fast system is

$$\begin{aligned} \left\{ \begin{aligned} \dot{\phi }&=\epsilon \psi ,\\ \dot{\psi }&=\epsilon \nu \\ \dot{\nu }&=-(c-\phi )\nu +(c-2k)\phi -\frac{1+b}{2}\phi ^2+\frac{b-1}{2}\psi ^2-\epsilon \psi . \end{aligned} \right. \end{aligned}$$

(39)

Setting $\epsilon =0$, we get the critical manifold to be

$$\begin{aligned} M_0=\left\{(\phi ,\psi ,\nu ):(c-\phi )\nu =(c-2k)\phi -\frac{1+b}{2}\phi ^2+\frac{b-1}{2}\psi ^2\right\}. \end{aligned}$$

Now, $M_0$ consists of equilibrium points of (39) for $\epsilon =0$. The linearization is given by

$$\begin{aligned} \left( \begin{array}{ccc} 0 &{} \ \ 0 &{} \ \ \ \ 0\\ 0 &{} \ \ 0 &{} \ \ \ \ 0\\ c-2k+\nu -(1+b)\phi &{} \ \ \ \ (b-1)\psi &{} \ \ \ \ \phi -c\\ \end{array} \right) . \end{aligned}$$

(40)

Therefore, the critical manifold $M_0$ is normally hyperbolic with one stable normal direction. Consequently, it follows from Definition 3.1 that, for $\epsilon >0$ sufficiently small, there exists a two dimensional locally invariant manifold $M_\epsilon$ lying $O(\epsilon )$ close to $M_0$ in the $C^1$ topology, and given by

$$\begin{aligned} {M}_\epsilon =\left\{(\phi ,\psi ,\nu ):(c-\phi )\nu =(c-2k)\phi -\frac{1+b}{2}\phi ^2+\frac{b-1}{2}\psi ^2+\epsilon g(\phi ,\psi ,\epsilon )\right\}, \end{aligned}$$

(41)

from which it follows that the flow on $M_{\epsilon }$ satisfies the following equation

$$\begin{aligned} \left\{ \begin{aligned} \phi '&=\psi ,\\ (c-\phi )\psi '&=(c-2k)\phi -\frac{1+b}{2}\phi ^2+\frac{b-1}{2}\psi ^2+\epsilon g(\phi ,\psi ,\epsilon ),\\ \end{aligned} \right. \end{aligned}$$

(42)

which is seen to be a regular perturbation of (6) with $\epsilon =0$. Then, we calculate the perturbation term. Since $M_{\epsilon }$ is locally invariant, we differential the equation

$$\begin{aligned} (c-\phi )\nu =(c-2k)\phi -\frac{1+b}{2}\phi ^2+\frac{b-1}{2}\psi ^2+\epsilon g(\phi ,\psi ,\epsilon ) \end{aligned}$$

(43)

with respect to $\xi$ to get

$$\begin{aligned} (c-2k)\phi '+\phi '\nu +(\phi -c)\nu '-(1+b)\phi \phi '+(b-1)\psi \psi '+O(\epsilon )=0. \end{aligned}$$

(44)

We substitute the expressions for $\phi ',\psi ',\nu '$ from (39) and also the expression for $\nu$ given by (43) into (44), and, after cancelling the O(1) terms, we get

$$\begin{aligned}g(\phi ,\psi ,\nu )&=-\frac{\psi }{(c-\phi )^2} \left( \frac{-b^2+b+4}{2}\phi ^2\right. \nonumber \\&\quad \left. +\frac{b^2-b}{2}\psi ^2+(2-2b)k\phi +2c^2-2ck-4c\phi \right) +O(\epsilon ). \end{aligned}$$

(45)

Therefore, restricted to the slow manifold $M_\epsilon$, (42) is

$$\begin{aligned} \left\{ \begin{aligned} \phi '&=\psi ,\\ (c-\phi )\psi '&=(c-2k)\phi -\frac{1+b}{2}\phi ^2+\frac{b-1}{2}\psi ^2\\&\quad -\frac{\varepsilon \psi }{(c-\phi )^2}\left( \frac{-b^2+b+4}{2}\phi ^2+\frac{b^2-b}{2}\psi ^2+(2-2b)k\phi +2c^2-2ck-4c\phi \right) \\&\qquad \qquad \qquad +O(\epsilon ^2).\\ \end{aligned} \right. \end{aligned}$$

(46)

Within a small neighborhood of the unperturbed homoclinic orbits $\Gamma$, $c-\phi$ is always positive. So (45) is equivalent to

$$\begin{aligned} \left\{ \begin{aligned} \dot{\phi }&=(c-\phi )\psi ,\\ \dot{\psi }&=(c-2k)\phi -\frac{1+b}{2}\phi ^2+\frac{b-1}{2}\psi ^2\\&\ \ -\frac{\varepsilon \psi }{(c-\phi )^2} \left( \frac{-b^2+b+4}{2}\phi ^2+\frac{b^2-b}{2}\psi ^2+(2-2b)k\phi +2c^2-2ck-4c\phi \right) +O(\epsilon ^2),\\ \end{aligned} \right. \end{aligned}$$

(47)

where $\dot{\ }=\frac{d}{(c-\phi )d\xi }$. Moreover, we have already known the first integral

$$\begin{aligned} H_b(\phi ,\psi )=\left( -\frac{1}{2}\phi ^2-\frac{2k}{b}\phi -\frac{2ck}{b(b-1)}+\frac{1}{2}\psi ^2\right) (c-\phi )^{b-1}, \end{aligned}$$

where $b\ne -1,0,1$. In order to study the homoclinic orbit $\Gamma _b$ which goes through the origin, we set $H_b(\phi ,\psi )=H_b(0,0)$ and calculate the intersection points on the $\phi -$axis.

Our aim is to seek homoclinic orbits for (46) with small $\epsilon$, which depends on the value of c. From the original equations, one can see that O(0, 0) remains a critical point and must lie on $M_\epsilon$. We thus look for orbits homoclinic to O(0, 0). The critical point O(0, 0) can be constructed as a surface of critical points, parameterized by $c,\epsilon$. This in turn spawns an unstable manifold $W^u$ and stable manifold $W^s$, which meet at $\epsilon =0$.

Hence, in the set {$\psi =0$}, we parameterize $W^u$ and $W^s$[18] as $\phi =h^-(c,\epsilon )$ and $\phi =h^+(c,\epsilon )$. We define

$$\begin{aligned} d(c,\epsilon )=h^-(c,\epsilon )-h^+(c,\epsilon ) \end{aligned}$$

and observe that zeroes of d render homoclinic orbits. Since there are homoclinic orbits independently of c when $\epsilon =0$, we have $d(c,0)=0$, and thus that $d(c,\epsilon )=\epsilon \tilde{d}(c,\epsilon )$. The Melnikov function is here given by

$$\begin{aligned} \tilde{d}(c,0)=M(c)=\left(\frac{\partial {h^-}}{\partial \epsilon }-\frac{\partial {h^+}}{\partial \epsilon }\right)|_{\epsilon =0}. \end{aligned}$$

(48)

It is a simple application of the Implicit Function Theorem to see that there is a curve of homoclinic orbits given by $c=c(\epsilon )$ for $\epsilon$ small, if there exists a c, at which

$$\begin{aligned} M(c)=0, M'(c)\ne 0. \end{aligned}$$

Then we can calculate this Melnikov function

$$\begin{aligned} \begin{aligned}&\ \ \ \ M(c)\\&\quad =\int _{-\infty }^{+\infty } { \left| \begin{array}{cccc} (c-\phi )^{b-1}\psi &{} \ \ \ \ 0 \\ (c-\phi )^{b-2}\left( (c-2k)\phi -\frac{1+b}{2}\phi ^2+\frac{b-1}{2}\psi ^2\right) &{} \ \ \ \ -\frac{\psi }{(c-\phi )^{4-b}}\left( \frac{-b^2+b+4}{2}\phi ^2+\frac{b^2-b}{2}\psi ^2+2c^2\right. \\ &{}\quad \left. +(2-2b)k\phi -2ck-4c\phi \right) \\ \end{array}\right| }d\tilde{\zeta }\\&\quad =\int _{-\infty }^{+\infty } {-(c-\phi )^{2b-5}\psi ^2\left( \frac{-b^2+b+4}{2}\phi ^2+\frac{b^2-b}{2}\psi ^2+(2-2b)k\phi +2c^2-2ck-4c\phi \right) }d\tilde{\zeta },\\ \end{aligned} \end{aligned}$$

(49)

where $d\tilde{\zeta }=\frac{d\phi }{(c-\phi )^{b-1}\psi }$. We always consider the case $c>2k>0$ in this section.

Since it is difficult to calculate the fractional order equations and equations with logarithmic terms, we can not get the display expression of the intersection between the $\phi$-axis and the unperturbed homoclinic. We can only deal with two situations: $b=2,3$, which have explicit solutions.

• b = 2

It is the case: Camassa-Holm equation. We consider the following equation:

$$\begin{aligned} u_t-u_{xxt}+2ku_x+3uu_x+\epsilon (u_{xx}+u_{xxxx})=2u_xu_{xx}+uu_{xxx}. \end{aligned}$$

(50)

According to Li and Du’s work [14], the corresponding Melnikov integral is given by

$$\begin{aligned} \begin{aligned} M(c)&=\int _{-\infty }^{+\infty } { \left| \begin{array}{cccc} (c-\phi )\psi &{} \ \ \ \ 0 \\ (c-2k)\phi -\frac{3}{2}\phi ^2+\frac{1}{2}\psi ^2 &{} \ \ \ \ -\frac{\psi }{(c-\phi )^2}(\phi ^2+\psi ^2-2k\phi +2c^2-2ck-4c\phi )\\ \end{array}\right| }d\zeta \\&=\int _{-\infty }^{+\infty } {-(c-\phi )^{-1}\psi ^2(\phi ^2+\psi ^2-2k\phi +2c^2-2ck-4c\phi )}d\zeta ,\\ \end{aligned} \end{aligned}$$

where $d\zeta =\frac{d\phi }{(c-\phi )\psi }$, $\phi ,\psi$ are evaluated on the unperturbed homoclinic $\Gamma _2$ which satisfies

$$\begin{aligned} (\phi -c)\psi ^2-\phi ^3-(2k-c)\phi ^2=0. \end{aligned}$$

(51)

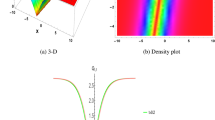
By calculation, when $2k<c<\frac{2k}{-19+\sqrt{385}}$, the function M(c) is concave; when $c>\frac{2k}{-19+\sqrt{385}}$, the function M(c) is strictly uniformly convex. Also, we have

$$\begin{aligned} \begin{aligned} M(2k)=\frac{d}{dc}M(2k)=0, \\ M\rightarrow -\infty , as\ c\rightarrow +\infty ,\\ \end{aligned} \end{aligned}$$

which indicates there is a unique simple zero of the function M(c) somewhere larger than $\frac{2k}{-19+\sqrt{385}}$, which is depicted in Fig.9(a). Therefore, by Implicit Function Theorem, for each fixed $2k>0$, there is a unique persistent homoclinic orbit for $0<\varepsilon \le 1$.

Fig. 9

Numerical simulations of Melnikov function M(c)

• b = 3

It is the case: Degasperis-Procesi equation. We consider the following equation with $k>0$:

$$\begin{aligned} u_t-u_{xxt}+2ku_x+4uu_x+\epsilon (u_{xx}+u_{xxxx})=3u_xu_{xx}+uu_{xxx}. \end{aligned}$$

(52)

By calculation, we get the critical manifold to be

$$\begin{aligned} \tilde{M}_0=\{(\phi ,\psi ,\nu ):(c-\phi )\nu =(c-2k)\phi -2\phi ^2+\psi ^2\}, \end{aligned}$$

and the two dimensional locally invariant manifold $\tilde{M}_\epsilon$, which lies $O(\epsilon )$ close to $\tilde{M}_0$ in the $C^1$ topology, is given by

$$\begin{aligned} \tilde{M}_\epsilon =\{(\phi ,\psi ,\nu ):(c-\phi )\nu =(c-2k)\phi -2\phi ^2+\psi ^2+\epsilon \tilde{g}(\phi ,\psi ,\epsilon )\}. \end{aligned}$$

(53)

Also, we calculate $\tilde{g}$ to be

$$\begin{aligned} \tilde{g}(\phi ,\psi ,\nu )=-\frac{\psi }{(c-\phi )^2}(-\phi ^2+3\psi ^2-4k\phi +2c^2-2ck-4c\phi )+O(\epsilon ). \end{aligned}$$

(54)

Then, the DP-KS equation’s Melnikov function can be represented as

$$\begin{aligned} \begin{aligned} M(c)&=\int _{-\infty }^{+\infty } { \left| \begin{array}{cccc} (c-\phi )^2\psi &{} \ \ \ \ 0 \\ (c-\phi )((c-2k)\phi -2\phi ^2+\psi ^2) &{} \ \ \ \ -\frac{\psi }{c-\phi }(-\phi ^2+3\psi ^2-4k\phi +2c^2-2ck-4c\phi )\\ \end{array}\right| }d\zeta \\&=\int _{-\infty }^{+\infty } {-(c-\phi )\psi ^2(-\phi ^2+3\psi ^2-4k\phi +2c^2-2ck-4c\phi )}d\zeta ,\\ \end{aligned} \end{aligned}$$

where $d\zeta =\frac{d\phi }{(c-\phi )^2\psi }$. For further calculation, we set

$$\begin{aligned} H_3(\phi ,\psi )=\frac{1}{2}\phi ^4+\frac{2k-3c}{3}\phi ^3-\frac{2ck-c^2}{2}\phi ^2-\frac{(c-\phi )^2}{2}\psi ^2+\frac{c^3k}{3}=H_3(0,0) \end{aligned}$$

(55)

to find the intersection on the $\phi -$axis to be $(\phi ^*,0)=(\frac{-2k+3c-\sqrt{4k^2+6ck}}{3},0)$. Changing variable $\varphi =c-\phi$, we get

$$\begin{aligned} \begin{aligned} M(c)&=-2\int _0^{\phi ^*}{(c-\phi )^2\psi ^2(-\phi ^2+3\psi ^2-4k\phi +2c^2-2ck-4c\phi )\frac{d\phi }{(c-\phi )^2\psi }}\\&=-2\int _0^{\phi ^*}{\frac{\phi }{(c-\phi )^4}\sqrt{\phi ^2+\frac{4k-6c}{3}\phi ^2+c^2-2ck}(2(c-\phi )^4-2c^3k)}d\phi \\&=2\int _c^{c-\phi ^*}\frac{c-\varphi }{\varphi ^4}\sqrt{\varphi ^2-\frac{4k}{3}\varphi -\frac{2ck}{3}}(2\varphi ^4-2c^3k)d\varphi . \end{aligned} \end{aligned}$$

(56)

This is the calculation about the original functions of rational polynomials, we get the final result to be

$$\begin{aligned} \begin{aligned} M(c)=&8c^3k\{\frac{-432c^3k^2-3968k^5-2592k^3c^2-5184k^4c-\frac{1024k^6}{c}}{\left( 12ck+8k^2+4k\sqrt{4k^2+6ck}\right) ^3}\\&-\frac{\left( 1600k^4+432k^2c^2+1536k^3c+\frac{512k^5}{c}\right) \sqrt{6ck+4k^2}}{\left( 12ck+8k^2+4k\sqrt{4k^2+6ck}\right) ^3}\\&-\frac{-8c^5+\frac{736k^2c^3}{27} -\frac{256k^3c^2}{27}+\left( 8c^4+\frac{32ck^3}{27}+8kc^3-\frac{416c^2k^2}{27}\right) \sqrt{c^2-2ck}}{\left( 2c^2-\frac{4ck}{3}-2c\sqrt{c^2-2ck}\right) ^3}\\&-(1+\frac{2k}{3c})\left( \frac{2ck}{3}\right) ^{-\frac{1}{2}} \left[ \arctan \left( \left( \frac{2ck}{3}\right) ^{-\frac{1}{2}}\frac{2k+\sqrt{4k^2+6ck}}{3}\right) \right. \\&\qquad \qquad \qquad \left. -\arctan \big (\left( \frac{2ck}{3}\right) ^{-\frac{1}{2}}\left( c-\sqrt{c^2-2ck}\right) \right] \big \}\\&+2\left( c-\frac{2k}{3}\right) \left( \frac{4k^2}{9}+\frac{2ck}{3}\right) \ln \frac{3c-2k+3\sqrt{c^2-2ck}}{\sqrt{4k^2+6ck}}-\left( \frac{2c^2}{3}+\frac{8k^2}{9}\right) \sqrt{c^2-2ck}, \end{aligned} \end{aligned}$$

(57)

which is described by numerical simulation in Fig. 9(b).

It explicitly shows that there is a unique simple zero of the function M(c). We get therefore from the Implicit Function Theorem that for each fixed $k>0$, there is a unique persistent homoclinic orbit for $0<\epsilon \le 1$. This proves the following theorem:

Theorem 3.1

For any $k>0$. For sufficiently small $\epsilon >0$, there is a unique solitary wave to Degasperis-Procesi Kuramoto–Sivashinsky equation (52).

Compare these two representative graphs, we can draw the conjecture due to their similarities.

Conjecture 3.1

For any fixed $k>0$. For sufficiently small $\epsilon >0$, there is a unique solitary wave to b-class Kuramoto–Sivashinsky equation when $b\in [2,3]$.