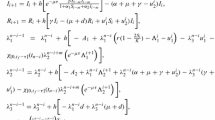Introduction

Epidemiology is the discipline that focuses on the study of the dynamics of infectious diseases as well as the relationship between these diseases and the various factors involved in their appearance and evolution, in order to implement fight against this spread. Despite its young age, mathematical modeling is a valuable tool for understanding the mechanisms of disease transmission, plays an increasingly important role in epidemiology and has already contributed to great successes.

One of the main mathematical tools being used to formulate many epidemiological models is differential equations, whether they are ordinary, partial or stochastic [1,2,3,4,5,6]. The focus in such epidemiological models has been on the incidence rate which is the number of new cases per population at risk in a given time period at which people move from the class of susceptible individuals to the class of infective individuals. These incidence rates were mainly modeled by the bilinear incidence function, called also the mass action, and other generalized functional responses such as: the Beddington-DeAnglis functional response [7, 8], the Crowley-Martin functional response [9], the Hattaf functional response [10] and the Hattaf-Yousfi functional response [11].

On the other hand, optimal control has been used as a strategy to control the epidemic propagation. The main idea behind using the optimal control in epidemics is to search for, among the available strategies, the most effective strategy that reduces the infection rate to a minimum level while optimizing the cost of deploying a therapy or a preventive vaccine that is used for controlling the disease progression. Recently, many optimal control models pertaining to epidemic diseases have appeared in the literature. Tuberculosis model [12], where Silva and Torres proposed optimal control strategies to minimize the cost of interventions using data from Angola, delayed HIV model [13], where Hattaf and Yousfi used optimal controls to represent the efficiency of drug treatment in inhibiting viral production and preventing new infections, and stochastic SIVR model [14], where Witbooi et al. designed an efficient strategy for the roll-out of vaccination in order to minimize the number of infected individuals.

In this paper, we propose a generalized SIVR stochastic epidemic model, in which we consider two controls, namely, vaccination together with non-pharmaceutical interventions such as education and awareness. Our aim is to reduce the number of infected individuals and the costs. To do this, the paper is organized as follows. “Presentation of the model” describes the mathematical model. In “Deterministic optimal control problem” and “Stochastic optimal control problem”, the optimal control problems are formulated and analyzed. In “Numerical simulations” , the resulting numerical simulations are presented. Finally, a brief discussion and conclusion are given in “Discussion and conclusion”.

Presentation of the model

In reality, for every epidemic, there are many factors that must be considered mathematically in the definition of the model. This means that for an epidemiological study to be closer to reality, more informations are needed about the epidemic and the nature of its spread, including the effect of environmental noise. Therefore, there are several variations of stochastic models, with different properties, for describing the epidemic propagation [11, 14,15,16,17,18,19]. In this paper, one of these variations is examined. Precisely, we propose a new stochastic SIVR model with nonlinear functional response and two control functions governed by the following stochastic differential equations (SDEs):

$$\begin{aligned} \left\{ \begin{array}{ll} dS(t)&{}=\left( \Lambda -\mu S(t)-\displaystyle \frac{\left( 1-u_1 (t)\right) \beta S(t)I(t)}{\Psi \left( S(t),I(t)\right) }+\delta V(t)-u_2(t)S(t)\right) d(t)\\ \\ &{}\quad -\displaystyle \frac{\sigma S(t)I(t)}{\Psi \left( S(t),I(t)\right) }dB(t),\\ \\ dI(t)&{}=\left( \displaystyle \frac{\left( 1-u_1 (t)\right) \beta S(t)I(t)}{\Psi \left( S(t),I(t)\right) }+\displaystyle \frac{\rho \left( 1-u_1 (t)\right) \beta V(t)I(t)}{\Phi \left( V(t),I(t)\right) }-(\mu + \gamma )I(t)\right) d(t)\\ \\ &{}\quad +\sigma I(t)\left( \displaystyle \frac{ S(t)}{\Psi \left( S(t),I(t)\right) }+\displaystyle \frac{ \rho V(t)}{\Phi \left( V(t),I(t)\right) }\right) dB(t), \\ \\ dV(t)&{}=\left( u_2(t)S(t)-\displaystyle \frac{\left( 1-u_1 (t)\right) \rho \beta V(t)I(t)}{\Phi \left( V(t),I(t)\right) }-(\mu +\delta )V(t)\right) d(t)\\ \\ &{}\quad-\displaystyle \frac{\sigma \rho V(t)I(t)}{\Phi \left( V(t),I(t)\right) }dB(t),\\ \\ dR(t)&{}=\left( \gamma I(t)-\mu R(t)\right) dt, \end{array}\right. \end{aligned}$$
(1)

where S(t), I(t), V(t) and R(t) are four compartments describing the different populations and denote the number of susceptible, infected, vaccinated and removed individuals at time t, respectively. The variable \(u_1(t)\) represents the control on the successful practice of non-pharmaceutical interventions for susceptible to protect themselves from attack of the disease and \(u_2(t)\) is the control on vaccination of susceptible in a time interval \([0,t_f]\). The parameters \(\Lambda\) and \(\mu\) represent the recruitment rate and the natural death rate of the population, respectively, \(\gamma\) is a recovery rate of the infected individuals. The terms \(\beta S/\Psi (S,I)\) and \(\beta S/\Phi (S,I)\) are in the form of the incidence rate proposed by Hattaf et al. [10] with \(\Psi (S,I)=1+\alpha _{1}S+\alpha _{2}I+\alpha _{3}SI\) and \(\Phi (V,I)=1+\alpha _{4}V+\alpha _{2}I+\alpha _{5}VI\), where \(\beta\) is the infection coefficient and \(\alpha _i \ge 0,\ i=1,...,5\), are the saturation factors measuring the psychological or inhibitory effect. It is very important to note that this functional response is used in [3] and it covers many common types of incidence rate cited previously. The vaccination may reduce but not completely eliminate susceptibility to infection, so a factor \(\rho\), \(0\le \rho \le 1\), is included in the contact rate of vaccinated members with \(\rho = 0\) meaning that the vaccine is perfectly effective and \(\rho = 1\) meaning that the vaccine has no effect. We suppose also that the vaccination loses effect at a proportional rate \(\delta\). Finally, B(t) is a standard Brownian motion defined on a complete probability space \((\Omega ,{\mathcal {F}},{\mathbb {P}})\) with a filtration \(\{{\mathcal {F}}_{t}\}_{t\ge 0}\) satisfying the usual conditions (i.e., it is increasing and right continuous while \({\mathcal {F}}_{0}\) contains all P-null sets) and \(\sigma\) represents the intensity of B(t).

Note that R does not appear in the first three equations of system (1); this allows us to study only the following system

$$\begin{aligned} \left\{ \begin{array}{ll} dS(t)&{}=\left( \Lambda -\mu S(t)-\displaystyle \frac{\left( 1-u_1 (t)\right) \beta S(t)I(t)}{\Psi \left( S(t),I(t)\right) }+\delta V(t)-u_2(t)S(t)\right) d(t)\\ \\ &{}\quad -\displaystyle \frac{\sigma S(t)I(t)}{\Psi \left( S(t),I(t)\right) }dB(t),\\ \\ dI(t)&{}=\left( \displaystyle \frac{\left( 1-u_1 (t)\right) \beta S(t)I(t)}{\Psi \left( S(t),I(t)\right) }+\displaystyle \frac{\rho \left( 1-u_1 (t)\right) \beta V(t)I(t)}{\Phi \left( V(t),I(t)\right) }-(\mu + \gamma )I(t)\right) d(t)\\ \\ &{}\quad +\sigma I(t)\left( \displaystyle \frac{ S(t)}{\Psi \left( S(t),I(t)\right) }+\displaystyle \frac{ \rho V(t)}{\Phi \left( V(t),I(t)\right) }\right) dB(t), \\ \\ dV(t)&{}=\left( u_2(t)S(t)-\displaystyle \frac{\rho \left( 1-u_1 (t)\right) \beta V(t)I(t)}{\Phi \left( V(t),I(t)\right) }-(\mu +\delta )V(t)\right) d(t)\\ \\ &{}\quad-\displaystyle \frac{\sigma \rho V(t)I(t)}{\Phi \left( V(t),I(t)\right) }dB(t). \end{array}\right. \end{aligned}$$
(2)

It is important to note that system (2) includes and improves the stochastic model presented by Witbooi et al. [14], when \(\Lambda =\mu\), \(\delta =0\), \(u_1=0\) and \(\alpha _i=0, i=1,...,5\). The authors examine only the case when the vaccine does not lose its effectiveness and introduced one type of control that characterize the vaccination for susceptible where the optimal control problem was about minimizing the number of infected individuals balanced against the cost of vaccination. Further, our system (2) includes the stochastic model proposed by Tornatore et al. [19], when \(u_1=0\), \(u_2\) is a constant, \(\delta =0\) and \(\alpha _i=0, i=1,...,5\). Finally, in the absence of the perturbations (i.e. \(\sigma =0\)), many deterministic epidemic models existing in the literature are a special case of our proposed model such as [20, 21].

Deterministic optimal control problem

In this section, we formulate and solve the deterministic version of the control problem for the system (2) in the absence of perturbation (i.e. \(\sigma =0\)). We wish to design an optimal controls \(u^{*}_1(t)\) and \(u^{*}_2(t)\) which minimize the number of infected individuals and the costs of successful practice of non-pharmaceutical interventions and vaccination over a certain time horizon \([0,t_f]\). For simplicity, we rewrite the system (2) without perturbation as follows

$$\begin{aligned} dX(t)=F\left( X(t),u(t)\right) dt, \end{aligned}$$
(3)

where

$$\begin{aligned} X=(S,I,V),\ u=(u_1,u_2),\ F=(f_1,f_2,f_3)^{T }, \end{aligned}$$

with

$$\begin{aligned} f_1=\, & \Lambda -\mu S-\displaystyle \frac{\left( 1-u_1\right) \beta SI}{\Psi \left( S,I\right) }+\delta V-u_2 S, \\ f_2=\, & \displaystyle \frac{\left( 1-u_1\right) \beta SI}{\Psi \left( S,I\right) }+\displaystyle \frac{\rho \left( 1-u_1\right) \beta VI}{\Phi \left( V,I\right) }-\left( \mu + \gamma \right) I, \\ f_3=\, & u_2S-\displaystyle \frac{\rho \left( 1-u_1\right) \beta VI}{\Phi \left( V,I\right) }-\left( \mu +\delta \right) V. \end{aligned}$$

Here \(T\) denotes the transpose of a matrix.

Now, we can formulate the optimization problem.

Problem 3.1

Minimize the objective functional

$$\begin{aligned} J(u_1,u_2)=\displaystyle {\int _{0}^{t_f}}\left( I(s)+\displaystyle \frac{C_1 }{2}u^{2}_{1}(s)+\displaystyle \frac{C_2 }{2}u^{2}_{2}(s)\right) ds, \end{aligned}$$
(4)

subject to (3) and \(S(0)=S_0\ge 0,\ I(0)=I_0\ge 0,\ V(0)=V_0\ge 0\), where \(C_1\) and \(C_2\) represent the positive weights on the cost.

The control functions are assumed to be \(L^1(0,t_f)\) functions, belonging to a set of admissible controls \({\mathcal {U}}\) defined by

$$\begin{aligned} {\mathcal {U}}=\left\{ u=\left( u_1,u_2\right) : u_i \text { measurable },\quad 0\le u_i(t)\le 1, t\in [0,t_f], i=1,2\right\} . \end{aligned}$$
(5)

To show the existence of the optimal control for the problem under consideration, we notice that the set of admissible controls \({\mathcal {U}}\) is, by definition, closed and bounded. It is also convex because \([0, 1]\times [0,1]\) is convex in \({\mathbb {R}}^2\). It is obvious that there is an admissible pair \((u_{1}^{*},u_{2}^{*})\) for the problem. For example, one can select \(u_1(t) =0\) and \(u_2(t)=1\) for all \(t\in [0,t_f]\) and solve the resulting differential Eq. (3) to obtain the corresponding solution of the system. Moreover, the solution is bounded, since the state variables and the history functions are continuous and the domain is bounded. Also, the objective functional J is convex in the controls \(u_1(t)\) and \(u_2(t)\). Hence, the existence of the optimal control comes as a direct result from Corollary 4.1. [22]. Therefore, we have the following result.

Theorem 3.2

Consider the optimal control problem (4) subject to (3). Then there exists an optimal pair of controls \((u_1{^*},u_2{^*})\) and a corresponding optimal states \((S^*,I^*,V^*)\) that minimizes the objective function \(J(u_1,u_2)\) over the set of admissible controls \({\mathcal {U}}\).

Now, we derive the first order necessary conditions for the existence of optimal control by constructing the Hamiltonian \({\mathcal {H}}\) and then applying the Pontryagin’s maximum principle [23].

The Hamiltonian of the problem is given by

$$\begin{aligned} {\mathcal {H}}\left( S,I,V,u_1,u_2\right) =I(t)+\displaystyle \frac{C_1 }{2}u^{2}_{1}(t)+\displaystyle \frac{C_2 }{2}u^{2}_{2}(t)+\displaystyle {\sum _{i=1}^{3}}\lambda _i f_i (t). \end{aligned}$$
(6)

By applying Pontryagin’s Maximum Principle, we obtain the following theorem.

Theorem 3.3

Given optimal controls \(u^*=(u^{*}_{1},u^{*}_{2})\), and solutions \(S^*\), \(I^*\) and \(V^*\) of the corresponding state system (3), there exist adjoint variables, \(\lambda _1\), \(\lambda _2\) and \(\lambda _3\) satisfying the following equations

$$\begin{aligned} \lambda _{1}^{\prime }(t)&=\displaystyle \frac{\beta \left( \lambda _1(t)-\lambda _2(t)\right) \left( 1+\alpha _2 I^*(t)\right) \left( 1-u^{*}_1(t)\right) }{\Psi \left( S^{*}(t),I^{*}(t)\right) ^2}+\left( \lambda _1(t)-\lambda _3(t)\right) u^{*}_2(t) + \lambda _1(t)\mu ,\nonumber \\ \lambda _{2}^{\prime }(t)&=\beta \left( \displaystyle \frac{\left( \lambda _1(t)-\lambda _2(t)\right) \left( 1+\alpha _1 S^{*}(t)\right) }{\Psi \left( S^{*}(t),I^{*}(t)\right) ^2} + \displaystyle \frac{\rho \left( \lambda _3(t)-\lambda _2(t)\right) \left( 1+\alpha _4 V^{*}(t)\right) }{\Phi \left( V^{*}(t),I^{*}(t)\right) ^2} \right) \left( 1-u^{*}_1(t)\right) , \nonumber \\&\quad + \lambda _2(t)(\mu +\gamma ) - 1,\nonumber \\ \lambda _{3}^{\prime }(t)&= \displaystyle \frac{\rho \beta \left( \lambda _3(t)-\lambda _2(t)\right) \left( 1+\alpha _2 I^{*}(t)\right) \left( 1-u^{*}_1(t)\right) }{\Phi \left( V^{*}(t),I^{*}(t)\right) ^2} + \left( \lambda _3(t)-\lambda _1(t)\right) \delta + \lambda _3(t)\mu , \end{aligned}$$
(7)

with transversality conditions

$$\begin{aligned} \lambda _i(t_f)=0, \ i=1,...,3. \end{aligned}$$
(8)

Moreover, the optimal control is given by

$$\begin{aligned} u_{1}^{*}(t)&= \min \left\{ 1,\max \left\{ 0,\displaystyle \frac{\beta I^{*}(t)}{C_1}\left( \displaystyle \frac{S^{*}(t)\left( \lambda _2(t)-\lambda _1(t)\right) }{\Psi \left( S^{*}(t),I^{*}(t)\right) } + \displaystyle \frac{\rho V^{*}(t)\left( \lambda _2(t)-\lambda _3(t)\right) }{\Phi \left( V^{*}(t),I^{*}(t)\right) } \right) \right\} \right\} , \nonumber \\ u_{2}^{*}(t)&=\min \left\{ 1,\max \left\{ 0,\displaystyle \frac{ S^{*}(t)}{C_2}\left( \lambda _1(t)-\lambda _3(t)\right) \right\} \right\} . \end{aligned}$$
(9)

Proof

The adjoint equations and transversality conditions can be obtained by using Pontryagin’s Maximum Principle [23] such that

$$\begin{aligned}&\lambda _{1}^{\prime }(t) =-\displaystyle \frac{\partial {\mathcal {H}}}{\partial S}(t),\quad \lambda _{2}^{\prime }(t) =-\displaystyle \frac{\partial {\mathcal {H}}}{\partial I}(t),\quad \lambda _{3}^{\prime }(t) =-\displaystyle \frac{\partial {\mathcal {H}}}{\partial V}(t), \nonumber \\&\quad \lambda _i(t_f)=0,\ i=1,...,3. \end{aligned}$$
(10)

The optimal controls \(u^{*}_1\) and \(u^{*}_2\) can be solved from the optimality conditions

$$\begin{aligned} \displaystyle \frac{\partial {\mathcal {H}}}{\partial u_1}(t)=0,\quad \displaystyle \frac{\partial {\mathcal {H}}}{\partial u_2}(t)=0. \end{aligned}$$
(11)

This implies that

$$\begin{aligned} \displaystyle \frac{\partial {\mathcal {H}}}{\partial u_1}( t)=\, & C_1 u_1(t)+\beta I(t)\left( \displaystyle \frac{ S(t)\left( \lambda _1(t)-\lambda _3(t)\right) }{\Psi \left( S(t),I(t)\right) } + \displaystyle \frac{\rho V(t)\left( \lambda _3(t)-\lambda _2(t)\right) }{\Phi \left( V(t),I(t)\right) }\right) =0, \nonumber \\ \displaystyle \frac{\partial {\mathcal {H}}}{\partial u_2}(t)=\, & C_2 u_2(t)+S(t)\left( \lambda _3(t)-\lambda _1(t)\right) =0. \end{aligned}$$
(12)

By the bounds in \({\mathcal {U}}\) of the controls, it is easy to obtain \(u^{*}_1\) and \(u^{*}_2\) in the form of (9), respectively. \(\square\)

Stochastic optimal control problem

Here, we formulate the stochastic version of the optimization problem and describe its solution. For the purposes of optimization, we rewrite the system (2) as follows

$$\begin{aligned} dX(t)=F\left( X(t),u(t)\right) dt+G\left( X(t)\right) dB(t), \end{aligned}$$
(13)

where \(G=(g_1,g_2,g_3)^{T }\) with

$$\begin{aligned} g_1 = -\displaystyle \frac{\sigma SI}{\Psi \left( S,I\right) },\quad g_2 =\sigma I\left( \displaystyle \frac{ S}{\Psi \left( S,I\right) }+\displaystyle \frac{ \rho V}{\Phi \left( V,I\right) }\right) ,\quad g_3 = -\displaystyle \frac{\sigma \rho VI}{\Phi \left( V,I\right) }. \end{aligned}$$

Our goal is to find an optimal control for non-pharmaceutical interventions and vaccination that minimizes the objective functional which for an initial state \(X_0\) is defined by

$$\begin{aligned} E_{0,X_0}\left[ \displaystyle {\int _{0}^{t_f}}\left( I(s)+\displaystyle \frac{C_1 }{2}u^{2}_{1}(s)+\displaystyle \frac{C_2 }{2}u^{2}_{2}(s)\right) ds\right] . \end{aligned}$$
(14)

Here the expectation is obtained on the condition that the initial state (at time \(t= 0\)) of the system is \(X_0\). In step with the deterministic problem of earlier, the class of admissible control laws is

$$\begin{aligned} {\mathcal {A}}=\left\{ u=\left( u_1,u_2\right) : u_i\ {\mathcal {F}}_t\text {-adapted, and } 0\le u_i(t)\le 1\ p.s, t\in [0,t_f], i=1,2.\right\} . \end{aligned}$$
(15)

To solve this stochastic control problem, we define the performance criterion as follows:

$$\begin{aligned} J\left( t,X,u\right) =E_{t,X}\left[ \displaystyle {\int _{t}^{t_f}}\left( I(s)+\displaystyle \frac{C_1 }{2}u^{2}_{1}(s)+\displaystyle \frac{C_2 }{2}u^{2}_{2}(s)\right) ds\right] , \end{aligned}$$
(16)

where the expectation is conditional on the state of the system being a fixed value X at time t. We define the value function as follow

$$\begin{aligned} U(t,X)=\displaystyle {\inf _{u\in {\mathcal {A}}}}J\left( t,X,u\right) =J\left( t,X,u^*\right) . \end{aligned}$$
(17)

We determine a control law that minimizes the expected value \(J: {\mathcal {A}}\rightarrow {\mathbb {R}}^+\) given by (16). We can now formulate the stochastic analogue of the optimal control problem, subsequent to which we present the solution formulae.

Problem 4.1

Given the system (13) and \({\mathcal {A}}\) as in (15) with J as in (16), find the value function

$$\begin{aligned} U(t,X)=\displaystyle {\inf _{u\in {\mathcal {A}}}}J\left( t,X,u\right) , \end{aligned}$$
(18)

and an optimal control functions

$$\begin{aligned} (u_1^{*}(t),u_2^{*}(t))=u^{*}(t)=\arg \displaystyle {\inf _{u\in {\mathcal {A}}}}J\left( t,X,u\right) . \end{aligned}$$
(19)

From [24], we denote by \({\mathcal {L}}\) the differential operator associated with the functions displayed in (13), defined for a function \(U(t,x)\in C^{1,2}([0,+\infty )\times {\mathbb {R}}^{3})\) by

$$\begin{aligned} {\mathcal {L}}U=\displaystyle \frac{\partial U}{\partial t}+F^{T }\displaystyle \frac{\partial U}{\partial x}+\displaystyle \frac{1}{2}Tr\left[ G^{T }\displaystyle \frac{\partial ^{2} U}{\partial x^{2}}G\right] , \end{aligned}$$
(20)

where

$$\begin{aligned}&\displaystyle \frac{\partial U(t,x)}{\partial x}:=\left( U_{x_1},U_{x_2},U_{x_3}\right) ^{T }=\left( \displaystyle \frac{\partial U(t,x)}{\partial x_{1}},\displaystyle \frac{\partial U(t,x)}{\partial x_{2}},\displaystyle \frac{\partial U(t,x)}{\partial x_{3}}\right) ^{T }, \\&\displaystyle \frac{\partial ^{2} U(t,x)}{\partial x^{2}}:=(U_{x_i x_j})_{i,j}=\left( \displaystyle \frac{\partial ^{2} U(t,x)}{\partial x_{i}\partial x_{j}}\right) _{i,j}\ ,\quad i=1,...,3, \end{aligned}$$

and Tr means trace of a matrix.

We can find an expression for the optimal controls \(u^{*}_{1}\) and \(u^{*}_{2}\) through the following theorem.

Theorem 4.2

A solution to the optimal vaccination problem stated in Problem (15) is of the form

$$\begin{aligned} u_{1}^{*}(t)=\, & \min \left\{ 1;\max \left\{ 0;\displaystyle \frac{\beta I^{*}(t)}{C_1}\left( \displaystyle \frac{S^{*}(t)\left( U_I(t)-U_S(t)\right) }{\Psi \left( S^{*}(t),I^{*}(t)\right) } + \displaystyle \frac{\rho V^{*}(t)\left( U_I(t)-U_V(t)\right) }{\Phi \left( V^{*}(t),I^{*}(t)\right) } \right) \right\} \right\} , \nonumber \\ u_{2}^{*}(t)=\, & \min \left\{ 1;\max \left\{ 0;\displaystyle \frac{S^{*}(t)}{C_2}\left( U_S(t)-U_V(t)\right) \right\} \right\} . \end{aligned}$$
(21)

Proof

We determine (21) via the dynamic programming approach. First we calculate \({\mathcal {L}}(U(t))\) as follows

$$\begin{aligned} {\mathcal {L}}(U(t))=\, & f_1(t)U_S(t)+f_2(t)U_I(t)+f_3(t)U_V(t)+\displaystyle \frac{1}{2}g_{1}^{2}U_{SS}(t)+\displaystyle \frac{1}{2}g_{2}^{2}U_{II}(t)\\&+\displaystyle \frac{1}{2}g_{3}^{2}U_{VV}(t) +g_{1}g_{2}U_{SI}(t)+g_{1}g_{3}U_{SV}(t)+g_{2}g_{3}U_{VI}(t)\\\\=\, & \left( \Lambda -\mu S(t)-\displaystyle \frac{\left( 1-u_1 (t)\right) \beta S(t)I(t)}{\Psi \left( S(t),I(t)\right) }-u_2 (t)S(t)+\delta V(t)\right) U_S(t)\\\\&+\left( \displaystyle \frac{\left( 1-u_1 (t)\right) \beta S(t)I(t)}{\Psi \left( S(t),I(t)\right) }+\displaystyle \frac{\rho \left( 1-u_1 (t)\right) \beta V(t)I(t)}{\Phi \left( V(t),I(t)\right) }-\left( \mu + \gamma \right) I(t)\right) U_I(t)\\\\&+\left( u_2 (t)S(t)-\displaystyle \frac{\rho \left( 1-u_1 (t)\right) \beta V(t)I(t)}{\Phi \left( V(t),I(t)\right) }-(\mu +\delta )V(t)\right) U_V(t)\\\\&+\displaystyle \frac{1}{2}\left( \displaystyle \frac{\sigma S(t)I(t)}{\Psi \left( S(t),I(t)\right) }\right) ^2U_{SS}(t)+\displaystyle \frac{1}{2}\left( \displaystyle \frac{\sigma \rho V(t)I(t)}{\Phi \left( V(t),I(t)\right) }\right) ^2U_{VV}(t)\\\\&+\displaystyle \frac{1}{2}\left( \displaystyle \frac{ \sigma S(t)I(t)}{\Psi \left( S(t),I(t)\right) }+\displaystyle \frac{ \sigma \rho V(t)I(t)}{\Phi \left( V(t),I(t)\right) }\right) ^2U_{II}(t)\\\\&-\left[ \displaystyle \frac{\sigma S(t)I(t)}{\Psi \left( S(t),I(t)\right) }\left( \displaystyle \frac{ \sigma S(t)I(t)}{\Psi \left( S(t),I(t)\right) }+\displaystyle \frac{ \sigma \rho V(t)I(t)}{\Phi \left( V(t),I(t)\right) }\right) \right] U_{SI}(t)\\\\&-\left[ \displaystyle \frac{\sigma V(t)I(t)}{\Phi \left( V(t),I(t)\right) }\left( \displaystyle \frac{ \sigma S(t)I(t)}{\Psi \left( S(t),I(t)\right) }+\displaystyle \frac{ \sigma \rho V(t)I(t)}{\Phi \left( V(t),I(t)\right) }\right) \right] U_{VI}(t) \\\\&+\displaystyle \frac{\sigma ^2\rho S(t)V(t)I^2(t)}{\Psi \left( S(t),I(t)\right) \Phi \left( V(t),I(t)\right) }U_{SV}(t). \end{aligned}$$

Applying the Hamilton-Jacobi-Bellman theory [25], we must find the infimum:

$$\begin{aligned} \displaystyle {\inf _{u\in {\mathcal {A}}}}\left[ I(t)+\displaystyle \frac{C_1 }{2}u^{2}_{1}(t)+\displaystyle \frac{C_2 }{2}u^{2}_{2}(t)+{\mathcal {L}}(U(t))\right] . \end{aligned}$$
(22)

For this purpose, we need to find the partial derivative of the expression

$$\begin{aligned} I(t)+\displaystyle \frac{C_1 }{2}u^{2}_{1}(t)+\displaystyle \frac{C_2 }{2}u^{2}_{2}(t)+{\mathcal {L}}(U(t)) \end{aligned}$$
(23)

with respect to \(u_1\) and \(u_2\), respectively, and these derivatives should vanish. This leads to the equations

$$\begin{aligned}&C_1u_{1}(t)+\displaystyle \frac{\beta S(t)I(t)\left( U_S-U_I\right) }{\Psi \left( S(t),I(t)\right) } + \displaystyle \frac{\rho \beta V(t)I(t)\left( U_V-U_I\right) }{\Phi \left( V(t),I(t)\right) }=0, \nonumber \\&C_2u_{2}(t)+S(t)\left( U_V-U_S\right) =0. \end{aligned}$$
(24)

We consider the bounds on \(u_1\) and \(u_2\), respectively, and by an argument similar to that in the proof of the deterministic case; the asserted expressions for \(u^{*}_{1}\) and \(u^{*}_{2}\), respectively, emerge. \(\square\)

Numerical simulations

In this section, we give some numerical simulations of the stochastic model (2) and the corresponding deterministic system (3), we use the parameter values given in Table 1. These realistic hypothetical parameter values are chosen in the case when the population is not vaccinated and has not yet undergone any non-pharmaceutical interventions (i.e \(u_1=u_2=0\)). In addition, we choose the following initial values \(S_0=0.2\), \(I_0=0.1\) and \(V_0=0\). The efficacy of the vaccine is \(\rho =0.1\), the rate at which vaccinated lose immunity is \(\delta =0.2\) UT\(^{-1}\), the weight constant values in the objective functional are \(C_1=C_2=1\) and the intensity of perturbation is \(\sigma =0.15\).

Table 1 Parameters, their symbols and values used in the model (2)
Full size table

In the deterministic case, we used the numerical algorithm developed by [26] and presented in [27,28,29] which is a semi-implicit finite difference method and describes the approximation method for obtaining the optimal control. For the stochastic case, we used the results of deterministic control problem to find an approximate numerical solution for the stochastic control problem (see,Witbooi et al. [14]). In particular, we used \(\lambda _ 1- \lambda _3\), \(\lambda _ 2- \lambda _1\), and \(\lambda _ 2- \lambda _3\) as a proxy of \(U_S -U_V\), \(U_I -U_S\) and \(U_I -U_V\), respectively, for the calculation of \(u^{*}_{1}\) and \(u^{*}_{2}\). It is noted that the presence of S(t), I(t) and V(t) makes U into a stochastic variable even with the said proxy.

We investigate and compare numerical results in the following three possible strategies for the control of the disease. The computations is done for \(t_f=30\) days.

Only Vaccination Control (\(u_1=0\))

With this strategy, only the vaccination control \(u_2\) is used to optimize the objective functions (4) and (14), while the non-pharmaceutical interventions control \(u_1\) is set to zero.

In Figs. 1 and 2, we observe that there is a slight decrease in the density of susceptible individuals vaccinated compared with those not vaccinated, with a slight decrease in the density of infected individuals.

Fig. 1
figure 1

Evolution of S and I for deterministic model with only vaccination control

Full size image
Fig. 2
figure 2

Evolution of S and I for stochastic model with only vaccination control

Full size image

Only Non-pharmaceutical interventions control (\(u_2=0\))

With this strategy, only the non-pharmaceutical interventions control \(u_1\) is used to optimize the objective functions (4) and (14) while the vaccination control \(u_2\) is set to zero.

In Figs. 3 and 4, we observe that there is a significant increase in the density of susceptible individuals undergoing non-pharmaceutical interventions, with a significant decrease in the density of infected individuals.

We see that the control in Figs. 3 and 4 always needs to be greater than a certain threshold while the control in Figs. 1 and 2 can be reduced after the first 10 days. Hence, we can firstly practice the non-pharmaceutical interventions for susceptible to protect themselves from attack of the disease in order to increase the the number of susceptible individuals to above a certain threshold, and we begin to decrease this control after 10 days. After, we start to apply more of vaccination control to decrease the number of infected individuals.

Fig. 3
figure 3

Evolution of S and I for deterministic model with only non-pharmaceutical interventions control

Full size image
Fig. 4
figure 4

Evolution of S and I for stochastic model with only non-pharmaceutical interventions control

Full size image

Combined Vaccination and Non-pharmaceutical interventions controls

With this strategy, we use both the non-pharmaceutical interventions control \(u_1\) and the vaccination control \(u_2\) to optimize the objective functionals (4) and (14).

In Figs. 5 and 6, we observe that there is increase in the density of susceptible individuals with a significant decrease in the density of infected individuals controlled compared with those not controlled.

Fig. 5
figure 5

Evolution of S and I for deterministic model with booth controls

Full size image
Fig. 6
figure 6

Evolution of S and I for stochastic model with booth controls

Full size image

Discussion and conclusion

In this work, we analyzed an optimal control problem for the proposed stochastic SIVR epidemic model with specific nonlinear incidence rate. Two types of control are used: one characterizes the effectiveness of successful practice of non-pharmaceutical interventions, and the other characterizes the vaccination for susceptible individuals. This optimal control problem was for minimizing the number of infected individuals and the cost(s) of controls.

Using the simple relation between the optimal forms of control for the stochastic model and the corresponding deterministic model, we found approximate solutions for optimal stochastic control by exploiting the similarity between the two forms of control. We showed the advantage of each case studied with a comparison between the numerical simulations they provided. We have identified three possible strategies for the control of the disease. Control programs that follow these strategies can effectively reduce the density of infected individuals with minimal costs. The results confirm the need to use both successful practice of non-pharmaceutical interventions and the vaccination strategy all the time to prevent the spread of the disease.

The approximation method of the numerical solution of the optimal stochastic control problem is a viable alternative. A more formal approach will be considered in our future work.