SIVR epidemic model with stochastic perturbation

Abstract

We propose a stochastic disease model where vaccination is included and such that the immunity is permanent. The existence, uniqueness, and positivity of the solution and the stability of the disease-free equilibrium are studied.

1 Introduction

The mathematical models, deterministic and stochastic, are wide used in order to describe the spread of a disease into a population.

Most models descend from the classical SIR model of Kermack e Meckendrick [10]. In the SIR model, the population is subdivided into three distinct classes: susceptible, infective, and removed denoted by S,   I, and R respectively.

The fundamental parameter that governs the spread of the disease into a population is “the basic reproduction number” denoted by ${\mathfrak{R}}_0$. It is defined as “the average number of secondary case caused by an infectious individual in a totally susceptible population.” When ${\mathfrak{R}}_0\leq 1$ the disease dies out while, when ${\mathfrak{R}}_0>1$ the disease is endemic.

After the model of Kermack e Meckendrick, many its extensions and other models have been proposed and studied (see [3, 13]).

The introduction of a stochastic perturbation in these models is justified by observation that the real life is full of social and environmental random variations. The presence of a stochastic noise in a model modifies the behavior of solution of correspondent deterministic system and modifies the thresholds of the system for an epidemic to occur. In [14], the authors studied how the noise induce effects in a populations dynamics. In [5], the authors studied a dynamical model for epidemiological infection with a noise source with memory. In [6], the authors analyzed a model for epidemic dynamics by using a pulse noise model with memory. In [16], a stochastic SIR model has been studied and has been showed as the thresholds vary.

There is an increasing interest in the analysis and control of infectious disease. Attention has been give to vaccination and treatment policies. The study of vaccination related to disease transmission has been the subject of intense theoretical analysis (see [1, 2, 11, 15, 17]). In modeling the disease transmission in which a vaccination program is in effect, the main problem is that the vaccination is not complectly efficient. Vaccines may have low efficacy and be leaky (i.e., after a certain time, vaccinated individual may have only partial protection from infection); moreover, data support the fact that a vaccine usually wanes, thus providing only temporary protection. We consider a SIR-type disease when a vaccination program is in effect

$$ \left\{\begin{array}{l} S^{\prime}(t)=\mu-{\beta} S(t)I(t)-(\mu+\phi) S(t)+\theta V(t)\\ I^{\prime}(t)=\beta S(t) I(t)+\rho{\beta} V(t)I(t) -(\lambda+\mu) I(t)\\ V^{\prime}(t)=\phi S(t) -\rho{\beta} V(t)I(t)-(\mu+\theta) V(t)\\ R^{\prime}(t)=\lambda I(t)-\mu R(t) \end{array}\right. $$

(1)

precisely the population can be in one of four states: susceptible, infective, vaccinated, and removed denoted by S,  I,  V, and R respectively. In the model, we suppose that in the unit time, a fraction ϕ of the susceptible class is vaccinated. The vaccination may reduce but not completely eliminate susceptibility to infection, so in the model is included a factor ρ, 0 ≤ ρ ≤ 1, in the contact rate of vaccinated members with ρ = 0 meaning that the vaccine is perfectly effective and ρ = 1 meaning that the vaccine has no effect. We suppose also that the vaccination loses effect at a proportional rate θ and that the immunity is permanent so that a fraction λ of infective goes in the removed class. We assume that the birth occurs in the system with the same constant rate μ of death and that all newborns enter in susceptible class. Consequently, the total population is constant and the variables are normalized to N = 1, that is, S(t) + I(t) + V(t) + R(t) = 1 for all t ≥ 0. Of course ${\mu, \lambda, \phi, \theta, {\beta}\in \mathbb{R}_+}$.

In this paper, we examine the case when the vaccine does not lose its effectiveness (i.e., θ = 0). One can modify the basic model, based on this assumption in order to get the system

$$ \left\{\begin{array}{l} S^{\prime}(t)=\mu-{\beta} S(t)I(t)-(\mu+\phi) S(t)\\ I^{\prime}(t)=\beta S(t) I(t)+\rho{\beta} V(t)I(t) -(\lambda+\mu) I(t)\\ V^{\prime}(t)=\phi S(t) -\rho{\beta} V(t)I(t)-\mu V(t)\\ R^{\prime}(t)=\lambda I(t)-\mu R(t). \end{array}\right. $$

(2)

Denoted by ${\mathfrak{R}}_0=\frac{\beta}{\mu+\lambda}$ the basic reproduction number and by

$$ {\mathfrak{R}}_{\phi}={\mathfrak{R}}_0\left(\frac{\mu+\rho \phi}{ \mu+\phi}\right) $$

the basic reproduction number in a population in which a proportion ϕ has been vaccinated. It is known that in the absence of the disease (I = 0) there is a unique disease-free equilibrium

$$ E_0 \left(\frac{\mu }{\mu + \phi}, 0, \frac{\phi}{\mu + \phi},0 \right) $$

that is globally asymptotically stable if ${\mathfrak{R}}_{\phi}<1$.

If ${\mathfrak{R}}_{\phi}>1$ for some parameters values, the model exhibits a backward bifurcation leading to the existence of multiple endemic equilibria and news subthreshold, which may be important when it comes to designing vaccination strategies (see [2, 4]).

The real world is not deterministic so it is important to examine the inclusion of stochastic effects into deterministic models. We introduce a stochastic perturbation in the system (2) and obtain the following system

$$ \left\{\begin{array}{l} dS(t)=(\mu-{\beta} S(t)I(t)-(\mu+\phi) S(t))dt -\sigma S(t) I(t)dW(t) \\ dI(t)=(\beta S(t) I(t)+\rho{\beta} V(t)I(t) -(\lambda+\mu) I(t))dt +\sigma (S(t)+\rho V(t))I(t)dW(t) \\ dV(t)=(\phi S(t) -\rho{\beta} V(t)I(t)-\mu V(t))dt-\rho\sigma V(t)I(t)dW(t) \\ dR(t)=(\lambda I(t)-\mu R(t))dt \end{array}\right. $$

(3)

where σ is a positive constant and W is a real Wiener process defined on a stochastic basis $(\Upomega, \mathcal{F}, (\mathcal{F}_t)_{t\geq 0}, \bf P)$.

In this paper, we want to prove the existence of the solution of (3) with suitable initial conditions and study the stability of the disease-free equilibrium.

2 Nonnegative solutions

In this section, we prove the existence of the solution of system (3).

We introduce the notation

$$ {\mathbb{R}}^4_+=\{x\in {\mathbb{R}}^4 : x_i>0 \quad \hbox{for all} \quad i=1,2,3,4\}. $$

To begin the analysis of the model, define the subset

$$ \Upomega=\{(S,I,V,R) : S\geq 0, I\geq 0, V\geq 0, R\geq 0, S+I+V+R=1\;\} $$

to ensure that the model is well posed and thus biologically meaningful, we need to prove that the solution remains in $\Upomega$.

We study (3) with the following initial conditions

$$ (S(0),I(0),V(0),R(0))\in{\mathbb{R}}^4_+,\quad S(0)+I(0)+V(0)+R(0)=1. $$

(4)

Since the coefficients of the system (3) are locally Lipschitz, there is the following result of local existence of solutions.

Theorem 2.1

(Theorem 1.1, [5]) If (4) holds, then there exists τ > 0 and a unique solution (S(t), I(t), V(t), R(t)) to the system (3) on $t\in [0,\tau[$ almost surely.

There is the following remark.

Remark 2.1

Let (S(t), I(t), V(t), R(t)) be the solution of the system (3) in [0,τ[; if S(s) > 0, I(s) > 0, V(s) > 0, R(s) > 0 for all 0 ≤ s ≤ τ a.s., then

$$ 0<S(s)< 1, \quad 0<I(s)<1, \quad 0<V(s)< 1,\quad 0<R(s)<1 $$

for all 0 ≤ s ≤ τ a.s..

Proof

It is sufficient to observe that the total population is constant, that is, S(t) + I(t) + V(t) + R(t) = 1 for all 0 < t < τ almost surely, in fact summing the equations of the system (3), we obtain

$$ d(S+I+V+R)=0. $$

Now, we consider a integer k ₀ > 4 sufficiently large such that $(S(0), I(0), V(0), R(0))\in [\frac{1}{k_0},k_0]^4$. For each integer k > k ₀, we define the stopping time

$$ \tau_k=\inf \ \left\{t\in[0,\tau[ : (S(t), I(t), V(t), R(t)) \notin \left[\frac{1}{k},k\right]^4 \ \right\}.$$

(5)

We shall show that the solution of (3) with initial condition (4) is nonnegative and global by using the idea exposed in [7].

Theorem 2.2

There exists a unique solution (S(t), I(t), V(t), R(t)) to the system (3) with initial condition (4) on t ≥ 0 and the solution will remain in ${\mathbb{R}^4_+}$ with probability 1, namely ${(S(t), I(t), V(t), R(t))\in \mathbb{R}^4_+}$ for all t ≥ 0 almost surely.

For the proof of the theorem, we need the following lemma.

Lemma 2.1

Let (S(t), I(t), V(t), R(t)) be the solution of the system (3) with initial condition (4), then

$$ E(\log^2 S(\tau_k\wedge t)+\log^2 I(\tau_k\wedge t)+\log^2 V(\tau_k\wedge t)+\log^2 R(\tau_k\wedge t))\leq C(t)\quad \forall t\geq 0 $$

(6)

where τ _k is the stopping time given by (5) and C(t) is the solution of the Cauchy problem

$$ \left\{\begin{array}{l} y^{\prime}(t)= B+B^{\prime}y(t) \\ y(0)=\log^2S(0)+\log^2 I(0)+\log^2 V(0)+\log^2 R(0)\\ \end{array}\right. $$

where B and $B^{\prime}$ are constants defined by

$$ \begin{aligned} B&=(2(1+\rho)\beta+8\mu+2\varphi+2\lambda+2\sigma ^2(1+\rho^2)+2\sigma^2(1+\rho)^2);\\ B^{\prime}&=4(2(1+\rho)\beta+8\mu+2\varphi+2\lambda +\sigma^2(1+\rho^2)+\sigma^2(1+\rho)^2). \end{aligned} $$

(7)

Proof

We consider a C ²-function, ${\Upphi:\mathbb{R}^4_+\to \mathbb{R}_+}$ by

$$ \Upphi(x)=\sum_{i=1}^{4}\log^2x_i, $$

(8)

In virtue of stopping time defined in (5), $(S(\tau_k\wedge t), I(\tau_k\wedge t), V(\tau_k\wedge t), R(\tau_k\wedge t))\in[\frac{1}{k},k]^4$ and by using Ito formula, we have

$$ \begin{aligned} &\log^2 S(\tau_k\wedge t)+\log^2 I(\tau_k\wedge t)+\log^2 V(\tau_k\wedge t)+\log^2 R(\tau_k\wedge t)\\ &\leq \log^{2}S(0)+\log^2 I(0)+\log^2 V(0)+\log^2 R(0)+A_1+A_2+A_3, \end{aligned} $$

(9)

where

$$ \begin{aligned} &A_1=2\int\limits_0^{\tau_k\wedge t}\left[\left(\frac{\mu}{S(t^{\prime})}-\beta I(t^{\prime})-(\mu+\phi)-\frac{\sigma^2}{2}I^2(t^{\prime})\right) \log S(t^{\prime})+\right.\\ & \quad +(\beta (S(t^{\prime})+\rho V(t^{\prime}))-(\lambda+\mu)-\frac{\sigma^2}{2} (S(t^{\prime})+\rho V(t^{\prime}))^2)\log I(t^{\prime})\\ \quad &+(\phi\frac{S(t^{\prime})}{V(t^{\prime})}-\beta \rho I(t^{\prime})-\mu-\frac{\sigma^2}{2}\rho^2 I^2(t^{\prime})) \log V(t^{\prime})+\\ &\quad \left.+(\lambda\frac{I(t^{\prime})}{R(t^{\prime})}-\mu)\log R(t^{\prime})\right]{\hbox{d}}t^{\prime};\\ &A_2= \sigma^2\int\limits_0^{\tau_k\wedge t}[(1+\rho^2)I^2(t^{\prime})+(S(t^{\prime})+\rho V(t^{\prime}))^2)]{\hbox{d}}t^{\prime};\\ &A_3=2\sigma\int\limits_0^{\tau_k\wedge t}[-I(t^{\prime})\log S(t^{\prime})+(S(t^{\prime})+\rho V(t^{\prime}))\log I(t^{\prime})-\rho I(t^{\prime})\log V(t^{\prime})]{\hbox{d}}W(t^{\prime}). \end{aligned} $$

In virtue of Remark 2.1, we can neglect the terms

$$ \begin{aligned} &\int\limits_0^{\tau_k\wedge t}\frac{\mu}{S(t^{\prime})}\log S(t^{\prime}){\hbox{d}}t^{\prime}, \quad \int\limits_0^{\tau_k\wedge t}\beta (S(t^{\prime})+\rho V(t^{\prime}))\log I(t^{\prime}){\hbox{d}}t^{\prime},\\ &\int\limits_0^{\tau_k\wedge t}\phi\frac{S(t^{\prime})}{V(t^{\prime})}\log V(t^{\prime}){\hbox{d}}t^{\prime},\quad \int\limits_0^{\tau_k\wedge t}\lambda\frac{I(t^{\prime})}{R(t^{\prime})}\log R(t^{\prime}){\hbox{d}}t^{\prime} \end{aligned} $$

and we estimate the terms of right-hand side of (9) by the following inequalities

$$ |A_1| \leq [2(1+\rho)\beta+8\mu+2\varphi+2\lambda+\sigma^2(1+\rho^2) +\sigma^2(1+\rho)^2]\int\limits_0^{\tau_k\wedge t}[|\log S(t^{\prime})| +|\log I(t^{\prime})|+|\log V(t^{\prime})|+|\log R(t^{\prime})|]{\hbox{d}}t^{\prime}; $$

and

$$ |A_2| \leq (\sigma^2(1+\rho^2)+\sigma^2(1+\rho)^2) t $$

substituting these relations into (9) and taking expectation, we obtain

$$ \begin{aligned} &E(\log^2 S(\tau_k\wedge t)+\log^2 I(\tau_k\wedge t) +\log^2V(\tau_k\wedge t))\log^2 R(\tau_k\wedge t))\leq \\ & \log^2S(0)+\log^2 I(0)+\log^2 V(0)+\log^2 R(0) +B t\\ &\quad +B^{\prime}\int\limits_0^tE(\log^2 S(\tau_k\wedge t^{\prime})+\log^2 I((\tau_k\wedge t^{\prime})+\log^2 V((\tau_k\wedge t^{\prime})+\log^2 R(\tau_k\wedge t^{\prime})){\hbox{d}}t^{\prime}, \end{aligned} $$

where B and $B^{\prime}$ are constants given by (7).

We set

$$ Y(t)=E(\log^2 S(\tau_k\wedge t)+\log^2 I(\tau_k\wedge t)+\log^2 V(\tau_k\wedge t)+\log^2 R(\tau_k\wedge t)), $$

then, we obtain

$$ Y(t)\leq Y(0) +Bt+B^{\prime}\int\limits_0^t Y(t^{\prime}){\hbox{d}}t^{\prime}, $$

from which it follows that

$$ Y(t)\leq C(t)\quad \forall t\geq 0, $$

where C(t) is the solution of Cauchy problem

$$ \left\{\begin{array}{l} y^{\prime}(t)= B+B^{\prime}y(t)\\ y(0)=\log^2S(0)+\log^2 I(0)+\log^2 V(0)+\log^2 R(0) \end{array}\right. $$

and the lemma is proved. □

Proof of the Theorem 2.2

From the Theorem 2.1, there exists τ > 0 and the solution (S(t), I(t), V(t), R(t)) to the system (3) on $t\in[0,\tau[;$ to show that this solution is global, we need to show that $\tau=\infty$ a.s. Consider the stopping time defined in (5). Clearly, (τ _k ) is an increasing sequence. Set $\tau_\infty=\lim_{k\to\infty}\tau_k$, whence $\tau_\infty<\tau,$ a.s. If we can show that $\tau_\infty=\infty$ a.s. then $\tau=\infty$ a.s. and consequently the solution ${(S(t), I(t), V(t),R(t))\in \mathbb{R}^4_+}$ for all t ≥ 0 a.s. For if this statement is false, then there are two constants T > 0 and $\epsilon\in (0,1)$ such that

$$ P(\{\omega \in \Upomega : \tau_\infty(\omega)\leq T\})>\epsilon. $$

Consequently, there exists an integer k ₁ ≥ k ₀ such that

$$ P(\{\omega\in\Upomega :\tau_k(\omega)\leq T\})\geq\epsilon\quad \forall k\geq k_1. $$

Set $\Upomega_k=\{\omega\in \Upomega: \tau_k(\omega)\leq T\}$ for each k ≥ k ₁, we have $P(\Upomega_k)\geq \epsilon$. Note that for every $\omega\in \Upomega_k$ there is some component of (S(τ _k ), I(τ _k ), V(τ _k ), R(τ _k )) equals a k or $\frac{1}{k}$ and hence by (8)

$$ \Upphi((S(\tau_k), I(\tau_k), V(\tau_k),R(\tau_k)),\omega)\geq \log ^2 k. $$

From (6), we deduce that

$$ C(T)\geq E(1_{\Upomega_k}\Upphi((S(\tau_k), I(\tau_k), V(\tau_k)),\omega)\geq \epsilon\log ^2 k $$

where $1_{\Upomega _k}$ is the indicator function of $\Upomega _k$. Letting $k\to \infty$ leads to the contradiction, so we must have $\tau_\infty=\infty$ a.s. □

We observe that Theorem 2.2 and Remark 2.1 show that $\Upomega$ is the invariant set of the solutions of the system (3).

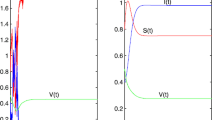
It is well known that the presence of a noise source can modify the behavior of deterministic evolution of the system. For this reason, we use numerical simulations based on the Euler-Maruyama scheme and Matlab software and refer to [9] for comparing the behavior of stochastic solution of (3) with that one of deterministic solution of (2). If we choose the parameters values such that ${\mathfrak{R}}_{\phi}<1$ (see Figs. 1, 2) with different values of σ, the numerical simulations show that the stochastic solution (see the continuous line) as that deterministic one (see the straight line) goes to the disease-free equilibrium. If we choose the parameters values such that ${\mathfrak{R}}_{\phi}>1$ we can observe different situations. The random fluctuations can eradicate the infectious disease (see Fig. 3) or the stochastic solution can fluctuate around the deterministic endemic equilibrium (see Fig. 4).

Fig. 1

Number of susceptible, infective and vaccinates in a deterministic and stochastic SIVR model. S(0) = 0.8, I(0) = 0.1, V(0) = 0.05, λ = 0.05,  μ = 0.005, ϕ = 0.2, ρ = 0.1, β = 0.4, σ = 1.62 and ${\mathfrak{R}}_{\phi}=0.8869<1$

Fig. 2

Number of susceptible, infective and vaccinates in a deterministic and stochastic SIVR model. S(0) = 0.8, I(0) = 0.1, V(0) = 0.05, λ = 0.05,  μ = 0.005, ϕ = 0.2, ρ = 0.1, β = 0.4, σ = 1.02 and ${\mathfrak{R}}_{\phi}=0.8869<1$

Fig. 3

Number of susceptible, infective and vaccinates in a deterministic and stochastic SIVR model. S(0) = 0.8, I(0) = 0.1, V(0) = 0.05, λ = 0.1,  μ = 0.2, ϕ = 0.2, ρ = 0.1, β = 0.8, σ = 1.22 and ${\mathfrak{R}}_{\phi}=1.4667>1$

Fig. 4

Computer simulations of mathematical model where S(0) = 0.8, I(0) = 0.1, V(0) = 0.05, λ = 0.1,  μ = 0.2, ϕ = 0.2, ρ = 0.1, β = 0.8, σ = 0.2 and ${\mathfrak{R}}_{\phi}=1.4667>1$

3 Stability of disease-free equilibrium

In this section, we prove the stability of the disease-free equilibrium in order to provide the threshold condition for disease control or eradication. Here recall the definition of stability of equilibrium states of a stochastic differential equation as introduced in [12]. Consider the following n-dimensional stochastic equations system

$$ dX(t)=f(t,X(t))dt+g(t,X(t))dW(t) $$

(10)

where f(t, x) is a function in ${\mathbb{R}^n}$ defined in ${ [t_0, +\infty[\times \mathbb{R}^n, }$ and g(t, x) is a n × m matrix, f,  g are locally Lipschitz functions in x and W(t) is an m-dimensional Wiener process. If ${x_0\in \mathbb{R}^n}$, denote by x(t;t ₀,x ₀) the solution of (10) with initial condition x(t ₀) = x ₀.

Definition 3.1

The stochastic process x(t;t ₀,x ₀) = x ₀ is a stationary solution of the stochastic system (10) if

$$ f(t,x_0)=0,\quad g(t,x_0)=0. $$

If x ₀ = 0, the stationary solution is called a trivial solution.

Definition 3.2

The trivial solution of system (10) is said to be p-th moment exponentially stable if there are two positive constants C and $\tilde{C}$ such that

$$ E(|x(t;t_0,x_0)|^p)\leq \tilde{C} |x_0|^p e^{-Ct} $$

for all ${x_0\in \mathbb{R}^n}$. When p = 2, it is usually said to be exponentially stable in mean square.

Now, we want to prove our main result

Theorem 3.1

If the conditions ${\mathfrak{R}}_0+\frac{\sigma^2(1+\rho)}{2}<\frac{1}{1+\rho}$ holds, then the disease-free equilibrium is exponentially stable in mean square for system (3).

Proof

Consider the second equation of (3), the Ito formula gives us

$$ dI^2=\left(2\beta(S+\rho V)-2(\mu+\lambda)+\sigma^2(S+\rho V)^2\right)I^2dt+2\sigma (S+\rho V)I^2dW $$

by using Theorem 2.2, we have

$$ dI^2\leq \left(2\beta(1+\rho )-2(\mu+\lambda)+\sigma^2(1+\rho )^2\right)I^2dt+2\sigma (1+\rho )I^2dW. $$

(11)

Set

$$ C_1=-\left(2\beta(1+\rho )-2(\mu+\lambda)+\sigma^2(1+\rho )^2\right)>0, $$

then, from (11), we have

$$ \frac{d}{dt}E(I^2)\leq -C_1E(I^2), $$

by using the comparison theorem of stochastic equation, we obtain

$$ E(I^2)\leq I^2(0)e^{-C_1 t}\quad \forall t\geq 0. $$

(12)

The Ito formula apply to the last equation of (3) gives us

$$ dR^2=(2\lambda IR-2\mu R^2)dt, $$

(13)

by using the Holder inequalities, we can observe that

$$ 2\lambda IR=2\lambda\left(\sqrt{\frac{\lambda}{\mu}}I\cdot \sqrt{\frac{\mu}{\lambda}}R\right)\leq \mu R^2+\frac{\lambda^2}{\mu}I^2 $$

substituting this relation into (13) and taking the expectation, we obtain

$$ \frac{d}{dt}E(R^2)\leq -\mu E(R^2)+\frac{\lambda^2}{\mu}E(I^2) $$

by using (12), we have

$$ \frac{d}{dt}E(R^2)\leq -\mu E(R^2)+\frac{\lambda^2}{\mu}I^2(0)e^{-C_1t}\quad \forall t\geq 0, $$

then we obtain

$$ E(R^2)\leq E(R^2(0))e^{-\mu t}+e^{-\mu t}\int\limits_0^t \frac{\lambda^2}{\mu}I^2(0)e^{(\mu-C_1)s}{\hbox{d}}s $$

the last integral is

$$ \left\{\begin{array}{ll} \frac{\lambda^2}{\mu}I^2(0)e^{-\mu t} & \mu=C_1 \\ \frac{\lambda^2}{\mu(\mu-C_1)}I^2(0)\left(e^{-C_1 t}-e^{-\mu t}\right) & \mu\not =C_1 \end{array} \right. $$

so, we have

$$ E(R^2)\leq C_3 e^{-C_2 t}\quad \forall t\geq 0 $$

(14)

where

$$ C_2=\left\{ \begin{array}{ll} \mu & \mu=C_1 \\ \min\{\mu, C_1\} & \mu\not=C_1 \end{array} \right. $$

$$ C_3=\left\{\begin{array}{ll} R^2(0)+\frac{\lambda^2}{\mu^2}I^2(0) & \mu=C_1 \\ R^2(0)+ \frac{\lambda^2}{\mu|\mu-C_1|}I^2(0) & \mu\not =C_1. \end{array}\right. $$

Consider the first equation of (3) near the disease-free equilibrium

$$ d\left(S-\frac{\mu}{\mu+\phi}\right)=\left(-\beta(S-\frac{\mu}{\mu+\phi})I +\frac{\beta \mu}{\mu+\phi}I-(\mu+\phi)(S-\frac{\mu}{\mu+\phi})\right)dt-\sigma SI dW $$

the Ito formula gives us

$$ d\left(S-\frac{\mu}{\mu+\phi}\right)^2=\left[-2\beta(S-\frac{\mu}{\mu+\phi})^2I +\frac{2\beta \mu}{\mu+\phi}(S-\frac{\mu}{\mu+\phi})I-2(\mu+\phi)\left(S -\frac{\mu}{\mu+\phi}\right)^2\right]dt-2\sigma(S-\frac{\mu}{\mu+\phi}) SI dW $$

neglected the term $-2\beta(S-\frac{\mu}{\mu+\phi})^2I$, we have

$$ \frac{d}{dt}E\left(S-\frac{\mu}{\mu+\phi}\right)^2\leq \frac{2\beta \mu}{\mu+\phi}E\left(\left(S-\frac{\mu}{\mu+\phi}\right)I\right)-2(\mu+\phi) E\left(S-\frac{\mu}{\mu+\phi}\right)^2. $$

We can estimate the following term

$$ \left|\frac{2\beta \mu}{\mu+\phi}\left((S-\frac{\mu}{\mu+\phi})I\right)\right|\leq (2\phi+\mu)(S-\frac{\mu}{\mu+\phi})^2+\frac{\beta^2 \mu}{(\mu+\phi)^2(2\phi+\mu)}I^2, $$

hence

$$ \frac{d}{dt}E\left(S-\frac{\mu}{\mu+\phi}\right)^2\leq -\mu E\left(\left(S-\frac{\mu}{\mu+\phi}\right)^2\right)+\left(\frac{\beta^2 \mu}{(\mu+\phi)^2(2\phi+\mu)}+\sigma^2\right)E(I^2) $$

taking into account (14), we obtain

$$ \frac{d}{dt}E\left(S-\frac{\mu}{\mu+\phi}\right)^2\leq -\mu E\left(\left(S-\frac{\mu}{\mu+\phi}\right)^2\right)+\left(\frac{\beta^2 \mu}{(\mu+\phi)^2(2\phi+\mu)}+\sigma^2\right)I^2(0)e^{-\mu t} $$

hence

$$ E(S-\frac{\mu}{\mu+\phi})^2\leq C_4 e^{-C_2 t}\quad \forall t\geq 0 $$

(15)

where

$$ C_4=\left\{\begin{array}{ll} (S(0)-\frac{\mu}{\mu+\phi})^2+\left(\frac{\beta^2 }{(\mu+\phi)^2(2\phi+\mu)}+\sigma^2\right)I^2(0) & \mu=C_1 \\ (S(0)-\frac{\mu}{\mu+\phi})^2+(\frac{\beta^2\mu }{(\mu+\phi)^2(2\phi+\mu)}+\sigma^2)\frac{I^2(0)}{|\mu-C_1|} & \mu\not =C_1. \end{array}\right.$$

Consider the third equation of (3) near the disease-free equilibrium

$$ \begin{aligned} d\left(V-\frac{\phi}{\mu+\phi}\right)& =\left(\phi \left(S-\frac{\mu}{\mu+\phi}\right)- \rho\beta\left(V-\frac{\phi}{\mu+\phi}\right) {I}-\frac{\rho\beta \mu}{\mu+\phi}{I}-\right.\\ & \left.\mu\left(V-\frac{\phi}{\mu+\phi}\right)\right)dt- \sigma\rho VIdW \end{aligned} $$

the Ito formula gives us

$$ \begin{aligned} d\left(V-\frac{\phi}{\mu+\phi}\right)^2 &=\left[2\phi \left(S-\frac{\mu}{\mu+\phi}\right)\left(V-\frac{\phi}{\mu+\phi}\right) -2\rho \beta\left(V-\frac{\phi}{\mu+\phi}\right)^2I- \frac{2\rho\beta \mu}{\mu+\phi}\left(V-\frac{\phi}{\mu+\phi}\right)I-\right.\\ &\left.2\mu\left(V-\frac{\phi}{\mu+\phi}\right)^2+\sigma^2\rho^2V^2I^2\right]dt -\sigma\rho \left(V-\frac{\phi}{\mu+\phi}\right)VI dW \end{aligned} $$

neglected the term $-2\rho\beta(V-\frac{\phi}{\mu+\phi})^2I$ and estimated the following terms

$$ \left|2\phi(S-\frac{\mu}{\mu+\phi})(V-\frac{\phi}{\mu+\phi})\right|\leq \frac{2\phi^2}{\mu}(S-\frac{\mu}{\mu+\phi})^2+\frac{\mu}{2} (V-\frac{\phi}{\mu+\phi})^2 $$

and

$$ \left|\frac{2\rho\beta \mu}{\mu+\phi}\left((V-\frac{\phi}{\mu+\phi})I\right)\right|\leq \frac{\mu}{2}(V-\frac{\phi}{\mu+\phi})^2+\frac{2\rho^2\beta^2\phi^2 }{(\mu+\phi)^2\mu}I^2 $$

we have

$$ \frac{d}{dt}E(V-\frac{\phi}{\mu+\phi})^2\leq -\mu E\left((V-\frac{\phi}{\mu+\phi})^2\right)+\frac{2\phi^2} {\mu}E(S-\frac{\mu}{\mu+\phi})^2+\left(\frac{2\rho^2\beta^2\phi^2 }{(\mu+\phi)^2\mu}+\sigma^2\rho^2\right)E(I^2) $$

taking into account (12) and (14), we obtain

$$ \frac{d}{dt}E(V-\frac{\phi}{\mu+\phi})^2\leq -\mu E\left((V-\frac{\phi}{\mu+\phi})^2\right)+\frac{2\phi}{\mu}C_4e^{-C_2 t}+\left(\frac{2\rho^2\beta^2\phi^2 }{(\mu+\phi)^2\mu}+\sigma^2\rho^2\right)I^2(0)e^{-C_1 t} $$

hence

$$ E(V-\frac{\phi}{\mu+\phi})^2\leq C_5 e^{-C_2 t}\quad \forall t\geq 0 $$

(16)

where

$$ C_5=\left\{\begin{array}{ll} (V(0)-\frac{\phi}{\mu+\phi})^2+\frac{2\phi^2}{\mu}C_4 +\left(\frac{2\rho^2\beta^2\phi^2 }{(\mu+\phi)^2\mu)}+\sigma^2\rho^2\right)I^2(0) & \mu=C_2 \\ (V(0)-\frac{\phi}{\mu+\phi})^2+\frac{2\phi^2}{\mu}C_4 +\left(\frac{2\rho^2\beta^2\phi^2 }{(\mu+\phi)^2\mu)}+\sigma^2\rho^2\right)\frac{1}{|\mu-C_2|} & \mu\not =C_2. \end{array} \right. $$

Hence, denoting by $x(t)=(S(t)-\frac{\mu}{\mu+\phi},I(t), V(t)-\frac{\phi}{\mu+\phi}, R(t))$, by using (12), (14), (15), and (16), we obtain

$$ E(|x(t)|^2)\leq \tilde{C} e^{-Ct}\quad \forall t\geq 0 $$

for some constants $C, \tilde{C}$, hence the disease-free equilibrium is exponentially stable in mean square. □