Introduction

Provision of additional food to predators and its effect on the dynamics of prey predator system have been a source of interest to many scientists. Much experimental work has been carried out in the context of biological control phenomenon viz., spreading insecticides, fungicides or fertilizers that pollute the environment and also it remains as residuum in the entire ecosystem. Predators are generally carnivores by nature. Due to this fact, it is generally ignored that these carnivores also require plant derived foods as a source of energy. The degree of dependence on the primary food by the predators is different. Wackers and van Rijn [1] distinguish between the various categories of life-history omnivores, temporal omnivores or permanent omnivores. Life history omnivores are those natural enemies that derives their food rigorously from plants during their life time, such as hoverflies. Temporal omnivores also add the carnivorous diet during their life time and permanent omnivores sustain a mixed diet throughout their lifetime.

Biological control mechanisms involves the conservation of natural enemies in an environment. Over the last forty years, artificial food sprays are used to increase the ratio of natural enemies of anthropod pests but due to its inconsistent performance, this approach is not feasible in every biological control program. The mirid predator Macrolophus pygmaeus uses the eggs of the Mediterranean moth Ephestia kuehniella for its mass production and consumption of pollen as an additional food by Macrolophus pygmaeus was studied. Different quantities of Ephestia kuehniella eggs were provided to the predator along with the different amounts of pollen as an additional food and the changes occured in the developmental period, survival rate, mortality rate etc. were observed [2,3,4]. It is assessed that diet consisting of both eggs and pollen in appropriate manner is much advantageoous for rearing these predators [1]. Much experimentation has been done to valuate the role of additional food in improving the biological control programs as can be seen in [5,6,7,8].

Some of the experiments conducted have been supported by the theoretical results and they comprehended over the use of different types of food as an additional source to predators and their efficiency to attain biological control [1, 9,10,11]. Effort has been made to find resolution for the control of pests in the field [12,13,14,15].

Some natural enemies are adapted to depend entirely on prey as their mode of nutrition but the importance of non prey food has been acknowledged and attempts are made to examine the interactions between the natural enemies and non prey foods for underlying its importance to raise the level of biological pest control [16,17,18,19]. It is found that consumption of alternative food is significant not just in maintaining the ecological balance but also in biological control programs.

Work has been done in assessing the action of pest for the prey which includes the study of control and eradication of pest by predators by offering the alternative/additional food to the predators which has been studied as one predator and two prey mathematical model [20]. This depicts that supplementing additional food along with the prey food in the diet of predators has an effect on prey density i.e. focal prey by reducing the population of prey which results into an interspecific competiton called as apparent competition as it facilitates by the alternative prey [20, 21].

Some theoretical studies concluded that the introduction of alternative prey results in apparent competition, by which the prey density is restraint but some observational and experimental evidences show that alternative food not always trail to biological control. It is found that the success rate of biological control programs depend on the role of additional food [11, 20, 22]. Harwood and Obrycki [11] found out that providing non pest food to predators is significant in ways as it is advantageous to predators for increasing the fertility and the existence of alternative food results in reduced pest consumption.

In [12], a model has been suggested and made to study the effect of additional food in the prey predator system. The system has been analysed by taking the holling type II functional response for predators. It has also been observed that the quantity and quality of additional food plays a significant role in the system controllability. The analysis in [23] presented an unbounded growth of predators when they are dependent on additional food only. The model thus improved by inserting a limiting factor known as mutual interference between predators which is commonly seen in ecosystem and has a drastic role to play [24,25,26,27,28,29].

Both the Beddington–DeAngelis form of functional response and ratio-dependent functional response have been widely used in various models and studied in different aspects [5, 30]. It is similar to the well known Holling type II functional response but it incorporates mutual interference between predators. Ratio-dependent predator prey models are also a source of interest to many biologists and it also comprises of mutual interference by predators, but depicts singular behavior at low densities and has been a source of criticism for many.

In [24], Beddington–DeAngelis functional response has been incorporated and mutual interference concept is framed within to study the role of additional food in the predator prey system. Additional food quality is also defined as the ratio of handling times between the additional food and prey [12].

In this article, Beddington–DeAngelis functional response has been used in the prey predator system to assess the role of mutual interference between the predators. The present model is incorporated with two classes of predators; one with the predators who are consuming the additional food/alternative food along with the prey food and the other class of predators that are not consuming the additional food and having the only source of nutrition as prey food. Further, interference within the predators and also between the preys and predators have been considered.

The present article is as follows: The next section introduces the prey predator model with two classes of predators along with the additional food concept. Section 3 presents the conditions for the existence of various equilibrium points. In Sect. 4, local stability analysis has been done and global analysis is carried out in Sect. 5. Last section comprises of the discussion and conclusions following the numerical simulations in Sect. 6.

The model

The prey-predator dynamics using the Beddington–DeAngelis type of functional response with mutual interference between predators is given in [5, 30] is as follows,

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{dN}{dT}=rN\Big (1-\frac{N}{K}\Big )-\frac{cNP}{a+N+\rho P},\\ \frac{dP}{dT}=\frac{bNP}{a+N+\rho P}-mP, \end{array}\right. } \end{aligned}$$
(2.1)

where, \( N\equiv N(T),P\equiv P(T)\) are the prey and predator density respectively with \( N(0)\ge 0, P(0)\ge 0\) and the parameters r, K, m denote the growth rate of prey, carrying capacity of the prey and mortality rate of predators in the absence of prey respectively.

\(\rho \) is the strength of mutual interference between the predators and mathematically, defined as \( \rho =\frac{e_{P}h_{P}}{e_{N}h_{N}}\) where \(e_{P},e_{N}\) are the constants dependent on the rate of movement of predators in the search of prey or predators and \(h_{N},h_{P}\) denote the handling time of predator per prey and interaction time among predators [7]. The prey predator system mentioned in (2.1) has been considered from many ways and is well studied in literature [9, 30,31,32,33,34,35,36,37,38,39].

In [24], predators are provided with additional food with quantity A and the prey predator model takes the following form as:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{dN}{dT}=rN\Big (1-\frac{N}{K}\Big )-\frac{cNP}{a+\alpha \eta A+N+\rho P},\\ \frac{dP}{dT}=\frac{b(N+\eta A)P}{a+N+\rho P}-mP, \end{array}\right. } \end{aligned}$$
(2.2)

where, \( N\equiv N(T), P\equiv P(T)\), r, K and m have the same meanings as explained before.

\(\rho \) is the strength of mutual interference between the predators. \(h_{A}\) is the handling time of the predator per unit quantity of the additional food and \( e_{A}\) is the constant dependent on the rate of movement of predators in the search of additional food, then \( \alpha =\frac{h_{A}}{h_{N}}\) and \( \eta =\frac{e_{A}}{e_{N}}.\)

Additional food is said to be of low quality if \(\alpha \) is greater than the ratio between the maximum growth rate and the starvation rate and is said to be of high quality if \(\alpha \) is less than the ratio between the maximum growth rate and the starvation rate [12, 24]. The term \(\eta A \) is the effectual additional food level [7, 23].

Now, we know that predators can often be distinguished based on their feeding behaviour. Let us assume that there is a class of predators \( P_{1}\) that consumes both the prey food and the additional food of biomass A i.e. they are omnivores (both carnivores and herbivores) in nature whereas \( P_{2} \) is the class of predators that are just dependent on prey food i.e. they are carnivores and this class doesnot consume the alternative food such as pollen, nectar, grass etc. Then the above model reduces to the following form as:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{dN}{dT}=rN\Big (1-\frac{N}{K}\Big )-\frac{c_{1}NP_{1}}{a_{1}+\alpha \eta A+N+\rho _{1} P_{1}}-\frac{c_{2}NP_{2}}{a_{1}+N+\rho _{2} P_{2}},\\ \frac{dP_{1}}{dT}=\frac{b_{1}(N+\eta A)P_{1}}{a_{1}+\alpha \eta A +N+\rho _{1} P_{1}}-m_{1}P_{1}-m_{2}P_{1}^2-\gamma _{1}P_{1}P_{2},\\ \frac{dP_{2}}{dT}=\frac{b_{2}NP_{2}}{a_{1}+N+\rho _{2} P_{2}}-n_{1}P_{2}-n_{2}P_{2}^2-\gamma _{2}P_{1}P_{2}, \end{array}\right. } \end{aligned}$$
(2.3)

with non negative initial conditions governs the dynamics of additional food on one prey and two predator system using Beddington–DeAngelis functional response.

Here \(c_{1}\) and \(c_{2} \) represents the highest rate of predation by class \( P_{1}\) and \(P_{2}\) respectively. \(b_{1}\) and \(b_{2}\) represents the highest growth rate of predators \(P_{1}\) and \(P_{2}\) respectively. \( m_{2} \) and \( n_{2}\) are the rate of interaction among the predators \(P_{1}\) and \( P_{2}\) respectively. Similarly, \(\gamma _{1}\) and \(\gamma _{2}\) are the rate of interaction between the predators \(P_{1}\) and \(P_{2}\) respectively.

Now, the model given by (2.3) can be reduced in the following form using the conversions as:

$$\begin{aligned} x= & {} \frac{N}{a_{1}}, \quad y_{1}=\frac{c_{1}P_{1}}{ra_{1}}, \quad y_{2}=\frac{c_{2}P_{2}}{ra_{1}}, \quad t=rT, \quad \epsilon _{1}=\frac{r\rho _{1}}{c_{1}}, \\ \epsilon _{2}= & {} \frac{r\rho _{2}}{c_{2}}, \quad \alpha _{0}=\frac{\gamma _{1}a_{1}}{c_{2}}, \quad \delta _{1}=\frac{m_{1}}{r},\\ \delta _{2}= & {} \frac{m_{2}a_{1}}{c_{1}}, \quad \mu _{1}=\frac{n_{1}}{r}, \quad \mu _{2}=\frac{n_{2}a_{1}}{c_{2}}, \quad \beta _{0}=\frac{\gamma _{2}a_{1}}{c_{1}}, \quad L=\frac{K}{a_{1}}, \\ \xi _{1}= & {} \frac{\eta A}{a_{1}}, \quad \beta _{1}=\frac{b_{1}}{r}, \quad \beta _{2}=\frac{b_{2}}{r}, \end{aligned}$$

and the system becomes:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{dx}{dt}= x\Big (1-\frac{x}{L}\Big )-\frac{xy_{1}}{1+\alpha \xi _{1}+x+\epsilon _{1}y_{1}}-\frac{xy_{2}}{1+x+\epsilon _{2}y_{2}},\\ \frac{dy_{1}}{dt}=\frac{\beta _{1}(x+\xi _{1})y_{1}}{1+\alpha \xi _{1}+x+\epsilon _{1}y_{1}}-\delta _{1}y_{1}-\delta _{2}y_{1}^{2}-\alpha _{0}y_{1}y_{2},\\ \frac{dy_{2}}{dt}=\frac{\beta _{2}xy_{2}}{1+x+\epsilon _{2}y_{2}}-\mu _{1}y_{2}-\mu _{2}y_{2}^{2}-\beta _{0}y_{1}y_{2}. \end{array}\right. } \end{aligned}$$
(2.4)

The following are the two lemma proving the positivity and boundedness of solutions of the system (2.8).

Lemma 1

Every solution of the system (2.4) w.r.t the non negative initial conditions, remain positive \( \forall \) \( t > 0 \).

Proof

The system (2.4) with the imposed initial conditions can be written in the matrix equation form as:

$$\begin{aligned} \frac{dX}{dt}=G(X(t)), \end{aligned}$$
(2.5)

where, \(X(t)=(x,y_{1},y_{2})^{T}, X(0)=(x(0),y_{1}(0),y_{2}(0))^{T}\in R_{+}^{3}\) and

$$\begin{aligned} G(X(t))=\left( \begin{array}{c} G_{1}(X(t)) \\ G_{2}(X(t)) \\ G_{3}(X(t)) \\ \end{array} \right) =\left( \begin{array}{c} x\Big (1-\frac{x}{L}\Big )-\frac{xy_{1}}{1+\alpha \xi _{1}+x+\epsilon _{1}y_{1}}-\frac{xy_{2}}{1+x+\epsilon _{2}y_{2}}\\ \frac{\beta _{1}(x+\xi _{1})y_{1}}{1+\alpha \xi _{1}+x+\epsilon _{1}y_{1}}-\delta _{1}y_{1}-\delta _{2}y_{1}^{2}-\alpha _{0}y_{1}y_{2}\\ \frac{\beta _{2}xy_{2}}{1+x+\epsilon _{2}y_{2}}-\mu _{1}y_{2}-\mu _{2}y_{2}^{2}-\beta _{0}y_{1}y_{2} \end{array} \right) , \end{aligned}$$

where,

\(G:C^{\infty }( R^{3})\rightarrow R_{+}^{3}\) and \(G\in C^{\infty }(R^{3}).\) It is clear that, whenever \(X(0)\in R_{+}^{3}\), then using classical theorem by Nagumo [40], the solution of matrix equation with initial condition \(X_{0}\in R_{+}^{3}, \) say \(X(t)=X(t, X_{0})\) is positive for all finite and positive time t.

Indeed, from the first equation of system (2.4), we have,

$$\begin{aligned} \frac{dx}{dt}= & {} x\Big (1-\frac{x}{L}\Big )-\frac{xy_{1}}{1+\alpha \xi _{1}+x+\epsilon _{1}y_{1}}-\frac{xy_{2}}{1+x+\epsilon _{2}y_{2}},\\= & {} x\biggl (\left( {1-\frac{x}{L}}\right) -\frac{y_{1}}{1+\alpha \xi _{1}+x+\epsilon _{1}y_{1}}-\frac{y_{2}}{1+x+\epsilon _{2}y_{2}}\biggl ). \end{aligned}$$

So, \(x=x(0) \exp \biggl ({(1-\frac{x}{L}})-\frac{y_{1}}{1+\alpha \xi _{1}+x+\epsilon _{1}y_{1}}-\frac{y_{2}}{1+x+\epsilon _{2}y_{2}}\biggl )>0\) \(\forall \) \( t\ge 0.\)

Similarly, we may proceed for other equations as well of system (2.4) which confirms the positivity of solution of system. \(\square \)

Lemma 2

All solutions of the system (2.4) starting in the interior of the positive quadrant are bounded.

Proof

We define \(w=x+\frac{1}{\beta _{1}}y_{1}+\frac{1}{\beta _{2}}y_{2}.\)

Now we consider for \(\eta > 0\),

$$\begin{aligned} \frac{dw}{dt}+\eta w= & {} \frac{dx}{dt}+\frac{1}{\beta _{1}}\frac{dy_{1}}{dt}+\frac{1}{\beta _{2}}\frac{dy_{2}}{dt}+\eta x+\frac{\eta }{\beta _{1}}y_{1}+\frac{\eta }{\beta _{2}}y_{2},\\= & {} x\Big (1-\frac{x}{L}\Big )+\frac{\xi _{1}y_{1}}{1+\alpha \xi _{1}+x+\epsilon _{1}y_{1}}-\frac{\delta _{1}y_{1}}{\beta _{1}}-\frac{\delta _{2}y_{1}^{2}}{\beta _{1}}-\frac{\alpha _{0}y_{1}y_{2}}{\beta _{1}}\\&-\frac{\mu _{1}y_{2}}{\beta _{2}}-\frac{\mu _{2}y_{2}^2}{\beta _{2}}-\frac{\beta _{0}y_{1}y_{2}}{\beta _{2}}+\eta x+\frac{\eta }{\beta _{1}}y_{1}+\frac{\eta }{\beta _{2}}y_{2},\\= & {} \Big (1-\frac{x}{L}+\eta \Big )x-\Big (\frac{\delta -\eta }{\beta _{1}}\Big )y_{1}-\Big (\frac{\mu _{1}-\eta }{\beta _{2}}\Big )y_{2}-\frac{\delta _{2}y_{1}^2}{\beta _{1}}-\frac{\alpha _{0}y_{1}y_{2}}{\beta _{1}}\\&-\frac{\beta _{0}y_{1}y_{2}}{\beta _{2}}-\frac{\mu _{2}y_{2}^{2}}{\beta _{2}}+\frac{\xi _{1}y_{1}}{1+\alpha \xi _{1}+x+\epsilon _{1}y_{1}},\\\le & {} x\Big (1-\frac{x}{L}+\eta \Big )+\frac{\xi _{1}y_{1}}{1+\alpha \xi _{1}+x+\epsilon _{1}y_{1}},\\\le & {} x\Big (1-\frac{x}{L}+\eta \Big )+\frac{\xi _{1}}{\epsilon _{1}},\\\le & {} L(1+\eta )+\frac{\xi _{1}}{\epsilon _{1}}. \end{aligned}$$

Hence, we obtain,

$$\begin{aligned} \frac{dw}{dt}+\eta w \le P\Big (=L(1+\eta )+\frac{\xi _{1}}{\epsilon _{1}}\Big ). \end{aligned}$$

By the application of differential inequality [41], we get,

$$\begin{aligned} 0 \le w(t)\le \frac{P}{\eta }(1-e^{-\eta t})+w(0)e^{-\eta t}. \end{aligned}$$

So, as \(t \rightarrow \infty \), we have \(0< w(t)< \frac{P}{\eta }\) which implies that the solutions of system (2.4) are bounded. \(\square \)

Existence of equilibria

System (2.4) has six possible non-negative equilibria, namely,

$$\begin{aligned} E_{0}(0, 0, 0), \quad E_{1}(L, 0, 0), \quad E_{2}(0, \overline{y_{1}}, 0), \quad E_{3}(\widetilde{x}, \widetilde{y_{1}}, 0), \quad E_{4}(\widehat{x},0, \widehat{y_{2}}), \quad E_{5}(x^{*}, y_{1}^*, y_{2}^*). \end{aligned}$$

The equilibrium points \( E_{0}\) and \( E_{1}\) obviously exist. We now show the existence of other equilibrium points as follows.

Existence of \(E_{2}(0, \overline{y_{1}}, 0)\)

\(\overline{y_{1}}\) is the positive solution of the equation,

$$\begin{aligned}&\frac{\beta _{1}\xi _{1}y_{1}}{1+\alpha \xi _{1}+\epsilon _{1}y_{1}}-\delta _{1}y_{1}-\delta _{2}y_{1}^2=0,\\&\quad \Rightarrow \beta _{1}\xi _{1}-\delta _{2}(1+\alpha \xi _{1}+\epsilon _{1}y_{1})y_{1}=\delta (1+\alpha \xi _{1}+\epsilon _{1}y_{1}). \end{aligned}$$

On further solving, we get a quadratic equation in \(y_{1}\) as follows.

$$\begin{aligned} A_{1}y_{1}^2+B_{1}y_{1}-H_{1}=0. \end{aligned}$$

Taking only the positive root, we have,

$$\begin{aligned} y_{1}= \overline{y_{1}} =\frac{-B_{1}+\sqrt{B_{1}^2+4A_{1}H_{1}}}{2A_{1}}, \end{aligned}$$

where,

\(A_{1}=\delta _{2}\epsilon _{1}\),    \(B_{1}=\delta _{2}+\alpha \xi _{1}\delta _{2}+\epsilon _{1}\delta _{1}\),    \(H_{1}=\beta _{1}\xi _{1}-\delta _{1}-\alpha \xi _{1}\delta _{1}\).

Thus, the equilibrium point \(E_{2}(0, \overline{y_{1}}, 0)\) exists if \(\beta _{1}\xi _{1} > \delta _{1}(1+\alpha \xi _{1})\).

Existence of \( E_{3}(\widetilde{x}, \widetilde{y_{1}}, 0)\)

\(\widetilde{x}, \widetilde{y_{1}}\) is the positive solution of the system of equations as follows,

$$\begin{aligned}&\Big (1-\frac{x}{L}\Big )-\frac{y_{1}}{1+\alpha \xi _{1}+x+\epsilon _{1}y_{1}}=0, \end{aligned}$$
(3.1)
$$\begin{aligned}&\frac{\beta _{1}(x+\xi _{1})}{1+\alpha \xi _{1}+x+\epsilon _{1}y_{1}}-\delta _{1}-\delta _{2}y_{1}=0. \end{aligned}$$
(3.2)

To show the existence of the equilibrium point \( E_{3}(\widetilde{x}, \widetilde{y_{1}}, 0)\), we proceed by proving the intersection of isoclines at a unique point which is as follows.

In eq. (3.1), if \(x\rightarrow 0 \), then, \(y_{1} \rightarrow y_{1a}\),

where, \(y_{1a}=\frac{1+\alpha \xi _{1}}{1-\epsilon _{1}}\) and \( y_{1a} > 0\), provided \(\epsilon _{1}< 1.\)

Similarly, if \(y_{1}\rightarrow 0\), then, \( x\rightarrow x_{1a},\) where, \(x_{1a}=L\).

Now, using eq. (3.1), we get,

$$\begin{aligned} \frac{dy_{1}}{dx}|_{\widetilde{x}, \widetilde{y_{1}}}=\frac{C_{1}}{D_{1}}, \end{aligned}$$

where, \(C_{1}=-(1+\alpha \xi _{1}+\widetilde{x}+\epsilon _{1}\widetilde{y_{1}})^2+L\widetilde{y_{1}}\), \(D_{1}=L(1+\alpha \epsilon _{1}+\widetilde{x})\).

Now, for \( \frac{dy_{1}}{dx}|_{\widetilde{x}, \widetilde{y_{1}}}< 0\),

\((1+\alpha \xi _{1}+\widetilde{x}+\epsilon _{1}\widetilde{y_{1}})^2 > L\widetilde{y_{1}} \) must hold.

Similarly, in eq. (3.2).

If \(x\rightarrow 0\), then \(y_{1}\rightarrow y_{1b}\), where, \(y_{1b}=\frac{-q+\sqrt{q^{2}-4pr}}{2p}\),

where,

$$\begin{aligned} q=\delta _{1}\epsilon _{1}+\delta _{2}(1+\alpha \xi _{1}), p=\delta _{2}\epsilon _{1}, r=\delta _{1}(1+\alpha \xi _{1})-\beta _{1}\xi _{1}. \end{aligned}$$

Now, \(y_{1b}> 0\), provided, \( r < 0\).

Similarly, in eq. (3.2), when, \(y_{1}\rightarrow 0\), then, \(x\rightarrow x_{1b}\),

where, \(x_{1b}= \frac{\delta _{1}+\delta _{1}\alpha \xi _{1}-\beta _{1}\xi _{1}}{\beta _{1}-\delta _{1}}\).

Now, using eq. (3.2), we get,

\(\frac{dy_{1}}{dx}|_{\widetilde{x}, \widetilde{y_{1}}}=\frac{C_{2}}{D_{2}}\), where, \( C_{2}=\beta _{1}(1+\alpha \xi _{1}+\widetilde{x}+\epsilon _{1}\widetilde{y_{1}})-(\beta _{1}\widetilde{x}+\beta _{1}\xi _{1}), D_{2}=(\beta _{1}\widetilde{x}+\beta _{1}\xi _{1})\epsilon _{1}+\delta _{2}(1+\alpha \xi _{1}+\widetilde{x}+\epsilon _{1}\widetilde{y_{1}})^2.\)

For, \( \frac{dy_{1}}{dx}|_{\widetilde{x}, \widetilde{y_{1}}} < 0 \) ,

\( (1+\alpha \xi _{1}+\widetilde{x}+\epsilon _{1}\widetilde{y_{1}}) < (\widetilde{x}+\xi _{1}) \) must hold.

From the analysis done above, it can be concluded that the isoclines given by (3.1) and (3.2) intersect at a unique point \( (\widetilde{x}, \widetilde{y_{1}})\), provided the above conditions are satisfied along with the inequality as;

\(y_{1a} > y_{1b}\) and \(x_{1b} > x_{1a}\) or \(y_{1a} < y_{1b}\) and \(x_{1b} < x_{1a}\). This completes the existence of \(E_{3}\).

In a very similar way, existence conditions of the equilibria \( E_{4}(\widehat{x}, 0, \widehat{y_{2}}) \) can be determined.

Existence of \( E_{5}(x^*, y_{1}^*, y_{2}^*)\)

\(x^*, y_{1}^* \) and \( y_{2}^* \) is the positive solution of the system of equations given as follows.

$$\begin{aligned}&\Big (1-\frac{x}{L}\Big )-\frac{y_{1}}{1+\alpha \xi _{1}+x+\epsilon _{1}y_{1}}-\frac{y_{2}}{1+x+\epsilon _{2}y_{2}}=0, \end{aligned}$$
(3.3)
$$\begin{aligned}&\frac{\beta _{1}(x+\xi _{1})}{1+\alpha \xi _{1}+x+\epsilon _{1}y_{1}}-\delta _{1}-\delta _{2}y_{1}-\alpha _{0}y_{2}=0, \end{aligned}$$
(3.4)
$$\begin{aligned}&\frac{\beta _{2}x}{1+x+\epsilon _{2}y_{2}}-\mu _{1}-\mu _{2}y_{2}-\beta _{0}y_{1}=0. \end{aligned}$$
(3.5)

Solving (3.4) and (3.5), we get,

\(f(y_{1}, y_{2})=[y_{2}(\alpha _{0}+\alpha _{0}\alpha \xi _{1})+\delta _{1}+\delta _{1}\alpha \xi _{1}-\beta _{1}\xi _{1}+y_{1}\delta _{1}\epsilon _{1}-y_{1}\delta _{2}-y_{1}\delta _{2}\alpha \xi _{1}-y_{1}^2\delta _{2}\epsilon _{1}+\alpha _{0}\epsilon _{1}y_{2}y_{1}][\beta _{2}-\mu _{1}-\mu _{2}y_{2}-\beta _{0}y_{1}]-[\beta _{0}y_{1}+\mu _{1}+y_{2}(\epsilon _{2}\mu _{1}+\mu _{2}+\epsilon _{2}\mu _{2}y_{2}+\beta _{0}y_{1}\epsilon _{2})][\beta _{1}-\delta _{1}-\delta _{2}y_{1}-\alpha _{0}y_{2}].\)

In \(f(y_{1},y_{2})=0.\)

If \(y_{1}\rightarrow 0,\) then, \(y_{2} \rightarrow y_{2c}\),

where, \(y_{2c}\) is a unique positive real root of the equation given by,

\((y_{2}(\alpha _{0}+\alpha _{0}\alpha \xi _{1})+\delta _{1}+\delta _{1}\alpha \xi _{1}-\beta _{1}\xi _{1})(\beta _{2}-\mu _{1}-\mu _{2}y_{2})-(\mu _{1}+y_{2}(\epsilon _{2}\mu _{1}+\mu _{2}+\epsilon _{2}\mu _{2}y_{2}))(\beta _{1}-\delta _{1}-\alpha _{0}y_{2})=0\).

Similarly, as \(y_{2}\rightarrow 0 \), then, \(y_{1}\rightarrow y_{1c}\),

where, \( y_{1c} \) is a unique positive real root of the equation,

\((\delta _{1}+\delta _{1}\alpha \xi _{1}-\beta _{1}\xi _{1}+y_{1}\delta _{1}\epsilon _{1}-y_{1}\delta _{2}-y_{1}\delta _{2}\alpha \xi _{1}-y_{1}^2\delta _{2}\epsilon _{1})(\beta _{2}-\mu _{1}-\beta _{0}y_{1})-(\beta _{0}y_{1}+\mu _{1})(\beta _{1}-\delta _{1}-\delta _{2}y_{1})=0.\)

Using above,

\(\frac{dy_{2}}{dy_{1}}|_{(y_{1}^*, y_{2}^*)}=\frac{-C_{3}}{D_{3}}\),

where, \(C_{3}=(\delta _{1}\epsilon _{1}-\delta _{2}-\delta _{2}\alpha \xi _{1}-2y_{1}^*\delta _{2}\epsilon _{1}+\alpha _{0}\epsilon _{1}y_{2}^*)(\beta _{2}-\mu _{1}-\mu _{2}y_{2}^*-\beta _{0}y_{1}^*)-(\beta _{0}+\beta _{0}\epsilon _{2}y_{2}^*)(\beta _{1}-\delta _{1}-\delta _{2}y_{1}^*-\alpha _{0}y_{2}^*)+(y_{2}^*(\alpha _{0}+\alpha _{0}\alpha \xi _{1})+\delta _{1}+\delta _{1}\alpha \xi _{1}-\beta _{1}\xi _{1}+y_{1}^*\delta _{1}\epsilon _{1}-y_{1}^*\delta _{2}-y_{1}^*\delta _{2}\alpha \xi _{1}-{y_{1}^*}^2\delta _{2}\epsilon _{1}+\alpha _{0}\epsilon _{1}y_{2}^*y_{1}^*)(-\beta _{0})+(\beta _{0}y_{1}^*+\mu _{1}+y_{2}^*(\epsilon _{2}\mu _{1}+\mu _{2}+\epsilon _{2}\mu _{2}y_{2}^*+\beta _{0}y_{1}^*\epsilon _{2})\delta _{2})\) and \(D_{3}=(((\alpha _{0}+\alpha _{0}\alpha \xi _{1})+\alpha _{0}\epsilon _{1}y_{1}^*)(\beta _{2}-\mu _{1}-\mu _{2}y_{2}^*-\beta _{0}y_{1}^*)+(y_{2}^*(\alpha _{0}+\alpha _{0}\alpha \xi _{1})+\delta _{1}+\delta _{1}\alpha \xi _{1}-\beta _{1}\xi _{1}+y_{1}^*\delta _{1}\epsilon _{1}-y_{1}^*\delta _{2}-y_{1}^*\delta _{2}\alpha \xi _{1}-{y_{1}^*}^2\delta _{2}\epsilon _{1}+\alpha _{0}\epsilon _{1}y_{1}^*y_{2}^*)(-\mu _{2}))-((\epsilon _{2}\mu _{1}+\mu _{2}+2\epsilon _{2}\mu _{2}y_{2}^*+\beta _{0}y_{1}^*\epsilon _{2})(\beta _{1}-\delta _{1}-\delta _{2}y_{1}^*-\alpha _{0}y_{2}^*)+(\beta _{0}y_{1}^*+\mu _{1}+y_{2}^*(\epsilon _{2}\mu _{1}+\mu _{2}+\epsilon _{2}\mu _{2}y_{2}^*+\beta _{0}y_{1}^*\epsilon _{2}))(-\alpha _{0})).\)

For \(\frac{dy_{2}}{dy_{1}}|_{(y_{1}^*, y_{2}^*)} < 0\),

Either, \(C_{3} > 0 \) and \(D_{3} > 0 \) or \(C_{3} < 0 \) and \(D_{3} < 0\) hold.

Now using, eq. (3.4) and eq. (3.5) in eq. (3.3) and on simplifying, we get,

$$\begin{aligned} g(y_{1},y_{2})= & {} L\Bigg [1-\frac{y_{1}(\delta _{1}+\delta _{2}y_{1}+\alpha _{0}y_{2})(\beta _{2}-\mu _{1}-\mu _{2}y_{2}-\beta _{0}y_{1}^*)}{\beta _{1}\xi _{1}(\beta _{2}-\mu _{1}-\mu _{2}y_{2}-\beta _{0}y_{1})+\beta _{1}(1+\epsilon _{2}y_{2})(\mu _{1}+\mu _{2}y_{2}+\beta _{0}y_{1})}\\&-\frac{y_{2}(\mu _{1}+\mu _{2}y_{2}+\beta _{0}y_{1})(\beta _{2}-\mu _{1}-\mu _{2}y_{2}-\beta _{0}y_{1})}{\beta _{2}(1+\epsilon _{2}y_{2})(\mu _{1}+\mu _{2}y_{2}+\beta _{0}y_{1})}\Bigg ]. \end{aligned}$$

In \(g(y_{1},y_{2})=0\),

If \(y_{1}\rightarrow 0,\) then, \(y_{2} \rightarrow y_{2d}\),

where, \(y_{2d}\) is a positive real root of the equation given by,

\( L\Big (1-\frac{y_{2}(\beta _{2}-\mu _{1}-\mu _{2}y_{2})}{\beta _{2}(1+\epsilon _{2}y_{2})}\Big ). \)

Similarly, if \(y_{2}\rightarrow 0\), then, \(y_{1}\rightarrow y_{1d}\), where, \(y_{1d}\) is given by the positive root of the following equation,

\( L\Big (1-\frac{y_{1}(\delta _{1}+\delta _{2}y_{1})(\beta _{2}-\mu _{1}-\beta _{0}y_{1})}{\beta _{1}\xi _{1}(\beta _{2}-\mu _{1}-\beta _{0}y_{1})+\beta _{1}(\mu _{1}+\beta _{0}y_{1})}\Big ).\)

Using above,

$$\begin{aligned} \frac{dy_{2}}{dy_{1}}|_{(y_{1}^*, y_{2}^*)}=\frac{-C_{4}}{D_{4}}, \end{aligned}$$

where,

$$\begin{aligned}&\begin{aligned} C_{4}&=L\Bigg [\frac{(-(\delta _{1}+2\delta _{2}y_{1}^*+\alpha _{0}y_{2}^*)(\beta _{2}-\mu _{1}-\mu _{2}y_{2}^*-\beta _{0}y_{1}^*)+y_{1}^*(\delta _{1}+\delta _{2}y_{1}^*+\alpha _{0}y_{2}^*)\beta _{0})(E)-F((-\beta _{0}\beta _{1}\xi _{1})+\beta _{1}\beta _{0})}{E^2}\\&\quad -\frac{(((y_{2}^*\beta _{0}(\beta _{2}-\mu _{1}-\mu _{2}y_{2}^*-\beta _{0}y_{1}^*)+y_{2}^*(\mu _{1}+\mu _{2}y_{2}^*+\beta _{0}y_{1}^*)(-\beta _{0}))(G)-H(\beta _{2}(1+\epsilon _{2}y_{2}^*)\beta _{0})}{P^2}\Bigg ]. \end{aligned}\\&\begin{aligned} D_{4}&=L\Bigg [\frac{((\alpha _{0}y_{1}^*(\beta _{2}-\mu _{1}-\mu _{2}y_{2}^*-\beta _{0}y_{1}^*)-\mu _{2}y_{1}^*(\delta _{1}+\delta _{2}y_{1}^*+\alpha _{0}y_{2}^*))E+B\mu _{2}\beta _{1}\xi _{1})}{E^2}\\&\quad \frac{-\beta _{1}\epsilon _{2}(\mu _{1}+\mu _{2}y_{2}^*+\beta _{0}y_{1}^*)-\beta _{1}\mu _{2}(1+\epsilon _{2}y_{2}^*))}{E^2} \\&\quad -\frac{((\mu _{1}+\mu _{2}y_{2}^*+\beta _{0}y_{1}^*)(\beta _{2}-\mu _{1}-\mu _{2}y_{2}^*-\beta _{0}y_{1}^*)+\mu _{2}y_{2}^*(\beta _{2}-\mu _{1}-\mu _{2}y_{2}^*-\beta _{0}y_{1}^*))P}{E^2}+\\&\quad \frac{(y_{2}^*(\mu _{1}+\mu _{2}y_{2}^*+\beta _{0}y_{1}^*)(-\mu _{2}))P-H(\epsilon _{2}\beta _{2}(\mu _{1}+\mu _{2}y_{2}^*+\beta _{0}y_{1}^*)+\beta _{2}(1+\epsilon _{2}y_{2}^*)\mu _{2}))}{P^2}\Bigg ] \end{aligned} \end{aligned}$$

and E, F, H, P are given by,

$$\begin{aligned} E= & {} \beta _{1}\xi _{1}(\beta _{2}-\mu _{1}-\mu _{2}y_{2}^*-\beta _{0}y_{1}^*)+\beta _{1}(1+\epsilon _{2}y_{2}^*)(\mu _{1}+\mu _{2}y_{2}^*+\beta _{0}y_{1}^*),\\ F= & {} y_{1}^*(\delta _{1}+\delta _{2}y_{1}^*+\alpha _{0}y_{2}^*)(\beta _{2}-\mu _{1}-\mu _{2}y_{2}^*-\beta _{0}y_{1}^*),\\ H= & {} y_{2}^*(\mu _{1}+\mu _{2}y_{2}^*+\beta _{0}y_{1}^*)(\beta _{2}-\mu _{1}-\mu _{2}y_{2}^*-\beta _{0}y_{1}^*),\\ P= & {} \beta _{2}(1+\epsilon _{2}y_{2}^*)(\mu _{1}+\mu _{2}y_{2}^*+\beta _{0}y_{1}^*). \end{aligned}$$

For \(\frac{dy_{2}}{dy_{1}}|_{(y_{1}^*, y_{2}^*)} < 0\),

Either, \(C_{4} > 0 \) and \(D_{4} > 0 \) or \(C_{4} < 0 \) and \(D_{4} < 0 \).

Based on the analysis done above, it is to be noted that \(f(y_{1}, y_{2})\) and \(g(y_{1}, y_{2})\) intersect at a unique point \((y_{1},y_{2})\) provided the above conditions are satisfied along with the inequalities \(y_{1c} > y_{1d}\) and \(x_{1c}< x_{1d}\) or \(y_{1c} < y_{1d}\) and \(x_{1c} > x_{1d}\).

On knowing the values of \(y_{1}^*\) and \( y_{2}^* \), we can find the value of \( x^* \) as follows.

$$\begin{aligned} x^*=\frac{(\beta _{0}y_{1}^*+\mu _{1})+y_{2}^*(\epsilon _{2}\mu _{1}+\mu _{2}+\epsilon _{2}\mu _{2}y_{2}+\beta _{0}y_{1}^*\epsilon _{2})}{(\beta _{2}-\mu _{1}-\mu _{2}y_{2}^*-\beta _{0}y_{1}^*)}, \end{aligned}$$

and \(x^* \) exists provided \(\beta _{2} > (\mu _{1}+\mu _{2}y_{2}^*+\beta _{0}y_{1}^*).\)

Local stability analysis

The variational matrix of the system (2.4) is given by,

$$\begin{aligned} J= \left( \begin{array}{ccc} m_{11} &{} m_{12} &{} m_{13} \\ m_{21} &{} m_{22} &{} m_{23} \\ m_{31} &{} m_{32} &{} m_{33}\\ \end{array} \right) , \end{aligned}$$

where,

$$\begin{aligned}&m_{11}=\Big (1-\frac{2x}{L}\Big )-\frac{y_{1}(1+\alpha \xi _{1}+x+\epsilon _{1}y_{1})-xy_{1}}{(1+\alpha \xi _{1}+x+\epsilon _{1}y_{1})^2}-\frac{y_{2}(1+x+\epsilon _{2}y_{2})-xy_{2}}{(1+x+\epsilon _{2}y_{2})^2} ,\\&m_{12}=\frac{-x(1+\alpha \xi _{1}+x+\epsilon _{1}y_{1})+xy_{1}\epsilon _{1}}{(1+\alpha \xi _{1}+x+\epsilon _{1}y_{1})^2},\\&m_{13}=\frac{-x(1+x+\epsilon _{2}y_{2})+xy_{2}\epsilon _{2}}{(1+x+\epsilon _{2}y_{2})^2}, m_{21}=\frac{\beta _{1}y_{1}(1+\alpha \xi _{1}+x+\epsilon _{1}y_{1})-\beta _{1}y_{1}(x+\xi _{1})}{(1+\alpha \xi _{1}+x+\epsilon _{1}y_{1})^2},\\&m_{22}=\frac{\beta _{1}(x+\xi _{1})(1+\alpha \xi _{1}+x+\epsilon _{1}y_{1})-\beta _{1}(x+\xi _{1})y_{1}\epsilon _{1}}{(1+\alpha \xi _{1}+x+\epsilon _{1}y_{1})^2}-\delta _{1}-2y_{1}\delta _{2}-\alpha _{0}y_{2},\\&m_{23}=-\alpha _{0}y_{1},\\&m_{31}=\frac{\beta _{2}y_{2}(1+x+\epsilon _{2}y_{2})-\beta _{2}xy_{2}}{(1+x+\epsilon _{2}y_{2})^2}, m_{32}=-\beta _{0}y_{2},\\&m_{33}=\frac{\beta _{2}x(1+x+\epsilon _{2}y_{2})-\beta _{2}xy_{2}\epsilon _{2}}{(1+x+\epsilon _{2}y_{2})^2}-\mu _{1}-2y_{2}\mu _{2}-\beta _{0}y_{1}.\\ \end{aligned}$$

(a). At the equilibria \( E_{0}(0, 0, 0)\), eigenvalues of the above matrix corresponding to the system (2.4) is given by,

$$\begin{aligned} 1, \frac{\beta _{1}\xi _{1}}{(1+\alpha \xi _{1})}-\delta _{1}, -\mu _{1} . \end{aligned}$$

It is always an unstable equilibrium point.

(b). At the equilibria \( E_{1}(L, 0, 0)\), eigenvalues of the matrix J corresponding to the system (2.4) is given by,

$$\begin{aligned} -1, \frac{\beta _{1}(L+\xi _{1})}{1+\alpha \xi _{1}+L}-\delta _{1}, \frac{\beta _{2}L}{(1+L)-\mu _{1}}. \end{aligned}$$

So, the equilibrium solution \( E_{1}(L, 0, 0)\) is locally asymptotically stable under the condition,

$$\begin{aligned} \frac{\beta _{1}(L+\xi _{1})}{1+\alpha \xi _{1}+L}< \delta _{1}\hbox { and }(1+L) < \mu _{1}. \end{aligned}$$

(c). At the equilibria \( E_{2}(0, \overline{y_{1}}, 0)\), conditions for the locally asymptotically stable become as follows,

$$\begin{aligned} 1<\frac{\overline{y_{1}}}{(1+\alpha \xi _{1}+\epsilon _{1}\overline{y_{1}})}\hbox { and } \delta _{1}+2\delta _{2}\overline{y_{1}} < \frac{\beta _{1}\xi _{1}(1+\alpha \xi _{1})}{(1+\alpha \xi _{1}+\epsilon _{1}\overline{y_{1}})^2} . \end{aligned}$$

(d). The equilibrium point \(E_{3}(\widetilde{x}, \widetilde{y_{1}}, 0)\) is locally asymptotically stable if,

\(st > pq \), \( s+t < 0\) and \(n < 0\) where,

$$\begin{aligned} s= & {} \Big (1-\frac{2\widetilde{x}}{L}\Big )-\frac{\widetilde{y_{1}}(1+\alpha \xi _{1}+\widetilde{x}+\epsilon _{1}\widetilde{y_{1}})-\widetilde{x}\widetilde{y_{1}}}{(1+\alpha \xi _{1}+\widetilde{x}+\epsilon _{1}\widetilde{y_{1}})^2} , p= \frac{-\widetilde{x}(1+\alpha \xi _{1}+\widetilde{x})}{(1+\alpha \xi _{1}+\widetilde{x}+\epsilon _{1}\widetilde{y_{1}})^2},\\ q= & {} \frac{\beta _{1}\widetilde{y_{1}}(1+\alpha \xi _{1}+\epsilon _{1}\widetilde{y_{1}})-\beta _{1}\widetilde{y_{1}}\xi _{1}}{(1+\alpha \xi _{1}+\widetilde{x}\epsilon _{1}\widetilde{y_{1}})^2},\\ t= & {} \frac{\beta _{1}(\widetilde{x}+\xi _{1})(1+\alpha \xi _{1}+\widetilde{x})}{(1+\alpha \xi _{1}+\widetilde{x}+\epsilon _{1}\widetilde{y_{1}})^2}-\delta _{1}-2\widetilde{y_{1}}\delta _{2}, n= \frac{\beta _{2}\widetilde{x}}{(1+\widetilde{x})}-\mu _{1}-\beta _{0}\widetilde{y_{1}}. \end{aligned}$$

(e). The equilibrium point \(E_{4}(\widehat{x}, 0, \widehat{y_{2}})\) is locally asymptotically stable using Routh Hurwitz criteria if the following conditions are satisfied.

(i). \(PRQ-MQT > 0,\)

(ii). \(QT+MQ+MT-PR > 0,\)

(iii). \((QT+QM+MT-PR)(Q-T-M) > (PRQ-MQT), \)

where,

$$\begin{aligned} P= & {} \frac{-\widehat{x}(1+\widehat{x})}{(1+\widehat{x}+\epsilon _{2}\widehat{y_{2}})^2},\\ R= & {} \frac{\beta _{2}\widehat{y_{2}}(1+\epsilon _{2}\widehat{y_{2}})}{(1+\widehat{x}+\epsilon _{2}\widehat{y_{2}})^2} ,\\ M= & {} \Bigg (1-\frac{2\widehat{x}}{L}\Bigg )-\frac{\widehat{y_{2}}(1+\epsilon _{2}\widehat{y_{2}})}{(1+\widehat{x}+\epsilon _{2}\widehat{y_{2}})^2},\\ T= & {} \frac{\beta _{2}\widehat{x}(1+\widehat{x})}{(1+\widehat{x}+\epsilon _{2}\widehat{y_{2}})^2}-\mu _{1}-2\mu _{2}\widehat{y_{2}}, \\ Q= & {} \frac{\beta _{1}(\widehat{x}+\xi _{1})}{(1+\alpha \xi _{1}+\widehat{x})}-\delta _{1}-\alpha _{0}\widehat{y_{2}}. \end{aligned}$$

(f). The equilibrium point \(E_{5}(x^*,y_{1}^*,y_{2}^*)\) is locally asymptotically stable under the following conditions as,

(i). \((M^*R^* + M^* V+R^* V-NQ^*+US^*-T^*P^*) > 0\),

(ii). \((M^*US^*+NQ^*V+R^*T^*P^*-S^*T^*N-Q^*UP^*-M^*R^*V) > 0\),

(iii). \(-(V+R^*+M^*)(M^*R^* + M^* V+R^* V-NQ^*+US^*-TP^*) > (M^*US^*+N^*Q^*V+R^*TP^*-S^*T^*N-Q^*UP^*-M^*R^*V)\).

Where,

$$\begin{aligned} M^*= & {} \Big (1-\frac{2x^*}{L}\Big )-\frac{y_{1}^*(1+\alpha \xi _{1}+x^*+\epsilon _{1}y_{1}^*)-x^*y_{1}^*}{(1+\alpha \xi _{1}+x^*+\epsilon _{1}y_{1}^*)^2}-\frac{y_{2}^*(1+x^*+\epsilon _{2}y_{2}^*)-x^*y_{2}^*}{(1+x^*+\epsilon _{2}y_{2}^*)^2},\\ R^*= & {} \frac{\beta _{1}(x^*+\xi _{1})(1+\alpha \xi _{1}+x^*+\epsilon _{1}y_{1}^*)-\beta _{1}(x^*+\xi _{1})y_{1}^*\epsilon _{1}}{(1+\alpha \xi _{1}+x^*+\epsilon _{1}y_{1}^*)^2}-\delta _{1}-2y_{1}^*\delta _{2}-\alpha _{0}y_{2}^*,\\ V= & {} \frac{\beta _{2}x^*(1+x^*+\epsilon _{2}y_{2}^*)-\beta _{2}x^*y_{2}^*\epsilon _{2}}{(1+x^*+\epsilon _{2}y_{2}^*)^2}-\mu _{1}-2y_{2}^*\mu _{2}-\beta _{0}y_{1}^*,\\ N= & {} \frac{-x^*(1+\alpha \xi _{1}+x^*+\epsilon _{1}y_{1}^*)+x^*y_{1}^*\epsilon _{1}}{(1+\alpha \xi _{1}+x^*+\epsilon _{1}y_{1}^*)^2},\\ Q^*= & {} \frac{\beta _{1}y_{1}^*(1+\alpha \xi _{1}+x^*+\epsilon _{1}y_{1}^*)-\beta _{1}y_{1}^*(x^*+\xi _{1})}{(1+\alpha \xi _{1}+x^*+\epsilon _{1}y_{1}^*)^2},\\ S^*= & {} -\alpha _{0}y_{1}^*, T^*=\frac{\beta _{2}y_{2}^*(1+x^*+\epsilon _{2}y_{2}^*)-\beta _{2}x^*y_{2}^*}{(1+x^*+\epsilon _{2}y_{2}^*)^2},\\ U= & {} -\beta _{0}y_{2}^*, P^*=\frac{-x^*(1+x^*+\epsilon _{2}y_{2}^*)+x^*y_{2}^*\epsilon _{2}}{(1+x^*+\epsilon _{2}y_{2}^*)^2}. \end{aligned}$$

Global stability analysis

In this section, we prove the equilibrium point \(E^*\) to be globally stable using the method of Lyapunov function and the result can be stated as follows.

The positive equilibrium \(E^*\) is globally asymptotically stable for all solutions starting in the interior of the positive region if the following conditions hold.

(a)\(\Big (\frac{1+\alpha \xi _{1}+x^*}{M_{1}}+\frac{k_{1}\beta _{1}(1+\alpha \xi _{1})-\xi _{1}k_{1}\beta _{1}+k_{1}\beta _{1}\epsilon _{1}y_{1}^*}{M_{1}}\Big )^2 < \Big (\frac{1}{L}+\frac{y_{1}^*}{M_{1}}+\frac{y_{2}^*}{M_{2}}\Big )\Big (k_{1}\delta _{2}+\frac{\epsilon _{1}\xi _{1}k_{1}\beta _{1}}{M_{1}}+\frac{\epsilon _{1}k_{1}\beta _{1}x^*}{M_{1}}\Big )\),

(b) \(\Big (\frac{1+x^*}{M_{2}}+\frac{k_{2}\beta _{2}+k_{2}\beta _{2}\epsilon _{2}y_{2}^*}{M_{2}}\Big )^2 < \Big (\frac{1}{L}+\frac{y_{1}^*}{M_{1}}+\frac{y_{2}^*}{M_{2}}\Big ) \Big (k_{2}\mu _{2}+\frac{k_{2}\beta _{2}\epsilon _{2}x^*}{M_{2}}\Big )\),

(c) \( \Big (-k_{1}\alpha _{0}-k_{2}\beta _{0}\Big )^2 < \Big (k_{1}\delta _{2}+\frac{\epsilon _{1}\xi _{1}k_{1}\beta _{1}}{M_{1}}+\frac{\epsilon _{1}k_{1}\beta _{1}x^*}{M_{1}}\Big )\Big (k_{2}\mu _{2}+\frac{k_{2}\beta _{2}\epsilon _{2}x^*}{M_{2}}\Big ) ,\)

where,

$$\begin{aligned} M_{1}= & {} \Big (1+\alpha \xi _{1}+x^*+\epsilon _{1}y_{1}^*\Big )\Big (1+\alpha \xi _{1}+x^*+\epsilon _{1}y_{1}^*\Big ),\\ M_{2}= & {} \Big (1+x^*+\epsilon _{2}y_{2}^*\Big )\Big (1+x^*+\epsilon _{2}y_{2}^*\Big ). \end{aligned}$$

It can be proved by considering the following positive definite function about \( E^* \) as.

$$\begin{aligned} V(x, y_{1},y_{2})= & {} \left( x-x^*-x^*ln\left( \frac{x}{x^*})\right) +k_{1}\left( y_{1}-y_{1}^*-y_{1}^*ln\left( \frac{y_{1}}{y_{1}^*}\right) \right) \right. \\&\left. +k_{2}(y_{2}-y_{2}^*-y_{2}^*ln\left( \frac{y_{2}}{y_{2}^*}\right) \right) , \end{aligned}$$

where \( k_{1}\) and \(k_{2}\) are the positive arbitrary constants to be chosen mutually.

Differentiating V with respect to t, we get,

$$\begin{aligned} \dot{V}= & {} \frac{-1}{L}(x-x^*)^2-(x-x^*)\Bigg [\frac{y_{1}}{1+\alpha \xi _{1}+x+\epsilon _{1}y_{1}}-\frac{y_{1}^*}{1+\alpha \xi _{1}+x^*+\epsilon _{1}y_{1}^*}\Bigg ]\\&-(x-x^*)\Bigg [\frac{y_{2}}{1+x+\epsilon _{2}y_{2}}-\frac{y_{2}^*}{1+x^*+\epsilon _{2}y_{2}^*}\Bigg ]-k_{1}\delta _{2}(y_{1}-y_{1}^*)^2\\&-k_{1}\alpha _{0}(y_{1}-y_{1}^*)(y_{2}-y_{2}^*)\\&+k_{1}\beta _{1}(y_{1}-y_{1}^*)\Bigg [\frac{x+\xi _{1}}{1+\alpha \xi _{1}+x+\epsilon _{1}y_{1}}-\frac{x^*+\xi _{1}}{1+\alpha \xi _{1}+x^*+\epsilon _{1}y_{1}^*}\Bigg ]\\&-k_{2}\mu _{2}(y_{2}-y_{2}^*)^2-k_{2}\beta _{0}(y_{1}-y_{1}^*)(y_{2}-y_{2}^*)\\&-k_{2}\beta _{2}(y_{2}-y_{2}^*)\Bigg [\frac{x}{1+x+\epsilon _{2}y_{2}}-\frac{x^*}{1+x^*+\epsilon _{2}y_{2}^*}\Bigg ], \end{aligned}$$

after simplifying the above expression, we get,

$$\begin{aligned} \dot{V}= & {} -\Bigg (\frac{1}{L}+\frac{y_{1}^*}{M_{1}}+\frac{y_{2}^*}{M_{2}}\Bigg )(x-x^*)^2-\Big (k_{1}\delta _{2}+\frac{\epsilon _{1}\xi _{1}k_{1}\beta _{1}}{M_{1}}+\frac{\epsilon _{1}k_{1}\beta _{1}x^*}{M_{1}}\Big )(y_{1}-y_{1}^*)^2\\&-\Bigg (k_{2}\mu _{2}+\frac{k_{2}\beta _{2}\epsilon _{2}x^*}{M_{2}}\Bigg )(y_{2}-y_{2}^*)^2\\&+(x-x^*)(y_{1}-y_{1}^*)\Bigg [\frac{1+\alpha \xi _{1}+x^*}{M_{1}}+\frac{k_{1}\beta _{1}(1+\alpha \xi _{1})-\xi _{1}k_{1}\beta _{1}+k_{1}\beta _{1}\epsilon _{1}y_{1}^*}{M_{1}}\Bigg ]\\&+(x-x^*)(y_{2}-y_{2}^*)\Bigg [\frac{1+x^*}{M_{2}}+\frac{k_{2}\beta _{2}+k_{2}\beta _{2}\epsilon _{2}y_{2}^*}{M_{2}}\Bigg ]\\&+(y_{1}-y_{1}^*)(y_{2}-y_{2}^*)\Big [-k_{1}\alpha _{0}-k_{2}\beta _{0}\Big ]. \end{aligned}$$

This is equivalent to the following as,

$$\begin{aligned} \dot{V}= & {} \frac{-1}{2}a_{11}(x-x^*)^2+a_{12}(x-x^*)(y_{1}-y_{1}^*)-\frac{1}{2}a_{22}(y_{1}-y_{1}^*)^2-\frac{1}{2}a_{11}(x-x^*)^2\\&+a_{13}(x-x^*)(y_{2}-y_{2}^*)-\frac{1}{2}a_{33}(y_{2}-y_{2}^*)^2-\frac{1}{2}a_{22}(y_{1}-y_{1}^*)^2\\&+a_{23}(y_{1}-y_{1}^*)(y_{2}-y_{2}^*)-\frac{1}{2}a_{33}(y_{2}-y_{2}^*)^2, \end{aligned}$$

where,

$$\begin{aligned} a_{11}= & {} \Bigg (\frac{1}{L}+\frac{y_{1}^*}{M_{1}}+\frac{y_{2}^*}{M_{2}}\Bigg ),\\ a_{12}= & {} \Bigg [\frac{1+\alpha \xi _{1}+x^*}{M_{1}}+\frac{k_{1}\beta _{1}(1+\alpha \xi _{1})-\xi _{1}k_{1}\beta _{1}+k_{1}\beta _{1}\epsilon _{1}y_{1}^*}{M_{1}}\Bigg ], \\ a_{22}= & {} \Bigg (k_{1}\delta _{2}+\frac{\epsilon _{1}\xi _{1}k_{1}\beta _{1}}{M_{1}}+\frac{\epsilon _{1}k_{1}\beta _{1}x^*}{M_{1}}\Bigg ),\\ a_{33}= & {} \Bigg (k_{2}\mu _{2}+\frac{k_{2}\beta _{2}\epsilon _{2}x^*}{M_{2}}\Bigg ),\\ a_{13}= & {} \Bigg [\frac{1+x^*}{M_{2}}+\frac{k_{2}\beta _{2}+k_{2}\beta _{2}\epsilon _{2}y_{2}^*}{M_{2}}\Bigg ],\\ a_{23}= & {} \Big [-k_{1}\alpha _{0}-k_{2}\beta _{0}\Big ]. \end{aligned}$$

So, the sufficient condition for \(\dot{V} \) to be negative definite are as follows,

\(a_{12}^2 < a_{11}a_{22}\), \(a_{13}^2 < a_{11}a_{33}\), \(a_{23}^2 < a_{22}a_{33}\),

where, \(a_{11}, a_{12}, a_{13}, a_{22}, a_{33}\) and \( a_{23}\) have same meanings as described above.

Numerical simulations

This section deals with the numerical simulations of the system by taking the assumed values for the parameters. By assuming the values of the parameters as \( L=20, \alpha =0.8, \xi _{1}=25, \epsilon _{1}=0.4, \epsilon _{2}=0.5,\beta _{1}=0.6, \beta _{2}=0.4, \mu _{1}=0.3, \mu _{2}=0.5, \beta _{0}=0.2, \delta _{1}=0.6, \delta _{2}=0.4, \alpha _{0}=0.2\). System becomes:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{dx}{dt}= x\Big (1-\frac{x}{20}\Big )-\frac{xy_{1}}{1+20+x+0.4y_{1}}-\frac{xy_{2}}{1+x+0.5y_{2}},\\ \frac{dy_{1}}{dt}=\frac{0.6(x+25)y_{1}}{1+20+x+0.4y_{1}}-0.6y_{1}-0.4y_{1}^{2}-0.2y_{1}y_{2},\\ \frac{dy_{2}}{dt}=\frac{0.4xy_{2}}{1+x+0.5y_{2}}-0.3y_{2}-0.5y_{2}^{2}-0.2y_{1}y_{2}. \end{array}\right. } \end{aligned}$$
(6.1)

Now the system (6.1) has the trivial equilibrium points as \( E_{0}(0, 0, 0), E_{1}(20, 0, 0)\). The existence condition for the equilibrium point \( E_{2} \) is satisfied and (0, 0.267179, 0) is one of the equilibrium point satisfying condition \(H_{1}(=2.4) > 0\). Existence conditions of the equilibrium point \(E_{3}\) is \(C_{2}(=-2.357)<0 \) which is satisfied by taking the above parameters and so the equilibrium point \( E_{3}(19.9296,0.144275,0)\) exists. Also, for the system (6.1), equilibrium point \( E_{4}(19.8483,0,0.158739) \) exists. Now, by substituting the values of the parameters in the eqs. (3.4) and (3.5), we get the values of \(y_{1}^* \) and \(y_{2}^*\) as 0.0824207 and 0.12634 respectively. Also, \(\beta _{2}=0.4\) and \((\mu _{1}+\mu _{2}y_{2}^*+\beta _{0}y_{1}^*)=0.3+0.06317+0.032=0.39517\). So, the condition \(\beta _{2} > (\mu _{1}+\mu _{2}y_{2}^*+\beta _{0}y_{1}^*)\) is valid and the equilibrium point \(x^*\) is a positive value. So, the nonzero equilibrium point \(E_{5}(x^*,y_{1}^*,y_{2}^*)\) exists.

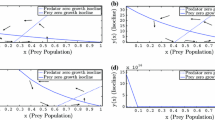
Further, the dynamics of the system is studied by taking some fixed parameters and some varying control parameters as given in Tables 1 and 2. Predator population shows different behaviour when the quantity of additional food is changed i.e when \(\alpha =0.8\) and \(\xi _{1}=25\). It is to be noted that there is a stable coexistence between the three species population when the system has additional food as its component and there is comparatively higher growth rate of predators consuming additional food as compared to the other class (Fig. 1).

When the control parameters \(\alpha \) and \( \xi \) are changed to increase the quantity of additional food, then a drastic change in the behaviour of predators population is seen. Population of predators show high growth rate with the increase in additional food and as a result, prey population decreases due to high predation and the mutual interference between predators with high strength but less than one results in the low density of predators that are not consuming additional food (Fig. 2).

Table 1 Numerical Values of Parameters
Full size table
Table 2 Parameter values of \(\alpha ,\xi ,\epsilon _{1},\epsilon _{2}\)
Full size table

In Fig. 4, where a tremendous decrease in the population of predators in the absence of prey population coincides with the ecological aspect and as the prey population increases, there is variability in the abundance of predators in the presence of low additional food which conveys the ecological meaning that predators will be solely dependent on preys for the survival but because of the additional food their population existed even when there were no preys.

In Figs. 2 and 4, there is difference in the strength of mutual interference i.e. Fig. 2 with high strength and Fig. 4 with low but both the systems with strength less than 1. Due to low mutual interference in the presence of additional food, the predators consuming food suppresses the prey and other class of predator population. It supports in the eradication of prey population and other predator population. Unlike, in Fig. 5 when the strength of mutual interference is high, greater than 1, keeping all other parameters as same results in supporting the prey population and the population of predators suppresses. It can be concluded that additional food availability along with the strength of mutual interference has an important role in the dynamics of the system and hence useful in biological control.

Also, it is to be pointed out that when the strength of mutual interference is high, then both the families of predators show similar behavior in the presence of additional food (Fig. 5). Thus, it can be concluded that high level of mutual interference represses the role of additional food in predators.

Fig. 1
figure 1

Numerical solution for the model 5.1

Full size image
Fig. 2
figure 2

Numerical solution with parameter set in Table 1 for the model with \(\alpha =4/5, \xi _{1}=25, \alpha \xi _{1}=20\)

Full size image

Further, when the value of \(\alpha \) increases from 1 and rest all parameters same as in Fig. 2, we observe that the class of predators not consuming the additional food(z axis) shows higher population rate as compared to other class of predators(y axis) with the case \(\alpha > 1\) which conveys the meaning that when handling time towards additional food is greater than the time taken to handle preys, then the family of predators(z) is behaving in a different way as compared to other systems when \(\alpha < 1\). In this case, the other class of predators(z) suppresses the predators class(y) which is true from the ecological point of view as the suppressed class is dependent on additional food as well (Fig. 7). Also, it is to be noted that when the value of \(\alpha \) is increased to 2 with the low level mutual interference, then it leads to an unstable behaviour of the system due to the high level of additional food and low interference among predators which results in the rise of predator population. As an outcome, prey density decreases and the predators completely dependent on preys for food will suffer. In due course of time, predators population will also decline and ultimately disturbs the ecosystem.

Fig. 3
figure 3

Numerical solution with parameter set in Table 1 for the model with \(\alpha =2/25, \xi _{1}=250, \alpha \xi _{1}=20\)

Full size image
Fig. 4
figure 4

Numerical solution with parameter set in Table 1 for the model with \(\alpha =4/5, \xi _{1}=25, \alpha \xi _{1}=20, \epsilon _{1}=0.004,\epsilon _{2}=0.005\)

Full size image
Fig. 5
figure 5

Numerical solution with parameter set in Table 1 for the model with \(\alpha =4/5, \xi _{1}=25, \alpha \xi _{1}=20, \epsilon _{1}=7,\epsilon _{2}=7\)

Full size image
Fig. 6
figure 6

Numerical solution with parameter set in Table 1 for the model with \(\alpha =2, \xi _{1}=25, \alpha \xi _{1}=50\)

Full size image
Fig. 7
figure 7

Numerical solution with parameter set in Table 1 for the model with \(\alpha =2, \xi _{1}=250, \alpha \xi _{1}=500\)

Full size image
Fig. 8
figure 8

Numerical solution with parameter set in Table 1 for the model with \(\alpha =2, \xi _{1}=25, \alpha \xi _{1}=50, \epsilon _{1}=0.004,\epsilon _{2}=0.005\)

Full size image

Conclusions

The consequences of providing additional food to predators has long been studied both theoretically and experimentally [12,13,14,15, 22]. This study has been a source of interest to researchers from the point of view of biological control by controlling pests by means of natural ways. It has also been studied that both the quality and quantity of additional food plays a vital role in controlling the prey [16,17,18]. Work has been done in improving the model based on additional food by incorporating the mutual interference between the predators along with the use of Beddington–DeAngelis functional response and significant results have been obtained [24, 38].

In [42], a prey predator model in which the effects of additional food and the harvesting efforts are discussed. It has been studied in the paper that the alternative food does not always lead to benefit the system. The final amount of both prey and predator biomass has been examined through the optimal control theory. In [43], a predator prey system has been investigated where population of the top level predators is provided with the alternative food. Thereafter, the model is examined by the local stability analysis of the various equilibrium points and optimal control of harvesting is acknowledged using Pontryagins maximum principle. The analysis carried out shows that the provision of alternative food, population of predator species can be prevented from extinction at the higher rate of harvesting. Study has been performed to demonstrate the significance of alternative food in the disease induced prey predator model and the analysis is done in regard to local stability, persistence and bifurcation. Results are illustrated by the way of numerical simulation to depict the role of alternative food in the disease free system [44].

The predator’s functional response can be defined as the characterisation of predators per capita feeding rate which is considered to be a function of prey density say ’N’(Holling 1959). Holling type II functional response states that the average feeding rate of predators is dependent on the searching time for prey and the handling time(includes the processing time) by predators. It takes the form as:

$$\begin{aligned} f=\frac{a'N}{1+b'N}, \end{aligned}$$

where, a’ and b’ specifies the influence of capturing rate and handling time on the feeding rate of predators. This functional response ignores the influence of interference among the predators and presumes that depletion in the prey density is a means by which competition occurs in predators. Beddington [5] and DeAngelis et al. [30] proposed a functional response which exhibits the aspect of interference in predators and assumes that predator population allocates time not only in the quest of prey and in processing prey but also time is expended in encountering with other predators which determines an another functional called as Beddington functional response. The Beddington DeAngelis functional response relies on the fact that handling and interfering are the two exclusive behaviour but Crowley and Martin in 1989 removed this presumption and acknowledged for admitting the interference in predators irrespective of whether a predator is handling prey or searching for prey. The Beddington DeAngelis model envisages that under high prey density, the impact of predator interference on feeding rate gets insignificant but Crowley–Martin model anticipates that interference role on feeding rate is significant under same conditions [45].

In this paper, an attempt has been made to further improve the prey- predator dynamical model incorporating the concept of additional food with the distinction being made in the class of predators. There are carnivorous predators and omnivorous predators existing in the ecosystem with discrimination being done on the basis of consuming the type of food. Proposed model consists of two classes of predators and role of additional food has been considered a significant factor along with the mutual interference factor. In this paper, Beddington–DeAngelis functional response has been considered due to the presence of mutual interference between the predators with \(\rho _{1}\) and \(\rho _{2}\) being the mutual interference factor between the class \(P_{1}\) and \(P_{2}\) of the predators. The growth rate of the predator class \(P_{1}\) is demonstrated with the functional response \( \frac{b_{1}(N+\eta A)P_{1}}{a_{1}+\alpha \eta A +N+\rho _{1} P_{1}} \) and the growth of predator class \(P_{2}\) with \( \frac{b_{2}NP_{2}}{a_{1}+N+\rho _{2} P_{2}}\). It is to be noted that the additional food term \(\eta A\) is induced in the growth rate of predator class \(P_{1}\) only. Thereafter, the dynamic behaviour of the system has been analysed and various conditions of stability have been derived.

Global stability analysis has been performed in the present article using Lyapunov functional method. The interior unique equilibrium point \(E^{*}(x^*,y_{1}^*,y_{2}^*)\) is globally stable under the conditions \(a_{12}^2 < a_{11}a_{22}\), \(a_{13}^2 < a_{11}a_{33}\), \(a_{23}^2 < a_{22}a_{33}\). Although the formation of Lyapunov function is not an easy task but the approach is extensively used in many studies as it facilitates the global stability study [46,47,48]. Numerical simulations to support the theoretical results are done.