Introduction

Fractional calculus is a generalization of ordinary calculus which introduces derivatives and integrals of fractional order (see [1,2,3,4,5,6,7, 9]). In the last 2 decades, the use of fractional order operators and operations has been shown as a powerful tool to model the behavior of a number of mechanical and electrical dynamic systems [10,11,12, 14]. In 2006, Magin provided a simple but illustrative example of memory effect of a fractional derivative [13]. Recently, fractional calculus is therefore generally accepted by physical considerations, such as memory and hereditary effects, favor the use of fractional derivative-based models [8, 15]. In particular, it is reasonable to think that the physicochemical nature of biological processes will result in a dynamic behavior with memory such as fermentations, enzymatic reactions, cell growth, etc. [8]. They also show that the kinetics of those reactive systems can be accurately represented by using fractional calculus without the need of empirical considerations.

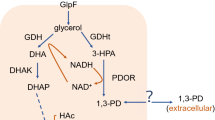
The microbial conversion process for synthesizing 1,3-PD has been studied since the 1980s  [16, 28]. An experimental investigation about the multiple inhibitions of the fermentation process is given in [17, 29], and studies based on metabolic flux and metabolic pathway analysis are given in [18,19,20,21,22, 26]. Mathematical models of the microbial conversion process, together with various process control strategies, have been considered in [23,24,25, 27]. There are three common methods of microbial fermentation: batch culture, continuous culture, and fed-batch culture. At the beginning of the batch culture, the bacteria and substrate are added to the bioreactor, and nothing is added to the batch culture during the process. In continuous culture, fresh medium flows into the fermentor continuously to replenish consumed substrate. Fed-batch culture is a mixture of the batch and continuous cultures: the time horizon is divided into periods, and the fermentation process switches between a continuous phase (in which substrate is added continuously to the reactor) and a batch phase (in which no substrate is added to the reactor). In this paper, we focus on the batch culture process with glycerol as the substrate.

Motivated by the use of fractional calculus in reactive biological systems, in this paper, we intend to extend the existing ordinary order mathematical model to the fractional order model, which can more accurately describe the batch culture in the microbial fermentation process for producing 1,3-PD. The existence and uniqueness of solutions to the system and the continuity of solutions with respect to the parameters are discussed. A parameter identification model is developed, and its identifiability is proved. Subsequently, we construct an algorithm to solve the parameter identification problem. Numerical result shows the effectiveness of the algorithm and the agreement with the experimental data.

This paper is organized as follows. In the second section, we introduce a fractional model with new system parameters to describe the batch culture in microbial fermentation  [15]. Then the properties of the solutions to the system are discussed in the next section. Subsequently, a parameter identification model is constructed in following section. Then, we develop a particle swarm optimization method for solving the parameter identification problem in the next section. Finally, numerical results are reported in last section.

Fractional Model for Biological Fermentation

Some relativity mature models for producing 1,3-PD have already been established in last 2 decades [23,24,25, 27]. Motivated by the applications of fractional calculus and the fractional model for reactive biological system proposed by Toledo-Hernandez [15], we propose a fractional order differential equation model to simulate the microbial fermentation. This fractional order fermentation model is based upon the mechanism of our original ordinary differential equations model [23] and the Caputo fractional derivative (see [30, 31]).

Assume that nothing is added to or removed from the batch reactor during the batch culture process. Further, assume that the concentration of reactions of reactor reactants are uniform. According to [25], mass balance of biomass, substrate and products in batch culture are written as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} \dot{x_1}&{}=\mu x_1(t),\\ \dot{x_2}&{}=-q_2x_1(t), \quad \quad \quad t\in I,\ i=3,4,5,\\ \dot{x_i}&{}=q_ix_1(t),\\ x_i^0&{}=x_i(0), \end{aligned} \end{array}\right. } \end{aligned}$$
(1)

where \(x_1,x_2,x_3,x_4,x_5\) are biomass, glycerol, 1,3-PD, acetate and ethanol concentrations at time t in the reactor, respectively. I denotes the time interval of microbial fermentation. \(x^0:=(x_1^0,x_2^0,x_3^0,x_4^0,x_5^0)^{\top }\) denotes the initial state. The specific cell growth rate \(\mu \), specific consumption rate of substrate \(q_2\) and specific formation rate of products \(q_i,\ i=3,4,5\), are expressed by the following equations on the basis of [24].

$$\begin{aligned} {\left\{ \begin{array}{ll} \mu = {\mu }_m \displaystyle {{\frac{x_2(t)}{x_2(t)+k_s}\underset{i=2}{\overset{5}{\prod }}} \Big (1-\frac{x_i(t)}{x_i^{*}}\Big )},\\ q_2=m_2+\frac{\mu }{Y_2},\\ q_i=m_i+\mu Y_i,\ i=3,4,5. \end{array}\right. } \end{aligned}$$

Under anaerobic conditions at \(37^{\circ }\) and PH = 7.0, the maximum specific growth rate of cells \({\mu }_m=0.67\) /h and Monod saturation constant \(k_s = 0.28\) mmol/L. The critical concentrations of biomass glycerol, 1,3-PD, acetate and ethanol for cell growth are \(x_1^{*} = 10\) g/L, \(x_2^{*} = 2039\) mmol/L, \(x_3^{*} = 939.5\) mmol/L, \(x_4^{*} = 1026\) mmol/L and \(x_5^{*} = 360.9\) mmol/L, respectively. \(m_i\) and \(Y_i,\ i = 2,3,4,5\), are parameters given in [24]. Since the concentrations of biomass, glycerol and products are restricted in a certain range according to the practical production, we consider the system on a subset of \(R^5,\ W_{ad}:=\{x \in R^5 \vert x_1\in [0.001,x_1^{*}],\ x_i \in [0,x_i^{*}],\ i=2,3,4,5\}\).

To establish fractional order fermentation model, two fractional derivative definitions, the Riemann-Liouville definition and the Caputo definition, together with the initial condition [7] are introduced. The Riemann-Liouville fractional derivative is

(2)

where \(n=[\alpha ]+1\), and \([\alpha ]\) means the integer part of \(\alpha \). The initial conditions corresponding to (2) are of the form

$$\begin{aligned} \frac{d^{\alpha -k}}{dt^{\alpha -k}}y(t)\vert _{t=0^{+}}:=c_k,\ k=1,2,\ldots ,n, \end{aligned}$$
(3)

with given values \(c_k\). In practical applications, these specified fractional initial values are frequently not available, and it may not even be clear what their physical meanings are (see[32, 33]). The Caputo fractional order derivative is

(4)

with specified initial conditions in the classical form

$$\begin{aligned} y^{(k)}(0)=y_0^{(k)},\ k=0,1,\ldots ,n-1. \end{aligned}$$
(5)

Because the physical meaning of the fractional derivative of y is not clear when dealing with the fermentation model, nor is how such a quantity can be measured, the Caputo definition is applied in the following fractional fermentation model.

Since the amount of acetate and ethanol generated in the process is very small, we only consider one kind of product, 1,3-PD, i.e., the first three equations (the biomass, the substrate and the 1,3-PD) of system (1) are considered. Then we assume that nothing is added to, or removed from, the batch reactor during the batch culture process. And also, the stir in the reactor is sufficient so that the concentrations of reactants are uniform. In [15], the classical Lotka-Volterra model was extended to the fractional model. Analogy to [15], we extend the existed ordinary differential model of system (1) to a fractional model. In [15], the author only consider the influence of cell mortality to biomass. However, cell death also inhibit the consumption of the substrate and the growth of the product. In this paper, considering the influence of cell mortality to biomass, product and substrate, we present a novel fractional fermentation model.

Based on [15], it is reasonable to assume that the biomass growth depends only on the substrate, and the increase of biomass is proportional to the biomass-substrate interaction (a product of \(x_1\) and \(x_2\)). Moreover, the inhibition of cell death to biomass is proportional to the biomass. So the rate of change of biomass concentration can be represented as follows:

(6)

A similar derivation is used for the substrate and the product differential equations. Assume that the concentration of substrate decreases proportionally to the biomass-substrate interaction (\(x_1x_2\)). Also, the cell death will inhibit the glycerol consumption and the rate of change of substrate concentration is shown as follows:

(7)

The 1,3-PD concentration depends on the same biomass-substrate interaction and the cell death, so we have

(8)

The kinetics constants \(k_i,\ i=1,2,3\), represent biomass growth, glycerol consumption, and 1,3-PD formation, respectively. And \(k_i,\ i=4,5,6\), represent cell death, the inhibition of glycerol consumption, and the 1,3-PD growth by cell death, respectively. For simplicity, we introduce \(\alpha :=({\alpha }_1,{\alpha }_2,{\alpha }_3)^{\top },\ k:=(k_1,k_2,k_3,k_4,k_5,k_6)^{\top }\), and \(x:=(x_1,x_2,x_3)^{\top }\).

Since the concentration of biomass, glycerol and 1,3-PD are restricted in a certain range according to practical production, we consider the system on a subset of \(R^3\), let

$$\begin{aligned} W_{ad}:=\{x\in R^3 \vert x_i \in [x_{i*},x_i^{*}],\ i = 1,2,3\}, \end{aligned}$$

be the permitted capability of state variables, where \(x_{i*}\) and \(x_i^{*}\) are the lower and the upper bound of biomass, glycerol and product, respectively. And

$$\begin{aligned} P_{ad}:=\{(\alpha ,k)\vert {\alpha }_i\in (0,1),k_j\in [0,1],\ i=1,2,3,\ j=1,\ldots ,6\}, \end{aligned}$$

is the parameter admission set. For brevity, let us define that \(p:=({\alpha }^{\top },k^{\top })\) and

$$\begin{aligned} f(t,x(t),p) := (f_1(t,x(t),p),f_2(t,x(t),p),f_3(t,x(t),p))^{\top }, \end{aligned}$$
(9)

where \(f_i(t,x(t),p), i=1,2,3\), represent the right hands of the Eqs. (6–8), respectively. Then the fractional material balance equations for the process of microbial batch culture is given by the following equations:

(10)

where \(t\in I:=[0,T]\) and T is the terminal time. Next, we will study the existence and uniqueness of solutions to the fractional system (10).

Properties of the Solution for the System

To discuss the existence and uniqueness of the solutions to the system and the continuity of solutions with respect to the parameters, some important properties of the Eq. (9) are discussed in this section. We denote the space of continuous functions from I into \(R^3\) with \(C(I,R^3)\), equipped with the sup norm \({\Vert x \Vert }:=\sup \{ |x(t) |: t\in I \}\) for \(x\in C(I,R^3)\), where \(|\cdot |\) is the Euclidean norm.

Property 3.1

For a given \(p\in P_{ad}\), function f defined in Eq. (9) is twice continuously differentiable on \(x\in W_{ad}\). Further, there exists a constant \(M\in (0,\infty )\) satisfying

$$\begin{aligned} \Vert f(t,x,p)\Vert \le M, \end{aligned}$$
(11)

for all \(x\in W_{ad}\).

Property 3.2

There exists a constant K, for all given \(t\in I, x^1,x^2\in W_{ad}\), and all \(p_1,p_2\in P_{ad}\), function (9) satisfies the following Lipschitz condition

$$\begin{aligned} \Vert f(t,x^1,p^1)-f(t,x^2,p^2)\Vert \le K(\Vert x^1-x^2\Vert + \Vert p^1 -p^2 \Vert ). \end{aligned}$$
(12)

Proof

Under Property  3.1 and the Mean Value Theorem, it is easy to complete the proof.

\(\square \)

Definition 3.1

A function \(x(\cdot )\in C(I,R^3)\) is said to be a solution of the fractional order system (10) if x satisfies the equation a.e. on I and the condition that \(x(0)=x^0\).

Property 3.3

(existence and uniqueness) For all \((x_0,p)\in W_{ad}\times P_{ad}\), there exists an unique solution x to the fractional system (10) in \(C(I,R^3)\).

Proof

Obviously, f is continuous in \(I\times W_{ad}\). Further, Based on Property  3.1, \(\Vert f(t,x,p)\Vert \) is bounded when \((t,x,p)\in I\times W_{ad}\times P_{ad}\). Let \(q=\frac{2}{3}\alpha ,\ \beta =\frac{\alpha -1}{1-q}\), we have

$$\begin{aligned} \Big \Vert \displaystyle {\frac{2M}{\varGamma {(\alpha )}(1+\beta )^{1-q}}}\Big \Vert \le 4M. \end{aligned}$$

According to Property  3.1, there exists a constant \(l_0\in R_+\) and let \(k_1\in (0,\frac{1}{l_0})\), satisfying

$$\begin{aligned} \Vert f(t,x^1,p)-f(t,x^2,p)\Vert \le L_0\Vert x^1-x^2 \Vert , \end{aligned}$$

where \(\ L_0=\max \{k_1x_2\vert k_1\in P_{ad},\ x_2\in W_{ad}\}\). Let

$$\begin{aligned} ln(\tau )={\frac{1}{q}\Big (ln(L_0)+(1+\beta )(1+q)ln(T)-ln(\varGamma {(q)})-(1-q)ln(1+\beta )+qln(q)\Big )}, \end{aligned}$$

then we have

$$\begin{aligned} \displaystyle {\frac{L_0}{\varGamma {(q)}}\frac{T^{(1+\beta )(1-q)}}{(1+\beta )^{1-q}}\left( \frac{q}{\tau }\right) ^{q}}\le 1. \end{aligned}$$

According to Theorem 3.16 in [34], the proof of existence and uniqueness of the solution to the fractional order system (10) is completed. \(\square \)

Lemma 3.1

Function \(x(\cdot )\in C(I,R^3)\) is said to be a solution of the fractional order system (10), if it satisfies the following integral equation:

$$\begin{aligned} x(t,p)=x^0+\displaystyle {\frac{1}{\varGamma {(\alpha )}}\int _0^t(t-\tau )^{\alpha -1}f(\tau ,x,p)d\tau },\quad t\in I. \end{aligned}$$
(13)

Property 3.4

The solution \(x(\cdot ;p)\) of the fractional order system (10) is continuous on \(p\in P_{ad}\).

Proof

For all \(p^1,\ p^2\in P_{ad}\), we have

$$\begin{aligned} \Vert x(t,p^1) - x(t,p^2)\Vert= & {} \Vert x(t,{\alpha }^1,k^1)-x(t,{\alpha }^2,k^2)+x(t,{\alpha }^2,k^1)-x(t,{\alpha }^2,k^2) \Vert \nonumber \\\le & {} \Vert x(t,{\alpha }^1,k^1)-x(t,{\alpha }^2,k^1)\Vert + \Vert x(t,{\alpha }^2,k^1) - x(t,{\alpha }^2,k^2) \Vert .\nonumber \\ \end{aligned}$$
(14)

Combining (9) with Lemma  3.1 yields

$$\begin{aligned} \Vert x(t,{\alpha }^1,k^1) - x(t,{\alpha }^2,k^1)\Vert= & {} \Big \Vert \frac{1}{\varGamma {({\alpha }^1)}}\int _0^t(t-s)^{{\alpha }^1-1}f(s,x,{\alpha }^1,k^1)ds\\&-\frac{1}{\varGamma {({\alpha }^2)}}\int _0^t(t-s)^{{\alpha }^2-1}f(s,x,{\alpha }^2,k^1)ds \Big \Vert \\\le & {} \Big \Vert \int _0^t \frac{1}{\varGamma {({\alpha }^1)}}(t-s)^{{\alpha }^1-1}\Big [f(s,x,{\alpha }^1,k^1)\\&-f(s,x,{\alpha }^2,k^1)\Big ] ds\Big \Vert \\&+ \Big \Vert \int _0^t \Big [ \frac{1}{\varGamma {({\alpha }^1)}}(t-s)^{{\alpha }^1-1}\\&- \frac{1}{\varGamma {({\alpha }^2)}}(t-s)^{{\alpha }^2-1}\Big ]f(s,x,{\alpha }^2,k^1) ds \Big \Vert . \end{aligned}$$

According to Property  3.1 and Property  3.2, the equation can be simplified as follows:

$$\begin{aligned} \Vert x(t,{\alpha }^1,k^1) - x(t,{\alpha }^2,k^1)\Vert\le & {} K\Big \Vert \int _0^t\frac{1}{\varGamma {({\alpha }^1)}}(t-s)^{{\alpha }^1 -1}ds\Big \Vert \cdot \Vert {\alpha }^1-{\alpha }^2\Vert \\&+M\Big \Vert \int _0^t \Big [\frac{1}{\varGamma {({\alpha }^1)}}(t-s)^{{\alpha }^1 -1} -\frac{1}{\varGamma {({\alpha }^2)}}(t-s)^{{\alpha }^2-1}\Big ]ds\Big \Vert . \end{aligned}$$

Let \(N_1=K \Big \Vert \displaystyle {\frac{T^{{\alpha }^1}}{\varGamma {({\alpha }^1+1)}}}\Big \Vert ,\ N_2=\displaystyle {\frac{MT^{\Vert {\alpha }^1\Vert }}{\varGamma {(\min \{\Vert {\alpha }^1\Vert ,\Vert {\alpha }^2\Vert \}+1)}}}\), then we obtain

$$\begin{aligned} \Vert x(t,{\alpha }^1,k^1) - x(t,{\alpha }^2,k^1)\Vert \le N_1\Vert {\alpha }^1-{\alpha }^2\Vert + N_2|1 - t^{\Vert {\alpha }^2-{\alpha }^1\Vert } |. \end{aligned}$$

For all \(\epsilon >0\), let \({\delta }_1=\frac{\epsilon }{2N}\) where \(N=\max \{N_1,N_2\}\), when \(\Vert {\alpha }^1 -{\alpha }^2\Vert <\delta \), the following

$$\begin{aligned} \Vert x(t,{\alpha }^1,k^1) - x(t,{\alpha }^2,k^1)\Vert \le \frac{\epsilon }{2}, \end{aligned}$$
(15)

holds. For all \(k^1,k^2\in P_{ad}\), the second part of the equation (14) can be expressed as follows:

$$\begin{aligned} \Vert x(t,{\alpha }^2,k^1)-x(t,{\alpha }^2,k^2)\Vert= & {} \Big \Vert \frac{1}{\varGamma {({\alpha }^2)}}\int _0^t(t-s)^{{\alpha }^2-1}f(s,x,{\alpha }^2,k^1)ds\\&-\frac{1}{\varGamma {({\alpha }^2)}}\int _0^t(t-s)^{{\alpha }^2-1}f(s,x,{\alpha }^2,k^2)ds\Big \Vert \\\le & {} K \Big \Vert \int _0^t \frac{(t-s)^{{\alpha }^2-1}}{\varGamma {({\alpha }^2)}}ds\Big \Vert \cdot \Vert k^1-k^2 \Vert . \end{aligned}$$

Let \(N_3=K\Vert \displaystyle {\frac{T^{{\alpha }^2}}{\varGamma {({\alpha }^2+1)}}}\Vert ,\ {\delta }_2=\frac{\epsilon }{2N_3}\), when \(\Vert k^1-k^2\Vert <{\delta }_2 \) we have

$$\begin{aligned} \Vert x(t,{\alpha }^2,k^1)-x(t,{\alpha }^2,k^2)\Vert \le \frac{\epsilon }{2}. \end{aligned}$$
(16)

Based upon (14–16), we obtain the desired results. \(\square \)

Parameter Identification

Under the specified initial data \(x^0=(x_1(0),x_2(0),x_3(0))^{\top }\), we did l times concentration measurement during fermentation process. Denote the experimental data at time \(t_j,\ j\in I_l:=\{1,2,\ldots ,l\}\), by \(y^j:=(y_1^j,y_2^j,y_3^j)^{\top }\in {\mathbb {R}}^3\), where \(y_1^j, y_2^j\) and \(y_3^j\) represent the experimental concentration of the biomass, glycerol, and 1,3-PD at that time, respectively. Further, let \(x^j:=(x_1(t_j,p),x_2(t_j,p),x_3(t_j,p))^{\top }\) be the solution of the fractional order fermentation system (10) under the initial value \(x_0\) at time \(t_j\), where \(j\in I_l\) and \(p:=({\alpha }_1,{\alpha }_2,{\alpha }_3,k_1,k_2,k_3,k_4,k_5,k_6)\in P_{ad}\). Then, the parameter identification problem that makes the calculated values \(x^j\) from the system (10) achieve a best approximation with the empirical data \(y^j\) can be described as follows:

$$\begin{aligned} \begin{aligned} (P) \quad \quad \quad&\min J(p)=\displaystyle {\sum _{i=1}^3\sum _{j=1}^l \frac{|x_i(t_j,p)-y_i^j|}{|y_i^1-y_i^l|}}\\&s.t \quad p \in P_{ad},\\&\quad \quad 0\le t\le T. \end{aligned} \end{aligned}$$
(17)

We define the solution set to the fractional order system (10) as follows:

$$\begin{aligned} S:=\{x(\cdot ;p)\in C(I,R^3)\vert \ x(\cdot ;p)\ \text {is the solution to the system } (10),\ p\in P_{ad}\}. \end{aligned}$$
(18)

According to Property  3.4 and the compactness of \(P_{ad}\), we can obtain the following results.

Lemma 4.1

For a given \(x(\cdot ) \in W_{ad}\), the set S defined in (18) is compact in \(C(I,R^3)\).

Theorem 4.1

Assume that for a given \(p\in P_{ad}\), the system (10) is controllable and observable, then there exists an optimal solution \(p^{*}\in P_{ad}\) of the Problem (P), such that the following

$$\begin{aligned} J(p^*)\le J(p),\quad \forall p\in P_{ad}, \end{aligned}$$
(19)

holds.

Proof

It follows from Property  3.4 that the mapping from \(p\in P_{ad}\) to \(x(\cdot ;p)\in S\) is continuous. In view of the continuity of the mapping from x to J(p) and the compactness of S, we conclude that problem (P) has an optimal solution, denoted by \(p^*\), that is, \(J(p^*)\le J(p)\), for all \(p\in P_{ad}\). \(\square \)

Particle Swarm Optimization Algorithm and Numerical Results

The problem (P) is a dynamic optimization problem with the fractional dynamic differential equations, and we want to adjust the parameters so that our numerical results conform to the experiment data. To get the numerical solution of the fractional derivative equations, we introduce the predictor-corrector method in [8]. Considering the global nature of the solution and the rate of the convergence, we introduce a modified Particle Swarm Optimization algorithm (PSO) to solve this problem. We will make a brief introduction of the predictor-corrector method first.

The fundamental algorithm for the solution of initial value problems with Caputo derivatives is derived by Diethelm in [8], and the algorithm is a generalization of the classical Adams-Bashforth-Moulton integrator. We recall the results of numerical method for the fractional differential equations. A general fractional differential equation system can be described as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} D^{\alpha }y(t)=f(t,y(t)), \quad \quad \quad \quad \\ y^{(k)}(0)=y_0^{(k)},\ k=0,1,\ldots ,[\alpha ]+1. \end{array}\right. } \end{aligned}$$
(20)

And the system (20) is equivalent to the following:

$$\begin{aligned} y(t)=\displaystyle {\sum _{k=0}^{\lceil {\alpha }\rceil -1}\frac{t^k}{k!}y_0^{(k)}}+ \displaystyle {\frac{1}{\varGamma {(\alpha )}}\int _0^t(t-\tau )^{\alpha -1}f(\tau ,y(\tau ))d\tau }, \end{aligned}$$

where \(\lceil {\alpha }\rceil \) is the smallest integer lager than or equal to \(\alpha \). The integral is then replaced by a two-point quadrature formula. To be brief, the predictor step is calculated through the following equation:

$$\begin{aligned} y_N^p(t_{n+1})=\displaystyle {\sum _{k=0}^{\lceil {\alpha }\rceil -1} \frac{t_{n+1}^k}{k!}y_0^{(k)}}+\displaystyle {\frac{1}{\varGamma {(\alpha )}}\sum _{j=0}^{n} b_{j,n+1}f(t_j,y_h(t_j))}, \end{aligned}$$
(21)

where

$$\begin{aligned} b_{j,n+1}=\frac{h^{\alpha }}{\alpha }((n+1-j)^{\alpha }-(n-j)^{\alpha }). \end{aligned}$$
(22)

And the corrector formula is calculated by the following equation:

$$\begin{aligned} y_h(t_{n+1})= & {} \displaystyle {\sum _{k=0}^{\lceil {\alpha }\rceil -1} \frac{t_{n+1}^k}{k!}y_0^{(k)}}+\displaystyle {\frac{h^{\alpha }}{\varGamma {(\alpha +2)}}f(t_{n+1},y_h^p(t_{n+1}))}\nonumber \\&+\displaystyle {\frac{h^{\alpha }}{\varGamma {(\alpha +2)}}\sum _{j = 0}^n a_{j,n+1}f(t_j,y_h(t_j))}, \end{aligned}$$
(23)

where

$$\begin{aligned} a_{j,n+1}= {\left\{ \begin{array}{ll} n^{\alpha +1}-(n-\alpha )(n+1)^{\alpha },&{} \text {j = 0},\\ (n-j+2)^{\alpha +1}+(n-j)^{\alpha +1}-2(n-j+1)^{\alpha +1},&{} 1\le j\le n,\\ 1,&{} \text {j = n+1}. \end{array}\right. } \end{aligned}$$
(24)

The basic algorithm, fractional Adams-Bashforth-Moulton method, is fully described by equations (21) and (23) with the weights \(b_{j,n+1}\) and \(a_{j,n+1}\) being defined according to (22) and (24), respectively.

PSO optimizes a problem by having a population of candidate solution, and moving these particles around in the search-space according to simple mathematical formulae over the particles position and velocity. PSO is a metaheuristic as it makes few or no assumptions about the problem being optimized and can search very large spaces of candidate solutions. More specifically, PSO does not use the gradient of the problem being optimized, which means PSO does not require that the optimization problem be differentiable as is required by classic optimization methods such as gradient descent and quasi-Newton methods. And it can be simplified as follows:

Notations:

  • N is the total number of the particles in the swarm.

  • \(K_{\max }\) is the maximum iteration step.

  • \(\tau \) is the convergence tolerance.

  • \(c_1\) and\(c_2\) are the minimum and maximum inertia weights.

  • \(v_{\max }\) and \(v_{\min }\) are vectors containing the maximum and minimum particle velocities.

  • \(p_{\max }\) and \(p_{\min }\) are the upper and the lower bound of the particles. The following variables in the PSO algorithm are updated as the algorithm proceeds.

  • w is the inertia weight.

  • q is the iterative step.

  • J(q, n) is the value of the nth individual particle at the qth iteration.

  • \(\tilde{J}(q,n)\) is the best objective value found by the nth individual particle in the qth iteration.

  • \(\tilde{p}^n\) is the best control strategy found by the nth individual particle.

  • \(\tilde{J}^{*}\) is the best objective value found by any member of the swarm.

  • \(\tilde{p}^{*}\) is the best control strategy found by any member of the swarm.

Algorithm:

  • Step 1. Initialize the following parameters: \(K_{\max }, \tau , c_1, c_2, w_0, v_{\max }, v_{\min },p_{\max }, p_{\min }\).

  • Step 2. Randomly generate positions of the N particles in the rectangular region defined by constrains of (17). And randomly generate the particle velocities in the rectangular region defined by \(v_{\max }\) and \(v_{\min }\). Let \(p^n:=({\alpha }_1^n,{\alpha }_2^n,{\alpha }_2^n,k_1^n,k_2^n,k_3^n,k_4^n,k_5^n,k_6^n)\) denotes the position of the nth particle, and let \(v^n:=(v_1^n,v_2^n,v_3^n,v_4^n,v_5^n,v_6^n,v_7^n,v_8^n,v_9^n)\) denotes the velocity of the nth particle, where \( n = 1,2,\ldots ,N\).

  • Step 3. According to (21–24), we get the numerical solution of the fractional order system (10). Then for each \(n=1,2,\ldots ,N\), calculate the corresponding objective value J(q, n) according to (17) and initialize \(\tilde{J}(1,n),\ \tilde{J}^{*}\) and \(\tilde{p}^n,\ \tilde{p}^{*}\).

  • Step 4. If \(J(q,n)<\tilde{J}(q,n)\), then set \(\tilde{J}(q,n)=J(q,n)\) and \(p^n=\tilde{p}^n\).

  • Step 5. If \(J(q,n)<\tilde{J}^{*}\), then set \(\tilde{J}^{*}=J(q,n)\) and \(p^n=\tilde{p}^{*}\).

  • Step 6. If \(\tilde{J}^{*}<\tau \) then stop. Otherwise go to Step 7.

  • Step 7. Update the velocities, for each \(n=1,2,\ldots ,N,\ j=1,2,\ldots ,9\),

    $$\begin{aligned} v^n(j)=w_0\times v^n(j)+c_1\times r_1\times (p_{best}^n(j)-p^n(j))+c_2\times r_2\times (p_{best}^{*}(j)-p^n(j)), \end{aligned}$$

    where \(r_1\in (0,1)\) and \(r_2\in (0,1)\) are random numbers, and \(v^n(j)\) denotes the jth index of the nth particle.

  • Step 8. For each \(n=1,2,\ldots ,N,\ j=1,2,\ldots ,9\) update the velocity of the particles according to the following formula:

    $$\begin{aligned} v^n(j)= {\left\{ \begin{array}{ll} v_{\min }, \quad v^n(j)<v_{\min },\\ v^n(j), \quad v^n(j)\in [v_{\min },v_{\max }],\\ v_{\max }, \quad v^n(j)>v_{\max }. \end{array}\right. } \end{aligned}$$

  • Step 9. Update the inertia term according to the following formula:

    $$\begin{aligned} w=0.4+0.5 \times \exp {(-3\times (q/K_{\max })^2)}. \end{aligned}$$

  • Step 10. For each \(n=1,2,\ldots ,N,\ j=1,2,\ldots ,9\), compute

    $$\begin{aligned} p^n(j)=p^n(j)+w\times v^n(j). \end{aligned}$$

  • Step 11. For each \(n=1,2,\ldots ,N,\ j=1,2,\ldots ,9\), update the position of the particles according to the following formula

    $$\begin{aligned} p^n(j)= {\left\{ \begin{array}{ll} p_{\min }, \,\,\quad \ {p^n(j)<p_{\min }},\\ p^n(j), \quad {p^n(j)\in [p_{\min },p_{\max }]},\\ p_{\max }, \,\,\quad {p^n(j)>p_{\max }}. \end{array}\right. } \end{aligned}$$

  • Step 12. Set \(q=q+1\) and return to Step 3.

Numerical Results

By combining the PSO algorithm with the predictor-corrector approach for the numerical solution of fractional differential equations, we solved the parameter identification problem and obtained the fractional orders and the optimal kinetics parameters for the fractional order system (10). The results are listed in Table 1. Further, the average relative errors are calculated according to the following form

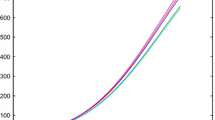
$$\begin{aligned} {\epsilon }_i = \displaystyle {\sum _{j=1}^l\frac{|x_i(t_j,p)-y_i^j |}{y_i^j}},\ i=1,2,3. \end{aligned}$$

Then the experimental data and the numerical results with the obtained parameters are shown in Fig. 1, where ‘+’ and ‘−’ represent the experimental data and the numerical data, respectively. According to Fig. 1, we can conclude that the fractional order system (10) can present the intermittent fermentation process properly.

Table 1 Parameters values in dynamical systems (10)
Full size table
Fig. 1
figure 1

Comparison of biomass, glycerol and product concentration between experimental data and computational results

Full size image

Conclusion

The bioconversion of glycerol to 1,3-propanediol is an intricate bioprocess, and we had a relatively mature system to represent microbial fermentation already. In this paper, we introduce a novel fractional model. Fractional derivatives are defined by integrals, and they are non-local operators. The calculation of the fractional derivative of a function at a given time contains information about all of the values of the function at earlier times. We believe that the dynamic behavior of a microbial batch culture does not depend only on their conditions at the current point in time, but also in their earlier time points. One of the advantages is that the fractional system can be used to model memory effects without the need for a series of ordinary differential equations involving a number of parameters. The structure of the fractional system is simpler than the previous fermentation model and bring us much convenience when dealing with constraint optimization problems. Further, according to the numerical results of the system, we can conclude that the fractional order model with identified parameters can describe the batch culture appropriately.