Introduction

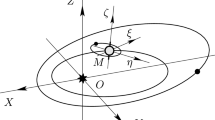
Let us briefly recall that the restricted three-body problem (R3BP) consists of two massive bodies (primaries) moving in orbits (circular or elliptic) around their common barycenter and a third body of negligible mass being influenced, but not influencing them. The elliptic R3BP (ER3BP) describes the three-dimensional motion of a particle under the gravitational attraction force of two finite bodies which revolve on elliptic orbits in a plane around their common center of mass. A typical example of the ER3BP is the motion of an asteroid, an artificial satellite or a space probe under the gravitational attraction of the Sun–Jupiter or the Earth–Moon systems. There exist five co-planar equilibrium points in the R3BP, three collinear with the primaries (collinear points), and two form equilateral triangles with the line (\(\xi \)-axis) joining the primaries. The collinear points are generally unstable; while the triangular points are conditionally stable [9, 12, 18, 78]. As a result of rotational motion, long and short periodic orbits exist around these points. The shapes, orientation and sizes of the orbits are determined by the eccentricities, inclination and the semi-major axes of the orbits. The three-body problem in general relativity has also been a subject of several studies [33, 53, 54].

The classical restricted three-body problem considers the bodies to be strictly spherical, but in the solar (e.g., Sun, Earth, Jupiter and Saturn), [24, 57, 58, 64, 82] and stellar (e.g., Achernar, Alfa Arae, Regulus, VFTS 102, Vega and Altair) systems, some planets, stars and their satellites (Moon, Charon) are sufficiently oblate. This justifies the inclusion of oblateness in the study of motion of celestial bodies. The oblateness or triaxiality of a body can produce perturbations-deviations in the two-body motion. The most striking example of perturbations arising from oblateness in the solar system is the orbit of the fifth satellite of Jupiter, Amalthea. This planet is so oblate and the satellite’s orbit is so small that its line of apsides advances about \(900^\mathrm{o}\) in a year [49]. The extremely fast rotation of stars produces an equatorial bulge due to centrifugal force [13, 15, 28, 46, 47, 79, 83]. Neutron stars and black dwarfs (the result of the cooling of white dwarfs) may due to their rapid rotation after formation also be considered oblate. On formation, a neutron star can rotate at a rate of nearly a thousand rotations per second [7, 8, 14, 20–22, 26, 27, 43, 50, 63]. The millisecond pulsar PSR B1937+21, spinning about 642 times a second and the pulsar PSR J1748-2446ad, spinning 716 times a second are some of the swiftest spinning pulsars [23]. It is notable that the effect of having an arbitrary shape is only important for close neighbors. For instance, the Earth’s gravitational field is the major controller of the orbit of an artificial Earth satellite [25, 29, 30, 32, 53–56]. Here the line of nodes and the perigee point move very rapidly under the force field arising from the oblateness of the Earth. This inspired several researchers (Elipe and Ferrer [17], Sharma et al. [66]) to include oblateness of the primaries in their studies of the R3BP. Sharma and Rao (1976) considered the primary in their investigation of triangular points as an oblate spheroid whose equatorial plane coincides with the plane of motion, and proved that the range of the mass parameter leading to stable solutions decreases due to oblateness. Taking both primaries as triaxial rigid bodies with one of the axes as axis of symmetry and its equatorial plane coinciding with the plane of motion, Elipe and Ferrer [17] examined three rigid bodies under central forces in the CRP and obtained collinear and triangular solutions, while Sharma et al. [66] described the stability of the equilibrium points when the bigger primary is a triaxial rigid body and a source of radiation and found that collinear points are unstable, whereas the triangular points are conditionally stable.

In addition, Sharma [62], Singh and Ishwar [68], Ishwar and Kushvah [35], Tsirogiannis et al. [77], AbdulRaheem and Singh [1, 2], Vishnu et al. [80], Mital et al. [48], Sahoo and Ishwar [61], Singh and Umar [69–72], Abouelmagd [3], Ammar [6] have included oblateness of one or both primaries in their communications. Taking account of the oblateness of the Earth, Ammar (2012) have conducted an analytic theory of the motion of a satellite and solved the equations of the secular variations in a closed form, while Abouelmagd [3] analyzed the effect of oblateness of the more massive primary up to \(\hbox {J}_{4}\) in the planar CR3BP and proved that the positions and stability of the triangular points are affected by this perturbation. The quadruple mass moment \(\hbox {J}_{2}\) of an aspherical body disturbs the motion of a satellite also at the Post-Newtonian level (Soffel et al. 1989), so also does a body’s octupolar mass moment \(\hbox {J}_{4}\). \(\hbox {J}_{4}\) has important effects particularly in the satellite’s secular perturbation and orbital precessions. These shifts are quite significant in a number of practical applications including global gravity field determination [38, 55] and fundamental physics in space [24–27, 73].

The orbits of most celestial and stellar bodies are elliptic rather than circular; as a result, the study of the elliptic restricted three-body problem (ER3BP) can have significant effects. When the primaries’ orbit is elliptic, a nonuniformly rotating-pulsating coordinate system is commonly used. This new coordinate system has the felicitous property that, the positions of the primaries are fixed; however, the Hamiltonian is explicitly time-dependent [76]. Such an oscillating coordinate system has been introduced by using the variable distance between the primaries as a unit of length of the system by which distances are divided. Several studies ([5, 40–42, 45, 60, 71–73, 84], Singh and Umar [74]) have examined the influence of the eccentricity of the orbits of the primary bodies with or without radiation pressure(s). Zimovshchikov and Tkhai [84] established the conditions of stability for the collinear and triangular points for various values of the eccentricity of the Keplerian orbits and the mass ratio of the primary bodies. Finally, Singh and Umar [70–72] considering both luminous primaries to be oblate spheroids as well, investigated the existence of triangular, collinear and the out of plane equilibrium points in the ER3BP respectively.

A vast number of researches ([10, 19, 37, 39, 51, 52, 66, 76], Sharma et al. 2003, 2007 and [59]) have been carried out on periodic orbits in the R3BP under various assumptions. The consideration of the primaries as either point masses or spherical in shape and with circular orbits may neglect a good number of practical problems. This is as a result of the fact that most celestial and stellar bodies are axisymmetric and their orbits are elliptic. The re-entry of artificial satellites and the minimization of station keeping have shown the importance of periodic orbits. The existence of two families of periodic motions near the Lagrangian solutions in the planar CR3BP was proved for arbitrary values of the parameter \(\upmu \) by Charlier [10] and Plummer [39], while Sarris [60] studied the families of symmetric-periodic orbits in the three-dimensional elliptic problem with a variation of the mass ratio \(\upmu \) and the eccentricity e. Khanna and Bhatnagar [37], Sharma et al. [66], Singh and Begha [67] have studied the long and short periodic orbits around the Lagrangian point(s). Also, Mital et al. [48] in examining periodic orbits, determined periodic orbits for different values of the mass parameter \(\upmu \), energy constant h, and oblateness factor [4, 59] explored the effect of the oblateness of Saturn on the regions of quasi-periodic motion around both primaries in the Saturn–Titan system, and combined effects of oblateness and radiation on periodic orbits in the circular framework of the restricted three-body problem respectively. The oblateness of the Earth and the Moon has continued to fascinate and intrigue many researchers [11, 16, 81]. It is a fundamental property of the Earth under stable rotation. Poincare surface section (PSS) was used by Winter [81] and Dutt and Sharma [16] to study the location and stability of periodic orbits and quasi-periodic motion, for the Earth–Moon system and they identified periodic solutions, quasi-periodic and chaotic regions in the CRTBP.

General relativity describes the gravitational field by curved space-time and introduces into the R3BP apart from the Newtonian gravitational potential a third force that attracts the particle slightly more strongly than the Newtonian gravity, especially at small radii. This third force causes the particle’s elliptical orbit to precess in the direction of the rotation. The R3BP is determined by the so called famous three-body problem. The motions of natural and artificial bodies in their orbits under the mutual gravitational fields of stars and of point-like objects fields similar to those in astrophysical scenarios constitute a two-body problem. This has resulted in three of the most famous and empirically investigated gravitomagnetic features; Lense-Thirring [44] effect, the gyroscope precession and the gravitomagnetic clock effect.

This paper investigates in the elliptic framework of the problem, the long and short periodic orbits around the triangular points when both primary bodies and the third body of infinitesimal mass are oblate spheroids. The analytic results obtained are applied to the Earth–Moon–Artificial satellite system.

The paper is organized as follows: “Equations of Motion” section provides the equations of motion for the system under investigation; “Periodic Orbits” section computes the long and short periodic orbits; and “Elliptic orbits” section examines the eccentricities, semi-major and semi-minor axes; while “Numerical Applications” sections are the numerical applications and conclusion respectively.

Equations of Motion

The equations of motion of an axisymmetric body (artificial satellite) in the vicinity of oblate primaries in the ER3BP are presented [73] as

$$\begin{aligned} \xi ^{{\prime }{\prime }}-2\eta ^{{\prime }}&= \varOmega _\xi ,\quad \eta ^{{\prime }{\prime }} +2\xi ^{{\prime }}=\varOmega _\eta , \quad \zeta ^{{\prime }{\prime }}=\varOmega _\zeta \end{aligned}$$
(1)
$$\begin{aligned} \varOmega&= (1-e^{2})^{-\frac{1}{2}}\,\left[ \frac{\xi ^{2}+\eta ^{2}}{2}+\frac{1}{n^{2}}\left\{ \frac{\left( {1-\mu }\right) }{r_1 }+\frac{\mu }{r_2}+\frac{\left( {1-\mu }\right) A}{2r_1^3 }+\frac{\mu A}{2r_2^3}\right. \right. \nonumber \\&\left. \left. +\frac{\left( {1-\mu }\right) A_1}{2r_1^3 }+\frac{\mu A_2}{2r_2^3} \right\} \right] , \end{aligned}$$
(2)

where

$$\begin{aligned} r_1^2&= (\xi +\mu )^{2}+\eta ^{2}+\zeta ^{2},\quad r_2^2 =(\xi +\mu -1)^{2}+\eta ^{2}+\zeta ^{2},\end{aligned}$$
(3)
$$\begin{aligned} n^{2}&= \frac{\left( {1+e^{2}} \right) ^{\frac{1}{2}}\left( {1+\frac{3A_1 }{2}+\frac{3A_2 }{2}} \right) }{a(1-e^{2})}=\frac{1}{a}\left( {1+\frac{3e^{2}}{2}+\frac{3A_1}{2}+\frac{3A_2}{2}}\right) . \end{aligned}$$
(4)

And \(\upmu \) is the ratio of the mass of the smaller primary to the sum of the masses of the primaries; \(0<\hbox {\textit{A}}_{ i}<<1\,(\hbox {{ i}}=1,\,2)\) and \(\hbox {\textit{A}}<<1\), are the factors characterizing oblateness of the primaries and the third body respectively; while n is the mean motion of the primaries; a and e are the semi-major axis and eccentricity of their orbits respectively. The prime represents differentiation w.r.t. the eccentric anomaly E.

Periodic Orbits

The triangular Lagrangian points \(L_{4,5}\,\left( {\xi _0,\pm \eta _0}\right) \) are given by [73]

$$\begin{aligned} \xi _0&= \frac{1}{2}-\mu +\frac{1}{2}\left( {A_1-A_2}\right) ,\nonumber \\ \eta _0&= \pm \left[ {a^{2/3}(1-e^{2}-A_1+A_1a^{-2/3}+Aa^{-2/3}-A_2 -\frac{1}{4}(1+2A_1-2A_2)}\right] ^{\frac{1}{2}}. \end{aligned}$$
(5)

We give these points a small displacement (x, y) and obtain the characteristic equation as [70]

$$\begin{aligned} \lambda ^{4}-\left( {\Omega _{\xi \xi }^0 +\Omega _{\eta \eta }^0 -4} \right) \lambda ^{2}+\Omega _{\xi \xi }^0\Omega _{\eta \eta }^0 -\left( {\Omega _{\xi \eta }^0}\right) ^{2}=0. \end{aligned}$$

The superscript 0 indicates that the partial derivatives are to be evaluated at the triangular points \(\left( {\xi _0,\pm \eta _0}\right) \). We substitute \(\hbox {\textit{a}}=1-\upalpha \), and neglect second and higher order terms and their products with \(\upalpha ,\,\hbox {\textit{A}},\,\hbox {\textit{A}}_{ i}\) and \(\hbox {\textit{e}}^{2}\) in evaluating these partial derivatives. The characteristic eqn. has pure imaginary roots in the interval \(0<\upmu <\upmu _\mathrm{c}\). Thus, the motion in this region is bounded and made up of two harmonic motions with frequencies \(\hbox {\textit{s}}_{1}\) and \(\hbox {\textit{s}}_{2}\) given by

$$\begin{aligned} x&= C_1 \cos s_1 E+ S_1 \sin s_1 E +C_2 \cos s_2 E + S_2 \sin s_2 E, \\ y&= {\overline{C}}_1 \cos s_1 E + {\overline{S}}_1 \sin s_1 E +{\overline{C}}_2 \cos s_2 E+ {\overline{S}}_2 \sin s_2 E, \end{aligned}$$

where

$$\begin{aligned} s_1&= \left[ {\frac{27\mu \left( {1-\mu }\right) }{4}+\frac{45}{4}\mu \left( {1-\mu }\right) e^{2}+3\mu \left( {1-\mu }\right) \alpha +9\mu \left( {1-\mu }\right) \left( {A+A_1+A_2}\right) }\right] ^{\frac{1}{2}},\nonumber \\ s_2&= \left[ 1-\frac{3}{4}e^{2}-\frac{3}{2}A-\frac{3(1-\mu )}{2}A_1 -\frac{3\mu }{2}A_2-\frac{9}{2}\mu \left( {1-\mu }\right) \left( {A+A_1+A_2}\right) \right. \nonumber \\&\left. -\frac{3}{2}\mu \left( {1-\mu }\right) \alpha - \frac{27\mu \left( {1-\mu } \right) }{8} {-\frac{45}{4}\mu \left( {1-\mu } \right) e} \right] , \end{aligned}$$
(6)

and

$$\begin{aligned} {\overline{C}}_i \!=\!\Gamma _i (2nS_i s_i \!-\!\Omega _{\xi \eta } C_i ); \quad {\overline{S}}_i \!=\!-\Gamma _i (2nC_i c_i \!-\!\Omega _{\xi \eta }^0 S_i ); \quad \Gamma _i \!=\!\frac{1}{S_i^2 +\Omega _{\eta \eta }^0 }\!>\!0, \quad i\!=\!1, 2 \end{aligned}$$

The terms \(C_1,S_1,{\overline{C}}_1\,\mathrm{and}\,{\overline{S}}_1\) are called the long period terms while \(C_2,S_2,{\overline{C}}_2\,\mathrm{and}\,{\overline{S}}_2\) the short period terms, while E is the eccentric anomaly.

Elliptic Orbits

The function \(\Omega \) around the triangular point \(\hbox {L}_{4}\) can be expressed as

$$\begin{aligned} \Omega =\Omega ^{0}+\frac{\Omega _{\xi \xi }^0 }{2}(x^{2})+\Omega _{\xi \eta }^0 (xy)+\frac{\Omega _{\eta \eta }^0 }{2}(y^{2})+0(x^{3}y^{3}), \end{aligned}$$
(7)

which is a quadratic form in x and y, indicating that the periodic orbits around \(\hbox {L}_{4}\) are elliptic and we write it as \(\Omega =Px^{2}+Qxy+Ry^{2}+L\), with

$$\begin{aligned} P&= \left[ {\frac{3}{8}+\frac{\alpha }{4}+\frac{9}{16}e^{2}+\left( {\frac{9}{8}-\frac{3\mu }{2}} \right) A_1 +\left( {\frac{3\mu }{2}-\frac{3}{8}} \right) A_2 } \right] ,\nonumber \\ R&= \left[ {\frac{9}{8}-\frac{\alpha }{4}+\frac{3}{16}e^{2}+\frac{3}{2}A+\frac{3}{8} (A_1 +A_2 )} \right] ,\nonumber \\ Q&= \pm \frac{\sqrt{3}}{2}\left[ \left( {\frac{3}{2}-3\mu } \right) +\left( {\frac{1}{2}-\frac{2\mu }{3}} \right) \alpha +\left( {\frac{5}{4}-\frac{5\mu }{2}} \right) e^{2}+\left( {1-2\mu } \right) A \right. \nonumber \\&+\left. \left( {\frac{5}{2}-2\mu } \right) A_1 -\left( {\frac{1}{2}+2\mu } \right) A_2 \right] ,\nonumber \\ L&= \left[ \frac{3}{2}+\frac{\mu }{2}(1-\mu )-\frac{1}{4}(3-\mu (1-\mu ))e^{2}-\alpha -2A-\left( {1+\frac{\mu }{2}} \right) A_1\right. \nonumber \\&\left. -\left( {\frac{3}{2}-\frac{\mu }{2}} \right) A_2 \right] . \end{aligned}$$
(8)

Using the transformation \(x={\overline{x}}\cos \psi -{\overline{y}}\sin \psi ;y={\overline{x}}\sin \psi +{\overline{y}}cos\psi \) by introducing the variables \({\overline{x}}\,and\,{\overline{y}}\), we obtain what is equivalent to a rotation of the coordinate system x, y through an angle \(\uppsi \). The new quadratic form is thus \(\Omega ={\overline{P}}x^{2}+{\overline{Q}}xy+{\overline{R}}y^{2}+{\overline{L}}\).

$$\begin{aligned} \Omega&= \left[ {\frac{3}{2}+\frac{\mu }{2}(1-\mu )-\frac{1}{4}(3-\mu (1-\mu ))e^{2}-\alpha -2A-\left( {1+\frac{\mu }{2}} \right) A_1 -\left( {\frac{3}{2}-\frac{\mu }{2}} \right) A_2 } \right] \\&+\left( {P\cos ^{2}\psi +RSin^{2}\psi +Q\frac{\sin 2\psi }{2}} \right) {\overline{x}}^{2}+\left( {Q\cos 2\psi -P\sin 2\psi +R\sin 2\psi } \right) {\overline{x}} {\overline{y}}\\&+\left( {P\sin ^{2}\psi -Q\frac{\sin 2\psi }{2}+R\cos ^{2}\psi } \right) {\overline{y}}^{2}, \end{aligned}$$

where

$$\begin{aligned} {\overline{P}}&= \left[ {\frac{3}{8}+\frac{\alpha }{4}+\frac{9}{16}e^{2} \pm \left( {\frac{9}{8}-\frac{3\mu }{2}} \right) A_1 +\left( {\frac{3\mu }{2}-\frac{3}{8}} \right) A_2 } \right] \cos ^{2}\psi ,\nonumber \\&\pm \frac{\sqrt{3}}{2}\left[ \left( {\frac{3}{2}-3\mu } \right) +\left( {\frac{1}{2}-\frac{2\mu }{3}} \right) \alpha +\left( {\frac{5}{4}-\frac{5\mu }{2}} \right) e^{2}+2\left( {1-2\mu } \right) A\right. \nonumber \\&+\left. \left( {\frac{5}{2}-2\mu } \right) A_1 +\left( {-\frac{1}{2}-2\mu } \right) A_2 \right] \frac{\sin 2\psi }{2}\nonumber \\&+\left[ {\frac{9}{8}-\frac{\alpha }{4}+\frac{3}{16}e^{2}+\frac{3}{2}A+\left( {\frac{3}{8}} \right) (A_1 +A_2 )} \right] \sin ^{2}\psi ,\nonumber \\ {\overline{Q}}&= \left[ \left\{ \pm \frac{\sqrt{3}}{2}\left[ \left( {\frac{3}{2}-3\mu } \right) +\left( {\frac{1}{2}-\frac{2\mu }{3}} \right) \alpha +\left( {\frac{5}{4}-\frac{5\mu }{2}} \right) e^{2}\right. \right. \right. \nonumber \\&\left. \left. \left. +\left( {1-2\mu }\right) A\left( {\frac{5}{2}-2\mu }\right) A_1+\left( {-\frac{1}{2}-2\mu }\right) A_2\right] \right\} \cos 2\psi \right. \nonumber \\&\left. -\left[ \left\{ \frac{3}{8}+\frac{\alpha }{4}+\frac{9}{16}e^{2}+\frac{3}{2}A+\left( {\frac{9}{8}-\frac{3\mu }{2}} \right) A_1 +\left( {\frac{3\mu }{2}-\frac{3}{8}} \right) A_2 \right\} \right. \right. \nonumber \\&+\left. \left. \left\{ \frac{9}{8}-\frac{\alpha }{4}+\frac{3}{16}e^{2}+\frac{3}{2}A+\left( {\frac{3}{8}} \right) (A_1 +A_2 )\right\} \right] s\hbox {in}2\psi \right] ,\nonumber \\ {\overline{R}}&= \left[ \left\{ \frac{3}{8}+\frac{\alpha }{4}+\frac{9}{16}e^{2}+\left( {\frac{9}{8}-\frac{3\mu }{2}} \right) A_1 +\left( {\frac{3\mu }{2}-\frac{3}{8}} \right) A_2 \right\} \sin ^{2} \right. \psi \nonumber \\&\left. -\left\{ \pm \frac{\sqrt{3}}{2}\left[ \left( {\frac{3}{2}-3\mu } \right) +\left( {\frac{1}{2}-\frac{2\mu }{3}} \right) \alpha +\left( {\frac{5}{4}-\frac{5\mu }{2}} \right) e^{2}\right. \right. \right. \nonumber \\&\left. \left. +\left( {1-2\mu } \right) A \left( {\frac{5}{2}-2\mu } \right) A_1 +\left( {-\frac{1}{2}-2\mu }\right) A_2\right] \right\} \frac{\sin 2\psi }{2}\nonumber \\&+\left. \left[ \frac{9}{8}-\frac{\alpha }{4}+\frac{3}{16}e^{2}+\frac{3}{2}A+\left( {\frac{3}{8}} \right) (A_1 +A_2 ) \right] \cos ^{2}\psi \right] ,\nonumber \\ {\overline{L}}&= \left[ \frac{3}{2}+\frac{\mu }{2}(1-\mu )-\frac{1}{4}(3-\mu (1-\mu ))e^{2}-\alpha -2A-\left( {1+\frac{\mu }{2}} \right) A_1\right. \nonumber \\&\left. -\left( {\frac{3}{2}-\frac{\mu }{2}} \right) A_2\right] . \end{aligned}$$
(9)

Now, we choose \(\uppsi \) such that the term containing xy in \(\Omega \) vanishes, that is \({\overline{Q}}=0\), which provides us with

$$\begin{aligned} \tan 2\psi =\frac{\sin 2\psi }{\cos 2\psi }=\frac{H}{G}, \end{aligned}$$

where

$$\begin{aligned}&H=\left[ \left\{ \pm \frac{\sqrt{3}}{2}\left[ \left( {\frac{3}{2}-3\mu } \right) +\left( {\frac{1}{2}-\frac{2\mu }{3}} \right) \alpha +\left( {\frac{5}{4}-\frac{5\mu }{2}} \right) e^{2}+\left( {1-2\mu } \right) A\right. \right. \right. \\&\,\,\,\,\quad \left. \left. \quad +\left( {\frac{5}{2}-2\mu }\right) A_1 -\left( {\frac{1}{2}+2\mu } \right) A_2 \right\} \right] \\&G=\left[ \frac{3}{4}-\frac{\alpha }{2}-\frac{3}{8}e^{2}+\frac{3}{2}A+\left( {-\frac{3}{4}+\frac{3\mu }{2}} \right) A_1 +\left( {\frac{3}{4}-\frac{3\mu }{2}} \right) A_2 \right] . \end{aligned}$$

Eccentricities of the Ellipses

The function around the triangular point is given by Eq. (7), but the Jacobian constant \(\hbox {C}=2\Omega \) implies that

$$\begin{aligned} C&= \left\{ {3+\mu (1-\mu )-2\alpha -4A-\left( {2+\mu } \right) A_1 -(3-\mu )A_2 -\frac{3}{2}e^{2}+\frac{\mu }{2}\left( {1-\mu } \right) e^{2}} \right\} \\&+\left\{ {\frac{3}{4}+\frac{\alpha }{2}+\frac{9}{8}e^{2}+\left( {\frac{9}{4}-3\mu } \right) A_1 +\left( {3\mu -\frac{3}{4}} \right) A_2 } \right\} x^{2}\\&+\left\{ {\frac{9}{4}-\frac{\alpha }{2}+\frac{3}{8}e^{2}+\frac{3}{2}A+\left( {\frac{3}{4}} \right) (A_1 +A_2 )} \right\} y^{2}\\&\times \left\{ {\pm \sqrt{3}\left[ {\left( {\frac{3}{2}-3\mu } \right) +\left( {\frac{1}{2}-\frac{2\mu }{3}} \right) \alpha +\left( {\frac{5}{4}-\frac{5\mu }{2}} \right) e^{2}+\left( {1-2\mu } \right) A} \right. } \right. \\&+\left. {\left. {\left. {\left( {\frac{5}{2}-2\mu } \right) A_1 +\left( {-\frac{1}{2}-2\mu } \right) A_2 } \right] } \right\} } \right| xy\\&=ax^{2}+bxy+cy^{2}+d. \end{aligned}$$

The determinant of which is

$$\begin{aligned} =\left[ {\frac{27\mu \left( {1-\mu } \right) }{4}+\frac{45}{4}\mu \left( {1-\mu } \right) e^{2}+3\mu \left( {1-\mu } \right) \alpha +9\mu \left( {1-\mu } \right) \left( {A+A_1 +A_2 } \right) } \right] . \end{aligned}$$

The characteristic equation of the associated matrix is thus

$$\begin{aligned}&\lambda ^{2}-3\left( {1+\frac{e^{2}}{2}+A+(1-\mu )A_1 +\mu A_2 } \right) \lambda +\frac{27}{4}\mu (1-\mu )+3\mu (1-\mu )\alpha \nonumber \\&\quad +\frac{45}{4}\mu (1-\mu )e^{2} +9\mu (1-\mu )(A+A_1 +A_2 )=0. \end{aligned}$$
(10)

Its roots are

$$\begin{aligned} \lambda _1&= 3+3A+3(1-\mu )A_1 +3\mu A_2 -3\mu (1-\mu )(A+A_1 +A_2 )-\mu (1-\mu )\alpha +\frac{3}{2}e^{2},\\&-\frac{9}{4}\mu (1-\mu )-\frac{15}{4}\mu (1-\mu )e^{2}\\ \lambda _2&= \frac{9}{4}\mu (1-\mu )+\frac{15}{4}\mu (1-\mu )e^{2}+\mu (1-\mu )\alpha +3\mu (1-\mu )(A+A_1 +A_2 ). \end{aligned}$$

The eccentricities of the ellipses are given by [76]

$$\begin{aligned} e_i=(1-\phi _i^2)^{\frac{1}{2}}, \quad \phi _i=\frac{2s_i}{s_i^2+{\overline{\lambda }}} \end{aligned}$$

where \({\overline{\lambda }}\) is one of the roots of Eqn. (10). For \(\hbox {i}=1\), we have

$$\begin{aligned} \phi _1^2&= 3\mu (1-\mu )-9\mu ^{2}(1-\mu )^{2}+\frac{4}{3}\mu (1-\mu )\alpha -8\mu ^{2}(1-\mu )^{2}\alpha +2\mu (1-\mu )e^{2}\nonumber \\&-\,30\mu ^{2}(1-\mu )^{2}e^{2} -6\mu (1-\mu )A-6\mu (1-\mu )^{2}A_1 -6\mu ^{2}(1-\mu )A_2 \nonumber \\&+\,4\mu (1-\mu )(A+A_1 +A_2 )-24\mu ^{2}(1-\mu )^{2}(A+A_1 +A_2 ),\nonumber \\ \phi _2^2&= \frac{1}{4}-\frac{3}{8}e^{2}-\frac{9}{16}\mu (1-\mu )-\frac{243}{64}\mu ^{2}(1-\mu )^{2}-\frac{\mu }{4}(1-\mu )\alpha -\frac{27\mu ^{2}}{8}(1-\mu )^{2}\alpha \nonumber \\&-\,\frac{57}{32}\mu (1-\mu )e^{2} \frac{405}{32}\mu ^{2}(1-\mu )e^{2} -\frac{3}{4}A-\frac{27}{16}\mu (1-\mu )A\nonumber \\&-\,\frac{3}{4}\mu (1-\mu )(A+A_1 +A_2) -\frac{81}{8}\mu ^{2}(1-\mu )^{2}(A+A_1 +A_2 )\nonumber \\&-\,\frac{3(1-\mu )}{4}A_1 -\frac{27}{16}\mu (1-\mu )^{2}A_1 -\frac{3\mu }{4}A_2 -\frac{27}{16}\mu ^{2}(1-\mu )A_2. \end{aligned}$$
(11)

And therefore

$$\begin{aligned} e_1&= 1-\frac{3}{2}\mu (1-\mu )+\frac{9}{2}\mu ^{2}(1-\mu )^{2}-\frac{2}{3}\mu (1-\mu )\alpha +4\mu ^{2}(1-\mu )^{2}\alpha +3\mu (1-\mu )A,\nonumber \\&-2\mu (1-\mu )(A+A_1 +A_2 ) +3\mu (1-\mu )^{2}A_1 +3\mu ^{2}(1-\mu )A_2\nonumber \\&+12\mu ^{2}(1-\mu )^{2}(A+A_1 +A_2 )-\mu (1-\mu )e^{2}+15\mu ^{2}(1-\mu )^{2}e^{2},\nonumber \\ e_2&= \pm \frac{\sqrt{3}}{2}\left[ 1+\frac{e^{2}}{4}+\frac{3}{8}\mu (1-\mu )+\frac{81}{32}\mu ^{2}(1-\mu )^{2}+\frac{\mu }{6}(1-\mu )\alpha +\frac{9}{4}\mu ^{2}(1-\mu )^{2}\alpha \right. \nonumber \\&\left. +\frac{19}{16}\mu (1-\mu )e^{2}+ \frac{135}{16}\mu ^{2}(1-\mu )e^{2}+\frac{\mu }{2}(1-\mu )(A+A_1 +A_2 )\right. \nonumber \\&\left. +\frac{27}{4}\mu ^{2}(1-\mu )^{2}(A+A_1 +A_2 )+\frac{(1-\mu )}{2}A_1+ \frac{9}{8}\mu (1-\mu )^{2}A_1 +\frac{9}{8}\mu ^{2}(1-\mu )A_2\right. \nonumber \\&\left. +\frac{\mu }{2}A_2 +\frac{A}{2}+\frac{9}{8}\mu (1-\mu )A \right] . \end{aligned}$$
(12)
Table 1 Relevant orbital and physical parameters of the Earth and Moon with resulting GL0660B solution from Grail primary mission
Full size table

Semi-major and Semi-minor Axes

The semi-major and semi-minor axes of the periodic orbits are given by

$$\begin{aligned} a_i=\left( {\xi _0^2+\frac{\eta _0^2}{\phi _i^2}}\right) ^{\frac{1}{2}}\quad \mathrm{and}\quad b_i=\left( {\phi _i^2\xi _0^2+\eta _0^2}\right) ^{\frac{1}{2}}(i=1,2) \end{aligned}$$

respectively. Now, using Eqs. (5) and (6), we obtain

$$\begin{aligned} a_1&= \frac{\sqrt{5}}{2}\left[ {1+\frac{1}{10\mu }-\frac{2}{5}\mu (1-\mu )-\frac{3}{5}\mu \left( 1-\frac{\mu }{2}\right) -\frac{2}{45}\left( {\frac{(1-\mu )}{\mu }+\frac{2(1+\mu )}{\mu }} \right) \alpha } \right. \nonumber \\&-\,\frac{(1-\mu )}{15\mu }e^{2}\!+\!\frac{3}{5}(1-\mu )^{2}e^{2}\!-\! \frac{2}{15\mu }(\mu \! +\!1)e^{2}\!+\!\left( {\frac{(1-\mu )}{15\mu }\!+\!\frac{2(1\!+\!\mu )}{15\mu }\!+\!\frac{2(1-\mu )^{2}}{5}} \right) A\nonumber \\&+\,\frac{2}{5}\left( {\mu -\frac{1}{2}} \right) (A_1 -A_2 )-\left( {\frac{(1+\mu )}{15\mu }+\frac{(1-\mu )^{2}}{5}} \right) (A_1 +A_2 )\nonumber \\&+\left( {\frac{4(1-\mu )^{2}}{5}-\frac{2(1-\mu )}{15\mu }} \right) (A+A_1 +A_2 )\left. {+\frac{(1-\mu )^{2}}{5\mu }A_1 +\frac{(1-\mu )}{5}A_2 } \right] ,\nonumber \\ a_2&= \frac{\sqrt{13}}{2}\left[ {1+\frac{23}{26}\mu (1-\mu )+\frac{729}{104}\mu ^{2}(1-\mu )^{2}-\frac{16}{39}\alpha -\frac{6\mu }{13}(1-\mu )\alpha } \right. \nonumber \\&+\,\frac{81}{13}\mu ^{2}(1-\mu )^{2}\alpha +\frac{e^{2}}{13} +\frac{99}{52}\mu (1-\mu )e^{2}+\frac{1215}{52}\mu ^{2}(1-\mu )e^{2}\nonumber \\&+\left( {2+\frac{117}{26}\mu (1-\mu )} \right) A+\left( {\frac{18(1-\mu )}{13}+\frac{81\mu (1-\mu )^{2}}{26}} \right) A_1\nonumber \\&+\left( {\frac{18\mu }{13}+\frac{81\mu ^{2}(1-\mu )}{26}} \right) A_2 +\left( {\frac{18\mu (1-\mu )}{13}+\frac{243\mu ^{2}(1-\mu )^{2}}{13}} \right) (A+A_1 +A_2 )\nonumber \\&-\left. {\left( {\frac{4}{13}+\frac{9}{13}\mu (1-\mu )} \right) (A_1 +A_2 )} \right] , \end{aligned}$$
(13)

and

$$\begin{aligned} b_1&= \frac{\sqrt{3}}{2}\left[ {1+\mu (1-\mu )-7\mu ^{2}(1-\mu )^{2}+12\mu ^{3}(1-\mu )^{3}} \right. \nonumber \\&-\left( {\frac{4}{3}-\frac{2}{3}\mu (1-\mu )+\frac{38}{3}\mu ^{2}(1-\mu )^{2}-40\mu ^{3}(1-\mu )^{3}} \right) e^{2}\nonumber \\&-\left( {\frac{8}{9}-\frac{4}{9}\mu (1-\mu )+\frac{40}{9}\mu ^{2}(1-\mu )^{2}-\frac{32}{3}\mu ^{3}(1-\mu )^{3}} \right) \alpha \nonumber \\&+\left( {\frac{4}{3}-2\mu (1-\mu )+8\mu ^{2}(1-\mu )^{2}} \right) A -\left( {\frac{2}{3}+2\mu (1-\mu )^{2}-8\mu ^{2}(1-\mu )^{3}} \right) A_1\nonumber \\&-\left( {\frac{2}{3}+2\mu ^{2}(1-\mu )-8\mu ^{3}(1-\mu )^{2}} \right) A_2 +\mu (1-\mu )\left( {4\mu -2} \right) \left( {1-3\mu (1-\mu )} \right) \nonumber \\&\left. \times {(A_1 \!-\!A_2 )\!+\!\left( \mu (1\!-\!\mu )\left( \frac{4}{3}\!-\!\frac{40}{3}\mu (1\!-\!\mu )\!+\!32\mu ^{2}(1-\mu )^{2}\right. \right) (A+A_1 +A_2 )} \right] ^{\frac{1}{2}},\nonumber \\ b_2&= \frac{\sqrt{13}}{4}\left[ {1-\frac{25}{52}\mu (1-\mu )-\frac{99}{208}\mu ^{2}(1-\mu )^{2}+\frac{243}{52}\mu ^{3}(1-\mu )^{3}-} \right. \frac{8}{13}(A_1 +A_2 )\nonumber \\&-\,\frac{1}{13}\left( {\frac{32}{3}+\frac{19}{2}\mu ^{2}(1-\mu )^{2}+\mu (1-\mu )-54\mu ^{3}(1-\mu )^{3}} \right) \alpha \nonumber \\&-\,\frac{1}{13}(4\mu -2)\left( {1-\frac{9}{4}+\frac{243}{16}\mu (1-\mu )} \right) \mu (1-\mu )(A_1 -A_2 )\nonumber \\&-\,\frac{1}{13}\left( {\frac{35}{2}+\frac{9}{8}\mu (1-\mu )+\frac{177}{8}\mu ^{2}(1-\mu )^{2}-\frac{405}{2}\mu ^{3}(1-\mu )^{3}} \right) e^{2}-\frac{3}{13}\mu (1-\mu )\nonumber \\&\times \left( {1+\frac{19}{2}\mu (1-\mu )-54\mu ^{2}(1-\mu )^{2}} \right) (A+A_1 +A_2 )\nonumber \\&+\left. {\frac{3}{13}\left( {\frac{13}{3}A-(1-\mu )A_1 -\mu A_2 } \right) } \right] ^{\frac{1}{2}}. \end{aligned}$$
(14)

Numerical Applications

Following [73] (in which double pulsars were applied to the collinear and triangular points of the axisymmetric bodies in the ER3BP under consideration), we use the relevant orbital and physical parameters of the Earth–Moon system given in Table 1 to compute the frequencies of the long and short periodic orbits, their eccentricities, semi-major and semi-minor axes by the aid of Eqs. (6), (10), (11)& (12) and present them in Table 3 for some assumed oblateness of an artificial satellite, where the mass ratio of the Earth–Moon–Satellite system \(\upmu =0.0121537\). The Earth’s global gravity field has after nearly half a century of precise orbit determination of dozens of geodesy-satellite orbit around the Earth been solved to high harmonic degrees. In one of the most recent global Earth’s gravity solutions, we present the results of [31] in Table 2 for \(\ell =2,\,3,\,4,\,5,\,6,\,7\) from the GOCE/GRACE-base solution GOCO01S [36] where \(J_{\ell }=-\sqrt{(2\ell +1)C}_{\ell ,0}\), with C as the normalized Stokes coefficient and \(\sigma {\overline{C}}_{\ell ,0}\) the formal statistical errors. And also in Table 1 are the solutions for the Moon’s GM degree 2 and 3 GRAIL PM, normalized without permanent tide (with bar) and unnormalized (without bar) [38].

Table 2 Zonal harmonics from the GOCE/GRACE-base solution GOCO01S
Full size table
Table 3 Frequencies of the long and short periods, the eccentricities, semi-major and semi-minor axes of the Earth–Moon system
Full size table

Conclusions

By considering the primaries and the third body as oblate spheroids moving in elliptic orbits around their common barycenter, the expressions for the frequencies of the long and short periods around the triangular points with their orientations, eccentricities, semi-major and semi-minor axes have been obtained. They have been found to be influenced by the eccentricity of the orbits, oblateness and semi-major axis of the primaries and of the third body.

In a numerical exploration, the effect of oblateness of an artificial satellite in orbit around the Earth–Moon system is investigated. Table 3 shows clearly the effect of oblateness of an artificial satellite on the long and short periods around the Earth–Moon system. The frequency of the long period increases with increase in oblateness while that of the short period decreases. This agrees with [2] in the circular case with the absence of small perturbations in the Coriolis and centrifugal forces in their study. In the circular case \((\hbox {e}=0)\), our results also validate (Sharma et al. 2001, [34]) when the smaller primary is non-luminous and the bigger is spherical in shape.

Equation (10) gives the eccentricities of the long and short periods; they increase with increase in oblateness of third body (Table 3). The eccentricity of the orbits and the effect of oblateness of the satellite are shown graphically in Figs. 1, 2, 3, 4, 5, 6, 7, 8 for the Earth–Moon system. We see reduction in the sizes of the periodic orbits with increase in oblateness in this axisymmetric ER3BP. In the absence of these perturbations, the results are in accordance with [76]. An interesting study which could yield significant results is the consideration of misaligned bulges of the primaries, this we shall treat in future.

Fig. 1
figure 1

Long periodic orbit around \(\hbox {L}_{4}\) of the Earth–Moon system for zero oblateness

Full size image
Fig. 2
figure 2

Short periodic orbit around \(\hbox {L}_{4}\) of the Earth–Moon system for zero oblateness

Full size image
Fig. 3
figure 3

Long periodic orbit around \(\hbox {L}_{4}\) of the Earth–Moon system for satellite oblateness \(\hbox {A}=0.05\)

Full size image
Fig. 4
figure 4

Short periodic orbit around \(\hbox {L}_{4}\) of the Earth–Moon system for satellite oblateness \(\hbox {A}=0.05\)

Full size image
Fig. 5
figure 5

Long period around \(\hbox {L}_{4}\) of the Earth–Moon system for satellite oblateness \(\hbox {A}=0.09\)

Full size image
Fig. 6
figure 6

Short periodic orbit around \(\hbox {L}_{4}\) of the Earth–Moon system for satellite oblateness \(\hbox {A}=0.09\)

Full size image
Fig. 7
figure 7

Effect of increasing oblateness [0, 0.05, 0.1] of the satellite on the short periodic orbit around \(\hbox {L}_{4}\) of the Earth–Moon system

Full size image
Fig. 8
figure 8

Effect of increasing oblateness [0, 0.02, 0.04] of the satellite on the short periodic orbit around \(\hbox {L}_{4}\) of the Earth–Moon system

Full size image