1 Introduction

Over the last two decades the role of hemodynamics in the progression of atherosclerosis disease has been an interesting topic of study in fluid mechanics. Atherosclerosis occurs due to deposition of lipids and accumulation of macrophages beneath the endothelial layer of the artery. This reduces(stenosis) the lumen area of the artery which may lead to increases in pressure and blood velocity across the stenosis in large as well as in medium sized arteries [17]. Computational studies show that a recirculation zone (or flow separation zone) occurs downstream of the stenosis, and the size of the zone depends on percentage stenosis and Reynolds number [22]. Recirculation zones are characterized by low wall shear stress, and low wall shear stress is reported to result in an atherogenic phenotype [13]. It is reported that multiple stenosis may occur downstream of single arterial stenosis [24] and, in such cases, the severity of the primary stenosis most affects the pressure gradient across the artery [8]. Thus, the growth of atherosclerotic plaques depends on hemodynamic factors at downstream of the stenosis such as wall shear stress and flow streamlines which are disturbed by primary stenosis [18]. The growth- whether it is in the flow direction,i.e., by increasing length of stenosis, or in the direction normal to flow,i.e., by increasing radius or percentage stenosis- depends on the size and nature of recirculation behind stenosis. It is difficult to predict the progression of stenosis using the knowledge of hemodynamic factors because, thus far, there is no formula for the same. Prior to developing a formula/equation, it is essential to determine what aspects of a single stenosis influence the flow and wall shear stress downstream, and also whether stenosis multiplicity will affect these variables. We do so in this article using computational simulations to assess the effect of multiple stenosis in pulsatile flow.

Fig. 1
figure 1

Schematic diagram of stenosed channel

Full size image
Fig. 2
figure 2

Transformation of physical into computational domain

Full size image

Blood flow through an artery with single or double stenosis have been studied using computations by many authors. Early studies used the Navier-Stokes model (aka Newtonian model) to describe the rheology of blood, and we review those first. Computational studies on the steady flow of Newtonian fluid at Re < 200 in a rigid-walled pipe with axisymmetric stenosis were performed by [6] and validated using available experimental data; An approximate solution is given in [12]. Blood flow in the arteries is unsteady in nature and is predominantly pulsatile. For pulsatile flow in a rigid-walled pipe with a large axisymmetric stenosis (75 % occlusion), [35] used finite-element method(FEM) and showed the presence of recirculation which moved from downstream of the stenosis to upstream of the stenosis as the pressure gradient varied from positive to negative. The effect of double stenoses with gap was studied in [11] for Re of 5–200, and concluded that the value of maximum wall vorticity at the second constriction is always less than that at the first constriction. FEM with predictor corrector time-marching was used for pulsatile flow in a rigid pipe with a mild axisymmetric stenosis, and the effect of varying stenosis percentage, stenosis length, Reynolds number (Re), and Womersley number (Wo) on flow variables was documented in [34]. The effect of stenosis morphology on three-dimensional (3-D) pulsatile flow in severely stenosed (≤75 %) vessels was investigated by [31]. They reported that, along with percentage stenosis, surface irregularity and stenosis aspect ratio also affect the plaque stresses. A flexible elastic wall for the pipe was incorporated in [7], and performed simulation of 3-D pulsatile flow that showed collapse of the wall. Steady flow in a rigid-walled pipe with double stenosis, and the impact of the second stenosis and gap between stenosis on pressure drop, wall shear stress, and reattachment length were studied in [14].

It is well known that blood exhibits non-Newtonian characteristics like shear-thinning [5] and viscoelasticity [33]. Models for the flow of non-Newtonian fluid through stenosed pipes have been widely studied computationally. The models considered include Casson [4] and Herschel-Bulkley [3, 29]: these concluded that flow is affected both by percentage stenosis and wall flexibility. Flow of power-law model in a stenosed pipe was simulated by [16], and reported that irregular stenosis experienced greater wall shear stress than cosine shape stenosis (for a given percentage stenosis). Further, studies with shear-thinning fluid models consistently reported flow separation and recirculation downstream of stenosis: [30] for power-law model, and [19] for Carreau-Yasuda model. The steady flow of a shear-thinning Oldroyd-B model (proposed in [36]) in a rigid-walled mildly stenosed pipe was simulated by [26]. Simulations for various shear-thinning Oldroyd-B type models in a rigid-walled stenosed pipe were performed in [2]. They observed significant differences arising in the results, compared to Newtonian fluid, due to the shear-thinning viscosity and the relaxation time.

Fig. 3
figure 3

Variation of peak WSS with %stenosis and \(L_0\) (single stenosis, Re = 4000)

Full size image
Fig. 4
figure 4

Stream lines for steady flow in stenosed channel; \(L_0=1.5,\) Re = 4000

Full size image

Although more advanced constitutive models to describe blood have since been developed in [1], and [23], we will use the shear-thinning relation proposed by Yeleswarapu [36] as a first step in our numerical studies of flow in double-stenosed channel. In pulsatile flow in a cylindrical pipe, Yeleswarapu’s shear-thinning viscoelastic model gives higher flow rate amplitude, and an extra phase-lag, as compared to the classical Oldroyd-B model [25]. A Marker and-Cell finite difference scheme [9] is used to solve the pressure and momentum balance equations for steady flow (\(Re \le 100\)) using Yeleswarapu’s model in a rigid-walled pipe with a cosine-shaped stenosis: Results were reported for the axial variation of wall shear stress, and the effect of stenosis size (≤33 %) and Re (≤100) on peak wall shear stress. We showed that shear-thinning fluid using Yeleswarapu relation will predict higher shear stress than Newtonian fluid in [22] and [21]: this extended the study of the shear-thinning model from Re < 150 and stenosis <10 %, done in [15], to Re of 4000 and stenosis of 25 %.

The present work is a computational study of 2D steady and pulsatile flow of blood in a rigid-walled channel with double stenosis. We study flow with double stenosis, and document the influence of stenosis size, length, and gap between double stenosis on wall shear stress: this is done in anticipation of developing a purely mechanical model for atherosclerosis growth. Blood is modeled as a shear-thinning fluid using the relation proposed by [36]. Governing equations are formulated in terms of stream function and vorticity, and solved using full-multi grid algorithm for a finite-difference formulation. We consider Re as 4000 which is characteristic of blood flow in the human aorta, and consider stenosis of size (percentage) ≤25 %. We compare the results from shear-thinning and Newtonian fluid for the pulsatile flow case with double stenosis.

Fig. 5
figure 5

Variation of WSS with % stenosis (double stenosis, Re = 4000)

Full size image
Fig. 6
figure 6

WSS (at primary stenosis) versus \(L_0\) & \(L_g\) for Re = 4000

Full size image

2 Problem formulation

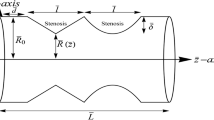
2D-steady and pulsatile blood flow through square channel with double stenosis is considered in a cartesian co-ordinate system (x, y). The hydraulic diameter of the channel is equal to the hydraulic diameter of a cylindrical pipe (in our case, human aorta), and the Reynolds number is set to 4000, so that the results from these simulations can be compared with flow in human aorta. We assume flow is fully developed at the entrance and center line (\(y=0\)) is considered as the plane of symmetry. The complete geometry of the flow domain is given in Fig. 1. The shape of the stenosis is described by a cosine function. Thus the function of the wall, f(x), is given by:

$$\begin{aligned} f(x)&= 1 ;\quad x\le (L_1-L_0), \end{aligned}$$
(1)
$$\begin{aligned} f(x)&= 1-{1 \over 2} h \left[ {1+\hbox{cos}{ \pi (x-L_1) \over L_0}} \right] ;\quad (L_1-L_0) < x < (L_1+L_0), \end{aligned}$$
(2)
$$\begin{aligned} f(x)&= 1 ;\quad (L_1+L_0) \le x \le (L_2-L_0), \end{aligned}$$
(3)
$$\begin{aligned} f(x)&= 1-{1 \over 2} h \left[ {1+\hbox{cos}{ \pi (x-L_2) \over L_0}} \right] ;\quad (L_2-L_0) < x < (L_2+L_0), \end{aligned}$$
(4)
$$\begin{aligned} f(x)&= 1 ;\quad x\ge (L_2+L_0). \end{aligned}$$
(5)

In our simulations, we set the half-width of the channel to be H = 0.0125 m, which is the same as the radius of the human aorta [17]. The length of the section is set to be L = 30H. \(L_1 = 11.0\)H is the location of the peak in first stenosis. In our simulations we vary the the percentage stenosis (100 h/H), and length of stenosis \(L_0\) (for given percentage) = 1H, 1.5H, 2H for single and double stenosis. For the case of double stenosis, we also vary the gap between stenosis \(L_g\) = 0H, 2H, 4H. The location of peak in secondary stenosis \(L_2\) is calculated as \(L_2=L_1+2L_0+L_g\).

Fig. 7
figure 7

WSS versus time for \(L_0=1\) , \(L_g=4L_0\) and Re = 4000

Full size image
Fig. 8
figure 8

% difference of mean WSS versus Wo (\(L_0=1\) , \(L_g=4L_0\) and Re = 4000)

Full size image

2.1 Model for blood

Blood is modeled as an incompressible, homogeneous fluid which exhibits shear thinning properties. The model is described by:

$$\begin{aligned} \mathbf {\tau } = -p \mathbf {1} + \mu _d ({\dot{\gamma }} )[\triangledown \mathbf {v} + (\triangledown \mathbf {v})^T], \end{aligned}$$
(6)

where 1 is the unit tensor, and v is the velocity field. The shear-rate is given by:

$$\begin{aligned} \dot{\gamma } = \left[ \frac{1}{2} tr[\triangledown \mathbf {v} + (\triangledown \mathbf {v})^T]^2 \right] ^\frac{1}{2}. \end{aligned}$$
(7)

The shear dependent dynamic viscosity of blood is \(\mu _d \) and is a function of \( \dot{\gamma }\) , as described in [36]:

$$\begin{aligned} \mu _d ( \dot{\gamma }) = \eta _\infty +\left( \eta _0 - \eta _\infty \right) {\left[ {1+ \hbox{ln}(1+ \Lambda \dot{\gamma })}\right] \over 1+\Lambda \dot{\gamma } }. \end{aligned}$$
(8)

The above equation has been experimentally proved to give good results for blood flow in rigid-walled pipes [37]. It contains three parameters: \(\Lambda = 14.81\) sec denotes the shear-thinning index, \(\eta _0 = 0.0736\) Pas denotes the asymptotic zero shear-rate viscosity as \(\dot{\gamma } \rightarrow \) 0, and \(\eta _\infty = 0.005\) Pas denotes the asymptotic infinite shear-rate viscosity as \(\dot{\gamma }\) \(\rightarrow \infty \).

2.2 Governing equations

To study the steady and pulsatile flow in a multiple stenosed channel, the governing equations considered are the standard mass and momentum balance. The flow field is given by: \(\mathbf {v} = u_d{\hat{\mathbf{e}}}_x + v_d{\hat{\mathbf{e}}}_y\). The variables in the governing equations are non-dimensionalised as follows:

$$\begin{aligned} u &= \frac{u_d}{U},\quad v = \frac{v_d}{U},\quad x = \frac{x_d}{H},\quad y = \frac{y_d}{H},\quad \omega _0 = \frac{U}{H}, \nonumber \\ t &=\frac{t_dU}{H},\quad \mu = \frac{\mu _d}{\mu _\infty },\quad \psi = \frac{\psi _d}{\psi _0},\quad \omega = \frac{\omega _d}{\omega _0},\quad Re = \frac{\rho UH}{\mu _\infty }. \end{aligned}$$
(9)

The subscript ‘d’ in Eq. (9) refers to the dimensional quantities. U is the centerline velocity at the inlet, and H is the half channel width. The stream function (\(\psi \)) and vorticity (\(\omega \)) are calculated from the velocity profile. The viscosity is non-dimensionalised by dividing with \( \eta _\infty \), and is given below:

$$\begin{aligned} \mu ( \dot{\gamma }) = 1 +\left( \lambda - 1 \right) {\left[ {1+ ln(1+ \Lambda \dot{\gamma })}\right] \over 1+\Lambda \dot{\gamma } }, \end{aligned}$$
(10)

where \(\lambda = \frac{\eta _0}{\eta _\infty }\).

The dimensional governing equations for the given blood model are described as:

The continuity equation is

$$\begin{aligned} {\partial u_d \over \partial x_d}+ {\partial v_d \over \partial y_d} = 0 \end{aligned}$$
(11)

X-momentum equation:

$$\begin{aligned} \rho \left[ {\partial u_d \over \partial t_d} + u_d{\partial u_d \over \partial x_d} + v_d{\partial u_d \over \partial y_d} \right] &= -{\partial p_d \over \partial x_d} + \mu _d ({\dot{\gamma }} ) \left[ {\partial ^2 u_d \over \partial x_d^2} + {\partial ^2 u_d \over \partial y_d^2} \right] \nonumber \\&+2 \left[ {\partial u_d \over \partial x_d}{\partial \mu _d \over \partial x_d} \right] +\left[ {\partial \mu _d \over \partial y_d}\left( {\partial u_d \over \partial y_d} + { \partial v_d \over \partial x_d} \right) \right] \end{aligned}$$
(12)

Y-momentum equation:

$$\begin{aligned} \rho \left[ {\partial v_d \over \partial t_d} + u_d{\partial v_d \over \partial x_d} + v_d{\partial v_d \over \partial y_d} \right]&= -{\partial p_d \over \partial y_d} + \mu _d ({\dot{\gamma }} ) \left[ {\partial ^2 v_d \over \partial x_d^2} + {\partial ^2 v_d \over \partial y_d^2} \right] \nonumber \\&\quad +2 \left[ {\partial v_d \over \partial y_d}{\partial \mu _d \over \partial y_d} \right] + \left[ {\partial \mu _d \over \partial x_d}\left( {\partial u_d \over \partial y_d} + { \partial v_d \over \partial x_d} \right) \right] \end{aligned}$$
(13)

The stream function (\(\psi _d\)) and vorticity (\(\omega _d\)) are calculated from the velocity using the following formulae:

$$\begin{aligned} u_d &= {\partial \psi _d \over \partial y_d} \end{aligned}$$
(14)
$$\begin{aligned} v_d &= -{\partial \psi _d \over \partial x_d} \end{aligned}$$
(15)
$$\begin{aligned} \omega _d &= {\partial v_d \over \partial x_d}-{\partial u_d \over \partial y_d} \end{aligned}$$
(16)

The dynamic vorticity balance equation is obtained from the momentum balance equations by subtracting \(\partial / \partial y\) (Eq. 12) from \(\partial / \partial x\) (Eq. 13). The non-dimensionalized stream-function vorticity formulation is given by Eqs. (17) and (18).

$$\begin{aligned}&\omega = - \left( {\partial ^2 \psi \over \partial x^2} + {\partial ^2 \psi \over \partial y^2} \right) . \end{aligned}$$
(17)
$$\begin{aligned}&\left[ { \partial \omega \over \partial t} + {\partial (u \omega ) \over \partial x} + {\partial (v \omega ) \over \partial y} \right] = {1 \over Re} \Big [ \mu \left( { \partial ^2 \omega \over \partial x^2} + { \partial ^2 \omega \over \partial y^2} \right) \nonumber \\&\quad +{ \left( {\partial \mu \over \partial y} {\partial \omega \over \partial y} + {\partial \mu \over \partial x} {\partial \omega \over \partial x} \right) } +2 {{\partial }^2 \mu \over \partial y \partial x} \left( {\partial v \over \partial y} - {\partial u \over \partial x} \right) \nonumber \\&\quad +\left( { \partial ^2 \mu \over \partial x^2} - { \partial ^2 \mu \over \partial y^2} \right) \left( {\partial v \over \partial y} + {\partial u \over \partial x} \right) \Big ]. \end{aligned}$$
(18)

We now transform the physical domain into the computational domain as shown in Fig. 2. This is done using the transformation:

$$\begin{aligned} \zeta &= x, \end{aligned}$$
(19)
$$\begin{aligned} \eta &= \frac{y}{f(x)}. \end{aligned}$$
(20)

The velocity components in the transformed coordinates are obtained (using chain rule):

$$\begin{aligned} u &= \frac{1}{f} {\partial \psi \over \partial \eta } \end{aligned}$$
(21)
$$\begin{aligned} v &= -{\partial \psi \over \partial \zeta } + \frac{\eta f'}{f} {\partial \psi \over \partial \eta }. \end{aligned}$$
(22)

Equations (17) and (18) are written in the transformed coordinates as:

$$\begin{aligned} \omega &= -\Big [ {\partial ^2 \psi \over \partial \zeta ^2} + \left( {2\eta \left( \frac{f'}{f} \right) ^2 - \eta \frac{f''}{f}}\right) {\partial \psi \over \partial \eta } \nonumber \\&+\left( \frac{ [{1+ (\eta f')^2}]}{f^2}.{\partial ^2 \psi \over \partial \eta ^2} \right) - 2\eta \left( \frac{f'}{f} \right) { \partial ^2 \psi \over \partial \zeta \partial \eta } \Big ], \end{aligned}$$
(23)
$$\begin{aligned} { \partial \omega \over \partial t} &= - \left[ {\partial (u \omega ) \over \partial \zeta } - \frac{\eta f'}{f} {\partial ( u \omega ) \over \partial \eta } + \frac{1}{f} { \partial (u \omega ) \over \partial \eta } \right] + \frac{\mu (\dot{\gamma })}{Re}\nonumber \\ &. \left[ {\partial ^2 \omega \over \partial \zeta ^2}+ \left( { 2\eta \left( \frac{f'}{f} \right) ^2 - \eta \frac{f''}{f} } \right) { \partial \omega \over \partial \eta } \right.\nonumber \\ &+\left.\left( \frac{[1+(\eta f')^2]}{f^2}.{\partial ^2 \omega \over \partial \eta ^2} \right) -2\eta \left( \frac{f'}{f} \right) { \partial ^2 \omega \over \partial \zeta \partial \eta } \right]\nonumber \\ &+\frac{1}{Re} \left[ {\partial \mu \over \partial \zeta }-{\frac{\eta f'}{f}} {\partial \mu \over \partial \eta } \right] {\partial \omega \over \partial \zeta }\nonumber \\&-\frac{1}{Re} \left[ {\frac{\eta f'}{f}} {\partial \mu \over \partial \zeta } - \frac{(1+(\eta f')^2)}{f^2} {\partial \mu \over \partial \eta } \right] {\partial \omega \over \partial \eta }\nonumber \\ &+\frac{2}{Re} \left[ \frac{1}{f} {\partial ^2 \mu \over \partial \zeta \partial \eta } - \frac{\eta f'}{f^2} { \partial ^2 \mu \over \partial \eta ^2} - \frac{f'}{f^2}{\partial \mu \over \partial \eta } \right] \nonumber \\&.\left( -{\partial u \over \partial \zeta }+\frac{\eta f'}{f} {\partial u \over \partial \zeta }+ \frac{1}{f} {\partial v \over \partial \eta } \right) \nonumber \\ &+\frac{1}{Re} \Big [ {\partial ^2 \mu \over \partial \zeta ^2} + \Big [ 2 \eta \left( \frac{f'}{f} \right) ^2 - \eta \frac{f''}{f} \Big ] {\partial \mu \over \partial \eta }\nonumber \\ &+\frac{ \left[ (\eta f')^2-1 \right] }{f^2} {\partial ^2 \mu \over \partial \eta ^2}-2\eta \left( \frac{ f'}{f} \right) {\partial ^2 \mu \over \partial \zeta \partial \eta } \Big ]\nonumber \\ &.\left( \frac{1}{f} {\partial u \over \partial \eta } + {\partial v \over \partial \zeta }- \frac{\eta f'}{f} {\partial v \over \partial \eta } \right) , \end{aligned}$$
(24)

respectively. In the time-dependent vorticity equation, \(\dot{\gamma }\) that appears in the viscosity, \(\mu (\dot{\gamma })\), is given by:

$$\begin{aligned} \dot{\gamma } &= {U \over H} \root \of {2 \left[ \left( {\partial u \over \partial \zeta } \right) ^2 + \left( \frac{1}{f}{\partial v \over \partial \eta } \right) ^2 \right] + \left( \frac{1}{f}{\partial u \over \partial \eta }+ {\partial v \over \partial \zeta }\right) ^2 }. \end{aligned}$$
(25)

The initial and boundary conditions used to solve Eqs. (23) and (24) are given next.

2.3 Boundary conditions

The inlet boundary conditions for steady flow and pulsatile flow case are different. The boundary conditions for steady flow case are as follows:

Fully developed flow at inlet (\(\zeta = 0\)) at initial time:

$$\begin{aligned} u &= 1- \eta ^2,\\ v &= 0,\nonumber \\ \psi &= \eta - \frac{\eta ^3}{3},\nonumber \\ \omega &= 2 \eta .\nonumber \end{aligned}$$
(26)

Symmetry condition at centerline (\(\eta = 0\)):

$$\begin{aligned} {\partial \psi \over \partial \zeta } &= 0 \end{aligned}$$
(27)

No slip condition at rigid wall (\(\eta = 1\)):

$$\begin{aligned} {\partial \psi \over \partial \zeta } &= {\partial \psi \over \partial \eta } = 0 \end{aligned}$$
(28)

The updated vorticity at the rigid wall is derived from Eq. (23):

$$\begin{aligned} \omega _{wall} &= -2\frac{\partial ^2 \psi }{\partial \eta ^2} \frac{\left[ 1+(\eta f')^2 \right] }{f^2}; \quad \eta = \pm 1 \end{aligned}$$
(29)

A periodic boundary condition in the axial direction is specified at the outlet (\(\zeta = 1\)). By periodic boundary condition, we mean that the inlet flow is repeated at the outlet and this is a standard boundary condition for extended flow domain used in computational fluid dynamics literature (see [28, 32]).

In the pulsatile flow problem, the steady state solution obtained at the end of pseudo-time stepping for the model in consideration (Shear-thinning or Newtonian) is used as the inlet velocity at the initial step.

3 Numerical solution

The numerical scheme used here has been detailed earlier in [22]. The governing Eqs. (23) and (24) are discretized using finite difference scheme. A second-order central difference scheme is used to discretized advective terms in dynamic vorticity equation: upwinding is also present in case high velocities are encountered, but this is not the case for the study done here. A second-order central differencing scheme is applied to discretize diffusive terms of Eq. (24) and all the terms of Eq. (23). To solve dynamic vorticity equation, an explicit time marching procedure is used in the simulation. The steps in algorithm of numerical solution are as follows:

  1. 1.

    Initialize all variables such as ‘\(\psi \)’ , ‘u’, ‘v’ ,‘\(\omega \)’ at all grid points using initial & boundary conditions.

  2. 2.

    Update ‘\(\omega \)’ at the new time step by solving Eq. (24) using an explicit time marching technique.

  3. 3.

    Evaluate ‘\(\psi \)’ at the next time step by solving the Poisson equation for vorticity (Eq. 23) using values from previous time step. Here we used iterative scheme to solve vorticity equation. A full multi-grid technique is used to accelerate the convergence. A convergence criterion of residual less than \(10^{-8}\) is used.

  4. 4.

    Calculate, ‘u’, ‘v’ at all grid points using Eqs. (21) and (22) and also update ‘\(\omega \)’ using Eq. (29) at wall boundary.

These steps are repeated so as to obtain the flow variables in successive time steps.

3.1 Validation and grid independence

Validation of the code was performed as detailed in [22]: results were obtained for oscillatory flow using the new code for the same parameters as in [25], and the difference in peak wall shear stress (\(|\tau |_{w}\)) was only 2 %. Grid independence of the computed solution was verified by comparing peak wall shear stress on three grids (\(\zeta \times \eta \)): \(256 \times 32\), \(512 \times 32\), and \(512\times 64\). It was found that, for the case of double stenosis separated by a finite gap (\(L_g=4L_0, L_0=2\)), there was only 4.4 and 4.7 % difference in \(|\tau |_{w}\) between the \(256 \times 32\) grid and the two other finer grids. We therefore concluded that no significant change in \(|\tau |_{w}\) will be seen with the finer grid, and reported all results for the \(256 \times 32\) grid. Note that the time step required in a study with the \(512 \times 64\) mesh will be much less than that for the \(256 \times 32\) mesh: the CFL number (\(U\Delta t/\Delta x\)) for the \(256 \times 32\) grid is 0.0643 which is much smaller than 1.

4 Results and discussion

In steady flow, the effects of the restriction length ‘\(L_0\)’ of stenosis as well as size of (percentage) stenosis on peak wall shear stress and downstream recirculation were reported for single and double stenosis. We also report the change in peak wall shear stress due to variation of gap between stenosis. Next, in pulsatile flow, we studied variation of peak wall shear stress over primary and secondary stenosis with time and different Womersley numbers for double stenosis.

4.1 Steady flow

4.1.1 Variation with length (for single stenosis)

Atherosclerotic plaque growth coincides with zones of low wall shear stress. So we first studied the effect of different restriction length and percentage stenosis on peak wall shear stress (WSS) in a single stenosed channel (see [22] for variation of velocity & wall shear stress along axial length). In Fig. 3a, peak WSS decreases with decreasing percentage stenosis for single stenosis. In Fig. 3b it is seen that, for given percentage stenosis, the peak WSS increases with increase in restriction length \(L_0\) and seems to asymptote as length increases.

4.1.2 Variation with length and gap (for double stenosis)

A secondary stenosis may occur in the downstream artery because the primary stenosis creates recirculation and changes the dynamics of flow. Hence, assuming that a second stenosis is formed, we studied the variation of peak WSS, and effect on streamlines, due to presence of the second stenosis. The stream line contours in steady flow for single and double stenosis are reported in Fig. 4 for 25 % stenosis, \(L_0=1.5\)H and Reynolds number of =4000. In this case,the recirculation zone is located downstream of both the primary stenosis as well as secondary stenosis which leads to zones with low wall shear stress; however, further downstream, and away from the recirculation zone, the shear stress recovers its initial pre-stenosis value.

The presence of the second stenosis (separated by gap) significantly reduces the wall shear stress felt on the primary stenosis (Fig. 5a): this is because the recirculation bubble for each stenosis slows down the flow at the peak stenosis location, and more recirculation bubbles (with little gap between them) lead to further slowing down of the velocity at the primary stenosis. However, when the gap between the recirculation bubbles increases the effect of the second stenosis is not so much as we shall see in Fig. 6b. Further, the recirculation bubble between two stenosis of same size reduces the velocity of downstream fluid. Thus, the primary stenosis attained higher peak wall shear stress than the secondary stenosis (see Fig. 5b). It is also noted from Fig. 6a that the WSS at primary stenosis increases with increases in either the percentage stenosis or stenosis length: Increase in length (for 25 % stenosis) from \(L_0\) to \(2L_0\) changed peak WSS at primary stenosis by 57.02 %. In constrast, the gap (\(L_g\)) between the two stenosis plays only a subdued role on peak WSS. The peak WSS on primary stenosis increases with gap ‘\(L_g\)’ until \(L_g = 4L_0\) but the difference is only 2.39 % compared to zero gap (Fig. 6b); there is negligible change (0.068 %) in peak wall shear stress with further increases in gap length.

4.2 Pulsatile flow

Blood flow in the aorta is unsteady and pulsatile [10], and we consider pulsatile flow in double stenosed channel The non-dimensionalised pulsatile pressure gradient and Womersley number are described by:

$$\begin{aligned} -{\partial p \over \partial \zeta } &= A \left[1+0.1\hbox{sin} \left(\frac{2 \pi }{T} t \right) \right]. \end{aligned}$$
(30)
$$\begin{aligned} Wo &= H \root \of {\Big (\frac{2 \pi \rho }{T \mu } \Big )}. \end{aligned}$$
(31)

We have already shown [22] that the solution for the above pressure gradient is pulsatile for single stenosis. We note that the difference of peak WSS between shear thinning and Newtonian fluid is finite (5.63 % at mid-cycle) for \(Wo=16\), and Re = 4000 for single stenosis (\(L_0=1\)), and a similar difference (5.75 %) is seen at the primary stenosis (for double stenosis, \(L_0=1\)) in Fig. 7a. Importantly, for double stenosis with gap 4\(L_0\) and \(L_0=1\), the peak WSS at primary stenosis is higher than that at secondary stenosis at t = 0 in Fig. 7b. However it is clearly observed that higher peak WSS shifts to the secondary stenosis after t = 24 in first half-cycle. In the next half cycle, it is observed that the higher peak WSS shifts back to the same location on the primary stenosis after t = 60. This suggests that pulsatility may play an important role in plaque growth behind stenosis. Figure 8 shows that at primary stenosis percentage difference of the mean peak WSS (obtained at \(t=\frac{2}{3}T\)) between shear thinning and Newtonian decreases with Womersley number (2.79 % at \(Wo=16\)).

5 Conclusion

We have obtained a computational solution for 2D, steady and pulsatile flow in a double stenosed channel. In steady flow, it was observed that the peak wall shear stress increases with stenosis length \(L_0\) and achieved higher value in single stenosis case compared to primary stenosis in double stenosis case. Further wall shear stress was higher at primary stenosis compared to secondary stenosis, which is consistent with the results of [11]. Stenosis length was more important compared to gap between stenosis in affecting the wall shear stress: 57.02 % increase for doubling of length from \(L_0\) to \(2L_0\) compared to 2.39 % difference for increase in gap from 0 to \(4L_0\) (and further increase in gap produced near 0 % difference).

Our study extends the results in [15] in that we have validated the pulsatile flow results, clearly showed the presence of recirculation at higher Reynolds number, and documented the effect of Womersley number on peak WSS. Also, we found that, for a given Re (4000), the wall shear stress at a single stenosis of length \(2L_0\) is greater than the wall shear stress experienced by two stenoses each of length \(L_0\): this is a useful supplement to the experimental result of [27] who observed that, for a given pressure gradient, flow reduction is greater for multiple short stenosis than for single stenosis of equivalent length. Importantly, it was seen that pulsatility may play an important role in dynamics of plaque growth in atherosclerosis because the location of peak WSS shifts from primary to secondary stenosis during a time cycle. This is an important point to consider when developing a model for atherosclerosis based purely on mechanical factors, and we will take this up in a subsequent paper.

5.1 Limitations and extensions

The entire study is based on the premise of laminar flow in the human aorta at Re = 4000. This assumption can be questioned because aortic flows are experimentally noted to be on the edge of turbulence [10]. We have therefore neglected the onset of turbulence, and assumed laminar flow based on the discussion in [20] who state that conditions like variable viscosity and cell concentration can prevent turbulence from developing. We also assume that the channel walls are highly smooth so as to prevent the onset of turbulence even in the presence of stenosis. A proper method to test this assumption will involve formulating the equations for channel flow in 3D, and solving numerically to see if the solution exhibits turbulence: this is however, beyond the scope of our study. Further, the hemodynamic factors such as WSS for 2D study will be different from those obtained in a more advanced 3D study, but we do not expect the qualitative nature of our conclusions to change even if our study is preliminary compared to a 3D study which also neglects turbulence.