Fading characteristics of maritime propagation channel for beyond geometrical horizon communications in C-band

Abstract

The design of a maritime communication system requires the understanding of the wireless propagation channel above the sea. For broadband communication systems, a carrier frequency in the C-band is of interest because of allocatable spectrum. Therefore, the German Aerospace Center performed a long-distance channel measurement campaign at 5.2 GHz on the North sea to investigate large and small-scale fading characteristics. The results show that our measurement data conforms with the ITU-R and the Bullington’s path loss model to predict the power loss caused by diffraction over the Earth’s surface. Further, the first tap of the channel impulse response experiences Rician fading due to superposition of a strong line-of-sight (LoS) path and multipath components originating from the sea surface and ship body. We found that the fading of the second tap follows a Rician distribution, but with a much smaller K-factor compared to the first tap. The K-factor showed a dependence on the distance between the transmitter and receiver. Particularly, the K-factor of the first tap decreases significantly when the distance between the transmitter and receiver is larger than the clearance distance of the first Fresnel zone. Therefore, we propose a distance-dependent K-factor model for the first and the second tap.

1 Introduction

Today, several maritime communication systems exist with each of them offering a dedicated service. Most of them are narrowband systems in the (HF) and very high frequency (VHF) band. Satellite broadband communication systems are rather expensive and have a significant footprint that reduces the effective throughput for each vessel in densely populated areas. In densely populated areas, such as harbors, proprietary solutions exist today based on formerly defined land-based terrestrial communication systems, such as WiMAX [1] and long-term evolution (LTE). However, there are a few vessels that use these systems and it is expected that the number of vessels making use of broadband links for different operational purposes is increasing. In the 5–8 GHz band, a spectrum is identified by the European Conference of Postal and Telecommunication Administrations (CEPT) in conjunction with European Telecommunication Standards Institute (ETSI) to offer maritime broadband radio communications in the near future [2, 3].

To develop new algorithms for future communication and navigation systems on ships, it is essential to understand the wireless propagation characteristics particularly fading characteristics in the maritime environment. Large-scale fading has been widely studied based on channel measurement campaigns [4,5,6,7,8]. Related measurements were conducted with a bandwidth up to 20 MHz. Most of these measurements were conducted for short to medium distances with carrier frequencies below 5 GHz. Short-distance-based channel measurement results for small-scale fading at 5.2 GHz with a signal bandwidth of 20 MHz have been presented in Wang et al.  [9]. However, the small-scale fading characteristic has not been thoroughly investigated for wideband systems.

In this paper, we evaluated large- and small-scale fading characteristics based on broadband propagation measurement data. The measurement data was gathered during a measurement campaign on the North sea conducted by the German Aerospace Center (DLR). The findings show that the clearance of the first Fresnel zone is important for both large- and small-scale fading. The analysis is structured as follows: First, the received power of the broadband signal is analyzed and compared with several theoretical models such as the ITU-R path loss model [10] and the Bullington’s model [11]. The results conform with both models. In the second part, investigations of the small-scale fading for individual channel taps are presented. The first tap experiences Rician fading because of the presence of a strong line-of-sight (LoS) component. The results show a distance-dependent K-factor. Particularly, the K-factor of the first tap decreases significantly when the distance between the transmitter and receiver is larger than the clearance distance of the first Fresnel zone. As a whole, we present a distance-dependent K-factor model for the first and the second tap of the channel impulse response (CIR).

The paper is structured as follows: in Sect. 2, the setup of the channel measurement campaign is addressed. Section 3 presents the data processing methods and the results, and Sect. 4 concludes the paper.

Fig. 1

Measurement scenario on the North sea: (a) receiver location on the land. (b) Ship route during the measurement, visualized by the blue line, while the receiver was located in the harbor marked by the red cross. The maximum distance between the transmitter and receiver was around 35 km. (c) View of the ship “Hermann Marwede” where the transmit antenna was mounted on

2 Channel measurement campaign

The measurements were conducted using the Medav RUSK DLR broadband channel sounder. To sound the channel, the transmitter sent a broadband signal—in particular a multitone signal—at center frequency of 5.2 GHz. During the measurement, the CIR snapshots, measured periodically with a period $t_g$, are denoted as $h (t_k,\tau _n )$, where $t_k=k\cdot t_g$, with $k=1,2\ldots ,$ being the time index of the measured CIR snapshot, and $\tau _n=n\cdot \tau _{\Delta }=\frac{n}{B}$, with $n=0,\ldots ,N-1,$ being the delay of sample n while B is the bandwidth. $\tau _{\Delta }$ is the delay resolution. The corresponding transfer function is denoted as $H(t_k,f_n)$, where $f_n$ is the frequency associated to bin n. A summary of the measurement parameter setup is given in Table 1.

Table 1 Channel sounder settings

During the measurement, the receiver was located on the land in Heligoland, Germany as depicted in Fig. 1a. A vertically polarized directional antenna was used to receive the signal, with a half power beam width of 40$^{\circ }$. The direction of the directional antenna was set such that its main lobe pointed towards the ship. The receive antenna height is 6 m. The transmitter was located on a ship, named “Hermann Marwede”, of the German Maritime Search and Rescue Service (DGzRS) visualized in Fig. 1c. A vertically polarized signal was periodically transmitted with a repetition rate of $T_p= 25.6~{\upmu \mathrm{s}}$, such that a maximum detour propagation distance¹ of 7.6 km larger than the distance between the transmitter and receiver can be measured. The transmit antenna height is around 16 m. The ship was moving at most time instants with a speed between 4 and 9 m/s. Figure 1b visualizes the ship traveling route during the measurement with a maximum distance between the transmitter and receiver of 35 km.

To obtain the antenna positions at each time instant $t_k$, geodetic global navigation satellite system (GNSS) receivers were used at the transmitter and the receiver site. The GNSS receivers are able to receive satellite signals from the Global Positioning System (GPS), the GLObal NAvigation Satellite System (GLONASS) and the Galileo system. The measured data were later post-processed by the software GrafNav$^{\circledR }$ using real-time kinematic to achieve positioning accuracy in the sub-meter level. To achieve time synchronization between the transmitter and receiver, two Rubidium clocks were used, one on each side. In the beginning of every measurement day, a reference measurement, where the transmit antenna had a clear LoS to the receiver antenna, was performed to measure the time offset between the transmitter and receiver clocks. To compensate the relative clock drift between the transmitter and receiver clocks, the GNSS receivers’ clocks driven by the Rubidium frequency normal were compared to the GPS time. Therefore, the relative clock drift between the transmitter and receiver clocks can be obtained by the GPS time information. A more detailed description of clock monitoring using GPS measurements can be found in Schneckenburger et al. [12]. Furthermore, the attitude of the ship was measured by inertial measurement units (IMUs) in terms of pitch, yaw and roll angles. The IMU data were time stamped with the GPS time obtained from a GNSS receiver. Therefore, the IMU data can be synchronized to the measured CIRs that is also stamped by GPS time.

During the measurement, the significant wave height $h_\mathrm{{s}}$ of ocean waves was around 3 m [13]. The salinity of the sea water was around $3.4\%$. Water temperature was around $6~^\circ \mathrm {C}$. Detailed environment data within the measurement time period can be found in the database of the Federal Maritime and Hydrographic Agency of Germany (BSH) [14]. Furthermore, an Automatic Identification System (AIS) receiver was used to record the positions of other vessels close to Heligoland during the measurement time period.

Fig. 2

Exemplarily measured CIRs over 180 s and the ship traveled 1381 m

Fig. 3

Exemplary Doppler spectrum and shift of the LoS path over 180 s. The x-axis represents the corresponding time of individual segments

3 Results analysis

Exemplarily measured CIRs $h (t_k,\tau _n )$ are visualized in Fig. 2 where the ship traveled 1381 m within 180 s. While the ship was moving away from the receiver, the delay of the LoS path increases. The multipath component caused by objects on land were suppressed because of the directional antenna on land. The dominant multipath propagation is caused by the sea surface and local scatterers on the ship. As a result, there are no strong multipath components at large delays compared to the LoS path delay.

To calculate the delay-Doppler spectrum, the obtained CIR snapshots are divided into segments with index l. Each segment $Z({l,\tau _n})$ represents a time duration of $T_f$ and is defined as:

$$\begin{aligned} Z({l,\tau _n})=[h({t_{k_l}),\tau _n},\ldots ,h({t_{k_{l+1}-1},\tau _n})], \end{aligned}$$

(1)

where $t_{k_l}$ denotes the time index of the CIR where the lth segment starts. On the one hand, $T_f$ should be small such that the channel within the duration of $T_f$ can be assumed to be stationary, i.e., the Doppler does not change significantly. On the other hand, the number of CIR snapshots within $T_f$ should be sufficiently large to obtain a high resolution of the Doppler spectrum. In the following, we choose $T_f= 0.5~{\mathrm{s}}$. The delay-Doppler spectrum $S_l\left( \nu ,\tau _n\right)$ of the l-th segment is calculated as:

$$\begin{aligned} S_l({\nu ,\tau _n})=\mathscr {F}_{t}({Z({l,\tau _n}})) , \end{aligned}$$

(2)

where $\nu$ is the Doppler frequency and $\mathscr {F}_{t}\left( \cdot \right)$ represents the discrete Fourier transform with respect to the variable t. Thereafter, the Doppler spectrum of the LoS path can be obtained from the delay-Doppler spectrum at the LoS delay:

$$\begin{aligned} \tau _0=\arg \max _{\tau _n}({|h (t_k,\tau _n)|^2}) . \end{aligned}$$

(3)

Figure 3a shows the obtained Doppler spectrum $S_l\left( \nu ,\tau _0\right)$ of the LoS path over a measurement time period of 180s. The x-axis represents the corresponding starting time of individual segments. While the ship was moving forward, the Doppler spectrum varied due to the changing speed and attitude of the ship affected by the sea waves. The Doppler shift of the LoS path is obtained by:

$$\begin{aligned} \nu _l^0=\arg \max _{\nu }({|S_l\left( \nu ,\tau _0\right) |^2}) . \end{aligned}$$

(4)

Figure 3b visualizes the obtained $\nu _l^0$ by the blue curve over a measurement time period of 180s. To verify the obtained Doppler shift, the red curve visualizes the calculated Doppler shift using the GNSS-estimated positions and -velocities. It can be noticed that the variations of the Doppler shifts of both measurements are similar to each other.

In the following, a detailed analysis on the channel measurement data in terms of large- and small-scale fading characteristics is presented.

3.1 Large-scale fading

The received power $P_r(t_k)$ is obtained as:

$$\begin{aligned} P_r\left( t_k\right) =10\log _{10}\Bigg \{\sum _{n=0}^{N-1}|\Gamma \left( h (t_k,\tau _n )\right) |^2\Bigg \} , \end{aligned}$$

(5)

where $\Gamma \left( \cdot \right)$ represents a threshold function at the $99.9\%$ quantile of the noise distribution to discard noise samples. Figure 4 shows an example of measured CIR by the blue curve which consists of noise samples at delays outside the region between 1 and 3 ${\upmu \mathrm{s}}$. The calculated threshold is visualized by the red line, and the outcome after thresholding is given by the green curve.

Figure 5 visualizes the obtained power values (in blue color) versus the distance d between the transmitter and receiver. A few “deep fades” in the received power can be observed. As an example, a power fade of $15~{\mathrm{dB}}$ occurs at the distance around $d= 6.9$ km. It can be explained by the fact that another vessel blocked the LoS path. Figure 6 visualizes the geographical positions of the receiver (by the red cross) and the ship “Hermann Marwede” when the “deep fade” occurs (by the blue dots). The black line represents the LoS path between the transmitter and receiver at $d=6.85~{\mathrm{km}}$. Based on the AIS measurement, we can identify another ship blocking the LoS path. The identified ship, named “Meerkatze” is depicted in Fig. 7 and belongs to the German Federal Waterways and Shipping Administration (WSV). It is approximately $72~{\mathrm{m}}$ long and 25 m tall. Figure 6 also shows the position of the ship “Meerkatze” (by the cyan dot) at the moment when the receiver was located at $d= 6.85~{\mathrm{km}}$. It is worth noting that the deep fades at larger distance, e.g., larger than 12 km, may be also caused by other vessels that block the LoS path. However, in the AIS measurement there is no record of other vessels that might have blocked the LoS path. It may be due to the limited coverage of the AIS receiver or small vessels without AIS device on board.

Fig. 4

Exemplarily measured CIR and calculated threshold to mitigate noisy samples

Fig. 5

Measured received power in comparison with different theoretical path loss models. The black line and the orange line overlap with each other after $d> 12~{\mathrm{km}}$. The cyan- and black-dashed lines stand for the distance $d_\mathrm{{C}}$ and $d_\mathrm{{H}}$, respectively

Fig. 6

Geometry of measurement scenario for the measurement instant where the distance between the transmitter and receiver was around 7 km.The red cross point and the blue dots represent the transmitter and receiver positions, respectively. Black line indicates the LoS path and the cyan dot shows the position of the ship “Meerkatze”

Fig. 7

Photo of the ship “Meerkatze” belonging to the German Federal Waterways and Shipping Administration (WSV)

Table 2 Statistical parameters of the error $\varepsilon$ in (dB)

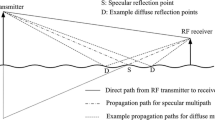
To predict the system coverage, a suitable path loss model is important. LoS propagation is dominant for the propagation channel over sea. To compare the measured power levels, the theoretical free space path loss model is visualized by the black line in Fig. 5. Apart from the direct propagation between the transmitter on the ship and receiver on the land, the interaction between the sea surface and the signal need to be considered, particularly the specular reflection on the sea surface. The power of the reflected path depends on the reflection coefficient $\Gamma _r$ of the rough sea surface [4, 15, 16]:

$$\begin{aligned} \Gamma _r=S_a^2 D_v \Gamma e^{-8\left( \frac{\pi h_0 \cos (\beta )}{\lambda }\right) ^2} , \end{aligned}$$

(6)

with the divergence factor $D_v$ that can be calculated as in Parsons [16], the wavelength $\lambda$, the the root mean square (RMS) water wave height $h_0$ and the incident angle $\beta$. $\Gamma$ is the reflection coefficient for a perfectly smooth sea surface that can be calculated as in Ulaby [17]. Due to the sea surface roughness, an additional shadowing factor $S_\mathrm{{a}}$ [4, 15, 18] for the calculation of the reflected power is considered.

As a comparison, the simulated power considering both LoS and reflected path are plotted in Fig. 5 by the orange line. Due to the curvature of the earth, the LoS path can be blocked by the ground. According to the geometry, the distance $d_\mathrm{{H}}$ where the beyond geometrical horizon occurs can be calculated as:

$$\begin{aligned} d_\mathrm{{H}}=\sqrt{h_1^2+2h_1R}+\sqrt{h_2^2+2h_2R} , \end{aligned}$$

(7)

where R is the earth radius in (km), $h_1$ and $h_2$ are the antenna heights in (km) above the mean sea level (MSL) for transmitter and receiver, respectively. The obtained distance $d_\mathrm{{H}}$ is 23.5 km and plotted as the black-dashed line in Fig. 5². It can be noticed that the predicted power values fit well to the measurement data for distances $d< 12~{\mathrm{km}}$. For $d> 12~{\mathrm{km}}$, the free space path loss model over-predicts the received power. This can be explained by the blockage of the first Fresnel zone. If the clearance of the first Fresnel zone is not sufficient (i.e., less than $60\%$ of the Fresnel zone radius), additional diffraction loss must be considered [19]. The clearance distance $d_\mathrm{{C}}$ for $60\%$ of the Fresnel zone radius is approximated as in [10] by:

$$\begin{aligned} d_\mathrm{{C}}=\frac{0.00015949\cdot f_c\cdot h_1\cdot h_2\cdot \left( \sqrt{h_1}+\sqrt{h_2}\right) }{0.0000389\cdot f_c\cdot h_1\cdot h_2+4.1\left( \sqrt{h_1}+\sqrt{h_2}\right) } , \end{aligned}$$

(8)

where $f_c$ is the carrier frequency in (MHz), $d_C$ in (km), $h_1$ and $h_2$ are the antenna heights in (m). The obtained $d_\mathrm{{C}}$ is 11.7 km and plotted as the cyan-dashed line in Fig. 5.

To consider the additional diffraction loss, we evaluate two methods: the ITU-R P.$1546-5$ model [10] and the Bullington’s model [11]. For the ITU-R model, we consider the percentage time of $50\%$ that indicate the median of the power values. Bullington proposed a diffraction loss model for propagation via the curvature of earth. Based on the Bullington’s model, the two path effect (i.e., the LoS path and the reflected path) are considered. Figure 5 shows the predicted power values for the ITU-R and the Bullington’s model by a green and a red curve, respectively. Both models are of low complexity but can predict the received power well, especially for $d>d_\mathrm{{C}}$.

To evaluate the qualitative performances between different power prediction models, an error $\varepsilon \left( t_k\right)$ is defined as:

$$\begin{aligned} \varepsilon \left( t_k\right) =P_r\left( t_k\right) -\hat{P}_r\left( t_k\right) . \end{aligned}$$

(9)

where $\hat{P}_r\left( t_k\right)$ represents the predicted power in [dB]. The statistical parameters of the error $\varepsilon \left( t_k\right)$ of the four models in Fig. 5 are summarized in Table 2. The root mean-squared logarithmic error (RMSLE) of the error is calculated for each model as in Guan et al. [20]:

$$\begin{aligned} \varsigma =\sqrt{E_\mathbf{{l}} \{ {|\varepsilon ({t_k}) |^2} \} }. \end{aligned}$$

(10)

It can be seen that using the Bullington’s or the ITU-R model, the power can be predicted with small errors. Particularly, the ITU-R model is more accurate than the Bullington’s model, where the RMSLE of the Bullington’s model is 0.7 dB larger than the ITU-R model. Therefore, we can conclude that the ITU-R model predicts well the received power for large distances in C-band, although the ITU-R model is developed for carrier frequencies up to 3GHz. However, as reported in previous work [4, 21], the ITU-R model does not consider power variations caused by the reflected path on the water surface.

3.2 Small-scale fading

Prior to the processing, the CIR is time aligned such that the first CIR tap has the strongest magnitude. Given the measurement bandwidth of 120 MHz, the resolution in delay domain is 8.33 ns corresponding to a propagation distance of 2.5 m. Therefore, the tap with index n refers to a detour distance of $n\cdot 2.5~{\mathrm{m}}$ compared to the LoS path. Figure 8 visualizes the ellipses indicating the positions of scatterers such that the multipath has a detour length of $n\cdot ~2.5{\mathrm{m}}$ with $n=1,2$.

The large-scale fading (e.g., the distance dependent path loss) has to be removed from the obtained magnitude of each tap: Similar to [22, 23], the power of individual taps is normalized to the average power taken over a certain traveled distance $d_{\Delta }$ where the channel is regarded to be stationary. In this paper, a distance of $d_{\Delta }=170\lambda$ is used to remove large-scale fading. Figure 9 shows the normalized magnitude of the first three taps (i.e., $n=0,1,2$) in linear scale. The first tap contains the strong LoS path accompanied by multipath components with detour distances smaller than 2.5 m . The variance on the magnitude of the first tap is significantly smaller than on the other two taps. Particularly, the magnitude of the third tap varies most among all three considered taps. While the distance increases, the variances of the magnitude for all three taps increase.

Fig. 8

Geometry of ellipse corresponding to different detour distance

Fig. 9

Normalized magnitude of the first, the second and the third tap

3.2.1 Magnitude distribution

As a first step to characterize the small-scale fading behavior of the magnitude for individual taps, the distribution of the magnitude is verified. A popular approach to characterize the distribution is the Kolmogorov–Smirnov (KS) test statistic serving as a goodness of fit (GoF) indicator [22, 23]. The so-called test statistic $\rho$ is calculated as:

$$\begin{aligned} \rho =\sup _{x}|F_X(x)-F(x)| , \end{aligned}$$

(11)

where $\sup _{x}$ is the supremum operator, $F_X(x)$ and F(x) are the empirical and theoretical cumulative distribution functions (CDFs) of x, respectively. A lower value for $\rho$ indicates a better fit of the distribution to the empirical CDF calculated using the measurement samples. Figure 10 visualizes the GoF indicator $\rho$ for the magnitude of the first three taps. In this paper, five distributions are considered within the test. It can be seen that the Rician distribution fits best to the empirical distribution of the magnitude for the first tap. The value of $\rho$ for the normal distribution is close to the Rician distribution. Therefore, the Rician K-factor, i.e., the Rician distribution, can be approximated well by a normal distribution. For the second tap, the Rician distribution is found to provide the best fit, where the value of $\rho$ is close to the results of the Weibull, normal and Rayleigh distribution fits. It can be noticed that the Weibull distribution is the best fit for the magnitude of the third tap. The values of $\rho$ for the Rician and Rayleigh distribution fits are close. As shown in Bernado et al.  [22], the Weibull distribution is defined as

$$\begin{aligned} f(x;\chi ,k)=\left\{ \begin{array}{ll} \frac{k}{\chi }\left( \frac{x}{\chi }\right) ^{k-1}e^{-\left( \frac{x}{\chi }\right) ^k}, &{} {x \ge 0} \\ 0, &{} {x <0} \end{array} \right. , \end{aligned}$$

(12)

with shape parameter k and scale parameter $\chi$. When the shape parameter k of $f(x;\chi ,k)$ equals to two, the Weibull distribution is identical with the Rayleigh distribution. If the shape parameter is larger than two, the Weibull distribution becomes similar to the Rician distribution. Table 3 shows the estimated scale and shape parameters of the Weibull distribution for the first three taps. It can be seen that the shape parameter k for the first tap is much larger than two, which indicates that the magnitude of the first tap is Rician distributed. On the other side, k is close to two for the third tap, indicating that the magnitude of the third tap may be fitting well to a Rayleigh distribution also.

Table 3 Estimated scale and shape parameters of the Weibull distribution for the first three taps

Fig. 10

GoF of the first, the second and the third tap for different distributions

3.2.2 Rician K-factor

As described in Sect. 3.2.1, the magnitudes of the first and the second tap can be characterized as being Rician distributed. The third tap experiences a Rayleigh fading that is a special case of the Rician distribution. Only the first two taps are considered for calculating the K-factor because of the weak power of the third tap compared to the LoS. The Rician distribution can be represented as

$$\begin{aligned} f(x)= & {} \frac{2\left( K+1\right) x}{\Omega }\cdot e^{-K-\frac{\left( K+1\right) x^2}{\Omega }} \nonumber \\&\times \, I_0\left( 2\sqrt{\frac{K\left( K+1\right) }{\Omega }}x\right) , \end{aligned}$$

(13)

where x stands for the magnitude, $I_0$ the 0th order modified Bessel function of the first kind, $\Omega =\text {E}\left\{ x^2\right\}$, and K is the Rician K-factor, i.e., the power ratio of the dominant path to the multipath components. In general, the K-factor is defined as:

$$\begin{aligned} K=\frac{A^2}{2\sigma ^2} , \end{aligned}$$

(14)

where A denotes the peak amplitude of the dominant component and $\sigma$ the root mean square value of the amplitude. To calculate K the moment-based method [24] with

$$\begin{aligned} K=\frac{\sqrt{1-\gamma }}{1-\sqrt{1-\gamma }} , \end{aligned}$$

(15)

and

$$\begin{aligned} \gamma =\frac{\text {Var}\left\{ x^2\right\} }{\left( \text {E}\left\{ x^2\right\} \right) ^2} , \end{aligned}$$

(16)

is widely used. The notations $\text {Var}\left\{ \cdot \right\}$ and $\text {E}\left\{ \cdot \right\}$ stand for the sample variance and expectation estimators, respectively. To use the sample variance and expectation estimators, a spatial window length has to be considered that is no longer than the window length for removing the large-scale fading. Therefore, a window length of $~150\lambda$ is used to calculate the K-factor, which contains around 500 magnitude samples. The number of samples per window length changes because of the varying speed of the ship. Figure 11 shows the empirical CDF of the estimated K-factor for the first and the second tap. It can be seen that the K-factor of the first tap is larger than the value of the second tap.

Fig. 11

CDF of the K-factor for the first two taps

Figures 12 and 13 show the estimated K-factor of the first tap versus the distance between the transmitter and receiver. The value of the K-factor of the first tap is much larger compared to the second tap because of the presence of the strong LoS component in the first tap. Particularly, similar “deep fades” to the receiver power in Fig. 5 can be noticed in the estimated K-factor values. For instance, at distance d = 7 km the “Meerkatze” obstructs the LoS path resulting in a decreased power of the dominant LoS path. Thus, the value of the K-factor decreases.

For distance $d<d_\mathrm{{C}}\approx 12~{\mathrm{km}}$, the K-factor of the first tap does not significantly change over distance, whereas for $d>d_\mathrm{{C}}$ the K-factor decreases with increasing distance d. For the distance $d>d_\mathrm{{C}}$, additional diffraction loss occurs and the power of the dominant component decreases. It can be also seen that the value of the K-factor for the second tap does not change significantly over distance d.

Fig. 12

K-factor estimates of the first tap

Fig. 13

K-factor estimates of the second tap

To model the distance-dependent K-factor of the first tap, a stepwise model is proposed as

$$\begin{aligned} \hat{K}=\left\{ \begin{array}{ll} -2.3561\cdot d + 222.4231, &{} {d\le d_\mathrm{{C}}} \\ -0.1251\cdot d^2 - 5.1484\cdot d + 279.1343, &{} {d>d_\mathrm{{C}}} \end{array} \right. , \end{aligned}$$

(17)

where $\hat{K}$ is the predicted K-factor in linear scale and d is the distance in (km). The parameter estimation of the linear model is performed in the least square sense.

To model the distance-dependent K-factor of the second tap, a simple linear model is used as:

$$\begin{aligned} \hat{K}=-0.0123\cdot d+2.4201 , \end{aligned}$$

(18)

where $\hat{K}$ is the predicted K-factor in linear scale and d is the distance in (km). Similar to (17), the parameters are fitted in the least square sense.

Furthermore, we study the deviation of the model to the measurements by:

$$\begin{aligned} \Delta K_L=10\log _{10}K-10\log _{10}\hat{K} , \end{aligned}$$

(19)

where K and $\hat{K}$ are the estimated and predicted K-factors, respectively. Figure 14 shows the estimated probability density function (PDF) of the deviation $\Delta K_L$ by using a Gaussian kernel estimator with bandwidth $1.06\cdot \sigma _L\cdot N_L^{-1/5}$ where $N_L$ denotes the length of the data samples and $\sigma _L$ is the standard deviation [25]. It is found that the Laplacian distribution shows a good fit to the estimated PDF for the deviation $\Delta K_L$.

Fig. 14

Estimated PDF of the deviation $\Delta K_L$ compared with the theoretical Laplacian distribution

4 Conclusions

To investigate fading characteristics of long-distance ship-to-land wireless propagation, a channel measurement campaign at 5.2 GHz with a bandwidth of 120 MHz was performed on the North sea. In this paper, a detailed description of the channel measurement campaign and investigations on the fading characteristics are presented.

In the first part, the large-scale fading in terms of the received power is analyzed. The diffraction loss due to the curvature of earth’s surface has to be considered in the path loss model, even when the line-of-sight path is present. The ITU-R path loss model and the Bullington’s model are evaluated based on measurement data. The results show that both models are able to predict the received power well. Particularly, the ITU-R model allows to predict the received power for large distances in the C-band, although the ITU-R model is developed for a carrier frequency up to 3 GHz. However, for short distances, the ITU-R model does not consider the power variation caused by the reflection on the sea surface.

In the second part, the small-scale fading of individual channel taps is investigated. The results show that the first tap experiences Rician fading due to the presence of a strong LoS path. The second tap also experiences Rician fading, but with much smaller K-factor (mean value of around 3 dB) compared to the K-factor of the first tap (mean value of around 22 dB). Furthermore, a distance dependency of the K-factor has been found. Particularly, the K-factor of the first tap decreases significantly when the distance between the transmitter and receiver is larger than the clearance distance of the first Fresnel zone. It is due to the fact that the first Fresnel zone is partially blocked by the sea surface and, thus, the power of the dominant LoS path is reduced. Distance-dependent K-factor models are proposed for the first and the second tap.