Modeling of Maritime Wireless Communication Channel

Abstract

Influenced by radian of the Earth and the waves, also the shelter of ships and sea waves, wireless channels above the sea have the effects of deep fading and multipath. Microwaves of very high frequency and ultrahigh frequency are analyzed in oceanic environments. We considered the direct path, paths of mirror reflection, and diffuse scattering, and we calculated the power of mirror reflection and diffuse scattering theoretically. Area of effective diffuse scattering and partitioning was introduced to calculate the power of multipath. We built a generalized channel model with different frequency band and communication range.

1 Introduction

Hainan is the province with the largest ocean area in China, with a sea area of 2 million square kilometers, accounting for 42.3% of Chinese ocean area [1]. The production and living areas of people from land to sea are constantly expanding, such as the development of ocean-going fisheries, marine environment detection and oil exploration, maritime safety and other communication service issues [2], so there is an urgent need to find a solution to marine communication. The problem of the development of high-speed data communication in modern ports and near-shore ships is becoming more and more prominent [3]. The establishment of a universal wireless channel model can provide a scientific basis for the design of communication systems and thereby reduce the blind marine radio wave propagation and channel modeling research in engineering design [4].

2 Simple Prediction Model of Ocean Radio Wave Propagation Loss

2.1 Radio Wave Propagation Theory

Suppose there is an isotropic emission source in free space, and the total power radiated in all directions is Pt watts (ideal) (Fig. 1).

Fig. 1

Flux density generated by isotropic source

The flux density across the sphere from the source R meters is

$$F = \frac{{P_{t} }}{{4\pi R^{2} }}{\text{W/m}}^{ 2}$$

(1)

The antenna gain G(θ) is defined as the ratio of the radiated power per unit solid angle in the direction of θ to the average radiated power per unit solid angle

$$G\left( \theta \right) = \frac{P\left( \theta \right)}{{{{P_{o} } \mathord{\left/ {\vphantom {{P_{o} } {4\pi }}} \right. \kern-0pt} {4\pi }}}}$$

(2)

Among them, P(θ) is the radiated power per unit solid angle of the antenna; P_o is the total radiated power of the antenna; G(θ) is the gain of the antenna in the angular direction. The antenna gain takes the value of G(θ) when θ = 0, which is used to measure the radiant flux density of the antenna. Assuming that the transmitter output power is P_t, a lossless antenna is used, and the antenna gain is G_t, then the flux density at a distance R in the direction of the line of sight is

$$F = \frac{{P{\text{t}}G_{\text{t}} }}{{4\pi R^{2} }}{\text{W}}/{\text{m}}^{ 2}$$

(3)

where P_tG_t is called effective isotropic radiated power (EIRP), which means an equivalent isotropic source with power P_tG_t watt, θ = 0. If an ideal receiving antenna with an aperture area of A m² is used, as shown in Fig. 2, the received power P_r can be calculated by the following formula

Fig. 2

Power received by an ideal antenna in an area of A m² (the incident flux density is F and the received power is $P_{r} = F \times A = P_{t} G_{t} A/4\pi R^{2} \;{\text{W}}$)

$$P_{r} = F \times A{\text{ W}}$$

(4)

The received power of the actual antenna cannot be calculated using the above formula. Because of the energy incident on the antenna aperture, part of it is reflected into free space and part of the energy is absorbed by the lossy element. A_e is the effective aperture, and A_r is the actual aperture area, then

$$A_{e} = \eta AAr$$

(5)

where η_A is the aperture efficiency, reflecting all losses between the incident wavefront and the antenna output. The power received by the actual antenna is

$$P_{r} = \frac{{P_{t} G_{t} A_{e} }}{{4\pi R^{2} }}{\text{ W}}$$

(6)

Among them, the limited area of the receiving antenna

$$A_{e} = \frac{{\lambda^{2} }}{4\pi }G_{r} \quad$$

(7)

where G_r is the effective gain of the receiving antenna. The relationship between antenna gain and area: G = 4πA_e/λ², where λ is the wavelength corresponding to the operating frequency. Using Eqs. (6) and (7), the link equation is

$$P_{r} = {\text{EIRP}} + G_{r} - L_{p} \quad {\text{dBW}}$$

(8)

where EIRP = lg(P_tG_t) dBW, G_r= lg(4πA_e/λ²) dBW

$$L_{p} = 10\lg \left[ {\left( {{{4\pi R} \mathord{\left/ {\vphantom {{4\pi R} \lambda }} \right. \kern-0pt} \lambda }} \right)} \right]^{2} = 20\lg \left( {{{4\pi R} \mathord{\left/ {\vphantom {{4\pi R} \lambda }} \right. \kern-0pt} \lambda }} \right)$$

(9)

Equation (8) represents the ideal situation. In practice, the attenuation caused by oxygen, water vapor, and rainfall, the sea surface reflection propagation loss, the internal loss generated by the antenna at both ends of the link, and the pointing error loss must also be considered.

$$P_{r} = {\text{EIRP}} + Gr - Lp - La - Lta - Lra\quad {\text{dBW}}$$

(10)

where L_a is the atmospheric loss, L_ta is the loss caused by the transmitting antenna, and L_ra is the loss caused by the receiving antenna.

2.2 Popagation Loss in Free Space

When radio waves propagate in free space, the energy in per unit area will be attenuated by diffusion. This reduction is called free space propagation loss. The L_p can be expressed in decibels as

$$Lp = 32.45 + 20\lg d({\text{km}}) + 20\lg f({\text{MHz}})\quad dB$$

(11)

In this formula, f represents the operating frequency (MHz), and d represents the distance (km) between the transmitting and receiving antennas.

2.3 Sea Surface Reflection Propagation Loss

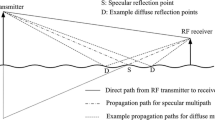
As shown in Fig. 3, the total received signal of the receiver should be a composite signal of direct and sea reflection.

Fig. 3

Sea surface reflection propagation model

The reflection propagation model of radio waves on a smooth sphere is shown in Fig. 4, where T represents the signal emission point and AB line represents the tangent line through point C. The reflection process of radio waves on a smooth sphere must satisfy the angle of incidence equal to the angle of reflection. Therefore, when the height of the antenna at both ends of the path is h₁, h₂, and the station distance d is determined, the reflection point position C is a certain value, and the position d₁ of point C meets the following conditions

Fig. 4

Reflecting point calculation chart

$$d_{1}^{3} - \frac{3}{2}dd_{1}^{2} - \left[ {Ka\left( {h_{1} + h_{2} } \right) - \frac{{d^{2} }}{2}} \right]d_{1} + Kadh_{1} = 0$$

(12)

In the above formula, d₂ = d − d₁, K represents the earth’s equivalent radius coefficient, and we assume

$$P = 1.5925Kd\left( {h_{2} - h_{1} } \right)$$

(13)

$$Q = \frac{{d^{2} }}{12} + 2.125K\left( {h_{2} + h_{1} } \right)$$

(14)

$$\varphi = ar\cos \frac{P}{{Q^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} }}$$

(15)

$$d_{1} = \frac{d}{2} + 2\sqrt Q \cos \left( {\frac{\phi }{3} + 240} \right)$$

(16)

The tangent line AB through the reflection point C cuts the antenna heights h₁ and h₂ at both ends into two parts.

$$h_{1} = h_{1}^{'} + \Delta h_{1} \quad \Delta h_{1} = \frac{{d_{1}^{2} }}{2Ka}$$

(17)

$$h_{2} = h_{2}^{'} +\Delta h_{2} \quad\Delta h_{2} = \frac{{d_{2}^{2} }}{2Ka}$$

(18)

where a is the radius of the earth; $h_{1}^{'}$ and $h_{2}^{'}$ are the effective height of the antenna. The reflection fading loss thus obtained is

$$L_{f} = 10\lg \frac{{\left( {{{4\pi d} \mathord{\left/ {\vphantom {{4\pi d} \lambda }} \right. \kern-0pt} \lambda }} \right)^{2} }}{{1 + D_{0}^{2} - 2D_{0} \cos \left( {\frac{{4\pi h_{1}^{'} h_{2}^{'} }}{d\lambda }} \right)}}$$

(19)

where D₀ is the ground equivalent reflection coefficient. Figure 5 shows that the frequency f is 300 MHz, 3 GHz, and 30 GHz, respectively; the transmitter height h₁ is 100 m, the mobile station height h₂ is 50 m, the communication distance d is 0–80 km, the earth radius a is 6400 km, and the earth is equivalent when the radius coefficient K = 4/3 and the ground equivalent reflection coefficient D₀ = 1, the curve relationship between the reflection loss L_f and the distance d between the transmitting and receiving antennas.

Fig. 5

Curves of reflection loss and transmission distance at different frequencies

3 Modeling of Marine Wireless Transmission Channels

3.1 Model Parameters of the Marine Channel

RMS of wave height

Wind and waves on the sea surface are an important factor that causes changes in the ocean channel. Sea state is a method of describing the state of the sea surface in the form of numerical series. In Table 1, WMO and Douglas, both divide the sea state by wave height [5]. Root mean square (RMS) of wave height refers to the root mean square value of sea surface wave height.

Table 1 Division of sea state

Roughness of the sea

Roughness of the sea g used to describe the degree of sea surface undulation. The expression is as follows

$$g = \frac{{\sigma_{h} \sin \varphi }}{\lambda }$$

(20)

where λ is the wavelength of the carrier wave, σ_h is RMS of wave height, and φ is the incident angle of the radio wave.

Dielectric constant of seawater

Dielectric constant of seawater ε_c is a complex number, which is related to the electromagnetic wave wavelength λ, the sea surface conductivity σ_e and the dielectric constant ε_r

$$\varepsilon c = \varepsilon r - j60\lambda \sigma e$$

(21)

Dielectric constant of seawater ε_c is used in the calculation of Fresnel’s reflection coefficient.

Fresnel’s reflection coefficient

According to the polarization method, it can be divided into the Fresnel coefficient under vertical polarization $\Gamma V$ and the Fresnel coefficient under horizontal polarization $\Gamma H$.

$$\Gamma V = \frac{{\varepsilon c\sin \varphi - \sqrt {\varepsilon c - \cos^{2} \varphi } }}{{\varepsilon c\sin \varphi + \sqrt {\varepsilon c - \cos^{2} \varphi } }}$$

(22)

$$\Gamma H = \frac{{\sin \varphi - \sqrt {\varepsilon c - \cos^{2} \varphi } }}{{\sin \varphi + \sqrt {\varepsilon c - \cos^{2} \varphi } }}$$

(23)

3.2 Modeling of Maritime Wireless Channels

Mirror reflection coefficient

In fact, the specular reflection multipath comes from a reflection area, but it is treated as a single reflection point during modeling. Ament gives the formula [6]

$$\rho s = \exp \left[ { - 2\left( {\frac{2\pi \sigma h\sin \varphi }{\lambda }} \right)} \right]$$

(24)

where λ = c/f, c = 3 × 10⁸ m/s. Later, Miller modified Ament’s formula [7] and proved that the mirror reflection coefficient after the zero-order modified Bessel function I₀(P_s) is closer to the sea surface [8].

$$Ps = 2\left( {\frac{2\pi \sigma h\sin \varphi }{\lambda }} \right)^{2}$$

(25)

$$\rho s = \exp \left[ {Ps} \right]I0\left( {Ps} \right)$$

(26)

Because the surface of the earth is not horizontal, the influence of the curvature of the earth on the specular reflection coefficient should also be considered [9]. Suppose the horizontal distance from the transmitter to the mirror reflection point is G₁, the horizontal distance from the mirror reflection point to the receiver is G₂, and the radius of the earth is R_e. Earth’s curvature factor D is

$$D = \left( {1 + \frac{2G1G2}{{R_{e} \left( {G1 + G2} \right)\sin \varphi }}} \right)^{{ - \frac{1}{2}}}$$

(27)

The transmitting signal platform is 1 km from the horizontal plane, the receiving signal platform is 250 m from the horizontal plane, the horizontal distance between the two is 10 km, the RMS wave height is 0.3 m, the carrier frequency is 100 MHz, 1 GHz, 10 GHz, and 100 GHz, corresponding to the wavelength of 3 m, 0.3 m, 0.03 m, and 0.003 m. As shown in Fig. 6, as the incident angle continues to increase, the curvature of the earth also increases.

Fig. 6

Earth curvature

It can be seen from Fig. 7 that, without considering the Earth’s curvature, when other conditions remain unchanged, the specular reflection coefficient becomes smaller as the carrier frequency increases; when other conditions remain unchanged, the reflection coefficient becomes smaller when the incident angle increases. Considering the influence of the curvature of the earth, the smaller the incident angle, the greater the influence of the curvature of the earth on the mirror reflection coefficient.

Fig. 7

Mirror reflection coefficient

Specular energy

It is assumed that the signal voltage of the direct path relative to the direct path is 1 V. The voltage loss value of the specular reflection path is relative to the direct path signal.

$$\frac{Vm}{Vd} = \rho s\sqrt {G_{\text{ant}} } |\Gamma V|\rho {\text{veg}}$$

(28)

Diffuse area

Define the diffuse area boundary as

$$\beta \lim = \frac{k\beta 0}{\sqrt 2 }$$

(29)

k is the standard coefficient of variance. It is assumed that the diffuse reflection area is a flat plane. According to Fig. 8, the unit vectors set in the directions of R₁ and R₂ are U₁ and U₂, the coordinates of the reflection point are (x, 0, z), the coordinates of the transmitting end are (0, H_t, 0), and the coordinates of the receiving end are (G, H_r, 0), then

Fig. 8

Effective diffuse reflection area

$$\begin{aligned} U1 & = {{\left( { - xi + Htj - zk} \right)} \mathord{\left/ {\vphantom {{\left( { - xi + Htj - zk} \right)} {R1}}} \right. \kern-0pt} {R1}} \\ U2 & = {{\left( {\left( {G - x} \right)i + Hrj - zk} \right)} \mathord{\left/ {\vphantom {{\left( {\left( {G - x} \right)i + Hrj - zk} \right)} {R2}}} \right. \kern-0pt} {R2}} \\ \end{aligned}$$

(30)

Definition β₀ is the root mean square of the inclined surface of the sea on any small diffuse reflection area [10]. Definition β is the radian value of the angle formed by the bisector of R₁ and R₂ and the vertical direction. Then, the unit vector and β in the direction of the angle bisector can be expressed as

$$UB = {{\left( {U1 + U2} \right)} \mathord{\left/ {\vphantom {{\left( {U1 + U2} \right)} {|U1 + U2|}}} \right. \kern-0pt} {|U1 + U2|}}$$

(31)

$$\beta \lim = \frac{k\beta 0}{\sqrt 2 }$$

(32)

The range calculated when β = β_lim is the diffuse reflection range C_B

$$\begin{aligned} CB & = \cos \left( {\beta_{\lim } } \right) = \cos \left( {\frac{k\beta 0}{\sqrt 2 }} \right) = UB \cdot j \\ & = \frac{{{{Ht} \mathord{\left/ {\vphantom {{Ht} {R1 + {{Hr} \mathord{\left/ {\vphantom {{Hr} {R2}}} \right. \kern-0pt} {R2}}}}} \right. \kern-0pt} {R1 + {{Hr} \mathord{\left/ {\vphantom {{Hr} {R2}}} \right. \kern-0pt} {R2}}}}}}{{\sqrt {\left( {\frac{ - x}{R1} + \frac{G - x}{R2}} \right)^{2} + \left( {\frac{Ht}{R1} + \frac{Hr}{R2}} \right)^{2} + \left( {\frac{ - z}{R1} + \frac{ - z}{R2}} \right)^{2} } }} \\ \end{aligned}$$

(33)

As shown in Fig. 9, the effective diffuse reflection area is approximately an ellipse. When the value of k becomes larger, the diffuse reflection area becomes larger.

Fig. 9

Diffuse area

Diffuse energy

Literature [11, 12] provides a basis for calculating the multipath of diffuse reflection area. Let the direct path voltage be 1 V. The formula for calculating the voltage loss of the diffuse reflection path relative to the direct path signal is

$$\frac{Vd}{Vr} = \sqrt {\frac{1}{4\pi }\left( {\frac{R}{R1R2}} \right)^{2} \frac{1}{{\beta 0^{2} }}\exp \left( { - \frac{{\beta^{2} }}{{\beta 0^{2} }}} \right)dA} |\Gamma V| \cdot \sqrt {G_{\text{ant}} } \cdot \rho {\text{roughness}} \cdot \sqrt {Sf}$$

(34)

where R, $R1$ and $R2$ are the direct path lengths, and $dA$ represent an arbitrarily small area on the diffuse reflection area. $\rho {\text{roughness}}$ represents the diffuse reflection coefficient. The $\exp \left( { - {{\beta^{2} } \mathord{\left/ {\vphantom {{\beta^{2} } {\beta 0^{2} }}} \right. \kern-0pt} {\beta 0^{2} }}} \right)$ obeys Gaussian distribution, and $\sqrt {Sf}$ represents the shadow effect coefficient. The diffuse reflection coefficient of any small area in the effective diffuse reflection area is a function of the specular reflection coefficient in the vicinity.

$$\rho {\text{roughness}} = \sqrt {\rho d\left( {\varphi 1} \right)\rho d\left( {\varphi 2} \right)} \, = \sqrt[4]{{\left( {1 - \rho s^{2} \left( {\varphi 1} \right)} \right)\left( {1 - \rho s^{2} \left( {\varphi 2} \right)} \right)}}$$

(35)

And $\sqrt {Sf}$ is actually the probability that the receiver can be received.

$$\begin{aligned} Li & = \frac{{\beta 0 \cdot \exp \left[ {\left( { - \frac{\tan \varphi i}{\beta 0}} \right)^{2} } \right]}}{\sqrt \pi \cdot \tan \varphi i} - erfc\left( {\frac{\tan \varphi i}{\beta 0}} \right) \\ Sfi & = \left[ {1 - \frac{1}{2}erfc\left( {\frac{{tan{\varphi }i}}{{\upbeta0}}} \right)^{2} } \right]/\left( {Li + 1} \right) \\ Sf & = Sf1 \cdot Sf2 \\ \end{aligned}$$

(36)

where

Simulation results and data analysis

Set carrier frequency 100 MHz, RMS wave height 0.25 m, $\sigma e = 0.00 1$, $\varepsilon r = 3$, k is 2, use omnidirectional dipole antenna.

It can be seen from Fig. 10 that the value of the incident angle is small, and the farther away from the transmitter, the smaller the value of the incident angle. It can be seen from Fig. 11 that the delay energy of the multipath signal caused by diffuse reflection is attenuated in a decreasing trend. The difference between the delay time of the direct reflection path and the direct reflection path is small.

Fig. 10

Variation of incident angle

Fig. 11

Multipath shock response curve

4 Conclusions

The calculation methods of the RMS wave height of sea channel parameters, sea surface roughness, seawater dielectric constant, and Fresnel reflection coefficient are given. Combined with the actual sea surface environment, a multipath model at sea was established. Relative to the direct path energy, the specular reflection path energy is mainly related to the specular reflection coefficient at the specular reflection point; the diffuse reflection path energy is related to the diffuse reflection area, sea wave height, diffuse reflection surface roughness coefficient, shadow effect coefficient, etc. Finally, through simulation, it is found that the time delay of the mirror reflection path is small, and the energy loss of the diffuse reflection path signal increases with the increase of the time delay.