Dynamical analysis of rendezvous and docking with very large space infrastructures in non-Keplerian orbits

Abstract

A space station in the vicinity of the Moon can be exploited as a gateway for future human and robotic exploration of the solar system. The natural location for a space system of this kind is about one of the Earth–Moon libration points. The study addresses the dynamics during rendezvous and docking operations with a very large space infrastructure in an EML2 Halo orbit. The model takes into account the coupling effects between the orbital and the attitude motion in a circular restricted three-body problem environment. The flexibility of the system is included, and the interaction between the modes of the structure and those related with the orbital motion is investigated. A lumped parameter technique is used to represents the flexible dynamics. The parameters of the space station are maintained as generic as possible, in a way to delineate a global scenario of the mission. However, the developed model can be tuned and updated according to the information that will be available in the future, when the whole system will be defined with a higher level of precision.

1 Introduction

In the last two decades, humanity achieved amazing goals with space missions in Low Earth Orbit, creating the base for what can be called prolonged human habitation in space. In the same time, robots have been targeted throughout the solar system to explore different planets and numerous celestial objects. Now, the time for another step forward in space exploration has come. In fact, the future exploration of solar system will be driven by a cooperation of astronauts and robots in space missions that will be aimed progressively further away from the Earth. The roadmap to drive this ambitious program has been already proposed by the International Space Exploration Group (ISECG) [1], and one of the key points in the whole mission scenario is the so-called Evolvable Deep Space Habitat: a modular space station in lunar vicinity.

At the current level of study, the optimum location for space infrastructure of this kind has not yet been determined, but a favorable solution can be about one of the Earth–Moon libration points, such as in a Earth–Moon Lagrangian Point n^o 2 (EML2) Halo orbit. Moreover, the final configuration of the entire system is still to be defined, but it is already clear that to assemble the structure, several rendezvous and docking activities will be carried out, many of which to be completely automated.

Unfortunately, the current knowledge about rendezvous in cis-lunar orbits is minimal and it is usually limited to point-mass dynamics. The aim of this paper is to present some preliminary results about a possible rendezvous scenario with a large space infrastructure in non-Keplerian orbits. The dynamical analysis is based on a coupled orbit-attitude model of motion in a circular restricted three-body problem (CR3BP) environment, and includes the flexibility of the structure with a lumped parameter technique.

The research is started with the definition of a possible rendezvous strategy that can be inserted as a part of a broad mission framework in cis-lunar space. It exploits invariant manifolds associated with unstable periodic orbits, such as EML2 Halo orbits, by finding a heteroclinic connection between two different orbits. A tool to optimize this class of transfers is developed and discussed. Moreover, a tool to simulate the relative dynamics during final approach phases is also presented. The analysed rendezvous strategy is an example of application of the simulation tools and the coupled dynamical model that have been and are being developed from the authors. A separate section is dedicated to highlight the effects of the extended flexible bodies on the dynamics in non-Keplerian orbits.

This work is intended to pose a preliminary base for further developments within the research area on very large and flexible structure in three-body problem environments. The purpose is the definition of a new astrodynamics tool, able to simulate such a class of space systems. At the current stage of development, the model does not yet include perturbing effects, such as solar radiation pressure and fourth-body (Sun) gravity, and the analysis is still concentrated on a single element of the structure. However, the model has been founded on a “multi-body-friendly” approach, and the extension of the results is of easy implementation.

Looking at recent literature, it is possible to find other research works that investigated the coupled orbit-attitude dynamics in non-Keplerian environment. For example, the works of Guzzetti and Knutson [2, 3] considered both planar and full three-dimensional motion, providing a method to study families of periodic orbit-attitude solutions. More recently, Colagrossi [4] investigated the coupling between orbit-attitude dynamics and the flexibility of the structure in a slightly different way than the one presented in this paper. A comparison between the two different approaches of the authors will be discussed in the conclusions of this paper.

2 Theoretical background

The present research is based on circular restricted three-body problem modelling approach, which consider the motion of three masses $m_1$, $m_2$, and m, where $m\ll m_1,m_2$ and $m_2 < m_1$. $m_1$ and $m_2$ are denoted as primaries, and are assumed to be in circular orbits about their common center of mass. The motion of m does not affect the trajectories of the primaries.

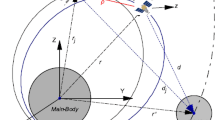
The dynamics is written in a rotating reference frame, S, which is called synodic frame and is represented in Fig. 1. It is centered at the center of masses, $m_1$ and $m_2$, of the system, O; the first axis, $\hat{\mathbf {x}}$, is aligned with the vector from $m_1$ to $m_2$; the third axis, $\hat{\mathbf {z}}$, is in the direction of the angular velocity of S, $\varvec{\omega }=\omega {\hat{\mathbf {z}}}$; ${\hat{\mathbf {y}}}$ completes the right-handed triad. The system can be defined by the mass parameter:

$$\begin{aligned} \mu =\frac{m_2}{m_1+m_2}, \end{aligned}$$

(1)

the magnitude of the angular velocity of S,

$$\begin{aligned} \omega =\sqrt{\frac{G(m_1+m_2)}{r_{12}^3}}, \end{aligned}$$

(2)

and the distance between the primaries $r_{12}$. The equations of motion are usually normalized with respect to $r_{12}$, $\;\omega$ and the total mass of the system $m_{T}=m_1+m_2$. After the normalization, the universal constant of gravitation is $G=1$.

The mass m is an extended body, and the model is currently based on a simple and generic structural element: a rigid rod. In this way, it is possible to have a solid foundation, which can be easily extended to more complex configurations of the space system, with a multi-body technique [5]. The body m has five degrees of freedom: the position of its center of mass B, ${\mathbf {r}}_B$, and two independent parameters to define the orientation of the versor aligned with the rod, ${\hat{\mathbf {u}}}$.

Fig. 1

Synodic reference frame

The equations of motion can be derived starting from a Lagrangian Formulation, where the Lagrangian function, ${\mathcal {L}}={\mathcal {T-G}}$, includes the kinetic energy, ${\mathcal {T}}$, and the generalized potential, $\mathcal {G}$.

The kinetic energy $\mathcal {T}$ of the rigid body can be expressed as the kinetic energy of the translational motion of the center of mass plus the kinetic energy of the rotational motion of m as follows:

$$\begin{aligned} {\mathcal {T}}=\frac{1}{2}m\,{\mathbf {\dot{r}}}_B\cdot {\mathbf {\dot{r}}}_B+\frac{1}{2}\varvec{\Omega }\cdot {\mathbf {I}}_B\cdot \varvec{\Omega }, \end{aligned}$$

(3)

where ${\mathbf {\dot{r}}}_B$ is the velocity of B, $\varvec{\Omega }$ is the angular velocity of the body relative to the S frame, and ${\mathbf {I}}_B$ is the inertia tensor about B.

The generalized potential $\mathcal {G}$ is related with the gravitational forces and with the inertia forces, since the synodic frame S is a non-inertial reference frame that is rotating with the two primaries. It can be expressed as the sum of the ordinary gravitational potential, $V_g=V_{g_1}+V_{g_2}$, and the generalized potential of the inertia forces, $V_i$.

The gravitational action exerted by the ith spherical primary on m can be derived from:

$$\begin{aligned} V_{g_i}=-\frac{{Gm}_im}{r_{B_i}}+\frac{{Gm}_i}{r_{B_i}^3}\left[ \frac{3}{2}({\hat{\mathbf {r}}}_{B_i}\cdot {\mathbf {I}}_{B_i}\cdot {\hat{\mathbf {r}}}_{B_i})-\mathrm {tr}({\mathbf {I}}_B)\right] , \end{aligned}$$

(4)

where $r_{B_i}$ and ${\hat{\mathbf {r}}}_{B_i}$ are, respectively, magnitude and direction of ${\mathbf {r}}_{B_i}$: position vector of m with respect to the i-th primary. The previous expression is an expansion up to the second order of the gravitational potential generated by a spherical attractor on a small extended body [6].

The generalized potential of the inertia forces is needed to write the equations of motion in S, and it can be expressed as follows:

$$\begin{aligned} V_i=\frac{m}{2}{\mathbf {r}}_B\cdot \left[ \varvec{\omega }\times (\varvec{\omega }\times {\mathbf {r}}_B)+2\varvec{\omega }\times {\mathbf {\dot{r}}}_B \right] -\frac{1}{2}\varvec{\omega }\cdot {\mathbf {I}}_B\cdot (\varvec{\omega }+2\varvec{\Omega }). \end{aligned}$$

(5)

It is important to remember that a generic generalized potential ${\mathcal {V}}({\mathcal {P}},{\mathcal {\dot{P}}})$, where $\mathcal {P}$ is the position and $\mathcal {\dot{P}}$ the velocity, is defined in a way that the related force can be computed as follows:

$${\mathcal{F}} = \frac{{\rm{d}}}{{\rm{dt}}}\left( {\frac{{\partial {\mathcal{V}}}}{{\partial {\dot{\mathcal{P}}}}}} \right) - \frac{{\partial {\mathcal{V}}}}{{\partial {\mathcal{P}}}} .$$

(6)

To write the normalized equation of motion, $\mathcal {L}$ has to be written in non-dimensional form. In fact, from now on, all the variables will be intended to be non-dimensional: lengths will be divided by $r_{12}$, masses by $m_{T}$ and times by $1/\omega$. In the same way, from now on, the time derivative will be taken with respect to the non-dimensional time $\tau =\omega t$: $\dot{\circ }=\mathrm{d}\circ /\mathrm{d}\tau$.

At this point, it is possible to derive the equations of motion as follows:

$$\frac{{\rm{d}}}{{{\rm{d}}\tau }}\left( {\frac{{\partial {\mathcal{L}}}}{{\partial \dot{q}_{j} }}} \right) - \frac{{\partial {\mathcal{L}}}}{{\partial q_{j} }} = A_{j} ,$$

(7)

where $q_j, j=1,\dots ,5$ are the generalized coordinates, and $A_j$ the generalized non-dimensional contributions due to different external forces, such as the solar radiation pressure or the presence of a fourth body. In the present analysis, $A_j=0$.

Applying the previous equations to the case of the rigid rod m of length l, $\mathcal {L}$ can be expressed as follows:

$$\begin{aligned} \mathcal {L}=\mathcal {L}_0+\epsilon _0^2\mathcal {L}_2+\epsilon _0^3\mathcal {L}_3+\cdots , \end{aligned}$$

(8)

where $\epsilon _0$ is the non-dimensional length of the rod: $\epsilon _0=l/r_{12}$, and it is usually a small number.

Limiting the expansion to the second order, our system of equations becomes:

$$\frac{{\rm{d}}}{{{\rm{d}}\tau }}\left( {\frac{{\partial {\mathcal{L}}_{0} }}{{\partial \dot{x}}}} \right) - \frac{{\partial {\mathcal{L}}_{0} }}{{\partial x}} = \epsilon _{0}^{2} \frac{{\partial {\mathcal{L}}_{2} }}{{\partial x}}$$

(9)

$$\frac{{\rm{d}}}{{{\rm{d}}\tau }}\left( {\frac{{\partial {\mathcal{L}}_{0} }}{{\partial \dot{y}}}} \right) - \frac{{\partial {\mathcal{L}}_{0} }}{{\partial y}} = \epsilon_{0}^{2} \frac{{\partial {\mathcal{L}}_{2} }}{{\partial y}}$$

(10)

$$\frac{{\rm{d}}}{{{\rm{d}}\tau }}\left( {\frac{{\partial {\mathcal{L}}_{0} }}{{\partial \dot{z}}}} \right) - \frac{{\partial {\mathcal{L}}_{0} }}{{\partial z}} = \epsilon_{0}^{2} \frac{{\partial {\mathcal{L}}_{2} }}{{\partial z}}$$

(11)

$$\frac{{\rm{d}}}{{{\rm{d}}\tau }}\left( {\frac{{\partial {\mathcal{L}}_{2} }}{{\partial \dot{\theta }}}} \right) - \frac{{\partial {\mathcal{L}}_{2} }}{{\partial \theta }} = 0$$

(12)

$$\frac{{\rm{d}}}{{{\rm{d}}\tau }}\left( {\frac{{\partial {\mathcal{L}}_{2} }}{{\partial \dot{\varphi }}}} \right) - \frac{{\partial {\mathcal{L}}_{2} }}{{\partial \varphi }} = 0,$$

(13)

where x, y, and z are the non-dimensional cartesian coordinates of B in S, while $\theta$ and $\varphi$ are, respectively, the in-plane and out-of-plane libration angles that define univocally the orientation of $\hat{\mathbf {u}}$.

It is interesting to note that limiting $\mathcal {L}$ to the main order ${\mathcal {L}}_0$, Eqs. (9)–(13) reduce to the usual circular restricted three-body problem equations. In this case, the size of the rigid rod disappears from the problem.

The attitude dynamics of a one-dimensional body, such a rod, is fully defined by $\theta$ and $\varphi$. However, it is possible to use another set of attitude parameters that, despite it can be redundant, it is usually more convenient, and allows more intuitive analyses [7]. In this work, a set of Euler angles in 1–2–3 sequence, commonly called Bryant Angles [8], is employed. The singularity condition of these attitude parameters happens when $\hat{\mathbf {u}}$ is perpendicular to the orbital plane, which is not likely to happen in this research work. The angles associated with the 1–2–3 rotations are, respectively, $\phi _1$, $\phi _2$, and $\phi _3$; they allows to express orientation of m as follows:

$$\begin{aligned} \hat{\mathbf {u}}= & {} [\cos {\phi _2}\cos {\phi _3}, \cos {\phi _1}\sin {\phi _3}+\sin {\phi _1}\sin {\phi _2}\cos {\phi _3},\nonumber \\&\sin {\phi _1}\sin {\phi _3}-\cos {\phi _1}\sin {\phi _2}\cos {\phi _3}]. \end{aligned}$$

(14)

The equations of motion in terms of Bryant angles can be derived using a Newton–Euler formulation. In fact, the angular momentum at B, ${\mathbf {h}}_B$, is related to the torque applied to the center of mass, ${\mathbf {m}}_B$, as follows:

$$\begin{aligned} \frac{\mathrm{d}\,\mathbf {h}_B}{\mathrm{d}t}=\mathbf {m}_B. \end{aligned}$$

(15)

A new system of reference attached to the rod can be defined: it is centered in B; ${\hat{\mathbf {u}}}_1={\hat{\mathbf {u}}}$; ${\hat{\mathbf {u}}}_2$ is aligned with the direction of the variation of ${\hat{\mathbf {u}}}$, $\dot{\hat{\mathbf {\mathbf {u}}}}$; ${\hat{\mathbf {u}}}_3$ completes the right-handed frame as in Fig. 2. In this body frame, the angular momentum of m is as follows:

$$\begin{aligned} {\mathbf {h}}_B=I_B\Omega _\perp {\hat{\mathbf {u}}}_3, \end{aligned}$$

(16)

where $\Omega _\perp =|{\hat{\mathbf {u}}\times \dot{\hat{\mathbf {\mathbf {u}}}}}|=|\dot{\hat{\mathbf {\mathbf {u}}}}|$, and $I_B$ the moment of inertia of the rod with respect to B.

Fig. 2

Body reference frame

From Eqs. (15) and (16), with some algebraic manipulation, it is possible to write a system of three equations with the time evolution of $\Omega _\perp$, ${\hat{\mathbf {u}}}_1$ and ${\hat{\mathbf {u}}}_3$. However, exploiting the Bryant angles to describe the orientation of the body frame with respect to S, the attitude equations of motion are four. In non-dimensional form, they are:

$$\begin{aligned}&\frac{\mathrm{d}\phi _1}{\mathrm{d}\tau }=-\frac{M_2}{\omega \,\Omega _\perp I_B}\frac{\cos {\phi _3}}{\cos {\phi _2}}\end{aligned}$$

(17)

$$\begin{aligned}&\frac{\mathrm{d}\phi _2}{\mathrm{d}\tau }=-\frac{M_2}{\omega \,\Omega _\perp I_B}\sin {\phi _3}\end{aligned}$$

(18)

$$\begin{aligned}&\frac{\mathrm{d}\phi _3}{\mathrm{d}\tau }=\frac{\Omega _\perp }{\omega }+\frac{M_2}{\omega \,\Omega _\perp I_B}\cos {\phi _3}\tan {\phi _2}\end{aligned}$$

(19)

$$\begin{aligned}&\frac{1}{\omega }\frac{\mathrm{d}\Omega _\perp }{\mathrm{d}\tau }=\frac{M_3}{\omega ^2 I_B}, \end{aligned}$$

(20)

where $M_2$ and $M_3$ are the components of ${\mathbf {m}}_B$ along the second and the third direction of the body frame. It must be noted that in the present analysis, all the torques are normal to the rod, and this conditions must be respected in the framework of this research. The torque ${\mathbf {m}}_B$ is computed from the forces that are derived from the already presented potentials in Eqs. (4) and (5). Both the inertial forces and the gravitational forces must be considered to compute ${\mathbf {m}}_B$, because this research is carried out in the synodic frame S. In this paper, any other external force is neglected.

The coupled orbit-attitude dynamical model is, therefore, represented by Eqs. (9)–(11) and (17) to (20).

The astrodynamics tool that is presented and discussed in this paper is based on the dynamical model that has been previously described, and it is intended to simulate the orbit-attitude dynamics of large and flexible space infrastructures in cis-lunar environment. In particular, it is mainly dedicated to analyse transfer trajectories and rendezvous dynamics with extended space systems in non-Keplerian orbits. The structural properties of the proposed space station are not completely known yet, but its probable dimensions and typical structural characteristics of the existing space systems require to analyse and simulate the dynamics with the inclusion of flexible effects. The main reason is to highlight possible couplings between orbit-attitude dynamics and flexible dynamics. In fact, orbital and rotational motion of the space station may be perturbed by the natural vibrations of the flexible structure or, inversely, the frequencies associated with the non-Keplerian dynamics may be an issue with respect to possible resonances of the flexible system. At the current stage of development of the dynamical tool, the flexibility of the system is included in the model with a lumped parameters technique, exploiting lumped masses connected to a rigid structure with a massless spring; in a way to have an equivalent spring–mass system, able to represent a pseudo-mode of vibration [9, 10].

The spring–mass systems are attached to the rod in arbitrary points at a fixed distance from B. Their motion is excited from the dynamics of the rod itself. In this preliminary analysis, it is assumed that the lumped masses do not interact directly with the gravitational field. Their effect is inserted in the equations of motion through $\mathbf {m}_B$; in fact, the spring generates a force on the rod and, therefore, a torque with respect to B. The net force on B is neglected; hence, the flexibility effect is considered only in the attitude dynamics. However, the orbital motion is influenced by the coupling with the attitude equations.

Each i-th spring–mass system, represented in Fig. 3, is located at a distance $l_i$ from the barycenter of the rod, and it is defined by a pseudo-modal mass $\widetilde{m}_i$ and an equivalent stiffness $\widetilde{k_i}$. All the modal masses are scaled to 1, and each pseudo-mode is entirely represented through $\widetilde{k_i}$. From the natural frequency of each mode of the structure $\widetilde{\omega _i}$, the stiffness can be computed as follows:

$$\begin{aligned} \widetilde{k_i}=\widetilde{\omega }_i^2\widetilde{m}_i. \end{aligned}$$

(21)

Fig. 3

Spring–mass system

The motion of the spring–mass systems is constrained to be orthogonal to the rod to simulate only the bending modes. The elongation of the spring, with respect to the linking point, is $\widetilde{\mathbf {z}}_i$. The acceleration of the linking point is $\ddot{\widetilde{\mathbf {y}}}_i$, and it can be easily computed knowing the dynamics of the body m. In addition, in this case, the equations of motion have to be normalized with the same process that has been described for the rigid body dynamics; all the aforementioned variables are in non-dimensional form. For each spring–mass system, it is possible to write:

$$\begin{aligned} \widetilde{m}_i(\ddot{\widetilde{\mathbf {z}}}_i+\ddot{\widetilde{\mathbf {y}}}_i)+\widetilde{k_i}\widetilde{\mathbf {z}}_i=0. \end{aligned}$$

(22)

The torque exerted on the rod, with respect to B, by a single spring–mass system is as follows:

$$\begin{aligned} {\mathbf {m}}_{{B_k}_i}=l_i{\hat{\mathbf {u}}}_1 \times \widetilde{k_i}\widetilde{\mathbf {z}}_i. \end{aligned}$$

(23)

The results that are presented in this paper refer to a configuration with two spring–mass systems at the ends of the rod. In this way, it is possible to simulate the first bending mode of two cantilever beams attached to B.

3 Rendezvous definition

Rendezvous in space involves a spacecraft already in a operational orbit, which is commonly called target, and a spacecraft that is approaching to it, chaser. The different phases of a generic rendezvous have been extensively studied in the past and consist of a series of orbital manoeuvres and controlled trajectories, which have to progressively bring the chaser into the vicinity of the target [11].

The rendezvous between two spacecrafts in Earth orbits, i.e., in the framework of the restricted two body problem, is nowadays well studied and tested, thanks to the experience of the International Space Station (ISS). However, this delicate phase is strongly supported by the direct control of the astronauts. The technology to support completely automated and unmanned rendezvous missions has not yet reached an high level of maturity. Moreover, if the autonomous rendezvous operations have to be conducted in CR3BP, the studies are even more preliminary and not completely developed yet. Furthermore, as already said, studies in the literature were always limited to point-mass spacecrafts.

Possible rendezvous strategies have been recently proposed with a target on a Earth–Moon L2 Halo orbit by different authors [12,13,14]. An example involving the same family of operational orbits is presented in this paper, in accordance with the existing feasibility studies about the cis-lunar space station mentioned above. However, the tool that is being developed from the authors is already able to work around the other collinear Lagrangian points, even though only L1 can be a valid alternative for this kind of space infrastructures.

The automated transfer vehicles (chaser) will have to reach the cis-lunar space station (target) from different locations, such as the Earth, the Moon, or a different non-Keplerian orbit, within a reasonable time and cost. Therefore, a preliminary analysis involves the design of a trajectory connecting the operational Halo orbit with the desired location. A vast literature addresses this problem, and many solutions were proposed to solve it. For example, the one proposed in the same department of the authors [15] injects the spacecraft on an highly eccentric orbit from a Low Earth Orbit (LEO) or Low Lunar Orbit (LLO), and near the apogee, a dedicated manoeuvre pushes the spacecraft on a stable manifold, which is progressively converging to the operational Halo orbit.

By assuming the evolvable space infrastructure on an EML2 Halo orbit, it is reasonable to have the injection point of the stable manifold in the vicinity of the Moon. In this way, it is possible to find many injection points that can be easily reached from an LEO, an LLO, the Lunar surface, or a safe parking orbit. The complete scenario of logistic transfers and operational missions on the Moon is out of the scope of this work, and it is just employed to contextualize the presented solution, which considers a parking Halo orbit for the chaser and the operational Halo orbit of the target.

According to the definition introduced by Koon [16], this kind of rendezvous can be denoted as Halo Orbit Insertion (HOI), being the chaser on a different Halo orbit when the sequence of manoeuvres is started. The other type of rendezvous is called Stable Manifold Orbit Insertion (MOI), because in that case, the chaser is travelling from the Earth, or the Moon, and is directly inserted in the stable manifold of the operational orbit.

The rendezvous that is presented in this work is composed by the following phases, similar to what has been proposed by Lizy–Déstrez [12]:

• Starting phase  The chaser and the target are orbiting their own Halo orbits, which are characterized by two different values of maximum elongation in z, $A_z$.

• Departure  The chaser is injected in an unstable manifold of the parking orbit with a first manoeuvre, $\Delta v_1$.

• Switching manoeuvre  The chaser is injected in the stable manifold of the target operational orbit. The injection point is at the intersection of the unstable and the stable manifolds. A second manoeuvre, $\Delta v_2$, is needed. If an MOI rendezvous is considered, the starting point is here.

• Approach manoeuvre  The chaser arrives in proximity of the target and, with a third manoeuvre, $\Delta v_3$, is moved very close to the operational Halo orbit. The relative distance between chaser and target is maintained within the safety standards.

• Closing phase  A fourth manoeuvre, $\Delta v_4$, aligns the chaser with the docking axis of the space station. This phase starts as soon the chaser enters in the field of view of the space station.

• Final approach  A series of manoeuvres, $\Delta v_5$ and $\Delta v_{51}$, progressively reduces the relative distance between cargo and space station. The chaser is maintained aligned with the docking axis of the space station, which is rotating.

• Mating phase  A continuous manoeuvre, $\Delta v_6$, is performed to reduce to zero the relative distance between the two spacecrafts and brings the chaser at the docking port, before the final contact.

Fig. 4

Operational and Parking Halo orbits in normalized S

The case that is presented in this paper involves an operational EML2 Halo orbit with $A_z={10{,}000}$ km in positive direction, Northern Halo. The chaser’s parking orbit is a different Northern EML2 Halo orbit with $A_z={8000} km$. The switching point is assumed to be in the vicinity of the Moon, in the space between Earth and Moon: $x_{SP}<1-\mu$. This choice is motivated from the willing to simulate a possible cyclic chaser that is continuously transferring between the operational and the parking Halo orbit; the passage between Earth and Moon allows an easy encounter with a cargo coming from the Earth, the Moon, or a Low Lunar orbit. The chaser is a point mass, while the target (space station) is a rod with $l_T={100}$ m, and mass $m_T={300{,}000}$ kg. The docking axis is aligned with the rod axis, ${\hat{\mathbf {u}}}_{1_T}$. The halo orbits considered in this work are shown in Fig. 4, with data reported in Table 1.

Table 1 Operational and Parking Halo parameters

4 Rendezvous simulation

The dynamical tool that is used to simulate the rendezvous of the chaser with the target propagates the coupled orbit-attitude dynamics of the space station and the point-mass orbital motion of the chaser.

First of all, it is important to find an heteroclinic connection between the two Halo orbits: the transfer trajectory. In this work, it has been assumed that the chaser and the target are approximately phased in their own orbits according to the chosen transfer, i.e., the target needs the time of the transfer, $t_\mathrm{transfer}$, to move from its starting point to the ending point of the heteroclinic connection. Such requirement can be always satisfied with a Phasing Phase to be conducted before the Starting Phase of the rendezvous operations; moreover, the proximity operations after the heteroclinic transfer are able to correct some errors in the phasing of chaser and target.

Fig. 5

Possible heteroclinic connections for $x_{SP}<1-\mu$

The heteroclinic connection is individuated, computing the unstable manifold of the parking orbit and the stable manifold of the operational orbit. Manifolds can be computed from the eigenvectors of the Monodromy Matrix, $\mathbf {M}$, which is the State Transition Matrix, $\varvec{\Phi }$, evaluated after one orbital period, $\mathrm {T}$. The intersections of the two manifolds are analysed on a Poincarè section and different sub-optimal solutions are located for $x_{SP}<1-\mu$. Then, a correction procedure is applied to all the sub-optimal solutions, to exactly connect in position starting point, switching point, and ending point. In Fig. 5, the sub-optimal solutions are shown before and after the correction procedure. Among the selected sub-optimal solution, the best one is chosen as the one with the smallest $\Delta v_\mathrm{transfer}=\Delta v_1+\Delta v_2+\Delta v_3$. This best sub-optimal transfer is then optimized with an optimization algorithm.

The transfer optimization algorithm starts from the already mentioned sub-optimal connection and slightly varies the state vector of the chaser at the starting point, ${\mathbf {sv}}_\mathrm{Start}=[x_\mathrm{Start},y_\mathrm{Start},z_\mathrm{Start},{\dot{x}}_\mathrm{Start},{\dot{y}}_\mathrm{Start},{\dot{z}}_\mathrm{Start}]$. The starting position, ${\mathbf {r}}_{B_\mathrm{Start}}=[x_\mathrm{Start}, y_\mathrm{Start}, z_\mathrm{Start}]$, is constrained to lie on the Halo orbit. Moreover, also the state vector at the switching point can be varied with the constraint to preserve the continuity in position with the stable manifold of the operational Halo orbit. The algorithm is based on a constrained multiple-shooting corrector with a multi-variable Newton methods [17]. The optimum solution is searched with a derivative-free method. The result of the transfer optimization algorithm is shown in Fig. 6, and the characteristics of the best heteroclinic transfer are reported in Table 2. From these data, the low-cost transfer capabilities of invariant manifolds are evident, but the time of flight during this connection can be somewhat too long for certain applications, e.g., humans’ transportation or emergency cargos. However, this is only a limit for transfers that have to pass between Earth and Moon; in fact, for $x_{SP}>1-\mu$, the typical time of transfer is in the order of few days.

Table 2 Optimal transfer parameters

Fig. 6

Optimal transfer

After $\Delta v_3$, the relative distance between chaser and target is usually in the order of few hundreds of kilometers; in the presented example $|{\mathbf {r}}_\mathrm{Rel} |\simeq {150}$ km. In the following phases, the dynamical tool performs more convenient analyses exploiting a local vertical local horizontal (LVLH) reference frame, similar to what is usually done in LEO. The CR3BP LVLH reference frame is centered at the barycenter B of the target; $\hat{\mathbf {z}}_{LVLH}$ (R-bar) is always directed towards the Lagrangian point associated with the studied Halo; $\hat{\mathbf {y}}_{LVLH}$ is opposite to the direction of the orbital momentum vector; $\hat{\mathbf {x}}_{LVLH}$ (V-bar) completes the right-handed frame, as shown in Fig. 7.

Fig. 7

LVLH reference frame

When the chaser enters in view of the target along the R-Bar, $\Delta v_4$ is performed to align the chaser with the docking axis, ${\hat{\mathbf {u}}}_{1_T}$, of the space station. After this closing phase manoeuvre, the chaser is maintained always aligned with the docking axis of the target, within the field of view along ${\hat{\mathbf {u}}}_{1_T}$. During the final approach phase, this alignment is checked at different interface points; the first is at a distance of 200 km from the target, the second at 10 km, and the third at 500 m. These interface points are needed to break the rendezvous trajectory with some check-and-go points, to have a more gradual and safe final approach.

The different phases after the transfer are computed and optimized with a constrained optimization algorithm. The cost of the manoeuvre at each interface point and the difference in velocity between chaser and target at the end of the arc, as a preliminary measure of the next $\Delta v$, are the objective functions of the optimization algorithm. In this way, the rendezvous path is evaluated minimizing the cost of all the proximity manoeuvres. The constraint is used to reduce the relative distance and maintain the alignment between chaser and target. Thus, at each interface point, the chaser reaches the desired location with a desired attitude relative to the target. The velocity of the chaser is used as design variable to connect the different interface points minimizing the overall $\Delta v$ cost. It has been assumed to control the dynamics with impulsive manoeuvres, and, therefore, the actual design variable is not directly the velocity of the chaser, but the instantaneous $\Delta v$ that are applied at the interface points to control the chaser along the rendezvous trajectory with the minimum possible cost. If the optimization algorithm converges to a feasible solution, the result is a trajectory that matches the final position vector of the target and minimizes the $\Delta v$ cost. The initial guesses at each interface point are obtained randomly. The programming algorithm chosen in this work is a particular version of the barrier method [18, 19], belonging to the class of the so-called interior point methods [20].

Fig. 8

Proximity operations in synodic frame

Fig. 9

Proximity operations in LVLH frame, x–z view: closing and final approach phases

Fig. 10

Final approach in LVLH frame, x–z view

In Figs. 8 and 9, the proximity phases are shown in the synodic and in the LVLH frame. Both frames are useful to analyse the rendezvous, but the latter is more insightful when the distance between chaser and target is in the order of few hundreds of kilometers. In Fig. 9, it can be noted how the closing phase starts when the chaser enters in the field of view along the R-bar, then the following phases are maintained within the field of view in direction of the docking axis. Moreover, in the same figure, the approach along ${\hat{\mathbf {u}}}_1$ is evident; the interface points follow the approach axis that is changing in time because of the rotation of the space station.

Figure 10 shows a more detailed view of the final approach phase, while the mating phase can be analysed in Fig. 11. In the aforementioned pictures, the typical behaviour of relative motion in CR3BP is confirmed: the approaching trajectories are almost rectilinear and the carving feature of LEO rendezvous trajectories is missing.

In Fig. 11, the interface point before $\Delta v_6$, 500 m from the target, is characterized by an hold in the procedures. In fact, for safety reasons, the chaser cannot enter in the Keep-Out Sphere until the authority to proceed is obtained. After the final approach, the mating phase begins.

Fig. 11

Mating phase in LVLH frame, x–z view

In this dynamical analysis tool, the guidance during the mating phase is assumed to be continuous. The trajectory is computed using a Linear Quadratic Regulator (LQR) and a linearised model of the CR3BP dynamics for the chaser [21]. The relative distance between chaser and center of mass of the target is reported in Fig. 12, as a function of the time of flight in the mating phase, which lasts for approximately 3 h and brings the chaser few meters away from the docking port. In Fig. 13, the evolution of the relative velocity in this phase is presented as a function of the target-chaser distance. In Table 3, time of flight and $\Delta v$s during the proximity operations are reported. Hence, remembering the data in Table 2, the analysed rendezvous lasts for 29.5 days and requires a total $\Delta v$ of 165.93 m/s.

Table 3 Proximity operations parameters

Fig. 12

Relative distance during mating phase

Fig. 13

Relative velocity during mating phase as a function of relative distance

5 Flexible orbit-attitude analysis

In the previous analyses, the coupled orbit-attitude model has been used to simulate the dynamics of the large space flexible infrastructure (target). However, the effects of this refined model are not so evident from the previously shown results. This section reports some analyses that have been conducted to preliminarily study the effects of the flexible extended structure on the dynamics in non-Keplerian orbits.

Fig. 14

Orbit-attitude motion on Halo orbit with $A_z={30{,}000}$ km

In Fig. 14, the attitude evolution of the rod infrastructure is reported. The attitude motion that has been examined in this analysis is set to be quasi-periodic with the orbital period: the space station performs almost one rotation in the first orbital period.

An interesting analysis is reported in Figs. 15 and 16, where the motion is propagated along four different Halo orbits, which are different in $A_z$. In this way, the influence between the orbital frequencies and the spring–mass frequencies is highlighted and some preliminary considerations are possible. The spring–mass systems have $\widetilde{\omega _i}=50\;\mathrm {(nd)}$. The most elongated orbits have a particular influence on the oscillations of the Bryant angles, while more the orbit is close to be planar, more the variations are evident in $\Omega _\perp$. This results can be explained considering that in the limit of planar orbits, all the torques are exerted along ${\hat{\mathbf {u}}}_3$.

Fig. 15

Bryant angles evolution along one orbital period

Fig. 16

Angular velocity, $\Omega _\perp$, evolution along one orbital period

A different preliminary study is targeted to point out the influence of the natural frequencies of the structure on the orbital motion. The difference in x, y, and z of the coupled flexible model with respect to the point-mass CR3BP model is shown in Fig. 17. However, in this case, a unique trend does not exist among the different components and the different Halo orbits. Each orbit has its peculiar frequency in each spatial direction, and the influence on flexible systems with different natural frequency must be analysed isolating each single effect and coupling term.

Fig. 17

Difference with respect to the point-mass CR3BP dynamics

6 Conclusions

This paper presented an example of a possible rendezvous scenario with a very large and flexible space infrastructure in an EML2 Halo orbit. The example has been used to show a dynamical analysis tool that is being developed by the authors. Moreover, some reference parameters for such a rendezvous have been presented, and they can be exploited to assess the feasibility of a cyclic mission between two different Halo orbits, when the cargo has to pass on the Earth side of the Moon.

At this point, as introduced in Sect. 2, it is relevant to note that in a different research work of the authors [4], an additional model has been developed and exploited to represent and study the dynamics of large and flexible space structures in non-Keplerian orbits. The other dynamical model resulted in a more efficient and adaptable way to study this kind of space systems. In fact, that dynamical representation can be easily integrated with more complex structural model, such as distributed parameters semi-analytical techniques, or with additional control devices, such as dual-spinning rotors. For these reasons, the future research will be addressed with that formulation. Notwithstanding, what has been presented in this paper, gave to the authors many information on orbit–attitude–flexible couplings and on rendezvous and docking operations; the extensions and the refinements of the additional modelling approach cannot overlook the present results.

Future works will increase the fidelity of the simulations, including some perturbing phenomena in the rendezvous analyses and enhancing the modelling approach with the aforementioned additional developed model. An extensive study on the possible couplings between the structural frequencies of the space infrastructure and the control action is needed. This is because the higher frequencies associated with an active control system can be more dangerous with respect to possible resonances of the flexible system. Finally, further investigations on the entire system configuration and on the proposed assembly strategies are necessary to highlight some drivers for the whole lunar infrastructure design.