1 Introduction

The theory of spacecraft (s/c) formation flying has become the focus of considerably extensive research and development effort during the last decades. Earlier design techniques addressed rendezvous and docking missions such as those of the Apollo space program, which had the Lunar Excursion Module and the Command and Service Module being assembled in orbit. The purpose is not to correct the Earth relative orbit itself during this maneuver, but rather to adjust and control the relative orbit between two vehicles. The relative distance is decreased to zero in a very slow and controlled manner during the docking maneuver [17].

The modern-day focus of s/c formation flying has extended to maintain a formation of various s/c. Several formation flying missions are currently operating or in the design stage: synthetic aperture interferometers for Earth observation (e.g., TanDEM-X/TerraSAR-X), dual s/c telescopes (e.g., VTDM) and laser interferometer for the detection of gravitational waves (e.g., LISA). It became obvious that the formation flying concept overcomes significant technical challenges and even avoids financial limitations. Indeed, the distribution of sensors and payloads among several s/c allows higher redundancy, flexibility and new applications that would not be achievable with a single s/c [2]. Recently, formation flying with non-cooperative objects has emerged as a new focus, motivated through the increasing number of such objects, especially in low Earth orbit. The exploitation of satellite-based resources has led to an ever-increasing number of non-cooperative objects such as defunct satellites and rocket upper stages termed as space debris. A collisional cascading effect has been postulated by Kessler in the late 1970s [12] and seems more real than ever since 2009 when two intact artificial satellites, Iridium 33 (operational) and Kosmos 2251 (out of service), collided distributing debris across thousands of cubic kilometers. Using the NASA long-term orbital debris projection model (LEGEND), Liou showed that, besides already implemented mitigation measures, the annual active debris removal (ADR) of 5–10 prioritized objects from orbit is required in order to stabilize the low Earth orbit (LEO) environment [14]. Those results have been backed by several other studies [11] and are meanwhile widely accepted in the space debris community.

This evolution has led to a substantial research effort to develop a theory that could simply and explicitly address the relative motion and collision avoidance issue in control design. Thus the development of the upcoming theories, such as ROE and eccentricity/inclination (E/I) vector separation, originally developed for collocation of geostationary satellites [10], was conducted.

The control of satellite formation is performed by the activation of on-board thrusters. Typically, impulsive control (very short-duration thrust) is preferred to continuous control (finite-duration thrust). This is due to historical limitations on propulsion technologies, typical payload requirements especially for scientific missions and the simplicity of impulsive maneuver planning often allowing pure analytical maneuver design. Recent advances in propulsion and computer technologies suggest a deeper study of continuous maneuver planning. This approach is not only justified by the precision of continuous maneuvers planning (the finite duration is explicitly addressed, and no impulsive assumptions are made) but also because of the typical advantages of low thrust propulsion systems, such as reduced mass, limited required power and variable exhaust velocity.

A vast amount of literature exists on formation reconfiguration maneuvers with impulsive thrust mainly modeled with Clohessy-Wiltshire (CW) and Lawden’s equations of relative motion. The Gauss’ variational equations (GVE) of motion however offer an ideal mathematical framework for designing impulsive control laws [3]. These equations have been extensively used in the last decades for absolute orbit keeping of single s/c, but have only recently been exploited for formation flying control in LEO as introduced by Schaub et al. [16] and subsequently by Vaddi et al. [19], Breger et al. [8] and D’Amico [9]. The reason for such slow development is that GVE describe the effect of control acceleration on the time derivative of the Keplerian orbital elements which were normally used to parameterize the motion of a single s/c but not the relative motion of a formation [8].

In this paper, we build upon the previously mentioned references and give the following original contributions. Firstly, a comprehensive literature survey of the relative motion parameterization and Gauss’ variational equations for relative motion is presented demonstrating the convenience of ROE and GVE-based maneuver planning as opposed to Cartesian parameterization. Secondly, GVE for relative motion using finite-duration thrust are derived for a specific set of ROE. Thirdly, an impulsive maneuver plan based on [2] is extended to the general case of nonzero relative semimajor axis and finally translated to the case of finite-duration thrust. The paper is organized as follows: in Sect. 2, an overview of the theory of relative motion, including ROE, is presented. In Sect. 3, an overview of the GVE and their application in relative orbit control is presented and the integrated GVE are derived. Section 4 is dedicated to the study of the effects of impulsive and finite-duration thrust on ROE. Subsequently the impulsive and finite-duration maneuver schemes are derived in Sect. 5 and verified via numerical simulation.

2 Dynamics of relative motion

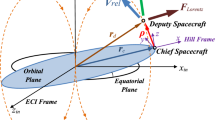
First of all we define some notations adopted in this paper. The motion of a single s/c orbiting the Earth is described in the Earth-centered inertial (ECI) frame. The relative motion of two s/c orbiting the Earth is described in the radial–tangential–normal (RTN) frame (Fig. 1).

The \(\Delta (\cdot )\) operator indicates arithmetic differences between absolute Cartesian or orbital parameters. The \(\delta (\cdot )\) operator indicates the relative Cartesian position and velocity in the RTN frame. It refers generally to a nonlinear combination of the absolute Cartesian/orbital parameters.

The s/c about which all other s/c motions are referenced is called the Target and is denoted with subscript \((\cdot )_1\). The second s/c, referred to as Chaser, is to fly in formation with the Target and is denoted with the subscript \((\cdot )_2\). Absolute Cartesian and orbital parameters without subscript are to be understood as Target parameters.

2.1 Linearized equations of relative motion

The Target position vector in the ECI is noted \(\underline{r}_1\). The relative orbit will be described in the rotating local orbital frame RTN in terms of the Cartesian coordinate vector \(\delta \underline{r} =\begin{pmatrix} x&y&z \end{pmatrix}^{\mathrm T}\).

Fig. 1
figure 1

Illustration of a s/c formation in RTN frame

Full size image

We introduce dimensionless spatial coordinates \(\delta \underline{\rho }\) and a dimensionless time \(\tau\) via the equations:

$$\begin{aligned} \delta \underline{\rho } = \frac{\delta \underline{r}}{r_1} = \begin{pmatrix} \bar{x}&\bar{y}&\bar{z} \end{pmatrix}^{\mathrm T} \quad \text{ and } \quad \mathrm {d} \tau = n \mathrm {d}t \end{aligned}$$
(1)

with n the mean motion. The differentiation with respect to the independent variable \(\tau\) is written here as

$$\begin{aligned} \left( \right) '\equiv \frac{\mathrm {d}\left( \right) }{\mathrm {d}\tau }. \end{aligned}$$
(2)

The dimensionless state vector is then noted

$$\begin{aligned} \delta \underline{\zeta } =\begin{pmatrix} \delta \underline{\rho }&\delta \underline{\rho }\, ^{\prime } \end{pmatrix}^{\mathrm T}. \end{aligned}$$
(3)

The CW equations of motion take a very elegant numerically advantageous form if written in a non-dimensional form [1]:

$$\begin{aligned} \bar{x}''-2 \bar{y}'-3\bar{x}&= 0 \end{aligned}$$
(4a)
$$\begin{aligned} \bar{y}''+2\bar{x}'&= 0 \end{aligned}$$
(4b)
$$\begin{aligned} \bar{z}''+\bar{z}&=0. \end{aligned}$$
(4c)

Note that these equations of motion are valid only if:

  • the Target orbit is circular,

  • \(\left\| \delta \underline{\rho }\right\| \ll r_1\),

  • the Target and Chaser s/c have a pure Keplerian motion.

Further, the out-of-plane component \(\bar{z}\) in Eq. (4c) decouples from the radial and along-track directions (in-plane). A more detailed view on how the equations are obtained can be found in [1, 17].

2.1.1 State-space approach

From a system theoretical perspective, based on Eq. (4), one can describe the dynamics of motion in state-space form:

$$\begin{aligned} \delta \underline{\zeta }'= \underline{\underline{A}} \delta \underline{\zeta } + \underline{\underline{B}} \delta \underline{u} + \underline{d} \end{aligned}$$
(5)

where \(\underline{\underline{A}}\) is the state matrix, \(\underline{\underline{B}}\) the control input matrix and \(\underline{d}\) the process disturbances induced through environmental perturbations. The state matrix is described by Eq. (6), where \(\underline{\underline{0}}_3\) is a 3 × 3 null matrix and \(\underline{\underline{I}}_3\) is a 3 × 3 identity matrix.

(6)

2.2 Solution of the linearized equations of motion

CW equations (4) are a set of three coupled ordinary homogeneous second-order equations with constant coefficients. Six independent constants are thus required to determine a unique solution for a relative orbit. The general homogenous solution can be written as the product of a state transition matrix \(\underline{\underline{\varPhi }}(\tau ,\tau _0)\) with an integration constant vector \(\underline{c}\). A possible representation is:

$$\begin{aligned} \delta \underline{\zeta }\left( \tau \right) = \underline{\underline{\varPhi }}\left( \tau ,\tau _0\right) \underline{c}, \quad \text {with} \end{aligned}$$
(7)
$$\begin{aligned} \underline{\underline{\varPhi }}\left( \tau ,\tau _0\right)&= \begin{bmatrix} 1&0&-\cos {\tau }&-\sin {\tau }&0&0 \\ -\frac{3}{2}\left( \tau -\tau _0 \right)&1&2\sin {\tau }&-2\cos {\tau }&0&0 \\ 0&0&0&0&\sin {\tau }&-\cos {\tau } \\ 0&0&\sin {\tau }&-\cos {\tau }&0&0 \\ -\frac{3}{2}&0&2\cos {\tau }&2\sin {\tau }&0&0 \\ \end{bmatrix}\ \ \text {and} \\ \underline{c}&= \begin{pmatrix} c_1&\cdots&c_6 \end{pmatrix}^{\mathrm T}. \end{aligned}$$

\(\underline{c}\) is a vector containing a set of six independent integration constants as described in [15]. To study the geometry of the relative path we rewrite the first three rows of Eq. (7) in amplitude-phase form

$$\begin{aligned} \bar{x}&= c_1 - c_{34} \cos {\left( \tau - \varphi \right) } \end{aligned}$$
(8a)
$$\begin{aligned} \bar{y}&= c_2 - c_1 \frac{3}{2}\left( \tau -\tau _0 \right) + 2c_{34} \sin {\left( \tau - \varphi \right) } \end{aligned}$$
(8b)
$$\begin{aligned} \bar{z} \,= +\, c_{56} \sin {\left( \tau - \theta \right) }. \end{aligned}$$
(8c)

The amplitudes \(c_{34}, c_{56}\) and phases \(\varphi , \theta\) of the in-plane and out-of-plane relative motion oscillations are

$$\begin{aligned} c_{34}&=\sqrt{c_3^2 + c_4^2} \quad c_{56} =\sqrt{c_5^2 + c_6^2}\end{aligned}$$
(9)
$$\begin{aligned} \varphi&=\arctan \left( \frac{c_4}{c_3}\right) \quad \theta =\arctan \left( \frac{c_6}{c_5}\right) . \end{aligned}$$
(10)
Fig. 2
figure 2

Illustration of the integration constants in the projected instantaneous (no drift) relative motion ellipse at \(\tau =\tau _0\)

Full size image

We can easily see from (8) that the Chaser moves in an elliptical-like pattern around the Target as illustrated in Figs. 1 and 2. Indeed:

  • The projection of the relative path in the RT plane is an ellipse centered in \(\left( c_1 , c_2\right)\). Because of the drift term \(c_1 \frac{3}{2}\left( \tau -\tau _0 \right)\) the ellipse is instantaneous and the \(\bar{y}\)-value of the center is valid only at \(\tau =0\). Bounded relative motion is hence obtained for \(c_1=4 \bar{x}_0 +2\bar{y}_0' = 0\).

  • The RN projection is an ellipse centered in \(\left( c_1 , 0\right)\) for \((\varphi -\theta ) \in \left\{ 0, \pi \right\}\) which gets tighter and dwindle to a line for \((\varphi -\theta )\rightarrow \frac{\pi }{2}\). In the case of bounded relative motion (\(c_1=0\)) the Target lies on this line which leads to collision risk if along-track position uncertainties exist and suggests choosing \((\varphi -\theta ) \in \left\{ 0, \pi \right\}\) to minimize this risk. This presumption will be discussed in Sect. 2.4.

2.3 Relative orbital elements

In conventional analysis, the set of independent variables \(\underline{c}\) could be computed using the initial conditions consisting of the position \(\underline{r}\) and velocity \(\underline{v}\) at some specific initial time \(t_0\), often taken at zero for convenience. However, any six independent constants can describe the solution, with the physical nature of the problem usually dictating the choice. Many authors worked on that issue searching combinations of Keplerian elements of the co-orbiting s/c to describe their relative motion [18]. The motivation for this effort was the advantages of the Keplerian elements description, experienced for single s/c in the last decades, compared with the classical position-velocity description. Similar advantages were expected and could be noticed. This new approach provides direct insight into the formation geometry and allows the straightforward adoption of variational equations such as the Gauss’ ones to study the effects of orbital perturbations on the relative motion.

In this paper a set of non-singular orbital elements \(\underline{\alpha }= \begin{pmatrix} a&u&e_x&e_y&i&\Omega \end{pmatrix}^{\mathrm T}\) is used to describe the absolute orbit of a s/c with \(u=M+\omega\), \(e_x =e\cos \omega\), and \(e_y= e\sin \omega\) where a denotes the semimajor axis, e the eccentricity, i the inclination, \(\Omega\) the right ascension of the ascending node, \(\omega\) the argument of periapsis, M the mean anomaly and u the mean argument of latitude.

We define the ROE introduced by D’Amico [9]:

$$\begin{aligned} \delta \underline{\alpha } = \begin{pmatrix} \delta a \\ \delta \lambda \\ \delta e_x \\ \delta e_y\\ \delta i_x \\ \delta i_y \end{pmatrix} = \begin{pmatrix} \left( a_2-a_1 \right) a_1^{-1}\\ \left( u_2-u_1\right) + \left( \Omega _2 -\Omega _1\right) \cos i_1 \\ e_{x_2} -e_{x_1} \\ e_{y_2} -e_{y_1} \\ i_2-i_1 \\ \left( \Omega _2 -\Omega _1\right) \sin i_1 \end{pmatrix} \ \ \ , \end{aligned}$$
(11)

where \(\delta \lambda\) denotes the relative mean longitude, \(\delta \underline{e}\) and \(\delta \underline{i}\) the relative eccentricity and inclination vectors, subscripts 1 and 2, respectively, Target and Chaser. The ROE defined in Eq. (11) are all invariants of the unperturbed relative motion with the exception of \(\delta \lambda\), which evolves linearly with time. The variable \(\delta \dot{\lambda }\) can be approximated to first order as

$$\begin{aligned} \delta \dot{\lambda } = \Delta \dot{u} = n_2 - n_1 =-\frac{3}{2}n_1 \frac{\Delta a}{a_1} \end{aligned}$$
(12)

The general linearized relative motion of the Chaser relative to the Target is provided in terms of ROE by

$$\begin{aligned} \delta \alpha _j(t) = \delta \alpha _{j_0} - \frac{3}{2}\left( u(t)-u_0 \right) \delta \alpha _{1_0} \ \delta _j^2 \end{aligned}$$
(13)

where j denotes the vector index \((j = 1, \ldots , 6)\), the subscript 0 indicates quantities at the initial time \(t_0\) and \(\delta _j^2\) is the Kronecker delta. Note that the only assumptions made here are pure Keplerian motion and \(\Delta u , \Delta a<< r_1\). These equations are hence valid for arbitrary eccentricities.

2.4 Final comments

These ROE have the distinct advantage of matching exactly the integration constants of Eq. (7) [9]. It follows

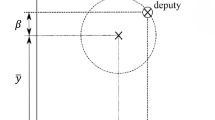
$$\begin{aligned} (c_1, c_2, c_{34}, c_{56}) = a(\delta a ,\delta \lambda ,\left\| \delta \underline{e} \right\| ,\left\| \delta \underline{i} \right\| ) \end{aligned}$$
(14)

The variables \(\varphi\) and \(\theta\) are the arguments of the vectors \(\delta \underline{e}\) and \(\delta \underline{i}\) in polar coordinates as depicted in Fig. 3.

Fig. 3
figure 3

Illustration of the relative orbital elements in the projected instantaneous (no drift) relative motion ellipse at \(u=u_0\)

Full size image

That means that the vector \(\underline{c}\) is not only an integration constant vector which could be geometrically interpreted in the relative trajectory (Fig. 2) but also receives a geometrical meaning by means of Chaser’s and Target’s Keplerian elements. Statements about the relative orbit geometry can directly be made based on the absolute Keplerian elements without solving any equation. For example if \(\Delta i\) and \(\Delta \Omega\) are found to be zero, then it can immediately be concluded that the amplitude of the out-of-plane motion is zero (\(c_{56} = \left\| \delta \underline{i} \right\| = \sqrt{(\Delta i)^2 + (\Delta \Omega \sin i_1)^2}\)).

Furthermore, we obtain a mapping tool between the relative state vector \(\delta \underline{x}\left( \tau \right)\) at a generic time \(\tau\) and the initial ROE vector \(\delta \underline{\alpha }(\tau _0)\). Keeping in mind the equivalence between mean argument of latitude u and the independent variable \(\tau\), we write:

$$\begin{aligned} \delta \underline{\zeta }(u)= \underline{\underline{\varPhi }}(u,u_0) \delta \underline{\alpha }(u_0) \end{aligned}$$
(15)

Of practical use is mainly the inverse linear mapping from the relative state vector to the initial ROE vector with

$$\begin{aligned} \underline{\underline{\varPhi }}^{-1}(u,u_0) = \begin{bmatrix} 4&0&0&0&2&0 \\ 6(u-u_0)&1&0&-2&3 (u-u_0)&0 \\ 3\cos u&0&0&\sin u&2 \cos u&0 \\ 3\sin u&0&0&-\cos u&2 \sin u&0 \\ 0&0&\sin u&0&0&\cos u \\ 0&0&-\cos u&0&0&\sin u \end{bmatrix}. \end{aligned}$$
(16)

It may be noted that this choice of the ROE maintains the decoupling of the motion. In other words \(\delta a\), \(\delta \lambda\) and \(\delta \underline{e}\) describe the in-plane motion, whereas \(\delta \underline{i}\) describes the out-of-plane motion.

Moreover, the usage of ROE increases the accuracy of the CW general solution because it retains higher-order terms which are normally dropped using Cartesian description [17]. For example the first-order Cartesian constraint for bounded relative motion (\(c_1=4 \bar{x}_0 +2\bar{y}_0'=0\)) translated in ROE yields \(\delta a=0\). This is in fact the only condition on two inertial orbits to have a closed relative orbit since their energies are equal. The ROE constraint is thus universally valid (no linearization).

Because of the coupling between semimajor axis and orbital period, small uncertainties in the initial position and velocity result in a corresponding drift error and thus in a growing along-track error [9]. Long-term predictions of the relative motion between Chaser and Target are therefore sensitive to both orbit determination errors and maneuver execution errors. In order to minimize the collision risk of the two s/c in the presence of along-track position uncertainties, they must be properly separated in RN directions. As expected from the results of Sect. 2.2 and shown in [10] this can be achieved by a (anti-)parallel alignment of the \(\delta \underline{e}\) and \(\delta \underline{i}\) vectors (\((\varphi -\theta ) \in \left\{ 0, \pi \right\}\)). In this case RN separations never vanish at the same time and provide a minimum safe separation between the s/c at all times. This principle is termed E/I separation.

Perturbations of the motion such as \(J_2\) and atmospheric drag effects can be easily incorporated through the convenient orbital elements description. From these two, the only perturbation which affect the E/I separation is the Earth oblateness [9]. It turned out that choosing \(\delta i_x = 0\) avoids a secular motion of \(\delta \lambda\) and \(\delta \underline{i}\) due to \(J_2\) and provides hence a more stable configuration. Therefore the passively safe and stable configuration given through \(\delta \underline{\alpha }_\mathrm{nom} = \begin{pmatrix} \delta a&\delta \lambda&0&\pm ||\delta e||&0&\pm ||\delta i||\end{pmatrix}^{\mathrm T}\) is adopted as nominal configuration in this work.

Finally, all six relative state variables (position and velocity) are fast varying variables, meaning that they vary throughout the orbit. Using ROE simplifies the relative orbit computation because even within a perturbed orbit, e.g., gravitational perturbations, ROE will only change slowly. Due to its curvilinear nature large rectilinear distances can be captured by small ROE variations. This property is exploited and illustrated by the use of GVE for the relative control as described in the next section.

3 Gauss’ variational equations

The GVE derived in [3] describe the alteration of Keplerian orbital elements due to a disturbance acceleration \(\underline{\gamma }_p=(\gamma _\mathrm {R}, \gamma _\mathrm {T}, \gamma _\mathrm {N})^T\) in radial, tangential and normal direction. If the perturbation acceleration is due to a control thrust, GVE show what effect such a control thrust would have on the Keplerian orbital elements. Based on the general GVE description in [3] it is possible to derive the GVE in terms of the non-singular orbital elements vector \(\underline{\alpha }\) and build the limit for \(e\rightarrow 0\) for a circular orbit. As a result we get

$$\begin{aligned} \frac{\mathrm da}{\mathrm dt} = 2a \frac{\gamma _{_{\mathrm T}}}{na} \end{aligned}$$
(17a)
$$\begin{aligned} \frac{\mathrm du}{\mathrm dt} = n -2 \frac{\gamma _{_{\mathrm R}}}{na} -\frac{\sin u}{\tan i} \frac{\gamma _{_{\mathrm N}}}{na} \end{aligned}$$
(17b)
$$\begin{aligned} \frac{\mathrm de_x}{\mathrm dt} = 2 \cos u \frac{\gamma _{_{\mathrm T}}}{na} +\sin u \frac{\gamma _{_{\mathrm R}}}{na} \end{aligned}$$
(17c)
$$\begin{aligned} \frac{\mathrm de_y}{\mathrm dt} = 2 \sin u \frac{\gamma _{_{\mathrm T}}}{na} -\cos u \frac{\gamma _{_{\mathrm R}}}{na} \end{aligned}$$
(17d)
$$\begin{aligned} \frac{\mathrm d i}{\mathrm dt} = \cos u \frac{\gamma _{_{\mathrm N}}}{na} \end{aligned}$$
(17e)
$$\begin{aligned} \frac{\mathrm d \Omega }{\mathrm dt} = \frac{\sin u}{\sin i} \frac{\gamma _{_{\mathrm N}}}{na} \end{aligned}$$
(17f)

Given a constant acceleration \(\underline{\gamma }_p\) at a generic time \(t _{_{ \mathrm M }}\), the integration of the system of equations (17) over the thrust duration provides the relation between the maneuver \(\Delta \underline{v} _{_{ \mathrm M }}\) and the subsequent change in orbital elements \(\Delta \underline{\alpha }\) where

$$\begin{aligned} \Delta \underline{v} _{_{ \mathrm M }} = \int ^{t^{+}_{\mathrm M}}_{t^{-}_{\mathrm M}} \underline{\gamma }_p \mathrm dt = \int ^{t_{\mathrm M} +\epsilon }_{t_{\mathrm M}-\epsilon } \underline{\gamma }_p \mathrm dt . \end{aligned}$$
(18)

The subscript \((\cdot ) _{_{ \mathrm M }}\) denotes the maneuver execution time; \(2\epsilon\) denotes the thrust duration. For impulsive maneuver planning, the velocity increment is given by \(\lim \nolimits _{\epsilon \rightarrow 0} \Delta \underline{v}_\text {M}\). For proximity operations, these equations can be generalized from describing the motion of single spacecraft to the description of the relative motion of two spacecraft. This approach is the most natural way to control relative orbital elements and have the main advantage that it allows us to translate the aforementioned advantages of the ROE parameterization into maneuver planning.

3.1 Impulsive thrust

We can extend the result above for relative motion. The alteration in ROE can be expressed as a function of the absolute orbital elements of Target and Chaser. We obtain the direct relation between velocity increments in the RTN frame and the consequent change of ROE:

$$\begin{aligned} \Delta \delta \underline{\alpha } (u) = \frac{1}{n_2 a_2} \underline{\underline{G}}(u,u _{_{ \mathrm M }} )\Delta \underline{v} _{_{ \mathrm M }} ,\quad \text{with} \end{aligned}$$
(19)
$$\begin{aligned} \underline{\underline{G}}(u,u _{_{ \mathrm M }} ) = \begin{bmatrix} 0&2&0 \\ -2&-3(u-u _{_{ \mathrm M }} )&0 \\ \sin u _{_{ \mathrm M }}&2 \cos u _{_{ \mathrm M }}&0 \\ -\cos u _{_{ \mathrm M }}&2 \sin u _{_{ \mathrm M }}&0 \\ 0&0&\cos u _{_{ \mathrm M }} \\ 0&0&\sin u _{_{ \mathrm M }} \end{bmatrix} \ . \end{aligned}$$

The variables \(\Delta \delta \underline{\alpha }\) denote the alteration of the ROE, \((\cdot ) _{_{ \mathrm M }}\) the maneuver execution time and \(\Delta \underline{v} _{_{ \mathrm M }}\) the velocity increment. It is possible to summarize the factor \(1/n_2a_2\) and \(\Delta \underline{v} _{_{ \mathrm M }}\) to obtain the dimensionless velocity increment \(\Delta \underline{\rho }' _{_{ \mathrm M }}\). Taking into account the evolution of the ROE described in Eq. (13) we deduce that the alteration of \(\delta \lambda\) evolves after the maneuver linearly according to the following law

$$\begin{aligned} \Delta \delta \lambda = \delta \lambda _{_{ \mathrm M }} -3(u-u _{_{ \mathrm M }} ) \end{aligned}$$
(20)

This result has been already incorporated in Eq. (19), so that \(\underline{\underline{G}}(u _{_{ \mathrm M }} ,u _{_{ \mathrm M }} )\) describes the instantaneous change in ROE at \(u _{_{ \mathrm M }}\) while \(\underline{\underline{G}}(u,u _{_{ \mathrm M }} )\) takes into account the linear evolution of \(\delta \lambda\) after \(u _{_{ \mathrm M }}\).

3.2 Relation to the state transition matrix

It is worth noting that the inverse state transition matrix \(\underline{\underline{\varPhi }}^{-1}(u,u_0)\) in Eq. (16) and the variation matrix \(\underline{\underline{G}}(u,u _{_{ \mathrm M }} )\) in Eq. (19) are closely connected. We rewrite the mapping rule for convenience:

$$\begin{aligned} \Delta \delta \underline{\alpha }(u) = \underline{\underline{G}}(u,u_0) \Delta \underline{\rho }' _{_{ \mathrm 0 }} \end{aligned}$$
(21a)
$$\begin{aligned} \delta \underline{\alpha }(u_0) = \underline{\underline{\varPhi }}^{-1}(u,u_0) \delta \underline{\zeta }(u) \end{aligned}$$
(21b)

If we set \(\delta \underline{\rho }=0\), implying that both spacecrafts have the same position but different velocities in the inverted linear motion model of Eq. (21b), we obtain the effect of an instantaneous velocity increment on the ROE vector [9]. Let \(\underline{\underline{\varPhi }}^{-1}\) in Eq. (16) be divided into four \(3\times 3\) blocks \(\underline{\underline{\varPhi }}^{-1}_{ij}(u,u_0)\); it follows

$$\begin{aligned} \delta \underline{\alpha }(u_0) = \begin{bmatrix} \underline{\underline{\varPhi }}^{-1}_{12}(u,u_0)&\underline{\underline{\varPhi }}^{-1}_{22}(u,u_0) \end{bmatrix} \delta \underline{\rho }'(u) \end{aligned}$$
(22)

Equations (22) and (19) are equivalent; the only difference between them is the opposite sign in the term \(-3(u-u _{_{ \mathrm M }} )\). This is due to the fact that the result is calculated for different mean argument of latitudes: u refers to after the maneuver, while \(u_0\) refers to the initial state.

The equations above assume impulsive maneuver which would require a propulsion source of infinite thrust. In practice thrusts have always a finite duration which can be approximated as follows:

$$\begin{aligned} \Delta t _{_{ \mathrm M }} = m_2 \left\| \Delta \underline{v} _{_{ \mathrm M }} \right\| /F_\mathrm{max}, \end{aligned}$$
(23)

with \(m_2\) the mass of the Chaser and \(F_\mathrm{max}\) the available thrust level. Considering the execution as impulsive is a valid assumption for small maneuvers and thus adequate for maneuver planning. For large maneuvers the finite duration of the thrust has to be considered explicitly.

3.3 Finite-duration thrust

Depending on the amplitude of the maneuver, the mass of the s/c and the available thrust level, it is possible that the computed maneuver duration in Eq. (23) is too large to be considered as impulsive. In this case, \(u _{_{ \mathrm M }}\) cannot be considered constant during the maneuver anymore. Let \(\underline{\gamma } _{_{ \mathrm M }}\) be the available level of acceleration in the RTN directions and \([t_1 , \; t_2]\) the maneuver execution time interval. Based on Eqs. (17) and (19), integration over \([t_1 , \; t_2]\) yields

$$\begin{aligned} \Delta \delta \underline{\alpha } = \frac{1}{n_2^2a_2} \underline{\underline{H}}(\tilde{u} _{_{ \mathrm M }} , \hat{u} _{_{ \mathrm M }} ) \underline{\gamma } _{_{ \mathrm M }} \ \ \text{, } \text{ with } \end{aligned}$$
(24)
$$\begin{aligned} & \underline{\underline{H}}(\tilde{u} _{_{ \mathrm M }} , \hat{u} _{_{ \mathrm M }} )\nonumber \\ =& \left[\begin{matrix} 0& 2 \hat{u} _{_{ \mathrm M }}& 0 \\ -4\hat{u} _{_{ \mathrm M }}&- \frac{3}{2}\left( 2\hat{u} _{_{ \mathrm M }} \right) ^2& 0 \\ 2 \sin \tilde{u} _{_{ \mathrm M }} \sin \hat{u} _{_{ \mathrm M }}& 4 \cos \tilde{u} _{_{ \mathrm M }} \sin \hat{u} _{_{ \mathrm M }}& 0 \\ - 2 \cos \tilde{u} _{_{ \mathrm M }} \sin \hat{u} _{_{ \mathrm M }}& 4 \sin \tilde{u} _{_{ \mathrm M }} \sin \hat{u} _{_{ \mathrm M }}& 0 \\ 0& 0& 2 \cos \tilde{u} _{_{ \mathrm M }} \sin \hat{u} _{_{ \mathrm M }} \\ 0& 0& 2 \sin \tilde{u} _{_{ \mathrm M }} \sin \hat{u} _{_{ \mathrm M }} \end{matrix}\right] , \end{aligned}$$
(25)
$$\begin{aligned} \tilde{u} _{_{ \mathrm M }} = \frac{u(t_2)+ u(t_1)}{2} \quad \text{ and } \quad \hat{u} _{_{ \mathrm M }} = \frac{u(t_2)- u(t_1)}{2} \end{aligned}$$
(26)

Note that \(\hat{u} _{_{ \mathrm M }}\) is the halved dimensionless maneuver duration and \(\tilde{u} _{_{ \mathrm M }}\) the mean argument of latitude at the middle point of the maneuver.

4 Assessment of orbital maneuvers

We assume that there are three different thrust directions: radial, along-track and normal. The fuel consumption (F) due to a single impulse is proportional to the norm of the impulse vector. One impulse in normal direction is required to reconfigure the out-of-plane motion, while two in RT-direction are needed to reconfigure the in-plane motion. Based on the results of Vaddi et al. [19] and D’Amico [9] we choose \(\pi\) as the optimal separation between two impulses.

Based on Eq. (19), one can deduce that radial maneuvers are safer than along-track ones since they do not affect the relative semimajor axis and thus do not induce an evolving change (drift) in mean longitude. However, they are twice as expensive as along-track and are not able to achieve complete formation reconfiguration because the relative semimajor axis can only be changed using along-track maneuvers. In this paper far-range formation (several kilometers) is considered, in which an approach via drift is desirable and thus exclusively along-track maneuvers are used for in-plane control. The insecurity is compensated through appropriate separation in RN-direction.

4.1 Impulsive thrust maneuvers

4.1.1 Out-of-plane maneuvers

The desired variation in the inclination vector can be obtained using maneuvers in normal direction. The influence of impulsive thrusts is given by Eq. (19) where \(\Delta v _{_{ \mathrm N }}\) is the normal impulsive thrust (scalar value) and \(u _{_{ \mathrm N }}\) the location of the thrust. The non-trivial solution is given by a single thrust located at \(u _{_{ \mathrm N1 }}\) or \(u _{_{ \mathrm N1 }} +\pi\). Depending on the actual position on the orbit, the closest solution to the actual position can be chosen. However, operational constraints may suggest splitting the out-of-plane maneuver in two components located at \(u_{_{N1}}\) and \(u_{_{N1}}+\pi\). This allows for example to correct maneuver execution errors. Let p be the thrust distribution coefficient, the double thrust solution is:

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta v_{_{N1}}= p na || \Delta \delta \underline{ i} || & \quad \text {at}\,u_{_{N1}}= \arctan \left( \frac{\Delta \delta i_y}{\Delta \delta i_x} \right) \\ \Delta v_{_{N2}}=( p-1) na|| \Delta \delta \underline{ i} || & \quad \text {at}\,u_{_{N2}= u_{_{N1}} + \pi , \ p \in [0,1] } \end{array}\right. } \end{aligned}$$
(27)

4.1.2 Out-of-plane delta-v budget

Single and double thrust impulsive maneuvers have the same delta-v budget:

$$\begin{aligned} F=| \Delta v_{_{N1}} | + | \Delta v_{_{N2}} | = na||\Delta \delta \underline{ i} || \end{aligned}$$
(28)

4.1.3 In-plane maneuvers

The desired variation of the relative eccentricity vector \(\delta \underline{e}\), relative semimajor axis \(\delta a\) and relative mean longitude \(\delta \lambda\) can be obtained using maneuvers in along-track and/or radial direction. The influence of impulsive thrusts is given by Eq. (19) where \(\Delta v _{_{ \mathrm R }}\) and \(\Delta v _{_{ \mathrm T }}\) are, respectively, the radial and along-track impulsive thrusts (algebraic values); \(u _{_{ \mathrm R }}\) and \(u _{_{ \mathrm T }}\) are the locations of the thrusts.

It is possible to control the relative eccentricity with a single thrust. The side effect is a persistent variation of the mean semimajor axis and thus, an increasing change of the mean longitude. Besides operational constraints suggesting the splitting of maneuvers, a double thrust solution can limit the instantaneous variation of semimajor axis between the thrust. That means that, for \(p=0.5\), there is no change of the semimajor axis but a change of the mean longitude at the end of the maneuver.

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta v_{_{T1}}= p \frac{1}{2}na || \Delta \delta \underline{ e} || &{} \text {at}\, u_{_{T1}}= \arctan \left( \frac{\Delta \delta e_y}{\Delta \delta e_x} \right) \\ \Delta v_{_{T2}}=( p-1)\frac{1}{2} na|| \Delta \delta \underline{ e} || &{} \text {at } u_{_{T2}}= u_{_{T1}} + \pi , \ p \in [0,1] \end{array}\right. } \end{aligned}$$
(29)

The pair of along-track maneuvers planned to settle the new \(\delta \underline{e}\) vector changes temporarily the relative semimajor axis \(\delta a\) and thus causes a change of \(\delta \lambda\). The caused drift between the maneuvers is \(\Delta \delta \lambda = \pm \frac{3}{2}p \pi || \Delta \delta \underline{ e} ||\). Along-track maneuvers can be exploited to correct additionally the semimajor axis [2]. One solution for the control of \(\delta a\) and \(\delta \underline{e}\) is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta v_{_{T1}}= \frac{1}{4} na\left( +|| \Delta \delta \underline{ e} || + \Delta \delta a \right) &{} \text {at} \, u_{_{T1}}= \arctan \left( \frac{\Delta \delta e_y}{\Delta \delta e_x} \right) \\ \Delta v_{_{T2}}=\frac{1}{4} na\left( -|| \Delta \delta \underline{ e} || + \Delta \delta a \right) &{} \text {at}\, u_{_{T2}}= u_{_{T1}} + \pi \end{array}\right. } \end{aligned}$$
(30)

The double thrust solution induces a non-vanishing semimajor axis difference that makes the spacecraft drift from each other. We have to take that into account in our control strategy and plan a second pair of maneuvers to stop the drift and acquire the desired mean longitude \(\delta \lambda\) alteration (along-track separation). To stop (counteract) the variation of \(\delta \lambda\) we aim a (slightly non) zero at the end of the second pair of maneuvers which make the spacecraft maintain the Target separation (drift back). The caused drift between the maneuvers remains \(\Delta \delta \lambda = \pm \frac{3}{4} \pi || \Delta \delta \underline{ e} ||\).

4.1.4 In-plane delta-v budget

Since the choice of p does not influence the total fuel consumption we set \(p=0.5\) and obtain a homogeneous distribution.

$$\begin{aligned} F=| \Delta v_{_{T1}} | + | \Delta v_{_{T2}} | = \frac{1}{2}na||\Delta \delta \underline{e} || \end{aligned}$$
(31)

4.2 Finite-duration thrust maneuvers

4.2.1 Out-of-plane maneuvers

The equation describing the influence of finite-duration thrusts on the out-of-plane motion is given by Eq. (24) where \(\Delta t _{_{ \mathrm N }}\) is the duration of the thrust, \(\gamma _{_{ \mathrm N }}\) the normal thrust acceleration (scalar value) and \(\tilde{u} _{_{ \mathrm N }}\) the location of the thrust. The solution is given by:

$$\begin{aligned} \Delta t _{_{ \mathrm N }} = \frac{2}{n} \hbox{arcsin} \left( n^2a \frac{|| \Delta \delta \underline{i} || }{2 |\gamma _{_{ \mathrm N }} |} \right) \ \ \text{ at } \ \ \tilde{u} _{_{ \mathrm N }} = \arctan \left( \frac{\Delta \delta i_y}{\Delta \delta i_x} \right) \end{aligned}$$
(32)

Analogously to the impulsive case, the solution for a homogeneous distribution (\(p=0.5\)) is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta t_{_{N1}}= \frac{2}{n} \hbox{arcsin} \left( n^2a \frac{|| \Delta \delta \underline{i} || }{4 |\gamma _{_{ \mathrm N }} |} \right) \ \ &{} \text{ at } \ \ \tilde{u}_{_{N1}}= \arctan \left( \frac{\Delta \delta i_y}{\Delta \delta i_x} \right) \\ \Delta t_{_{N2}}= \frac{2}{n} \hbox{arcsin} \left( n^2a \frac{|| \Delta \delta \underline{i} || }{4 |\gamma _{_{ \mathrm N }} |} \right) \ \ &{} \text{ at } \ \ \tilde{u}_{_{N2}}=\tilde{u}_{_{N1}} + \pi \end{array}\right. } \end{aligned}$$
(33)

where \(\gamma _{_{ \mathrm N }} = \pm | \gamma _{_{ \mathrm N }} |\).

4.2.2 Out-of-plane delta-v budget

Without loss of generality, we consider the simple case of \(p=0.5\). The index refers to the number of maneuvers

$$\begin{aligned} {\left\{ \begin{array}{ll} F_\mathrm{single}= |\gamma _{_{ \mathrm N }} | \Delta t _{_{ \mathrm N }} &{}\\ F_\mathrm{double}=\sum _k |\gamma _{_{ \mathrm N }} | \Delta t_{_{Nk}} = |\gamma _{_{ \mathrm N }} |\left( \Delta t _{_{ \mathrm N1 }} + \Delta t _{_{ \mathrm N1 }} \right) &{} \end{array}\right. } \end{aligned}$$
(34)

Lemma 1

The splitting of out-of-plane maneuvers reduces the propellant consumption.

Proof

We define the function \(h(x) = \hbox{arcsin} \left( \frac{x}{2}\right) - \frac{1}{2} \hbox{arcsin} \left( x\right)\). It can be shown that this function is monotonically decreasing for \(x \in [-1,1]\) . The following relations hold

$$\begin{aligned} \left. \begin{array}{ll} h(0)=0 \\ h \text { monotone decreasing} \end{array} \right\} \Rightarrow h(x) < 0 \ \ \forall x \in {]0,1]} \\ \end{aligned}$$

it follows \(\ \ \ \Rightarrow \hbox{arcsin} \left( \frac{x}{2}\right) < \frac{1}{2} \hbox{arcsin} \left( x\right)\)

we set \(x = n^2a \frac{|| \Delta \delta \underline{i} || }{2 |\gamma _{_{N}}|} \in {]0,1]}\)

$$\begin{aligned}&\Rightarrow \hbox{arcsin} \left( n^2a \frac{|| \Delta \delta \underline{i} || }{4 |\gamma _{_{ \mathrm N }} |}\right)< \frac{1}{2} \hbox{arcsin} \left( n^2a \frac{|| \Delta \delta \underline{i} || }{2 |\gamma _{_{ \mathrm N }} |}\right) \\&\Rightarrow \Delta t _{_{ \mathrm N1 }} < \frac{1}{2} \Delta t _{_{ \mathrm N }} \end{aligned}$$

\(\Rightarrow F_\mathrm{double} < F_\mathrm{single}\) \(\square\)

In a physical sense we can derive this result in the following way. The finite-duration thrust takes place along the arc length \(\hat{u} _{_{ \mathrm M }}\). The effectiveness of the maneuver is at maximum near the middle point \(\tilde{u} _{_{ \mathrm M }}\). Splitting the maneuver provides two arcs separated by \(\pi\) and thus increases the effectiveness of the maneuver since the length of the portion in vicinity of \(\tilde{u} _{_{ \mathrm M }}\) (two in our case) increases as depicted in Fig. 4.

Lemma 2

The minimum of the (splitted) out-of-plane maneuver cost is given by a homogenous distribution \((p=0.5)\)

Proof

Let \(h(p) = \hbox{arcsin} \left( kp\right) + \hbox{arcsin} \left( k (1-p)\right)\), where k is a positive constant and p a real variable in [0, 1].

$$\begin{aligned} \frac{\mathrm d }{\mathrm dp}h(p) = 0&\Leftrightarrow k[(1-(kp)^2 )^{-1} -( 1-k^2(1-p)^2 )]=0 \\&\Leftrightarrow p^2 =(1-p)^2 \\&\Leftrightarrow p=0.5 \end{aligned}$$

Since \(\frac{\mathrm d^2 }{\mathrm dp^2}h(0.5)>0\), we deduce that h(p) has a global minimum at \(p=0.5\). \(\square\)

In a physical sense, we can derive this result in the following way. The length of the arc in vicinity of \(\tilde{u} _{_{ \mathrm M }}\) is maximized for homogenous distribution, and thus, the effectiveness of the maneuver is maximized for \(p=0.5\).

Fig. 4
figure 4

Illustration of maneuver splitting

Full size image

4.2.3 In-plane maneuvers

The equation describing the influence of finite-duration thrusts on the in-plane motion is given by Eq. (24) where \(\Delta t _{_{ \mathrm R }} /\Delta t _{_{ \mathrm T }}\) is the duration of the thrust, \(\gamma _{_{ \mathrm R }} /\gamma _{_{ \mathrm T }}\) the radial/along-track thrust acceleration (scalar value) and \(u _{_{ \mathrm R }} / u _{_{ \mathrm T }}\) the location of the thrust. Analogously to the impulsive case, the solution for a homogeneous distribution \((p=0.5)\) is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta t _{_{ \mathrm T1 }} = \frac{2}{n} \hbox{arcsin} \left( n^2a \frac{|| \Delta \delta \underline{e} || }{8 |\gamma _{_{T}}|} \frac{1}{\cos \left( \frac{1}{2} n \frac{a n \Delta \delta a}{4| \gamma _{_{ \mathrm T }} |}\right) } \right) +\frac{a n \Delta \delta a}{4| \gamma _{_{ \mathrm T }} |} \\ \Delta t _{_{ \mathrm T2 }} = \frac{2}{n} \hbox{arcsin} \left( n^2a \frac{|| \Delta \delta \underline{e} || }{8 |\gamma _{_{T}}|} \frac{1}{\cos \left( \frac{1}{2} n \frac{a n \Delta \delta a}{4| \gamma _{_{ \mathrm T }} |}\right) } \right) -\frac{a n \Delta \delta a}{4| \gamma _{_{ \mathrm T }} |} \end{array}\right. } \end{aligned},$$
(35)

respectively, at \(\tilde{u} _{_{ \mathrm T1 }} = \arctan \left( \frac{\Delta \delta e_y}{\Delta \delta e_x} \right)\) and \(\tilde{u} _{_{ \mathrm T2 }} = \tilde{u}_{_{T1}}+ \pi\) with \(\gamma _{_{ \mathrm T }} = \pm | \gamma _{_{ \mathrm T }} |\)

4.2.4 In-plane delta-v budget

The delta-v budget for single and double thrust maneuvers is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} F_\mathrm{single}= |\gamma _{_{ \mathrm T }} | \Delta t _{_{ \mathrm T }} &{}\\ F_\mathrm{double}=\sum _k |\gamma _{_{ \mathrm T }} | \Delta _{_{ \mathrm Tk }} = |\gamma _{_{ \mathrm T }} |\left( \Delta t _{_{ \mathrm T1 }} + \Delta t _{_{ \mathrm T1 }} \right) &{} \end{array}\right. } \end{aligned}$$
(36)

5 Control of relative motion

5.1 Control scheme

The control scheme in this paper is based on the following considerations:

  • The presented dynamics of relative motion does not take gravitational and atmospheric perturbations into account while planning the maneuvers. However, the simulation environment presented in section 5.2.1 incorporates disturbances. The atmospheric drag and the gravitational perturbation are also not considered during the maneuver planning because they do not have a significant impact on the achievement of the desired formation as shown in section 5.2. The incorporation of disturbances has been discussed in [9] and will be subject of future work.

  • Three different thrust directions (radial, along-track and normal) are available. This increases the fuel consumption in case skewed thrusts are needed but is still a valid assumption since maneuvers are typically constraint to certain directions.

  • The reconfiguration of \(\delta \underline{e}\) using two along-track maneuvers is an optimal solution in that case [9, 19].

  • The two along-track thrusts can be used to simultaneously reconfigure \(\delta e_x\), \(\delta e_y\) and \(\delta a\) (and hence a non-vanishing variation of \(\delta \lambda\)). This is still an adequate suboptimal solution for the in-plane reconfiguration since generally \(\delta a\) remains small.

  • To stop a drift (i.e., set \(\delta a\) to zero) we need two pulses so that only \(\delta a\) is affected. Obviously, \(\delta \lambda\) is also affected from the maneuver but has a constant value after the execution. \(\delta e_x\) and \(\delta e_y\) change only between the two maneuvers and finally take on their initial values at the end of the maneuvers.

Fig. 5
figure 5

Exemplary maneuver sequence for complete formation reconfiguration

Full size image

The formation reconfiguration and formation keeping are performed using the concept illustrated in Fig. 5 which is valid for the general case of \(\delta a \ne 0\) and for the finite-duration thrust case. The desired change of the relative semimajor axis is split into \(\Delta \delta a =\Delta \delta a_{\mathrm {I}}+\Delta \delta a_{\mathrm {II}}\). Two along-track maneuvers settle a change of the relative eccentricity vector \(\Delta \delta \underline{e}\) and the intermediate change of the relative semimajor axis \(\Delta \delta a_{\mathrm {I}}\). Due to the new settled semimajor axis \(\delta \lambda\) will evolve with a constant rate until a second pair of along-track maneuvers provoke the second semimajor axis change \(\Delta \delta a_{\mathrm {II}}\). Commonly the second pair will stop the drift by setting \(\delta a\) to zero. \(\Delta \delta a_{\mathrm {I}}\) has to be chosen in a way so that the total drift (inclusive between the maneuver pairs) corresponds to the desired change \(\Delta \delta \lambda\). For the out-of-plane motion a single-pulse split in two equivalent pulses will reconfigure \(\delta \underline{i}\).

5.1.1 Impulsive scheme

Based on the results of the last section, we derived the six impulsive thrusts as follows:

$$\begin{aligned} \Delta v _{_{ \mathrm T1 }}&= \frac{1}{4} na\left( \Delta \delta a_I + || \Delta \delta \underline{ e} ||\right) \quad \text {at } \quad u _{_{ \mathrm T1 }} = \varphi \end{aligned}$$
(37a)
$$\begin{aligned} \Delta v _{_{ \mathrm T2 }}&= \frac{1}{4} na\left( \Delta \delta a_I - || \Delta \delta \underline{ e} ||\right) \quad \text {at } \quad u _{_{ \mathrm T2 }} = u _{_{ \mathrm T1 }} + \pi \end{aligned}$$
(37b)
$$\begin{aligned} \Delta v _{_{ \mathrm T3 }}&= \frac{1}{4} na \Delta \delta a_{\mathrm {II}} \quad \text {at } \quad u _{_{ \mathrm T3 }} = u _{_{ \mathrm T2 }} + nT \end{aligned}$$
(37c)
$$\begin{aligned} \Delta v _{_{ \mathrm T4 }}&= \frac{1}{4} na \Delta \delta a_{\mathrm {II}} \quad \text {at } \quad u _{_{ \mathrm T4 }} = u _{_{ \mathrm T3 }} + \pi \end{aligned}$$
(37d)
$$\begin{aligned} \Delta v _{_{ \mathrm N1 }}&= + \frac{1}{2}na || \Delta \delta \underline{ i} || \quad \text {at } \quad u _{_{ \mathrm N1 }} = \theta \end{aligned}$$
(37e)
$$\begin{aligned} \Delta v _{_{ \mathrm N2 }}&= - \frac{1}{2}na || \Delta \delta \underline{ i} || \quad \text {at } \quad u _{_{ \mathrm N2 }} =u _{_{ \mathrm N1 }} +\pi \end{aligned}$$
(37f)

The intermediate change of the relative semimajor axis can be determined analytically [4]:

$$\begin{aligned} \Delta \delta a_{\mathrm {I}} =\frac{ -\frac{2\Delta \delta \lambda }{3} -\frac{\pi ||\Delta \delta \underline{e}||}{2} -\delta a_0 \left( u _{_{ \mathrm T1 }} -u_0 +nT+ 2\pi \right) -\frac{\Delta \delta a }{2} }{nT+\pi } \end{aligned}$$
(38)

5.1.2 Finite-duration scheme

Based on Eq. (24), we extended the solution in Eq. (37) to the case of finite-duration thrusts

$$\begin{aligned} \hat{u} _{_{ \mathrm T1 }}&= \hbox{arcsin} \left( \frac{n^2a || \Delta \delta \underline{e} || }{8 |\gamma _{_{T}}|\cos \left( \frac{n^2a \Delta \delta a_{\mathrm {I}}}{8| \gamma _{_T}|}\right) } \right) +\frac{a n^2 \Delta \delta a_{\mathrm {I}}}{8| \gamma _{_T}|} \end{aligned}$$
(39a)
$$\begin{aligned} \hat{u} _{_{ \mathrm T2 }}&= \hbox{arcsin} \left( \frac{n^2a|| \Delta \delta \underline{e} || }{8 |\gamma _{_{T}}|\cos \left( \frac{n^2a \Delta \delta a_{\mathrm {I}}}{8| \gamma _{_T}|}\right) } \right) -\frac{a n^2 \Delta \delta a_{\mathrm {I}}}{8| \gamma _{_T}|} \end{aligned}$$
(39b)
$$\begin{aligned} \hat{u} _{_{ \mathrm T3 }}&= +\frac{a n^2 \Delta \delta a_{\mathrm {II}}}{8| \gamma _{_T}|} \end{aligned}$$
(39c)
$$\begin{aligned} \hat{u} _{_{ \mathrm T4 }}&= +\frac{a n^2 \Delta \delta a_{\mathrm {II}}}{8| \gamma _{_T}|} \end{aligned}$$
(39d)
$$\begin{aligned} \hat{u} _{_{ \mathrm N1 }}&= \frac{2}{n} \hbox{arcsin} \left( n^2a \frac{|| \Delta \delta \underline{i} || }{4 |\gamma _{_{N}}|} \right) \end{aligned}$$
(39e)
$$\begin{aligned} \hat{u} _{_{ \mathrm N1 }}&= \frac{2}{n} \hbox{arcsin} \left( n^2a \frac{|| \Delta \delta \underline{i} || }{4 |\gamma _{_N}|} \right) \end{aligned}$$
(39f)

Note that the middle point of each maneuver \(\tilde{u} _{_{ \mathrm M }}\) matches exactly the pulse location \(u _{_{ \mathrm M }}\) of the IT above. Furthermore \(\Delta \delta a_{\mathrm {I}}\) involves solving a transcendental equation and cannot be calculated analytically in case of finite-duration maneuvers. One possible approach is to approximate \(\Delta \delta a_{\mathrm {I}}\) to the value computed via impulsive planning in Eq. (38) [5]. The transcendental equation can be approximated to a polynomial equation and solved via numerical iteration. First tests show that sufficiently accurate results are obtained after three to six iteration steps. This issue will not be treated in this paper.

5.2 Simulation results

5.2.1 Simulation scenario

In this section the proposed control schemes are verified through a numerical integration of the nonlinear differential equations of motion using a MATLAB–Simulink simulation environment. The simulation environment includes additionally modeling blocks to incorporate gravitational and atmospheric perturbations. An assessment of the achievable performance via closed-loop simulation is presented. The boundary conditions were defined assuming an active debris removal mission scenario via rendezvous and docking. As Chaser we assume a spacecraft of 500 kg and a maximal thrust level of 0.4 N. Table 1 shows the detailed orbital parameters of a selected representative high-risk debris object which will be used as a test case in this work: a rocket upper stage (Zenit) with an inclination of about 70° which has been identified as the object with the highest environmental criticality [6, 11] in LEO.

Table 1 Selected high-risk objects for active debris removal
Full size table

As described in Sect. 2.4 a passively safe and stable configuration has been defined as \(\delta \underline{\alpha }_\mathrm{nom} = \begin{pmatrix} \delta a&\delta \lambda&0&\pm ||\delta e||&0&\pm ||\delta i||\end{pmatrix}^{\mathrm T}\). The dedicated formation flying scenario is that of the Chaser being injected in almost the same orbit as the Target with an initial along-track separation of −8 km. The Chaser gets position measurements via GNSS. The Target is uncooperative and can only be observed from ground using radar measurements at an update frequency of 12 h. The initial and targeted final ROE used in the simulation are listed in Table 2.

Table 2 Formation initial and final configurations
Full size table

The scenario is simulated using a \(J_{40,40}\) gravity model, NRLMSISE-00 atmospheric model and a Runge–Kutta fourth-order integration algorithm with a step size of 1 s.

Two initial position errors can be assumed, the radar orbit determination (radar/OD) measurement error, affecting the Target, and the GNSS orbit determination (GNSS/OD) measurement error, affecting the Chaser. To overcome the 12-h gap of Target radar-based measurements, orbit propagation is then considered. Two different navigation strategies based on on-ground absolute propagation and on-board relative propagation are possible. For relative orbit propagation the relative position is needed und thus both GNSS/OD and radar/OD errors have to be taken into account for the initial error. However, if the relative state is derived from absolute orbit propagation, the GNSS/OD measurement does not influence the position of the Target and the Chaser is assumed to be supported the whole time via GNSS/OD measurements. For this reason the GNSS/OD inaccuracy should not be incorporated as an initial error but has to be considered over the entire propagation time as a possible offset. In addition to the position errors, also errors in velocity can occur, for example due to uncertainties in thrust vector, activation time and spacecraft mass. These errors cannot be directly observed using relative propagation. A study of the navigation solution with a non-cooperative Target is discussed in detail in [6].

In this work however, we do not take navigation uncertainties and environmental perturbations into account while planning the maneuver reconfiguration. The main reason for that is that we are essentially interested on validating the derived guidance equations. The guidance algorithm assumes a precise knowledge of the state and does not incorporate drag or Earth oblateness terms. However, the Simulink-based simulation environment models gravitational and atmospheric perturbations and—as presented in the next section—the desired formation is nevertheless achieved with very good accuracy. The passively safe and stable final configuration defined in Table 2 guarantees a collision-free formation flight by setting a safe radial–normal separation as explained in Sect. 2.4.

5.2.2 Formation reconfiguration

We examine an approach phase including a complete formation reconfiguration (FR) and keeping (FK) with a maneuver set interval \(\Delta t = \Delta u / n\) corresponding to the radar measurement update period of 12 h. The implemented algorithm compares the measured configuration (initial) to the desired one (final) and computes a set of six maneuvers based on the finite-duration scheme. This step is repeated after 12 h to compute a maneuver set for formation keeping in case the desired configuration has not been reached or did not remain stable.

Fig. 6
figure 6

Temporal evolution of the ROE during formation reconfiguration and in-plane formation keeping maneuvers

Full size image
Fig. 7
figure 7

Temporal evolution of the out-of-plane motion ROE during formation reconfiguration maneuvers

Full size image

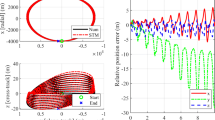
Figures 6 and 7 show the temporal evolution of the individual ROE. The desired formation is achieved with high precision within the first 12 h and remains stable so that no maneuvers are needed for the formation reconfiguration. The error is 10 m for \(a \delta \lambda\) and remains under 1 m for the rest of the ROE. The temporal evolution of the elements coincides with the predicted behavior described in Sect. 5.1 with the exception of small variations in \(a \delta e_x\) and \(a \delta i_x\) which are supposed to remain zero. This would be the case if the maneuvers are executed in an impulsive manner. Since maneuvers are executed along an arc centered at \(u _{_{ \mathrm M }}\) a temporal change is induced which sums up to zero at the end of the maneuver. Further small discrepancies are explained as linearization errors and effects of orbits disturbance.

Fig. 8
figure 8

3D trajectory and its projection on the RT and RN planes

Full size image

Figure 8 shows the three-dimensional trajectory of the formation and its projection on the radial–tangential and radial–normal planes. The ellipsoid depicted at the start position of the Target shows typical two-line-element (TLE) initial position uncertainties [7, 13]. The desired formation configuration has through the application of the E/I separation technique a safe separation in radial and normal direction and thus guarantees a collision-free formation as depicted in Fig. 8. Velocity uncertainties have been neglected, which is a common practice in collision risk estimations [13]. For a more rigorous assessment, these uncertainties have to be incorporated and the complete state vector errors have to be propagated until the next measurement is available. Uncertainty propagation can be achieved using different methods as described in [7, 13] and is subject of future work.

5.2.3 Integrated GVE as error assessment tool

It is possible to use the integrated GVE as precise (opposed to the standard GVE) analytical tool to propagate the effect of thrust maneuvers on ROE. We approximate the duration of maneuvers \(\Delta t _{_{ \mathrm M }}\) for impulsive thrusts using (23). Inserting this \(\Delta t _{_{ \mathrm M }}\) in Eq. (24) yields the induced alteration in ROE. This provides an analytical tool to estimate the error induced through impulsive planning. Depending on mission profile, this allows us to determine a threshold value (targeted alteration in ROE), for which impulsive planning is sufficient to achieve the required precision. Figure 9 depicts the analytical error estimation for \(a\delta e_y\) and \(a\delta i_y\). The estimated errors (1.6% for \(a\delta e_y\) and 2% for \(a\delta i_y\)) coincide with simulation results.

Fig. 9
figure 9

Analytical assessment of formation error induced through impulsive planning

Full size image

6 Conclusion and future work

The major contribution offered by this work is delivering a control method for finite-duration thrust maneuver. This method allows a clear amelioration of the achieved formation accuracy in terms of \(a\delta \underline{e}\) and \(a\delta \underline{i}\) which are the key for safe formation flight. To compute the finite-duration control scheme an approximation has been made to determine the intermediate change of the relative semimajor axis \(\Delta \delta a_I\) as detailed in Sect. 5.1.2. This approximation is sufficient for the purpose of safe formation reconfiguration but could provoke an undesired relative semimajor difference and hence triggers an undesired drift. To solve this problem, the transcendental equation evoking \(\Delta \delta a_I\) has to be numerically solved. First tests show that sufficiently accurate results are obtained after three to six iteration steps. Furthermore, the gravitational and atmospheric perturbations could be incorporated analytically in a generalized perturbed equation of motion and thus taken into account while computing the control scheme.