Experimental evaluation of model predictive control and inverse dynamics control for spacecraft proximity and docking maneuvers

Abstract

An experimental campaign has been conducted to evaluate the performance of two different guidance and control algorithms on a multi-constrained docking maneuver. The evaluated algorithms are model predictive control (MPC) and inverse dynamics in the virtual domain (IDVD). A linear–quadratic approach with a quadratic programming solver is used for the MPC approach. A nonconvex optimization problem results from the IDVD approach, and a nonlinear programming solver is used. The docking scenario is constrained by the presence of a keep-out zone, an entry cone, and by the chaser’s maximum actuation level. The performance metrics for the experiments and numerical simulations include the required control effort and time to dock. The experiments have been conducted in a ground-based air-bearing test bed, using spacecraft simulators that float over a granite table.

1 Introduction

Rendezvous and proximity operations (RPO) are essential for a wide range of future space missions [1,2,3]. Ground-based experimental evaluations of emerging guidance, navigation, and control (GNC) approaches may be used to raise their technological readiness level and determine their performance and limitations on flight-equivalent hardware (i.e., sensors, actuators, and computational systems) [2].

An experimental campaign to evaluate the performance of the model predictive control (MPC) and inverse dynamics in the virtual domain (IDVD) guidance methods has been performed at the Naval Postgraduate School POSEIDYN¹ air-bearing test bed [4]. The focus of this research is limited in scope to the guidance and control of the simulated spacecraft. The navigation problem is solved by the POSEIDYN test bed motion capture system, which, augmented by onboard sensors, is used to provide accurate navigation data. The test vehicles operating in the POSEIDYN test bed float on top of a 4-by-4 m granite table and exhibit a drag-free and weightless motion on a plane [4]. These test vehicles are referred to as floating spacecraft simulators, or simply as FSS.

A spacecraft docking problem is selected for the experimental evaluation of these two different control approaches. A keep-out zone, an entry cone, and a maximum force constraint are added to the docking scenario to evaluate the constraint handling abilities of the two different controllers. A linear–quadratic MPC (LQ-MPC) algorithm with a quadratic programming (QP) solver and an IDVD algorithm with a nonlinear programming (NLP) solver have been chosen for this comparative study. These two controllers have been implemented and, when executed in real-time on board the FSS, they are successful in autonomously guiding the chaser FSS towards its docking target.

The MPC approach is a receding horizon control that results in a QP problem when a linear–quadratic-based approach is used  [5]. This type of programming problem can be efficiently solved, has guaranteed convergence regardless of the initial guess (as long as the problem is feasible), and an upper bound on the number of required computations can be predetermined [6]. The drawback of an LQ-based MPC is that the problem constraints must be linear. Any nonlinear constraints must be linearized before the LQ-MPC problem can be formulated. This linearization may over-constrain the problem, providing a sub-optimal solution when compared to the solution of the original nonlinear problem. The use of MPC has been recently proposed for spacecraft RPO [7] and experimental evaluations using a kinematic test bed have already been conducted [8, 9], but to the best knowledge of the authors, this is the first time that the use of MPC is experimentally demonstrated for spacecraft RPO in a dynamically representative test bed. After conducting the experiments presented in this paper, the authors have experimentally demonstrated the use of a nonlinear MPC approach for spacecraft docking maneuvers [10].

The IDVD control approach is a direct optimization method based on the inversion of the system’s dynamics and the parametrization of the trajectory using a family of functions [11, 12]. This approach is also operated as a feedback controller but, unlike MPC, the IDVD approach optimizes the full length of the trajectory. As an NLP problem arises from the IDVD formulation, the IDVD approach can directly handle any nonlinear (and nonconvex) constraints. This capability comes at the expense of having to solve a more complex programming problem. In this research effort, the resultant NLP problem is solved onboard the FSS using the open-source NLP Interior Point OPTimizer (IPOPT) solver [13]. The application of the IDVD approach for spacecraft RPO has been extensively studied in the past by the authors, both on simulation [12, 14,15,16], and experimentally in the POSEIDYN test bed [17, 18]. Notably, none of the previously reported experimental results included a keep-out zone constraint. As the IDVD optimizes the full maneuver and does not need to linearize the constraints, the IDVD approach is expected to yield more propellant-efficient maneuvers.

Similar comparative studies have already been conducted in the POSEIDYN test bed. In particular, it is worth mentioning the comparison of artificial potential functions (APF) and adaptive APF for docking maneuvers [19]. In that case, the chaser spacecraft is required to avoid several obstacles before docking with the target. More recently, an LQ-MPC has been compared against a nonlinear MPC for a docking maneuver in the presence of multiple obstacles [10], and a nonlinear MPC approach has been used to experimentally demonstrate docking with a rotating target [20]. Moreover, a near-optimal real-time guidance approach using harmonic potential functions and a modified rapid random tree (RRT) approach has also bee experimentally tested in the POSEIDYN test bed for multi-constrained docking maneuvers [21].

Other optimization-based guidance approaches, based on convex optimization and potentially suitable for onboard implementation and real-time applications, have also been proposed [22, 23], but, to the best knowledge of the authors, not tested in a hardware-in-the-loop setup. These proposed and experimentally tested optimization-based guidance and control approaches contrast with the ones used on operational spacecraft. Historically, chaser spacecraft have conducted V-bar or R-bar approaches that are either manually piloted [24, 25] or controlled by a proportional-integral-derivative or H-infinity controller tracking a pre-defined straight-line (or quasi-straight) trajectory [26, 27]. For a historical review on the guidance and control algorithms used in spacecraft rendezvous and proximity operations refer to [28, 29].

The main contribution of this paper is to experimentally evaluate, for the first time, the performance of an LQ-MPC formulation for a multi-constrained spacecraft docking scenario using a hardware-in-the-loop setup in a dynamically representative test bed. The LQ-MPC formulation is then compared to the previously studied IDVD approach. Another contribution of this paper is to experimentally demonstrate the ability of the IDVD approach to handle keep-out zone constraints. By experimentally evaluating these guidance approaches in a dynamically representative test bed, their feasibility can be demonstrated with realistic dynamics, realistic actuator and navigation noises, as well as with real-time computational constraints. These experimental tests help raise the technology readiness level of the MPC and IDVD approaches for spacecraft RPO.

In this paper, the docking problem that has been used to evaluate the LQ-MPC and IDVD approaches is outlined first. Then a brief overview of the experimental setup is provided. The problem formulation of the two different control approaches is then presented. The practical implementation details, as well as the simulation and experimental results, are then given. Finally, a discussion about the experimental results and the differences between the two control approaches is provided.

2 Problem formulation

A multi-constrained docking scenario has been selected to experimentally compare the LQ-MPC and IDVD control approaches in the POSEIDYN test bed. Figure 1 schematically shows the test setup with the problem’s constraints and the vehicle’s initial conditions in the POSEIDYN test bed. One FSS is used as the chaser, another is used as a non-moving target, and a third is used as a non-moving obstacle.

Fig. 1

Experiment initial conditions in the POSEIDYN test bed

The specific parameters used for this test case are provided in Table 1. The selected test case is a straight-on docking with a non-moving obstacle and an entry cone constraint.

Table 1 Numeric values for the test case parameters

The keep-out zone constraint is only imposed on the chaser’s nominal position, which, for practical reasons, is approximately set at its geometric center. This chaser’s reference point is indicated in Fig. 2 by a black cross. To ensure a collision-free maneuver, the keep-out zone has been sized so that no collision can occur if the chaser’s geometric center remains outside it, i.e., regardless of the chaser’s relative orientation with respect to the obstacle. It is also important to note that the chaser needs to actively avoid the keep-out zone, as this one is placed along what would be the optimal straight-line trajectory if no obstacle was included. This can be clearly seen in Fig. 1. In addition, the entry cone constraint is also only imposed on the chaser’s geometric center. The apex of the cone is located at the chaser’s desired end state, thus showing an offset with respect to the target’s FSS position.

The focus of this experimental campaign is to compare two control approaches and thus the navigation problem is considered solved. The obstacle and the target’s positions are made available to the chaser vehicle. Additionally, the algorithms to be evaluated are only used to control the vehicle’s position, with its attitude being controlled by a combination of a propellant-optimal slew [30] and a proportional-derivative (PD) controller. Therefore, only the translation forces are considered when computing the resultant control effort.

2.1 Experimental setup

The experiments are conducted using three, approximately 10 kg test vehicles. These vehicles float via three planar air bearings over a 4-by-4 m granite table. Due to the air bearings as well as the planarity and horizontallity of the granite surface, the FSS experiences a weightless and a quasi-frictionless motion in two translation and one rotation degree-of-freedom, i.e., planar motion [4]. Figure 2 shows the target, chaser, and obstacle FSS over the POSEIDYN granite surface in the initial conditions used for this particular comparative study.

Fig. 2

Floating spacecraft simulators on top of the 4-by-4 m granite surface in the initial conditions used for the experiment campaign

Eight cold-gas thrusters provide autonomous motion capability to the FSS [31]. An onboard tank of compressed air provides the propellant required to operate the thrusters and the air bearings. An onboard power system and an onboard computer complete the FSS equipment. All the required processing (e.g., sensor readings, communications, navigation, guidance and control, and actuator commanding) is handled by the onboard computer.

Absolute navigation data is provided by an overhead motion capture system, VICON. The position and attitude information provided by this system is augmented by an onboard one-axis fiber-optic gyroscope (FOG) using a discrete-time Kalman filter [4]. Communications among multiple FSS, the VICON workstation, and other external PCs (used for telemetry monitoring) is achieved via UDP streams over an ad hoc Wi-Fi network [32].

Air-bearing tables provide an acceptable approximation of the dynamics experienced by spacecraft during close proximity operations. These types of test beds have been extensively used in the past to conduct hardware-in-the-loop testing and research in spacecraft RPO [33, 34].

2.2 FSS dynamic model

The motion of the FSS in the POSEIDYN test bed can be modeled as a double integrator with two translational and one rotational degree of freedom. The equations of motion of the FSS translation degrees of freedom can be written as follows:

$$\begin{aligned} \ddot{x}=\frac{F_x}{m} \end{aligned}$$

(1a)

$$\begin{aligned} \ddot{y}=\frac{F_y}{m} \end{aligned}$$

(1b)

where m denotes the mass of the FSS and $F_x, \ F_y$ the control forces. These equations can be re-written in state-space form as:

$$\begin{aligned} \dot{{\mathbf {x}}} = {\mathbf {A}}{\mathbf {x}} + {\mathbf {B}}{\mathbf {u}} \end{aligned}$$

(2)

The state vector is denoted by ${\mathbf {x}} = [x, \ y, \ \dot{x}, \ \dot{y}]^\mathrm{T}$, the control vector by ${\mathbf {u}} = [F_x, \ F_y]^\mathrm{T}$, and ${\mathbf {A}}\in \mathbb {R}^{4\times 4},$ and ${\mathbf {B}}\in \mathbb {R}^{4\times 2}$ represent the corresponding state and control matrices, respectively. With ${\mathbf {0}}_{2\times 2}$ denoting a $2\times 2$ zero matrix and ${\mathbf {I}}_{2\times 2}$ a $2\times 2$ identity matrix, the ${\mathbf {A}}$ and ${\mathbf {B}}$ matrices can be defined as follows:

$$\begin{aligned} {\mathbf {A}}= \begin{bmatrix} {\mathbf {0}}_{2\times 2}&{\mathbf {I}}_{2\times 2}\\ {\mathbf {0}}_{2\times 2}&{\mathbf {0}}_{2\times 2} \end{bmatrix} \end{aligned}$$

(3a)

$$\begin{aligned} {\mathbf {B}}= \begin{bmatrix} {\mathbf {0}}_{2\times 2} \\ \frac{1}{m}{\mathbf {I}}_{2\times 2} \end{bmatrix} \end{aligned}$$

(3b)

A control method can then be designed to control the linear-time invariant system described by Eq. (2). In this case, the LQ-MPC and IDVD algorithms are used to control these translation states.

The attitude or orientation of the FSS is also modeled as a double integrator:

$$\begin{aligned} \ddot{\theta }=\frac{\tau }{I_{zz}} \end{aligned}$$

(4)

In this last equation, $I_{zz}$ denotes the FSS’ moment of inertia about the vertical axis and $\tau$ the control torque. The FSS’ attitude is controlled through a propellant-optimal, bang-off-bang controller [30], and when the attitude is within $\pm {10^\circ }$ of the desired target attitude (i.e., the docking attitude), it switches to a PD control law to maintain it.

3 Controller design

The two different control approaches that have been experimentally evaluated are briefly described in this section.

3.1 Linear–quadratic model predictive control (LQ-MPC)

MPC is a receding horizon control approach that can be used to solve constrained trajectory optimization problems. The LQ-MPC is fundamentally based on the linear–quadratic optimal control problem. The constraint handling ability of the LQ-MPC distinguishes it from the standard linear–quadratic control [5]. In the LQ-MPC approach, only linear inequality constraints are allowed, resulting in a QP problem. This type of optimization problems can be efficiently solved while enjoying deterministic convergence properties [6].

Implementation of MPC for spacecraft RPO maneuvers has been studied in the past [7]. A survey of guidance algorithms that can be used for onboard RPO trajectory planning is presented in [35], including an MPC implementation in simulation. The experimental validation of an MPC algorithm presented in this paper provides further confidence in its ability to be implemented onboard real systems. Simulation results of applications of MPC to a constrained rendezvous problem have also been shown in [36, 37]. The type of constraints enforced in these simulations include thrust constraints, a line-of-sight constraint linearized through polyhedral approximations [36], and an obstacle avoidance constraint linearized through a rotating hyperplane [7, 37]. These references provide the basic framework for the LQ-MPC formulation implemented for this experimental campaign.

As an LQ-based method, LQ-MPC can be used to solve a constrained optimization problem, where a quadratic cost function is minimized subject to linear dynamics and linear inequality constraints. This problem formulation results in a convex QP problem that can be solved using readily available solvers [38]. The obstacle avoidance constraint is linearized through a rotating hyperplane method [37]. The approach cone constraint is linearized by constructing two hyperplanes that define the edges of the cone, intersecting at the target docking point. When these constraints are activated, the FSS is forced to stay within the two hyperplanes until docking is achieved. The LQ-MPC problem, in discrete form, is formed as follows:

$$\begin{aligned} {\text {Minimize }}J &= ({\mathbf {x}}(N)-\mathbf {x}_{t})^\mathrm{T} {\mathbf {P}}({\mathbf {x}}(N)-\mathbf {x}_{t}) \nonumber \\&+\sum \limits _{i=0}^{N-1} ({\mathbf {x}}(k+i)-\mathbf {x}_{t})^\mathrm{T} {\mathbf {Q}}({\mathbf {x}}(k+i)-\mathbf {x}_{t})\nonumber \\&+\sum \limits _{i=0}^{N-1}{\mathbf {u}}(k+i)^\mathrm{T} {\mathbf {R}}{\mathbf {u}}(k+i) \end{aligned}$$

(5a)

$$\begin{aligned} {\text {Subject to }}{\mathbf {x}}(k+1)& = {\mathbf {A}}_d{\mathbf {x}}(k) + {\mathbf {B}}_d{\mathbf {u}}(k) \end{aligned}$$

(5b)

$$\begin{aligned} |{u_{1}(k)}|\le & {} u_{\mathrm {max}} \end{aligned}$$

(5c)

$$\begin{aligned} |{u_{2}(k)}|\le & {} u_{\mathrm {max}} \end{aligned}$$

(5d)

$$\begin{aligned} \hat{{\mathbf {n}}}_{\mathrm {obs}} \cdot {\mathbf {r}}(k)\ge & {} \hat{{\mathbf {n}}}_{\mathrm {obs}} \cdot {\mathbf {p}}_{\mathrm {obs}} \end{aligned}$$

(5e)

$$\begin{aligned} \hat{{\mathbf {n}}}_{c1} \cdot {\mathbf {r}}(k)\ge & {} \hat{{\mathbf {n}}}_{c1} \cdot {\mathbf {p}}_{\mathrm {dock}} \end{aligned}$$

(5f)

$$\begin{aligned} \hat{{\mathbf {n}}}_{c2} \cdot {\mathbf {r}}(k)\le & {} \hat{{\mathbf {n}}}_{c2} \cdot {\mathbf {p}}_{\mathrm {dock}} \end{aligned}$$

(5g)

The length of the horizon is denoted by N, and ${\mathbf {A}}_d, \ {\mathbf {B}}_d$ are the discrete state and control matrices, which can be derived from the continuous dynamics in Eq. (2) when using a sampling time $T_\mathrm{s}$. The term ${\mathbf {x}}_t$ denotes the targeted final condition. As mentioned before, only the translational motion is included in the MPC formulation. The matrices ${\mathbf {P}}\in \mathbb {R}^{4\times 4}$, ${\mathbf {Q}}\in \mathbb {R}^{4\times 4}$, and ${\mathbf {R}}\in \mathbb {R}^{2\times 2}$ in Eq. (5a) define the cost function weights on the final condition, state, and control variables, respectively. Equation (5b) defines the equality constraint enforcing the dynamics of the system. Equations (5c) and (5d) enforce constraints on the control variables. Finally, Eqs. (5e)–(5g) enforce the hyperplane constraints for the obstacle and cone, where ${\mathbf {r}}=\left[ x,y\right] ^\mathrm{T}$ denotes the position of the chaser, $\hat{{\mathbf {n}}}_{()}$ defines the normal vector of the hyperplane, and ${\mathbf {p}}_{()}$ defines a point on the hyperplane. The $\left( \cdot \right) _{\mathrm {dock}}$, $\left( \cdot \right) _{\mathrm {obs}}$, and $\left( \cdot \right) _{\mathrm {c1,c2}}$ subscripts in Eq. (5) help differentiate the quantities related to the docking point, obstacle, and entry cone constraint, respectively.

The problem in Eq. (5) is transformed into a QP problem [38], and solved using a publicly available MATLAB-based solver. The QP solver outputs the required control inputs for the entire horizon. Once the QP problem is solved, the first control input of the obtained sequence is extracted from the solution and applied for the $T_\mathrm{s}$ sampling period. The QP problem is then resolved using the previous solution control sequence and the current FSS state to obtain the solution to be used in the next step. This feedback action introduces a degree of nominal (inherent) robustness to uncertainty.

The MPC (and also the IDVD) produces a control input that needs to be actuated by the FSS thrusters. This piecewise constant control input needs to be modulated to generate a pulse train to fire the different FSS thrusters to generate an equivalent effect than the requested control input. To achieve this binary thruster actuation, i.e., ON–OFF, the output of the MPC (and also of the IDVD) is passed through a delta–sigma modulator [4].

The LQ-MPC formulation is implemented in Simulink as an embedded MATLAB function, which is suitable for automatic code generation. C code is then automatically generated from the Simulink model and compiled (targeting the embedded hardware architecture). Finally, this compiled model is executed onboard the FSS’ real-time operating system [4].

3.2 Inverse dynamics in the virtual domain (IDVD)

The IDVD method is a near-optimal guidance technique where the trajectory and time are parameterized using a family of functions that depend on a finite number of coefficients (e.g., polynomials or splines) [11, 12]. Some of these function parameters are determined to automatically enforce the initial and final conditions. The remaining parameters can be adjusted to minimize a cost function while meeting certain predefined constraints. In general, the parameter optimization problem results in a nonlinear programming problem. Once all the function parameters have been adjusted, the vehicle’s trajectory is fully determined and the required control inputs can be easily derived. This optimization procedure can be repeated at regular intervals, employing IDVD as a near-optimal feedback controller. The IDVD approach has been extensively studied for spacecraft docking problems both in simulation [14,15,16, 39] and experimentally in the POSEIDYN test bed [17, 18].

In this IDVD implementation, the trajectory is constructed as a polynomial of order $n_{x}$ and $n_{y}$ that is a function of the virtual time $\kappa \in [0,\kappa _{f}]$:

$$\begin{aligned} x\left( \kappa \right) =\sum _{i=0}^{n_{x}}a_{i}\kappa ^{i} \end{aligned}$$

(6a)

$$\begin{aligned} y\left( \kappa \right) =\sum _{i=0}^{n_{y}}b_{i}\kappa ^{i} \end{aligned}$$

(6b)

The time t for each of the trajectory components is also modeled as a polynomial of the virtual time $\kappa$ of order $n_{t}$:

$$\begin{aligned} t_{x}\left( \kappa \right) =\sum _{i=1}^{n_{t}}d_{ai}\kappa ^{i} \end{aligned}$$

(7a)

$$\begin{aligned} t_{y}\left( \kappa \right) =\sum _{i=1}^{n_{t}}d_{bi}\kappa ^{i} \end{aligned}$$

(7b)

The time is also parameterized to provide additional optimization variables, reducing the final control effort and improving the constraint handling capabilities. To fully specify the trajectory and thus solving the problem, the $a_{i},b_{i},d_{ai},{\text { and }}d_{bi}$ coefficients have to be determined.

It is worth noting that different polynomial orders can be used for each of the trajectory components $n_{x}\ne n_{y}$. Additionally, different virtual time polynomials (see Eq. (7)) can be used for each of the trajectory components, imposing equal final times $t_{x} (\kappa _{f})=t_{y} (\kappa _{f})$. It is also worth pointing out that the time t has to be monotonically increasing and thus $t'=\mathrm{d}t/\mathrm{d}\kappa$ needs to be positive $t'>0$, making the time t univocally determined by $\kappa$.

$$\begin{aligned} t'=\frac{\mathrm{d}t}{\mathrm{d}\kappa }=\sum _{i=1}^{n_{t}}id_{i}\kappa ^{i-1}>0 \end{aligned}$$

(8)

The time derivatives of the trajectory can be computed as follows:

$$\begin{aligned} t''\left( \kappa \right) =\frac{\mathrm{d}^{2}t}{\mathrm{d}\kappa }=\sum _{i=2}^{n_{t}}i\left( i-1\right) d_{i}\kappa ^{i-2} \end{aligned}$$

(9a)

$$\begin{aligned} \dot{x}=\frac{\mathrm{d}x}{\mathrm{d}t}\frac{\mathrm{d}\kappa }{\mathrm{d}\kappa }=\frac{x'}{t'} \end{aligned}$$

(9b)

$$\begin{aligned} x'=t'\dot{x}\end{aligned}$$

(9c)

$$\begin{aligned} \ddot{x}=\frac{\mathrm{d}\dot{x}}{\mathrm{d}t}\frac{\mathrm{d}\kappa }{\mathrm{d}\kappa }=\frac{\mathrm{d}(x'/t')}{\mathrm{d}\kappa }\frac{1}{t'} =\frac{x''}{t'^{2}}-\frac{x'}{t'^{3}}t''=\frac{x''}{t'^{2}}-\frac{\dot{x}}{t'^{2}}t'' \end{aligned}$$

(9d)

$$\begin{aligned} x''=t'^{2}\ddot{x}+t''\dot{x} \end{aligned}$$

(9e)

The trajectory derivatives with respect to the virtual time are computed as follows:

$$\begin{aligned} x'=\sum _{i=1}^{n_{x}}ia_{i}\kappa ^{i-1} \end{aligned}$$

(10a)

$$\begin{aligned} x''=\sum _{i=2}^{n_{x}}i\left( i-1\right) a_{i}\kappa ^{i-2} \end{aligned}$$

(10b)

From the accelerations (see Eq. (9e)) the forces required to follow the trajectory can be obtained using Eq. (1).

The trajectory must comply with the initial ${\mathbf {x}}\left( 0\right)$ and desired final states ${\mathbf {x}} (t_{f})$ as well as with a final acceleration $\ddot{x}(t_{f}),\ddot{y}(t_{f})$. These initial and final conditions are used to set the first five trajectory coefficients ($a_{i}$ and $b_{i}$ with $i\le 4$). The polynomial order needs to be larger than or equal to four $n_{x,y}\ge 4$ to have any remaining coefficients left for the optimization, or to ensure that the resultant trajectory meets the constraints.

$$\begin{aligned} {\mathbf {x}}(0)& = \mathbf {x}_{0} \end{aligned}$$

(11a)

$$\begin{aligned} {\mathbf {x}}(t_{f})& = {\mathbf {x}}_{f} \end{aligned}$$

(11b)

In general, for a docking scenario, the final acceleration is set to zero: $\ddot{x} (t_{f})=\ddot{y} (t_{f})=0,$ and the final velocity may be also set to zero or to a certain small terminal value to ensure a successful latching.

The coefficients available to minimize the cost function while meeting constraints are the trajectory coefficients $a_{i}$ and $b_{i}$ with $i\ge 5$, the virtual time coefficients $d_{i}$, with $i\ge 1$, and the final virtual time $\kappa _{f}$. It has to be noted that if different time polynomials are used for the different components then the $d_{b1}$ is set so that $t_{x} (\kappa _{f})=t_{y} (\kappa _{f})$ is met.

With respect to the constraints, it is imposed that the final time $t (\kappa _{f})$ shall be less than a maximum user defined time $t_{\mathrm {max}}$.

$$\begin{aligned} t (\kappa _{f})<t_{\mathrm {max}} \end{aligned}$$

(12)

Additionally, the time shall be monotonically increasing with $\kappa$ (see Eq. (8)). This last constraint has been enforced by imposing a lower bound on the $d_{i}$ coefficient as $d_{i}>0$. This stricter constraint simplifies the optimization but, as it is over-constraining, potentially reduces the solution’s optimality.

The cost function of the optimization problem is then selected as the $L^{1}$-norm of the control input (see Eq. (13a)). The complete IDVD optimization problem is formulated as follows:

$$\begin{aligned} {\text {Minimize }}J=\int _{t_{0}}^{t_{f}}||{\mathbf {u}}||_{1} \mathrm{d}t \end{aligned}$$

(13a)

$$\begin{aligned} {\text {Subject to }} \mathbf {\dot{x}}= {\mathbf {A}}{\mathbf {x}} + {\mathbf {B}}{\mathbf {u}} \end{aligned}$$

(13b)

$$\begin{aligned} d_{i} & > 0\quad {\text {for }}i=1,\ldots ,n_{t} \end{aligned}$$

(13c)

$$\begin{aligned} t (\kappa _{f}) & < t_{\mathrm {max}} \end{aligned}$$

(13d)

$$\begin{aligned} t_{x} (\kappa _{f}) & = t_{y} (\kappa _{f}) \end{aligned}$$

(13e)

$$\begin{aligned} |{u_{1}(t)}| & \le u_{\mathrm {max}}\end{aligned}$$

(13f)

$$\begin{aligned} |{u_{2}(t)}| & \le u_{\mathrm {max}}\end{aligned}$$

(13g)

$$\begin{aligned} \hat{{\mathbf {n}}}_{c1} \cdot {\mathbf {r}}(t) & \ge \hat{{\mathbf {n}}}_{c1} \cdot {\mathbf {p}}_{\mathrm {dock}}\end{aligned}$$

(13h)

$$\begin{aligned} \hat{{\mathbf {n}}}_{c2} \cdot {\mathbf {r}}(t) & \le \hat{{\mathbf {n}}}_{c2} \cdot {\mathbf {p}}_{\mathrm {dock}}\end{aligned}$$

(13i)

$$\begin{aligned} \left||{\mathbf {r}}(t)-\mathbf {r}_{\mathrm {obs}}\right||_{2} & \ge R_{\mathrm {obs}} \end{aligned}$$

(13j)

As in the LQ-MPC formulation, the force that the FSS can produce is limited, imposing the constraint in Eqs. (13f), (13g). The entry cone constraint is included in Eqs. (13h), (13i) in an equivalent manner as the one introduced in the LQ-MPC formulation. Finally, the scenario’s keep-out zone is directly added as a nonlinear and nonconvex constraint in Eq. (13j).

The IDVD problem, as implemented here, is inherently nonlinear and nonconvex. The open-source nonlinear programming Interior Point OPTimizer (IPOPT) [13] solver is used to find the solution to the IDVD problem at each time step. In this case the solution, if found, can only be guaranteed to be the locally optimal.

It is also worth noting that the constraints are only imposed on a finite number of points S along the trajectory. These points are equally spaced along the virtual time $\kappa$.

In an equivalent manner as in the LQ-MPC approach, the IDVD approach is implemented as a feedback controller, thus obtaining an inherent degree of robustness to uncertainty. The IDVD problem is resolved at regular intervals $T_\mathrm{s}$, with the current solution being used to extract the current control input.

The IPOPT optimization routine is wrapped as a Simulink S-function suitable for automatic code generation. The resulting C code is compiled for the target hardware and executed in the real-time operating system on board the FSS.

4 Simulation and experimental results

A numerical simulator that recreates the FSS dynamics and simulates the different onboard sensors and actuators is first used to design, validate, and tune the controllers. The two different controllers were initially independently and manually tuned to achieve acceptable results. This independent tuning resulted in different maneuver durations for the two controllers. To obtain a fairer control effort comparison, the controllers were then re-tuned to achieve a similar maneuver duration than the other controller with their respective initial tuning.

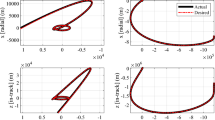
Table 2 shows the initial parameters used for the LQ-MPC algorithm to run both the simulated and experimental cases, where $\bar{{\mathbf {P}}}\in \mathbb {R}^{4\times 4}$ is the solution to the Algebraic Riccati equation for the discrete LQR problem. Table 3 shows the parameters used after re-tuning the controller to achieve a similar docking time as the initial IDVD case. Figure 3 shows the simulated and experimental trajectories, with the initial tuning. In the trajectory figures, the solid black circles located along the trajectory represent the control effort expended during the last 5 s, thus visually indicating the distribution of the control effort along the trajectory. As these black circles are evenly spaced in time, they also visually indicate the velocity at which the FSS traversed the trajectory.

Table 2 LQ-MPC parameters (initial tuning)

Table 3 LQ-MPC parameters (re-tuned)

Fig. 3

Simulated and experimental trajectories for LQ-MPC after initial tuning

Table 4 shows the initial parameters used for the IDVD controller. Table 5 shows the parameters after re-tuning the controller to achieve similar docking time as the initial LQ-MPC case. Figure 4 shows the simulated and experimental trajectories, with the initial tuning. As the polynomials orders have been set to $n_{x}=n_{y}=5$ and $n_{t}=2$, the total number of coefficients that remain available for the maneuver optimization is 6 ($a_{5}$, $b_{5}$, $d_{a1}$, $d_{a2}$, $d_{b2}$ and $\kappa _{f}$)—as 8 of them ($a_{i}$ and $b_{i}$ with $i\le 4$) are used to set the initial and final conditions, and $d_{b1}$ is used to impose $t_{x} (\kappa _{f})=t_{y} (\kappa _{f})$.

As the IDVD approach has a tendency to hug the constraints, it was observed that small cone constraint violations could occur on the external edge of the cone. These violations, only occurring during the experiments and not in the simulations, are attributed to noise on the actuated control, which briefly displaces the FSS into a region where the cone constraints are violated. To alleviate the concern of not meeting the problem’s cone constraint as defined in Table 1, the cone range is extended in the IDVD formulation so that the original constraint is always met. Moreover, since the cone constraints are enforced on states, this issue could also be addressed by adding auxiliary slack variables in the cone constraints [7].

Table 4 IDVD parameters (initial tuning)

Table 5 IDVD parameters (re-tuned)

Fig. 4

Simulated and experimental trajectories for IDVD after the initial tuning

Figure 5 shows the simulated and experimental trajectories obtained with the re-tuned LQ-MPC controller. Figure 6 shows the simulated and experimental trajectories obtained with the re-tuned IDVD controller.

Fig. 5

Simulated and experimental trajectories for LQ-MPC after re-tuning

Fig. 6

Simulated and experimental trajectories for IDVD after re-tuning

Finally, Table 6 provides the performance metrics for the LQ-MPC and IDVD controllers when executed on the simulator. Table 7 provides the performance metrics for the experiment campaign. The control effort, $u_{T}$, measuring the efficiency of the guidance and control approach, is defined as follows:

$$\begin{aligned} u_{T}=\int _{t_{0}}^{t_{f}}||{\mathbf {u}}||_{1} \mathrm{d}t \end{aligned}$$

(14)

An $L^{1}$-norm has been selected for the control effort $u_{T}$ as its output is given in N s, providing results that are intuitive and that can be easily converted into other meaningful quantities (e.g., quantity of expelled propellant or thrusters on-time).

Table 6 Comparison of simulation performance metrics for LQ-MPC and IDVD

Table 7 Comparison of experiment performance metrics for LQ-MPC and IDVD

5 Discussion

The results presented in the previous section clearly show that both algorithms successfully reach the final docking condition while meeting the imposed constraints. It is also worth mentioning that the numerical simulation and the experimental results are quite similar (thus validating the simulator).

The slight differences between the numerical simulations and the experiments are to be expected, given that the physical attributes of the test bed cannot be fully recreated in the numerical simulation environment. Thruster misalignment and thruster level uncertainties account for most of the differences [4]. An additional source of variability is the navigation. Although the navigation problem has been considered solved, the VICON motion capture system only provides position and attitude information. A discrete-time Kalman filter is used to obtain the velocity estimates, which, in the case of the angular rate, are augmented by an onboard FOG [4]. Therefore, in the experimental cases, the position and the velocities suffer from a certain amount of noise which does inevitably affect the controller’s behavior. Both controllers are able to successfully dock despite these navigation noise and actuation uncertainties, indicating that both controllers are somewhat capable of rejecting the navigation noise and are robust with respect to actuation uncertainty.

It is also worth pointing out that the simulation results for the IDVD algorithm are smoother, in terms of thrust, when compared to their experiment counterparts. In the IDVD approach, the resulting trajectory tends to get close to the constraint boundaries. Small uncertainties in the state estimation and thruster uncertainties can place the FSS in a trajectory that may violate these constraints in the immediate future. The IDVD controller attempts to immediately correct this situation, resulting in short-lived aggressive thrusting. This phenomena accounts for the unexpected peaks of thruster actuation levels during the experimental trajectories (specially clear in Fig. 4b).

When the IDVD polynomial order increases, the IDVD tends to converge to the true optimal solution, which, given its cost function, resembles a propellant-optimal bang-off-bang type solution. Although the polynomial order does not change during the experiments, the IDVD enjoys increasing optimization freedom as the trajectory gets traversed. Less distance remaining with respect to the target state allows a more flexibile trajectory generation. Therefore, the IDVD solution progressively evolves and converges to a bang-off-bang type solution. On the last part of the maneuver, this results in a tendency to only decelerate when the FSS gets close to its target end state, i.e., eventually becoming an impulsive deceleration. This can be clearly seen on the simulation results (see Fig. 4) where the solid black circles are larger toward the end of the trajectory, signaling this aggressive deceleration.

This late aggressive deceleration, although efficient in terms of propellant usage, may actually be an undesirable effect, as safety and operational constraints may limit the velocity at which the chaser approaches the target, or limit the amount of thrusting allowed in the immediate vicinity of the target. To limit this aggressive deceleration, the force constraint on the IDVD controller has been artificially reduced, thus forcing a longer and milder deceleration period. For the initial tuning, the maximum available force has been lowered to a quarter of the actual achievable level by the FSS. This artificial limitation may reduce the ability of the FSS to overcome disturbances and reduce the set of feasible solutions. On the re-tuned case, the maximum force is lowered to only a half of its maximum value, as a shorter maneuver duration trajectory demands higher actuation levels. By adding an upper velocity constraint, a similar result could also be obtained (at the expense of increasing the number of constraints and the computational burden). This effect can be traced back to the IDVD cost function in Eq. (13a). By changing the cost function, a different type of behavior could be obtained [11]. To obtain a more equitable comparison, the LQ-MPC maximum force is also reduced, matching the values used in the IDVD approach.

In contrast, the LQ-MPC controller is more aggressive at the beginning of the maneuver, as can be seen in Figs. 3 and 5. This behavior is consistent with the notion that the LQ-MPC exhibits a “regulator type” of behavior. Under an LQ-MPC, the FSS strongly accelerates at the beginning of the maneuver, slowly reducing its velocity as it approaches the target, and exhibiting a reduced thruster activity toward the end of the docking maneuver.

When comparing the two algorithms from the results in Table 7, a few conclusions can be drawn. The IDVD algorithm provides a more propellant-efficient maneuver, with a lower control effort. This result is expected since the IDVD approach solves the full nonlinear optimization problem without approximating the obstacle keep-out zone. The LQ-MPC only considers a part of the trajectory (receding horizon) and approximates the nonlinear constraint through the rotating hyperplane method [7, 37]. The linearization of the keep-out zone tends to overconstrain the problem, leading to a less optimal solution. Additionally, the LQ-MPC cost function includes both state and control terms, whereas IDVD minimizes the control effort directly. This is illustrated by the fact that the LQ-MPC method minimizes both state error and control effort via the ${\mathbf {Q}}$ and ${\mathbf {R}}$ matrices, respectively.

An interesting difference between the LQ-MPC and the IDVD approach is that the IDVD approach includes an explicit maximum docking time constraint, with the optimal solution usually taking all the allowed time. In docking maneuvers it may be desired to explicitly bound the maneuver duration, as communication with ground assets and/or favorable illumination conditions may be time critical. The duration of the LQ-MPC maneuver is governed by the selection of the weight matrices and thus the final time is a matter of tuning. For example, by increasing the ${\mathbf {R}}$ weighting values, the resulting LQ-MPC trajectory would take longer, and also potentially use less control effort.

The IDVD and LQ-MPC controllers were initially tuned independently, resulting in two different maneuver durations. To allow a fairer comparison of control effort, the controllers were re-tuned to achieve a similar maneuver time. When the LQ-MPC controller was re-tuned to achieve a longer docking time, the hyperplane rotation rate was not adjusted. Therefore, the resulting trajectory did not get as close to the keep-out zone as the initial trajectory. If the rotation rate of the hyperplane was tuned for this case, the performance of the LQ-MPC could be further improved.

The computational cost of the MPC and IDVD approaches has not been directly measured and a direct quantitative comparison on this quantity cannot be made at this time. Despite this limitation, the results of a similar experimental campaign [10] offer some rough-order-of-magnitude data for the LQ-MPC approach. In that study, the authors used an LQ-MPC approach to perform docking maneuvers in the presence of two obstacles on the POSEIDYN test bed. In that case, the average computation time to solve the QP problem arising from the LQ-MPC formulation is around 0.3 s, and a maximum computation time of 2.85 s is observed, when the maximum 170 iterations on the QP solver are reached. In the case presented in this paper, the iteration limit is set to 100. This limit is only reached when the FSS finds itself within a region of local infeasibility. However, in these cases, the resulting LQ-MPC control input directs the FSS toward the feasibility region and thus the penalty of reaching this condition is rather mild.

The NLP problem resulting from the IDVD approach has no guaranteed convergence and thus more precautions are required. Due to the highly nonlinear behavior of the polynomials on the IDVD approach, a failure to converge to a feasible solution can produce a completely erroneous control input. To help the FSS to recover from these conditions, the IDVD algorithm is executed at a fast 5 Hz rate, setting a 15 iteration limit on the IPOPT solver. This low iteration limit can cause some cases to not reach convergence, while still providing a feasible solution. During the experiments, this iteration limit was frequently reached when the FSS found itself close to an infeasible region (e.g., close to a constraint boundary). The fast 5 Hz solution rate guarantees that the actuation of non-converged but feasible solutions or the gaps due to non-converged and infeasible solutions are brief (i.e., max. 0.2 s). Using the IPOPT warm start capabilities, convergence was usually achieved under ten iterations. It is also worth mentioning that executing the IDVD at a fast rate also helps the algorithm to consistently provide converged solutions. This behavior may be counterintuitive, but the IPOPT solver can greatly benefit from an initial guess that is very close to the actual solution. If that is the case, the optimization problem can be solved in a few iterations (thus in a short amount of time) and the risk of not finding a feasible solutions diminishes. If the IDVD is resolved at a fast rate, subsequent IDVD solutions are close to each other and thus the previous solution can be effectively used as the initial guess.

Although the IDVD approach results in an NLP problem, this one can be solved relatively fast. This is due to the relatively small dimension of the problem, which, in this case, only includes six optimization parameters ($a_{5}$, $b_{5}$, $d_{a1}$, $d_{a2}$, $d_{b2}$ and $\kappa _{f}$). The fast 5 Hz re-solving rate of IDVD contrasts with the $T_\mathrm{s}=5$ s re-solving period of the LQ-MPC approach. Due to this difference, and given that the LQ-MPC approach is, on average, solved in approximately 0.3 s, with the prediction horizon length set as 20 [10], the computational load of the IDVD approach is significantly larger than the computational load of the LQ-MPC.

6 Conclusions

A linear–quadratic model predictive control (LQ-MPC) and an inverse dynamics in the virtual domain (IDVD) guidance approach have been experimentally evaluated on a planar air-bearing test bed for a multi-constrained docking maneuver. Both approaches achieved a successful docking with no constraint violation. The IDVD approach exhibited a smaller control effort as it considers the full-length maneuver and does not linearize the constraints. The drawback associated with IDVD approach is the resulting nonlinear programming problem, which is highly nonlinear, without any guarantee of convergence, and computationally expensive to solve. The LQ-MPC approach seems to generate more expensive maneuvers, but its resulting quadratic programming problem has deterministic convergence properties. The research presented in this paper illustrates the trade-offs that must be considered between optimality and computational complexity.