A typical question in education research is about the effectiveness of a treatment, of which the treatment can be an education program, a curriculum, or a policy of interest, is that whether the treatment have a causal impact on the outcome of interest. For example, Jennings et al. (2017) developed a mindfulness-based professional development program to promote teachers’ social and emotional competence and improve the quality of classroom interactions. To investigate the effectiveness of the program, eligible teachers were randomly assigned to receive this program (treatment) or to receive standard professional development activities by their schools (control). Randomized control trials (RCTs), where treatment conditions are randomly assigned, are the most popular research designs because they can establish strong internal validity, the extent to which the research results support the causal effect. The What Works Clearinghouse (WWC) Procedures and Standards Handbook (Version 5) by the U.S. Department of Education’s Institute of Education (2022) provides standards and guidelines to review and summarize the quality of existing research in educational programs, products, practices, and policies. According to its report, the highest possible research rating on RCTs is “meeting WWC standards without reservations” when the assumptions of RCTs are satisfied. The strong internal validity of RCTs is supported by different logical frameworks for causal inference such as potential outcomes framework and directed acyclic graph framework (see the specific articles contained in this special issue).

However, there are situations where RCTs are not feasible or ethical, therefore, the methodology cannot be applied. Quasi-experimental designs aim to establish the causal effect of a treatment on an outcome in the absence of RCTs. The regression discontinuity design (RDD) is a quasi-experiment that can achieve high internal validity. As an example of the RDD, Wong et al. (2008) conducted a study in the U.S. They compared a group of children who were 4 years of age and completed state pre-kindergarten programs with another group of children who were the same age but did not participate in the programs. The aim was to investigate the effects of state pre-kindergarten programs on children’s receptive vocabulary, math, and print awareness skills. The pre-kindergarten program enrollment was not randomized, and it was determined by a continuous assignment variable: children’s date of birth.

Besides the RDD, there are other quasi-experimental designs such as difference-in-differences analysis (DiD), interrupted time series design (ITS), instrumental variable (IV) analysis, as well as propensity score analysis (PSA). First, we present a survey about the usage of quasi-experimental designs in education research. In each design, we use the potential outcomes framework to define the causal effects and overview the causal assumptions and statistical analyses with examples in education research.

Use of quasi-experimental designs in education research

We used the search engine hosted by EBSCO, to sum up the number of publications on different designs between 2016 and 2022 in the ERIC database using the following phrases: randomized (control) trial (or randomization), regression discontinuity, difference-in-differences (or gain score analysis), interrupted time series (or comparative interrupted time series), instrumental variable, and propensity score (or group equating, nonequivalent groups design).Footnote 1 Figure 1 shows the results. As expected, the usage of RCTs far exceeded all other designs. Among the quasi-experimental designs, PSAs were the most utilized, followed by DiDs, RDDs, IVs, and ITSs. There was a steady increase in the usage of DiDs. The frequencies of the usage of RDDs, ITSs, and IVs were stable yet infrequent over time.

Fig. 1
figure 1

Number of publications in ERIC between 2016 and 2022. This figure is based on the search in EBSCO using the following keywords. Randomized Control Trial: randomization, randomized trial, randomized control trial. Regression Discontinuity: regression discontinuity. Difference-in-Differences: difference-in-differences, gain score analysis. Interrupted Time Series: interrupted time series, comparative interrupted time series. Instrumental variable: instrumental variable. Propensity Score: propensity score, group equating, nonequivalent groups design

Full size image

Causal estimands and causal assumptions

We utilize the potential outcomes framework (Neyman et al., 1990; Rubin, 2006) to identify the causal estimands. Throughout the paper, we focus on a two-group design (treatment and control). For simplicity, we assume that the data have no missing values in every design and refer readers to textbooks on missing data analysis (Enders, 2022; Little & Rubin, 2019). Cham and West (2016) reviewed strategies to handle missing values in PSAs.

Let \({T}_{i}\) denote participant i’s treatment assignment (1 = treatment, 0 = control). Then, according to the potential outcomes framework, participant i has two potential (hypothetical) outcomes: the potential treatment outcome if participant i is assigned to the treatment group, \({Y}_{i}(T=1)\) or \({Y}_{i}(1)\), and the potential control outcome if participant i is assigned to the control group, \({Y}_{i}(T=0)\) or \({Y}_{i}\left(0\right)\). Participant i’s individual causal effect (ICE) is defined as \({Y}_{i}\left(1\right)-{Y}_{i}\left(0\right)\). Based on the ICE, there can be three causal estimands: the average treatment effect (ATE) is the average ICE across all participants (Eq. 1); the average treatment effect on the treated (ATT) is the average ICE among participants who are actually assigned to the treatment group (Eq. 2); the average treatment effect on the untreated (ATU) is the average ICE among participants who are actually assigned to the control group (Eq. 3).

$$ATE=E\left({Y}_{i}\left(1\right)-{Y}_{i}\left(0\right)\right)$$
(1)
$$ATT=E\left({Y}_{i}\left(1\right)-{Y}_{i}\left(0\right)|{T}_{i}=1\right)$$
(2)
$$ATU=E\left({Y}_{i}\left(1\right)-{Y}_{i}\left(0\right)|{T}_{i}=0\right),$$
(3)

where \(E(\cdot )\) is the expected value and | is the condition function.

The ICE suffers from the “fundamental problem of causal inference” (Holland, 1986), that is, it is impossible to measure the potential treatment and control outcomes, \({Y}_{i}\left(1\right)\) and \({Y}_{i}\left(0\right)\), at the same time. In different designs, the ATE, ATT, or ATU may be identified under different causal assumptions. For instance, in RCTs where participants are randomly assigned to either a treatment or a control group, the independence assumption is met (by design). This assumption means that \({Y}_{i}\left(1\right)\) and \({Y}_{i}\left(0\right)\) are independent of the treatment assignment \({T}_{i}\). This assumption implies that there is no confounding. Confounders are covariates that causally affect the treatment assignment and potential outcomes. The independence assumption guarantees internal validity for successfully implemented RCTs.

Given the independence assumption, the ATE, ATT, and ATU are identical in RCTs and are estimated as:

$$ATE=ATT=ATU=E\left({Y}_{i}|{T}_{i}=1\right)-E\left({Y}_{i}|{T}_{i}=0\right),$$
(4)

where \({Y}_{i}\) is participant i’s measured outcome. Simply speaking, the ATE, ATT, and ATU are sample mean differences of the outcome between the treatment and control groups. In quasi-experimental designs where participants are not randomly assigned, the independence assumption is not met without conditioning on or adjusting for a set of covariates so that the confounding bias is removed. Other assumptions are required to identify the causal estimands in quasi-experimental designs, which are presented later.

Stable unit treatment value assumption

To identify the causal estimands, all the research designs introduced in this paper need to fulfill the stable unit treatment value assumption (SUTVA) (Rubin, 2006). For simplicity, we will not mention the SUTVA when introducing each design thereafter. This assumption has two aspects. The first aspect is that all participant’s potential treatment and control outcomes are unaffected by the treatment assignment of other participants. This is also known as the no spillover effect. The second aspect is that the treatment and control conditions are homogenously implemented to all participants. This is also known as the perfect fidelity of treatment (Feely et al., 2018).

One example that violates the first aspect of the SUTVA (no spillover effect) is that a control group participant interacts with a treatment group participant. In the example of Jennings et al. (2017), imagine that a teacher in school A was randomly assigned to the treatment group, and another teacher in the same school was randomly assigned to the control group. It is possible and likely that teachers would exchange information about the treatment program, and thus, this part of the SUTVA would be violated. One solution is to isolate or separate the treatment and control groups. Another solution is a clustered design, which puts participants who are likely to interact with each other into the same cluster, and treatment assignment is conducted at the cluster level. In Jennings et al. (2017), a clustered RCT design was conducted at the school level; that is, teachers at the same school were all assigned to the treatment or control group.

One violation of the second aspect of the SUTVA (perfect fidelity of treatment) is that there are variations when implementing the treatment or control groups. In the example of Jennings et al. (2017), imagine that a facilitator of the treatment program intentionally dropped one program component because the facilitator thought that this component would not be effective. In practice, researchers shall assess the fidelity of treatment. In Jennings et al. (2017), two trained researchers assessed the completion of treatment program components. On average, 88% (range = 86–91%) of the facilitation activity components listed in the treatment program manual were completed. Feely et al. (2018) provided guidelines for assessing the fidelity of treatment.

While this section described the causal estimands and causal assumptions needed for all quasi-experimental designs, we now discuss different quasi-experimental designs, their rationales, and the specific causal assumptions needed to identify and estimate causal estimands.

Regression discontinuity design (RDD)

The regression discontinuity design (RDD), proposed by Donald Campbell (Cook, 2008), assigns participants to the treatment group or to the control group based on a cutoff value of a continuous variable. This design is also known as a sharp RDD. Equation 5 mathematically presents the treatment assignment in a sharp RDD (Bloom, 2012; Cunningham, 2021; Imbens & Lemieux, 2008):

$${T}_{i}=1\,if\,({X}_{i}\ge c)$$
(5)
$${T}_{i}=0\,if\,\left({X}_{i}<c\right),$$
(6)

where \({X}_{i}\) is participant i’s continuous assignment variable and c is the cutoff value of X.

In the example of Wong et al. (2008), they solicited officials from 38 states in the U.S. that had state pre-kindergarten (pre-K) programs. Five states (Michigan, New Jersey, Oklahoma, South Carolina, and West Virginia) agreed to join and offered support and cooperation for the study. The treatment group was composed of children who completed pre-K in the spring of 2004 and started kindergarten in the fall of 2004. The control group was composed of children who just started pre-K in the fall of 2004. A child’s age (in days) was used as the continuous assignment variable, and the cutoff value was the age of 4 years. The eligibility to enroll in a pre-K program required that the child reach the age of four by a clearly defined date in the fall. That is, if the child’s birth date was after the eligibility date (i.e., is not yet 4 years old), the child was not eligible for enrollment. We simulated a dataset based on the results of the pre-K effect on mathematical skills in Michigan. Figure 2A shows the scatterplot of the mathematical skills scores (y-axis) against the continuous assignment variable, the age of the child (x-axis).

Fig. 2
figure 2

Scatterplots of sharp regression discontinuity design. The grey areas in panels B and C are the 95% confidence bands

Full size image

Causal estimand

In a sharp RDD, the causal estimand is the average treatment effect at the cutoff value (ATEC) (Bloom, 2012; Cunningham, 2021; Imbens & Lemieux, 2008; Lee & Lemieux, 2010):

$$ATEC=E\left({Y}_{i}\left(1\right)-{Y}_{i}\left(0\right)|{X}_{i}=c\right)$$
(7)

In Wong et al. (2008), the ATEC is the average effect of state pre-K programs on the mathematical skills of the 4-year-old children at the cutoff (eligibility date).

Causal assumption

The sharp RDD requires the continuity assumption, meaning that the conditional regression functions of the potential treatment and potential control outcomes are continuous (smooth) functions of the assignment variable X across x (Bloom, 2012; Cunningham, 2021; Imbens & Lemieux, 2008; Lee & Lemieux, 2010):

$$E\left( {Y_{i} \left( 1 \right)|X_{i} = x} \right)\,{\text{and}}\,E\left( {Y_{i} \left( 0 \right)|X_{i} = x} \right) {\text{are continuous in }}x$$
(8)

The continuity assumption implies that \({Y}_{i}\left(1\right)\) and \({Y}_{i}\left(0\right)\) are conditionally independent of the treatment assignment \({T}_{i}\) at cutoff c (Cunningham, 2021; Rosenbaum & Rubin, 1983). In other words, there is no confounding at the cutoff c.

The continuity assumption requires that the assignment variable X is numeric and continuous. In practice, the assignment variable may not fulfill this requirement perfectly. Shadish et al. (2002) suggested that the statistical power of sharp RDDs increases when the assignment variable has a greater number of response categories. Suk et al. (2022) presented the identification and estimation of the causal estimand when the assignment variable is ordinal.

Another assumption researchers should check in sharp RDDs is whether all participants are assigned to the treatment or control groups according to the cutoff (Eq. 5). This is also known as compliance. Visualization can aid in examining this assumption. To illustrate, we use the same simulated data based on Wong et al. (2008) in Fig. 2, which has the assumption of compliance fulfilled. Figure 3 shows a line graph of the treatment receipt (y-axis) against the assignment variable (x-axis; Bloom, 2012; Wong et al., 2008). If compliance is fulfilled, there is a horizontal line lies on the y-axis = 0 when the x-axis < cutoff c. There is a sharp vertical increase from 0 to 1 on the y-axis at the cutoff on the x-axis, and then there is a horizontal line that lies on the y-axis = 1 when the x-axis > cutoff c (Fig. 3A). If compliance is not fulfilled, there are vertical bumps between 0 and 1 on the y-axis along the x-axis, usually around the cutoff c (Fig. 3B). In case of noncompliance, researchers can consider a fuzzy RDD (Imbens & Lemieux, 2008; Lee & Lemieux, 2010; see the specific articles contained in this special issue).

Fig. 3
figure 3

Line plots of actual treatment assignment against continuous assignment variable when compliance is fulfilled and is not fulfilled

Full size image

Statistical analysis

Given the continuity assumption in sharp RDDs, the ATEC can be estimated as (Bloom, 2012; Imbens & Lemieux, 2008; Lee & Lemieux, 2010):

$$ATEC=\underset{x\downarrow c}{\mathit{lim}}E\left({Y}_{i}|{X}_{i}=x\right)-\underset{x\uparrow c}{\mathit{lim}}E\left({Y}_{i}|{X}_{i}=x\right),$$
(9)

where \(\underset{x\downarrow c}{lim}\) and \(\underset{x\uparrow c}{lim}\) mean the limit of the function (here, \(E\left({Y}_{i}|{X}_{i}=x\right)\)) as x approaches the cutoff c. Figure 2A illustrates that there are no-treatment group participants when X < c, and no control group participants at when X ≥ c. Based on the treatment assignment rule in Eq. 5, positivity is violated, which is defined as (Imbens & Lemieux, 2008; Lee & Lemieux, 2010):

$$0<P\left({T}_{i}=1|{X}_{i}=x\right)<1,$$
(10)

where x is any value of X across its range (including cutoff c), and \(P\left(\cdot \right)\) is the probability function.

Regression analysis can be used to estimate the ATEC. The dependent variable is the measured outcome Y, and the independent variables are the continuous assignment variable X and the treatment assignment T (1 = treatment, 0 = control). Before running the regression analysis, it is suggested to fit the lowess (locally weighted scatterplot smoothing) curves of the outcome (y-axis) against the assignment variable (x-axis) of the treatment and control groups, respectively (Fig. 2B; Wong et al., 2008). The lowess curves, which are smooth curves created by fitting localized subsets of the data in scatterplots, help to determine the functional forms in regression. If the lowess curves (or regression lines) show a discontinuity at the cutoff value, then the estimated ATEC will be different from zero. In the simulated example based on Wong et al. (2008), the lowess curves of the treatment and control groups were linear and parallel (i.e., no interaction between the treatment assignment and the assignment variable). Equation 10 and Fig. 2C present the linear regression model for this example:

$${Y}_{i}={b}_{0}+{b}_{1}\left({X}_{i}-c\right)+{b}_{2}{T}_{i}+{e}_{i},$$
(11)

where \({e}_{i}\) is participant i’s residual, assignment variable X is centered at the cutoff c.

When using regression analysis to estimate the ATEC, all assumptions in regression analysis apply, such as the correct model specification assumption. For instance, if the lowess curves in Fig. 2B are nonlinear, other functional forms, including polynomial regression, spline regression, and kernel regression, can be utilized. If the lowess curves of the treatment and control groups are not parallel, the interaction between the assignment variable and treatment indicator (X × T) should be considered for inclusion.

Remarks: statistical power and generalizability

The statistical power of sharp RDDs is often lower than that of RCTs (Jacob et al., 2012; Reichardt, 2019) because of the collinearity between the treatment assignment and the assignment variables. The assignment variable’s cutoff value also determines statistical power, which is at its maximum when the cutoff is equal to the median of the assignment variable (Reichardt, 2019; Shadish et al., 2002). Shadish et al. (2002) suggested minimizing model overfit in regression analysis, which can reduce statistical power.

RDDs are inferior to RCTs in terms of generalizability. The ATEC is the ATE of the subpopulation of participants who score at the cutoff. Caution must be exercised when generalizing ATEC to participants who do not score at this cutoff.

Summary

While RDDs were underutilized (Fig. 1), they are an excellent alternative to RCTs, which can achieve high internal validity. Given the continuity assumption, there is no confounding at the limits approaching the cutoff. The violation of the assumption means that a confounder would have to (a) occur at the cutoff of the assignment variable and (b) cause the discontinuity in regression lines. In RDDs, Shadish et al. (2002) suggested considering if there is an event that could affect the outcome happening only to one group but not the other group. This is also known as a “history” confounder.

Difference-in-differences analysis (DiD)

As shown in Fig. 1, DiDs have been gaining popularity in education research. The DiD is a longitudinal design that requires a pre-treatment measurement and a post-treatment measurement of the outcome. DiDs do not require randomization nor any specific treatment assignment rule for the treatment and control groups. The simplicity of DiDs may be one reason for their increasing popularity. For instance, a DiD was utilized to investigate the effect of homework assignments on a college course midterm exam performance (Latif & Miles, 2020). In an introductory statistics course in a Canadian business school, students of all class sections were administered the same midterm exam #1 (pre-treatment measurement of the outcome). After midterm #1, students in the treatment class section received homework assignments, and students in the control class section had no homework assignments. Both class sections administered the same midterm exam #2 (post-treatment measurement of the outcome).Footnote 2

Causal estimand

In DiDs, participant i has two potential outcomes: the potential treatment outcome at post-treatment (subscript post) if participant i is assigned to the treatment group, \({Y}_{i,post}(1)\), and the potential control outcome at post-treatment if participant i is assigned to the control group, \({Y}_{i,post}\left(0\right)\). In DiDs, the ATT is the same as that in Eq. 2, except that it is the average ICE at post-treatment among the treatment group.

$$ATT=E\left({Y}_{i,post}\left(1\right)-{Y}_{i,post}\left(0\right)|{T}_{i}=1\right)$$
(12)

In the example, the ATT means the average of the midterm #2 scores of the students who were given homework assignments after midterm #1, compared to their midterm #2 scores if they were not given homework assignments.

Causal assumption

Because DiDs do not require randomization or any specific treatment assignment rules, neither the independence assumption in RCTs nor the continuity assumption in RDDs applies. Another causal assumption, termed the parallel trends assumption, is required in DiDs (Roth et al., 2023; Stuart et al., 2014). The parallel trends assumption means that the average difference between the post-treatment potential outcome (\({Y}_{i,post}\left(0\right)\)) and the measured pre-treatment outcome (\({Y}_{i,pre}\)) is the same between the treatment and control groups:

$$E\left({Y}_{i,post}\left(0\right)-{Y}_{i,pre}|{T}_{i}=1\right)=E\left({Y}_{i,post}\left(0\right)-{Y}_{i,pre}|{T}_{i}=0\right)$$
(13)

To illustrate the parallel trends assumption (Fig. 4), we simulated a data example based on Latif and Miles (2020). Note that \({Y}_{i,post}\left(0\right)\) cannot be measured among the treatment group participants. Therefore, the line for the treatment group is dashed after the treatment. The two quantities in Eq. 12 are parallel in Fig. 4, meaning that if the participants of the two groups would all receive the control condition, the two groups would have the same average level of change in the outcome. In the example of Latif and Miles (2020), the parallel trends assumption means that if both class sections were given no homework assignments, the average change between midterm #2 and midterm #1 scores would be equal between the two class sections.

Fig. 4
figure 4

Illustration of the parallel trends assumption in difference-in-differences design. The dashed line of the treatment group indicates that the potential outcome cannot be actually measured at post-measurement

Full size image

Statistical analysis

Given the parallel trends assumption, the ATT is identified as (Roth et al., 2023):

$$ATT=E\left({Y}_{i,post}-{Y}_{i,pre}|{T}_{i}=1\right)-E\left({Y}_{i,post}-{Y}_{i,pre}|{T}_{i}=0\right),$$
(14)

where \({Y}_{i,post}\) is participant i’s measured post-treatment outcome. Simply speaking, the ATT is the average outcome’s difference between post-treatment and pre-treatment of the treatment group minus that of the control group. Thus, the design is named “difference-in-differences”.

Multilevel regression analysis can be used to estimate the ATT in a DiD (Eq. 14). In this analysis, the dataset has a clustered structure in which each participant has two rows of data, one row for the pre-treatment measurements and one row for the post-treatment measurements.

$${Y}_{ti}={b}_{0}+{b}_{1}{time}_{ti}+{b}_{2}{T}_{i}+{b}_{3}\left({time}_{ti}\times {T}_{i}\right)+{u}_{0i}+{e}_{ti},$$
(15)

where the subscript i denotes the participant and the subscript t denotes the time point (pre-treatment or post-treatment, Y is the measured outcome, time is a dummy variable of time (0 = pre-treatment, 1 = post-treatment), \({u}_{0i}\) is the level-2 residual, and \({e}_{ti}\) is the level-1 residual. The \({b}_{0}\) coefficient is the average pre-treatment outcome of the control group; the \({b}_{1}\) coefficient is the post-minus pre-treatment outcome difference of the control group; the \({b}_{2}\) coefficient is the pre-treatment outcome difference between the treatment and control group; the \({b}_{3}\) coefficient is the ATT estimate, which is the post- minus pre-treatment difference between the treatment and control groups. Figure 5A presents the results from Eq. 14 of simulated data based on the findings of Latif and Miles (2020).

Fig. 5
figure 5

Results of difference-in-differences design

Full size image

Remarks: potential confounders

The success of DiDs relies heavily on the parallel trends assumption, yet it is untestable. Equivalence in the average measured pre-treatment outcome between the treatment and control groups can help to make the parallel trends assumption more credible (Shadish et al., 2002). DiDs can deal with time-invariant confounding. However, DiDs fail if confounding varies over time, that is, the confounders’ impact on the post-treatment outcome is not the same as their impact on the pre-treatment outcome. Researchers may include time-varying covariates to make the parallel trends assumption more likely. Shadish et al. (2002) suggested that researchers carefully consider the patterns of results to identify potential confounders. In the previous example, the homework assignments (treatment) group had lower pre-treatment midterm scores than the control group, and the treatment group had higher increases in post-treatment midterm scores than the control group. It could be argued that the treatment group students had a faster learning rate than the control group students, but not the treatment itself that caused the improvement (termed selection × maturation confounder; Shadish et al., 2002). In such a situation, the parallel trends assumption would be violated (Fig. 5B). Shadish et al. (2002) extensively discussed various design elements that can be added to detect or rule out the confounders or enhance and strengthen the research conclusions in DiDs. One design element is adding another time point for the pre-treatment measurement. This allows the examination of the parallel trends assumption by visualizing or testing whether the trends of the pre-treatment outcomes are parallel between the treatment and control groups. If design elements are not plausible, researchers shall measure the confounder and include it in the regression analysis.

Summary

The DiD has been gaining popularity in education research (Fig. 1). It can produce the ATT given that the parallel trends assumption is fulfilled. However, the parallel trends assumption is untestable. We recommend readers study the results and consider whether the parallel trends assumption is plausible.

Interrupted time series design (ITS)

The ITS is a within-subject longitudinal design where the unit of observation is time. Each participant is exposed to or receives both the treatment and control conditions. For simplicity, let’s consider there is one participant first. In ITSs, the control condition is no treatment. The participant receives multiple (> 1) pre-treatment outcome measurements over time. At a certain time point, the participant is exposed to or receives the treatment condition. Upon completion of the treatment, the participant receives multiple (> 1) post-treatment outcome measurements over time. Maynard and Young (2022) conducted an ITS to study the effect of a trait-based instructional approach (treatment) on third-grade students’ writing achievement. Before treatment, students were asked to complete one essay in response to a writing prompt each day for 5 days. Six weeks after the treatment, students were asked to complete one essay in response to a writing prompt each day for 5 days. In their study, 20 students joined the treatment. This study had a clustered data structure with repeated measures nested within students.

Causal assumptions and estimand

If time can be quantified as a continuous variable (e.g., second or day), the ITS is similar to the sharp RDD in which time is the continuous assignment variable (Kim & Steiner, 2016; Reichardt, 2019; West et al., 2014). In ITSs, researchers often are not only interested in the average treatment effect at the treatment time point (i.e., when the treatment occurs) but are also interested in the delayed treatment effect that occurs later than the treatment time point. ITSs assume that the potential control outcomes for the post-treatment period can be reliably predicted from the pre-treatment time series. Thus, it is necessary to assume the stability of the functional form learned from the pre-treatment time series across the post-treatment time points. In other words, the control time series is stable across the pre- and post-treatment time points. In addition, ITSs assume that no other alternative treatments that may impact the outcome can take place during the post-treatment time periods (termed history confounder; Reichardt, 2019; Shadish et al., 2002). Given these assumptions, the ATT is identified at the post-treatment time point.

Reichardt (2019) and Shadish et al. (2002) suggested considering the existence of a history confounder in an ITS. In the example of Maynard and Young (2022), imagine that the school library initiated an after-school writing tutoring program and welcomed any students joining the program. Some students in the study had joined the tutoring program, and the tutoring program is argued to improve students’ writing achievement. To examine the existence of this history confounder, we can add a comparison group of the third-grade students who were not in the study and joined the writing tutoring program. This design is known as a comparative interrupted time series design and will be discussed later.

Statistical analysis

Regression analysis can be used to estimate the ATT at any post-treatment time point in an ITS. In the regression model, the dependent variable is the outcome, and the independent variables are the continuous time variable and the treatment status T (1 = treatment, 0 = control). To illustrate the regression analysis, we simulated a dataset based on the results of Maynard and Young (2022). The dataset had a clustered structure with repeated measures (level-1) nested within participants (level-2). Each row in the dataset reflected one time point of a participant. In the analysis, the time variable was the day (centered at day 1 after treatment).

First, we visualized the relationships of the outcome (y-axis) against the time variable (x-axis) across the pre-treatment and post-treatment periods, respectively. This helps to determine the functional form of the times series. Figure 6A shows the line graphs of each student, together with the line graph of the sample mean. Results showed a flat linear change in writing achievement before treatment, an immediate increase in writing achievement right after treatment (suggesting a positive ATT at this post-treatment time point), and then a steady linear increase in writing achievement over time after treatment. The figure also shows that the trends are about parallel across students, suggesting that random slopes are not necessary in the multilevel regression model. Equation 15 shows the multilevel regression model with a linear trend of time as well as the interaction effect between time and treatment status included (Fig. 6B):

$${Y}_{ti}={b}_{0}+{b}_{1}{time}_{ti}+{b}_{2}{T}_{i}+{b}_{3}\left({time}_{ti}\times {T}_{i}\right)+{u}_{0i}+{e}_{ti},$$
(16)

where the subscript \(t\) is time and the subscript \(i\) represents the student, Y is the measured outcome (writing achievement), time = (− 5, − 4, …4) for the 1st to the 10th day (i.e., centered at day 1 after treatment, which is the treatment time point), T is treatment status (0 = control, 1 = treatment), \({e}_{ti}\) is level-1 residual and \({u}_{0i}\) is level-2 residual. The \({b}_{0}\) coefficient is the average outcome before treatment at the treatment time point; the \({b}_{1}\) coefficient is the linear slope of time before treatment; the \({b}_{2}\) coefficient is the ATT estimate on day 1 after treatment; the \({b}_{3}\) coefficient is the difference of average linear slope of \(time\) between post-treatment and pre-treatment. Researchers can re-center the time variable at a different post-treatment time point to estimate the ATT at that time (West et al., 2014).

Fig. 6
figure 6

Results of interrupted time series design

Full size image

Assumptions in multilevel regression apply to calculate an unbiased ATT estimate and correct statistical inferences. In particular, the regression model needs to be correctly specified (Kim & Steiner, 2016; West et al., 2014). Interested readers are referred to tutorials about other functional forms, including nonlinear growth patterns (e.g., quadratic, exponential) and cyclic patterns (e.g., sinusoidal) (Grimm & McArdle, 2023). If the time assignment variable is equally spaced, as in our example, some multilevel regression software allows different covariance structure of the level-1 residual \({e}_{ti}\), including autoregressive lag-1, autoregression moving average, and compound symmetry. Correct specification of the level-1 residual covariance structure can increase statistical power (Kwok et al., 2007; Reichardt, 2019).

Comparative interrupted time series (CITS)

As mentioned previously, CITSs extend from ITSs by adding another comparison group of participants who do not receive the treatment over the same time period. To avoid confusion, we used the term comparison group to distinguish it from the control status (pre-treatment). CITSs also extend from DiDs by adding multiple pre-treatment and post-treatment measurements of the outcome. Like DiDs, the assignment of participants to the treatment and comparison groups does not require randomization or specific assignment rules in CITSs.

Kim and Steiner (2016) and Wong et al. (2013) presented the causal estimands and assumptions of CITSs. The assumptions in ITSs and the parallel trends assumption in DiDs are applicable to both the treatment and comparison groups in CITSs. Similar to ITSs, we can visualize the relationships between the outcome (y-axis) and time (x-axis) of the treatment and comparison groups across the time period, respectively. This helps to determine the functional forms of the time series in the statistical model, as well as to check if the pre-treatment trends of the outcome are parallel between the treatment and comparison groups. Multilevel regression can be used. Consider that the comparison group that we discussed previously was added to Maynard and Young’s (2022) example. The multilevel regression model is:

$${Y}_{ti}={b}_{0}+{b}_{1}{time}_{ti}+{b}_{2}{T}_{i}+{b}_{3}\left({time}_{ti}\times {T}_{i}\right)+{b}_{4}{G}_{i}+{b}_{5}\left({time}_{ti}\times {G}_{i}\right)+{b}_{6}\left({T}_{i}\times {G}_{i}\right)+{b}_{7}\left({time}_{ti}\times {T}_{i}\times {G}_{i}\right)+{u}_{0i}+{e}_{ti},$$
(17)

where \(G\) is the dummy coded group assignment (0 = comparison, 1 = treatment). The \({b}_{0}\) coefficient is the average pre-treatment outcome of the comparison group at the treatment time; the \({b}_{1}\) coefficient is the pre-treatment linear slope of \(time\) for the comparison group; the \({b}_{2}\) coefficient is the (post- minus pre-treatment) difference of the comparison group at the treatment time; the \({b}_{3}\) coefficient is the difference of average linear slope of \(time\) between post- and pre-treatment of the comparison group; the \({b}_{4}\) coefficient is the pre-treatment difference between the comparison and treatment groups on day 1 after treatment; the \({b}_{5}\) coefficient is the difference of the pre-treatment slope of \(time\) between the comparison and treatment groups. If the two groups have parallel trends before treatment, the \({b}_{5}\) coefficient equals 0.

The \({b}_{6}\) and \({b}_{7}\) coefficients are the ATT estimates of interests (Kim & Steiner, 2016; Wong et al., 2013). The \({b}_{6}\) coefficient is the (post- minus pre-treatment) difference between the comparison and treatment groups on day 1 after treatment. The WWC (U.S. Department of Education, 2022) requires reporting this \({b}_{6}\) coefficient when using CITSs. The \({b}_{7}\) coefficient is the (post- minus pre-treatment) difference of the slope of \(time\) between the comparison and treatment groups. Figure 7 visualizes this model. In the example, the comparison group had a flat linear trend throughout the time series, meaning the after-school tutoring program (comparison group) had no effect on students’ writing achievement. The research conclusions about the treatment group (trait-based instructional approach) were strengthened.

Fig. 7
figure 7

Comparative interrupted time series design

Full size image

Summary

The ITS is similar to the sharp RDD in that time is the continuous assignment variable. ITSs were not frequently utilized in education research (Fig. 1). The ATT at the post-treatment time point is identified given the causal assumptions. The CITS, which extends from the ITS and the DiD, adds a no-treatment comparison group that can detect or rule out a history confounder.

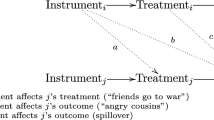
Instrumental variable (IV) analysis

We now come back to between-subject designs where a participant receives the treatment condition or the control condition. What if we are conducting a secondary data analysis, where the data were collected, and it is not possible to add a design element or to measure additional covariates to remove the confounding bias? The IV analysis, originated by Philip G. Wright, is an analytic technique to identify a causal estimand in the presence of unmeasured or omitted variables (Baiocchi et al., 2014; Cunningham, 2021; Huang et al., 2019). However, the IV analysis was not popular in education research (Fig. 1).

Causal assumptions

The IV analysis can identify the ATE for the entire population. It can also identify the local average treatment effect, which is the ATE among the participants who complete the assigned group and will be discussed later. An IV requires three assumptions: relevance, exclusion restriction, and exchangeability (Labrecque & Swanson, 2018; Lousdal, 2018).

  1. (a)

    Relevance: The IV is associated with treatment assignment (predictor). The IV does not need to cause the treatment assignment. If the association is high, the IV is also known as a strong IV. A low (weak) association is undesirable because it produces biased ATE estimates (for larger samples, it is less of an issue). In addition, a weak IV always results in inefficient effect estimates.

  2. (b)

    Exclusion restriction: The IV does not directly cause the outcome. It does not mean that the IV does not cause the outcome; it means that the IV causes the outcome only through the treatment (i.e., full mediation). This assumption is generally untestable.

  3. (c)

    Exchangeability: This assumption is sometimes known as the independence assumption. To avoid confusion with the independence assumption in RCTs, we used the term exchangeability instead in this paper. Exchangeability means that there is no confounding between the IV and the outcome. This assumption is generally untestable. Because exclusion restriction and exchangeability assumptions are untestable, it is recommended to select the IV based on the knowledge of research questions and contexts.

To identify the ATE in an IV analysis, another assumption is needed: Effect homogeneity. This assumption means that all participants have the same ICE. Later, we will introduce the monotonicity assumption which is less restrictive than the homogeneity assumption, yet the monotonicity assumption will produce a less generalizable causal estimand.

Statistical analysis

Given the assumptions above, two-stage least squares (TSLS) regression can be used to estimate the ATE. Nguyen et al. (2016) investigated the causal effect of educational attainment on dementia risk using the national Health and Retirement Study data between 1998 and 2010. Educational attainment was measured by self-reported years of schooling. The IV analysis can handle treatment with two or more (even continuous) groups. Nguyen et al. (2016) had two IVs that repeated the same statistical analysis using each IV separately. The first IV was years of compulsory schooling, and the second IV was a compositive score of three genome variables that were related to school attainment. The second IV could be viewed as a sensitivity analysis.

TSLS regression has two models that are estimated simultaneously. In the first stage model, the treatment is regressed on the IV:

$${D}_{i}={a}_{0}+{a}_{1}{IV}_{i}+{r}_{i},$$
(18)

where \({D}_{i}\) is participant i’s treatment (years of schooling), IV is an instrumental variable, r is the residual. The \({a}_{0}\) and \({a}_{1}\) coefficients are the regression intercept and slope, respectively. If the relevance assumption is fulfilled, the \({a}_{1}\) coefficient shall be high in level. To fulfill the exchangeability assumption and increase the estimator’s efficiency, measured covariates are often included in Eq. 17.

In the second stage model, the outcome is regressed on the predicted treatment values \({\widehat{D}}_{i}\) of the first stage model:

$${Y}_{i}={b}_{0}+{b}_{1}{\widehat{D}}_{i}+{e}_{i},$$
(19)

where Y is the measured outcome, and e is the residual. The \({b}_{0}\) coefficient is the regression intercept and the \({b}_{1}\) coefficient is the ATE estimate.

Noncompliance in RCTs

The IV analysis can identify a causal estimand when there is noncompliance (nonadherence) in an RCT. Noncompliance means that actual treatment receipt does not equal the planned treatment assignment. It can occur when participants fail to complete, comply with, or attend the assigned treatment or control condition.

When using IV analysis to account for noncompliance, the IV is treatment assignment (0 = control, 1 = treatment), and the predictor is treatment receipt (0 = control, 1 = treatment). Sagarin et al. (2014) reviewed several ways to measure compliance. In the RCT example of Jennings et al. (2017), the treatment involves 5 days of in-person sessions, and the participant’s attendance was assessed. They found that over 90% of the participants attended at least four of the 5 days (mean = 4.5) of the treatment program and concluded that no outstanding noncompliance needed to be corrected. Nevertheless, attendance rate can be used to determine or define treatment receipt.

The causal estimand can be expressed using the potential outcomes framework (Angrist et al., 1996). Denote D be the treatment receipt (0 = control, 1 = treatment). Given the exclusion restriction assumption, a participant i’s potential outcome according to the treatment receipt is \({Y}_{i}(D=d)\). The local average treatment effect (LATE), or complier average causal effect (CACE), is identified as the average potential outcome differences between the treatment receipts across compliers (Angrist et al., 1996; Sagarin et al., 2014):

$$LATE=E\left({Y}_{i}\left(D=1\right)-{Y}_{i}\left(D=0\right)|compliers\right)$$
(20)

To identify the LATE, the relevance assumption, the exclusion restriction assumption, the exchangeability assumption and the monotonicity assumption are needed (Sagarin et al., 2014). The relevance assumption means that the planned treatment assignment (IV) is associated with the treatment receipt (predictor). The exclusion restriction assumption means that the treatment assignment has no causal effect on the outcome other than via the treatment receipt (full mediation). As discussed previously, the monotonicity assumption is a less restrictive assumption than the homogeneity assumption. The monotonicity assumption means that there are no defiers. Defiers are the participants who do not comply with the assigned treatment group (also known as never-takers), and the participants who do not comply with the assigned control group (also known as always-takers; Angrist et al., 1996; Lousdal, 2018; Sagarin et al., 2014). TSLS regression in Eqs. 17 and 18 can be used to estimate the LATE. In the model, IV is the treatment assignment T (0 = control, 1 = treatment), D is the treatment receipt (0 = control, 1 = treatment), and Y is the measured outcome.

Summary

The IV analysis can be used to estimate the ATE in the presence of unmeasured confounders. Its assumptions require careful consideration according to the research contexts and questions to select an appropriate IV. The IV analysis can also be used to identify the LATE when noncompliance occurs in RCTs or RDDs. The LATE has lower generalizability than the ATE when compliance is fulfilled.

Propensity score analysis (PSA)

Based on our survey (Fig. 1), PSAs were the most popular quasi-experimental design in education research. We believe one reason is the availability of textbooks, tutorials, and statistical software for education and behavioral researchers since the late 2000s (e.g., Ho et al., 2007; Schafer & Kang, 2008). PSAs do not require randomization or a specific treatment assignment rule. PSAs also do not require a pre-treatment measurement of the outcome like DiDs. The PSA is an analytic technique used to adjust for the measured covariates between the treatment and control groups to estimate the ATE, ATT, and ATU (Rosenbaum & Rubin, 1983). For example, Hughes et al. (2018) compared students who were retained (hold back) in grades 1 to 5 (treatment group) and students who were continuously promoted (control group) on their high school completion (diploma, GED, or dropout). Grade retention can be caused by numerous factors, including cognitive and academic functioning, social-behavioral adjustment, self-regulatory skills, motivation, and personality. These factors can also impact the chance of high school completion, which can confound the hypothesized causal effect. They utilized a PSA to adjust for the measured covariates to estimate the causal estimand.

Causal estimands and causal assumptions

PSAs can identify the ATE, ATT, or ATU in Eqs. (2–4). PSAs require two assumptions: conditional independence and positivity. These two assumptions are also known as the strong ignorability assumption (Rosenbaum & Rubin, 1983). The conditional independence assumption is:

$${Y}_{i}\left(1\right), {Y}_{i}\left(0\right)\perp {T}_{i}|{{\varvec{Z}}}_{{\varvec{i}}},$$
(21)

where \(\perp\) means independence; \({{\varvec{Z}}}_{{\varvec{i}}}\) is a vector of measured covariates of participant i. This assumption means that that there is no confounding between the treatment assignment/selection \({T}_{i}\) and \({Y}_{i}\left(1\right)\) and \({Y}_{i}\left(0\right)\), after adjusting for the measured covariates Z.

The positivity assumption is the same as in Eq. 9, except that the probability is now conditional on \({{\varvec{Z}}}_{{\varvec{i}}}\) (Eq. 21). This assumption means that every participant i has some chance to be assigned to or select the treatment condition or the control condition, given the measured covariates.

$$0<P\left({T}_{i}=1|{{\varvec{Z}}}_{{\varvec{i}}}\right)<1$$
(22)

Why not regression or analysis of covariance?

Regression or analysis of covariance, where measured covariates Z are included as independent variables to the model, is seemingly the most straightforward analytic technique to adjust for the measured covariates. Regression specifies the relationships of covariates Z and treatment assignment/selection T to the outcome simultaneously. In other words, covariate adjustment and causal effect estimation are done together. This facilitates p-hacking (or fishing for significant results), in that researchers can peek at the estimated causal effect. As introduced in the next section, PSA separates covariates adjustment and causal effect estimation into different steps, which reduces the chance of p-hacking. Another major reason for not using regression is its linearity assumption. In terms of causal assumptions, both the PSA and regression assume conditional independence. The PSA assumes positivity, while regression does not. In regression analysis, if the covariates space of Z of the treatment group does not fully overlap with that of the control group, the estimation of ATE requires extrapolation (Schafer & Kang, 2008). In the following, we introduce each step in PSA.

Step 1: selecting covariates

The conditional independence assumption is fulfilled when the measured covariates that affect the treatment assignment/selection and the outcome are balanced between groups. Steiner et al. (2010) conducted an experiment to show that a “convenient” set of covariates, which includes only the participants’ demographic information (e.g., age and gender), may not be sufficient to fulfill this assumption. Two theory-driven approaches for covariate selection have been proposed (Steiner et al., 2010). The first approach involves identifying the covariates based on background knowledge before data collection. This approach requires a solid theoretical knowledge of the research question and hypothesis. The second approach is more beneficial when the researcher has limited knowledge to identify covariates. This approach involves first identifying a large set of theoretical domains that possibly influence the treatment assignment/selection process or the outcome. Then, a large sample of covariates is selected from those domains. For example, Hughes et al. (2018) identified covariates that had been shown in prior research to be associated with grade retention and school dropout at the levels of the individual child, the family, the school, and the home-school relationship. Readers can also refer to the directed acyclic graph causal framework, which provides rules for selecting covariates (Pearl, 2009; Steiner et al., 2023; see the specific article contained in this special issue).

Step 2: estimating propensity scores

The propensity score (PS) is the conditional probability of treatment assignment/selection predicted by the measured covariates, which is \(P\left({T}_{i}=1|{{\varvec{Z}}}_{{\varvec{i}}}\right)\) in Eq. 21. A balanced PS distribution between the treatment group and control group implies the distribution of the measured covariates are balanced between the two groups (Rosenbaum & Rubin, 1983). The PS estimation model needs to be correctly specified (Cham, 2022). Considering that the PS model is rarely of research interest, methods that automate model specification have been developed and tested. Simulation studies showed the utilities of typical machine learning techniques in PS estimation, including classification trees (Lee et al., 2010), random forests (Cannas & Arpino, 2019; Lee et al., 2010), generalized boosted models (Lee et al., 2010; McCaffrey et al., 2004), support vector machines (Tarr & Imai, 2021), and neural networks (Cannas & Arpino, 2019). Imai and Ratkovic (2014) developed an iterative algorithm that uses the generalized method of moments to maximize the balance of the measured covariates. After PS estimation, it is helpful to visualize the PS distributions of the treatment and control groups (e.g., histogram, kernel density plot). The positivity assumption requires an overlap of the PSs between groups. Lack of overlap limits the choice of equating methods and results in a larger standard error of the causal estimand. The positivity assumption is violated if a large proportion of control group participants have PSs close to 0 and a large proportion of treatment group participants have PSs close to 1. Kang et al. (2016) proposed a method using classification and regression tree for this situation.

Step 3: balancing groups on propensity scores

There are three classes of typical methods to balance the treatment and control groups on the estimated PSs: matching, stratification, and inverse probability weighting. Matching pairs the treatment group participants with the control group participants based on the similarity of their PSs. The simplest matching algorithm, exact matching, pairs a treatment group participant with a control group participant who has an identical PS. Besides exact matching, there are many matching algorithms (Austin, 2014). Stratification (or subclassification) groups the treatment and control group participants based on the similarity of their PSs (e.g., 0 to 20th percentile, 21 to 40th percentile, and so on). Inverse probability weighting converts PSs into sampling weights. There are several methods to calculate PS weights (Cham, 2022). For example, the PS weights of the Horvitz-Thompson estimator for ATE is. \(1/P\left({T}_{i}=1|{{\varvec{Z}}}_{{\varvec{i}}}\right)\) for the treatment group and \(1/(1-P\left({T}_{i}=1|{{\varvec{Z}}}_{{\varvec{i}}}\right))\) for the control group.

Step 4: examining covariate balance

As mentioned, the distribution of the measured covariates is balanced between groups in expectation if PSs are balanced. We can test if the distributions of measured covariates between the treatment and control groups are equal via graphical methods (e.g., histograms, kernel density plots) and analytical methods (e.g., standardized mean difference, variance ratio; Austin, 2009). Null hypothesis testing is not recommended because it favors PS distributions with smaller overlapping regions (Austin, 2009).

If PSs do not produce satisfactory balance on the measured covariates (e.g., WWC requires standardized mean difference ≤ 0.05 to achieve balance), researchers can respecifyspecify the PS estimation model (e.g., adding interaction terms, modifying model tuning parameters), use a different PS estimation method (e.g., changing from logistic regression to a machine learning technique), or balance the treatment and control groups using a different method (e.g., changing from exact matching to a different matching algorithm or inverse probability weighting).

Step 5: estimating causal estimand and sensitivity analysis

Different balancing methods have different formulas to estimate the ATE, ATT, or ATU. In exact matching, where one treatment group participant is paired with one control group participant with identical PS, the causal estimand can be estimated as the simple mean difference of the outcome between the paired treatment and control groups (i.e., \(E\left({Y}_{i}|{T}_{i}=1\right)-E({Y}_{i}|{T}_{i}=0)\)). If all the treatment and control group participants are paired, the mean difference estimates the ATE; if only all the treatment group participants are paired, the mean difference estimates the ATT; if only all the control group participants are paired, the mean difference estimates the ATU.

In stratification, if every treatment and control participant is grouped, ATE is estimated as:

$$\begin{gathered} \widehat{ATE} = \mathop \sum \limits_{s = 1}^{S} \left( {\frac{{N_{s} }}{N} \times D_{s} } \right) \hfill \\ D_{s} = E\left( {Y_{i} |T_{i} = 1, S = s} \right) - E(Y_{i} |T_{i} = 0,S = s) {\text{of stratum }}s, \hfill \\ \end{gathered}$$
(23)

where \({D}_{s}\) is the outcome mean difference between the treatment and control of stratum s, \(N\) is the total sample size, \({N}_{s}\) is the sample size of stratum s.

In weighting, the ATE (ATT or ATU) is the weighted mean difference of the outcome between treatment and control groups. Researchers can incorporate the weights in weighted least squares regression or survey sampling procedures that account for sampling weights to estimate ATE.

Because PSAs assume all covariates needed to remove the entire confounding bias are measured, it is suggested to conduct a sensitivity analysis examining the robustness of the results to violations of the conditional independence assumption.

As mentioned previously, a clustered design can be used to fulfill the no spillover effect assumption within the SUTVA. Clustering in PSAs can be more complicated than other designs in this paper. The PS estimation method and the PS balancing method should both account for the clustered data structure (Arpino & Mealli, 2011; Collier et al., 2022; Leite et al., 2015; Thoemmes & West, 2011).

Other covariate-adjusting methods

There are several promising covariate-adjusting methods as alternatives to PSAs. All these covariate-adjusting methods require the conditional independence assumption. First, entropy balancing uses a maximum entropy reweighting scheme to balance the measured covariates’ sample moments between the treatment group and the control group (Hainmueller, 2012). Second, genetic matching balance the weighted Mahalanobis distance of the measured covariates between the groups (Diamond & Sekhon, 2013). Third, regression estimation builds two prediction models where the measured covariates predict the measured outcome (Schafer & Kang, 2008). The first prediction model is estimated using the treatment group data, and this model is used to predict the potential treatment outcome \({Y}_{i}\left(1\right)\) for all participants; the second prediction model is estimated using the control group data, and this model is used to predict the potential control outcome \({Y}_{i}\left(0\right)\) for all participants. The mean difference of the predicted potential treatment outcomes and potential control outcomes estimates the ATE. Fourth, there is a class of doubly robust methods that utilize regression estimation (or regression) and the inversed probability weighting in PSA simultaneously to estimate the causal estimands. Kang and Schafer (2007) suggested that these doubly robust methods may not always be superior, and careful considerations about which combinations of covariate-adjusting methods and PS estimation methods may be needed for good performance.

Summary

The PSA is a useful tool to minimize confounding bias by adjusting for the measured covariates. The selected covariates must meet the conditional independence assumption (i.e., be able to remove the entire confounding bias). PSAs can be combined with other quasi-experimental designs to adjust for the measured covariates.

Conclusion

This article overviews RDDs, DiDs, ITSs, IV analyses, and PSAs. Table 1 summarizes the design characteristics, causal estimands, and causal assumptions for each design. We conducted a survey in ERIC and found that RCTs were still the dominating experimental design in education research. PSAs were the most popular among all the quasi-experimental designs introduced in this article. One likely reason is its availability of learning resources and software implementation in recent years. We hope this article and other articles in this issue are useful learning resources for education researchers to apply various quasi-experimental designs for high internal validity.

Table 1 Summary of design characteristics, causal estimands, and causal assumptions of quasi-experimental designs
Full size table