1 Introduction

Latent factor models are typically used to summarize multivariate data for the purpose of deriving or relating factor scores to other covariates [3], and are widely used in biomedical and epidemiological studies. In environmental epidemiology studies, for example, factor models are used to summarize several air pollution exposures [4, 10, 17]. Factor models relate observed variables that reflect the underlying latent factors through a system of regression equations termed the measurement model. However, in order to maintain a consistent and valid interpretation of the latent factors, certain measurement invariance conditions need to be satisfied [16]. Measurement invariance (MI) means the parameters in the measurement model are the same regardless of how the data are grouped in terms of covariates. Otherwise, measurement bias is introduced because the effect of variables other than the latent factor on the observed variables is not accounted for [15]. For instance, when MI is violated the factor scores derived from the model will be biased estimates of the underlying latent factor. The two most critical invariance conditions are invariance of the intercept and factor loadings in the measurement model. Simulation studies have shown that it is harder to detect bias coming from non-constant factor loadings [2].

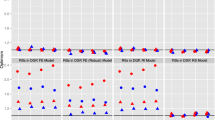
This work was motivated by research conducted as part of the Early Life Exposure in Mexico to Environmental Toxicants (ELEMENT) project. The ELEMENT project was designed to examine the influence of environmental pollutants, including metals such as lead (Pb), on child development; data for ELEMENT are collected from mother–child pairs enrolled in three birth cohorts in Mexico City. Latent factor models have been used to summarize biomarkers for lead exposure, collected from mothers near the time of their child’s birth, in order to assess the influence of lead exposure on the children’s mental development and physical growth [22]. In this setting, the latent factor represents the underlying but unobserved true prenatal exposure for the infants. However, since Téllez-Rojo et al. [27] show that lead metabolism in human bodies may vary by age, we raise the question of whether the factor loadings may vary across maternal age. Preliminary stratified factor analyses of these biomarkers suggest the factor loading for lead concentration in cord blood lead may vary by maternal age (Fig. 1), hence potentially violating the measurement invariance assumption. If the factor loadings do vary by maternal age, the estimated factors would be a biased measure of the latent exposure and potentially bias exposure–outcome associations. In this study, we focus specifically on approaches examining the measurement invariance assumption in factor models that are used to derive exposure estimates.

Fig. 1
figure 1

Factor loadings of different lead measurements from stratified confirmatory factor analyses. In these analyses one latent factor is used to summarize the underlying prenatal lead exposure. The data are evenly split into six age groups, and each dot on the plot represents the factor loading from the analysis of one stratum. Cord blood lead and blood lead 1 month after delivery are analyzed under the logarithmic scale

Full size image

Assessing the measurement invariance assumption is an established model diagnostic step for factor models in social and behavioral studies, where measurement invariance is traditionally studied through multi-group factor analysis [3]. Multi-group factor analysis divides the data into groups according to covariates, for example, age and gender. Then a different measurement model is fitted for each covariate group, and differences in parameters across groups are tested. The main disadvantage of this approach is its less satisfactory bias detection rate, especially when the measurement bias is related to a continuous covariate and is due to arbitrary group membership assignment that results in less accuracy and efficiency of parameter estimates [1, 2].

Novel models that allow factor loadings to vary as continuous functions of some covariates offer alternative strategies for addressing the issue of measurement invariance [2, 33, 34]. Zhang et al. [34] and Zhang and Lee [33] use bootstrap simulations to construct confidence intervals for non-constant factor loadings and examine whether a factor loading varies across covariate values. Barendse et al. [2] compare the ability of restricted factor analysis (RFA) and multi-group models to detect measurement bias. The simulation study of Barendse et al. [2] shows RFA models have better bias detection rates than multi-group models.

In this paper we develop a strategy to test if a factor loading deviates significantly from a constant. Our approach is based on estimating factor loadings that vary smoothly across the entire range of covariate values. We use penalized splines to model the factor loadings as varying coefficients [11], where the spline coefficients are treated as random, and the smoothing process is incorporated into the likelihood [18]. We then test whether a factor loading is constant by using a LRT that tests whether the variance of the spline coefficients differs from zero.

However, because the null value of the variance is zero and is at the boundary of its support, the asymptotic null distribution of the LRT statistic is not easy to derive. This test for non-zero variance components has been extensively studied in the mixed model framework [5, 9, 13, 23, 26]. Except for Stoel et al. [25], we are not aware of this type of testing problem within the latent variable framework. Following Greven et al. [9], we use a parametric bootstrap method to approximate the null distribution of the LRT statistic and compare the power of the LRT in our model to the power of the LRT in the multi-group model. We investigate how the performance of the test for one factor loading changes with the estimation of other factor loadings.

We present the model and the hypothesis test of interest in Sect. 2. Section 3 details the estimation method and some technical aspects of the nested Monte Carlo EM (MCEM) algorithm in the context of our proposed methods [28]. We also discuss computing the likelihood using Monte Carlo integration and the construction of confidence intervals for the non-constant factor loadings. In Sect. 4 we carry out simulation studies to investigate the Type I error and power of the LRT for detecting non-constant factor loadings. We also study use of the parametric bootstrap for obtaining the critical value for the LRT. In Sect. 5 we apply the proposed methods to our motivating data from the ELEMENT project. Section 6 ends with a discussion and future directions.

2 Model and Hypothesis

We model the factor loadings as non-constant functions of covariates so that the measurement model can differ across covariate values. For ease of exposition, suppose there is only one latent variable \(\eta _i\) and one continuous covariate, \(z_i\), for \(i=1,2,\dots ,n\) subjects. Let \(y_{p,i}\) be the pth observed variable measured on subject i and \(\eta _i \overset{{\text {iid}}}{\sim }N(0,1)\) be the latent factor underlying the P observed variables. The observed variables are related to the latent factor as

$$\begin{aligned} y_{p,i} = \mu _{p,i}+\lambda _{p,i}\eta _i + \epsilon _{p,i}, \quad p = 1, \ldots , P, \quad i = 1, \ldots , n. \end{aligned}$$
(1)

In this model, the factor loading \(\lambda _{p,i}\) for the pth observed variable includes a subscript i because the factor loading is assumed to vary smoothly across continuous values of the covariate z, i.e., \(\lambda _{p,i}=\lambda _{p}(z_i)\) (more details below). We assume the residual error \(\epsilon _{p,i} \overset{{\text {iid}}}{\sim }N(0,{\varvec{\Sigma }}_\epsilon )\) is independent of \(\eta _i\). Without loss of generality, we assume \(\mu _{p,i}=0\) and omit it from the mean for \(y_{p,i}\) since \(y_{p,i}\) can easily be centered to have zero mean; centering observed variables \(y_{p,i}\) is a common data pre-processing practice in factor analysis [3]. Further, de-trending the observed dependent variables \(y_{p,i}\) to remove covariate effects on their mean can be readily implemented. In Sect. 5 we use residuals from additive models that regress \(y_{p,i}\) on z as the adjusted observed outcomes. By doing so, we ensure that non-constant values of \(\lambda _{p,i}\) are due to changes in the partial correlation among observed values across the range of z after we remove the effect of z on their means. Models where covariates are allowed to influence \(y_{p,i}\) are available [19]. Here, centering and de-trending the data enables the testing methods to focus specifically on differences in the factor loadings associated with covariate z, which give rise to a more challenging estimation problem and are harder to detect [2], and are hence our primary focus.

We use penalized regression splines to model \(\lambda _{p,i} = \lambda _{p,0} + f_p(z_i) = \lambda _{p,0} + \mathbf {x}_i {\varvec{\beta }}^*_p\), where \(f_p(z)\) has mean zero across the covariate values (i.e., \(\int f_p(z) dz = 0\)), which is needed for the identifiability of \(\lambda _{p,0}\). We note that when \(f_p(z)=0\), the model simplifies to standard factor analysis. In other words, \(f_p(z)\) represents the non-constant component of the factor loading. We use cubic B-spline basis functions to model \(f_p(z_i)\), and let \(\mathbf {x}_i\) be a row vector containing the value of each basis function evaluated at \(z_i\) [30]. The spline coefficients, which differ across the P observed variables, are \({\varvec{\beta }}^*_p\). We use a quadratic penalty, \(({\varvec{\beta }}^*_p)^\mathrm{{T}} \mathbf {S}^* {\varvec{\beta }}^*_p\), to penalize the magnitude of the coefficients, where \(\mathbf {S}^*\) is the first difference penalty matrix [7]. In comparison to other penalties, ours is straightforward to compute [30] and it has the advantage of shrinking the estimate of f to zero [7], thereby shrinking the factor loading to a constant. To implement the penalty on the splines, we use the fact that penalized splines can be represented as a mixed model [18, 31]. Hence, we rewrite (1) as a regression model:

$$\begin{aligned} \mathbf {y}_{p,.} = {\varvec{\eta }}\lambda _{p,0} + \mathbf {X}_\eta {\varvec{\beta }}_p + {\varvec{\epsilon }}_{p,.}, \end{aligned}$$
(2)

where \(\mathbf {y}_{p,.} = [y_{p,1}, \) \(\ldots ,\) \(y_{p,n}]^\mathrm{{T}}\), \({\varvec{\eta }}= [\eta _1, \ldots , \eta _n]^\mathrm{{T}}\), \(\mathbf {X}_\eta = [\mathbf {x}_1^\mathrm{{T}} \eta _1, \ldots , \mathbf {x}_n^\mathrm{{T}} \eta _n]^\mathrm{{T}} \mathbf {S}^{-1}\), \({\varvec{\epsilon }}_{p,.} = [\epsilon _{p,1}, \ldots , \epsilon _{p,n}]^\mathrm{{T}}\); and \( {\varvec{\beta }}_p = \mathbf {S}{\varvec{\beta }}^*_p\) where \(\mathbf {S}\) satisfies \(\mathbf {S}^\mathrm{{T}} \mathbf {S}= \mathbf {S}^*\) and can be derived according to the spectral decomposition of \(\mathbf {S}^*\). Under the parameterization of (2), the quadratic penalty on the coefficients equals to \({\varvec{\beta }}_p^\mathrm{{T}} {\varvec{\beta }}_p\) and is implemented by setting \({\varvec{\beta }}_p\) as random variables [18, 31]; specifically, \({\varvec{\beta }}_p \sim N(\mathbf {0}, \sigma ^2_{p,b} \mathbf {I}_K)\) (see more details in Sect. 3). In this approach, \(\sigma ^2_{p,b}\) takes the role of the smoothing parameter so that a smaller value of \(\widehat{\sigma }^2_{p,b}\) leads to a smaller value of \(\widehat{{\varvec{\beta }}}_p\), and when \(\widehat{\sigma }^2_{p,b} \rightarrow 0\), \(\widehat{f}_p \rightarrow 0\), which makes \(\widehat{\lambda }_{p,i} \rightarrow \widehat{\lambda }_{p,0}\).

We aim to test if, for a particular observed variable \(\mathbf {y}_{p,.}\), its factor loading is constant, i.e.,

$$\begin{aligned} H_0: \lambda _{p,i} = \lambda _{p,0} \quad \text {for all}\;\,i \quad \mathrm {vs.}\quad H_a: \lambda _{p,i} \ne \lambda _{p,0} \quad \text {for some}\;\,i. \end{aligned}$$
(3)

This is equivalent to testing \(H_0: {\varvec{\beta }}_p = 0 \quad \mathrm {vs.}\quad H_a: {\varvec{\beta }}_p \ne 0.\) The test in (3) then becomes

$$\begin{aligned} H_0: \sigma ^2_{p,b} = 0 \quad \mathrm {vs.}\quad H_a: \sigma ^2_{p,b} > 0. \end{aligned}$$
(4)

Note that we are only testing for the factor loading of one variable, that is, \(\sigma ^2_{p,b}\) for a particular p according to the test in (4). We let other variables not being tested have either constant or non-constant factor loadings under both the null and alternative hypotheses. Even though the hypotheses in (3) and (4) focus on one factor loading only, they could be expanded to include testing more than one factor loading simultaneously. Further, the model fitted under the null could include non-constant factor loadings for other variables than for the one being tested.

3 Estimation and Inference

3.1 Likelihood

We use the EM algorithm for estimation, and treat \(\eta _i\) and \({\varvec{\beta }}_p\) as the augmented missing data. The log-likelihood when conditioning upon the augmented data is \(\log \mathcal {L}({\varvec{\theta }}| \mathbf {y}, {\varvec{\eta }}, {\varvec{\beta }}_p)\) and is proportional to

$$\begin{aligned} - \frac{1}{2} \sum _{p=1}^P \left\{ n \log (\sigma ^2_{p,\epsilon }) + \frac{\Vert \mathbf {y}_{p,.} - {\varvec{\eta }}\lambda _{p,0} - \mathbf {X}_\eta {\varvec{\beta }}_p \Vert ^2}{\sigma ^2_{p,\epsilon }} + K \log (\sigma ^2_{p,b}) + \frac{\Vert {\varvec{\beta }}_p \Vert ^2}{\sigma ^2_{p,b}}, \right\} \qquad \end{aligned}$$
(5)

where \({\varvec{\theta }}= \{\lambda _{p,0}, {\varvec{\beta }}_p, \sigma ^2_{p,\epsilon }, \sigma ^2_{p,b} | p=1,\ldots ,P \}\) represents all the parameters. In (5), we assume all factor loadings are non-constant. However, if the factor loading for the pth observed variable is instead assumed as constant a priori, we only need to remove \(\sigma ^2_{p,b}\) from the likelihood and set \({\varvec{\beta }}_p = 0\). The details of the E-step and M-step are given in Supplementary Material A.1 and A.2. Computational considerations for speeding up the E–M using nested iterations are discussed in Supplementary Material A.3.

3.2 Likelihood Ratio Test (LRT)

Since we use random spline coefficients to incorporate the smoothing of splines into the likelihood, we can use the LRT to assess measurement invariance assumption. The LRT test statistic is constructed as \(2 \left\{ \log \mathcal {L}( \widehat{{\varvec{\theta }}}_a | \mathbf {y}) - \log \mathcal {L}( \widehat{{\varvec{\theta }}}_0 | \mathbf {y}) \right\} \), where \(\widehat{{\varvec{\theta }}}_a\) and \(\widehat{{\varvec{\theta }}}_0\) represent, respectively, the parameter estimates from the model under the null and alternative hypotheses. Supplementary Material A.4 discusses details to carry out Monte Carlo integration with importance sampling to obtain the likelihood. Since the test involves one or potentially more variance components, the null distribution of the test statistic will generally be unknown. Hence, we propose using a parametric bootstrap approach to generate the null distribution of the test statistic.

Since the parametric bootstrap can be computationally intensive, both because of the numerical algorithms used to fit the model and because of the very large number of simulations needed to approximate well the tail of the null distribution, it is desirable to look for faster and/or parametric approximations. The rest of this section focuses on the case of testing one factor loading, and thus one variance component, where faster approximations for the null distribution can be derived, compared to the standard parametric bootstrap [6].

Approaches to testing one variance component have been widely studied. Stram and Lee [26] prove that with linear mixed models, the asymptotic null distribution of the LRT statistic when testing for a single variance component, similar to (4), follows a 50–50 mixture of \(\chi ^2_0\) and \(\chi ^2_1\); we denote this mixture distribution as \(\frac{1}{2} \chi ^2_0 + \frac{1}{2} \chi ^2_1\). However, Crainiceanu and Ruppert [5] argue that using \(\frac{1}{2} \chi ^2_0 + \frac{1}{2} \chi ^2_1\) gives a conservative test, because the asymptotic assumption is rarely reached in real cases and also is not directly applicable to penalized regression spline models. Their approach is instead to find the exact null distribution of the LRT statistic numerically when there is only one variance component in the model. Greven et al. [9] propose an approximation to the parametric bootstrap that assumes the distribution of the test statistic under the null is a mixture of chi-square distribution following the form, \(\pi \chi ^2_0 + (1-\pi ) a \chi ^2_1\), where \(\pi \) is the mixture probability and also the probability of the statistic being zero, and a is a scaling factor that gives more flexibility for the distribution. For clarity we refer to Greven’s approximation of the parametric bootstrap as a “chi-square” bootstrap, and use the term “full bootstrap” to refer to the ordinary parametric bootstrap.

For a given data set, deriving the null distribution of the LRT statistics using chi-square bootstrap is straightforward. First, \(M^*\) parametric bootstrap data sets are generated using the parameters estimated from the null model. LRT statistics are computed for each of the \(M^*\) data sets and are used to estimate \(\pi \) and a using the method of moments as described by Greven et al. [9]. Since the 95th percentile of the null LRT is derived from a fitted parametric family of distributions, a fewer number of bootstrap samples \(M^*\) are needed to obtain equally precise estimates of the tail quantiles compared to the full bootstrap if the chi-square mixture approximates the true null distribution well (also see Greven et al. [9] for details). Our simulation results confirm this advantage of the chi-square bootstrap in our particular application to factor models (see Supplementary Material B). After computing estimates \(\widehat{p}\) and \(\widehat{a}\), for p and a, respectively, we set the 95th percentile of the null LRT statistic as \(\widehat{a}F^{-1}_{\chi ^2_1}\frac{0.95-\widehat{\pi }}{1-\widehat{\pi }}\), where \(F_{\chi ^2_1}\) represents the cumulative distribution function of a \(\chi ^2_1\) distribution. p-values can also be derived using \((1-\widehat{\pi }) F^{-1}_{\chi ^2_1} \left[ \frac{1}{\widehat{a}} (\mathrm {LRT~statistic}) \right] \). For the data application in Sect. 5, we use the chi-square bootstrap. This is because through simulation studies we find that chi-square bootstrap can perform as well as the full bootstrap (Supplementary Material B) and in practice we want to use chi-square bootstrap to reduce computational cost.

3.3 Confidence Intervals and Confidence Bands

Since the construction of LRT statistic and the ensuing parametric bootstrap is computationally intensive, we also examine the use of confidence intervals as a way to examine MI. Confidence intervals can be directly derived using samples obtained at the E-step. Supplementary Material C describes approaches to derive pointwise confidence intervals and confidence bands for the non-constant part of the factor loadings. Examining whether the confidence intervals or bands do not contain zero for some portion of the range of the covariate implicated in MI can give guidance as to the nature of the violation of MI. As shown in the simulations, this approach has high power and maintains Type I error. This approach also works well in practice, as show in the example section.

4 Simulation Study

4.1 Simulation Objectives and Set-Up

In this simulation study, we want to compare the Type I error and power of the LRT for testing the hypothesis in (3) using our proposed model and multi-group models under different scenarios. Under our model, we actually test (4), the hypothesis about the variance of the random spline coefficients using LRT. We can obtain the critical cutoff value for the LRT statistic using parametric bootstrap as detailed in Sect. 3.2. Ideally, for each simulated data set, we would carry out a full bootstrap or the chi-square bootstrap to obtain the cutoff value. However, in order to reduce computational cost, we instead use the 95th percentile of the LRT statistics calculated for all the simulated data sets from the null scenario. Therefore, the Type I error is exactly nominal. Then we use this correct cutoff value to examine the true power of the LRT for our model. This simulation represents the results we would obtain when we use a full bootstrap, because we are basically carrying out a bootstrap under the true parameter values (see Greven et al. [9] for a similar simulation approach). The results also reflect what would be obtained with the chi-square approximation for the full bootstrap, since the cutoff values from these two approaches match very closely (see Supplementary Material). As a comparison, we also examine the use of \(\frac{1}{2} \chi ^2_0 + \frac{1}{2} \chi ^2_1\) since it would lead to substantial computational savings over any bootstrap approach. For the multi-group model approach, we also use LRT, but the cutoff value is straightforward to obtain since the parameter values under the null are not in the boundary of the parameter space.

For all the scenarios that are further described below, we let each of 10,000 simulated data sets have three observed variables, \(\mathbf {y}_{p,.}, p = 1, 2, 3,\) and \(n=2000\); values of \(z_i\) are equally spaced within the range of [0, 1]. We set the total variance of the observed variables, \(\lambda _{p,0}^2 + \sigma ^2_{p,\epsilon } = 8\) and let \({\lambda _{p,0}^2 / (\lambda _{p,0}^2 + \sigma ^2_{p,\epsilon })} = 0.5\) so that we have a medium signal-to-noise ratio, which is also in the middle of the range of signal-to-noise ratio in our data example. The factor loadings are generated as \(\lambda _p = \lambda _{p,0} + f_p\).

We vary the shapes of \(f_1\) and \(f_2\) for different simulation scenarios. First, we set the first factor loading as non-constant, that is, \(f_1 \ne 0\), but set \(f_2 = 0\), \(f_3 = 0\). Since the shape of \(f_1\) could potentially impact the power of the various approaches, we let \(f_1\) take on two different shapes, (1) a cyclic shape: \(f_1(z_i) = \kappa \{-0.1 \cos (6\pi z_i)\}\), (2) a monotone trend added: \(f_1(z_i) = \kappa \{c + (1.6 z_i - 0.8 z_i^2) - 0.1 \cos (6\pi z_i)\}\). In the formulas, c is the constant that ensures \(\int _{z \in [0,1]} f_1(z) dz = 0\) and \(\kappa \) is an amplitude parameter that changes the magnitude of \(f_1\) so that we can examine the power of the test. Second, we let \(f_1\) be the same as above, but we let \(f_2(z_i) = 0.6 (z_i - 0.5)\), while \(f_3\) still remains equal to zero.

For each scenario, we estimate two variations of our proposed model: one where only \(f_1\) is estimated and one where both \(f_1\) and \(f_2\) are estimated. However, following Sect. 3.2, we only test for one non-constant factor loading, specifically \(f_1\). This allows us to assess any potential bias in tests when the fitted model is correct or misspecified. For example, we have a misspecified model when \(f_2 \ne 0\) and we omit its estimation. We can also examine the potential loss in power when the model is more flexible than necessary. This happens when \(f_2 = 0\) and we unnecessarily estimate it.

In a multi-group model, the factor loadings are allowed to be different across groups of data points, but the factor loading within each group is still assumed constant. Therefore, this approach can overlook important differences in the factor loadings and the estimation also depends on how the group is assigned [2]. In this study we use tertiles and quartiles of z to group the data, and we jointly model the different groups.

We repeat the same two variations of estimated models using the multi-group approach. The non-constant factor loadings in the model take the following form when we use tertiles of \(z_i\), \(\lambda _{p,i} = \lambda _{p,0} + \alpha _1 I(z_i \le Q_1) + \alpha _2 I(Q_1<z_i \le Q_2) + \alpha _3 I(z_i>Q_2)\), where \(Q_1\), \(Q_2\) represent the first and second tertiles of \(z_i\), respectively. For quartiles, the formula is similar. We constrain the residual variances to be the same across groups because they do not contribute to the measurement bias and also because our simulation objective is to estimate the factor loadings. We also use a LRT for testing non-constant factor loadings in the multi-group models. In this case, the LRT statistic asymptotically follows a chi-square distribution with degrees of freedom equal to two and three for tertile and quartile models, respectively.

4.2 Simulation Results

Type I error and power when the model is correctly specified. We first focus on Type I error, the rejection rate when \(\kappa = 0\) for the scenario where \(f_2 = 0\) and we only estimate \(f_1\). We can see that, in the row labeled ‘Null’ in Table 1, using \(\frac{1}{2} \chi ^2_0 + \frac{1}{2} \chi ^2_1\) as the null distribution leads to a 3.0% rejection rate. This is because the estimated spline was reduced to zero more than half of the time, and this makes \(\frac{1}{2} \chi ^2_0 + \frac{1}{2} \chi ^2_1\) a conservative null distribution. As stated above, because the cutoff value is determined from the 95th percentile of the true distribution of the null LRT statistic, the rejection rate from the ‘Exact’ column is 5%. Tests from multi-group analyses preserve their nominal rate since the distributions are known.

Table 1 Rejection rate for testing \(H_0\): \(f_1 = 0\) versus \(f_1 \ne 0\) when only \(f_1\) is non-zero and being estimated
Full size table

Next we use increasing values of \(\kappa \) so that \(f_1\) is non-zero, and the rejection rate reflects the power of the test. The rows labeled ‘Cyclic’ and ‘Monotone’ in Table 1 show the results. Here, \(f_2 = 0\) and is not estimated, so the model is correctly specified. The larger \(\kappa \) is, the more \(f_1\) deviates from zero, and thus the power increases. Since \(\frac{1}{2} \chi ^2_0 + \frac{1}{2} \chi ^2_1\) is conservative for the LRT, it also lowers the power of the test compared with the rejection rate from the ‘Exact’ column in Table 1, the true power of the LRT. The multi-group models have lower power than our model because they cannot always capture the shape of \(f_1\), especially when \(f_1\) has a cyclic pattern. For example, in scenarios where \(f_1\) is cyclic, these tests cannot detect a non-zero \(f_1\) when we use tertiles because \(f_1\) has a threefold repeated pattern.

When both \(f_1\) and \(f_2\) are non-zero, and both functions are estimated so that we have a more complex but correctly specified model, the power for testing \(H_0: f_1=0\) is similar to the results shown in Table 1 for all testing approaches (results not shown).

Type I error and power when the model is unnecessarily flexible or misspecified. When \(f_2 = 0\) but it is estimated, then we have an unnecessarily flexible model for \(f_2\). In Table 2 we see similar patterns for Type I error as described above, and we also see that no power is lost in this model, because (1) our proposed model gives a stable estimate of \(f_1\) whether \(f_2\) is estimated or not, and (2) when \(f_2\) is estimated unnecessarily, the model is able to shrink the estimate to zero a large proportion (\(>50\%\)) of the time, and the fitted model reflects the correct and simpler model.

Table 2 Rejection rate for testing \(H_0\): \(f_1 = 0\) versus \(f_1 \ne 0\) when the model fitted is more flexible than needed (i.e., \(f_2=0\) but is estimated as non-zero) or when it is misspecified (i.e., \(f_2 \ne 0\) but is fixed at zero)
Full size table

On the other hand, when \(f_2 \ne 0\) but \(f_2\) is not estimated, then the model is misspecified for \(f_2\). As can be expected for misspecified models, we find that this results in biased \(\widehat{f}_1\), shown in Fig. 2. For our specific models, \(\widehat{\lambda }_{2,i}\) will be positively biased for \(z_i < 0.5\) and negatively biased for \(z_i > 0.5\). This in turn influences \(\widehat{\lambda }_{1,i}\) in the same direction. Because of the bias, Type I error is inflated for the LRT. In Table 2, the rejection rate in the ‘Exact’ column is 8.0%. Here, the cutoff value is determined from the simulation scenario of Table 1, where \(f_2 = 0\) and \(f_2\) is not estimated, because this is the scenario we have wrongly assumed and it is also the scenario we would have used for the bootstrap. Even though the Type I error in the ‘\(\frac{1}{2} \chi ^2_0 + \frac{1}{2} \chi ^2_1\)’ column seems nominal (5.1%), compared with Table 1, this also reflects the inflation due to the biased \(\widehat{f}_1\).

Power is higher for the misspecified model than the correctly specified model in Table 1 under the scenario where \(f_1\) is cyclic. Aside from the inflated Type I error, the power increase is likely also due to the positive bias of the estimated amplitude of \(\widehat{f}_1\). However, despite the inflated Type I error, power is lower when \(f_1\) has a monotone trend because the amplitude is instead attenuated, which is also shown in Fig. 2. The multi-group approach suffers similar consequences when the model is misspecified.

Fig. 2
figure 2

Comparison of \(\widehat{f}_1\) from different scenarios in Table 1. The dotted line is the true \(f_1\). The solid line is \(\widehat{f}_1\) from the scenario where \(f_2 = 0\) and \(f_2\) is not estimated. The long dashed line is \(\widehat{f}_1\) from the scenario where \(f_2 \ne 0\) but \(f_2\) is incorrectly fixed at zero during estimation. The short dashed line is \(\widehat{f}_1\) from the scenario where \(f_2 \ne 0\) and \(f_2\) is estimated. a Cyclic shape, b monotone trend added

Full size image

Confidence intervals. Since the construction of the LRT statistic and the ensuing parametric bootstrap is computationally intensive, we also examined the use of confidence intervals for testing purposes. Pointwise confidence intervals and simultaneous confidence bands can be directly derived using samples obtained at the E-step and can be informally used to assess deviations from a non-constant factor loading; see Section C of the Supplementary Materials for more details. We find that using pointwise confidence intervals, but not simultaneous confidence bands, as a way to make this assessment yields a rejection rate around the nominal 5% level (5.2%), and power as high as the LRT described above.

5 Application to Prenatal Lead Measurements from the ELEMENT Study

We use data collected from 880 mother/child pairs from the Early Life Exposure in Mexico to Environmental Toxicants (ELEMENT) project. Mothers were between 18 and 44 years old at recruitment (mean = 25.8, SD = 5.0). The ELEMENT project consists of three sequentially enrolled cohorts of pregnant women and their offspring, recruited in Mexico City between 1994 and 2003 to investigate the long-term consequences of lead exposure on child development. The project took prenatal and postnatal measurements from mothers and also followed the children longitudinally [8, 27]. The four observed variables we are interested in are maternal levels of cord blood lead, blood lead one month after delivery, patella bone lead, and tibia bone lead. Since these lead biomarkers can be conceptualized as manifestations of latent lead exposure during pregnancy [22], we use a one factor model to summarize them. We are interested in looking at whether and how the factor loadings for each observed variable differ with maternal age because lead metabolism processes, such as bone resorption, depend on maternal age [27]. Thus, the correlation between blood and bone lead measures may vary with maternal age, which in turn causes the factor loadings to vary with maternal age. As described in Sect. 2, we first de-trend the four biomarkers for lead exposure to remove any potential covariate effects on the mean. To do so, we use an additive model [30] for each biomarker with indicators for participant’s cohort membership and a smooth term of maternal age. We take the residuals from these models as the input to our factor model.

Fig. 3
figure 3

The non-constant component for the factor loadings of cord blood lead and tibia bone lead. The solid line shows \(\widehat{f}_p(z_i)\) from Model A. The dashed line and the dotted line show the 95% pointwise confidence intervals and the simultaneous confidence band, respectively. a Cord blood lead, b tibia bone lead

Full size image

Theoretically some factor loadings can be shrunk exactly to a constant in our model when the variance of the random spline coefficients, \(\widehat{\sigma }^2_{p,b}\), is zero. However, the estimation is built on the normal distribution of \({\varvec{\beta }}_p\), so even when \(\widehat{\sigma }^2_{p,b}\) approaches zero as the algorithm converges, it will not be exactly zero since a non-degenerate distribution is needed to sample \({\varvec{\beta }}_p\). Thus, in an initial exploratory analysis where all four factor loadings were estimated as non-constant, we examined convergence of \(\sigma ^2_{p,b}\) for all four variables and decided to set the factor loading for blood lead after delivery and patella bone lead as constant and proceeded to model the factor loadings of cord blood lead and tibia bone lead as varying with maternal age.

Next we conducted analyses in two models to illustrate the testing approaches previously described. In Model A, the factor loadings of both cord blood lead and tibia bone lead are modeled as non-constant, while in Model B only one of the two observed variables, either cord blood lead (Model B1) or tibia bone lead (Model B2), has a non-constant factor loading. In both models, and for both biomarkers, we find that the factor loadings deviate from a constant, although the deviation for cord blood lead’s factor loading is much stronger (Fig. 3).

The patterns of the two factor loadings are similar between Model A and Model B. However, as we saw in the simulations, if a truly non-constant factor loading is estimated as constant, the estimation for the other non-constant factor loadings can be affected. By comparing Models A and B1, and Models A and B2, we find that the amplitudes of \(\widehat{f}_p\) for both cord blood lead and tibia bone lead, respectively, are attenuated when the other factor loading is estimated as constant (figure not shown). This attenuation can also be seen numerically in Table 3 by examining \(\widehat{\sigma }^2_{p,b}\), the variance of the random spline coefficients. A bigger \(\widehat{\sigma }^2_{p,b}\) is related to a more pronounced deviation of \(\widehat{f}_p\) from zero. We find that \(\widehat{\sigma }^2_{p,b}\) from Model B is smaller than Model A.

Table 3 Parameter estimates for the model fitted under the alternative hypothesis, and LRT p-values for the ELEMENT study data
Full size table

The pointwise confidence intervals in both Model A and B suggest that the factor loading of cord blood lead, but not tibia lead, is non-constant (Fig. 3). Results from LRT using critical values from either \(\frac{1}{2} \chi ^2_0 + \frac{1}{2} \chi ^2_1\) or \(\pi \chi ^2_0 + (1-\pi ) a\chi ^2_1\) , where \(\widehat{\pi }=0.7\) and \(\widehat{a}\approx 0.9\) for both Model A and B, confirm this conclusion (Table 3). The p-values obtained through the multiple group analyses depend on whether tertiles or quartiles of the maternal age distribution are used to group the observations. In particular, the p-value obtained when using tertiles is smaller for cord blood lead, which makes sense because the pattern of the factor loading is U-shaped, and thus age tertiles capture the difference of middle tertile compared to the other two more accurately. In contrast, the p-value for the tibia lead factor loading, which follows a linear pattern, is smaller when using quartiles than tertiles.

In these data, the factor loading of cord blood lead differs depending on maternal age. The non-linear pattern in the non-constant component of the factor loading for cord blood implies that the factor loading among the youngest and oldest mothers is lower compared to mothers in the center of the age distribution. This implies that the use of a latent factor model with constant factor loadings may introduce measurement bias into any resulting summaries. In other words, the factor scores created from a model assuming constant factor loadings may not correctly rank overall exposure levels among study participants, and the bias in rankings would be related to maternal age. We plan to examine the impact of this bias on estimated associations between this latent exposure factor and other factors in future work.

6 Discussion

The assumption of measurement invariance (MI) is common in latent factor models, as this assumption makes parameter estimation simple and provides straightforward interpretation of the derived factors. Assessing whether or not this assumption is violated is difficult when the covariates related to violation of MI are continuous; a widely used approach is to create categories, usually based on empirical quantiles, and assess for differences in measurement model parameters among these categories. We proposed an approach to examine this assumption, founded on the connections between varying coefficient models, splines and mixed effect models. We presented simulation-based evidence for the validity and power of our test, showed it is more efficient to existing approaches based on categories, and demonstrated its application to a motivating example. The approach was implemented in SAS proc IML, and code is available as a supplementary material.

Our methods are applicable to cases where both the latent factor and observed variables are continuous and normally distributed. Extensions to latent factor models where observed data follow other distributions are a potential avenue of further research. Such approaches could build upon existing latent variable methods for outcomes of mixed types [20, 24] and methods for testing variance components in the generalized linear mixed model framework [14, 32]. Violations of normality may preclude the use of the chi-square approximation to the parametric bootstrap that we proposed here. However, if diagnostics [21] indicate deviations from normality, alternate parametric bootstrap approaches [6] that do not rely on simulating data sets using normal distributions could be used; for example data sets could be generated by permuting conditional residuals for each observed variable across subjects from the model fit under the null hypothesis. While this approach would lose the computational efficiency afforded by the chi-square approximation to the parametric bootstrap, it would still provide correct inference.

We assessed the validity and power of our test for models where only one latent factor is assumed, and used a few items for the latent factor. The choice of the number of factors in factor analysis remains a balance between variance explained in interpretability of the model, and was thus not our focus. However, the number of latent factors determined empirically from a given data set could potentially depend on whether measurement invariance holds and vice versa. Often times, the number of factors may be determined a priori based on knowledge of the underlying constructs. In our example, we were interested in a single construct of lead exposure. Nevertheless, in models with more than one latent factor, diagnosing the measurement model of each factor separately is likely advantageous so that misspecification of the measurement model for one latent factor does not contaminate parameter estimates for other components of the model [12]. Still, extensions to include additional factors are of interest because in some instances an observed variable could load on more than one latent factor and also because a broader definition of measurement invariance involves the question of whether the number of latent factors is the same across groups. The mechanics of extending the model to include more latent factors is relatively straightforward, albeit more computationally expensive. Increasing the number of observed variables per each latent variable is also a straightforward extension, and results in greater power to detect lack of a constant factor loading for one variable at a time. This is because having more observed variables increases the ability to estimate the latent factor more accurately, i.e., reduces noise (not shown).

Although our simulation studies focused primarily on the validity and power for testing one factor loading, the simulation studies and the data example also demonstrated the feasibility of fitting more than one non-constant factor loading simultaneously using our proposed methods. We also demonstrated in simulations that pointwise and simultaneous confidence intervals for the non-constant factor loadings can be readily constructed using the posterior distribution of the spline coefficients. More importantly, we found that pointwise confidence intervals can be used to assess MI with essentially equal power as the proposed LRT. Importantly, given that smoothing induces a large degree of correlation among adjacent confidence intervals, Type I error is also maintained. Thus, constructing confidence intervals be a useful strategy to assess lack of constant factor loadings for several variables simultaneously. Developing fast approximations for formally testing (i.e., producing p-values) more than one factor loading at a time (i.e., more than one variance component) is a natural next step. We choose [9] parametric bootstrap over the exact method proposed by Crainiceanu and Ruppert [5] because the exact method requires the eigenvalues of \(\mathbf {X}_\eta \) in (2), but in our case \({\varvec{\eta }}\) is unobserved.

Our current methods assume that all covariates that could be responsible for measurement invariance have been identified and no missing values exist. Since non-constant factor loadings can be viewed as an interaction between the latent factor and a third variable, we suggest that variables for testing be selected on the basis of biological knowledge. In our data example, maternal age is known to affect lead metabolism, and could thus result in different correlations among lead biomarkers and imply non-constant factor loadings. Nevertheless, extensions of our methods to determine which, among a large set of covariates, could be responsible for measurement invariance are of interest. A potential avenue for this research could be to apply variable selection approaches to select non-zero variance components of the random effects used to parametrize the non-constant component of the factor loadings. However, given the computational nature of random effects approaches that are well suited for testing as presented here, variables to assess measurement invariance based on cross-validation (e.g., [34]) maybe better suited for selection of factor loadings that violate the MI assumption. Missing data could be incorporated within the EM algorithm we developed here, but it is unknown how varying degrees of missing data would influence the operating characteristics of the proposed test. We focused on data sets that have a relatively large sample size. Increasing/decreasing sample size would naturally increase/reduce power. However, extending existing sample size recommendations for latent variable models [29] would be useful in light of the additional sample size needed to estimate smooth terms.

In summary, we proposed novel approaches to test for measurement invariance that are based on estimating factor loadings that vary smoothly as functions of covariates. The supplementary materials contain SAS code to implement the approach and thus enhance the application of our proposed method in practice. Further, our approach lays the foundation for developing approaches to systematically and efficiently examine the measurement invariance assumption in other types of factor models.