A Multivariate Generalized Linear Model Approach to Mediation Analysis and Application of Confidence Ellipses

Abstract

Mediation analysis evaluates the significance of an intermediate variable on the causal pathway between an exposure and an outcome. One commonly utilized test for mediation involves evaluation of counterfactual effects, estimated from separate regression models, corresponding to a composite null hypothesis. However, the “compositeness” of this null hypothesis is not commonly acknowledged and accounted for in mediation analyses. We describe a generalized multivariate approach in which these separate regression models are fit simultaneously in a single parsimonious model. This multivariate modeling approach can reproduce standard mediation analysis and has notable advantages over separate regression models, including the ability to combine distributions in the exponential family with any link functions and perform likelihood-based tests of some relevant hypotheses using existing software. We propose the use of a novel visual representation of confidence intervals of the two estimates for the indirect path with the use of a confidence ellipse. The calculation of the confidence ellipse is facilitated by the multivariate approach, can test the components of the composite null hypothesis under a single experiment-wise type I error rate, and does not require estimation of the standard error of the product of coefficients from two separate regressions. This method is illustrated using three examples. The first compares results between the multivariate method and separate regression models. The second example illustrates the proposed methods in the presence of an exposure–mediator interaction, missing data and confounding, and the third example utilizes these proposed methods for an outcome and mediator with negative binomial distributions.

1 Introduction

Mediation analysis is an important and evolving method in both observational and clinical research, where investigators are interested in not only describing the overall association between an exposure variable and an outcome, but also the underlying mechanism of this relationship. A mediator is a variable that is hypothesized to be on the causal pathway relating an independent exposure variable to a dependent outcome. Regression-based approaches for evaluating mediation were first popularized by Baron and Kenny [2], and extensions are now widely used in psychology and epidemiologic research [15, 33]. A general framework for mediation influenced by causal inference literature has been proposed [20, 23], leading to counterfactual definitions of direct and indirect effects [31, 33, 34]. These effects can be estimated from the regression models of traditional mediation analysis for the case where the outcome and mediator are normal [20, 23] and when one or both are nonnormal [12, 14, 31].

Regression based mediation analysis traditionally requires the estimation of coefficients from at least two separate models, often with mixed variable types (e.g., continuous mediator and a binary outcome). While many advances have been made in the field, there remain concerns with the use of coefficients from separate models, and with aspects of the test of mediation [10, 14, 16, 33]. The primary concern is the estimation and testing of the product of regression coefficients from two separate models when the joint distribution is unknown. A variety of methods are available for estimating the standard errors and/or confidence intervals for the product of coefficients. The delta method approximation to the standard error can be used in a Wald test or confidence intervals using bootstrap or bias corrected bootstrap, permutation, or the true distribution of the product can be obtained [11, 27, 29]. These approaches, however, are not without fault [10, 13, 16, 33], and confidence limits based on these approaches are often inaccurate [17].

Alternative methods exist to test for mediation in addition to the regression-based approaches [1, 12, 21]. Briefly, path analysis in structural equation models (SEMs) allow for the modeling of potentially complex relationships and provide a framework for estimating the two regression equations simultaneously. SEMs are advantageous because they allow for the estimation of latent variables. However, in cases where latent variables are not utilized, SEMs and regression-based approaches will result in the same estimates and inferences, and one disadvantage to the SEM framework is the required knowledge of specialized software [3]. Utilization of the SEM approach for latent variables and adaptation to specialized software are outside of the scope of this work. Rather, we propose improvements upon the widely used regression-based approach.

Several important contributions to mediation analysis using regression-based methods for mixed variable types are expanded upon in this paper. A multivariate generalized linear model was implicitly utilized by Vanderweele [32] to estimate the 4-way decomposition of interaction in mediation and was only discernable from the code provided in the supplement. Our first contribution is to describe in detail, this multivariate approach to simultaneously model the outcome and mediator and to estimate counterfactual effects in the presence of confounders and interaction. For this approach, the joint density of the outcome and mediator, conditional on the exposure, is expressed as the product of two univariate distributions, both from the exponential family with specified link functions. The use of the multivariate generalized linear model approach allows for several extensions that have not previously been described: (1) derivation of counterfactual effects for any combination of variable types (binary, continuous, etc.) and estimation of regressions with mixed variables types using a more parsimonious procedure; (2) the simultaneous estimation of the joint distribution of both outcome and mediator to provide a single −2log likelihood that can be used to perform a likelihood ratio test for the coefficients of interest and (3) a novel application of confidence ellipses and simultaneous confidence intervals to provide simultaneous tests of the coefficients [25]. This multivariate approach to mediation analysis facilitates the likelihood ratio test of the joint hypothesis and the confidence ellipse. Three examples are provided to illustrate the concepts and address complications including missing data, confounding and exposure–mediator interaction. We demonstrate how this general analysis can be executed with readily available existing software (SAS PROC NLMIXED, SAS Institute Inc.: Cary, NC, 2011) and provide a specialized SAS macro to produce the confidence ellipse.

2 The Multivariate Generalized Linear Model Approach to Mediation Analysis

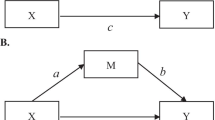
Consider the directed acyclic graph (DAG) where exposure A affects the mediator M, which in turn affects the outcome Y (Fig. 1). The traditional approach would be to model each component of the DAG separately. However, we describe an alternative to estimating parameters of interest from separate models, by modeling Y and M bivariately (i.e. simultaneously).

The joint density of Y and M conditional on A and confounders C can be expressed as the product of the distribution of M conditional on A and C and the distribution of Y conditional on M, A and C, i.e., $f\left( {y,m\,|\,a,c}\right) =f\left( {m\,|\,a,c}\right) f\left( {y\,|\,m,a,c} \right)$ where $f\left( {m\,|\,a}\right)$ is short for the probability $f\left( {m\,|\,a}\right) =P\left( {M=m \,|\, A=a}\right)$ if M is discrete, and $\int \limits _b^d {f\left( {m\,|\,a}\right) } =P\left( {b\le M\le d \,|\, A=a} \right)$ if M is continuous.

Fig. 1

Effect of exposure A on outcome Y mediated by M. If A*M interaction is present, $\theta _2$ may be replaced by $\varphi _a$ to denote that the path is now a function of a

Because $f\left( {y,m\,|\,a,c}\right)$ is the product of $f\left( {m\,|\,a,c}\right)$ and $f\left( {y\,|\,m,a,c}\right)$, M and Y can be modeled bivariately by treating them as two separate observations of a single dependent variable with likelihoods $f\left( {m\,|\,a,c} \right)$ and $f\left( {y\,|\,m,a,c}\right)$, respectively. Marshall et al. [18] and Vanderweele [32] similarly used this factorization to facilitate the analysis of M and Y simultaneously.

We assume that outcome Y obeys a generalized linear model with an exponential family density $f\left( {y|m,a,c}\right)$ and a link function, ${h}_{Y} \left\{ {E\left[ {{Y|a,m,c}} \right] }\right\} =\theta _0 +\theta _1 a+\theta _{2} m+\theta _3 am+{\theta }'_4 c_Y$ conditional on mediator M, exposure A and potential confounders $c_Y$, and where the product allows for an interaction between the mediator and exposure. We further assume that the mediator M obeys a generalized linear model with a second exponential family density $f\left( {m\,|\,a,c}\right)$ and a second link function, $h_m \left\{ {E\left[ {M\,|\,a,c}\right] }\right\} =\beta _0 +\beta _{1} a+{\beta }'_2 c_M$ conditional on exposure A and confounders $c_M$, where $c_Y$ and $c_M$ are vectors of covariates, and $\theta _{4}^{\prime }$ and $\beta _{2}^{\prime }$ are vectors of regression coefficients. Since the estimate for $\beta _{1}$ is a function of $f\left( {m\,|\,a,c} \right)$ alone, and the estimate of $\theta _{2}$ is a function of $f\left( {y\,|\,m,a,c}\right)$ alone, the estimates of $\beta _{1}$ and $\theta _{2}$ are independent conditionally (on A).

Under the counterfactual approach to mediation analysis [20, 23, 31, 32], the controlled direct effect (CDE), the natural direct effect (NDE), the natural indirect effect (NIE), and the total effect (TE) of exposure on the outcome can be estimated using coefficients from the above models and are defined on the scale of the inverse link function of the outcome. Similar derivations have been made for specific combinations of variable distributions (e.g., binary outcome, continuous exposure and mediator) in previous papers. Our contribution here is to provide derivations in the multivariate generalized linear model framework which are valid for all combinations of mixed variables. For a change in exposure from level $a^{*}$ to a (where $a^{*}$ denotes a counterfactual value not equal to a), these effects are given as

$$\begin{aligned}&\mathrm{CDE}=h_Y^{-1} \left\{ {\left( {\theta _1 +\theta _3 m} \right) \left( {a-a^{*}}\right) }\right\} ,\\&\mathrm{NDE}=h_y^{-1} \left\{ {\left[ {\theta _1 +\theta _3 h_M^{-1} \left\{ {\beta _0 +\beta _{1} a^{*}+\beta ^{\prime }_2 c}\right\} } \right] \left( {a-a^{*}}\right) }\right\} ,\\&\mathrm{NIE}=h_y^{-1} \left\{ {\left( {\theta _{2} +\theta _3 a} \right) \left[ {h_M^{-1} \left\{ {\beta _0 +\beta _{1} a+\beta ^ {\prime }_2 c}\right\} -h_M^{-1} \left\{ {\beta _0 +\beta _{1} a^{*}+\beta ^{\prime }_2 c}\right\} }\right] }\right\} \,\,\mathrm{and}\\&\mathrm{TE}=\mathrm{NDE}+\mathrm{NIE}, \end{aligned}$$

where $h_Y^{-1} \left\{ \right\}$ denotes the inverse function of $h_Y \left\{ \right\}$ and $h_M^{-1} \left\{ \right\}$ denotes the inverse function of $h_M \left\{ \right\}$. Details of these derivations and the simplified versions of no interaction or identity link functions, are included in Sect. 1 of Appendix.

If both Y and M have identity links, and there is no interaction, then ${h}_{M} \left\{ {{E}\left[ {{M|a,c}} \right] }\right\} ={E}\left[ {{M|a,c}}\right] =\beta _0 +\beta _{1} a+{\beta }'_2 c$, ${h}_{Y} \left\{ {{E}\left[ {{Y|a,m,c}}\right] }\right\} ={E}\left[ {{Y|a,m,c}}\right] =\theta _0 +\theta _1 a+\theta _{2} m+{\theta }'_4 c$, $\mathrm{CDE}=\mathrm{NDE}=\theta _1 \left( {a-a^{*}}\right)$ and $\mathrm{NIE}=\theta _{2} \beta _{1} \left( {a-a^{*}}\right)$. In this classic case, NIE depends on $a^{*}$ only through the difference $\left( {a-a^{*}}\right)$, and the product, $\beta _{1} \theta _{2}$, is often used to evaluate whether mediation is present.

More generally, if M has identity link, the Y link is arbitrary, and there is no interaction, then ${h}_{M} \left\{ {{E}\left[ {{M|a,c}}\right] }\right\} ={E}\left[ {{M|a,c}}\right] =\beta _0 +\beta _{1} a+{\beta }'_2 c$, ${h}_{Y} \left\{ {{E}\left[ {{Y|a,m,c}}\right] } \right\} =\theta _0 +\theta _1 a+\theta _{2} m+{\theta }'_4 c$, $\mathrm{CDE}=\mathrm{NDE}=h_Y^{-1} \left\{ {\theta _1 \left( {a-a^{*}}\right) } \right\} ,$ and $\mathrm{NIE}=h_y^{-1} \left\{ {\theta _{2} \beta _{1} \left( {a-a^{*}}\right) }\right\}$. In this case, NIE still depends on $a^{*}$ only through the difference $\left( {a-a^{*}}\right)$, and the product $\theta _{2} \beta _{1}$, is still often used to evaluate whether mediation is present since $\theta _{2} \beta _{1} \left( {a-a^{*}}\right) =h_y\left\{ \mathrm{NIE}\right\}$ is a monotone function of NIE. Note that in this case $h_y^{-1} \left\{ \right\}$ may map $\theta _{2} \beta _{1} \left( {a-a^{*}}\right) =0$ onto something nonzero. For example, if $h_y^{-1} \left\{ \right\} =\exp \left\{ \right\}$, $\exp \left\{ 0\right\} =1$ would indicate no mediation.

If M has identity link, the Y link is arbitrary, and there is an interaction, then

$$\begin{aligned} {h}_{Y} \left\{ {{E}\left[ {{Y|a,m,c}}\right] } \right\} =\theta _0 +\theta _1 a+\theta _{2} m+\theta _3 am+{\theta }'_4 c=\theta _0 +\theta _1 a+\varphi _a m+{\theta }'_4 c, \end{aligned}$$

where $\varphi _a =\theta _{2} +\theta _3 a$ denotes the effect of M when $A=a$, and $\mathrm{NIE}=h_y^{-1} \left\{ {\left( {\theta _{2} +\theta _3 a}\right) \beta _{1} \left( {a-a^{*}}\right) }\right\} =h_y^{-1} \left\{ {\varphi _a \beta _{1} \left( {a-a^{*}}\right) }\right\}$ with interaction is of the same form as $\mathrm{NIE}=h_y^{-1} \left\{ {\theta _{2} \beta _{1} \left( {a-a^{*}}\right) }\right\}$ without interaction after replacing $\theta _{2}$ with $\varphi _{a}$. This suggests that in the presence of interaction, the product, $\varphi _a \beta _{1}$, a monotone function of NIE, be used to evaluate whether mediation is present when $A=a$, just as $\theta _{2} \beta _{1}$ is used to evaluate mediation in the absence of interaction.

3 Approaches to Testing for Mediation

The multivariate approach offers more than a computational alternative to other approaches, as there is added benefit to using a single program that can both fit the models and then compute and test the significance of the nonlinear functions of interest without exterior macros. When using separate regression models, some statistical procedures utilize restricted maximum likelihood while others use maximum likelihood resulting in different degrees of freedom for variance estimates and subsequent difficulty in combining estimates to obtain standard errors of products (see Appendix 2). The multivariate approach avoids these issues, as all estimates are obtained by maximum likelihood. Because the Y and M are conditionally independent, their log likelihoods can simply be added to determine the multivariate generalized linear model log likelihood and the multivariate generalized linear model can be fit using software that can accommodate any user specified likelihoods and corresponding link functions. Additional details are provided in the supplementary material.

In standard multiple regression mediation analysis, one model estimates $\beta _{1}$ and its standard error, a second model estimates $\theta _{2}$ and its standard error. One approach to testing for a mediated effect, commonly referred to in the literature as the joint test for mediation, is to evaluate each regression coefficient individually, testing the two hypotheses $H_{01} :\beta _{1} =0 ; H_{02} : \theta _{2} =0$ and rejecting the null of no mediation only if $H_{01}$ and $H_{02}$ are both rejected. A second approach is to combine the separate model estimates for the null hypothesis, H$_{0}$:$\beta _{1} \theta _{2} =0$, which often is tested with the classical Wald test using an approximate delta method standard error [26]. This method includes the Sobel test which is considered an inferior approach [11] thought to perform poorly [1] that ultimately results in an inability to adequately address the proper significance level of a composite hypothesis. Other approaches use numerical integration to obtain the distribution of the product [17, 29], or resampling methods [27, 29] such as bootstrap or permutation [15, 27]. With the multivariate mediation approach proposed here, one can still test mediation with the Wald test of $H_0 :\beta _{1} \theta _{2} =0$, and in addition, a likelihood ratio test of the simultaneous hypothesis $H_0 :\beta _{1} =\theta _{2} =0$, since it is easy to set both $\beta _{1} =0$ and $\theta _{2} =0$ and rerun the multivariate model; then the difference in −2log likelihoods has an approximate chi-squared distribution with 2 degrees of freedom (df). Using the method of two separate regressions, a single −2log likelihood can also be obtained by summing the −2log likelihoods, but the likelihood ratio test would require four regression models to be fit.

A weakness shared by procedures attempting to test $H_0 :\beta _{1} \theta _{2} =0$ is their failure to account for the compositeness of the hypothesis. The composite null hypothesis $H_0 :\beta _{1} \theta _2 =0$ can be decomposed into individual null hypotheses, $H_0 :\beta _{1} =0$ or $H_0 :\theta _{2} =0$ or both $H_0 :\beta _{1} =\theta _2 =0$. The significance level should be the supremum (the largest) of the significance levels for each of the individual null hypotheses [5] or an experiment-wise error rate based on an appropriate multiple comparisons procedure. The general form of the null hypothesis for mediation $\mathrm{NIE}=h_y^{-1} \left\{ 0\right\}$ is also a composite since the argument of NIE, $\Psi =\left( {\theta _{2} +\theta _3 a}\right) \left[ {h_M^{-1} \left\{ {\beta _0 +\beta _{1} a+\beta ^{\prime }_2 c}\right\} -h_M^{-1} \left\{ {\beta _0 +\beta _{1} a^{*}+\beta ^{\prime }_2 c}\right\} } \right] =0$ if $\varphi _a =\theta _{2} +\theta _3 a=0$ or if $\beta _{1} =0$, or if both $\varphi _a =\beta _{1} =0$ and because $\mathrm{NIE}=h_y^{-1} \left\{ \psi \right\}$ is a monotone function of $\psi$. As mentioned earlier, $\psi =0$ may map onto a nonzero NIE, for example, $\mathrm{NIE}=\exp \left\{ 0\right\} =1$.

In the next section, a more ‘honest’ (in the sense of Tukey [30]) significance level is proposed based on a Scheffé -type confidence ellipse [25].

4 Confidence Ellipse

An advantage of the multivariate approach is the simplification in applying a confidence ellipse for the components of the composite null hypothesis under a single experiment-wise type-I error rate. Confidence ellipses and their projections have been used to provide confidence limits for nonlinear functions of parameters (e.g., [19, 36]). Here their use in mediation analysis is a novel application that clarifies and visualizes the components of mediation, without requiring an estimate of the standard error of the product of regression coefficients from different models, or for the NIE which can get complicated when nonidentity links are used. Here, we describe the use of the ellipse using $\beta _{1}$ and $\theta _{2}$, the components of the NIE that correspond to the test for mediation and the corresponding covariance matrix easily estimable from the multivariate approach. In the presence of an interaction, $\varphi _{a}$ is substituted for $\theta _{2}$.

According to Scheffé [25], assuming approximate bivariate normality of $\left( {\hat{{\beta }}_1 ,\hat{{\theta }}_2 } \right)$, an approximate 100 $(1-\alpha )$% confidence ellipse for $\left( \begin{array}{l} {\beta _{1} } \\ {\theta _{2} } \\ \end{array}\right)$ is provided by the set of points satisfying $\left( \begin{array}{l} {\beta _{1} -\hat{{\beta }}_1 } \\ {\theta _2 -\hat{{\theta }}_2 } \\ \end{array}\right) ^{\prime }\left( \begin{array}{ll} {{V}_{11} }&{} {{V}_{12} } \\ {\mathrm{V}_{12} }&{} {{V}_{22} } \\ \end{array}\right) ^{-1}\left( \begin{array}{l} {\beta _{1} -\hat{{\beta }}_1 } \\ {\theta _{2} -\hat{{\theta }}_2 } \\ \end{array}\right) \le 2{F}_{1-\alpha ,2,{v}}$ where the inverse of the variance-covariance matrix of $\left( \begin{array}{l} {\hat{{\beta }}_1 } \\ {\hat{{\theta }}_2 } \\ \end{array} \right)$ is $\left( \begin{array}{ll} {{V}_{11} }&{} {{V}_{12} } \\ {{V}_{12} }&{} {{V}_{22} } \\ \end{array}\right) ^{-1}=\left( \begin{array}{ll} {1/{V}_{11} }&{} 0 \\ 0&{} {1/{V}_{22} } \\ \end{array} \right)$, since $\hat{{\beta }}_1$ and $\hat{{\theta }}_2$ are conditionally independent (on A) for the proposed mediation analysis. $F_{1-\alpha ,2,{v}}$ is the $100(1-\alpha )$ percentage point of an F distribution with 2 and v degrees of freedom.

The projections of the ellipse on the $\beta _{1}$ and $\theta _{2}$ axes are $\beta _{1} =\hat{{\beta }}_1 \pm \sqrt{2\mathrm{F}_{1-\alpha ,2,{v}} }\sqrt{{V}_{11} }$, and $\theta _{2} =\hat{{\theta }}_2 \pm \sqrt{2{F}_{1-\alpha ,2,{v}} }\sqrt{{V}_{22} }$, respectively (see supplementary material). These two simultaneous projections are known as Scheffé’s simultaneous confidence limits for $\beta _{1}$ and $\theta _{2}$, and they define a rectangle that circumscribes the confidence ellipse (Fig. 3a). For a given value of $\beta _{1}$ between $\hat{{\beta }}_1 \pm \sqrt{2{F}_{1-\alpha ,2,{v}} }\sqrt{{V}_{11} }$, there are two solutions for $\theta _{2}$, one each at the minimum and maximum values that make up the border of the rectangle, defined as $\min \left[ {\theta _{2} \,|\,\beta _{1} } \right] =\hat{{\theta }}_2 -\sqrt{2\mathrm{F}_{1-\alpha ,2,{v}} -x^{2}}\sqrt{V_{22} }$ and $\max \left[ {\theta _{2} \,|\,\beta _{1} } \right] =\hat{{\theta }}_2 +\sqrt{2{F}_{1-\alpha ,2,{v}} -x^{2}}\sqrt{V_{22} }$ where $x=\left( {\beta _{1} -\hat{{\beta }}_1 } \right) /\sqrt{{V}_{11} }$. Plot points for the ellipse are determined by evaluating the $\min \left[ {\theta _{2} \,|\,\beta _{1} }\right]$ and $\max \left[ {\theta _{2} \,|\,\beta _{1} }\right]$ for a grid of $\beta _{1}$’s.

The ellipse constrains $\beta _{1}$ and $\theta _{2}$ to be within their simultaneous confidence limits. It also constrains the NIE, a nonlinear function of $\beta _{1}$ and $\theta _{2}$ to be within its simultaneous confidence limits. To determine these confidence limits, we construct a fine grid of $\left( {\beta _{1} ,\theta _{2} } \right)$ points within the ellipse, evaluate NIE at each point, and from these evaluations, determine the minimum and maximum values. See supplementary material for additional detail.

Fig. 2

Conclusions from the 5 possible confidence ellipse scenarios. Note that if $\beta _1 \ne 0$ and $\theta _2 \ne 0$ is concluded (Scenario a), then $\beta _1 \theta _2 \ne 0$ will be concluded, i.e., significant mediation; otherwise (Scenarios b through e), $\beta _1 \theta _2 =0$ will be concluded, i.e., no significant mediation

Figure 2 demonstrates five possible scenarios (a–e) for the ellipse and the conclusions that will ensue for four simultaneous hypothesis tests. The ellipse enables us to state with a single experiment-wise type I error rate, the following simultaneous test results:

• (1) the bivariate hypothesis $\left( {\beta _{1} ,\theta _{2} } \right) =\left( {0,0}\right)$ is rejected if the ellipse fails to cover the origin $\left( {0,0}\right)$, Fig. 2 scenarios a–d

• (2) $\beta _{1}$is declared significant if the simultaneous confidence interval for $\beta _{1}$ (the projection of the ellipse on the $\beta _{1}$ axis) fails to cover 0, scenarios a or c.

• (3) $\theta _{2}$ is declared significant if the simultaneous confidence interval for $\theta _{2}$ (the projection of the ellipse on the $\theta _{2}$ axis) fails to cover 0, scenarios a or b and

• (4) $\psi$ and hence NIE is declared significant if the simultaneous confidence interval for $\psi$ fails to cover 0 or equivalently, NIE on the inverse link scale is declared significant if the confidence interval for NIE fails to cover $h_y^{-1} \left\{ 0\right\}$ (the ellipse fails to cover either axis, scenario a).

To infer that the effect of A on Y passes through the indirect (mediating) path M, one would need to reject the null hypothesis for NIE or simultaneously reject both hypotheses, $\beta _{1} =0$ and $\theta _{2} =0$, by comparing $\hat{{\beta }}_1 /\mathrm{SE}\left( {\hat{{\beta }}_1 }\right)$ and $\hat{{\theta }}_2 /\mathrm{SE}\left( {\hat{{\theta }}_2 }\right)$ with the Scheffé constant $\sqrt{2{F}_{1-\alpha ,2,{v}} }$. In other words, the mediating path is a significant contributor to the effect of A on Y if and only if neither of the confidence interval overlaps zero (scenario a, Fig. 2).

The confidence ellipse avoids Wald tests based on delta method standard errors, clarifies and properly accounts for the compositeness of the null hypothesis $\mathrm{NIE}=h_y^{-1} \left\{ \psi \right\} =h_y^{-1} \left\{ 0\right\}$ (in special cases $\beta _{1} \theta _{2} =0)$ by examination of its components, and requires less computational time than a resampling approach. An interaction can be easily incorporated using the aforementioned relationship between $\varphi _{a}$ with interaction and $\theta _{2}$ without interaction as demonstrated in the example 2 below.

5 Examples

We will consider three special cases motivated by our research. Supplementary material provides the SAS code for these examples, as well as, an additional example not described here where we fail to reject the null hypothesis of no mediation. Mediation analysis should be utilized only after judicious consideration of the four assumptions for determining causality [33]. Such consideration, particularly investigation of all appropriate confounders has not been undertaken here, as our purpose is to use the examples to demonstrate analytic techniques and not to justify causal relationships.

Example 1

Normal Outcome with identity link, Normal Mediator with identity link

This example illustrates the equivalence of the univariate and the multivariate approaches and shows the application of the proposed methods for the important special case where both the mediator and the outcome have an identity link. Data come from a prospective longitudinal cohort study of 35 children with Cystic Fibrosis (CF) between the ages of 6 and 15 studied annually over 3 years [9, 24]. This study includes 28 subjects with baseline biomarker measurements of neutrophilic inflammation (A), visible airway counts from chest computed tomography (CT) scans after 1 year (M) and percent predicted forced expiratory volume in 1 s (FEV1$_\mathrm{pp})$ after 2 years (Y).

Table 1 Estimates and 95% confidence intervals (CI) for the example 1 (normal outcome, identity link; normal mediator, identity link): separate univariate regression model compared to multivariate model approach

Assuming M and Y are normally distributed with identity link functions, the exposure–mediator interaction was nonsignificant based on a likelihood ratio test comparing models with and without the interaction $\left( \chi ^{2}=280.12-278.80=1.32,\right. \left. \mathrm{df}=1,P=\,\,0.25\right)$. Table 1 compares results from the multivariate model with the separate regression models using the available SAS macro created by Valeri and VanderWeele [31]. The standard errors differ slightly due to the use of maximum likelihood versus restricted maximum likelihood for the computations (see Appendix 2 for details).

Tests for the individual components of the composite null hypothesis can be visualized using the confidence ellipse and confidence region. The bivariate hypothesis $\left( {\beta _{1} ,\theta _{2} } \right) =\left( {0,0}\right)$ is rejected since the ellipse excludes the origin $\left( {0,0}\right)$. The likelihood ratio test also rejects the simultaneous null hypothesis that $\beta _{1} =\theta _{2} =0 \left( {\chi ^{2}=300.06-280.12=19.94,\mathrm{df}=2,P<\,\,0.01}\right)$. In addition, both $\beta _{1}$ and $\theta _{2}$ are declared significant since their simultaneous confidence intervals exclude 0 (Fig. 3). Simultaneous confidence intervals based on the confidence ellipse are obtained using estimates from the multivariate approach (Table 2). The delta method from both separate and multivariate regression models, likelihood ratio test, confidence ellipse, and the bootstrap, indicate equivalent inferences: the significant product $\beta _{1} \theta _{2} =\mathrm{NIE}$ is consistent with a mediating effect of airway counts for the association between sputum neutrophil elastase and $\mathrm{FEV}1_{\mathrm{pp}}$. The bootstrap resulted in slightly more conservative confidence intervals compared with the delta method, and the confidence limits from the ellipse are more conservative than the bootstrap; however, only ellipse-based confidence limits are adjusted for the multiple comparisons and are therefore the only values protected from type-I errors (Table 2).

Example 2

Binary outcome with logit link, normal mediator with identity link, exposure–mediator interaction and confounder

This example illustrates the application of the proposed methods when an exposure–mediator interaction is present. In a prospective cohort study of adults with type-1 diabetes and controls [8], participants had two follow-up visits over 6  years to measure progression of coronary artery calcium (CAC), a subclinical marker of atherosclerosis and cardiovascular disease. It was hypothesized that log albumin creatinine ratio (M), a measure of kidney function, at least partially mediates the relationship between diabetes (A) and the presence of CAC progression upon follow-up (Y). Age was included as a confounder. The sample consisted of 1416 participants, 270 had missing values for either the exposure or the confounder and were therefore not included in the analysis, resulting in 1146 subjects for inclusion. Of these subjects, 145 had missing CAC progression values, and the following analysis includes those with missing outcomes and assumes they are missing at random.

Fig. 3

Simultaneous 95% confidence limits for $\beta _1$ and $\theta _2$ based on 95% confidence ellipse for the example 1 (normal outcome with identity link; normal mediator with identity link). The ellipse (gray hashed line) does not cover the origin, and the confidence intervals (black solid lines) do not contain 0, indicating the significance of the simultaneous test for $\beta _1 =\theta _2 =0$, and the individual tests for $\beta _1$ and $\theta _2$

Table 2 Comparison of estimates and inferences across various methods for the example 1

Table 3 Estimates and 95% confidence intervals (CI) for the example 2 (binary outcome, logit link; normal mediator, identity link) from multivariate model

The exposure–mediator interaction was significant based on a likelihood ratio test comparing models with and without the interaction $\left( \chi ^{2}=\,\,2374.28-2367.73=\right. \left. 6.55,\mathrm{df}=1,P=0.01\right)$. The effect of the mediator is significant $\left( {P<0.01}\right)$ for diabetics, and not significant (P = 0.70) for controls (Table 3). Tests for the individual components of the composite null hypothesis at a specified exposure level can be visualized using the confidence ellipse and the confidence region (Fig. 4). For diabetics $\left( {a=0}\right)$, the bivariate hypothesis $\left( {\beta _{1} ,\varphi _0 } \right) =\left( {0,0}\right)$ is rejected, the hypothesis $\beta _{1} =0$ is rejected, the hypothesis $\varphi _0 =0$ is rejected, and the hypothesis $\beta _{1} \varphi _0 =0$ is rejected since the ellipse excludes the origin $\left( {0,0}\right)$ and crosses neither axis (scenario a in Fig. 2). All results have a single experiment-wise 0.05 significance level. For controls $\left( {a=1}\right)$, hypothesis $\left( {\beta _{1} ,\varphi _1 }\right) =\left( {0,0} \right)$ is rejected, the hypothesis $\beta _{1} =0$ is not rejected, the hypothesis $\varphi _1 =0$ is rejected, and the hypothesis $\beta _{1} ,\varphi _1 =0$ is not rejected since the ellipse for $\left( {\beta _{1} ,\varphi _1 }\right)$ excludes the origin but crosses the $\beta _{1}$ axis (scenario c in Fig. 2). Again, all these results have a single experiment-wise 0.05 significance level. The simultaneous confidence intervals based on the confidence ellipse are obtained using estimates from the multivariate approach (Table 4). This suggests the effect of type-1 diabetes on subclinical cardiovascular disease is partially mediated through loss of kidney function. Furthermore, this loss of kidney function path does not appear important in people without type-1 diabetes. Likelihood ratio tests reject the simultaneous null hypothesis that $\beta _{1} =\upphi _0 =0 \left( {\chi ^{2}=193.2, \mathrm{df}=2, P<0.01}\right)$ for diabetics and also reject the null hypothesis $\beta _{1} =\upphi _1 =0$ for non-diabetics $\left( {\chi ^{2}=153.4, \mathrm{df}=2, P<0.01}\right)$.

Example 3

Negative binomial Outcome and Mediator both with log links

Fig. 4

Simultaneous 95% confidence limits for $\beta _1$ and $\varphi (a)$ based on 95% confidence ellipse from the example 3 (binary outcome with logit link; normal mediator with identity link; exposure–mediator interaction; confounder). Ellipses for diabetics (left) and for non-diabetics (right) are provided. For diabetics, the ellipse excludes the origin and crosses neither axis (scenario a). Hence, we conclude $\left( {\beta _1 ,\varphi _0 } \right) \ne \left( {0,0} \right)$, $\beta _1 \ne 0$, $\varphi _0 \ne 0$ and $\beta _1 \varphi _0 \ne 0$ all at the single experiment-wise significance level 0.05. For non-diabetics, the ellipse excludes the origin and crosses only the $\beta _1$ axis (scenario c). Hence, we conclude $\left( {\beta _1 ,\varphi _1 } \right) \ne \left( {0,0} \right)$, $\beta _1 \ne 0$, $\varphi _1 =0$, and $\beta _1 \varphi _1 =0$ all at the single experiment-wise significance level 0.05

Table 4 Simultaneous 95% confidence limits for $\beta _1$, $\varphi (a)$, and their product $\beta _1 \varphi (a)$ from the binary-normal example 2 based on 95% confidence ellipse

We use this example to illustrate (1) the calculation of the counterfactuals using the general equations for a combination of distributions and link functions that have not previously been reported and (2) that the confidence ellipse, which applies a simultaneous significance level for a composite hypothesis results in different inferences compared to other methods that ignore the compositeness of the mediation hypothesis. Conduct disorder is the most common disorder associated with substance dependence in adolescents [4, 7] and evidence suggests that having both attention-deficit hyperactivity disorder (ADHD) and conduct disorder increases the risk and severity of substance dependence in adolescence [7, 28]. In adolescent patients with ADHD and substance-use disorders who completed a 16-week multisite pharmacotherapy trial [22], we evaluated whether the relationship between having a past year conduct disorder diagnosis at baseline (A) and number of days cannabis was used during treatment (Y) is mediated by pretreatment drug use (i.e., proportion of days nontobacco substances were used in the month prior to treatment (M)). Of these 227 patients, 73 (32%) had a conduct disorder diagnosis at baseline. Y and M are both assumed to have negative binomial distributions, and an offset is included to adjust for variations in the observation times for Y.

Table 5 Estimates and 95% confidence intervals (CI) for example 3 (negative binomial outcome and mediator, log link)

Table 6 Comparison of estimates and inferences across various methods for the example 3

Fig. 5

Simultaneous 95% confidence limits for $\beta _1$ and $\theta _2$ based on 95% confidence ellipse from the example 3. The ellipse (grey hashed line) and the confidence intervals (black solid lines) cross the $\theta _2$ axis indicating the lack of significance for the joint test for $\beta _1$ and $\theta _2$, and the individual test for $\beta _1$

The exposure–mediator interaction was nonsignificant based on a likelihood ratio test $\left( {\chi ^{2}=\,\,4595.38-4593.68=1.70,\mathrm{df}=1, P=0.19}\right)$. Table 5 reports parameter estimates and their standard errors. The NIE and TE depend on a* which is set equal to 0. Using the delta method approach, the mediator is significantly associated with exposure $({\beta }_1 =0.21, P=0.03)$. The outcome remains significantly associated with exposure ($\theta _{1}=0.43$, $P<0.01$) and is significantly associated with the mediator $({\theta }_2 =0.06, P<0.01)$. The likelihood ratio test comparing the $\left( {\beta _{1} ,\theta _{2} }\right) =\left( {0,0}\right)$ is rejected $\left( {\chi ^{2}=\,\,4667.6-4595.4=72.2,\mathrm{df}=2,P<0.01} \right)$. The NIE is significant $\left( {\mathrm{NIE}=h_y^{-1} \left\{ \psi \right\} =\mathrm{1}.\mathrm{2}0,\psi =0.18}\right)$ using the bootstrap (Table 6). This suggests that the relationship between having a conduct disorder diagnosis and marijuana use during treatment is partially mediated by pretreatment drug use. Results based on the confidence ellipse of $\beta _{1}$ and $\theta _{2}$ disagree, however, as the test for $\beta _{1}= 0$ was not rejected (Fig. 5) and the confidence interval for NIE includes 1 (Table 6). With this example, different inferences would have been made using the different testing approaches, the likelihood ratio test is only testing the bivariate hypothesis and therefore agrees with the confidence ellipse (scenario b Fig. 2). The bootstrap test for the NIE, however, does not result in the same inference as the confidence ellipse yet the confidence ellipse is the only method that is properly accounting for the compositeness of the null hypothesis for testing mediation and incorporates all components.

6 Discussion

The multivariate method outlined in this paper describes a unifying framework for the regression approach to mediation analysis. This allows for the estimation of counterfactual effects in the presence of an exposure–mediator interaction for any combination of outcome and mediator variables having the same or different distributions from the exponential family and the same or different link functions. In the absence of interaction, there are a variety of methods available for estimating the standard errors and/or confidence intervals for the NIE, including the delta method approximation to the standard error of the product $\beta _{1} \theta _2$. Alternatively, confidence intervals may be obtained using bootstrap or bias-corrected bootstrap, permutation, or the true distribution of the product [11, 27, 29]. To the best of our knowledge, only the delta method approximation or bootstrap has been applied to mediation analyses in the presence of an interaction [31]. These approaches, however, are not without fault [10, 13, 16, 33], and confidence limits based on them are often inaccurate [17]. In lieu of the questionable Wald test, or the computationally intensive bootstrap approach, the multivariate approach estimates all relevant parameters in a single model and can simultaneously test the regression coefficients of interest with a likelihood ratio test that avoids estimation of the standard error of the product.

In the absence of interaction, it is seldom mentioned that the mediation hypothesis of interest $H_0 :\beta _{1} \theta _{2} =0$ is really a composite null hypothesis with individual components, $H_{01} :\beta _{1} =0$ or $H_{02} :\theta _{2} =0$ or both $H_{03} :\beta _{1} =\theta _{2} =0$. The significance level should then be the supremum of the significance levels for each of the individual null hypotheses or an experiment-wise error rate based on an appropriate multiple comparisons procedure. In this work, we chose the latter approach and propose a novel confidence ellipse approach to visualize and to clarify the components of mediation analysis while simultaneously testing the four null hypotheses, $H_{01} :\beta _{1} =0$, $H_{02} :\theta _{2} =0$, both $H_{03} :\beta _{1} =\theta _{2} =0$, and the product $H_{04} :\beta _{1} \theta _{2} =0$ (or more generally, the NIE) with a single experiment-wise type I error rate. Proper control of the experiment-wise error rate makes this confidence ellipse approach necessarily more conservative than approaches that naively ignore the compositeness of the null hypothesis [5]. For the case where there is an interaction, we substitute $\varphi _{a}$ for $\theta _{2}$ to examine mediation when $A=a$.

Here, we provide derivations for the estimation of the counterfactual effects for any combination of generalized linear regression models. In the particular case where $f\left( {y\,|\,m,a,c} \right)$ is binary with a logit link, $h_Y \left\{ {E\left[ {Y\,|\,a,m,c}\right] }\right\}$, and $f\left( {m\,|\,a,c}\right)$ is normal with an identity link, we have the logistic mediation scenario described previously [34]. Then on the logit, or equivalently, log(odds ratio) scale, CDE, PIE, and TE are easily derived using the more general equations provided here. Alternate formulas for CDE and TE have been provided for case–control studies where the binary outcome is rare such that the odds ratio is an approximation to the relative risk [31]. The suggested use of a binomial distribution with a log link function to obtain the correct interpretation [31] is also encompassed under the generalized framework proposed here.

The likelihood ratio test is currently available under the SEM framework using specialized packages (Mplus and PROC CALIS) or in Marginal Structural Models [6]. The SEM approach to mediation can be more difficult to implement for nonnormal outcomes, in part due to the use of specialized software. In addition, despite the advantages of the likelihood ratio test, confidence limits may be preferred as they provide a range of magnitudes for each parameter in addition to statistical significance. The confidence ellipse represents a novel application to mediation, addressing the compositeness of the null hypothesis.

Appendices

Appendix 1: Derivation of Counterfactual effects for the Generalized Linear Model

Note that many of these effects depend on the chosen values ${A}={a}*$, or ${M}={m}*$, or both.

Recall that

$$\begin{aligned}&{h}_{M} \left\{ {{E}\left[ {{M|a,c}} \right] } \right\} =\beta _0 +\beta _1 a+{\beta }'_2 c\,\mathrm{and}\\&{h}_{Y} \left\{ {{E}\left[ {{Y|a,m,c}} \right] } \right\} =\theta _0 +\theta _1 a+\theta _2 m+\theta _3 am+{\theta }'_4 c \\&\quad =\theta _0 +\theta _1 a+\left( {\theta _2 +\theta _3 a} \right) m+{\theta }'_4 c \\&\quad =\theta _0 +\theta _1 a+\varphi _a m+{\theta }'_4 c, \end{aligned}$$

where $\varphi _a =\theta _2 +\theta _3 a$ denotes the effect of M when $A=a$, c is a vector of covariates, and ${\beta }'_2$ and ${\theta }'_4$ are vectors of regression coefficients.

Note: If the two c’s from M and Y are not the same, we would have to condition on their union.

Controlled Direct Effect defined on the scale of the outcome (inverse link)

$$\begin{aligned} \mathrm{CDE}= & {} h_Y^{-1} \left[ {h_Y \left\{ {E\left[ {Y\,|\,a,m,c} \right] } \right\} -h_Y \left\{ {E\left[ {Y\,|\,a^{*},m,c} \right] } \right\} } \right] \\= & {} h_Y^{-1} \left[ {\left( {\theta _0 +\theta _1 a+\theta _2 m+\theta _3 am+{\theta }'_4 c} \right) -\left( {\theta _0 +\theta _1 a^{*}+\theta _2 m+\theta _3 a^{*}m+{\theta }'_4 c} \right) } \right] \\= & {} h_Y^{-1} \left[ {\left( {\theta _1 +\theta _3 m} \right) \left( {a-a^{*}} \right) } \right] , \end{aligned}$$

where $h_Y^{-1} \left\{ \right\}$ denotes the inverse function of $h_Y \left\{ \right\}$ and m is set to a specified value.

Natural direct effect evaluated at $M=m_\mathrm{a}^{*}$

$$\begin{aligned} \mathrm{NDE}= & {} h_Y^{-1} \left[ {h_Y \left\{ {E\left[ {Y\,|\,a,m_{a^{*}} ,c} \right] } \right\} -h_Y \left\{ {E\left[ {Y\,|\,a^{*},m_{a^{*}} ,c} \right] } \right\} } \right] \\= & {} h_Y^{-1} \left[ \left( {\theta _0 +\theta _1 a+\theta _2 m_{a^{*}} +\theta _3 am_{a^{*}} +\theta _4^{\prime } c} \right) \right. \\&\left. -\left( {\theta _0 +\theta _1 a^{*}+\theta _2 m_{a^{*}} +\theta _3 a^{*}m_{a^{*}} +\theta _4^{\prime } c} \right) \right] \\= & {} h_y^{-1} \left[ {\theta _1 \left( {a-a^{*}} \right) +\theta _3 m_{a^{*}} \left( {a-a^{*}} \right) } \right] \\= & {} h_y^{-1} \left[ {\left( {\theta _1 +\theta _3 m_{a^{*}}}\right) \left( {a-a^{*}} \right) } \right] \\= & {} h_y^{-1} \left[ {\left[ {\theta _1 +\theta _3 h_M^{-1} \left\{ {\beta _0 +\beta _1 a^{*}+\beta ^{\prime }_2 c} \right\} } \right] \left( {a-a^{*}} \right) } \right] , \end{aligned}$$

where $m_{a^{*}} =\mathrm{E}\left[ {\mathrm{M\,|\,a}^{\mathrm{*}}\mathrm{,c}} \right] =h_M^{-1} \left\{ {\beta _0 +\beta _1 a^{*}+{\beta }'_2 c} \right\}$.

Natural indirect effect

$$\begin{aligned} \mathrm{NIE}= & {} h_y^{-1} \left[ {h_Y \left\{ {E\left[ {Y\,|\,a,m_a ,c} \right] } \right\} -h_Y \left\{ {E\left[ {Y\,|\,a,m_{a^{*}} ,c} \right] } \right\} } \right] \\= & {} h_y^{-1} \left[ \left( {\theta _0 +\theta _1 a+\theta _2 m_a +\theta _3 am_a +\theta ^{\prime }_4 c} \right) \right. \\&\left. -\left( {\theta _0 +\theta _1 a+\theta _2 m_{a^{*}} +\theta _3 am_{a^{*}} +\theta ^{\prime }_4 c} \right) \right] \\= & {} h_y^{-1} \left[ {\left( {\theta _2 +\theta _3 a} \right) \left( {m_a -m_{a^{*}}}\right) } \right] \\= & {} h_y^{-1} \left[ {\left( {\theta _2 +\theta _3 a} \right) \left( {h_M^{-1} \left\{ {\beta _0 +\beta _1 a+{\beta }'_2 c} \right\} -h_M^{-1} \left\{ {\beta _0 +\beta _1 a^{*}+{\beta }'_2 c} \right\} } \right) } \right] \\= & {} h_y^{-1} \left[ {\varphi _a \left( {h_M^{-1} \left\{ {\beta _0 +\beta _1 a+{\beta }'_2 c} \right\} -h_M^{-1} \left\{ {\beta _0 +\beta _1 a^{*}+{\beta }'_2 c} \right\} } \right) } \right] , \end{aligned}$$

where $m_a =h_M^{-1} \left\{ {\beta _0 +\beta _1 a+{\beta }'_2 c} \right\}$,$m_{a^{*}} =h_M^{-1} \left\{ {\beta _0 +\beta _1 a^{*}+{\beta }'_2 c} \right\}$ and a is set to a specified value when $\theta _3 \ne 0$.

Total effect

$$\begin{aligned} \mathrm{TE}=\mathrm{NIE}+\mathrm{NDE} \end{aligned}$$

We propose that NIE be used to evaluate whether mediation is present. If there is an interaction, a in $\varphi _a =\theta _2 +\theta _3 a$ must be specified. If A is dichotomous (say $A=1$ for males and $A=0$ for females), then $\mathrm{NIE}\left( 1 \right)$ could estimate mediation for males and $\mathrm{NIE}\left( 0 \right)$ for females. If A is continuous, a might be chosen as the mean value of A.

If there is no interaction between the mediator and the exposure (i.e., $\theta _3 =0)$ and $\varphi _a =\theta _2$, then the counterfactuals simplify as follows

$$\begin{aligned}&\mathrm{CDE}=\mathrm{NDE}=h_Y^{-1} \left\{ {\theta _1 \left( {a-a^{*}} \right) } \right\} \,\,\mathrm{and}\\&\mathrm{NIE}=h_y^{-1} \left\{ {\theta _2 \left[ {h_M^{-1} \left\{ {\beta _0 +\beta _1 a+\beta ^{\prime }_2 c} \right\} -h_M^{-1} \left\{ {\beta _0 +\beta _1 a^{*}+\beta ^{\prime }_2 c} \right\} } \right] } \right\} . \end{aligned}$$

If the outcome and the mediator have identity links, such that ${E}\left[ {{Y|a,m,c}} \right] =\theta _0 +\theta _1 a+\theta _2 m+\theta _3 am+{\theta }'_4 c$ and ${E}\left[ {{M|a,c}} \right] =\beta _0 +\beta _1 a+{\beta }'_2 c$, then

$$\begin{aligned} \mathrm{CDE}&=\left( {\theta _1 +\theta _3 m} \right) \left( {a-a^{*}} \right) \\ \mathrm{NDE}&=\left( {\theta _1 +\theta _3}\right) \left( {\beta _0 +\beta _1 a^{*}+\beta ^{\prime }_2 c} \right) \left( {a-a^{*}} \right) \\ \mathrm{NIE}&=\left( {\theta _2 +\theta _3 a} \right) \beta _1 (a-a^{*})\\&=\varphi _a \beta _1 (a-a^{*}) \end{aligned}$$

as reported by Valeri and VanderWeele [31]. In this case, we propose that in the absence of an interaction, $\beta _1 \theta _2$, and in the presence of an interaction, $\beta _1 \varphi _a$, be used to evaluate whether mediation is present when $A=a$.

For the case where the outcome is binary and fit using a logistic regression, Valeri and VanderWeele [31] calculate the direct and indirect effect odds ratios. These can be derived from the estimates provided above as follows:

$$\begin{aligned}&\mathrm{OR}^\mathrm{CDE}=\exp \left\{ {\left( {\theta _1 +\theta _3 m} \right) \left( {a-a^{*}} \right) } \right\} ,\\&\mathrm{OR}^\mathrm{NDE}=\exp \left\{ {\left[ {\left( {\theta _1 +\theta _3}\right) h_M^{-1} \left\{ {\beta _0 +\beta _1 a^{*}+\beta ^ {\prime }_2 c} \right\} } \right] \left( {a-a^{*}} \right) } \right\} \,\,\mathrm{and}\\&\mathrm{OR}^\mathrm{NIE}=\exp \left\{ {\left( {\theta _2 +\theta _3 a} \right) \left[ {h_M^{-1} \left\{ {\beta _0 +\beta _1 a+\beta ^ {\prime }_2 c} \right\} -h_M^{-1} \left\{ {\beta _0 +\beta _1 a^{*}+\beta ^{\prime }_2 c} \right\} } \right] } \right\} . \end{aligned}$$

Appendix 2: Comparison of the Standard Errors Computed from the Multivariate Approach Implemented in NLMIXED and the Classical Separate Univariate Regression Method Used in the SAS Macro Provided by Valeri and VanderWeele [31]

Most regression programs, including REG and GENMOD used in SAS Macro provided by Valeri and VanderWeele [31], compute restricted maximum likelihood (REML) estimates of the residual variances of the regressions of M on A and Y on A and M, MSE$_{1}$ and MSE$_{2}$, respectively. Instead, NLMIXED computes maximum likelihood (ML) estimates $S_{11 }$ and $S_{22 }$ such that MSE$_{1}=n S_{11}/(n-2)$, and MSE$_{2}=n S_{22}/(n-3)$, where n is the number of subjects. The same proportionality will hold for variances of the regression coefficients. For example, $\mathrm{SE}_\mathrm{REML} \left( {\hat{{\theta }}_2}\right) =\mathrm{SE}_\mathrm{ML} \left( {\hat{{\theta }}_2 } \right) \sqrt{\frac{\mathrm{n}}{\mathrm{n}-3}}$, and $\mathrm{SE}_\mathrm{REML} \left( {\hat{{\beta }}_1}\right) =\mathrm{SE}_\mathrm{ML} \left( {\hat{{\beta }}_1}\right) \sqrt{\frac{{n}}{n-2}}$.