Two-way Concept-Cognitive Learning with Multi-source Fuzzy Context

Abstract

Concepts learning is the most fundamental unit in the process of human cognition in philosophy. Granularity is one of the fundamental concepts of human cognition. The combination of granular computing and concept learning is critical in the cognitive process. Meanwhile, efficiently and accurately using the information collected from different sources is the focus of data mining in the contemporary. Hence, how to sufficiently learn concepts under a multi-sources context is an essential concern in the field of cognition. This paper offers a new thought for two-way concept-cognitive learning based on granular computing in multi-source fuzzy decision tables. Firstly, based on the best possible guarantee of the classification ability, original information from different sources is fused by conditional entropy, which is the kind of multi-source fusion method (i.e., CE-fusion). Secondly, we learn concepts from a given object set, attribute set, or pair of object and attribute sets in the fused information table, and these three types of concept learning algorithms are designed. This analysis shows that two-way concept learning based on multi-source information fusion is a suitable method of multi-source concept learning. Some examples are valuable for applying these theories to deal with practical issues. Our work will provide a convenient novel tool for researching concept-cognitive learning methods with multi-source fuzzy context.

Introduction

The basic concept and scientific methodology of cognitive science are built on modern scientific analysis and engineering experiments to study cognition and intelligence. Up to now, cognitive computing has been viewed as the development of computer systems modeled on the human brain. As is well known, concepts are the most fundamental units of human cognition, and concept learning is the most fundamental unit in the process of human cognition in philosophy [1, 2]. The critical mission of conceptual knowledge presenting and processing is to obtain exact and accurate concepts from various aspects. Concept-cognitive learning (CCL), the idea of cognitive through concept formation and learning to reveal the systematic law of the human brain, is an effective cognitive mechanism [1, 3,4,5]. It should be noted that CCL will be an essential viewpoint for us to carry out cognitive science research in the current article.

As an emerging paradigm of intelligent computing methodologies, cognitive computing has the characteristic of integrating past experiences into itself. So it is a beneficial idea to learn concepts from the cognitive viewpoint. Note that concepts can be characterized by their extent and intent, which can be determined by each other [6,7,8]. The extent of the concept is the scope of application, which the object set can express that the concept denotes. The intent of concept is the unique attribute reflected by the concept, which the attribute can express a set that a concept connotes [8,9,10]. So concepts can be learned from two aspects of intent and extent. As an emerging paradigm of intelligent computing methodologies, cognitive computing has the characteristic of integrating past experiences into itself [3, 11, 12]. So it is a good idea to learn concepts from the cognitive viewpoint. Now, concept-cognitive learning, as the development of computer systems modeled on the human brain, is widely concerned [1, 13,14,15]. Note that authors [5, 16] firstly investigated learning concepts from the unknown through a pair of cognitive operators (i.e., extent-intent and intent-extent) to simulate human thought processes. Hence, two-way learning has become the primary method and theory basis for learning the concept from the multi-source information table in this paper.

Currently, big data has opened up a whole new era for cognitive science [17, 18]. As an essential basis to support cognitive science, data and knowledge fusion driven is related to the formulation of man-machine intelligence. One of the most urgent things is how to use data from different sources to discover effective knowledge. The deficiency of the single data can be made up via integrating data from different sources to achieve the mutual complement and confirmation of a variety of data sources. The means of multi-source fusion expand the application range of data and improve the accuracy of the analysis. Therefore, taking full advantage of multi-source information is crucial to learn concepts and knowledge. This paper emphasizes the concept-cognitive learning of multi-source fuzzy decision tables. It is also important to note that effective concepts may not be learned through existing concept learning methods in a single decision table. Thus, concept learning under multi-source information is worth paying attention to.

From a philosophical viewpoint, granular computing (GrC) is a structured way of thinking. From the application viewpoint, GrC is a general method for solving structured problems. From the calculation viewpoint, GrC is a typical method of information processing. At present, there are many studies on granular computing in references  [19,20,21,22]. Information granules are formalized in many different ways. They can be expressed in terms of the set, fuzzy set, rough set, formal concept, etc. Formal concept analysis (FCA) first proposed by Wille [8] is a popular human-centered tool for knowledge discovery, data mining, and bi-clustering and has widely been applied to lots of fields [14, 15, 23]. Note that these certain concept structures or lattices establish rigorous mathematical models and provide a formal semantics for data analysis in practice [24, 25]. In other words, meanings of real-world, concrete entities can be represented, and these certain concept structures can embody the semantics of abstract subjects. All in all, learning concepts (sometimes including their corresponding structure) have been investigated from various aspects. In addition, considering the computational complexity and the uncertainty of concept learning in multi-source decision tables, this paper focuses on two-way concept-cognitive learning with multi-source information fusion by granular computing.

Fig. 1

Block diagram of steps of the proposed approach

We proposed a two-way concept-cognitive learning approach to learn fuzzy concept from multi-source fuzzy decision tables. The block diagram of steps of the proposed approach is shown in Fig. 1. The main contributions of this paper are as follows:

• 1. We discuss a new thought of concept learning based on the multi-source decision table by connecting two-way learning, granular computing to multi-source information fusion theory. Furthermore, it attempts to construct a new concept learning method from a multi-source information fusion.

• 2. To take full advantage of multi-source information to learn concepts, we build two kinds of multi-source fuzzy decision fusion mechanisms, including conditional entropy fusion and mean-fusion. Moreover, some examples are used to verify the effectiveness of the two fusion mechanisms.

• 3. Compared with other CCL models, the two-way concept-cognitive learning method emphasizes learning concepts from clues. Therefore, the mechanic two-way concept-cognitive learning for given specific tasks or cues is more advantageous than the current many CCL model.

The remainder of this paper is organized as follows. The “Preliminaries” section briefly reviews some basic notions about granule computing and formal concept analysis. The “Two-way Concept-Cognitive Learning” section discusses a cognitive concept mechanism of transforming any information granule into a sufficient and necessary information granule. The definition of the multi-source fuzzy decision table and multi-source fusion is constructed to learn the concept based on entropy theory in the “Concept Learning in Multi-source Fuzzy Decision Tables” section. Furthermore, the “Conclusions” section concluded with a discussion for further work.

Preliminaries

This section briefly reviews some basic notions related to (1) fuzzy set, (2) an uncertainly measure in the rough set, and (3) fuzzy formal context. More detailed descriptions can reference the literatures [6, 26,27,28].

Fuzzy Set

Fuzzy set first proposed by Zadeh [28] attaches great importance to the idea of partial membership, which departs from the dichotomy. Fuzzy set theory is a generalization of the classical set theory. Let U be a nonempty finite set, and a fuzzy set $\tilde{X}$ of U can be expressed as:

$$\begin{aligned} \tilde{X}=\{<x,\mu _{\tilde{X}}(x)>| x \in U\}, \end{aligned}$$

where $\mu _{\tilde{X}}(x)$: $U\rightarrow [0, 1]$, $\mu _{\tilde{X}}(x)$ is called the membership degree of the object $x \in U$ with respect to $\tilde{X}$. Let $\mathscr {F}(U)$ customarily denote all fuzzy sets in the universe U. Given two fuzzy sets $\tilde{X}_{1}$, $\tilde{X}_{2} \in \mathscr {F}(U)$, for any $x \in U$, $\mu _{\tilde{X}_{1}}(x)\le \mu _{\tilde{X}_{2}}(x)$ if and only if $\tilde{X}_{1} \subseteq \tilde{X}_{2}$; $\mu _{\tilde{X}_{1}}(x)= \mu _{\tilde{X}_{2}}(x)$ if and only if $\tilde{X}_{1} \subseteq \tilde{X}_{2}$ and $\tilde{X}_{2}\subseteq \tilde{X}_{1}$. Let $\thicksim \tilde{X}$ represent the complement set of $\tilde{X}$, $\tilde{X}_{1}\cap \tilde{X}_{2}$ represents the intersection of $\tilde{X}_{1}$ and $\tilde{X}_{2}$, and $\tilde{X}_{1}\cup \tilde{X}_{2}$ represents the union of $\tilde{X}_{1}$ and $\tilde{X}_{2}$, and specific expressions are as follows:

$$\begin{aligned} \begin{array}{c} \thicksim \tilde{X}=\{<x,1-\mu _{\tilde{X}}(x)>| x \in U\}, \\ \tilde{X}_{1}\cap \tilde{X}_{2}=\{<x,\wedge \{\mu _{\tilde{X}_{1}}(x),\mu _{\tilde{X}_{2}}(x)\}>| x \in U\}, \\ \tilde{X}_{1}\cup \tilde{X}_{2}=\{<x,\vee \{\mu _{\tilde{X}_{1}}(x),\mu _{\tilde{X}_{2}}(x)\}>| x \in U\}. \end{array} \end{aligned}$$

A decision system is a quadruple $I=(U,A,V,f)$, where U is a nonempty finite universe; $A=C\cup D$ is the union of condition attribute set C and decision attribute set D, and $C\cap D=\emptyset$; V is the union of attribute domains, i.e., $V=\cup _{a\in A}V_{a}$; $f:U\times A \rightarrow V$ is an information function, i.e., $\forall a\in A$, $x\in U$, that $f(x,a)\in V_{a}$, where f(x, a) is the value of the object x under the attribute a. Generally, let $D=\{d\}$. Particularly, if the value range of V is from 0 to 1, then the decision system $I=(U,A,V,f)$ is called a fuzzy decision system which can be denoted by $\tilde{I}=(U,A,V,f)$.

An Uncertainty Measure in Rough Set

Rough set is one of effective mathematical tools for data analysis and knowledge discovery. Let U be a nonempty finite universe and R be an equivalence relation of $U\times U$. The equivalence relation R induces a partition of U, denoted by $U/R=\{[x]_{R}|x\in U\}$, where $[x]_{R}$ represents the equivalence class of x with regard to R. Then, (U, R) is called the Pawlak approximation space. For an arbitrary subset X of U, the lower and upper approximations of X are defined as follows:

$$\begin{aligned} \begin{array}{l} \overline{R}(X)=\{x\in U|[x]_{R}\cap X\ne \emptyset \}=\cup \{[x]_{R}|[x]_{R}\cap X\ne \emptyset \}, \\ \underline{R}(X)=\{x\in U|[x]_{R}\subseteq X\}=\cup \{[x]_{R}|[x]_{R}\subseteq X\}. \end{array} \end{aligned}$$

And $pos(X)=\underline{R}(X), neg(X)=\sim \overline{R}(X), \;bnd(X)=\overline{R}(X)-\underline{R}(X)$ are called the positive region, negative region, and boundary region of X, respectively. Objects definitely and not definitely contained in the set X form positive region pos(X) and negative region neg(X). Objects that may be contained in the set X constitute boundary region bnd(X).

The uncertainty measure is an important direction in rough set theory. The approximation precision proposed by Pawlak raised the proportion of correct classification by a equivalence relation. Let $I=(U,A,V,f)$ be a decision system and $U/D=\{D_{1},D_{2},\cdots , D_{m}\}$ be a classification of universe U. For an arbitrary attribute subset R of C, the R-lower and R-upper approximations of U/D are defined as

$$\begin{aligned} \underline{R}(U/D)=\underline{R}(D_{1}) \cup \underline{R}(D_{2}) \cup \cdots \cup \underline{R}(D_{m}), \end{aligned}$$

$$\begin{aligned} \overline{R}(U/D)=\overline{R}(D_{1}) \cup \overline{R}(D_{2}) \cup \cdots \cup \overline{R}(D_{m}). \end{aligned}$$

The approximation precision and the corresponding approximation roughness of U/D by R are defined as

$$\begin{aligned} \alpha _{R}(U/D)=\frac{\sum _{Y_{i}\in U/D}|\underline{R}(Y_{i})|}{\sum _{Y_{i}\in U/D}|\overline{R}(Y_{i})|}, \end{aligned}$$

$$\begin{aligned} Roughness_{R}(U/D)=1-\alpha _{R}(U/D). \end{aligned}$$

Fuzzy Formal Context

Formal concept analysis (FCA) proposed by Wille [8] provides comprehensive knowledge about a dataset called a formal context. The formal context is a triplet of an object set, an attribute set, and an information function about objects and attributes whose domain consists of 0 and 1. The formal context is fuzzy when the domain is the natural interval [0, 1]. Therefore, fuzzy information systems can be analyzed from the perspective of formal contexts. That is to say, fuzzy formal context is a triple $(U,A,\tilde{I})$, where $U=\{x_{1},x_{2},\cdots ,x_{n}\}$ is an object set and $A=\{a_{1},a_{2},\cdots ,a_{m}\}$ is an attribute set and $\tilde{I}$ is a fuzzy binary relation from U to A, $\tilde{I}=\{<(x,a),\mu _{\tilde{I}}(x,a)>|(x,a) \in U\times A\}$, $\mu _{\tilde{I}}(x,a): U\times A \rightarrow [0, 1]$.

The cognitive mechanism of forming concepts can be described as follows. Let X($X\subseteq U$) be an object set and B($B\subseteq A$) be an attribute set. A pair of operators firstly be defined, namely

$$\begin{aligned} X^{*}=\tilde{A}=\{<a,\mu _{\tilde{I}}(x)>| a \in A\}, \end{aligned}$$

$$\begin{aligned} \tilde{B}^{*}=\{x \in U | \tilde{I}(x,b) \ge \tilde{B}(b),b \in B\}. \end{aligned}$$

where $\tilde{A}(a)=\bigwedge _{x\in X}\mu _{\tilde{I}}(x,a)$, $\tilde{I}(x,b)= \mu _{\tilde{I}}(x,b)\in \nu$ and $\nu =\{\tilde{I}(x,a), x\in U, a \in A\}$. Particularly, we rule $\emptyset ^{*}=\tilde{A}=\{<a,0>| a \in A\}$. From the perspective of philosophy, a concept consists of two parts: extent Y which is a set of objects and intent C which is a set of attributes. In general, the more objects a concept denotes, the less attributes it connotes, and vice versa. That is to say, $X_{1}\subseteq X_{2}\Rightarrow X_{2}^{*}\subseteq X_{1}^{*}$ and $\tilde{B_{1}}\subseteq \tilde{B_{2}}\Rightarrow \tilde{B_{2}}^{*}\subseteq \tilde{B_{1}}^{*}$, where $X_{1}^{*}$ and $X_{1}^{*}$ denote the corresponding intents of $X_{1}$ and $X_{2}$ and $\tilde{B_{1}}^{*}$ and $\tilde{B_{1}}^{*}$ denote the corresponding extents of $\tilde{B_{1}}$ and $\tilde{B_{2}}$. From the perspective of cognitive psychology, the perception of the whole is more than the integration of perceptions of its parts. That is to say, $(X_{1}\cup X_{2})^{*}\supseteq X_{1}^{*}\cap X_{2}^{*}$ and $(\tilde{B_{1}}\cup \tilde{B_{2}})^{*}\supseteq \tilde{B_{1}}^{*}\cap \tilde{B_{2}}^{*}$. Moreover, the above two operators have the following properties:

• 1. $X_{1}\subseteq X_{2} \Rightarrow X_{2}^{*}\subseteq X_{1}^{*}$, $\tilde{B}_{1} \subseteq \tilde{B}_{2} \Rightarrow \tilde{B}_{2}^{*} \subseteq \tilde{B}_{1}^{*}$

• 2. $X \subseteq X^{**}, \tilde{B} \subseteq \tilde{B}^{**}$

• 3. $X^{*} = X^{***}, \tilde{B}^{*} = \tilde{B}^{***}$

• 4. $X \subseteq \tilde{B}^{*} \Leftrightarrow \tilde{B} \subseteq X^{*}$

• 5. $(X_{1} \cup X_{2})^{*} = X_{1}^{*} \cap X_{2}^{*}$, $(\tilde{B}_{1} \cup \tilde{B}_{2})^{*} = \tilde{B}_{1}^{*} \cap \tilde{B}_{2}^{*}$

• 6. $(X_{1} \cap X_{2})^{*} \supseteq X_{1}^{*} \cap X_{2}^{*}$, $(\tilde{B}_{1} \cap \tilde{B}_{2})^{*} \supseteq \tilde{B}_{1}^{*} \cap \tilde{B}_{2}^{*}$

A pair $(X,\tilde{B})$ is called a fuzzy concept, if $X^{*}=\tilde{B}$ and $X = \tilde{B}^{*}$, for $X \subseteq U$, $B \subseteq A$. X and $\tilde{B}$ are called the extent and intent of $(X,\tilde{B})$, respectively. It is clear that both $(X^{**}, X^{*})$ and $(\tilde{B}^{*},\tilde{B}^{**})$ are fuzzy concepts.

In order to more clearly explain the concept of learning process, we introduce a fuzzy formal context and detailed information is shown in Table 1. The universe is $U=\{x_1,x_2,x_3,x_4\}$ and the attribute set is $A=\{a,b,c,d\}$.

Table 1 A fuzzy formal context

According to intuitive perception and attention, we can obtain the result of the object-oriented and attribute-oriented operators, shown in Tables 2 and 3.

Table 2 Object-oriented operator

Table 3 Attribute-oriented operator

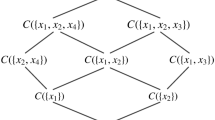
When $X^{*}=\tilde{B}$ and $X = \tilde{B}^{*}$, the pair $(X,\tilde{B})$ is called a fuzzy concept. According to the definition of the fuzzy concept and the result of two operators, concepts of the formal context introduced can be obtained as follows: $(\emptyset ,\{<a,1>,<b,1>,<c,1>,<d,1>\})$, $\ (\{x_1\},\{<a,0.6>,<b,0.2>,<c,0.5>,<d,0.3>\})$ , $\ (\{x_2\},\{<a,0.3>,<b,0.3>,<c,0.7>,<d,0.5>\})$, $\ (\{x_3\}, \{<a,0.7>,<b,0.6>,<c,0.2>,<d,0.9>\})$ , $\ (\{x_4\},\{<a,0.2>,<b,0.4>,<c,0.4>,<d,0.7>\})$, $\ (\{x_1,x_2\}, \{<a,0.3>,<b,0.2>,<c,0.5>,<d,0.3>\})$ , $\ (\{x_1,x_3\},\{<a,0.6>,<b,0.2>,<c,0.2>,<d,0.3>\})$, $\ (\{x_2,x_3\}, \{<a,0.3>,<b,0.3>,<c,0.2>,<d,0.5>\})$ , $\ (\{x_2,x_4\}, \{<a,0.2>,<b,0.3>,<c,0.4>,<d,0.5>\})$, $\ (\{x_3,x_4\}, \{<a,0.2>,<b,0.4>,<c,0.2>,<d,0.7>\})$, $\ (\{x_1,x_2,x_3\}, \{<a,0.3>,<b,0.2>,<c,0.2>,<d,0.3>\})$, $\ (\{x_1,x_2,x_4\}, \{<a,0.2>,<b,0.2>,<c,0.4>,<d,0.3>\})$, $\ (\{x_2,x_3,x_4\}, \{<a,0.2>,<b,0.3>,<c,0.2>,<d,0.5>\})$, $\ (\{x_1,x_2,x_3,x_4\}, \{<a,0.2>,<b,0.2>,<c,0.2>,<d,0.3>\})$.

Two-way Concept-Cognitive Learning

For a fuzzy formal context $(U,A,\tilde{I})$, ${2^U}$ and $2^A$ be the power sets of U and A, respectively. The $\tilde{\mathcal {F}}:{2^U} \rightarrow {2^A}$ and $\mathcal {P}:{2^A} \rightarrow {2^U}$ are considered as a pair of two-way learning operators, and they are abbreviated as $\tilde{\mathcal {F}}$ and $\mathcal {P}$, respectively. $L_1=P(U)$ and $\widetilde{L}_2=P(A)$ be complete lattices and fuzzy complete lattices, respectively.

Let $L_1$ and $\widetilde{L}_2$ be a pair of complete lattices, for any $X_1, X_2 \in L_1, \tilde{\mathcal {F}}: L_1 \rightarrow \widetilde{L}_2$ is an extent-intent cognitive operator if $\tilde{\mathcal {F}}$ satisfies the following:

• 1. $\tilde{\mathcal {F}}(0_{ L_1})=1_{\widetilde{L}_2}, \tilde{\mathcal {F}}(1_{L_1})=0_{\widetilde{L}_2}$,

• 2. $\tilde{\mathcal {F}}(X_1 \vee X_2) =\tilde{\mathcal {F}}(X_1) \wedge \tilde{\mathcal {F}}(X_2)$.

Similarly, for any $\tilde{B}_1, \tilde{B}_2 \in \widetilde{L}_2, \mathcal {P}: L_1 \rightarrow \widetilde{L}_2$ is an extent-intent cognitive operator if

• 1. $\mathcal {P}(0_{L_1})=1_{\widetilde{L}_2}, \mathcal {P}(1_{L_1})=0_{\widetilde{L}_2}$,

• 2. $\mathcal {P}(\tilde{B}_1 \vee \tilde{B}_2) = \mathcal {P}(\tilde{B}_1) \wedge \mathcal {P}(\tilde{B}_2)$.

where $O_{\widetilde{L}}$ and $1_{\widetilde{L}}$ are zero and the unit element, respectively.

Definition 1

Let $(U,A,\widetilde{I})$ be a fuzzy formal context, $L_1=P(U)$ and $\widetilde{L}_2=P(\widetilde{A})$ be two complete lattices, L and $\mathcal {P}$ be two cognitive operators (i.e., $(L_1, \widetilde{L}_2,\tilde{\mathcal {F}},\mathcal {P})$ is a cognitive system). For any $X \in L_1$, $\tilde{B}\in \widetilde{L}_2$, denote

$$\begin{aligned} {\widetilde{\mathcal{G}}}_{1}=\{(X,\tilde{B}| \tilde{B}\;\leqslant\;\tilde{\mathcal {F}}(X), X\;\leqslant\;\mathcal {P}(\tilde{B})\}, \end{aligned}$$

$$\begin{aligned} {\widetilde{\mathcal{G}}}_{2}=\{(X,\tilde{B}|\tilde{\mathcal {F}}(X)\;\leqslant\;\tilde{B}, \mathcal {P}( \tilde{B})\;\leqslant\;X\}. \end{aligned}$$

• 1. If $(X,\tilde{B}) \in \mathcal {G}_1$ , then $(X,\tilde{B})$ is a necessary fuzzy information granule and $\tilde{B}$ is necessary fuzzy attribute of X.

• 2. If $(X,\tilde{B}) \in \mathcal {G}_2$ , then $(X,\tilde{B})$ is a sufficient fuzzy information granule and $\tilde{B}$ is sufficient fuzzy attribute of X.

• 3. If $(X,\tilde{B}) \in \mathcal {G}_1 \cap \mathcal {G}_2$, then $(X,\tilde{B})$ is a sufficient and necessary fuzzy information granule, that is to say $X=\mathcal {P}(\tilde{B})$ and $\tilde{B}={\tilde{\mathcal{F}}}(X)$ and $\tilde{B}$ is a sufficient necessary fuzzy attribute of X.

• 4. If $(X,\tilde{B}) \notin \mathcal {G}_1 \cup \mathcal {G}_2$, then $(X,\tilde{B})$ is an inconsistent information granule.

From Definition 1, we only consider the situation that there exist three fuzzy information granule spaces in $(L_1, \widetilde{L}_2,\tilde{\mathcal {F}},\mathcal {P})$. Note that ${\widetilde{\mathcal{G}}}_1 \cap {\widetilde{\mathcal{G}}}_2$ be a fuzzy information granule space. Therefore, ${\widetilde{\mathcal{G}}}_1 \cap {\widetilde{\mathcal{G}}}_2$ is the concept space of $(L_1, \widetilde{L}_2,\tilde{\mathcal {F}},\mathcal {P})$. However, $(a,\tilde{B})\notin {\widetilde{\mathcal{G}}}_1 \cup {\widetilde{\mathcal{G}}}_2$ is not a fuzzy information granule of $(L_1, \widetilde{L}_2,\tilde{\mathcal {F}},\mathcal {P})$. Moreover, if necessary, sufficient and necessary fuzzy information granules do not exist at the beginning of $(L_1, \widetilde{L}_2,\tilde{\mathcal {F}},\mathcal {P})$. The approaches of volution of these fuzzy information granules are as follows.

Proposition 1

Let $(L_1, \widetilde{L}_2,\tilde{\mathcal {F}},\mathcal {P})$ be a cognitive system, ${\widetilde{\mathcal{G}}}_1$ be a necessary fuzzy information granule space, and ${\widetilde{\mathcal{G}}}_2$ be a sufficient fuzzy information granule space. If $X\in L_1$,$\tilde{B}\in \widetilde{L}_2$, then

• 1. $(X \wedge \mathcal {P}(\tilde{B}), \tilde{B} \vee \tilde{\mathcal {F}}(X)) \in {\widetilde{\mathcal{G}}}_1$

• 2. $(X \vee \mathcal {P}(\tilde{B}), \tilde{B} \wedge \tilde{\mathcal {F}}(X)) \in {\widetilde{\mathcal{G}}}_1$

• 3. $(\mathcal {P}(\tilde{B}), \tilde{B} \wedge \tilde{\mathcal {F}}(X)) \in {\widetilde{\mathcal{G}}}_1$

• 4. $(X \wedge \mathcal {P}(\tilde{B}), \tilde{\mathcal {F}}(X)) \in {\widetilde{\mathcal{G}}}_1$

• 5. $(\mathcal {P}\tilde{\mathcal {F}}(X), \tilde{B} \wedge \tilde{\mathcal {F}}(X)) \in {\widetilde{\mathcal{G}}}_1$

• 6. $(X \wedge \mathcal {P}(\tilde{B}), \tilde{\mathcal {F}} \mathcal {P}(\tilde{B})) \in {\widetilde{\mathcal{G}}}_1$  

• 7. $(X \vee \mathcal {P}(\tilde{B}), \tilde{\mathcal {F}} \mathcal {P}(\tilde{B})) \in {\widetilde{\mathcal{G}}}_2$  

• 8. $(\mathcal {P}\tilde{\mathcal {F}}(X), \tilde{B} \vee \tilde{\mathcal {F}}(X)) \in {\widetilde{\mathcal{G}}}_2$

Proposition 2

Let $(L_1, \widetilde{L}_2,\tilde{\mathcal {F}},\mathcal {P})$ be a cognitive system, ${\widetilde{\mathcal{G}}}_1$ be a necessary fuzzy information granule space, and ${\widetilde{\mathcal{G}}}_2$ be a sufficient fuzzy information granule space. If $(X_1, \tilde{B}_1)\in {\widetilde{\mathcal{G}}}_1$ and $(X_2, \tilde{B}_2)\in {\widetilde{\mathcal{G}}}_2$, then

• 1. $({X_1} \vee \mathcal {P}({\tilde{B}_1}), \tilde{\mathcal {F}}({X_1} \vee \mathcal {P} ({\tilde{B}_1})) \in {\widetilde{\mathcal{G}}}_1 \cap {\widetilde{\mathcal{G}}}_2$

• 2. $(\mathcal {P}({\tilde{B}_1} \vee \tilde{\mathcal {F}}({X_1})),{\tilde{B}_1} \vee \tilde{\mathcal {F}}({X_1})) \in {\widetilde{\mathcal{G}}}_1 \cap {\widetilde{\mathcal{G}}}_2$

• 3. $({X_2} \wedge \mathcal {P}({\tilde{B}_2}), \tilde{\mathcal {F}}({X_2} \wedge \mathcal {P}({\tilde{B}_2})) \in {\widetilde{\mathcal{G}}}_1 \cap {\widetilde{\mathcal{G}}}_2$

• 4. $(\mathcal {P}({\tilde{B}_2} \wedge \tilde{\mathcal {F}}({X_2})),{\tilde{B}_2} \wedge \tilde{\mathcal {F}}({X_2})) \in {\widetilde{\mathcal{G}}}_1 \cap {\widetilde{\mathcal{G}}}_2$

Let $(L_1, \widetilde{L}_2,\tilde{\mathcal {F}},\mathcal {P})$ be a cognitive system, ${\widetilde{\mathcal{G}}}_1$ be a necessary fuzzy information granule space, and ${\widetilde{\mathcal{G}}}_2$ be a sufficient fuzzy information granule space. If “$\vee$” and “$\wedge$” are defined operators of cognitive system, and

$$\begin{aligned} (X_1, \tilde{B}_1) \wedge (X_2, \tilde{B}_2) =(X_1 \wedge X_2, \tilde{\mathcal {F}}\mathcal {P}(\tilde{B}_1 \vee \tilde{B}_2 )) \end{aligned}$$

$$\begin{aligned} (X_1, \tilde{B}_1) \vee (X_2, \tilde{B}_2) = (\mathcal {P} \tilde{\mathcal {F}}(X_1 \vee X_2), \tilde{B}_1 \wedge \tilde{B}_2 ) \end{aligned}$$

Proposition 3

Let $(L_1, \widetilde{L}_2,\tilde{\mathcal {F}},\mathcal {P})$ be a cognitive system, $\mathcal {G}_1$ be a necessary information granule space, $\mathcal {G}_2$ be a sufficient information granule space, and $\mathcal {G}_1\cap \mathcal {G}_2$ be a sufficient and necessary information granule space. For arbitrary information granule $(X,\tilde{B}) \in \mathcal {G}_1 \cup \mathcal {G}_2$, there is only one sufficient and necessary information granule which is itself (i.e., $(X,\tilde{B})$); otherwise, we have two sufficient and necessary information granules, that is, $(\mathcal {P}\tilde{\mathcal {F}}(X),\tilde{\mathcal {F}}(X)$ and $(\mathcal {P}(B),\tilde{\mathcal {F}}\mathcal {P}(B))$.

Proof

Because $(L_1, \widetilde{L}_2,\tilde{\mathcal {F}},\mathcal {P})$ be a cognitive system, from Definition 1, we have three fuzzy information granule: $\mathcal {G}_1$, $\mathcal {G}_2$ and $(\mathcal {G}_1\cap \mathcal {G}_2)^c$, where $(\cdot )^c$ is the complement. Then, we divide it into three steps to prove it.

• 1. If $(X,\tilde{B})\in \mathcal {G}_1$, from Definition 1, we have $X\;\leqslant\;\mathcal {P}(\tilde{B})$ and $\tilde{B}\;\leqslant\;L(X)$. Thus, $X \vee \mathcal {P}(\tilde{B})=\mathcal {P}(\tilde{B})$, $\tilde{\mathcal {F}}(({X} \vee \mathcal {P}({\tilde{B}}))=\tilde{\mathcal {F}}\mathcal {P}(\tilde{B})$, ${\tilde{B}} \vee \tilde{\mathcal {F}}({X})=\tilde{\mathcal {F}}(X)$, $\mathcal {P}({\tilde{B}} \vee \tilde{\mathcal {F}}({X}))=\mathcal {P}\tilde{\mathcal {F}}(a)$; hence, two sufficient and necessary information granules are $(\mathcal {P}\tilde{\mathcal {F}}(X),\tilde{\mathcal {F}}(X))$ and $(\mathcal {P}(\tilde{B}),\tilde{\mathcal {F}}\mathcal {P}(\tilde{B}))$.

• 2. If $(X,\tilde{B})\in \mathcal {G}_2$, from Definition 1, we have $\tilde{\mathcal {F}}(X)\;\leqslant\;\tilde{B}$ and $\mathcal {P}(\tilde{B})\;\leqslant\;X$. Thus, $X \wedge \mathcal {P}(\tilde{B})=\mathcal {P}(\tilde{B})$, $\tilde{\mathcal {F}}(({X} \wedge \mathcal {P}({\tilde{B}}))=\tilde{\mathcal {F}}\mathcal {P}(\tilde{B})$, ${\tilde{B}} \wedge \tilde{\mathcal {F}}({X})=\mathcal {P}(\tilde{B})$, $\mathcal {P}({\tilde{B}} \wedge \tilde{\mathcal {F}}({X}))=\mathcal {P}\tilde{\mathcal {F}}(X)$; hence, two sufficient and necessary information granules are $(\mathcal {P}\tilde{\mathcal {F}}(X),\tilde{\mathcal {F}}(X))$ and $(\mathcal {P}(\tilde{B}),\tilde{\mathcal {F}}\mathcal {P}(\tilde{B}))$.

• 3. If $(X,\tilde{B})\notin \mathcal {G}_1 \cup \mathcal {G}_2$, it is immediate from Definition 1 and Proposition 2.

By combining 1), 2), and 3), this theorem is proven. #

Intuitively, Proposition 3 shows that $(\mathcal {P}\tilde{\mathcal {F}}(X),\tilde{\mathcal {F}}(X))$ and $(\mathcal {P}(B),\tilde{\mathcal {F}}\mathcal {P}(B))$ is a sufficient and necessary information granule in the two-way learning system. $(X,\tilde{B})=(\mathcal {P}\tilde{\mathcal {F}}(X),\tilde{\mathcal {F}}(X))=(\mathcal {P}(B),\tilde{\mathcal {F}}\mathcal {P}(B))$, if any $X\in L_1$ and $\tilde{B}\in L_2$, $(X,\tilde{B})$ is a sufficient and necessary information granule.

From the above discussion, we put forward a cognitive mechanism of transforming any information granule into sufficient and necessary fuzzy information granules as follows:

• Case 1: For any information granule $(X,\tilde{B})$, its sufficient, necessary, and sufficient and necessary fuzzy information granules can be obtained with the two-way concept-cognitive learning method, and the detailed conversion process is provided in Propositions 1 and 2.

• Case 2: From the definition of the sufficient and necessary fuzzy information granule and cognitive operators, it is true that $(\mathcal {P}\tilde{\mathcal {F}}(X),\tilde{\mathcal {F}}(X))$ is a fuzzy concept about a. So when one just knows the information from an object set X, a fuzzy concept can be obtained by computing $\mathcal {P}\tilde{\mathcal {F}}(X)$ and $\mathcal {P}\tilde{\mathcal {F}}(X)$.

• Case 3: From the definition of the sufficient and necessary fuzzy information granule and cognitive operators, it is obvious that $(\mathcal {P}(\tilde{B}),\tilde{\mathcal {F}}\mathcal {P}(\tilde{B}))$ is a fuzzy concept about $\tilde{B}$. So when one just knows the information from a fuzzy attribute set $\tilde{B}$, a fuzzy concept can be obtained by computing $\mathcal {P}(\tilde{B})$ and $\tilde{\mathcal {F}}\mathcal {P}(\tilde{B})$.

Concept Learning in Multi-source Fuzzy Decision Tables

It is well known that information about the same subject can be collected by different means with the development of technology. How to take full advantage of multi-source information to learn concepts is an imperative task during data processing. Considering the complexity of concept learning, we can divide the concept learning process of multi-source fuzzy decision tables into two steps. Firstly, multi-source information is fused based on some uncertainty measures. Secondly, fuzzy concepts are learned from the fused decision table.

Information from different sources is called multi-source information. In order to further deal with multi-source information, we first introduce a multi-source fuzzy decision table. The $MFI=\{\tilde{I_{i}}_{\{i\in N\}} |\tilde{I_{i}}=\{U,A_{i},V_{i},f_{i}\}\}$ can be called a multi-source fuzzy decision table with |N| single fuzzy decision tables, where U is a finite non-empty set of object, $A_{i}$, $V_{i}$ and $f_{i}$ are the finite non-empty set of attributes, the domain of all objects under all attributes, and the information function in the $i^{th}$ fuzzy decision table, respectively.

In each fuzzy information table $\tilde{I}_{k}=(U,A,V_{k},f_{k})$($k\in N$), for an arbitrary attribute $a \in A$, $\tilde{I}_{k}^{a}(x_{i})(k=1,2, \cdots , s,i=1,2,\cdots , n)$ represents the value of $x_{i}$ with respect to the attribute a in the $k^{th}$ fuzzy decision table. And for any $x \in U$, a similarity class of x with respect to a in the $\tilde{I}_{k}$ is defined as $T_{a}^{k}(x)=\{x_{i}||\tilde{I_{k}^{a}}(x_{i})-\tilde{I_{k}^{a}}(x)|\leqslant b\},$ where the threshold b is a given real number. It is obvious that $x_{i}\in T_{a}^{k}(x_{i})$ and $x_{i} \in T_{a}^{k}(x_{j}) \Leftrightarrow x_{j} \in T_{a}^{k}(x_{i})$.

For convenience, let $|N|=s$. $MFI=\{\tilde{I_{i}}_{\{i\in N\}} |\tilde{I_{i}}=\{U,A_{i},V_{i},f_{i}\}\}$ is composed of s single fuzzy decision table. In particular, if it is true that $A_{i}=A_{j}$ for all the $i\ne j$, then all the fuzzy decision tables have the same structure. Because the more information you have on the same thing learned knowledge should be more accurate. For the multi-source decision table, which has different structures, we may only need to find the ultimate goal as a middle bridge to establish the relationship between different information sources. However, the multi-source decision table, which has the same structure, will be required to achieve a higher goal in addition to the abovementioned middle bridge. So the research background of this paper is based on the multi-source fuzzy decision table which has the same structure and different information functions, namely, $MFI=\{\tilde{I_{i}}_{\{i=N\}}^{s} |\tilde{I_{i}}=\{U,A,V_{i},f_{i}\}\}$. For convenience, the multi-source decision table $MFI=\{\tilde{I_{i}}_{\{i=N\}}^{s} |\tilde{I_{i}}=\{U,A,V_{i},f_{i}\}\}$ is denoted as $MFI=\{\tilde{I_{1}} , \tilde{I_{2}}, \cdots , \tilde{I_{s}}\}$. Unless otherwise specified, all multi-source fuzzy decision tables in this paper are defined as above shown, namely, $MFI=\{\tilde{I_{1}} , \tilde{I_{2}}, \cdots , \tilde{I_{s}}\}$.

Multi-source Fuzzy Decision Fusion

By integrating data from different sources, the deficiency of single data can be made up. In order to make full use of multi-source information to realize the mutual complement and mutual confirmation of different information sources, all the signal fuzzy decision tables are fused based on the uncertainty measure. The detailed fusion process is shown in the following.

Conditional Entropy Fusion Mechanism

First of all, a critical issue is the reliability of information from different sources, namely the importance of information sources. In this paper, we select conditional entropy to measure the importance of information sources. A novel conditional entropy proposed by Dai et al. [26] is a great uncertainty measure that has monotonicity. The reason for selecting it is that the thinner the partition, the smaller the conditional entropy. That is to say, with the decrease of conditional entropy, available knowledge may be increased. Therefore, the smaller the conditional entropy is, the more critical the source will be. In general, other uncertainty measures can also be used to determine the importance of information sources according to different decision goals.

According to the paper [26], this proposed conditional entropy can be used to evaluate the importance of attributes. Let $I=(U,A,V,f)$ be a decision table, where $U=\{x_{1}, x_{2}, \cdots , x_{n}\}$ and $U/D=\{Y_{1}, Y_{2}, \cdots ,Y_{m}\}$. The conditional entropy (CE) of D regarding the attribute a in the I is defined as

$$\begin{aligned} H(D|a)=-\sum ^{n}_{i=1}\sum ^{m}_{j=1}\frac{|T_{a}(x_{i}) \cap Y_{j}|}{|U|} log \frac{|T_{a}(x_{i}) \cap Y_{j}|}{|T_{a}(x_{i})|}. \end{aligned}$$

where $T_{a}(x_{i})$ is the similarity class of $x_{i}$ with respect to a in the decision table I.

For the attribute a, the smaller the conditional entropy is, the more important the information source will be. So the following definitions in a fuzzy decision table are proposed.

Definition 2

Let $MFI=\{\tilde{I_{1}} , \tilde{I_{2}}, \cdots , \tilde{I_{s}}\}$ be a multi-source fuzzy decision table, $U=\{x_{1}, x_{2},\cdots ,x_{n} \}$ be the universe, and $U/D=\{Y_{1}, Y_{2}, \cdots ,Y_{m}\}$ be a classification of universe U. For any $a \in A$, the CE of D with respect to the attribute a in the $\tilde{I_{k}}$ of MFI is defined as

$$\begin{aligned} H_{a}(D|\tilde{I}_{k})=-\sum ^{|U|}_{i=1}\sum ^{m}_{j=1}\frac{|T_{a}^{k}(x_{i}) \cap Y_{j}|}{|U|} log \frac{|T_{a}^{k}(x_{i}) \cap Y_{j}|}{|T_{a}^{k}(x_{i})|}. \end{aligned}$$

where $T_{a}^{k}(x_{i})$ is the similarity class of $x_{i}$ with respect to a in the $\tilde{I}_{k}$.

The smaller the conditional entropy, the less uncertainty there is. Thus, we could select the best attribute among all multi-source according to the minimum principle and definition 2, as follows:

$$\begin{aligned} k_{a}=\underset{k\in \{1,2,\cdots ,s\}}{\mathop {\arg }min}(H_{a}(D|\tilde{I}_{k})). \end{aligned}$$

Then, the column of the attribute a in the ${k_{a}}^{th}$ table is extracted as the column of the attribute a in the fused table. After this operation is performed on all the attributes, a new decision table can be obtained. Let $NI(a)=\tilde{I}_{k_{a}}^{a},a \in A$ denote the operation on the attribute a and $NI=(\tilde{I}_{k_{a_1}}^{a_1},\tilde{I}_{k_{a_2}}^{a_2},\cdots ,\tilde{I}_{k_{a_m}}^{a_m})$ denote the new decision table, where m is the number of attribute.

Fig. 2

Multi-source fuzzy information fusion

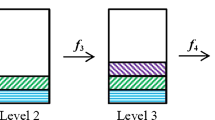
The process of fusion is visually displayed in Fig. 2. There is a multi-source fuzzy decision table $MFI=\{\tilde{I_{1}} , \tilde{I_{2}}, \cdots , \tilde{I_{s}}\}$ with s fuzzy decision table, and there are n objects and m attributes for each fuzzy decision table $\tilde{I_{i}},(i=1,2,\cdots ,s)$. For each fuzzy decision table, we can calculate the conditional entropy of the decision attribute set with respect to each condition attribute by Definition 2. For example, there are s conditional entropy of the attribute a calculated in the MFI, namely, $H_{a}(D|\tilde{I}_{1}),H_{a}(D|\tilde{I}_{2})\cdots ,H_{a}(D|\tilde{I}_{s})$. According to Definition 2, the attribute a in the ${k_{a}}^{th}$ table is extracted as the column of the attribute a in the fused table. In order to describe the results more vividly, we use different colors of rough lines to express the corresponding column extracted. These extracted columns construct a new fuzzy decision table. A more detailed presentation is shown in Fig. 2. Next, the proposed fusion theory is described by a specific example.

Example 1

This is a case study about the medical diagnosis. There are 10 patients who were suspected to be infected with the H1N1. In order to diagnose, four hospitals examined the following six indicators, respectively. The results of testing in four hospitals are shown in Tables 4, 5, 6, and 7, where A=$\{a_1, a_2, \cdots , a_6\}$ represent “White Blood Cell,” “Creatine Kinase,” “Aspartate Aminotransferase,” “Alanine Transaminase,” “Temperature,” and “Cough,” respectively. And U=$\{x_1, x_2, \cdots , x_{10}\}$ denotes 10 those suspected patients. These tables obtain a multi-source fuzzy decision table, and their similarity classes can be get by Definition 2.

Given the partition of the universe is U/D=$\{\{x_{1}$,$x_{4}$,$x_{7}\}$, $\{x_{2}$, $x_{5}$,$x_{8}\}$,$\{x_{3}$, $x_{6}$,$x_{9}$,$x_{10}\}\}$ and the value of b is 0.1, namely $b=0.1$. The results of the conditional entropy of each attribute are shown in Table 8.

Table 4 Information source $\tilde{I}_1$

Table 5 Information source $\tilde{I}_2$

Table 6 Information source $\tilde{I}_3$

Table 7 Information source $\tilde{I}_4$

The smaller the conditional entropy, the more important the information source. According to the result of Table 8, the reliable source of attributes $a_{1}$, $a_{3}$, $a_{5}$ is all $\tilde{I}_{4}$. Moreover, the reliable source of attributes $a_{2}$ and $a_4$ is all $\tilde{I}_{2}$ and the reliable source of attribute $a_{6}$ is $\tilde{I}_{3}$. Then, a new fuzzy decision table can be established by extracting the corresponding column of each attribute. The detailed information of the new table is displayed in Table 9.

Table 8 Conditional entropy of each attribute in the MFI

Table 9 The new decision table after CE-fusion

According to the theory of CE-fusion, an algorithm is designed for multi-source fuzzy information fusion. Detailed information is shown in Algorithm 1.

In Algorithm 1, we first calculate all the similarity class $T_{a}^{k}(x)$ of any $x \in U$ under attribute a in the $k_{th}$ fuzzy decision table. Then, the conditional entropy $H_{a}(D|\tilde{I}_{k})$ be calculated in the $k^{th}$ fuzzy decision table. Finally, the fuzzy decision table in which the conditional entropy of D with respect to a is minimal is selected as the reliable source of the attribute a. Then, a new fuzzy decision table can be established by extracting the corresponding column of each attribute, namely $NI=(\tilde{I}_{k_{a_{1}}}^{a_{1}},\tilde{I}_{k_{a_{2}}}^{a_{2}},\cdots ,\tilde{I}_{k_{a_{|A|}}}^{a_{|A|}})$. Taking into account the efficiency of the algorithm, we analyze the complexity of Algorithm 1, which is shown in Table 10.

Table 10 The computational complexity of Algorithm 1

In Algorithm 1, we compute all $T_{a}^{k}(x)$, for any $x \in U$ under attribute a in steps 4–5. Steps 6–14 calculate the conditional entropy for any attribute $a\in A$ in the $k^{th}$ information source. Steps 17–26 find the minimum conditional entropy of each attribute as their reliable sources. At last, return the results.

Uncertainty Measure of CE-Fusion

In order to show the advantages of the CE-fusion method, approximate precision and approximate quality are introduced to measure our methods. First, the definition of approximate precision is proposed in the following.

Definition 3

Let $\tilde{I}=(U,AT)$ be a fuzzy information system, where $U/D=\{Y_{1}, Y_{2},\cdots , Y_{m}\}$, $\tilde{I}^{a}(x_{j})(j=1,2,\cdots , n)$ is the value of $x_{j}$ with respect to a in the $\tilde{I}$. Given the constant $\theta$, for any $Y_{i}\in U/D(j=1,2,\cdots ,m)$, the lower and upper approximations of $Y_{j}$ are respectively defined as

$$\begin{aligned} \begin{array}{r} \underline{Apr}(Y_{i})=\{x \in U | T_{\theta }(x) \subseteq Y_{i}\}, \\ \overline{Apr}(Y_{i})=\{x \in U | T_{\theta }(x) \cap Y_{i} \ne \phi \} \end{array} \end{aligned}$$

where $T_{\theta }(x)=\{x_{i}|\underset{a \in AT}{\sum }{|\tilde{I^{a}}(x_{i})-\tilde{I^{a}}(x)}|\;\leqslant\;\theta \}$ is the similarity class of x with respect to a in the $\tilde{I}$. The lower approximation and upper approximation of U/D are $\underline{Apr}(U/D)=\underline{Apr}(Y_{1}) \cup \underline{Apr}(Y_{2}) \cup \cdots \cup \underline{Apr}(Y_{m})$ and $\overline{Apr}(U/D)=\overline{Apr}(Y_{1}) \cup \overline{Apr}(Y_{2}) \cup \cdots \cup \overline{Apr}(Y_{m})$, respectively.

The approximation precision (AP) and approximation quality (AQ) of U/D and in the $\tilde{I}$ can be defined as follows:

$$\begin{aligned} AP_{R}(U/D)=\frac{\sum _{Y_{i}\in U/D}|\underline{Apr}(Y_{i})|}{\sum _{Y_{i}\in U/D}|\overline{Apr}(Y_{i})|}. \end{aligned}$$

$$\begin{aligned} AQ_{R}(U/D)=\frac{\sum _{Y_{i}\in U/D}|\underline{Apr}(Y_{i})|}{|U|}. \end{aligned}$$

Then, the above theory is expounded by specific examples. Followed by example 1 and example 2, the approximation precision of U/D in the new tables of CE-fusion is calculated. Due to different science fields may require different similarity class thresholds, in this paper, the similarity class threshold $\theta$ varies from 0.3 to 1.4 with an increase of 0.1. The experimental results of CE-fusion are shown in Table 11.

Table 11 AP and AQ of CE-fusion method

Two-way Concept-Cognitive Learning of MFI

Concept learning is an important part of human cognition. People from different science fields have different means of information cognition. There are different approaches to learning concepts. Let $(U,A,\tilde{I})$ be a fuzzy formal context, $X \subseteq U$ be an object set, and $\tilde{B}$ be a fuzzy attribute set. There are 3 cases about concept learning from different perspectives.

• Case 1’: For any information granule $(X,\tilde{B})$, its sufficient, necessary, and sufficient and necessary fuzzy information granules can be obtained with the two-way concept-cognitive learning method, and the detailed conversion process is provided in the “Two-way Concept-Cognitive Learning” section.

• Case 2’: From the definition of the fuzzy concept and the property (3) of cognitive operators, it is true that $(\mathcal {P}\tilde{\mathcal {F}}(X),\tilde{\mathcal {F}}(X))$ is a fuzzy concept about X. So when one just knows the information from an object set X, a fuzzy concept can be obtained by computing $\mathcal {P}\tilde{\mathcal {F}}(X)$ and $\tilde{\mathcal {F}}(X)$. The corresponding calculation process is realized by Algorithm 2.

• Case 3’: According to the definition of the fuzzy concept and the property (3) of cognitive operators, it is obvious that $(\mathcal {P}(B),\tilde{\mathcal {F}}\mathcal {P}(B))$ is a fuzzy concept about $\tilde{B}$. So when one just knows the information from a fuzzy attribute set $\tilde{B}$, a fuzzy concept can be obtained by computing $\mathcal {P}(B)$ and $\tilde{\mathcal {F}}\mathcal {P}(B)$. The corresponding calculation process is realized by Algorithm 3.

When we only know the extent of a concept, it is our primary task to learn the intent of concept. The process of object-oriented concept learning is realized by Algorithm 2.

In Algorithm 2, step 2 initializes the intent and extent of the concept to be $\phi$, steps 5–7 seek attribute of the intent of the concept which we will learn, step 8 records the intent of the target concept to B, steps 11–17 search object of the extent of the target concept, and steps 18–20 add the object that is searched in steps 11–17 to Y. At last, return the result.

Moreover, the computational complexity of Algorithm 2 is analyzed, which is shown in Table 12.

Table 12 The computational complexity of Algorithm 2

When we only know the intent of a concept, it is our main task to learn the extent of the concept. The process of attribute-oriented concept learning is realized by Algorithm 3. By Algorithm 3, we know how to learn a fuzzy concept by an attribute set.

According to the discussion of Algorithm 3, we also analyze its complexity, which is shown in Table 13.

Table 13 The computational complexity of Algorithm 3

From the computation steps and the computational complexity, Algorithm 3 is similar to Algorithm 2. Step 2 initializes intent and extent of the concept, which we will learn to be $\phi$, steps 4–10 search the object of the extent of the target concept, and steps 11–13 record the object of the extent to Y. Steps 16–19 seek attribute of the intent of the target concept, and step 20 records the attribute of the intent to B. At last, return the result.

Currently, there is no unified standard in the multi-source fuzzy decision table. Based on the uncertainty measure in the rough set, we defined AP and AQ of concept as follows.

Definition 4

Let $(U,A,\tilde{I})$ be a fuzzy formal context, and $(X,\tilde{B})$ be a fuzzy concept. The AP and AQ of extent of $(X,\tilde{B})$ are defined as:

$$\begin{aligned} AP_{T_{\theta }}(X,\tilde{B})=\frac{|\underline{Apr}(X,\tilde{B})|}{|\overline{Apr}(X,\tilde{B})|},\\ AQ_{T_{\theta }}(X,\tilde{B})= \frac{|\underline{Apr}(X,\tilde{B})|}{|U|} \end{aligned}$$

where $\underline{Apr}(X,\tilde{B})=\{x \in U | T_{\theta }(x) \subseteq X\}$ and $\overline{Apr}(X,\tilde{B})=\{x \in U | T_{\theta }(x) \cap X \ne \phi \}$ are the lower and upper approximations of extent X of concept $(X,\tilde{B})$ and $T_{\theta }(x)=\{x_{i}|\underset{a \in AT}{\sum }{|\tilde{I^{a}}(x_{i})-\tilde{I^{a}}(x)}|\;\leqslant\;\theta \}$ is the similarity class of x about a in the $\tilde{I}$.

In order to display the advantage of concept learning based on CE-fusion in a multi-source fuzzy decision table, the AP and AQ of the extent of concepts are compared in a specific instance. The detailed process is shown in the following.

Example 2

According to the result of CE-fusion shown in Table 9 and the method of concept learning described in the “Two-way Concept-Cognitive Learning” section, the concepts related to the decision classes can be learned, which are

$$\begin{aligned} (X_{1},\tilde{A_{1}})\overset{\Delta }{\mathop {=}}(\{x_{1}, x_{4}, x_{7}\},\{<a_1, 0.19>,<a_2, 0.26>,<a_3, 0.71>,<a_4, 0.20>,<a_5, 0.46>,<a_6, 0.08> \}), \end{aligned}$$

$$\begin{aligned} (X_{2},\tilde{A_{2}})\overset{\Delta }{\mathop {=}}(\{x_{2}, x_{5}, x_{8}\},\{<a_1, 0.13>,<a_2, 0.19>,<a_3, 0.20>,<a_4, 0.59>,<a_5, 0.26>,<a_6, 0.37>\}), \end{aligned}$$

$$\begin{aligned} (X_{3},\tilde{A_{3}})\overset{\Delta }{\mathop {=}}(\{x_{3}, x_{6}, x_{9}, x_{10}\},\{<a_1, 0.28>,<a_2, 0.34>,<a_3, 0.16>,<a_4, 0.18>,<a_5, 0.20>,<a_6, 0.47>\}). \end{aligned}$$

Given $\theta$ = 1.4, the lower and upper approximations of extents of above concepts can be calculated as follows:

$$\begin{aligned} \underline{Apr}(X_{1},\tilde{A_{1}})=\{x_4,x_7\},\overline{Apr}(X_{1},\tilde{A_{1}})=\{x_1,x_3,x_4,x_5,x_7\}, \end{aligned}$$

$$\begin{aligned} \underline{Apr}(X_{2},\tilde{A_{2}})=\{x_8,x_9\},\overline{Apr}(X_{2},\tilde{A_{2}})=\{x_1,x_2,x_5,x_6,x_8,x_9\}, \end{aligned}$$

$$\begin{aligned} \underline{Apr}(X_{3},\tilde{A_{3}})=\{x_9,x_{10}\},\overline{Apr}(X_{3},\tilde{A_{3}})=\{x_1,x_2,x_3,x_6,x_9,x_{10}\}. \end{aligned}$$

Then according to the above discussion, the approximation precision of extents of the above concepts can be obtained, namely $AP_{T_{\theta }}(X_{1},\tilde{A_{1}})$=2/5, $AP_{T_{\theta }}(X_{2},\tilde{A_{2}})$=1/3, $AP_{T_{\theta }}(X_{3},\tilde{A_{3}})$=1/3; $AQ_{T_{\theta }}(X_{1},\tilde{A_{1}})$=1/5, $AQ_{T_{\theta }}(X_{2},\tilde{A_{2}})$=1/5, $AQ_{T_{\theta }}(X_{3},\tilde{A_{3}})$=1/5.

According to the results of concept learning, we can find that concepts are different for the same decision class in the new tables of CE-fusion. From the perspective of the approximation precision of the extent of concepts, CE-fusion in the multi-source fuzzy decision table is, to some extent, a suitable fusion method. Therefore, CE-fusion can be used as an effective technique in multiple cognition. Concept learning based on CE-fusion is a suitable concept learning method in the multi-source fuzzy decision table.

Experiment Evaluations

In this section, we first introduce the experimental setting and multi-source fuzzy context in the “Experimental Settings” subsection. In the “Outcome Evolution” subsection, we evaluate the outcome of the presented CE-fusion way for concept learning. Finally, we also reveal the effectiveness of CE-fusion with other methods on the public dataset.

Experimental Settings

In order to evaluate the effectiveness of our method for concept-cognitive learning in a multi-source fuzzy context, we conduct a series of experiments on public datasets from Keel and UCI Repository, namely, “User Knowledge Modeling,” “Balance,” “Pima,” “Vehicle,” “Winequality_red,” and “Wifi_localization_ok Objects.” Note that ten sources for each dataset are generated by blurring the original dataset and adding random noise to the original dataset. Detailed information about multi-source fuzzy context is shown in Table 14. This experimental program runs on a personal computer with hardware and software parameters, as shown in Table 15.

Table 14 The basic information of multi-source fuzzy context

Table 15 The description of experiment environment

The method of generating multi-source fuzzy decision context is proposed in the following. Firstly, to obtain a fuzzy decision context, each column of data is divided by the maximum value of the column in the original context. Then, a multi-source fuzzy decision context is constructed by adding Gauss and random noise to the fuzzy decision context.

Let $MFI=\{\tilde{I_{1}} , \tilde{I_{2}}, \cdots , \tilde{I_{s}}\}$ be a multi-source fuzzy decision context constructed by a fuzzy decision context $\tilde{I}$. Firstly, s numbers $(g_1,g_2,\cdots ,g_s)$ which obey the $N(0, \sigma )$ distribution are generated, where $\sigma$ is the standard deviation. The method of adding Gauss noise is defined as follows:

$$\begin{aligned} \tilde{I}_i(x,a)=\left\{ \begin{array}{lcl} \tilde{I}(x,a)+g_i&{} &{} if(0 \le \tilde{I}(x,a)+g_i \le 1)\\ \tilde{I}(x,a) &{} &{} else \\ \end{array} \right. \end{aligned}$$

where $\tilde{I}(x,a)$ is the value of object x under attribute a in fuzzy decision context, and $\tilde{I}_i(x,a)$ is the value of object x under attribute a in the $i^{th}$ fuzzy decision context $\tilde{I_{i}}$.

Then, s random numbers $(e_1,e_2,\cdots ,e_s)$ are generated and these numbers are between $-e$ and e, where e is random error threshold. The method of adding random noise is given in the following.

$$\begin{aligned} \tilde{I}_i(x,a)=\left\{ \begin{array}{lcl} \tilde{I}(x,a)+e_i&{} &{} if(0 \le \tilde{I}(x,a)+e_i \le 1)\\ \tilde{I}(x,a) &{} &{} else \\ \end{array} \right. \end{aligned}$$

where $\tilde{I}(x,a)$ represents value of object x under attribute a in fuzzy decision table, and $\tilde{I}_i(x,a)$ represents object x under attribute a in the $i^{th}$ fuzzy information source $\tilde{I_{i}}$.

Next, 35% objects are randomly selected from the fuzzy decision context $\tilde{I}$, and then Gauss noise is added to these objects. Thirty percent of objects are randomly selected from the rest of the context, and random noise is added. Finally, $MFI=\{\tilde{I_{1}} , \tilde{I_{2}}, \cdots , \tilde{I_{s}}\}$ can be obtained.

Outcome Evolution

In order to test the validity of fuzzy decision context after the CE-fusion method and concept learning mechanism, we select nine fuzzy set membership functions to conduct a series of experiments. Gauss form, Cauchy form, and $\Gamma$ form membership function are selected as the representation of fuzzy membership functions, which are divided into small, middle, and large types. In this process, drop half Cauchy form, Cauchy form, and L half Cauchy form are small type, middle, and large type, respectively. These nine different membership functions considered in this paper are small, middle, and large fuzzy membership functions of Gaussian, Cauchy, and $\Gamma$. For convenience, symbols SG, MG, LG, SC, MC, LC, $S\Gamma$, $M\Gamma$, and $L\Gamma$ denote the nine membership functions. Corresponding graphics are shown in Fig. 3.

Fig. 3

The nine kinds of membership functions

Based on the fuzzy membership functions and Algorithm 3, evaluate our methods’ approximation precision and approximation quality on six datasets (i.e., datasets 1–6). The details are shown in Tables 16, 17, 18, 19, 20, and 21. In different science fields, the standard deviation of Gauss noise and random error threshold of random noise may be different. In this paper, experiments are carried out five times for each dataset and let the standard deviation $\sigma$ and random error threshold e vary from 0.005 to 0.03 with an increase of 0.005 every time, denoted as noises 1–5. In this experiment, the thresholds b and $\theta$ are (0.1, 0.4).

Tables 16, 17, 18, 19, 20, and 21 record the measures values of five noises under nine membership functions, where AP and AQ represent the value of approximation precision and approximation quality. From these tables, we could find that all the measures (approximation precision and approximation quality) are higher than those of M-fusion methods on different datasets. All in all, based on the concept extension’s approximate precision and approximate precision, the conditional entropy fusion method (CE-fusion) and the mean value fusion method are compared in the experiment. The results show that the CE-fusion method is good in the concept learning of multi-source fuzzy decision tables.

Table 16 The average value of AP and AQ on User Knowledge Modeling Dataset

Table 17 The average value of AP and AQ on Balance Dataset

Table 18 The average value of AP and AQ on Pima Dataset

Table 19 The average value of AP and AQ on Vehicle dataset

Table 20 The average value of AP and AQ on Winequality_red dataset

Table 21 The average value of AP and AQ on Wifi_localization_ok Objects dataset

Parameters Analysis

In order to verify the effectiveness of the CE-Fusion method, in this subsection, we also compare and record the approximation precision and approximation quality of four fusion methods under different noises. Figures 4, 5, 6, 7, 8, and 9 show the approximation accuracy of four fusion methods, where the dark blue, light blue, orange, and red lines represent the approximation accuracy on six datasets under different noises of M-fusion, min-fusion, max-fusion, and CE-fusion. According to these pictures, we find that in most noises cases, the height of the yellow bar is higher than or equal to the other three bars, and the red line is higher than those of other colors, which illustrates the effectiveness of the CE-fusion method than the other three compared methods under different noises.

Fig. 4

The approximation accuracy of User Knowledge Modeling under nine noises

Fig. 5

The approximation accuracy of Balance under nine noises

Fig. 6

The approximation accuracy of Pima under nine noises

Fig. 7

The approximation accuracy of Vehicle under nine noises

Fig. 8

The approximation accuracy of Winequality_red nine noises

Fig. 9

The approximation accuracy of Wifi_localization_ok Objects under nine noises

In addition, we also take the approximation quality to analyze the advantage of the proposed method under different noises. The experimental results of approximation quality on six datasets are shown in Figs. 10, 11, 12, 13, 14, and 15 under nine membership functions. The graphic parameters are the same as those above. In these figures, we could find that the approximation quality is mostly higher than that of the other three compared methods except some cases. For Balance and Wifi_localization_ok Objects, the approximation quality of CE-fusion is all higher than that of the other three compared methods. Meanwhile, for User Knowledge Modeling, Pima, Vehicle, and Winequality_red, respectively, the CE-fusion method is higher than other M-fusions for 6, 6, 8, and 7 times in 9 experiments. All the experimental results verify the superiority of the CE-fusion method under different noises.

Fig. 10

The approximation quality of User Knowledge Modeling under nine noises

Fig. 11

The approximation quality of Balance under nine noises

Fig. 12

The approximation quality of Pima under nine noises

Fig. 13

The approximation quality of Vehicle under nine noises

Fig. 14

The approximation quality of Winequality_red nine noises

Fig. 15

The approximation quality of Wifi_localization_ok Objects under nine noises

Conclusions

To sum up, concept learning is a challenging, engaging, and promising research direction. Moreover, concept learning deserves to be studied based on granular computing from the perspective of cognitive computing, which may be beneficial to describing and understanding human cognitive processes in a conceptual knowledge way. In order to improve the efficiency and flexibility of concept learning, this paper mainly focuses on concept learning via granular computing from multi-source fuzzy decision tables. It is well known that different fusion methods will have different results when facing some multi-source fuzzy information. The article analyzes the cognitive mechanism of forming concepts from philosophy and cognitive psychology in multi-source fuzzy decision tables. We have considered a novel fusion method based on conditional entropy to fuse multi-source decision tables to describe the cognitive process. Then, granular computing has been combined with the cognitive concept to improve the efficiency of concept learning. The obtained results in this paper may be beneficial to simulating brain intelligence behaviors, including perception, attention, and learning.

Nevertheless, learning cognitive concepts from multi-source information is a challenging task. Although our work has put forward theoretical frameworks and methods to solve this problem, it is not enough in the application, for example, how to describe approximation of the intent of a cognitive concept in multi-source information tables. It includes the logical and semantic explanation of approximate cognitive concepts, theories, and methods of concept learning from an incomplete or multi-source information table and how to apply these theories in the real world. Some in-depth studies like these issues will be investigated in our future work.