Introduction

Brain computer interfaces (BCIs) establish direct passages between brain and external devices for communication and control [1]. Electroencephalogram (EEG) is the most widely used brain signal in BCIs, due to its advantages of portability, economy, and reliability. However, it is known that EEG is also very easily interfered by various artifacts. Electrooculogram (EOG) is one of the most important artifacts in EEG, causing influence on the performance of BCIs [2]. So, it is significant to remove EOG artifacts automatically while retaining more effective neural data.

In the existing literature, blind source separation (BSS) techniques are widely used in artifacts removal from EEG signals [3,4,5], which mainly can be classified into the following three categories. (1) Principal component analysis (PCA): its decomposition produces components from unrelated sources, but its orthogonality assumption is not often consistent with the EEG data in practice [6]. (2) Independent component analysis (ICA): it uses higher-order statistics to separate the recorded signals into some independent components [7] and thus increases the computational complexity greatly. Besides, ICA requires that no more than one source signal should obey the Gaussian distribution, which significantly limits its application in EEG data. (3) Canonical correlation analysis (CCA): it is an analysis method based on second-order statistics with using less processing time. CCA is used to generate components derived from their uncorrelated sources [8]. Previous studies have shown the superiority of CCA over ICA in removing artifacts from EEG [9, 10].

In summary, CCA method costs less processing time than ICA. At the same time, CCA does not need the conditions of orthogonality assumption and no more one source signal obeying the Gaussian distribution, which can overcome these shortcomings in PCA and ICA. However, if the identified EOG component is set to zero directly, some useful neural data contained would be removed. What is worse, this direct removal may cause bad final analysis results. Fortunately, empirical mode decomposition (EMD) is an adaptive signal decomposition method, which can be used to extract the neural data from the EOG component. It decomposes the EOG component into a set of intrinsic mode functions (IMFs). Then, the IMFs uncorrelated to EOG component, i.e., the IMFs containing neural data, are extracted and retained. But, EMD has the mode mixing problem [11], which will lead to extracting the desired IMFs inaccurately. The ensemble empirical mode decomposition (EEMD) is one improvement of EMD [12], and it has advantages of the EMD while solving the mixing mode problem.

This paper presents a novel method called CCA-EEMD approach to remove EOG artifacts from EEG data. In the proposed CCA-EEMD algorithm, CCA can quickly decompose the original EEG data into several uncorrelated components. Next, the EEMD is applied to extract the desired IMFs from the EOG component precisely. As a result, CCA-EEMD can remove EOG artifacts automatically and effectively as well as remains more desired data. In comparison with ICA and CCA methods, the proposed CCA-EEMD has better performance in EOG artifacts removal.

This paper is organized as follows: the “Methods” section describes the CCA, EEMD, and the proposed CCA-EEMD algorithms as well as EEG dataset. The outcomes and analyses of the study are given in the “Results and Discussion” section. Finally, the “Conclusion” section gives a brief conclusion to this paper.

Methods

BSS Using CCA

In the BSS, let S(t) = [s 1(t), s 2(t),  … , s l (t)]T denotes the l uncorrelated unknown source signals. With an unknown mixture for S(t), the observed EEG signals are acquired and denoted as X(t) = [x 1(t), x 2(t),  … , x l (t)]T, with t = 1,…, N, where N is the number of samples and l is the number of recorded channels. Thus, according to the BSS problem formulation, the relation between X(t) and S(t) is represented as

$$ X(t)= WS(t) $$
(1)

where W is the unknown mixing matrix. The aim of BSS is to find the mixing matrix W and recover the source signals S(t) satisfying

$$ S(t)={W}^{-1} X(t) $$
(2)

where W −1 is the inverse of W, called demixing matrix. CCA solves the BSS by decomposing the source signals to be maximally autocorrelated and mutually uncorrelated [13]. Moreover, the mixing matrix W can also be solved in the optimization process.

Let Y(t) be a delayed version of the raw EEG matrix Y(t) = X(t − 1). The \( \widehat{X}(t) \) and \( \widehat{Y}(t) \) can be obtained by centralizing X(t) and Y(t), respectively. Now by considering the linear combination in \( \widehat{X}(t) \) and \( \widehat{Y}(t) \), called the variates, we will have the following equations:

$$ \begin{array}{l}\mu ={a}_1{\widehat{x}}_1+{a}_2{\widehat{x}}_2+\dots +{a}_l{\widehat{x}}_l={A}^T\widehat{X}\\ {}\nu ={b}_1{\widehat{y}}_1+{b}_2{\widehat{y}}_2+\dots +{b}_l{\widehat{y}}_l={B}^T\widehat{Y}\end{array} $$
(3)

In this case, CCA aims to find the weighting vectors A = [a 1, a 2,  … , a l ]T and B = [b 1, b 2,  … , b l ]T that will maximize the correlation ρ between the variates μ and ν [9]:

$$ \rho =\frac{A^T{C}_{xy} B}{\sqrt{\left({A}^T{C}_{xx} A\right)\left({B}^T{C}_{yy} B\right)}} $$
(4)

where C xx and C yy are the autocovariance of μ and ν, respectively, and C xy is the crosscovariance matrix of μ and ν. In the fact, the maximum of ρ can be obtained by setting the derivatives of (4) to zero with respect to A and B and then one can obtain the following equations:

$$ \begin{array}{l}{C}_{xx}^{-1}{C}_{xy}{C}_{yy}^{-1}{C}_{yx} a={\lambda}^2 A\\ {}{C}_{yy}^{-1}{C}_{yx}{C}_{xx}^{-1}{C}_{xy} b={\lambda}^2 B\end{array} $$
(5)

where the canonical correlation coefficient λ can be determined as the square root of the eigenvalue, where A and B are the corresponding eigenvectors. The first pairs of A and B are the eigenvectors corresponding to the largest canonical correlation coefficient λ. The next pairs of A and B are the remaining eigenvectors in descending order of correlation coefficient [14], which are uncorrelated to previous pairs. In practice, X(t) and Y(t) contain almost the same data, so are the matrices of A and B. Thus, it only needs to solve (5) for A. The generated A can be used to separate the observed signals into maximally autocorrelated and mutually uncorrelated source signals, which is used as the estimation of W −1 in BSS. Furthermore, the generated variate μ can be used in the estimation of the source signals S(t).

On the other hand, kurtosis is a measure of signal peaks and it has simple computation [15]. It has been proved that the kurtosis values of EOG components are much higher than those of normal components. So, kurtosis values can be used to identify the EOG components. Kurtosis values of each component are computed by the next formula

$$ {k}_i={m}_4-3{m}_2^2 $$
(6)

where m n is the nth central moment: \( {m}_n= E\left\{{\left({s}_i(t)-{\tilde{s}}_i(t)\right)}^n\right\} \) (1 ≤ i ≤ l). By setting a threshold K v , EOG components can be identified automatically. The identified EOG components are denoted by O(t) = [o 1(t), o 2(t),  … , o m (t)]T, with m the number of EOG components. Then, the O(t) is used to be the input signal of EEMD method described below to extract the desired EEG data, which is described in the “Introduction to EEMD” section.

Introduction to EEMD

EMD and Mode Mixing

EMD is a signal decomposition method, which can decompose a time series signal into a set of IMFs, and also this decomposition of the signal is data driven. So, the EMD method has advantages of adaptivity and flexibility. More precisely, let o i (t) be an EOG component from O(t) = [o 1(t), o 2(t),  … , o m (t)]T (i = 1, 2…m). Then, the EMD can decompose the o i (t) into a set of IMFs denoted by \( {\left\{{c}_{ij}(t)\right\}}_{j=1}^n \) in the following equation:

$$ {o}_i(t)=\sum_{j=1}^n{c}_{i j}(t)+{r}_i(t) $$
(7)

where r i (t) is the residual of data after n IMFs are extracted from o i (t). In order to obtain some meaningful IMFs, the IMFs must satisfy the following two conditions [16]:

  1. (1)

    In the whole data series, the number of extrema and the number of zero crossings must be equal or differ at most by 1.

  2. (2)

    The mean value of the envelopes defined by local maxima and minima must be 0 at all points.

The IMFs can be obtained by using the following shifting procedure:

  1. (1)

    Find all of the extrema of o i (t), including maxima and minima.

  2. (2)

    By using cubic spline interpolation, interpolate between maxima to obtain an upper envelope q i (t) and minima to obtain a lower envelop p i (t), respectively.

  3. (3)

    Calculate the local mean, m i (t) = (q i (t) + p i (t))/2.

  4. (4)

    Subtract m i (t) from o i (t) to construct oscillating signalh i (t) = o i (t) − m i (t).

  5. (5)

    If h i (t) meets the above two conditions, c i (t) = h i (t) will become an IMF, and then, we can replace o i (t) with the residual r i (t) = o i (t) − c i (t) and repeat step (1); otherwise, we replace o i (t) with h i (t) and repeat step (1).

Finally, a set of IMFs, denoted by C i (t) = [c i1(t), c i2(t),  … , c in (t)], where n denotes the number of IMFs, are decomposed from the o i (t). However, if the given signal contains noise, it will eventually lead to the uneven distribution of extrema and thus will result in envelopes consisting of the noise envelope and the real signal envelope. Consequently, one IMF includes oscillations of dramatically disparate scales or a component of similar scale residing in different IMFs [17], which is called mode mixing. In fact, EOG component o i (t) may contain EOG signals and the signals uncorrelated to EOG (real EEG signals), so the mode mixing problem is unavoidable. As a result, the desired IMFs cannot be extracted and reserved accurately in current analysis.

EEMD Method

In order to solve the mode mixing problem of EMD, an improved method ensemble-EMD (EEMD) was proposed in [2]. Technically, the white noise is added to the given signal, which will provide a relatively uniform reference scale and distribution. Thus, the white noise will enhance the EEMD to avoid the mode mixing and help to extract the true signals in the given data [18]. The steps of EEMD method are described as follows:

  1. (1)

    Add a white noise series to the given signal.

  2. (2)

    By using the EMD, we can decompose the given signal with the added white noise into a set of IMFs.

  3. (3)

    Repeat step (1) and step (2) several times, and the added white noise must be different each time.

  4. (4)

    Obtain a set of IMFs, which are obtained from the ensemble mean of the corresponding IMFs achieved in step (2).

Finally, the given signal o i (t) is decomposed into a set of IMFs, denoted by C EEMD − i (t) = [c EEMD − i1(t), c EEMD − i2(t),  … , c EEMD − in (t)], where n is the number of IMFs.

CCA-EEMD Method

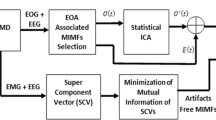
Based on previous analysis, we will propose a new CCA-EEMD approach for BSS. The flow chart of the proposed method is illustrated in Fig. 1. We will explain each step in more details.

Fig. 1
figure 1

Flow chart of CCA-EEMD

Full size image
  1. (1)

    The original EEG data X(t) = [x 1(t), x 2(t),  … , x l (t)]T from l channels is used as the input signal.

  2. (2)

    CCA is used to separate X(t) into l uncorrelated components, and they are denoted as S(t) = [s 1(t), s 2(t),  … , s l (t)]T. In this case, the mixing matrix W can also be obtained.

  3. (3)

    The kurtosis values of each component in S(t) are computed. Then, a threshold K v is setup. The components with kurtosis values larger than K v are identified as the EOG components, and they are denoted as O(t) = [o 1(t), o 2(t),  … , o m (t)]T, where m is the number of the identified EOG components.

  4. (4)

    The EEMD is applied to decompose these EOG component o i (t)(1 ≤ i ≤ m) into a set of IMFs, denoted as C EEMD − i (t) = [c EEMD − i1(t), c EEMD − i2(t),  … , c EEMD − in (t)]. Then, the correlation coefficient value between each IMF c EEMD − ij (t)(1 ≤ j ≤ n) and its corresponding EOG component o i (t) is computed, respectively. These IMFs with the correlation coefficient values smaller than the threshold K r are identified as the IMFs unrelated to EOG, denoted by C eeg − i (t) = [c eeg − i1(t), c eeg − i2(t),  … , c eeg − ik (t)], where k is the number of the IMFs uncorrelated to EOG. The identified IMFs C eeg − i (t) are retained and then are used to construct the new component o iclean(t). In the end, all of the new components o iclean(t) form a new vector, \( {O}_{\mathrm{clean}}(t)={\left[{o}_1^{\prime }(t),{o}_2^{\prime }(t),\dots, {o}_m^{\prime }(t)\right]}^T \).

  5. (5)

    Now, the clean EEG data denoted as \( {X}_{\mathrm{CCA}\hbox{-} \mathrm{EEMD}}(t)={\left[{x}_1^{\prime }(t),{x}_2^{\prime }(t),\dots, {x}_l^{\prime }(t)\right]}^T \) are reconstructed by the new components O clean(t) and other EEMD-unprocessed components.

EEG Dataset Description

In this paper, the dataset for seven healthy subjects is from the publicly available datasets of BCI Competition IV. For each subject, the two classes of motor imagery (MI) were selected from three classes of left hand, right hand, and foot imagery. Each class of MI contains 100 trails. The EEG dataset was sampled at 1000 Hz. More details are described in [19]. Fifteen channels most relevant to MI were chosen in this study: F3, F1, FZ, F2, F4, C5, C3, C1, CZ, C2, C4, C6, P1, PZ, and P2.

Results and Discussion

EEG Artifact Removal

Figure 2 shows a trail of the original EEG data randomly selected from the described EEG dataset. Obviously, the original EEG data contain a large number of EOG artifacts. Figure 3 shows 15 uncorrelated components separated from original EEG data by CCA. Then, the third component was identified as the EOG component automatically. Figure 4 shows the comparison of decomposition results for the EOG component using the EEMD and EMD. Figure 4a shows 12 IMFs decomposed by the EEMD. Visibly, the EOG data mainly concentrates in the first IMF. Figure 4b shows 14 IMFs decomposed by the EMD. Apparently, the decomposition results by using the EEMD are better than those by using the EMD. Figure 5 shows the comparison of correlation coefficient values using the EEMD and EMD. Each correlation coefficient value using the EMD is larger than the threshold value of 0.05. So, no IMFs can be extracted. This arises from the mode mixing problem of the EMD. In the contrary, the correlation coefficient values of the first IMF are up to 1 using the EEMD. In other words, the EOG data mainly concentrates in the first IMF. The second and third IMFs were automatically recognized as the IMFs uncorrelated with the EOG. They were retained. Besides, the correlation coefficient values of the second and third IMFs are less than all those of the IMFs decomposed by the EMD, which can further explain that the EEMD can solve the mode mixing problem better. Figure 6 shows the clean EEG data by using the proposed CCA-EEMD. In comparison with the original EEG data, it is obvious that the EOG artifacts are removed greatly in the clean EEG data. The remaining trails from the dataset were also processed, and similar results were obtained.

Fig. 2
figure 2

Original EEG data

Full size image
Fig. 3
figure 3

Fifteen components separated by CCA

Full size image
Fig. 4
figure 4

The comparison of decomposition results using EEMD and EMD. a Twelve IMFs decomposed by EEMD. b Fourteen IMFs decomposed by EMD

Full size image
Fig. 5
figure 5

Comparison of correlation coefficient values using EEMD and EMD

Full size image
Fig. 6
figure 6

Clean EEG data

Full size image

Quantification of Performance

In this section, the performance of the proposed CCA-EEMD method is quantified in three ways. Meanwhile, two existing methods, ICA [7] and CCA, were also used to make comparisons with the proposed method.

Root Mean Square Error

The root mean square error (RMSE) can measure how well the neural data are preserved in clean EEG data after removing EOG artifacts. The RMSE is defined as

$$ \mathrm{RMSE}=\sqrt{\sum_{k=1}^L{\left({\mathrm{EEG}}_{\mathrm{source}- k}-{\mathrm{EEG}}_{\mathrm{corrected}- k}\right)}^2} $$
(8)

where L is the number of electrodes, and EEGsource − k denotes the clear EEG of the kth electrode, which does not contain EOG artifacts from the same subject. Besides, EEGcorrected − k denotes the reconstructed signals of the kth electrode after EOG artifacts removal. The smaller RMSE value is, the more neural data in EEG will be preserved. The average values of seven subjects’ RMSE for CCA-EEMD, CCA, and ICA methods are calculated and shown in Table 1. One can see that the value of RMSE for CCA-EEMD is the smallest, i.e., the EEG signals after removing EOG artifacts by CCA-EEMD can preserve more neural data than other two methods.

Table 1 Comparison of average RMSE for CCA-EEMD, CCA, and ICA
Full size table

Signal Noise Ratio

The larger signal noise ratio (SNR) is, the better the effects of EOG artifacts removal are. The SNR is defined as

$$ \mathrm{SNR}=10 \log \frac{\sum_{k=1}^L{\left({\mathrm{EEG}}_{\mathrm{corrected}- k}\right)}^2}{\sum_{k=1}^L{\left({\mathrm{EEG}}_{\mathrm{source}- k}-{\mathrm{EEG}}_{\mathrm{corrected}- k}\right)}^2} $$
(9)

The average values of seven subjects’ SNR for CCA-EEMD, CCA, and ICA methods are shown in Table 2. The value of SNR for CCA-EEMD is the largest, i.e., the EEG signals processed by CCA-EEMD can remove more EOG artifacts than other two methods.

Table 2 Comparison of average SNR for CCA-EEMD, CCA, and ICA
Full size table

Classification Accuracy

To some extent, the classification accuracy can reflect the amount of residual information and the distortion degree of the EEG. So, the classification accuracy is also often used as one performance evaluation. As it is described in the “EEG Dataset description” section, two classes of left and right hand motor imagery tasks are classified in this study. In BCIs, common spatial patterns (CSP) method is the most widely used spatial filtering technique and can extract discriminative features for EEG-based BCI classification tasks. It essentially finds spatial filters that maximize the variance for one class and simultaneously minimize the variance for the other class. More details of CSP are described in [20]. There are a great many methods for classification, e.g., Sparse Bayesian [21,22,23], support vector machine (SVM), probabilistic neural network (PNN), and linear discriminant analysis (LDA) [24,25,26]. Among them, LDA has simple computation and is one of the most common classifiers. Here, CSP was used to extract a six-dimensional feature vector of the clean EEG, in which one spatial filter was used. Then, LDA was used to classify the extracted features. In the case of 20 times fivefold cross-validation, the average classification accuracies for three methods are shown in Table 3. In addition, the standard error is also added in Table 3. For each subject, it is obvious that the classification accuracy using CCA-EEMD is higher than that using CCA and ICA. The proposed CCA-EEMD has benefit for the feature extraction and classification than two other methods.

Table 3 Comparison of average classification accuracies for different and subjects and methods
Full size table

Discussion

In recent years, CCA and EMD have been increasingly applied to EEG analysis [27,28,29,30]. For

instance, CCA is applied to extract common basis [27]. Besides, an improved CCA method called multiset canonical correlation analysis (MsetCCA) is proposed to improve frequency recognition [28]. By using the EMD, the EEG signals of epilepsy patients are decomposed into several IMFs. The nonlinear features of IMFs are used for computer-aided diagnose of normal, inter-ictal, and ictal states in [29]. Moreover, multivariate extensions of empirical mode decomposition (MEMD) are employed with classification and its noise-assisted mode of operation (NA-MEMD) can provide a highly localized time-frequency representation [30].

In this study, a novel method called CCA-EEMD is proposed and applied to remove EOG artifacts automatically while retaining more neural data. Plenty of studies have shown that the EOG artifacts overlapped with the MI-based EEG signals in some frequency ranges. So, the EOG component may contain the useful information of MI tasks. In this paper, the EOG component can be identified automatically by its kurtosis value. The identified EOG component is not removed directly due to a fact that it contains useful information. Next, the desired information can be extracted and retained from the EOG component by EEMD. The proposed method can retain useful signals to a greater extent. According to three performance indexes, it is further proved that the proposed method is superior to other two common methods.

However, the size of the dataset used in this paper is relatively small. In future, large datasets will be created and put into the research to validate the proposed CCA-EEMD. In addition, the reference signal selected in CCA has a great influence on the results of decomposition [28].

Conclusion

In this paper, a novel method, called CCA-EEMD, is developed for EOG artifacts removal. The CCA method is one of the BSS methods, which has lower computational complexity. In the meantime, the EEMD method can extract the desired IMFs accurately, while keeping the integrity of EEG data to the maximum extent. Three ways are used to evaluate the performance of the proposed CCA-EEMD. From the experimental results, and after comparisons with CCA and ICA methods, one can see that the proposed method can not only remove EOG artifacts better but also retain more neural data of EEG. Thus, the proposed CCA-EEMD has great significance to the improvement of BCIs.