Research on Multi-Parametric Coupling Design Method of Deformable Boring Bar in Embedded Giant Magnetostrictive Actuator

Abstract

Deformable boring bar is the executive component of embedded giant magnetostrictive actuator (GMA), which plays a key role in the output performance of embedded GMA in precision machining of non-cylindrical piston pinhole. In this paper, a multi-parametric coupling design method was presented for deformable boring bar and giant magnetostrictive material. Firstly, the dynamic model of deformable boring bar was built. Second, the performance index of length-diameter ratio was introduced, and the problem of multi-parametric coupling design was solved by using the idea of nonlinear programming. The first-order natural frequency, the end output displacement and the output force of deformable boring bar were taken as the evaluation indexes to ensure the performance requirements of embedded GMA. Finally, according to project requirements and proposed method, an embedded GMA with high frequency response and large output displacement was further designed, which met the performance requirements of displacement and stiffness in precision machining of non-cylindrical piston pinholes and also verified the validity of the design method.

1 Introduction

Giant magnetostrictive actuator (GMA) is a kind of precision electromechanical component, which is widely used because of its nanometer output precision, high frequency and large thrust output [1, 2]. For example, GMA is used as displacement actuator in precision machining [3, 4], and as active vibration isolator component in vibration field [5].

GMA can be divided into direct GMA and embedded GMA according to its structure and magnetic circuit characteristics [1]. The giant magnetostrictive intelligent boring bar device designed in this paper belongs to embedded GMA, which can be used for precise boring of non-cylindrical piston pinholes to reduce it’s stress concentration [6]. At present, there have been many related studies about the design of direct GMA [7,8,9], and a relatively perfect design criterion has been formed, such as improving the intensity and uniformity of magnetic field, reducing eddy current loss and magnetic leakage, and improving electromagnetic conversion efficiency. However, the design of embedded GMA cannot directly apply the design criteria of direct GMA due to its own structural characteristics, which needs to be considered comprehensively, but there is little research on this aspect at present. Zhao et al. [10] established a three-dimensional finite element model of embedded GMA based on piezo-magnetic equation and Hamiltonian principle, and solved the model with the form of weak solution. However, the solution efficiency of designed model was low and the stiffness of corresponding deformable boring bar was insufficient. Zhang et al. [11] established a coupling optimization model of mechanical, electrical, magnetic and thermal fields to analyze embedded GMA. But the output displacement did not meet the requirements, and the specific method for solving the initial parameters of deformable boring bar was not given.

In GMA, flexible hinge mechanism is widely used as magnifying mechanism of magnetostrictive displacement because of its high dynamic performance [12, 13]. Deformable boring bar plays a role of displacement amplification in the embedded GMA, and its performance determines the machining quality of the non-cylindrical piston pinholes. However, the structure of the embedded GMA is compact, the deformation boring bar and GMM parameters are coupled with each other, the dimension parameters of GMM determine the output force and displacement of the embedded GMA, and the dimension parameters of the deformation boring bar determine its static and dynamic characteristics, so the design method of direct GMA cannot be applied directly. It is necessary to establish a model to reflect the performance of embedded GMA, and to find an effective multi parameter coupling design method, the most important of which is to model the deformable boring bar.

At present, the main methods to establish models of flexible hinge mechanisms are mathematical modeling method and finite element modeling method [14, 15]. Common mathematical modeling methods include Pseudo-rigid-body method [16, 17] and Castigliano second theorem method [18]. The pseudo-rigid-body modeling method can characterize the kinematic and dynamic characteristics of flexure hinge from mechanism. Castigliano second theorem involves the calculation of partial differential equation, which makes the solution of model complex. The mathematical modeling method mainly depends on the accuracy of the model, the deviation between mathematical model and experimental simulation may be as large as 50% [19]. Finite element method is a variational method and can minimize the error function, which is the most accurate modeling method for flexible hinge mechanism up to now. For example, Huang et al. [20] used FEA-based response surface methodology to solve the multi-objective optimization problem, which improved the static and dynamic characteristics of a flexure-based XY positioning platform. The response surface methodology can reduce the error caused by the mathematical model and shorten the calculation time. But if GMM's nonlinear characteristics are added to the finite element simulation, the analysis will become very complex. So the mathematical modeling method is more efficient for designing deformable boring bar of embedded GMA.

This paper put forward a multi-parametric coupling design method for embedded GMA. First of all, a dynamic model of deformable boring bar was built. Then, the problem of multi-parametric coupling design between GMM and the deformable boring bar was solved with the idea of nonlinear programming. Finally, according to the requirements of given project, an intelligent boring bar structure with high frequency and large output displacement was designed based on the proposed method in this paper, and finite element analysis and the relative key performance tests were carried out. The results showed that the designed intelligent boring bar met the required performance of displacement and stiffness, which indicated the effectiveness of design method.

2 Structure Scheme of Embedded GMA

As shown in Fig. 1, embedded GMA is mainly composed of GMM, deformable boring bar, magnetic conducting block, magnetic yoke, excitation coil, coil skeleton and coil shell. Among them, deformable boring bar, GMM and magnetic conducting block are combined into one part. The pre-pressure of GMM is adjusted by controlling the thickness of magnetic conducting block. Magnetic yoke, front and back magnetic conducting blocks and GMM form a closed magnetic circuit. Driven by excitation coil, GMM will generate axial elongation $\Delta L$. Through the amplification of deformable boring bar, the controllable radial displacement $\Delta R$ at the end of deformable boring bar will be put out. It is difficult to design embedded GMA because of the parameters interaction between GMM and deformable boring bar.

Fig. 1

Structure of embedded GMA. (1 deformable boring bar, 2 end cover, 3 coil shell, 4 excitation coil, 5 coil skeleton, 6 GMM, 7 magnetic conducting block)

3 Dynamic Modeling of Deformable Boring Bar

As shown in Fig. 2, the geometric model of deformable boring bar is simplified. The embedded GMA is a cantilever structure, which can be simplified as a damped forced vibration system with small angle assumption. According to Newton's second law and D'Alembert principle, the dynamic equation of the deformable boring bar is as Eq. (1):

$$ I_{\theta } \ddot{\theta } + C_{\theta } \ddot{\theta } + K_{\theta } \theta = F_{GMM} \left( t \right)l_{3 } - F_{y} \left( t \right)L_{0} $$

(1)

where $I_{\theta }$ is the total moment of inertia,$C_{\theta }$ is the total rotational damping, ${\text{K}}_{{\uptheta }}$ is the total rotational stiffness, $F_{{\text{y}}} \left( t \right)$ is the radial resistance, $F_{{{\text{GMM}}}}$ is the output force of GMM.

Fig. 2

Simplified geometric model of deformable boring bar

The evaluation indexes of the deformable boring bar include the maximum radial output displacement at the end of deformable boring bar $\Delta R_{\max }$, the radial output force $F_{{{\text{R}} - {\max}}}$ at the end of deformable boring bar corresponding to the maximum displacement, and the first-order natural frequency of deformable boring bar $f_{n}$.

3.1 The Maximum Radial Output Displacement

Due to the magnetostrictive saturation of GMM, the length of GMM should be long enough to meet the maximum strain requirement. Meanwhile, during the process of elongation, GMM is subjected to increasing compressive stress of the deformable boring bar, so the length of GMM is derived as follows:

$$ L_{{{\text{GMM}}}} = \frac{{\Delta L_{s} }}{{\varepsilon_{s} }} = \frac{{\Delta R_{\max } /K_{{\text{R}}} }}{{\delta^{\prime}\lambda_{s} - K_{{\text{t}}} \Delta R_{\max } /\left( {K_{{\text{R}}} E_{{{\text{GMM}}}} } \right)}} $$

(2)

where $\Delta L_{s}$ is the saturation elongation of GMM; $\varepsilon_{{\text{s}}}$ is the actual saturated strain of GMM, which is the difference of strain caused by saturated magnetostriction and compressive stress; $\delta^{\prime}$ is the mathematical factor, and the linear working displacement of general design is half of the saturation elongation, thus take $\delta^{\prime} = 0.5$; $K_{{\text{t}}}$ is the axial stiffness coefficient of the deformable boring bar, which is the ratio of the compressive stress of GMM on deformable boring bar to the axial elongation of the deformable boring bar. The larger $K_{{\text{t}}}$ is, the greater the stress ${\upsigma }$ variation of GMM, and more unfavorable to the elongation of GMM; $E_{{{\text{GMM}}}}$ is Young's modulus of GMM; $K_{{\text{R}}}$ is the displacement amplification ratio of the deformable boring bar, i.e., $K_{{\text{R}}} = l_{0} /l_{3}$, and thus:

$$ \Delta R_{\max } = \frac{{L_{{{\text{GMM}}}} \lambda_{{\text{s}}} \delta^{\prime}K_{{\text{R}}} E_{{{\text{GMM}}}} }}{{E_{{{\text{GMM}}}} + L_{{{\text{GMM}}}} K_{{\text{t}}} }} $$

(3)

3.2 The Output Force of the Deformable Boring Bar

For quasi-static loads, GMM can be simplified as a linear elastomer with a stiffness of $k_{{\text{g}}}$, The relationship between the output force and the output displacement at the end of deformable boring bar is derived as follows:

$$ F_{{\text{R}}} = F_{{\text{b}}} - \left( {K_{{\text{g}}} + K_{{\text{t}}} A_{{{\text{GMM}}}} } \right)\Delta R/K_{{\text{R}}}^{2} $$

(4)

where $F_{{\text{b}}}$ is the maximum output force of deformable boring bar when $\Delta R = 0$; $A_{{{\text{GMM}}}}$ is the cross sectional area of GMM. The stiffness of GMM is described as follows:

$$ K_{{\text{g}}} = \frac{{E_{{{\text{GMM}}}} A_{{{\text{GMM}}}} }}{{L_{{{\text{GMM}}}} }} $$

(5)

Due to the displacement amplification, the output force of GMM is derived as follows:

$$ F_{{\text{G}}} = F_{{\text{R}}} K_{{\text{R}}} + k_{{\text{t}}} A_{{{\text{GMM}}}} \Delta R/K_{{\text{R}}} + F_{0} = F_{{\text{b}}} K_{{\text{R}}} - K_{{\text{g}}} \Delta R/K_{{\text{R}}} + F_{0} $$

(6)

where $F_{0} = \sigma_{0} A_{{{\text{GMM}}}}$ is the pre-pressure of GMM. When GMM reaches the status of saturation magnetostriction, its output force becomes 0. For Eq. (2), take $\delta^{\prime } = 1$, and the saturated output displacement at the end of deformable boring bar is obtained as follows:

$$ \Delta R_{{\text{s}}} = \frac{{L_{{{\text{GMM}}}} \lambda_{{\text{s}}} K_{{\text{R}}} E_{{{\text{GMM}}}} }}{{E_{{{\text{GMM}}}} + L_{{{\text{GMM}}}} K_{{\text{t}}} }} $$

(7)

With $F_{{\text{R}}} \left( {\Delta R_{{\text{s}}} } \right) = 0$,

$$ F_{{\text{b}}} = \frac{{E_{{{\text{GMM}}}} A_{{{\text{GMM}}}} \lambda_{{\text{s}}} }}{{K_{{\text{R}}} }} $$

(8)

In conclusion, the relationship between the output force and the output displacement at the end of the deformable boring bar in embedded GMA is shown in Fig. 3.

Fig. 3

Relationships between the output force and the output displacement of the ideal GMM and embedded GMA

3.3 First-Order Natural Frequency of Deformable Boring Bar

According to Eq. (1), the first-order natural frequency of deformable boring bar

$$ f_{{\text{n}}} = \frac{1}{2\pi }\sqrt {\frac{{K_{\theta } }}{{I_{\theta } }}} $$

(9)

From the above modeling, it could be seen that the parameters in the design of embedded GMA are mutually coupled, and the existence of many contradictory design indicators will bring great difficulties to the parameter solution. Therefore, it is necessary to find an effective decoupling design method.

4 Coupling Dimension Design of Deformable Boring Bar and GMM

In order to simplify the design, the dimensions of the clamping part and the displacement amplification part of the deformable boring bar have been determined according to the requirements for embedded GMA applying for specific occasions, so the dimensions of $l_{2}$, $l_{5}$, $n$ and $d_{0}$ in Fig. 2 are given.

4.1 Determine the Thickness $m$ of Magnetic Conducting Block

The principle of determining the thickness of magnetic conducting block is that the thickness of the magnetic conducting block should be equal to the thickness of magnetic yoke. In order to reduce the cantilever length of the deformable boring bar, the thickness of magnetic conducting block with small size should be selected under the condition of preventing magnetic saturation and ensuring smooth magnetic circuit.

4.2 The Optimization Design of Deformable Boring Bar and GMM

4.2.1 Determine Design Variables, Design Objectives and Constraints

The design variables are length and radius of GMM, diameter of deformable section of deformable boring bar and radius of flexure hinge, which are as follows:

$$ X_{{\text{b}}} = \left( {L_{{{\text{GMM}}}} , R_{{{\text{GMM}}}} , d_{1} , R_{1} } \right) $$

(10)

The design objectives of embedded GMA are as follows:

$$ \left\{ {\begin{array}{*{20}l} {\Delta R_{\max } \ge \Delta R_{0} } \hfill \\ {F_{{{\text{R}}\_\max }} \ge F_{{{\text{y}}\_\max }} } \hfill \\ {f_{{\text{n}}} \ge f_{{{\text{n}}\_0}} } \hfill \\ \end{array} } \right. $$

(11)

where $\Delta R_{0}$, $F_{{{\text{y}}\_\max }}$ and $f_{{{\text{n}}\_0}}$ respectively denotes the maximum design output displacement of embedded giant magnetostrictive micro-feed mechanism driven by low frequency, the output force requirement for maximum output displacement, and the first-order natural frequency requirement of deformable boring bar.

Since the semi-cylindrical GMM is embedded in the groove of the deformable boring bar together with the front and rear magnetic conducting blocks, the dimensions of deformable boring bar and GMM are coupled mutually, making it impossible to design the deformable boring bar independently. Therefore, an effective decoupling design method needs to be found out.

By comparing design variables with design objectives, it is found that four design variables could not be accurately solved with three design objectives. Therefore, another constraint condition is introduced, that is the length-diameter ratio of deformable boring bar, $k_{{\text{d}}} = \left( {l_{1} + l_{2} } \right)/d_{1}$. For shaft parts, if $k_{{\text{d}}} < 5$, it is called a rigid shaft; If $k_{{\text{d}}} = 5 \sim 10$, it is called a moderately rigid axis; If $k_{{\text{d}}} > 10$, it is called a flexible axis [21]. Aiming at the embedded giant magnetostrictive micro-feed mechanism for specific occasions, the stiffness of deformable boring bar can be guaranteed by restricting the length-diameter ratio of deformable boring bar. So the constraint is as follows:

$$ k_{{\text{d}}} \le k_{{{\text{d}}\_0}} $$

(12)

where $k_{{{\text{d}}\_0}}$ is the length-diameter ratio of the deformable boring bar limited by requirements.

The length diameter ratio parameter $k_{{\text{d}}}$ characterizes the dimension relationship between the deformable boring bar and GMM, then it is possible to solve the four design variables of deformable boring bar and GMM by Eqs. (11) and (12). However, it could be seen from the modeling in the previous section that the design objectives are higher-order functions of design variables, which puts forward a difficult problem for the solution of design variables. But the feasible region of design variables can be found by using the method of nonlinear programming.

4.2.2 Select the Values of $R_{1}$ and $k_{{\text{d}}}$ and Draw the Influence Law Figures of Design Variables on Design Objectives

The typical value of radius $R_{1}$ of flexure hinge is determined according to the requirements. The selection principle of $R_{1}$ is as follows: under the condition of preventing stress concentration, choosing a smaller $R_{1}$ value could reduce the diameter $d_{1}$ of the deformable section of deformable boring bar and reduce the diameter of excitation coil on the premise of guaranteeing the performance of deformable boring bar. In order to ensure the rigidity of the deformable boring bar, generally, the smaller length diameter ratio $k_{{\text{d}}}$ of deformable boring bar is taken.

Due to the size limitation of GMM in common use, the range of each variable is set as Eq. (13).

$$ \left\{ {\begin{array}{*{20}l} {{\text{5mm }} \le {\text{ R}}_{{{\text{GMM}}}} { } \le {\text{ 25mm}}} \hfill \\ {{\text{40mm }} \le {\text{ d}}_{{1}} { } \le {\text{ 80 mm}}} \hfill \\ \end{array} } \right. $$

(13)

Set $R_{1} = 5{\text{mm}}$, $k_{{\text{d}}} = 5$ as an example, the effect of design variables on design objectives are shown in Fig. 4.

Fig. 4

Influences of design variables on design objectives; a $\Delta R_{\max }$, b $f_{{\text{n}}}$, and c $F_{{{\text{R}}\_\max }}$

According to Fig. 4, under the constraints of constant length-diameter ratio, with the increase of $R_{{{\text{GMM}}}}$ and $d_{1}$,the maximum output displacement at the end of deformable boring bar increases while the natural frequency of deformable boring bar decreases. The output force increases with the increase of $R_{{{\text{GMM}}}}$ and the decrease of $d_{1}$, and the value of $d_{1}$ seems to have little effect on the output force.

These rules can be explained as follows: under the condition of constant length-diameter ratio, the length of GMM and the cantilever length of deformable boring bar become longer with the increase of $d_{1}$, and the stiffness of deformable boring bar decreases with the increase of $R_{{{\text{GMM}}}}$. Therefore, with the increase of $R_{{{\text{GMM}}}}$ and $d_{1}$, the maximum output displacement at the end of deformable boring bar increases and the natural frequency decreases. The increase of $R_{{{\text{GMM}}}}$ makes the output force of GMM enlarge. Thus, the output force increases with the increase of $R_{{{\text{GMM}}}}$ when the displacement at the end of deformable boring bar reaches the maximum. However, assuming that $R_{{{\text{GMM}}}}$ is constant, with the increase of $d_{1}$, the stiffness of deformable boring bar increases and the displacement amplification ratio $k_{{\text{R}}}$ decreases. According to Eqs. (4) and (8), it could be seen that $F_{{\text{b}}}$ increases. However, with the increase of $k_{{\text{t}}}$ and $\Delta R_{\max }$, the output force $F_{{\text{R}}}$ corresponding to the maximum displacement at the end of deformable boring bar decreases, whereas, the effect is not significant.

4.2.3 Determine the Feasible Region of Design Variables by Nonlinear Programming Method

Based on the requirements of each design objective, the intersection lines between the design objectives’ sections and the surfaces of Fig. 4 are obtained to calculate the feasible region of design variables. If the feasible region could not be obtained, it means that there is no feasible solution among the current variables range, and thus the value of $R_{1}$ or length-diameter ratio $k_{{\text{d}}}$ needs to be adjusted until a feasible solution appears. The influence of $R_{1}$ and $k_{{\text{d}}}$ on the feasible region of design variables is shown in Figs. 5 and 6 respectively.

Fig. 5

Influence of $R_{1}$ on the feasible region of design variables when $k_{{\text{d}}} = 4.7$. (a $R_{1} = 0 \;{\text{mm}}$, b $R_{1} = 5 \;{\text{mm}}$, c $R_{1} = 10 \;{\text{mm}}$)

Fig. 6

Influence of ${\text{k}}_{{\text{d}}}$ on the feasible region of design variables when $R_{1} = 5\;{\text{mm}}$. (a $k_{{\text{d}}} = 4.6$, b $k_{{\text{d}}} = 4.7$, c $k_{{\text{d}}} = 4.8$)

From the above analysis, it could be seen that when the value of $k_{{\text{d}}}$ keeps constant, the feasible area of design variables increases with the increase of $R_{1}$. When $R_{1}$ is constant, the feasible area of design variables decreases with the increase of $k_{{\text{d}}}$. Therefore, in order to meet the requirements of design objectives, it is necessary to reasonably select the values of $R_{1}$ and $k_{{\text{d}}}$, so that the feasible region of design variables would exist.

4.2.4 Determine the Diameter of Deformable Bar $d_{1}$

In the case of feasible region, any value of $\left( {R_{1} , R_{{{\text{GMM}}}} , d_{1} } \right)$ in the feasible region can satisfy the requirements of design objective, and then the length of GMM can be calculated by Eq. (14).

$$ L_{{{\text{GMM}}}} = k_{{\text{d}}} d_{1} - l_{2} - n - 2m $$

(14)

As there are many feasible solutions, the solution with the smallest diameter of the deformable boring bar should be selected on the premise of satisfying the performance of the embedded GMA, which can reduce the length of GMM and the diameter of solenoid coil, so as to reduce the inductance and resistance of coil and reduce the driving power.

4.3 Discussion

Through the above four steps of multi-parametric coupling design method, using the idea of non-linear programming, the design problem of coupling parameters between the deformable boring bar and GMM is solved. Because $R_{1}$ and $k_{{\text{d}}}$ have influence on the feasible region, it is necessary to iterate the values of $R_{1}$ and $k_{{\text{d}}}$ repeatedly, so as to obtain the optimal solution with the minimum $d_{1}$, this process can be solved in MATLAB, and the design method will be used in the design of an intelligent boring bar for precise machining of non-cylindrical piston pinholes, and the validity of the design method is verified by finite element and experiment.

5 A Design Example of an Intelligent Boring Bar for Precision Machining of Non-Cylindrical Piston Pinholes

5.1 Design Objectives

The embedded GMA for precision machining of non-cylindrical piston pinholes, needs to meet the technical requirements of precision, frequency response, displacement, stiffness and cutting stability of non-cylindrical piston pinholes. In this example, In order to bore an elliptical hole with a radius difference of not less than 100 μm, the rotation speed of the boring bar is 3000r/min, so the vibration frequency of the embedded GMA is 100 Hz, the first-order natural frequency of the deformable boring bar should be far away from the vibration frequency of 100 Hz, it should be not less than 550 Hz according to our previous study. So the design objectives are as follows:

• (1) Maximum working trip: $\ge 100 {\mu m}$;

• (2) The output force must be sufficient enough to resist the radial cutting force;

• (3) First-order natural frequency: $\ge 550 {\text{Hz}}$;

According to reference of [21], the empirical formula of radial cutting force is described as follows:

$$ F_{y} = 9.81 \times 60^{{n_{{F_{y} }} }} C_{{F_{y} }} \cdot a_{p}^{{x_{{F_{y} }} }} \cdot f^{{ y_{{F_{y} }} }} \cdot v^{{n_{{F_{y} }} }} \cdot k_{{F_{y} }} $$

(15)

where $a_{{\text{p}}} , f, v$ are cutting depth, feed and cutting speed respectively; Coefficient $C_{{F_{y} }}$, index $n_{{F_{y} }} , x_{{F_{y} }} , y_{{F_{y} }}$ and correction coefficient $k_{{F_{y} }}$ could be obtained from “Metal Cutting Principles” [21]. For pistons made of aluminum, $C_{{F_{v} }}$, $+$, $Y_{{F_{v} }}$, $n_{{F_{v} }}$ and $k_{{F_{v} }}$ were 40, 0.9, 0.75, 0 and 1.0, respectively. The machining cutting parameters $a_{{\text{p}}} = \Delta R$, $f = 0.0515\;{\text{mm}}/{\text{r}}$ and $v = 5.485\;{\text{m/s}}$, therefore,

$$ F_{{{\text{R}}\_\max }} \ge F_{{\text{y}}} = 42.421\Delta R_{\max }^{0.9} $$

(16)

In order to ensure the stiffness of deformable boring bar, its length-diameter ratio must be kept less than 5 $\left( {k_{{\text{s}}} \le 5} \right)$. Then, the overall design objectives of high performance embedded GMA could be set as Eq. (17):

$$ \left\{ {\begin{array}{*{20}l} {\Delta R_{\max } \ge 100\;{\mu m}} \hfill \\ {F_{{{\text{R}}\_\max }} \ge F_{{\text{y}}} } \hfill \\ {f_{{\text{n}}} \ge 550\;{\text{Hz}}} \hfill \\ \end{array} } \right. $$

(17)

Withing ranges:

$$ \left\{ {\begin{array}{*{20}l} {5\;{\text{mm}} \le R_{{{\text{GMM}}}} \le 25\;{\text{mm}}} \hfill \\ {40\;{\text{mm}} \le d_{1} \le 80 \;{\text{mm}}} \hfill \\ {0\;{\text{mm}} \le R_{1} \le 5 \;{\text{mm}}} \hfill \\ {0 \le k_{{\text{s}}} \le 5} \hfill \\ \end{array} } \right. $$

(18)

5.2 Parameter solution

Set the thickness of magnetic conducting block as ${8}\;{\text{mm}}$ $\left( {m = 8\;{\text{mm}}} \right)$ and the length of measuring surface as $22\;{\text{mm}}$ $(n = 22\;{\text{mm}})$. After iterative calculation in MATLAB, when $k_{{\text{d}}} = 4.7$, $R_{1} = 5\;{\text{mm}}$, the feasible region of the structural parameter design variable of deformable boring bar was shown in Fig. 7. In order to reduce the diameter of driving coil, the minimum point of $d_{1}$ was selected as the initial variable value, where $d_{1} = 48.6\;{\text{mm}}$, $R_{{{\text{GMM}}}} = 14.4\;{\text{mm}}$, and $L_{{{\text{GMM}}}} = 49.6\;{\text{mm}}$.

Fig. 7

Design variable feasible region of deformable boring bar

Then, the initial design values can be rounded, $d_{1} = 50\;{\text{mm}}$, $R_{{{\text{GMM}}}} = 15\;{\text{mm}}$, and $L_{{{\text{GMM}}}} = 50\;{\text{mm}}$. The design objectives were verified to meet the requirements and the results were shown in Tables 1 and 2, which met the design requirements.

Table 1 Initial values and actual values of the design variables

Table 2 Actual values of design objectives

5.3 Finite Element Analysis of Deformable Boring Bar

In order to verify the design results, a finite element analysis was carried out in SolidWorks 2014 Edition. According to the installation method of the boring bar on the boring machine, the positioning axis and the step surface at the left end of the deformable boring bar were fixed. As depicted in Fig. 8, the model was meshed via element type of curvature based solid, and the semi-circular flexure hinge and the bottom of both sides of the groove are refined to ensure the mesh quality. The deformation boring bar is made of ASTM 304 stainless steel, it’s modal analysis results are shown in Fig. 9, and the first-order natural frequency is $558.85\;{\text{Hz}}$. When a force of 6100 N is applied on the GMM action surface, the output displacement on the end of the deformable boring bar is 102 μ m, as shown in Fig. 10a,The stress distribution of the deformable boring bar is shown in Fig. 10b, the maximum stress is 69.3 MPa, which is far less than the maximum yield of 206.8 MPa.

Fig. 8

FEA model of deformable boring bar

Fig. 9

Modal analysis of deformable boring bar

Fig. 10

Static simulation of deformable boring bar; a displacement distribution, b stress distribution

5.4 Key Performance Test

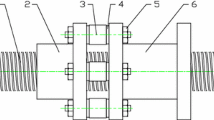
The designed embedded GMA intelligent boring system was shown in Fig. 11. The key performance of deformable boring bar was tested to verify whether it could meet the design performance requirements.

Fig. 11

Embedded GMA intelligent boring system

5.4.1 Static Stiffness Test of Deformable Boring Bar

Loads were applied to the deformable boring bar along ${\text{y}}$ direction and then the displacement on the response direction at the end of deformable boring bar was tested by an eddy current sensor(Model CWY-DO-810301–00-02–05-02). The experimental scheme is shown in Fig. 12, and the test results were shown in Fig. 13.

Fig. 12

Experimental scheme of static stiffness test of deformable boring bar

Fig. 13

Static stiffness test results of deformable boring bar

Thus, the static stiffness of deformable boring bar along is calculated as follows:

$$ k_{{\text{y}}} = \frac{1}{{0.226 \times 10^{ - 6} }} = 4.425 \times 10^{6} \;{\text{N/m}} $$

(19)

5.4.2 First-Order Natural Frequency Test of Deformable Boring Bar

The deformable boring bar was installed at the front of the spindle of the boring machine, and its natural frequency was measured by hammering method. A modal hammer(Model SALC02K) was used to apply the excitation to the deformable boring bar, the end displacement response of the deformable boring bar was measured by an eddy current sensor(Model CWY-DO-810301–00-02–05-02), and an NI acquisition card(Model PCI-6251) was used to record the data. The experiments are repeated three times. The frequency spectrum analysis of the displacement response curve of the deformable boring bar is carried out, the result is shown in Fig. 14, the natural frequency of the component is 370.7 Hz.

Fig. 14

Test result of first order natural frequency of deformable boring bar

5.4.3 Working Displacement Test

When the total turns of the actuated driving coil were 1140, a sinusoidal current of $0\sim 6\;{\text{A}}, 1\;{\text{Hz}}$ was applied, the displacement response was measured by the eddy current sensor, the result is shown in Fig. 15, the maximum displacement of embedded GMA output was $102.3\;{\mu m}$.

Fig. 15

Maximum displacement test result

6 Results and Discussions

The actual design results and test results of embedded GMA were shown in Table 3. From the comparative analysis of design and experimental results, it could be found that the static stiffness of intelligent boring bar was close to the design value. The finite element simulation results show that the natural frequency of the deformable boring bar is 558.85 Hz, which is close to the design result of 554.3 Hz, but in the experiment, the deformable boring bar was installed on the hydrostatic spindle and the stiffness of the oil film was low, which made the measured result of the whole component was 370.70 Hz, and it was reduced by $183.60\;{\text{Hz}}$ comparing to the designed value 554.30 Hz of the deformable boring bar. Therefore, in order to ensure the high frequency response characteristics of the whole mechanism, the design target of the first-order natural frequency of deformable boring bar should be appropriately increased. In addition, according to Fig. 15, the hysteresis of output displacement at low frequency is not obvious, the maximum output displacement was $102.3\;{\mu m}$. And according to Fig. 10, the maximum stress is 69.3 MPa, which is far less than the maximum yield of 206.8 MPa. In conclusion, the designed embedded GMA meets the design objectives.

Table 3 Comparisons between design results and experimental results

7 Conclusions

In order to solve the design problem of the dimension parameters coupling between the deformable boring bar and GMM in the embedded GMA. In this paper, a dynamic model of the deformable boring bar was derived and simulated. A multi-parametric coupling design method was proposed, and it was used in the specific design example of an embedded GMA for the precise boring of non-cylindrical piston pinholes, which were verified by finite element analysis and experiments. The following conclusions are obtained.

• (1) According to Newton's second law and D'Alembert's principle, a dynamic equation of deformable boring bar was given and the calculation formulas of three design indexes (maximum radial output displacement, output force and first-order natural frequency) are derived, providing a theoretical basis for the optimization design of embedded GMA.

• (2) The influences of key parameters in embedded GMA on the three design objectives were simulated and analyzed. The four steps of the multi-parametric coupling design method based on nonlinear programming were introduced in detail to solve the problem of the dimension parameters coupling between the deformable boring bar and GMM.

• (3) In order to precisely machine the non-cylindrical piston pinholes, the design objectives are: maximum displacement ≥ 100 μm, the end output force must greater than the maximum radial cutting force and the first-order natural frequency ≥ 550hz. The optimal design method of nonlinear programming was applied in the design process. The designed maximum displacement is 104.70 μ m, and the measured value is 102.30 μm. The maximum stress is 69.3 MPa by finite element simulation, which is far less than the yield stress of the material. The designed first-order natural frequency of the deformable boring bar is 554.3 Hz, which is close to the finite element simulation result of 558.85 Hz. However, the first-order natural frequency of the whole embedded GMA and spindle assembly is 370.70 Hz due to the low stiffness of the oil film, it is still far greater than the vibration frequency of 100 Hz in the process of non-cylindrical piston pinholes machining. Therefore, the design results meet the requirements, it shows that the multi-parametric coupling design method has a certain effect and provides a new idea for the optimal design of embedded GMA.