1 Introduction

The material characteristics of KDP crystal require high processing technology; only ultra-precision machining can achieve machining accuracy [1]. As a carrier of ultra-precision machining, ultra-precision fly-cutting machine tool (UFMT) directly determine the efficiency, accuracy, reliability and stability of machining quality. The research on dynamic characteristics of ultra-precision flying-cutting machine tool plays a decisive role in improving ultra-precision machining accuracy. Because of the slow feed speed and long processing time of ultra-precision machining, it is impractical to repeat experiments to explore the influence of dynamic parameters on ultra-precision machining. The dynamics method which can simulation rapidly and calculate accurately is particularly important in the dynamic design of ultra-precision machine tools.

There has been much research on the dynamics of the machine tool. Zaeh and Siedl [2] combined FEM with multibody simulation to simulate the dynamic machine tool. Liang et al. [3] established a FEM model and combined with Simulink to predict the machined surface. Liang et al. [4] also proposed an integrated dynamic-simulation model and found that the ratio of the cutting would cause the defects on the machined surface. Wu [5] used the extended transfer matrix method to establish the dynamics model of machine tool and analyzed its vibration characteristics. Zhang et al. [6] and Yao et al. [7] used dynamic simulation software ADAMS and finite element analysis software such as ANSYS, ABAQUS to analyze the static and dynamic vibration characteristics of the machine tool system, and found out the weak components. Yang et al. [8] obtained that dynamic characteristics of the air spindle are the main factor for the generation of strips on the surface after building a surface topography model and conducted dynamic finite element analysis of air spindle in ANSYS Workbench.

The UFMT system is a multi-rigid-and-flexible system with many closed loops. Using ordinary dynamics methods, the high order of the system leads to low computational efficiency. Besides, the modal method is difficult to use owing to the coupling of rigid and flexible bodies. Rui and his co-workers put forward transfer matrix method for multibody systems (MSTMM) [9,10,11] and automatic deduction method of overall transfer equation [12, 13]. MSTMM has been widely applied in the fields of complex weapon systems such as multiple launch rocket system [14], spacecraft [15], Stewart parallel system [16] and so on. In this method, the global dynamics equations of the system not need, and the order of involved matrix is much lower, and the computational speed is much higher than ordinary method, which provides a powerful tool for dynamics simulation of UFMT system. Lu et al. [17] studied dynamics response of ultra-precision single-point diamond fly-cutting machine tool by MSTMM, but the model and computing method are inadequate because the columns are modelled as flexible bodies and the modal order is only ten.

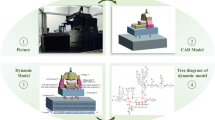
The purpose of this paper is to model and simulate the UFMT and find the relations between structure parameters and machined surface. Firstly, the dynamics model considering the flexible spindle of UFMT is established. And then, MSTMM is introduced to deduct the overall transfer matrix and equation to solve the vibration characteristics of UFMT system. Further, the modal method is applied to dynamics simulation of fly-cutting head tool-tip. The simulated results are verified by tests. Based on those, a geometric model is introduced to transfer relative displacement between the fly-cutting tool-tip and the workpiece into machined surface. At last, dynamics simulations of different parameters such as structure parameters and cutting process parameters are carried out (Fig. 1).

Fig. 1
figure 1

Research flow chart of this paper

Full size image

2 Modelling of the UFMT System

2.1 Machining Process

The photos of the UFMT from different perspectives are shown in Fig. 2, the key components such as the air-bearing spindle, fly-cutting head and slide are marked in the figure. During the ultra-precision machining process (shown in Fig. 3), the workpiece is placed on the slide which slowly removes in the feed direction, and the spindle rotates to drive the fly-cutting head cutting the workpiece. The values of cutting process parameters are listed in Table 1. As annotated in Figs. 2 and 3, the direction inversing the cutting depth direction is defined as z-direction, and the opposite direction of the feed direction is treated as y-direction and then x-direction is determined by Right Hand Rule.

Fig. 2
figure 2

Photos of the UFMT

Full size image
Fig. 3
figure 3

Sketch of the UFMT machining process

Full size image
Table 1 The values of cutting process parameters
Full size table

2.2 State Vectors of the UFMT System

The state vector is the mechanical state of a point which contains translational displacements, angular displacements, internal torques and internal forces at that point. For the UFMT system, the state vectors of the connection points or boundary points are defined as

$$ {\varvec{z}}_{i,j} = [x,y,z,\theta_{x} ,\theta_{y} ,\theta_{z} ,m_{x} ,m_{y} ,m_{z} ,q_{x} ,q_{y} ,q_{z} ]_{i,j}^{\text{T}} $$
(2.1)

where the subscripts i and j denote label of body and hinge elements. For example, if the connection point is the output end of body 2 and the input end of hinge 15, the state vector of that point is written as \( {\varvec{Z}}_{2,15} \). Where \( [x,y,z]_{i,j}^{{\text{T}}} \) and \( [\theta_{x} ,\theta_{y} ,\theta_{z} ]_{i,j}^{\rm T} \) represent translational and angular displacement in x, y, z physics coordinate; \( [m_{x} ,m_{y} ,m_{z} ]_{i,j}^{\rm T} \) and \( [q_{x} ,q_{y} ,q_{z} ]_{i,j}^{\rm T} \) are internal torque and force in x, y, z physics coordinate.

By introducing modal transform \( {\varvec{z}} = {\varvec{Z}}e^{i\omega t} \), such state vectors in modal coordinates are

$$ {\varvec{Z}}_{i,j} = [X,Y,Z,\Theta_{x} ,\Theta_{y} ,\Theta_{z} ,M_{x} ,M_{y} ,M_{z} ,Q_{x} ,Q_{y} ,Q_{z} ]_{i,j}^{\text{T}} $$
(2.2)

where variables in Eq. (2.2) represent the modal coordinates of corresponding variables in Eq. (2.1).

2.3 Transfer Equations and Transfer Matrices

The basic idea of MSTMM is dividing the whole system into elements such as body elements and hinge elements. Transfer equations of elements with single input end and single output end and elements with multi input ends and single output end are

$$ {\varvec{Z}}_{j,O} = {\varvec{U}}_{j} {\varvec{Z}}_{j,I} $$
(2.3)
$$ {\varvec{Z}}_{j,O} = \sum\limits_{k = 1}^{n} {{\varvec{U}}_{{j,I_{k} }} {\varvec{Z}}_{{j,I_{k} }} } $$
(2.4)

where subscripts j denote numbers of each element, subscripts I and O individually represent the input and output end of each element; Ik is the kth input end of element with multi input ends; Uj is the transfer matrix of element j.

For elements with multi input ends and single output end, the geometric relationships among different input ends are

$$ \left\{ {\begin{array}{*{20}l} {{\boldsymbol{\theta}}_{{I_{1} }} = {\boldsymbol{\theta}}_{{I_{k} }} } \hfill \\ {{\varvec{r}}_{{I_{1} }} = {\varvec{r}}_{{I_{k} }} + {\tilde{\varvec{l}}}_{{I_{1} I_{k} }} {\boldsymbol{\theta}}_{{I_{k} }} } \hfill \\ \end{array} } \right. $$
(2.5)

Equation (2.5) can be written in the matrix form as

$$ {\varvec{H}}_{{j,I_{k} }} {\varvec{Z}}_{{j,I_{k} }} = {\varvec{H}}_{{j,I_{1} }} {\varvec{Z}}_{{j,I_{1} }} (k = 2,3, \ldots ,n) $$
(2.6)

where

$$ {\varvec{H}}_{{I_{1} }} = \left[ {\begin{array}{*{20}c} {{\varvec{I}}_{3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } \\ {{\varvec{O}}_{3 \times 3} } & {{\varvec{I}}_{3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } \\ \end{array} } \right],{\varvec{H}}_{{I_{k} }} = \left[ {\begin{array}{*{20}c} {{\varvec{I}}_{3} } & {{\tilde{\varvec{l}}}_{{I_{1} I_{k} }} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } \\ {{\varvec{O}}_{3 \times 3} } & {{\varvec{I}}_{3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } \\ \end{array} } \right] $$
(2.7)

Transfer matrix of a rigid body is

$$ {\varvec{U}}_{{i,{\text{I}}_{ 1} }} = \left[ {\begin{array}{*{20}c} {{\varvec{I}}_{3} } & { - {\tilde{\varvec{l}}}_{{{\text{I}}_{ 1} {\text{O}}}} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } \\ {{\varvec{O}}_{3 \times 3} } & {{\varvec{I}}_{3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } \\ {m\omega^{2} {\tilde{\varvec{l}}}_{\text{CO}} } & { - \omega^{2} (m{\tilde{\varvec{l}}}_{{{\text{I}}_{ 1} {\text{O}}}} {\tilde{\varvec{l}}}_{{{\text{I}}_{ 1} {\text{C}}}} + {\varvec{J}}_{{I_{1} }} )} & {{\varvec{I}}_{3} } & {{\tilde{\varvec{l}}}_{{{\text{I}}_{ 1} {\text{O}}}} } \\ {m\omega^{2} {\varvec{I}}_{3} } & { - m\omega^{2} {\tilde{\varvec{l}}}_{{{\text{I}}_{ 1} {\text{C}}}} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{I}}_{3} } \\ \end{array} } \right] $$
(2.8)
$$ {\varvec{U}}_{{i , {\text{I}}_{k} }} = \left[ {\begin{array}{*{20}c} {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } \\ {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } \\ {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{I}}_{3} } & {{\tilde{\varvec{l}}}_{{{\text{I}}_{k} {\text{O}}}} } \\ {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{I}}_{3} } \\ \end{array} } \right] $$
(2.9)

where m and \( {\varvec{J}}_{{{\text{I}}_{1} }} \) is the mass and the inertia matrix relative to the first input point I1 of the rigid body, respectively. Assuming \( {\varvec{l}}_{\text{AB}} = \left[ {\begin{array}{*{20}c} {x_{\text{AB}} } & {y_{\text{AB}} } & {z_{\text{AB}} } \\ \end{array} } \right]^{\rm T} \), positon matrix \( {\tilde{\varvec{l}}}_{\text{AB}} \) is defined as

$$ {\tilde{\varvec{l}}}_{\text{AB}} = \left[ {\begin{array}{*{20}c} 0 & { - z_{\text{AB}} } & {y_{\text{AB}} } \\ {z_{\text{AB}} } & 0 & { - x_{\text{AB}} } \\ { - y_{\text{AB}} } & {x_{\text{AB}} } & 0 \\ \end{array} } \right] $$
(2.10)

Transfer matrix of a virtual body is

$$ {\varvec{U}}_{{v , {\text{I}}_{1} }} = \left[ {\begin{array}{*{20}c} {{\varvec{I}}_{3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } \\ {{\varvec{O}}_{3 \times 3} } & {{\varvec{I}}_{3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } \\ {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{I}}_{3} } & {{\varvec{O}}_{3 \times 3} } \\ {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{I}}_{3} } \\ \end{array} } \right],{\varvec{U}}_{{v , {\text{I}}_{k} }} = \left[ {\begin{array}{*{20}c} {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } \\ {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } \\ {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{I}}_{3} } & {{\varvec{O}}_{3 \times 3} } \\ {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{I}}_{3} } \\ \end{array} } \right] $$
(2.11)

Transfer matrix of a beam is

$$ {\varvec{U}}_{j} = \left[ {\begin{array}{*{20}c} {u_{1,1} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {u_{1,10} } & 0 & 0 \\ 0 & {u_{2,2} } & 0 & 0 & 0 & {u_{2,6} } & 0 & 0 & {u_{2,9} } & 0 & {u_{2,11} } & 0 \\ 0 & 0 & {u_{3,3} } & 0 & {u_{3,5} } & 0 & 0 & {u_{3,8} } & 0 & 0 & 0 & {u_{3,12} } \\ 0 & 0 & 0 & {u_{4,4} } & 0 & 0 & {u_{4,7} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {u_{5,3} } & 0 & {u_{5,5} } & 0 & 0 & {u_{5,8} } & 0 & 0 & 0 & {u_{5,12} } \\ 0 & {u_{6,2} } & 0 & 0 & 0 & {u_{6,6} } & 0 & 0 & {u_{6,9} } & 0 & {u_{6,11} } & 0 \\ 0 & 0 & 0 & {u_{7,4} } & 0 & 0 & {u_{7,7} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {u_{8,3} } & 0 & {u_{8,5} } & 0 & 0 & {u_{8,8} } & 0 & 0 & 0 & {u_{8,12} } \\ 0 & {u_{9,2} } & 0 & 0 & 0 & {u_{9,6} } & 0 & 0 & {u_{9,9} } & 0 & {u_{9,11} } & 0 \\ {u_{10,1} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {u_{10,10} } & 0 & 0 \\ 0 & {u_{11,2} } & 0 & 0 & 0 & {u_{11,6} } & 0 & 0 & {u_{11,9} } & 0 & {u_{11,11} } & 0 \\ 0 & 0 & {u_{12,3} } & 0 & {u_{12,5} } & 0 & 0 & {u_{12,8} } & 0 & 0 & 0 & {u_{12,12} } \\ \end{array} } \right] $$
(2.12)

where L is the length of the beam. \( u_{1,1} = u_{10,10} = \cos \left( {\beta L} \right) \), \( u_{1,10} = {{ - \sin \left( {\beta L} \right)} \mathord{\left/ {\vphantom {{ - \sin \left( {\beta L} \right)} {\left( {\beta EA} \right)}}} \right. \kern-0pt} {\left( {\beta EA} \right)}} \), \( u_{10,1} = \beta EA\sin \left( {\beta L} \right) \), \( u_{4,4} = u_{7,7} = \cos \left( {\gamma L} \right) \),\( u_{4,7} = {{\sin \left( {\gamma L} \right)} \mathord{\left/ {\vphantom {{\sin \left( {\gamma L} \right)} {\left( {\gamma GJ_{p} } \right)}}} \right. \kern-0pt} {\left( {\gamma GJ_{p} } \right)}} \), \( u_{7,4} = - \gamma GJ_{p} \sin \left( {\gamma L} \right) \), \( u_{2,2} = u_{6,6} = u_{9,9} = u_{11,11} = S(\lambda_{y} L) \), \( u_{3,3} = u_{5,5} = u_{8,8} = u_{12,12} = S(\lambda_{z} L) \), \( u_{2,6} = u_{9,11} = {{T(\lambda_{y} L)} \mathord{\left/ {\vphantom {{T(\lambda_{y} L)} {\lambda_{y} }}} \right. \kern-0pt} {\lambda_{y} }} \), \( u_{2,9} = u_{6,11} = {{U(\lambda_{y} L)} \mathord{\left/ {\vphantom {{U(\lambda_{y} L)} {\left( {EI_{z} \lambda_{y}^{2} } \right)}}} \right. \kern-0pt} {\left( {EI_{z} \lambda_{y}^{2} } \right)}} \), \( u_{2,11} = {{V(\lambda_{y} L)} \mathord{\left/ {\vphantom {{V(\lambda_{y} L)} {\left( {EI_{z} \lambda_{y}^{3} } \right)}}} \right. \kern-0pt} {\left( {EI_{z} \lambda_{y}^{3} } \right)}} \), \( u_{5,8} = {{T(\lambda_{z} L)} \mathord{\left/ {\vphantom {{T(\lambda_{z} L)} {\left( {EI_{y} \lambda_{z}^{{}} } \right)}}} \right. \kern-0pt} {\left( {EI_{y} \lambda_{z}^{{}} } \right)}} \), \( u_{3,5} = u_{8,12} = {{ - T(\lambda_{z} L)} \mathord{\left/ {\vphantom {{ - T(\lambda_{z} L)} {\lambda_{z} }}} \right. \kern-0pt} {\lambda_{z} }} \), \( u_{3,8} = u_{5,12} = {{ - U(\lambda_{z} L)} \mathord{\left/ {\vphantom {{ - U(\lambda_{z} L)} {\left( {EI_{y} \lambda_{z}^{2} } \right)}}} \right. \kern-0pt} {\left( {EI_{y} \lambda_{z}^{2} } \right)}} \), \( u_{3,12} = {{V(\lambda_{z} L)} \mathord{\left/ {\vphantom {{V(\lambda_{z} L)} {\left( {EI_{y} \lambda_{z}^{3} } \right)}}} \right. \kern-0pt} {\left( {EI_{y} \lambda_{z}^{3} } \right)}} \), \( u_{6,9} = {{T(\lambda_{y} L)} \mathord{\left/ {\vphantom {{T(\lambda_{y} L)} {\left( {EI_{z} \lambda_{y}^{{}} } \right)}}} \right. \kern-0pt} {\left( {EI_{z} \lambda_{y}^{{}} } \right)}} \), \( u_{5,3} = u_{12,8} = - \lambda_{z} V(\lambda_{z} L) \), \( u_{6,2} = u_{11,9} = \lambda_{y} V(\lambda_{y} L) \), \( u_{8,3} = u_{12,5} = - EI_{y} \lambda_{z}^{2} U(\lambda_{z} L) \), \( u_{9,2} = u_{11,6} = EI_{z} \lambda_{y}^{2} U(\lambda_{y} L) \), \( u_{9,6} = EI_{z} \lambda_{y}^{{}} V(\lambda_{y} L) \), \( u_{11,2} = EI_{z} \lambda_{y}^{3} T(\lambda_{y} L) \), \( u_{12,3} = EI_{y} \lambda_{z}^{3} T(\lambda_{z} L) \), \( \beta_{x} = \sqrt {{{\bar{m}\omega^{2} } \mathord{\left/ {\vphantom {{\bar{m}\omega^{2} } {(EA)}}} \right. \kern-0pt} {(EA)}}} \), \( \lambda_{y} = \sqrt[4]{{{{\bar{m}\omega^{2} } \mathord{\left/ {\vphantom {{\bar{m}\omega^{2} } {(EI_{z} )}}} \right. \kern-0pt} {(EI_{z} )}}}} \), \( \lambda_{z} = \sqrt[4]{{{{\bar{m}\omega^{2} } \mathord{\left/ {\vphantom {{\bar{m}\omega^{2} } {(EI_{y} )}}} \right. \kern-0pt} {(EI_{y} )}}}} \), \( \gamma = \sqrt {{{\rho J_{\text{P}} \omega^{2} } \mathord{\left/ {\vphantom {{\rho J_{\text{P}} \omega^{2} } {(GJ_{\text{P}} )}}} \right. \kern-0pt} {(GJ_{\text{P}} )}}} \). \( \rho ,E,G,A,I_{z} ,I_{y} \,{\text{and}}\,J_{p} \) are the density, elastic modulus, shear modulus, cross-sectional area, principal moments of inertia of cross-sectional area to z-axis, principal moments of inertia of cross-sectional area to y-axis and polar moment of inertia of cross-sectional area to z-axis, respectively.

Transfer matrix of a spatial spring-damper hinges is

$$ {\varvec{U}}_{k} = \left[ {\begin{array}{*{20}c} {{\varvec{I}}_{3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {\varvec{K}} \\ {{\varvec{O}}_{3 \times 3} } & {{\varvec{I}}_{3} } & {{\varvec{K^{\prime}}}} & {{\varvec{O}}_{3 \times 3} } \\ {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{I}}_{3} } & {{\varvec{O}}_{3 \times 3} } \\ {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{O}}_{3 \times 3} } & {{\varvec{I}}_{3} } \\ \end{array} } \right] $$
(2.13)

where

$$ {\varvec{K}} = \left[ {\begin{array}{*{20}c} { - \frac{1}{{k_{x} }}} & 0 & 0 \\ 0 & { - \frac{1}{{k_{y} }}} & 0 \\ 0 & 0 & { - \frac{1}{{k_{z} }}} \\ \end{array} } \right]\;,\quad {\varvec{K^{\prime}}} = \left[ {\begin{array}{*{20}c} {\frac{1}{{k^{\prime}_{x} }}} & 0 & 0 \\ 0 & {\frac{1}{{k^{\prime}_{y} }}} & 0 \\ 0 & 0 & {\frac{1}{{k^{\prime}_{z} }}} \\ \end{array} } \right] $$
(2.14)

\( k_{x} \), \( k_{y} \), \( k_{z} \) are the stiffness of linear springs, \( k^{\prime}_{x} \), \( k^{\prime}_{y} \), \( k^{\prime}_{z} \) represent the stiffness of rotary springs.

2.4 Dynamics Model of the UFMT System

According to the machining process in Sect. 2.1, various components in the UFMT are divided into 13 body elements combined by 18 spatial spring-damper hinges. Due to the shape and material of those 13 body elements, the spindle (not include fly-cutting head) is a flexible body, and the others are rigid bodies. The element type, number of ends and components of those 13 elements are shown in Table 2, and Fig. 4 displays the topology diagram of the dynamics model. The air-bearing of spindle and fly-cutting head are simplified as hinge 25 and hinge 31, respectively.

Table 2 Elements of UFMT system
Full size table
Fig. 4
figure 4

Topology diagram of dynamics model of UFMT system

Full size image

The transfer equations can be deduced according to Fig. 5 after cutting off closed loops in Fig. 4 marked by ‘scissor’ of the dynamics model.

Fig. 5
figure 5

Topology diagram of tree dynamics model of UFMT system

Full size image

The overall transfer equation of UFMT system can be deduced as

$$ {\varvec{U}}_{\text{all}} {\varvec{Z}}_{\text{all}} = {\varvec{0}} $$
(2.15)

where \( {\varvec{Z}}_{\text{all}} \) is a \( 72 \times 1 \) column matrix consisted of the state vectors of USDFMT system boundary points, that is

$$ {\varvec{Z}}_{\text{all}} = [{\varvec{Z}}_{ 1 4 , 0}^{\text{T}} ,{\varvec{Z}}_{ 2 1 , 0}^{\text{T}} ,{\varvec{Z}}_{ 2 2 , 0}^{\text{T}} ,{\varvec{Z}}_{ 2 8 , 0}^{\text{T}} ,{\varvec{Z}}_{ 3 0 , 0}^{\text{T}} ,{\varvec{Z}}_{ 3 1 , 0}^{\text{T}} ]^{\text{T}} $$
(2.16)

The overall transfer matrix \( {\varvec{U}}_{\text{all}} \) can be written as

$$ {\varvec{U}}_{\text{all}} = \left[ {\begin{array}{*{20}c} { - {\varvec{I}}} & {{\varvec{T}}_{21 - 14} + {\varvec{T}}_{6 - 14} {\varvec{C}}} & {{\varvec{T}}_{22 - 14} + {\varvec{T}}_{7 - 14} {\varvec{C}}} & {{\varvec{T}}_{28 - 14} + {\varvec{T}}_{{8 - 14,{\text{I}}_{2} }} {\varvec{C}}} & {{\varvec{T}}_{30 - 14} + {\varvec{T}}_{{8 - 14,{\text{I}}_{3} }} {\varvec{C}}} & {{\varvec{T}}_{31 - 14} + {\varvec{T}}_{{8 - 14,{\text{I}}_{4} }} {\varvec{C}}} \\ {\varvec{O}} & {{\varvec{G}}_{6 - 2} {\varvec{C}}} & {{\varvec{G}}_{7 - 2} {\varvec{C}}} & {{\varvec{G}}_{{8 - 2,{\text{I}}_{2} }} {\varvec{C}} + {\varvec{G}}_{28 - 2} } & {{\varvec{G}}_{{8 - 2,{\text{I}}_{3} }} {\varvec{C}}} & {{\varvec{G}}_{{8 - 2,{\text{I}}_{4} }} {\varvec{C}} + {\varvec{G}}_{31 - 2} } \\ {\varvec{O}} & {{\varvec{G}}_{6 - 2} {\varvec{C}}} & {{\varvec{G}}_{7 - 2} {\varvec{C}}} & {\varvec{O}} & {{\varvec{G}}_{30 - 2} } & {\varvec{O}} \\ {\varvec{O}} & {{\varvec{G}}_{6 - 2} {\varvec{C}} + {\varvec{G}}_{21 - 2} } & {{\varvec{G}}_{7 - 2} {\varvec{C}}} & {\varvec{O}} & {\varvec{O}} & {\varvec{O}} \\ {\varvec{O}} & {{\varvec{G}}_{6 - 2} {\varvec{C}}} & {{\varvec{G}}_{7 - 2} {\varvec{C}} + {\varvec{G}}_{22 - 2} } & {\varvec{O}} & {\varvec{O}} & {\varvec{O}} \\ {\varvec{O}} & {{\varvec{G}}_{6 - 3} {\varvec{C}}} & {{\varvec{G}}_{7 - 3} {\varvec{C}}} & {\varvec{O}} & {\varvec{O}} & {\varvec{O}} \\ {\varvec{O}} & {\varvec{O}} & {\varvec{O}} & {{\varvec{G}}_{{8 - 8,{\text{I}}_{2} }} {\varvec{C}} + {\varvec{G}}_{28 - 8} } & {\varvec{O}} & {{\varvec{G}}_{31 - 8} } \\ {\varvec{O}} & {\varvec{O}} & {\varvec{O}} & {{\varvec{G}}_{28 - 8} } & {{\varvec{G}}_{{8 - 8,{\text{I}}_{3} }} {\varvec{C}}} & {{\varvec{G}}_{31 - 8} } \\ {\varvec{O}} & {\varvec{O}} & {\varvec{O}} & {{\varvec{G}}_{28 - 8} } & {\varvec{O}} & {{\varvec{G}}_{{8 - 8,{\text{I}}_{4} }} {\varvec{C}} + {\varvec{G}}_{31 - 8} } \\ {\varvec{O}} & {\varvec{O}} & {\varvec{O}} & {{\varvec{G}}_{28 - 9} } & {\varvec{O}} & {{\varvec{G}}_{31 - 9} } \\ \end{array} } \right] $$
(2.17)

where the first line describes the main transfer equation of the system; the other lines show the geometrical equations of bodies 2, 3, 8 and 9 with multi input ends.

The main transfer equation is

$$ \begin{aligned} {\varvec{Z}}_{ 1 4 , 0}^{{}} &= ({\varvec{T}}_{21 - 14} + {\varvec{T}}_{6 - 14} {\varvec{C}}){\varvec{Z}}_{ 2 1 , 0}^{{}} { + (}{\varvec{T}}_{22 - 14} + {\varvec{T}}_{7 - 14} {\varvec{C}}){\varvec{Z}}_{ 2 2 , 0}^{{}} \\ &\quad +\, ({\varvec{T}}_{28 - 14} + {\varvec{T}}_{{8 - 14,{\text{I}}_{2} }} {\varvec{C}}){\varvec{Z}}_{ 2 8 , 0}^{{}} { + (}{\varvec{T}}_{30 - 14} + {\varvec{T}}_{{8 - 14,{\text{I}}_{3} }} {\varvec{C}}){\varvec{Z}}_{ 3 0 , 0}^{{}} \\ &\quad+\, ({\varvec{T}}_{31 - 14} + {\varvec{T}}_{{8 - 14,{\text{I}}_{4} }} {\varvec{C}}){\varvec{Z}}_{ 3 1 , 0}^{{}} \\ \end{aligned} $$
(2.18)

where

$$ \left\{ \begin{aligned} &{\varvec{T}}_{21 - 14} = {\varvec{U}}_{14} {\varvec{U}}_{1} {\varvec{U}}_{15} {\varvec{U}}_{{ 2 , {\text{I}}_{4} }} {\varvec{U}}_{21} \hfill \\& {\varvec{T}}_{6 - 14} = {\varvec{U}}_{14} {\varvec{U}}_{1} {\varvec{U}}_{15} {\varvec{U}}_{{ 2 , {\text{I}}_{ 1} }} {\varvec{U}}_{16} {\varvec{U}}_{{ 3 , {\text{I}}_{1} }} {\varvec{U}}_{19} {\varvec{U}}_{6} \hfill \\& {\varvec{T}}_{22 - 14} = {\varvec{U}}_{14} {\varvec{U}}_{1} {\varvec{U}}_{15} {\varvec{U}}_{{ 2 , {\text{I}}_{5} }} {\varvec{U}}_{22} \hfill \\& {\varvec{T}}_{7 - 14} = {\varvec{U}}_{14} {\varvec{U}}_{1} {\varvec{U}}_{15} {\varvec{U}}_{{ 2 , {\text{I}}_{ 1} }} {\varvec{U}}_{16} {\varvec{U}}_{{ 3 , {\text{I}}_{2} }} {\varvec{U}}_{20} {\varvec{U}}_{7} \hfill \\& {\varvec{T}}_{28 - 14} = {\varvec{U}}_{14} {\varvec{U}}_{1} {\varvec{U}}_{15} {\varvec{U}}_{{ 2 , {\text{I}}_{2} }} {\varvec{U}}_{17} {\varvec{U}}_{10} {\varvec{U}}_{29} {\varvec{U}}_{{ 8 , {\text{I}}_{1} }} {\varvec{U}}_{25} {\varvec{U}}_{{9,I_{2} }} {\varvec{U}}_{26} {\varvec{U}}_{13} {\varvec{U}}_{27} {\varvec{U}}_{5} {\varvec{U}}_{28} \hfill \\& {\varvec{T}}_{{8 - 14,I_{2} }} = {\varvec{U}}_{14} {\varvec{U}}_{1} {\varvec{U}}_{15} {\varvec{U}}_{{ 2 , {\text{I}}_{ 2} }} {\varvec{U}}_{17} {\varvec{U}}_{10} {\varvec{U}}_{29} {\varvec{U}}_{{8,I_{2} }} \hfill \\& {\varvec{T}}_{30 - 14} = {\varvec{U}}_{14} {\varvec{U}}_{1} {\varvec{U}}_{15} {\varvec{U}}_{{ 2 , {\text{I}}_{3} }} {\varvec{U}}_{18} {\varvec{U}}_{ 1 1} {\varvec{U}}_{30} \hfill \\& {\varvec{T}}_{{8 - 14,I_{3} }} = {\varvec{U}}_{14} {\varvec{U}}_{1} {\varvec{U}}_{15} {\varvec{U}}_{{ 2 , {\text{I}}_{ 2} }} {\varvec{U}}_{17} {\varvec{U}}_{10} {\varvec{U}}_{29} {\varvec{U}}_{{8,I_{3} }} \hfill \\& {\varvec{T}}_{31 - 14} = {\varvec{U}}_{14} {\varvec{U}}_{1} {\varvec{U}}_{15} {\varvec{U}}_{{ 2 , {\text{I}}_{2} }} {\varvec{U}}_{17} {\varvec{U}}_{10} {\varvec{U}}_{29} {\varvec{U}}_{{ 8 , {\text{I}}_{1} }} {\varvec{U}}_{25} {\varvec{U}}_{{9,I_{1} }} {\varvec{U}}_{24} {\varvec{U}}_{12} {\varvec{U}}_{23} {\varvec{U}}_{4} {\varvec{U}}_{31} \hfill \\& {\varvec{T}}_{{8 - 14,I_{4} }} = {\varvec{U}}_{14} {\varvec{U}}_{1} {\varvec{U}}_{15} {\varvec{U}}_{{ 2 , {\text{I}}_{ 2} }} {\varvec{U}}_{17} {\varvec{U}}_{10} {\varvec{U}}_{29} {\varvec{U}}_{{8,I_{4} }} \hfill \\ \end{aligned} \right. $$
(2.19)

As an example, the geometrical equation of the body element 9 shown in the last line in Eq. (2.17) is

$$ {\varvec{G}}_{31 - 9} {\varvec{Z}}_{ 3 1 , 0}^{{}} + {\varvec{G}}_{28 - 9} {\varvec{Z}}_{28,0}^{{}} = {\varvec{0}} $$
(2.20)

where

$$ \left\{ {\begin{array}{*{20}l} {{\varvec{G}}_{31 - 9} = - {\varvec{H}}_{{ 9 , {\text{I}}_{1} }} {\varvec{U}}_{24} {\varvec{U}}_{12} {\varvec{U}}_{23} {\varvec{U}}_{4} {\varvec{U}}_{31} } \hfill \\ {{\varvec{G}}_{28 - 9} = {\varvec{H}}_{{ 9 , {\text{I}}_{2} }} {\varvec{U}}_{26} {\varvec{U}}_{13} {\varvec{U}}_{27} {\varvec{U}}_{5} {\varvec{U}}_{28} } \hfill \\ \end{array} } \right. $$
(2.21)

Similarly, the geometrical equations of other bodies with multi input ends can be deduced and written in matrix form in Eq. (2.17).

The boundary conditions of USDFMT system are

$$ \left\{ \begin{aligned} &{\varvec{Z}}_{ 1 4 , 0}^{{}} = [0,0,0,0,0,0,M_{x} ,M_{y} ,M_{z} ,Q_{x} ,Q_{y} ,Q_{z} ]_{ 1 4 , 0}^{\text{T}} \hfill \\ &{\varvec{Z}}_{j , 0}^{{}} = [X,Y,Z,\Theta_{x} ,\Theta_{y} ,\Theta_{z} ,M_{x} ,M_{y} ,M_{z} ,Q_{x} ,Q_{y} ,Q_{z} ]_{j , 0}^{\text{T}} \hfill \\ &\quad\quad\quad\,\,(j = 21,22,28,30,31) \hfill \\ \end{aligned} \right. $$
(2.22)

substituting Eq. (2.22) into Eq. (2.15), the eigenfrequency equation of USDFMT system is obtained, that is

$$ \det {\bar{\varvec{U}}}_{\text{all}} = {\varvec{0}} $$
(2.23)

2.5 Vibration Characteristics of the UFMT System

Using the method of bisection, the first thirty natural frequencies \( \omega_{k} \) of UFMT system can be obtained by MSTMM (presented in Table 3). Then substituting the kth natural frequencies into the overall transfer equation, unknown boundary state variables of the UFMT system can be solved by using the matrix algebraic cofactor method. Furthermore, the state vectors at any point and the modal shapes of the UFMT system can be obtained through the transfer equations between state vectors. The structure parameters of body elements such as can be read out by UG software and the stiffness of hinge elements can be identified by MSTMM&GA.

Table 3 Natural frequencies and modal shapes of UFMT system
Full size table

3 Dynamics Simulation of the UFMT System

3.1 Body Element Dynamics Equations

For rigid bodies, assuming that force fi,p and torque \( {\varvec{m}}_{{i,p^{\prime}}} \) act on point \( {\text{P}}_{i,p} \), the dynamics equations are

$$ \begin{aligned} &m_{i} {\varvec{\ddot{r}}}_{i} - m_{i} {\varvec{l}}_{{I_{1} C,i}} {\varvec{\ddot{\theta }}}_{i} - \sum\limits_{n = 1}^{N} {{\varvec{q}}_{{I_{n} ,i}} + } {\varvec{q}}_{O,i} = \sum\limits_{p} {{\varvec{f}}_{i,p} } \hfill \\ &m_{i} {\tilde{\varvec{l}}}_{{I_{1} C,i}} {\varvec{\ddot{r}}}_{i} + {\varvec{J}}_{{I_{1} ,i}} {\varvec{\ddot{\theta }}}_{i} + \sum\limits_{n = 1}^{N} {{\varvec{m}}_{{I_{n} ,i}} - } {\varvec{m}}_{O,i} - \sum\limits_{n = 1}^{N} {{\tilde{\varvec{l}}}_{{I_{1} I_{n} ,i}} } {\varvec{q}}_{{I_{n} ,i}} + {\tilde{\varvec{l}}}_{{I_{1} O}} q_{O,i} = \sum\limits_{{p^{\prime}}} {{\varvec{m}}_{{i,p^{\prime}}} } + \sum\limits_{p} {{\tilde{\varvec{l}}}_{{I_{1} D,i}} {\varvec{f}}_{i,p} } \hfill \\ \end{aligned} $$
(3.1)

where \( m_{i} ,\ddot{r}_{i} \,{\text{and}}\,\ddot{\theta }_{i} \) are mass, translational acceleration and angular acceleration of rigid body i. \( {\varvec{J}}_{{I_{1} ,i}} \) is inertia matrix relative to the first input point I1, \( {\tilde{\varvec{l}}}_{{I_{1} C,i}} ,{\tilde{\varvec{l}}}_{{I_{1} O}} \text{ ,}{\tilde{\varvec{l}}}_{{I_{1} I_{n} ,i}} \,\text{and} \,{\tilde{\varvec{l}}}_{{I_{1} D,i}} \) are the coordinate matrices of center of mass, output point, input points expect the first input point and the force acting point relative the first input point I1. \( {\varvec{q}}_{{I_{n} ,i}} \), \( {\varvec{q}}_{O,i} \), \( {\varvec{m}}_{{I_{n} ,i}} \) and \( {\varvec{m}}_{O,i} \) are internal force and torque of the input ends and output end.

The virtual body is massless and un-volumetric, so the dynamics equation is

$$ - \sum\limits_{n = 1}^{N} {{\varvec{q}}_{{I_{n} ,i}} + } {\varvec{q}}_{O,i} = \sum\limits_{p} {{\varvec{f}}_{i,p} } $$
(3.2)

For flexible bodies, assuming that force \( {\varvec{f}}_{i,q} = [f_{x,q} ,f_{y,q} ,f_{z,q} ]^{\text{T}} \) and torque \( {\varvec{m}}_{i,q'} = [m_{x,q'} ,m_{y,q'} ,m_{z,q'} ]^{\text{T}} \) act on point \( {\text{Q}}_{i,q} \), the dynamics equations are

$$ \begin{array} {ll} EI_{z,i} \frac{{\partial^{4} y}}{{\partial x_{1}^{4} }} + \bar{m}_{i} \frac{{\partial^{2} y}}{{\partial t_{{}}^{2} }} = f_{y,q} (x_{1} ,t) - \frac{\partial }{{\partial x_{1}^{{}} }}m_{z,q'} (x_{1} ,t)&(0 \le x_{1} \le l_{i} ) \hfill \\ EI_{y,i} \frac{{\partial^{4} z}}{{\partial x_{1}^{4} }} + \bar{m}_{i} \frac{{\partial^{2} z}}{{\partial t_{{}}^{2} }} = f_{z,q} (x_{1} ,t) - \frac{\partial }{{\partial x_{1}^{{}} }}m_{y,q'} (x_{1} ,t)& (0 \le x_{1} \le l_{i} ) \hfill \\ \bar{m}_{i} \frac{{\partial^{2} z}}{{\partial t_{{}}^{2} }} - EA_{i} \frac{{\partial^{2} x}}{{\partial x_{1}^{2} }} = f_{x,q} (x_{1} ,t)& (0 \le x_{1} \le l_{i} ) \hfill \\ (\rho J_{p} )_{i} \frac{{\partial^{2} \theta_{x} }}{{\partial t_{{}}^{2} }} - (GJ_{p} )_{i} \frac{{\partial^{2} \theta_{x} }}{{\partial x_{1}^{2} }} = m_{x,q'} (x_{1} ,t)&(0 \le x_{1} \le l_{i} ) \end{array} $$
(3.3)

The dynamics equation of each body element in UFMT system can be easily obtained by rewriting Eqs. (3.1) and (3.3) as the following forms

$$ {\varvec{M}}_{i} {\varvec{v}}_{i,tt} + {\varvec{K}}_{i} {\varvec{v}}_{i} = {\varvec{f}}_{i} \quad (i = 1\sim13) $$
(3.4)

where i is the label of body element; \( {\varvec{v}}_{i} \) is the translational and angular displacements column matrix, and its subscript indicates the derivative order of time; \( {\varvec{M}}_{i} \) and \( {\varvec{K}}_{i} \) represents the mass and the spring forces matrix; \( {\varvec{f}}_{i} \) indicates the column matrix of external forces and torques.

3.2 Dynamics Equation of the UFMT System

For the system without damping, after deducing the body element dynamics equation, the dynamics equation of the system can be summarized as

$$ {\varvec{Mv}}_{tt} + {\varvec{Kv}} = {\varvec{f}} $$
(3.5)

where

$$ \begin{aligned} & {\varvec{M}} = diag({\varvec{M}}_{1} ,{\varvec{M}}_{2} , \ldots ,{\varvec{M}}_{13} ) \\ & {\varvec{K}} = diag({\varvec{K}}_{1} ,{\varvec{K}}_{2} , \ldots ,{\varvec{\rm K}}_{13} ) \\ & {\varvec{v}} = [{\varvec{v}}_{1}^{\text{T}} ,{\varvec{v}}_{2}^{\text{T}} , \ldots ,{\varvec{v}}_{13}^{\text{T}} ]^{\text{T}} \\ & {\varvec{f}} = [{\varvec{f}}_{{\varvec{1}}}^{\text{T}} ,{\varvec{f}}_{{\varvec{2}}}^{\text{T}} , \ldots ,{\varvec{f}}_{13}^{\text{T}} ]^{\text{T}} \\ \end{aligned} $$
(3.6)

For the UFMT system, the dynamics equation of the system can be deduced after adding a damping term into Eq. (3.5).

$$ {\varvec{Mv}}_{tt} + {\varvec{Cv}}_{t} + {\varvec{Kv}} = {\varvec{f}} $$
(3.7)

where C represents the damping force matrix.

Then the augmented eigenvector of the UFMT system is introduced to decouple Eq. (3.7), for the vibration of kth mode, the relationship between the augmented eigenvector and the system displacement array is

$$ {\varvec{V}}^{k} = {\varvec{v}}e^{{ - i\omega_{k} t}} $$
(3.8)

What’s more, using modal technology yields

$$ {\varvec{v}} = \sum\limits_{k = 1}^{n} {{\varvec{V}}^{k} q^{k} (t)} $$
(3.9)

where \( q^{k} (t) \) is the generalized coordinate for k-order mode.

Substituting (3.9) in (3.7) yields

$$ \sum\limits_{k = 1}^{n} {{\varvec{MV}}^{k} \ddot{q}^{k} (t)} + \sum\limits_{k = 1}^{n} {{\varvec{CV}}^{k} \dot{q}^{k} (t)} + \sum\limits_{k = 1}^{n} {{\varvec{KV}}^{k} q^{k} (t)} = {\varvec{f}} $$
(3.10)

The orthogonality of UFMT system augmented eigenvectors [9] can be applied to decoupling Eq. (3.10) by taking inner products with any augmented eigenvector \( {\varvec{V}}^{s} \) on both sides of the Eq. (3.10). Proportional damping \( \zeta_{s} = c_{s} /(2m_{s} \omega_{s} ) \) is also introduced to replace the damping term. Finally, the generalized coordinate equations of UFMT system can be obtained.

$$ \begin{array}{*{20}c} {\ddot{q}^{s} (t) + 2\zeta_{s} \omega_{s} \dot{q}^{s} (t) + \omega_{s}^{2} q^{s} (t) = f_{s} } & {(s = 1,2, \cdots ,n)} \\ \end{array} $$
(3.11)

where \( f_{s} = \frac{{ < {\varvec{f}},{\varvec{V}}^{s} > }}{{\varvec{M}}} \).

3.3 Dynamics Simulation of the UFMT System

In the ultra-precision machining process, the initial condition of the UFMT system is

$$ \left\{ {\begin{array}{*{20}l} {\left. {{\varvec{v}}(t)} \right|_{t = 0} = {\varvec{v}}_{0} = {\varvec{0}}\;} \hfill \\ {\left. {{\varvec{v}}_{t} (t)} \right|_{t = 0} = {\dot{\varvec{v}}}_{0} = {\varvec{0}}} \hfill \\ \end{array} } \right. $$
(3.12)

Taking Eq. (3.12) into Eq. (3.9), the initial condition in generalized coordinate is

$$ \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}l} {\left. {q_{{}}^{s} (t)} \right|_{t = 0} = q_{0}^{s} = \frac{{ < {\mathbf{v}}_{0} ,{\mathbf{MV}}^{s} > }}{{M^{s} }} = 0} \hfill \\ {\left. {\dot{q}_{{}}^{s} (t)} \right|_{t = 0} = \dot{q}_{0}^{s} = \frac{{ < {\dot{\mathbf{v}}}_{0} ,{\mathbf{MV}}^{s} > }}{{M^{s} }} = 0} \hfill \\ \end{array} }, & {(s = 1,2, \cdots ,30)} \\ \end{array} } \right. $$
(3.13)

Choosing the first 30 modes of the system, the translational and angular displacement of any point in the UFMT system, which is dynamics response can be solved by using numerical integration method and substituting the generalized coordinate \( q^{s} (t) \) in Eq. (3.9). Choosing the middle 2 s (106–108 s) in the cutting process to analyze, Figs. 6 and Fig. 7 separately plot dynamics simulation results of fly-cutting head tool-tip displacement and acceleration. Cutting process parameters are the speed of spindle: 300 RPM; the feed speed: 15 mm/min; the depth of cutting: 4 μm.

Fig. 6
figure 6

Dynamics simulation results of fly-cutting head tool-tip displacement

Full size image
Fig. 7
figure 7

Dynamics simulation results of fly-cutting head tool-tip acceleration

Full size image

4 Verification and Discussions

4.1 Vibration Characteristics

To verify the correction of the dynamics model and vibration characteristics by MSTMM, the modal test and finite element method (FEM) simulation are carried out. In the modal test (shown in Fig. 8), the impact hammer (sensitivity: 4.11 pC/N) is used to exert excitation, and the senor is set to measure acceleration response signal one point by one point. To describe the modal shape of the UFMT and the high-order mode shapes of key components, 224 measuring points were arranged in the test. The FEM model of the UFMT system (shown in Fig. 9) is built by Abaqus and then meshed into 1082790 solid elements (C3D8R and C3D4 element). Choosing the same structure parameters as MSTMM model, the vibration characteristics can be solves by Lanczos Method.

Fig. 8
figure 8

The modal test set up

Full size image
Fig. 9
figure 9

FEM model of UFMT system

Full size image

Table 3 lists the first eighteen and 29th typical natural frequencies and modal shape by simulation and modal test. Especially, the 3rd order mode and the 1st order mode are all related to the bed and foundation rotating around a rotating axis in z-direction, but the rotating directions are same in the 1st order and are different in the 3rd order, which is defined as antisymmetric mode (shown in Fig. 10). Analogously, besides 3rd order and the 1st order, the 4th and 5th order modes are the antisymmetric modes of 6th, 7th order modes, respectively, which have not been tested in modal test due to symmetrical structure itself and symmetrical arrangement of measuring points. The other modes simulated by MSTMM and FEM are both consistent with modal test results. Due to the different models and algorithms used in MSTMM and FEM, relative results are all in rational ranges. Such results verify the correctness of the UFMT dynamics model and MSTMM method.

Fig. 10
figure 10

Diagram of antisymmetric mode

Full size image

The FEM simulation model is made up of 1,082,790 degrees of freedom so that order of the FEM system is 1,082,790. However, the order of MSTMM system is only 66. The lower orders bring the advantage of faster computation speed.

The first eight modes of the machine tool system are only associated with machine tool and the foundation vibrating in different directions, which illustrates that the stiffness of each component and joint surface in the machine tool are high enough, and the structure design of the machine tool is reasonable. Besides, the mode shapes describing the motions of fly-cutting tool-tip in z-directions are the 11th, 12th, 18th and 29th. The frequencies of those four orders are 111.3 Hz, 177.9 Hz, 258.6 Hz and 585.5 Hz by MSTMM.

4.2 Dynamics Response

It can be seen in the Fig. 11 that, in the acceleration of tool-tip test, a dynamic signal recorder (Dong Hua DH5916) is fixed under the fly-cutting head and the senor (sensitivity: 1.000 V/g) is pasted under the tool carrier. When the machine tool is working, the senor and the signal recorder are rotating with fly-cutting head in order to test and save the acceleration of tool-tip. After the test, we can download the acceleration signal from the signal recorder and compare to the simulated results (in Fig. 12). Cutting process parameters are the speed of spindle: 300 RPM; the feed speed: 15 mm/min; the depth of cutting: 4 μm. The two curves in Fig. 12 mostly coincide, reflecting in their periodicity and amplitude. Both of the curves reach the peak value when the tool-tip contacts the workpiece at the same time and then gradually attenuate, which composes a cutting period. The average peak value in a period of the simulated results and test results are 0.065 mm/s2 and 0.066 mm/s2. Those prove the reliability of the proposed method and the parameters we choose. As for the FEM model, it is mostly impossible to simulate the complete cutting process without modal reduction due to the need for giant memory space of the computer.

Fig. 11
figure 11

Tool-tip acceleration test set up

Full size image
Fig. 12
figure 12

Simulated and experimental results fly-cutting head tool-tip acceleration in z-direction

Full size image

While, the quality of ultra-precision machining is finally determined by the relative displacements between the fly- cutting tool-tip and the workpiece surface in z-direction [18] which is simulated and plotted in Fig. 13. The curve also owns the same periodicity as the curve above and the average peak value in a period is 34 nm.

Fig. 13
figure 13

Simulated relative displacement between tool-tip and workpiece in z-direction

Full size image

What’s more, what we directly care about is the machined surface. The 3D locus of the UFMT is mentioned in [19], which describes how to translate 2D curve into 3D surface. In the cutting direction, it is the fact that every point is processed more than once, so the actual locus is composed by the minimum relative displacements between the fly-cutting tool-tip and the work piece surface in z-direction at every point which is called ‘tool interference’ phenomenon. Further, the geometric model of the 3D locus is rewritten as

$$ \left\{ {\begin{array}{*{20}l} {x = R\sin (2\pi f_{z} t)} \hfill \\ {y = R\cos (2\pi f_{z} t) + vt} \hfill \\ {z = \left\{ {\hbox{min} (z_{re} )_{1} ,\hbox{min} (z_{re} )_{2} , \ldots \hbox{min} (z_{re} )_{n} } \right\}} \hfill \\ \end{array} } \right. $$
(4.1)

where R denotes the radius of fly-cutting head, \( f_{z} \) means the velocity of the spindle, v means the feed speed, \( z_{re} \) is the relative displacements between the fly-cutting tool-tip and the workpiece surface in z-direction, n represents the number of points in the workpiece. Taking cutting process parameters and simulated results into Eq. (4.1), one can obtain the simulated surface.

Machined surface can be recorded and analyzed by Laser Interferometer (Zogo) in the same processing condition. Figure 14 presents the simulated surface and the measured surface which have the same trend that is the middle part of the surface is higher than surrounding area. The peak-to-valley value (PV) is directly used to evaluate the surface, which can be calculate by comparing the value in z direction of every point in the surface. The PV of the simulated surface and the measured surface are very similar (139.08 nm and 142.91 nm), shown in Table 4.

Fig. 14
figure 14

Machined surface of UFMT system

Full size image
Table 4 PV of surfaces
Full size table

In according to explore the relation between machined surface and dynamics parameters such as structure parameters and cutting process parameters, dynamics simulations of different parameters are carried out.

Firstly, air-bearing stiffness of spindle has been changing, but it has little influence on either vibration characteristics or dynamics response. Then, air-bearing stiffness of spindle has been changing in different directions in a reasonable range; results are plotted in Fig. 15. The angular air-bearing stiffness has a methodical effect on the machined surface that is the higher, the better. While the relations between radial and axial air-bearing stiffness and machined surface are not as that of the angular air-bearing stiffness. So, the dynamics design of the air-bearing stiffness of the flying-cutting head is indispensable.

Fig. 15
figure 15

Dynamics simulation results of different air-bearing stiffness of cutting-head

Full size image

Furthermore, the dynamics simulation results of different cutting process parameters are demonstrated in Fig. 16. When the speed of spindle increases and feed speed decreases in a reasonable range, the numbers of contacts between tool-tip and workpiece increase. As a result, the machined surface becomes smoother. On the other hand, cutting force is the main excitation of fly-cutting tool-tip, so the larger cutting force generates larger amplitude and broader bandwidth of tool-tip vibration which map to the surface. During actual processing, cutting force can indirectly downsize by diminishing depth of cutting and reducing tool wear as possible.

Fig. 16
figure 16

Dynamics simulation results of different cutting process parameters

Full size image

Consequently, the angular air-bearing stiffness of the flying-cutting head should increase and the radial and axial air-bearing should be optimized. As for the cutting process parameters, the speed of spindle should increase appropriately, while low feed speed and small cut force should be chosen in the ultra-precision machining.

5 Conclusions

Dynamics modelling and simulating of the ultra-precision fly-cutting machine tool (UFMT) is presented in this paper by using the transfer matrix method for multibody systems (MSTMM).

  1. 1.

    The dynamics model of UFMT multi-rigid-flexible system is proposed. In the model, the spindle is treated as a flexible body and the other parts are rigid bodies. The overall transfer equation, overall transfer matrix and the characteristic equation of the system are deduced theoretically by MSTMM, and first thirty modes of vibration characteristics are obtained by solving the eigenfrequency equation. The simulation results are consistent with the modal test results

  2. 2.

    The dynamics equations in the generalized coordinate of UFMT are derived after the body element dynamics equation has formulated simultaneously and are decoupled using augmented eigenvectors. The effective simulation of dynamics response can realize by MSTMM, and the simulation results have been verified by tool-tip acceleration test.

  3. 3.

    The machined surface is simulated by translating 2D dynamics response curve into a 3D surface. The peak-to-valley value and trend of the simulated surface is basically consistent with the measured surface. Both the air-bearing stiffness of the flying-cutting head and cutting process parameters affect the machined surface.