Research on the dynamic characteristics of the ultra-precision fly cutting machine tool and its influence on the mid-frequency waviness of the surface

Abstract

With the increasing demand for machining accuracy of machine tools, the dynamic characteristics of ultra-precision fly cutting machine tool (UFCMT) have increasingly prominent impacts on the machining accuracy. Based on the transfer matrix method for multibody systems (MSTMM), the dynamics model and its topology figure are established, and the dynamic response of the UFCMT is computed. The modal test of the UFCMT and the vibration test of the tool tip are carried out, which verifies the correctness of the dynamics model. To research causes of the formation of the mid-frequency waviness on the machined surface, the machined surfaces at different rotating speeds are measured. By extracting the characteristic frequencies of mid-frequency waviness of the machined surface and comparing with the results from the modal test and the vibration test, the dynamic characteristics of the spindle and the tool holder are main factors that form the mid-frequency waviness. By optimizing the connect stiffness between the tool holder and the fly cutting head, the displacement of the tool tip and the peak to valley (PV) value of the machined surface in the range of mid-frequency waviness is decreased.

1 Introduction

Ultra-precision fly cutting machine tool (UFCMT) is used to machine large-aperture planar potassium dihydrogen phosphate (KDP) crystals, aluminum alloy, copper, polycarbonate, and other ultra-precision optical elements used in the inertial confinement fusion (ICF) program [1]. In ultra-precision machining, the machined surface of the workpiece is formed by the cutting trajectory of the tool tip, which is decided by the relative movement between the tool tip and the workpiece. Therefore, all static and dynamic factors of machine tools will be imprinted on the surface topography and form waviness on the workpiece surface. The mid-frequency waviness (the spatial period in 2.5~33 mm) of the surface will cause a nonlinear increase and distortion of the refractive index of the input laser, and consequently decrease the laser-induced damage threshold, and even cause the damage of the optical elements [2]. Therefore, it is necessary to research the influence of the dynamic characteristics of the UFCMT on the mid-frequency waviness of the surface. Dynamic characteristics of machine tools include the dynamics model, natural frequencies, mode shapes, and the dynamics response. To improve the machining accuracy, the analysis of dynamic characteristics has always been the focuses and difficulties in the development of the UFCMT [3, 4].

In the published literatures, the main research institutes of the UFCMT are the Harbin Institute of Technology and China Academy of Engineering Physics (CAEP). Liang and his co-workers [5, 6] from Harbin Institute of Technology have done deep researches on the UFCMT. Liang and Chen proposed the design method of the UFCMT based on its dynamic characteristics. By establishing the whole finite element model of the UFCMT, the dynamic characteristics were analyzed and the machine tool structure was designed and optimized. Chen et al. [7] simplified the UFCMT as a spring-mass-damping system with 3 DOFs and analyzed the dynamics response of the tool tip. The influences of 3 modes natural frequencies of the UFCMT on the surface generation were investigated. An et al. [8] from Chengdu Fine Optic Engineering Research Center of CAEP proposed the Euler dynamics equations of the angular displacements of the aerostatic spindle. Its analytical solutions were also deduced. The mid-frequency waviness errors on the machined surface were determined by the ratio of inertia tensors of the spindle, which gave instructions to its structure design. Yang et al. [9] built a finite element model of the air spindle in Ansys and analyzed its dynamic characteristics. The vibration of the spindle under the cutting force caused the waviness at a space period of 17 mm on the machined surface, and its optimization was put forward. Chen et al. [10] built an unbalance dynamics model of the spindle considering the radial and axial directions and presented its transient analysis under the micro factors. Ding et al. [11] used the transfer matrix method to establish a dynamics model of the machine tool. However, the dynamics model is not precise enough and only the natural vibration characteristics are analyzed. In summary, some researchers use the spring-mass-damping model to model and analyze the UFCMT. The DOFs of this method are not enough, and the accuracy is not very good. Most researchers use the finite element method to research the UFCMT, which has high accuracy but needs huge amount of computation. This paper proposes a novel method (MSTMM) to analyze the dynamic characteristics of UFCMT, which has advantages of without global dynamics equations of the system, high programming, low order of the system matrix, and high computational speed [12, 13]. In this paper, a detailed model of the UFCMT and its dynamics topology figure are established. The dynamic characteristics are investigated. The main factors that introduced the mid-frequency waviness of the machined surface are analyzed. By studying the influence of the dynamics characteristics on the machined surface, the structure of the machine tool is improved.

2 Dynamic characteristics of the UFCMT based on MSTMM

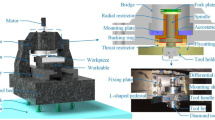
The UFCMT, as shown in Fig. 1, consists of foundation, machine tool bed, hydrostatic guideway, slider, columns, bridge, rotor, bearing spindle, aerostatic spindle, fly cutting head, and tool holder.

Fig. 1

UFCMT

Elements in this system are divided into body elements and hinge elements. Body elements include rigid body and flexible body, and hinge elements represent elastic hinges (EH).

The dynamics model of the UFCMT is shown in Fig. 2, and its topology figure is shown in Fig. 3. The ground is considered an infinite rigid body 0. The foundation, machine tool bed, slider, left and right side guideways, left and right upper guideways, left and right columns, bridge, rotor, bearing spindle, fly cutting head, and front and back tool holders are considered rigid bodies 43, 41, 9, 11, 13, 4, 7, 37, 39, 35, 23, 25, 33, 29, and 31, respectively. The aerostatic spindle is considered two beams, numbered 15 and 20. The two beams are connected by a massless rigid flake 18. All body elements are connected by spatial elastic hinges with translational stiffness k_x, k_y, k_z, and rotational stiffness ${k}_x^{\prime }$, ${k}_y^{\prime }$, and ${k}_z^{\prime }$. In conclusion, the UFCMT is a multi-rigid-flexible-body system, which consists of 16 rigid bodies, 2 beams, and 26 hinges. As can be seen in Fig. 3, there are 8 closed loops in the topology figure. By cutting the junctions of element 11/1, 11/3, 13/2, 13/6, 15/28, 20/17, 35 /22, and 39/27 marked by circles in Fig. 3, a tree topology figure can be achieved, as shown in Fig. 4. After cutting between i/j, artificial boundary states Z_{i, j} and Z_{i, 0} show up. The state vectors Z_{i, 0} marked by red colors in Fig. 4 are the state vectors at boundary points of the system. The circles represent body elements and arrows indicate hinge elements. The direction of the arrows denotes the transfer direction of state vectors.

Fig. 2

Dynamics model of UFCMT

Fig. 3

Topology figure of dynamics model of UFCMT

Fig. 4

Tree topology figure of UFCMT

2.1 Automatic deduction of overall transfer equation of the system

In MSTMM, elements are considered elements with single input and single output ends or elements with multiple input ends and single output end. The transfer equations of these elements can be formulated as

$$ {\boldsymbol{Z}}_{i,\mathrm{O}}=\sum \limits_{r=1}^N{\boldsymbol{U}}_{i,{\mathrm{I}}_r}{\boldsymbol{Z}}_{i,{\mathrm{I}}_r} $$

(1)

where

$$ {\boldsymbol{Z}}_{i,{\mathrm{I}}_r}={\left[{\boldsymbol{R}}^{\mathrm{T}},{\boldsymbol{\varTheta}}^{\mathrm{T}},{\boldsymbol{M}}^{\mathrm{T}},{\boldsymbol{Q}}^{\mathrm{T}}\right]}_{i,{\mathrm{I}}_r}^{\mathrm{T}} $$

(2)

and ${\boldsymbol{Z}}_{i,{\mathrm{I}}_r}$ is the state vector of the rth input end of element i; R^T = [X, Y, Z]^T,Θ^T = [Θ_x, Θ_y, Θ_z]^T, M^T = [M_x, M_y, M_z]^T, and Q^T = [Q_x, Q_y, Q_z]^T are the modal coordinates of translational displacements, angular displacements, internal torques and internal forces, respectively; ${\boldsymbol{U}}_{i,{\mathrm{I}}_r}$ is the corresponding transfer matrix of the rth input end of element i; and N is the total number of input ends of element i.

For a rigid body with multiple input ends and single output end, the further geometrical equation needs to be supplemented and can be given as

$$ {\boldsymbol{H}}_{i,{\mathrm{I}}_1}{\boldsymbol{Z}}_{i,{\mathrm{I}}_1}={\boldsymbol{H}}_{i,{\mathrm{I}}_r}{\boldsymbol{Z}}_{i,{\mathrm{I}}_r}\kern0.5em \left(r=2,3,\cdots, N\right) $$

(3)

where

$$ {\boldsymbol{H}}_{i,{\mathrm{I}}_{\mathrm{r}}}=\left[\begin{array}{cccc}{\boldsymbol{I}}_3& {\overset{\sim }{\boldsymbol{l}}}_{{\mathrm{I}}_1{\mathrm{I}}_{\mathrm{r}}}& {\boldsymbol{O}}_{3\times 3}& {\boldsymbol{O}}_{3\times 3}\\ {}{\boldsymbol{O}}_{3\times 3}& {\boldsymbol{I}}_3& {\boldsymbol{O}}_{3\times 3}& {\boldsymbol{O}}_{3\times 3}\end{array}\right]\left(r=1,\cdots, N\right) $$

(4)

and ${\tilde{\boldsymbol{l}}}_{{\mathrm{I}}_1{\mathrm{I}}_{\mathrm{r}}}$ refers to the skew-symmetric matrix of ${\boldsymbol{l}}_{{\mathrm{I}}_1{\mathrm{I}}_{\mathrm{r}}}$, which is the coordinate vector of the rth input end relative to the first input end.

Per the automatic deduction theorem of overall transfer equation of multibody systems [14] and the tree topology figure in Fig. 4, the overall transfer equation can be deduced as

$$ {\boldsymbol{U}}_{\mathrm{all}\ \left(114\times 132\right)}{\boldsymbol{Z}}_{\mathrm{all}\ \left(132\times 1\right)}=\boldsymbol{0} $$

(5)

where all the state vectors at boundary points of the system marked by red colors in Fig. 4 are given as

$$ {\displaystyle \begin{array}{l}{\boldsymbol{Z}}_{\mathrm{all}}=\Big[{\boldsymbol{Z}}_{44,0}^{\mathrm{T}},{\boldsymbol{Z}}_{1,0}^{\mathrm{T}},{\boldsymbol{Z}}_{2,0}^{\mathrm{T}},{\boldsymbol{Z}}_{3,0}^{\mathrm{T}},{\boldsymbol{Z}}_{6,0}^{\mathrm{T}},{\boldsymbol{Z}}_{17,0}^{\mathrm{T}},\\ {}\kern0.5em {\boldsymbol{Z}}_{22,0}^{\mathrm{T}},{\boldsymbol{Z}}_{27,0}^{\mathrm{T}},{\boldsymbol{Z}}_{28,0}^{\mathrm{T}},{\boldsymbol{Z}}_{29,0}^{\mathrm{T}},{\boldsymbol{Z}}_{31,0}^{\mathrm{T}}\Big]{}^{\mathrm{T}}\end{array}} $$

(6)

The overall transfer matrix is

$$ {U}_{\mathrm{all}}=\left[\begin{array}{ccccccccccc}-I& {T}_{1-44}+{T}_{11-44,{\mathrm{I}}_1}C& {T}_{2-44}+{T}_{13-44,{\mathrm{I}}_1}C& {T}_{3-44}+{T}_{11-44,{\mathrm{I}}_2}C& {T}_{6-44}+{T}_{13-44,{\mathrm{I}}_2}C& {T}_{17-44}+{T}_{20-44}C& {T}_{22-44}+{T}_{35-44}C& {T}_{27-44}+{T}_{39-44}C& {T}_{28-44}+{T}_{15-44}C& {T}_{29-44}& {T}_{31-44}\\ {}O& {G}_{1-9}& {G}_{2-9}& O& O& O& O& O& O& O& O\\ {}O& {G}_{1-9}& O& {G}_{3-9}& O& O& O& O& O& O& O\\ {}O& {G}_{1-9}& O& O& {G}_{6-9}& O& O& O& O& O& O\\ {}O& {G}_{11-11,{\mathrm{I}}_1}C& O& {G}_{11-11,{\mathrm{I}}_2}C& O& O& O& O& O& O& O\\ {}O& {G}_{1-41}+{G}_{11-41,{\mathrm{I}}_1}C& {G}_{2-41}& {G}_{3-41}+{G}_{11-41,{\mathrm{I}}_2}C& {G}_{6-41}& O& O& O& O& O& O\\ {}O& O& {G}_{13-13,{\mathrm{I}}_1}C& O& {G}_{13-13,{\mathrm{I}}_2}C& O& O& O& O& O& O\\ {}O& {G}_{1-41}& {G}_{2-41}+{G}_{13-41,{\mathrm{I}}_1}C& {G}_{3-41}& {G}_{6-41}+{G}_{13-41,{\mathrm{I}}_2}C& O& O& O& O& O& O\\ {}O& O& O& O& O& {G}_{17-18}& O& O& {G}_{15-18}C& O& O\\ {}O& O& O& O& O& {G}_{20-25}C& {G}_{22-25}& O& O& O& O\\ {}O& O& O& O& O& O& O& O& {G}_{28-33}& {G}_{29-33}& O\\ {}O& O& O& O& O& O& O& O& {G}_{28-33}& O& {G}_{31-33}\\ {}O& O& O& O& O& {G}_{17-35}+{G}_{20-35}C& {G}_{22-35}& O& {G}_{15-35}C& O& O\\ {}O& O& O& O& O& {G}_{17-35}& O& {G}_{27-35}& {G}_{15-35}C& O& O\\ {}O& O& O& O& O& {G}_{17-35}& O& O& {G}_{28-35}+{G}_{15-35}C& {G}_{29-35}& {G}_{31-35}\\ {}O& O& O& O& O& {G}_{17-35}& {G}_{35-35}C& O& {G}_{15-35}C& O& O\\ {}O& {G}_{1-41}& {G}_{2-41}& {G}_{3-41}& {G}_{6-41}& {G}_{17-41}+{G}_{20-41}C& {G}_{22-41}+{G}_{35-41}C& {G}_{27-41}& {G}_{28-41}+{G}_{15-41}C& {G}_{29-41}& {G}_{31-41}\\ {}O& {G}_{1-41}& {G}_{2-41}& {G}_{3-41}& {G}_{6-41}& O& O& {G}_{39-41}C& O& O& O\end{array}\right] $$

(7)

where

$$ \left\{\begin{array}{c}{T}_{1-44}={U}_{44}{U}_{43}{U}_{42}{U}_{41,{\mathrm{I}}_1}{U}_{10}{U}_{9,{\mathrm{I}}_1}{U}_1\\ {}{T}_{2-44}={U}_{44}{U}_{43}{U}_{42}{U}_{41,{\mathrm{I}}_1}{U}_{10}{U}_{9,{\mathrm{I}}_2}{U}_2\\ {}{T}_{3-44}={U}_{44}{U}_{43}{U}_{42}{U}_{41,{\mathrm{I}}_1}{U}_{10}{U}_{9,{\mathrm{I}}_3}{U}_5{U}_4{U}_3\\ {}{T}_{6-44}={U}_{44}{U}_{43}{U}_{42}{U}_{41,{\mathrm{I}}_1}{U}_{10}{U}_{9,{\mathrm{I}}_4}{U}_8{U}_7{U}_6\\ {}{T}_{11-44,{I}_1}={U}_{44}{U}_{43}{U}_{42}{U}_{41,{\mathrm{I}}_2}{U}_{12}{U}_{11,{\mathrm{I}}_1}\\ {}{T}_{11-44,{\mathrm{I}}_2}={U}_{44}{U}_{43}{U}_{42}{U}_{41,{\mathrm{I}}_2}{U}_{12}{U}_{11,{\mathrm{I}}_2}\\ {}{T}_{13-44,{\mathrm{I}}_1}={U}_{44}{U}_{43}{U}_{42}{U}_{41,{\mathrm{I}}_3}{U}_{14}{U}_{13,{\mathrm{I}}_1}\\ {}{T}_{13-44,{\mathrm{I}}_2}={U}_{44}{U}_{43}{U}_{42}{U}_{41,{\mathrm{I}}_3}{U}_{14}{U}_{13,{\mathrm{I}}_2}\\ {}{T}_{15-44}={U}_{44}{U}_{43}{U}_{42}{U}_{41,{\mathrm{I}}_4}{U}_{38}{U}_{37}{U}_{36}{U}_{35,{\mathrm{I}}_1}{U}_{19}{U}_{18,{\mathrm{I}}_1}{U}_{16}{U}_{15}\\ {}{T}_{17-44}={U}_{44}{U}_{43}{U}_{42}{U}_{41,{\mathrm{I}}_4}{U}_{38}{U}_{37}{U}_{36}{U}_{35,{\mathrm{I}}_1}{U}_{19}{U}_{18,{\mathrm{I}}_2}{U}_{17}\\ {}{T}_{20-44}={U}_{44}{U}_{43}{U}_{42}{U}_{41,{\mathrm{I}}_4}{U}_{38}{U}_{37}{U}_{36}{U}_{35,{\mathrm{I}}_2}{U}_{26}{U}_{25,{\mathrm{I}}_1}{U}_{21}{U}_{20}\\ {}{T}_{22-44}={U}_{44}{U}_{43}{U}_{42}{U}_{41,{\mathrm{I}}_4}{U}_{38}{U}_{37}{U}_{36}{U}_{35,{\mathrm{I}}_2}{U}_{26}{U}_{25,{\mathrm{I}}_2}{U}_{24}{U}_{23}{U}_{22}\\ {}{T}_{27-44}={U}_{44}{U}_{43}{U}_{42}{U}_{41,{\mathrm{I}}_4}{U}_{38}{U}_{37}{U}_{36}{U}_{35,{\mathrm{I}}_3}{U}_{27}\\ {}{T}_{28-44}={U}_{44}{U}_{43}{U}_{42}{U}_{41,{\mathrm{I}}_4}{U}_{38}{U}_{37}{U}_{36}{U}_{35,{\mathrm{I}}_4}{U}_{34}{U}_{33,{\mathrm{I}}_1}{U}_{28}\\ {}{T}_{29-44}={U}_{44}{U}_{43}{U}_{42}{U}_{41,{\mathrm{I}}_4}{U}_{38}{U}_{37}{U}_{36}{U}_{35,{\mathrm{I}}_4}{U}_{34}{U}_{33,{\mathrm{I}}_2}{U}_{30}{U}_{29}\\ {}{T}_{31-44}={U}_{44}{U}_{43}{U}_{42}{U}_{41,{\mathrm{I}}_4}{U}_{38}{U}_{37}{U}_{36}{U}_{35,{\mathrm{I}}_4}{U}_{34}{U}_{33,{\mathrm{I}}_3}{U}_{32}{U}_{31}\\ {}{T}_{35-44}={U}_{44}{U}_{43}{U}_{42}{U}_{41,{\mathrm{I}}_4}{U}_{38}{U}_{37}{U}_{36}{U}_{35,{\mathrm{I}}_4}\\ {}{T}_{39-44}={U}_{44}{U}_{43}{U}_{42}{U}_{41,{\mathrm{I}}_5}{U}_{40}{U}_{39}\end{array}\right. $$

(8)

$$ \left\{\begin{array}{c}{G}_{1-9}=-{H}_{9,{\mathrm{I}}_1}{U}_1\\ {}{G}_{2-9}={H}_{9,{\mathrm{I}}_1}{U}_2\\ {}{G}_{3-9}={H}_{9,{\mathrm{I}}_3}{U}_5{U}_4{U}_3\\ {}{G}_{6-9}={H}_{9,{\mathrm{I}}_4}{U}_8{U}_7{U}_6\\ {}{G}_{11-11,{\mathrm{I}}_1}=-{H}_{11,{\mathrm{I}}_1}\\ {}{G}_{11-11,{\mathrm{I}}_2}={H}_{11,{\mathrm{I}}_2}\\ {}{G}_{13-13,{\mathrm{I}}_1}=-{H}_{13,{\mathrm{I}}_1}\\ {}{G}_{13-13,{\mathrm{I}}_2}={H}_{13,{\mathrm{I}}_2}\\ {}{G}_{15-18}=-{H}_{18,{\mathrm{I}}_1}{U}_{16}{U}_{15}\\ {}{G}_{17-18}={H}_{18,{\mathrm{I}}_2}{U}_{17}\end{array}\right. $$

(9)

$$ \left\{\begin{array}{c}{G}_{20-25}=-{H}_{25,{\mathrm{I}}_1}{U}_{21}{U}_{20}\\ {}{G}_{22-25}={H}_{25,{\mathrm{I}}_2}{U}_{24}{U}_{23}{U}_{22}\\ {}{G}_{28-33}=-{H}_{33,{\mathrm{I}}_1}{U}_{28}\\ {}{G}_{29-33}={H}_{33,{\mathrm{I}}_2}{U}_{30}{U}_{29}\\ {}{G}_{31-33}={H}_{33,{\mathrm{I}}_3}{U}_{32}{U}_{31}\\ {}{G}_{15-35}=-{H}_{35,{\mathrm{I}}_1}{U}_{19}{U}_{18,{\mathrm{I}}_1}{U}_{16}{U}_{15}\\ {}{G}_{17-35}=-{H}_{35,{\mathrm{I}}_1}{U}_{19}{U}_{18,{\mathrm{I}}_2}{U}_{17}\\ {}{G}_{20-35}={H}_{35,{\mathrm{I}}_2}{U}_{26}{U}_{25,{\mathrm{I}}_1}{U}_{21}{U}_{20}\\ {}{G}_{22-35}={H}_{35,{\mathrm{I}}_2}{U}_{26}{U}_{25,{\mathrm{I}}_2}{U}_{24}{U}_{23}{U}_{22}\\ {}{G}_{27-35}={H}_{35,{\mathrm{I}}_3}{U}_{27}\\ {}{G}_{28-35}={H}_{35,{\mathrm{I}}_4}{U}_{34}{U}_{33,{\mathrm{I}}_1}{U}_{28}\\ {}{G}_{29-35}={H}_{35,{\mathrm{I}}_4}{U}_{34}{U}_{33,{\mathrm{I}}_2}{U}_{30}{U}_{29}\\ {}{G}_{31-35}={H}_{35,{\mathrm{I}}_4}{U}_{34}{U}_{33,{\mathrm{I}}_3}{U}_{32}{U}_{31}\end{array}\right. $$

(10)

$$ \boldsymbol{C}=\left[\begin{array}{cc}\boldsymbol{I}& \boldsymbol{O}\\ {}\boldsymbol{O}& -\boldsymbol{I}\end{array}\right] $$

(11)

The transfer matrices of rigid bodies, beams, and spatial elastic hinges and the detailed process of automatic deduction can be seen in Refs. [11, 15]. For boundary conditions, Z_{44, 0} is a boundary fixed to the ground. Therefore, the displacement and angle are zero while the forces and moments are unknown in Z_{44, 0}.

$$ {\boldsymbol{Z}}_{44,0}={\left[0,0,0,0,0,0,{M}_x,{M}_y,{M}_z,{Q}_x,{Q}_y,{Q}_z\right]}_{44,0}^{\mathrm{T}} $$

(12)

Z_{29, 0} and Z_{31, 0} are free boundary end. The displacement and angle are unknown while the forces and moments are zero.

$$ {\displaystyle \begin{array}{c}{\boldsymbol{Z}}_{i,0}={\left[X,Y,Z,{\Theta}_x,{\Theta}_y,{\Theta}_z,0,0,0,0,0,0,\right]}_{i,0}^{\mathrm{T}}\\ {}\left(i=29,31\right)\end{array}} $$

(13)

The remaining states are virtual boundaries after cutting the connections of the closed loops. The displacement, angle, forces, and moments are all unknown.

$$ {\displaystyle \begin{array}{c}{\boldsymbol{Z}}_{i,0}={\left[X,Y,Z,{\Theta}_x,{\Theta}_{y,}{\Theta}_z,{M}_x,{M}_y,{M}_z,{Q}_x,{Q}_y,{Q}_z\right]}_{i,0}^{\mathrm{T}}\\ {}\left(i=29,31\right)\end{array}} $$

(14)

Substituting Eqs. (12)–(14) into Eq. (5), a homogeneous linear algebraic equation can be obtained:

$$ {\overline{\boldsymbol{U}}}_{\mathrm{all}}{\overline{\boldsymbol{Z}}}_{\mathrm{all}}=\boldsymbol{0} $$

(15)

where ${\overline{\boldsymbol{Z}}}_{\mathrm{all}}$ is an array (114 × 1) by getting rid of the 18 known boundary conditions, and ${\overline{\boldsymbol{U}}}_{\mathrm{all}}$ is a matrix (114 × 114) by deleting the columns in U_all (114 × 132) corresponding to the 18 known boundary conditions in Z_all. The determinant of the system matrix is the characteristic equation of the system. The natural frequencies can be obtained by using the bisection method in Eq. (16).

$$ \det \left({\overline{\boldsymbol{U}}}_{\mathrm{all}}\right)=0 $$

(16)

And substituting the natural frequencies ω_k(k = 1, 2, ⋯) into Eq. (15) and using singular value decomposition of ${\overline{\boldsymbol{U}}}_{\mathrm{all}}$, ${\overline{\boldsymbol{Z}}}_{\mathrm{all}}$ can be solved. The state vector of each element in the system can be obtained by using Eq. (1) per the transfer direction shown in Fig. 4. Then, eigenvectors and mode shapes can be acquired.

2.2 Dynamics response of the system

Instead of overall dynamics equation of the system, body dynamics equations are used to solve the dynamic problems in MSTMM. The body dynamics equation of element i can be written as

$$ {\boldsymbol{M}}_i{\boldsymbol{v}}_{i, tt}+{\boldsymbol{C}}_i{\boldsymbol{v}}_{i,t}+{\boldsymbol{K}}_i{\boldsymbol{v}}_i={\boldsymbol{f}}_i $$

(17)

where v_i is the displacements and angles array of element i, and the subscript t represents the derivative of time. M_i, C_i, and K_i are the mass matrix, damping matrix, and spring matrix, respectively. f_i is the array of external forces and torques. In the dynamics model of the UFCMT, i refers to 4, 7, 9, 11, 13, 18, 23, 25, 29, 31, 33, 35, 37, 39, 41, 43, 15, and 20.

For rigid bodies, the M_i, C_i, and K_i can be written as

$$ {\displaystyle \begin{array}{c}{M}_i=\left[\begin{array}{cc}m{I}_3& -m{\overset{\sim }{l}}_{I_1C}\\ {}m{\overset{\sim }{l}}_{I_1C}& {J}_{I_1}\end{array}\right]\\ {}{C}_i=\left[\begin{array}{cc}-\sum \limits_{r=1}^N{\left.{I}_3{\mathrm{d}}^3\right|}_{{\mathrm{I}}_r}+{\left.{I}_3{\mathrm{d}}^3\right|}_{\mathrm{O}}& {O}_{3\times 3}\\ {}-\sum \limits_{r=2}^N{\left.{\overset{\sim }{l}}_{{\mathrm{I}}_1{\mathrm{I}}_r}{\mathrm{d}}^3\right|}_{{\mathrm{I}}_r}+{\left.{\overset{\sim }{l}}_{I_1\mathrm{O}}{\mathrm{d}}^3\right|}_{\mathrm{O}}& \sum \limits_{r=1}^N{\left.{I}_3{\mathrm{d}}^1\right|}_{{\mathrm{I}}_r}-{\left.{I}_3{\mathrm{d}}^1\right|}_{\mathrm{O}}\end{array}\right]\\ {}{K}_i=\left[\begin{array}{cc}-\sum \limits_{r=1}^N{\left.{I}_3{\mathrm{D}}^3\right|}_{{\mathrm{I}}_r}+{\left.{I}_3{\mathrm{D}}^3\right|}_{\mathrm{O}}& {O}_{3\times 3}\\ {}-\sum \limits_{r=2}^N{\left.{\overset{\sim }{l}}_{{\mathrm{I}}_1{\mathrm{I}}_r}{\mathrm{D}}^3\right|}_{{\mathrm{I}}_r}+{\left.{\overset{\sim }{l}}_{I_1\mathrm{O}}{\mathrm{D}}^3\right|}_{\mathrm{O}}& \sum \limits_{r=1}^N{\left.{I}_3{\mathrm{D}}^1\right|}_{{\mathrm{I}}_r}-{\left.{I}_3{\mathrm{D}}^1\right|}_{\mathrm{O}}\end{array}\right]\\ {}\left(i=4,7,\mathrm{9,11,13,18,23,25,29,31,33,35,37,39,41,43}\right)\end{array}} $$

(18)

where d³|_P, d¹|_P, D³|_P, and D¹|_P (P = I_r, O) are differential operators; d³|_P and d¹|_P are the damping forces and torques acting at P; and D³|_P and D¹|_P denote the internal forces and torques except the damping forces and torques, respectively.

For beams, these matrices can be written as

$$ {\displaystyle \begin{array}{l}{\boldsymbol{M}}_i=\mathrm{dia}g\left(\overline{m},\overline{m},\overline{m},\rho {J}_{\mathrm{P}}\right)\\ {}{\boldsymbol{C}}_i=\mathrm{dia}g\left({d}_x,{d}_y,{d}_z,{d}_x^{\prime}\right)\\ {}{\boldsymbol{K}}_i=\mathrm{dia}g\left(- EA\frac{\partial^2}{\partial {a}^2},{EI}_z\frac{\partial^4}{\partial {a}^4},{EI}_y\frac{\partial^4}{\partial {a}^4},-{GJ}_{\mathrm{P}}\frac{\partial^2}{\partial {a}^2}\right)\\ {}\left(i=15,20\right)\end{array}} $$

(19)

where $\overline{m}$ is mass per unit length, ρ is mass density, and J_P is the moment of cross section inertia, EA is compressive stiffness, GJ_P is torsional stiffness, and EI_z and EI_y are bending stiffness along z-axis and y-axis of the beam, respectively. d_x, d_y, and d_z are the damping force coefficients along the axes of the beam and ${d}_x^{\prime }$ is the damping torsional coefficient along x-axis of the beam.

By assembling the body dynamics equations one by one, the overall dynamics equation is

$$ {\boldsymbol{Mv}}_{tt}+{\boldsymbol{Cv}}_t+\boldsymbol{Kv}=\boldsymbol{f} $$

(20)

where

$$ {\displaystyle \begin{array}{l}\boldsymbol{M}=\operatorname{diag}\left({\boldsymbol{M}}_4,{\boldsymbol{M}}_7,\dots, {\boldsymbol{M}}_{20}\right)\\ {}\boldsymbol{K}=\operatorname{diag}\left({\boldsymbol{K}}_4,{\boldsymbol{K}}_7,\dots, {\boldsymbol{K}}_{20}\right)\\ {}\boldsymbol{v}={\left[{\boldsymbol{v}}_4^{\mathrm{T}},{\boldsymbol{v}}_7^{\mathrm{T}},\dots, {\boldsymbol{v}}_{20}^{\mathrm{T}}\right]}^{\mathrm{T}}\\ {}\boldsymbol{f}={\left[{\boldsymbol{f}}_4^{\mathrm{T}},{\boldsymbol{f}}_7^{\mathrm{T}},\dots, {\boldsymbol{f}}_{20}^{\mathrm{T}}\right]}^{\mathrm{T}}\end{array}} $$

(21)

The augmented eigenvectors of V^k are proposed in MSTMM and are defined by displacements and angles array of the first input end of all rigid bodies and mode shapes of all beams in the kth-order modal coordinates.

$$ {\boldsymbol{V}}^k=\left[{{\boldsymbol{V}}_4^k}^{\mathrm{T}},{{\boldsymbol{V}}_7^k}^{\mathrm{T}},\cdots, {{\boldsymbol{V}}_{20}^k}^{\mathrm{T}}\right]\kern0.5em \left(k=1,2,\cdots \right) $$

(22)

Due to the orthogonality of the augmented eigenvectors

$$ {\displaystyle \begin{array}{l}<{\boldsymbol{MV}}^k,{\boldsymbol{V}}^s>={\delta}_{k,s}{M}_s\\ {}<{\boldsymbol{KV}}^k,{\boldsymbol{V}}^s>={\delta}_{k,s}{K}_s\end{array}} $$

(23)

M_s and ${K}_s={\omega}_s^2{M}_s$ are the kth-order modal mass and stiffness.

Using the modal superposition method, the dynamics response is formulated as

$$ \boldsymbol{v}=\sum \limits_{k=1}^m{\boldsymbol{V}}^k{q}^k(t) $$

(24)

where m is the mode number. q^k(t) is the generalized coordinate of the kth mode.

Substituting Eq. (24) into Eq. (20) yields

$$ \sum \limits_{k=1}^m{\boldsymbol{MV}}^k{\ddot{q}}^k(t)+\sum \limits_{k=1}^m{\boldsymbol{CV}}^k{\dot{q}}^k(t)+\sum \limits_{k=1}^m{\boldsymbol{KV}}^k{q}^k(t)=\boldsymbol{f} $$

(25)

Taking inner products with V^s(s = 1, 2, ⋯, m) to Eq. (25), the differential equations of forced vibration of the system in generalized coordinates can be obtained as

$$ {\displaystyle \begin{array}{l}{M}_s{\ddot{q}}^s(t)+\sum \limits_{k=1}^m<{\boldsymbol{CV}}^k,{\boldsymbol{V}}^s>{\dot{q}}^k(t)+{K}_s{q}^s(t)=<\boldsymbol{f},{\boldsymbol{V}}^s>\kern0.5em \\ {}\left(s=1,2,\cdots, m\right)\end{array}} $$

(26)

Defining ${\zeta}_s=\frac{C_s}{2{\omega}_s{M}_s}$ and f_s = < f, V^s>, then Eq. (26) can be rewritten as

$$ {\displaystyle \begin{array}{l}{\ddot{q}}^s(t)+2{\zeta}_s{\omega}_s{\dot{q}}^s(t)+{\omega}_s^2{q}^s(t)={f}_s/{M}_s\kern0.5em \\ {}\left(s=1,2,\cdots, m\right)\end{array}} $$

(27)

where ζ_s is the sth-order modal damping ratio. f_s is the single-valued functions depending only on time t. The q^s(t)(s = 1, 2, ⋯, m) can be acquired by solving Eq. (27) using the numerical integration method. Substituting q^s(t)(s = 1, 2, ⋯, m) into Eq. (24), the dynamics response can be obtained.

3 Characteristic analysis of the mid-frequency in UFCMT

3.1 Extraction of the characteristic frequencies of the mid-frequency

When the feed rate is 12 mm/min, the cutting depth is 4 μm, and the rotating speed of the spindle is 200 rpm, 280 rpm, and 360 rpm, respectively; a pure copper workpiece was machined. The surface topology shown in Fig. 5 was measured by the FizCam 2000 Fizeau laser interferometer. The workpiece is feeding along the neigative x-direction, and the cutter is cutting along the negative y-direction.

Fig. 5

Machined surface topology at 200 rpm, 280 rpm, and 360 rpm

The machined surfaces in the range of PSD1 (the spatial period in 2.5~33 mm) were extracted by the Zygo MetroPro software, as shown in Fig. 6. There is obvious waviness on the machined surface along the cutting direction (the negative y-direction). With the increasing of the rotating speed, the waviness on the machined surface becomes sparser.

Fig. 6

Machined surface topology in the PSD1 period at 200 rpm, 280 rpm, and 360 rpm

To extract the characteristic frequencies of the mid-frequency waviness on the machined surface in the cutting direction, the arc cutting path of the tool tip on the machined surface is extracted by programming in MATLAB, as shown in Fig. 7.

Fig. 7

The arc cutting path of the tool tip in the PSD1 period on the machined surface

Fourier transform is used to calculate the corresponding spatial frequency of the arc cutting path. The spatial frequency can be converted into the frequency in the time domain by Eq. (28), as shown in Fig. 8.

$$ {\displaystyle \begin{array}{l}\omega = vf\\ {}v= N\pi D/60\end{array}} $$

(28)

where f denotes the spatial frequency and its unit is mm⁻¹, ω denotes the transformed frequency in the time domain and its unit is Hz, v denotes the tangent speed of the fly cutting head and its unit is mm/s, N denotes the speed of the spindle and its unit is rpm, and D denotes the diameter of the fly cutting head and its unit is mm.

Fig. 8

a Spatial frequency and b time frequency

The spatial frequencies of the cutting path at three different rotating speeds are obtained by Fourier transform shown in Fig. 9, and the corresponding spatial periods and frequencies in the time domain obtained by Eq. (28) are shown in Tables 1 and 2.

Fig. 9

The spatial frequencies at 200 rpm, 280 rpm, and 360 rpm

Table 1 Spatial periods and spatial frequencies at 200 rpm, 280 rpm, and 360 rpm

Table 2 Time frequencies at 200 rpm, 280 rpm, and 360 rpm

With the increasing of the spindle speed, the three spatial periods become larger and the three spatial frequencies become smaller. At different rotating speeds, the spatial frequencies and spatial periods of the mid-frequency waviness on the machined surface are different, while the frequencies in time domain remain unchanged, which are 195.3 Hz, 585.9 Hz, and 976.8 Hz, respectively, as shown in Table 2.

3.2 Vibration test of the tool tip

To research the causes of the formation of the characteristic frequencies of mid-frequency waviness, the vibration test of the tool tip and modal test of the UFCMT were carried out.

The micro dynamic data acquisition system DH 5916 was fixed at the bottom of the fly cutting head, and its connected acceleration sensor PCB 355B04 was glued to the tool holder near the tool tip, as shown in Fig. 10. When the feed rate is 12 mm/min, the cutting depth is 4 μm, and the rotating speed is 280 rpm; the vibration acceleration signal of the tool tip along the z-axis (the vertical direction) in the cutting process was measured, as shown in Fig. 11.

Fig. 10

The vibration test of the tool tip

Fig. 11

The vibration acceleration signal of the tool tip along the z-axis in the cutting process

Substituting the rotating speed 280 rpm and the diameter of the fly cutting head 650 mm into Eq. (28), the tangent speed is 9524.7 mm/s. The diameter of the workpiece in this experiment is 100 mm. When the spindle rotates for one cycle, the tool tip will cut the workpiece for only 0.01 s, as shown in Fig. 12a. Fourier transform is applied to the vibration signal of the tool tip in one cycle, and its corresponding frequency spectrum shown in Fig. 12b is obtained. The main vibration frequencies in the cutting process are 260 Hz, 579.8 Hz, and 948.5 Hz.

Fig. 12

The vibration acceleration signal of the tool tip in one circle: a time domain signal, b frequency spectrum

3.3 Modal test

A force hammer was used to carry out the modal test. There are 364 test points in UFCMT, as shown in Fig. 13.

Fig. 13

Distribution of test points for the modal test

The comparison of natural frequencies between the experiment and the above simulation in Section 2.1 is shown in Table 3. The relative errors between the simulated and experimental results are all less than 5%, which indicates the correctness of the established dynamics model.

Table 3 Experimental and simulated natural frequencies

By comparing the natural frequencies with the main frequencies of the tool tip response in Fig. 12b, the 12th, 14th, and 17th natural frequencies are consistent with the main frequencies of the tool tip response. The 12th, 14th, and 17th natural frequencies are 261.92 Hz, 582.37 Hz, and 961.16 Hz, respectively, and their mode shapes are shown from Figs. 14, 15, and 16 by using the pre-processor module and post-processor module of MSTMMsim [16]. In the 12th mode, the fly cutting head is moving along the z-axis in Fig. 14. The 14th mode shape is the deformation of the fly cutting head in Fig. 15. In the 17th mode, the tool holder is moving along the z-axis in Fig. 16. The 12th, 14th, and 17th mode shapes are all related to the motion of the tool tip and will influence the vibration of the tool tip in the machining process.

Fig. 14

The 12th mode shapes: a experimental, b Simulated

Fig. 15

The 14th mode shapes: a experimental, b simulated

Fig. 16

The 17th mode shapes: a experimental, b simulated

The characteristic frequencies of the mid-frequency waviness on the machined surface, the main frequencies of the tool tip response, and the 12th, 14th, and 17th natural frequencies are shown in Table 4, and they are in good agreement. Therefore, characteristic frequencies 195.3 Hz, 585.5 Hz, and 976.6 Hz of the mid-frequency are caused by the excitations of the 12th, 14th, and 17th natural frequencies in the machining process.

Table 4 Comparison of the frequencies (Hz)

4 Simulation and test verification

KISTLER 9119AA1 force sensor was used to measure the cutting force. As shown in Fig. 17, the cutting force increases abruptly when the tool tip cuts the workpiece and lasts for a short time. Therefore, the pulse function is used to simulate the cutting force in the machining process. When the tool tip cuts the workpiece, there is cutting force. When the tool tip does not cut the workpiece, the cutting force is 0. Substituting the simulated cutting force into Eq. (27), the dynamics response of the tool tip can be obtained.

Fig. 17

The cutting force along the z-axis: a Experimental, b simulated

The experimental and simulated accelerations of the tool tip are shown in Fig. 18 (a) and (b). The comparisons of experimental and simulated accelerations of the tool tip in one circle and in the cutting process are shown in Fig. 18 c and d. The simulated and experimental results are in good agreement, which verifies the correctness of the dynamics model.

Fig. 18

Experimental and simulated accelerations of the tool tip at 360 rpm: a experimental, b simulated, c in one circle, d in the cutting process

After obtaining the displacement of the tool tip as shown in Fig. 19, the simulated machined surface can be acquired by using the surface topography model considering the interference phenomenon of the cutting profile and geometry of the tool tip proposed in Ref. [17, 18]. The experimental and simulated machined surfaces in the PSD1 period are shown in Fig. 20. Their corresponding PV values are 67.44 nm and 78.95 nm. There also appears waviness on the simulated machined surface in cutting direction.

Fig. 19

Comparison of the tool tip displacement between the original and optimized UFCMT

Fig. 20

The experimental and simulated machined surfaces in PSD1 period: a experimental, b simulated

5 Structure improvement of the UFCMT

For the 14th mode shape of the deformation of the fly cutting head, some researchers have done relevant researches on the structure improvement of the fly cutting head. Yang et al. [9] added a cross rib under the fly cutting head to increase its stiffness and reduce its deformation. Wang et al. [19] changed the inner concave part of the fly cutting head to a conical shape to increase its stiffness and decrease the amplitude of the tool tip displacement.

For the 17th mode shape of the movement of the tool holder along the z-axis, the connect stiffness between the tool holder and the fly cutting head is increased to reduce the moving amplitude of the tool holder. The 17th modal frequency is increased from 946.69 Hz to 1051 Hz by increasing the z-axis stiffness of Hinge 30 from 9.5e7 to 1.2e8 N/m. The displacement of the tool tip of the improved machine tool is illustrated in Fig. 19. The vibration frequency of the tool tip displacement is changed, and the amplitude of the tool tip displacement is decreased after the improvement. The simulated machined surface in PSD1 period after the improvement is shown in Fig. 21. The PV value decreases by 11.2% from 78.95 to 70.09 nm.

Fig. 21

The optimized machined surface

6 Conclusion

The dynamic characteristics of the UFCMT and its influence on the mid-frequency waviness of the surface are analyzed theoretically, computationally, and experimentally in this paper. The conclusions are summarized as follows:

• 1. A detailed model of the UFCMT and its dynamics topology figure are developed by using MSTMM, and the overall transfer matrix is deduced. The dynamic characteristics got from the simulation and experiment have good agreements, which verifies the correctness of the dynamics model.

• 2. After analyzing the characteristic frequencies of mid-frequency waviness on the machined surface and comparing them with the simulated and experimental vibration results, the 14th and 17th natural frequencies (582.37 Hz and 961.16 Hz) excited by the cutting force are the main causes of mid-frequency waviness on the machined surface, which gives instructions on the optimization of the UFCMT.

• 3. By optimizing the connect stiffness between the tool holder and the fly cutting head, the displacement of the tool tip and the PV value of the machined surface in the PSD1 period is decreased.