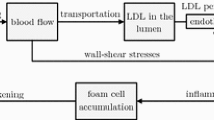
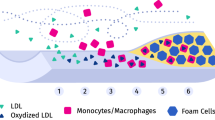
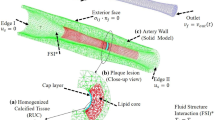
Abstract
Studying the formation and stability of atherosclerotic plaques in the hemodynamic field is essential for understanding the growth mechanism and preventive treatment of atherosclerotic plaques. In this paper, based on a multiplayer porous wall model, we established a two-way fluid–solid interaction with time-varying inlet flow. The lipid-rich necrotic core (LRNC) and stress in atherosclerotic plaque were described for analyzing the stability of atherosclerotic plaques during the plaque growth by solving advection–diffusion–reaction equations with finite-element method. It was found that LRNC appeared when the lipid levels of apoptotic materials (such as macrophages, foam cells) in the plaque reached a specified lower concentration, and increased with the plaque growth. LRNC was positively correlated with the blood pressure and was negatively correlated with the blood flow velocity. The maximum stress was mainly located at the necrotic core and gradually moved toward the left shoulder of the plaque with the plaque growth, which increases the plaque instability and the risk of the plaque shedding. The computational model may contribute to understanding the mechanisms of early atherosclerotic plaque growth and the risk of instability in the plaque growth.
Graphic abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Atherosclerosis (AS), a slowly progressing disease, grows with complex mechanisms of development due to endothelial dysfunction. A large number of studies have shown that AS plaque is mainly caused by the accumulation, reaction and oxidation of various lipids in the arterial intima [1,2,3,4], where low-density lipoprotein (LDL) penetrates into the superficial wall and is converted into oxidized LDL by free radical oxidation. The accumulation of oxidized LDL accelerates the generation of reactive oxygen species (ROS), while accelerating the formation and accumulation of macrophages and foam cells [5], thereby causing the biological activity of various lipids within the arterial walls, and finally leading to the occurrence of inflammation [1, 6]. However, it is generally considered that plaque destabilization (so-called vulnerable plaques) is a dominating cause of cardio-cerebrovascular disease and is responsible for the high mortality rate [2, 7]. Vulnerable plaques are usually characterized as a large LRNC with an overlying thin fibrous cap, and the necrotic core becomes an “attack receptor” for macrophages [7]. In addition, the death and accumulation of foam cells, macrophages, and vascular smooth muscle cells (VSMCs) in the intima accelerate the formation of necrotic cores within plaques [7, 8]. AS plaque has the risk of breakage as the LRNC volume inside a plaque is approximately 30–40% of the AS plaque [8].
It is important to study the growth of AS plaque and the development of necrosis core for plaque stability analysis [7, 8]. Theoretically, many mathematical models are used to make predictions in AS plaque evolution with a single-layer or a multi-layer transmission model. A Staverman–Kedem–Katchalsky membrane equation is usually applied to study the inner elastic layer (IEL) and transport in the endothelium [9]. However, there are two essential defects associated with this equation. First, the equation is based on the steady-state assumption, which may be too idealized. Second, the equation ignores the effect of boundaries when transporting across membranes [9]. Meanwhile, a large number of studies have shown that blood pressure and fluid shear stress have an impact on the material infiltration (such as LDL infiltration into the blood vessel wall in this paper) [10, 11]. For example, Mehrdad et al. established a multilayer fluid–structure interaction (FSI) model to study the LDL permeation under the wall shear stress (WSS). Their results showed that the expansion of the lumen will reduce the WSS of the wall, especially in patients with hypertension, which leaded to the increase of LDL permeability [12]. Calvez et al. established a growth model of early AS plaque using reaction–diffusion equations for considering the diffusions of oxidized LDL, foam cells, macrophages and other substances [13]. Wong et al. obtained the composition and distribution of AS plaque through a 3D vascular model, and successfully predicted how the cap and necrotic core of the plaque affected the biomechanical stress on the plaque [14]. Giuseppe established a one-dimensional mathematical model to elucidate the mechanisms of atherosclerotic plaque growth, and the model consists of a system of reaction–diffusion equations under Neumann boundary conditions [15]. According to the research report of Mirzaei et al., they developed a model consisting of multidimensional partial differential equations, which could depict the morphology of necrotic cores within plaques [16]. Furthermore, some studies have shown that inhibition of efferocytosis can postpone the development of the necrotic cores formed within AS plaques [17]. In addition, Hao et al. gave a mathematical model of AS plaque growth using partial differential equations and explored the effects of LDL and HDL on plaque growth, and predicted the probability of plaque occurrence [18], which has reference value for clinical treatment. It should be noted that the plaque stability is closely related to hemodynamics with the plaque growth, gradually leads to vascular stenosis, which in turn affects the blood flow distribution and the mechanical stress of arterial wall [19]. There is probably a close connection between hemodynamic stimulus and AS plaque stability.
Reports in clinical as well as experimental studies have revealed the non-uniform distribution of cellular components within AS plaques [20,21,22]. Local variations of the cell composition may be due to the direction of blood flow, producing the disturbed haemodynamics near AS plaques, changing the shear stress distribution of AS plaque surface, and affecting differences in the distributions of macrophages, macrophage-derived foam cells as well as smooth muscle cells inside AS plaques [21]. Thus, the haemodynamics may play a key role in vascular homeostasis as well as in the local onset, progression and stability of AS plaques. [23]. Therefore, it is very important to understand how the stress in AS plaque distributes and changes in hemodynamics.
In addition to the shear stress induced by blood fluid, a growing number of clinical experiments have indicated that hypertension, as a critical risk factor of cardiovascular disease, has been confirmed to be closely related to plaque rupture [24, 25]. Increments in blood pressure can cause a plethora of detrimental effects, such as promoting vascular endothelial injury and activation of inflammatory factors, as well as accelerating the progression of AS plaques [25].
Atherosclerotic progression is a highly complex process that involves relevant mechanisms of mechanics and biochemical reactions of substances under haemodynamic changes. Some researchers have improved and prospected the methods of treating aneurysms based on computational simulation and experimental research for taking into account the influence of hemodynamics [26]. In addition, Sugiyama et al. [27] used computational fluid dynamic (CFD) simulations to study the characteristics of hemodynamics when atherosclerosis occurs. Besides, some studies have revealed that the mass volume and location of atherosclerotic plaque have an important influence on the mechanical stress caused by hemodynamics [11, 28]. Although the hemodynamics, arterial tissue degradation and remodeling at the location of atherosclerosis have been reported for demonstrating the interactions between blood flow and plaque, a few studies showed how WSS-related and pressure-related variables affect wall permeability during AS plaque development [4, 19, 29, 30], and no studies showed the changes of mechanical properties during the formation of atherosclerotic plaque and took into account the influence of stenosis in hemodynamics [31]. Especially, abnormal blood pressure can lead to the occurrence and exacerbation of coronary heart disease [25]; however, its mechanical mechanism is still not clear.
Although there are many reports on the growth of AS plaques, they either studied the stability of fixed AS plaques [32] or studied the growth of atherosclerotic plaques alone [33,34,35,36]. At present, there are few studies on the stability of plaques in local hemodynamics through coupled multi-physics phase-field models. In this study, we established a fluid–solid two-way coupling model with pulse blood flow velocity, which can show the stress changes during AS plaque growth and is helpful to analyze the plaque stability. Combining the advantages of FSI in the plaque development, partial differential equations with time-dependent coupled model for the formation and development of atherosclerotic plaque was developed to plumb the plaque development both in healthy wall and in wall lesion, and to study the plaque stability by obtaining the stress distribution of plaques at different stages under the blood flow. The vessel wall was regarded as a four-layer porous medium. The model used the element method for solving convection–diffusion–reaction equations coupled with the Navier–Stokes equations, Darcy's law and structural mechanics in hydrodynamics field.
2 Mathematical Model and Methods
2.1 Blood Vessel Model
In Fig. 1, we assume that there is a local lesion on the intima of one side of vessel walls and a two-dimensional model with 100 mm × 20 mm. The length of blood vessel with 2 mm lesion is 100 mm, the inner radius of the lumen is 3 mm, and the total thickness of the blood vessel wall is 1 mm (The thickness of the intima is 0.2 mm, the media is 0.5 mm, and the adventitia is 0.3 mm). Blood is assumed to be an incompressible, homogeneous fluid, and vessel walls are composed of porous media. In this article, we mainly consider cell proliferation, migration, differentiation, apoptosis and transformation.
2.2 Mathematical model
2.2.1 Conservations of Momentum and Mass
This paper assumes blood flow has a constant viscosity coefficient. We also ignore the effects of gravitational force or other body forces. Therefore, the blood flow in the vessel lumen can be written as Navier–Stokes (laminar flow) and continuity equations:
where \(\mu\), \(p\), \(\vec{u}\) are hemodynamic viscosity, blood pressure and velocity vector, respectively, \(T\) represents the element diagonal matrix, \(\vec{F}\) is the volume force affecting the fluid.
The fluid at the entrance of the blood vessel enters the lumen in an unsteady velocity profile with a trigonometric function to achieve the maximum velocity of the pulsating waveform [37], and the pulsatile inlet velocity is defined by the following equations:
where the average velocity, \(U_{0} = 0.26\frac{m}{s},\) is assumed to be stable at the entrance, \(U_{{{\text{mean}}}}\) is obtained by multiplying the resulting value for 10–2.
The Darcy’s Law is used to describe the transmural flow in arterial wall [38]:
In the above equations, parameters \(u_{w}\), \(p_{w}\), \(\mu\), and \(k\) are the velocity of the transmural flow, the vessel inner-wall pressure, the blood plasma viscosity, and the Darcian permeability coefficient, respectively. It is believed that the blood vessel wall is composed of uniform isotropic material. Wall porosity \(\varepsilon_{p}\) varies with pressure, as shown below [39]:
where \(P0\) and \(P\) are the initial pressure and the blood pressure on the arterial wall at any other time, respectively. To facilitate the pressure drop through vessel wall, a constant-pressure value P0 = 2333.022 Pa (ie.17.5 mmHg) is used for the membrane–muscle interface [38]. Parameter \(b\) denotes the proportional constant determined by inflamed area.
2.2.2 Solid Models and Fluid–Solid Boundaries
In this paper, the stress magnitude and distribution in AS plaque are solved using linear elasticity and nonlinear structure theory. Thus, the governing equation for an elastic solid body can be expressed by the following equation [40]:
In Eq. (8), \(\sigma_{ij}\) and \(\varepsilon_{ij}\) are components of the stress tensor and displacement, respectively, and \(\sigma_{ij}\) can be obtained by solving the constitutive equations based on Newtonian fluid, \(\rho_{s}\) is the density of the solid, \(F_{i}\) are the body force loading on the isotropic solid. When a solid deforms, energy will be stored in the body. In addition, the energy is derived from the strain-energy–density function (Ψ):
where \(\epsilon_{j}\) are the components of the Green–Lagrange strain tensor, while \(S_{ij}\). is widely known as the second Piola–Kirchhoff stress tensor. There is no external force on the outer walls. A zero axial motion condition is imposed on the left and right edges of the solid domain.
Considering the coupled fluid and solid tissue interactions, the interface meets the following conditions:
In Eqs. (10–12), \(u\),\(n\),\(d\) and \(\sigma\) represent the velocity, boundary normal, displacement, and stress tensors, respectively. Subscript \(f\) represents the fid zone, subscript \(s\) represent solid zones, including plaque and vessel wall (see Table 1).
However, in fact, its mechanical properties will be changed during AS plaque growth [41, 42]. In this paper, we assume that the Young's modulus of the vascular wall tissue will change as the plaque grows and satisfies the following equation:
Here, \(E(t)\) represents Young’s modulus. We assume that parameter \(a\) is 1 × 106 Pa, \(\Delta h\) is the growth height of AS plaque. The value of \({E}_{0}\) is given in Table 2.
2.2.3 LDL Transport in the Arterial Wall
The concentration of LDL in blood vessels changes with time as follows [38]:
Here, \(C_{LDL,w}\) represents the LDL concentration, \(D_{LDL,w} { }\) is the LDL diffusion coefficient, \(u_{w}\) represents the convection coefficient based on flux conservation. In Eq. (14), \(d_{LDL}\) means the rate of LDL oxidation.
2.2.4 HDL Transport in the Arterial Wall
The concentration of HDL in the arterial wall is obtained as [33]
where \(C_{{{\text{HDL}},w}}\) is the HDL concentration, \(D_{{{\text{HDL}},w}}\) denotes the HDL diffusion coefficient. For the above-mentioned equation (15), \({r}_{{h}_{1}}\) is the HDL loss rate because of the reverse cholesterol transport (RCT) of foam cells, and the last term represents the HDL degradation rate.
2.2.5 LDLox Transport in the Arterial Wall
The convection and diffusion for LDLox transport are expressed by the following equation:
where \(C_{{{\text{LDLox}},w}}\) is the LDLox concentration in the arterial wall, \({D}_{LDLox,w}\) is the diffusion coefficient of LDLox [10]. Apart from the diffusion and convection terms in Eq. (16), the first item on the right, \({d}_{LDL}\), indicates the rate at which LDL is converted to oxidized LDL, \({LDL}_{oxr}\) represents the rate of which LDL is consumed by macrophages.
2.2.6 Macrophage Lipid Transport in the Arterial Wall
The concentration of macrophages is described by the following equation [33, 34]:
In Eq. (17),\({ }C_{M,w}\) and \(D_{M,w}\) represent the concentration and diffusion coefficient of macrophages, respectively. Similarly, on the right-hand side of Eq. (17), \(r_{m2}\) is the conversion rate of foam cells converted by macrophages per second, and the analysis of \(r_{m3}\) is the rate of loss of macrophages due to RCT. \(r_{m4}\) is the differentiation rate of macrophages, and \(r_{m5}\) denotes the rate proliferation of macrophages.
2.2.7 Foam Cell Production and Transport in the Arterial Wall
For the transport and diffusion of foam cells, it is expressed by the following equation:
Here, \(C_{F,w}\) is the foam cell concentration, \(D_{F,w}\) is the diffusion coefficient of foam cells. In this article, we assume that foam cells have the same diffusion coefficient as macrophages. On the right-hand side of Eq. (18), symbol \(r_{F1}\) denotes the conversion rate of foam cells transforming from macrophages, and \(r_{F2}\) indicates the reversible conversion rate at which some foam cells are transformed into macrophage pools due to RCT [33], \(r_{F3}\) means the number of LDLox converted into foam cells per second, and the last item represents the apoptosis of macrophages [38].
2.2.8 Transport of Monocyte Chemical Attractant in the Arterial Wall
The concentration variation of monocyte chemical attractant may be expressed by the following equation [33]:
where \(C_{P,w}\) means the concentration of monocyte chemical attractant, and parameter \(D_{P,w}\) denotes the diffusion coefficient for monocyte chemical attractant. Studies have shown that the value of \(D_{P,w}\) is very small because of the weak diffusion ability for monocyte chemical attractant [38]. The first term on the right-hand side of Eq. (19) corresponds to the growth number per second for monocyte chemical attractant producing by macrophage uptake of oxidized LDL, and the second term represents the reduction of monocyte chemical attractant due to apoptosis per second.
2.2.9 Transport of ES Cytokine Attractant in the Arterial Wall
In this paper, the concentration of monocyte chemical attractant can be written as
where \(C_{Q,w}\) is the concentration of ES cytokine attractant, parameter \(D_{Q,w}\) refers to the diffusion coefficient for ES cytokine attractant, respectively. Typically, the diffusion coefficient of monocyte chemical attractant is very small [33]. On the right side of Eq. (20) the first term denotes the growth rate for ES cytokine attractant producing from macrophages, and \(r_{Q2}\) represents the loss rate of ES cytokine attractant.
Figure 2 shows a schematic representation of the biochemical reactions taking place in the arterial wall for substances mentioned above [18, 35].
2.3 Initial Conditions and Boundary Conditions
2.3.1 Initial Conditions
In the arterial walls as shown in Fig. 1, the initial conditions at the initial moment for the equations mentioned above are as follows:
2.3.2 Boundary Conditions
We establish a two-dimensional Cartesian reference in which \(\Omega = \left\{ {\left( {x,y} \right),0 \le x \le L,0 \le y \le 2R0} \right\}\), and assume that, at the blood–wall interface, the boundary conditions satisfy the following expressions:
Generally speaking, the flux at the damage is relatively large, which is expressed by the following hypothetical formulas:
where \(\mathop m\limits^{ \wedge }\) is the inner membrane boundary, excluding the boundary that has been damaged, \(\mathop \theta \limits^{ \wedge }\) is the boundary of intimal injury, \(\mathop n\limits^{ \wedge }\) denotes a direction normal to the outer vessel wall, \(\Gamma 2\) and \(\Gamma 1\) represent the muscle–adventitia interface and blood–intima interface, respectively. \(\mathop \alpha \limits^{ \wedge }\) indicates the interface between the intima and the media. \(\mathop \beta \limits^{ \wedge }\) represents the interface between the media and adventitia. \(J\) is the boundary flux, \(R0\) is the lumen radius of blood vessel.
It is assumed that sigmoidal function increases linearly with the concentration [36]. Based on the binomial theorem expansion, we consider the nonlinear term in this paper. For convenience, we assume that the permeability of LDL is equal to that of HDL [43]:
Here, \({\text{WSS}}\) represents the shear stress of vessel wall, and the reference value of \({\text{WSS}}_{0}\) is \(1 {\text{N}}/{\text{m}}^{2}\)[43].
2.4 Formation of Plaque and Necrotic Core
We use finite-element method for solving partial differential equations involving multi-physical field coupling problem in porous media with COMSOL Multiphysics [44]. The continuity equation and Navier–Stokes equation are applied to predict the fluid flow, the pressure and the displacement of solid. In Fig. 1, a simple way is used to split the model into free triangle mesh with unit size, the maximum value of grid size is 2 mm, the muscle consists of 5587 triangular elements and 3107 mesh vertices, the blood flow consists of 9986 triangular units and 5379 mesh vertices, and the vessel wall consists of 5366 triangular units and 3303 mesh vertices. In our simulations, by combining boundary conditions, we will use the methods of freely moving and deformed meshes to solve Navier–Stokes equations in the fluid domain. ALE moving grid technique is utilized to deal with the growths of AS plaque and necrotic core. For the coupled system of solid and fluid equations, we use the PARDISO solver.
2.4.1 Plaque Growth
AS mentioned above, the “moving grid” model is employed to simulate the formation and development of AS plaque modified by foam and macrophages cells, in which the grid can move locally with the change of the concentrations of the foam and macrophages cells. Moreover, its mesh shape is deformed due to the diffusion mode with the boundary movement. Finally, the smooth mesh deformation of the computational region is obtained for solving partial differential equations. In addition, the Laplace smooth deformed grid coordinates is obtained as the following unsteady-state equations [45].
The node position and deformation are expressed by the function X = X (x, y, t) and Y = Y (x, y, t), where (x, y) is the coordinates of the fixed space, while (X, Y) represents the moving coordinates at time t. The radial variation of foam cell component in the model may be written as
To ensure that the simulation results are consistent with clinical phenomena, we choose the correction factor \(kr\) = 0.0779, which can accurately describe the arteriosclerosis development in vascular wall when characterizing the vessel wall deformation.
2.4.2 Necrotic Core Growth
To simplify the calculations, it is assumed that the main components of the necrotic core are dead foam cells and dead macrophages based on the growth mechanism of AS plaques [46, 47], and the specific reaction expression is as follows:
where \(C_{{{\text{dead}},w}}\) represents the total death concentration of foam cells and macrophages, \(D_{dead,w}\) denotes the diffusion coefficient and is equal to 0, r is the distance between the lumen center to the intimal boundary. On the right-hand side of Eq. (31), \({d}_{d1}\) and \({d}_{d2}\) are the death rate of macrophages and foam cells, respectively [18], \({d}_{de}\) represents the loss rate of dead cells in the arterial wall, and equals 7 × 10–7 1/s.
To reveal the growth characteristics of necrotic core, which the volume can be written as
In this model, \({l}_{p}(t)\) and \(R\left(t\right)\) are the length and height of the necrotic core at time \(t\), respectively.
3 Model Validation and Results
3.1 Model Validation
Based on the above equations and material parameters in Table 2, the growth and development of plaques are analyzed using the fluid–structure interaction model [53,54,55,56].
Figure 3 shows the annual volume change of LRNC and the comparison of experimental data from Jie’s report [57]. It is shown that plaques without intraplaque hemorrhage increase the LRNC volume about (-8.8 mm3 ± 29.9) per year. Chang et al. [58] concluded that cases through propensity-score matched analysis of risk factors, demographics, and number of obstructive vessels with imaging technique exhibited lesser fibrofatty and LRNC volumes (45.6 mm3 ± 68.8) and had no difference for calcified or total plaque volumes. Our simulation results showed that the LRNC volume increased by 4.99 mm from year 3 to year 4 and by 10.69 mm from year 4 to year 5. Results show that the LRNC volume changes from simulation are relatively close to the experimental results. Indeed, the LRNC progression in plaques may be influenced not only by living habits [59, 60], but also by clinical characteristics, such as intraplaque hemorrhage, wall thickness, and wall volume [57, 61].
3.2 Model Results
It is worth noting that the concentrations and distributions of foam cells and macrophages within AS plaque have the direct impact on the formation of necrotic cores [8]. Figure 4 shows that the change of foam cell concentration with time. It can be seen that the foam cells show a "downward" diffusion pattern in the plaque and eventually accumulate at the bottom. The simulation results are consistent with findings from observational studies [46].
Figure 5 shows the change of macrophage concentration during the same time periods as mentioned in Fig. 4. The concentration of macrophages in the downstream is higher than that in the upstream, which causes the asymmetric growth of the plaque. This may be the reason the shear stress at the AS plaque downstream is relatively small, increasing the LDL residence time, and thus causing a higher concentration of macrophages according to Eq. 29.
The growth of plaque can block the lumen and increase the risk of plaque instability with LRNC growth, causing the “vulnerable plaque” [62]. LRNC is one of the main characteristics for “vulnerable plaque” with LRNC is generally regarded as one of the decisive factors to determine whether the plaque will be broken [62, 63]. In Fig. 6, we obtained the volume–time curves of LRNC in the lower vessel wall, where LRNC began to accumulate around day 1080 and reached a volume of 15.86 mm3 at day 1800.
Figure 7a shows the radial height growth of the necrotic core in the lesion areas. Combined with the above-mentioned regional moving grid pattern, it can be observed that the necrotic core was formed at 1080 days, and increased by about 0.321 mm (Center distance). At the same time, the regional center displacement reached 1.636 mm at 1800 days. In addition, Fig. 7b shows the height growth along the radial orientation of the plaque, and the maximum height of the plaque reached approximately 4.681 mm at 1800 days.
To further explore the growth and development of AS plaques, we describe the process vividly in a two-dimensional space. It can be seen in Fig. 8 that the height at the downstream of the patch is higher than that at the upstream as a whole. With the AS plaque growth, the LRNC area reached 0.67 mm2 at 1080 days, 6.33 mm2 at 1440 days, and 18.13 mm2 at 1800 days, respectively. It's important to note that the plaque growth in the lesion area will squeeze the walls of healthy areas, it has been confirmed in medical imaging research [64,65,66].
Many studies have confirmed that lower shear stress, which has lower blood velocity, is considered as a risk factor of atherosclerosis [21, 23, 32, 67], while the existence of high blood flow may lower the risk of plaque formation [23, 32]. Therefore, the growth of AS plaques is associated with fluid hemodynamics and wall shear stress (WSS). Meanwhile, hypertension is also related to endothelial dysfunction [68, 69]. Figure 9 illustrates the effect of blood flow velocity on plaque growth. After 1800 days, the total surface area of the necrotic core are 4.24 mm2 at 0.5 m/s, 8.14 mm2 at 0.4 m/s, and 18.13 mm2 at 0.26 m/s, respectively. The reason may be that the increase of blood flow velocity leads to the decrease of wall shear stress, which leads to the decrease of lipid permeation. We can find that blood flow velocity has a significant effect on plaque and plaque necrotic core growth.
Figure 10 shows the effect of blood pressure on plaque growth. After 1800 days, the volume of necrotic core in lower vessel wall are 11.99 mm3 at 80 mmHg, 14.02 mm3 at 110 mmHg, and 15.86 mm3 at 140 mmHg, respectively. Therefore, controlling the body's blood pressure within the normal range is also the key to preventing or decreasing the occurrence of atherosclerosis.
Blood flow-induced shear stress covered at the plaque surface gets complexed during the plaque development due to interactions of the blood flow and plaque. Exploring the mechanism between shear stress and plaque can help us understand the possible risks for clinical treatment. Figure 11 shows the change curves of shear stress at the damaged wall during the plaque growth. It can be seen that the largest value of shear stress lies near the middle of the plaque, and the shear stresses at the upstream, on the whole, are higher than those at the downstream. The results are consistent with the results in Fig. 9.
4 Discussion
This study was the first to demonstrate the efficacy of hemodynamic intervention on the formation and development of AS plaque and necrotic core. We found that the shear stress was closely related to the AS plaque growth. As reported in references [21, 32, 70], the stress distribution in plaques was an important factor for evaluating the plaque rupture under variable fluid forces. Figure 12 shows the stress distribution in AS plaque at different times under the action of fluid. At 1080 days, the maximum stress of plaque was 34.4 N/m2, and the maximum blood flow velocity was 0.49 m/s. At 1440 days and 1800 days, the maximum stress reached 96.5 N/m2 and 1484.7 N/m2, respectively. At the same time, the maximum blood flow velocity was 0.72 m/s and 2.74 m/s, respectively. The maximum stress was mainly located at the necrotic core at the initial growth stage and gradually moved toward the left shoulder of the plaque with the AS plaque growth, which increases the plaque instability and the risk of the plaque shedding. In addition, necrotic core was thought to be the main parameter influencing plaque vulnerability, and the composition distribution in necrotic core may be more likely to induce high stress on the fibrous cap, and thus lead to rupture-prone plaque [70]. Our findings are consistent with the observed data [70,71,72].
AS mentioned above, hemodynamics has an important influence on the stability of the AS plaques. The main reason for this influence may likely be attributed to the roles of complex shear stress exerted on the plaque surface [20, 21]. In addition, AS plaques undergo a long-term pulsatile blood pressure ejected from the heart, especially for AS plaques with fibrous cap, may rupture when this loading exceeds the damage threshold stress of the plaque [73, 74]. Based on the calculation conditions as used in Fig. 10, Fig. 13 describes the impact of blood pressure on the stress distribution in plaque on day 1800. When the blood pressure was 80 mmHg, 110 mmHg and 140 mmHg, the maximum stress of plaque reached 634.9 N/m2, 927.6 N/m2 and 1484.7 N/m2, respectively. Especially, the plaque surface appears to have some fine cracks for the blood pressure of 140 mmHg. Blood pressure-derived tensile stress promoted the unstable (vulnerable) plaque prone to rupture and the consequent thrombosis [75]. It follows that high blood pressure is considered to be an important risk factor for cardiovascular disease [75, 76], and it is very helpful for preventing cardiovascular diseases by controlling blood pressure in a reasonable range.
AS illustrated in Fig. 9, there was a negative association between blood velocity and necrotic core volume and plaque volume. The reason may be that a reduction of blood flow rate may contribute to the WSS decrease, and increase the adhesion and deposition of lipids. In addition, a growing plaque can modify the local stress milieu in response to the changes of plaque geometry in the reconstructed hemodynamic environments [77]. This can be clearly seen from Fig. 14, which describes the distribution of stress in AS plaque under different blood velocities. The maximum stress of the plaque are 407.2 N/m2 for U0 = 0.5 m/s, 522.8 N/m2 for U0 = 0.4 m/s, and 1484.7 N/m2 for U0 = 0.26 m/s, respectively. Stress shows significant spatial oscillations with the plaque growth. Especially in geometrically irregular regions of plaques, the stresses can result in high spatial gradients [78]. It is worth noting that the maximum stress will migrate from the plaque center to the upstream shoulder of the plaque, affecting the plaque stability [21, 77].
It is widely accepted that [7, 17, 24, 41], apart from thin fibrous cap, a large acellular LRNC seems to be one important risk factor for plaque instability. This was mainly because the eccentric distribution of LRNC leads to a rearrangement of stress to the plaque shoulder regions and thus increases the vulnerability of these local regions to rupture [79]. These simulation results obtained in Figs. 12, 13 and 14 are generally consistent with the literature results [79]. In fact, the necrotic core may help to accelerate the calcification of the plaque, resulting in an increase in the Young’s modulus of the plaque, which may cause a large area of plaque to fall off [77]. If we assume that the value of \(a\) in Eq. 13 will become twice as much as the original when the necrotic core appears within atherosclerotic plaque, as seen from Fig. 15, there is an about 1% stress increase in the maximum stress, indicating a little effect on plaque stability for mild calcification and uniform calcification in the plaque center. However, calcification at the thin fibrous cap, or a speckled pattern of calcification in plaque may give rise to high stress concentrations and increase the risk of plaque instability [80, 81].
This paper aims to develop a qualitative model and attempts to help the researcher to understand the mechanical factors affecting AS plaque stability. This model not only demonstrates the formation and development of early AS plaque, but also predicts plaque instability in hemodynamics. One can set the model according to clinical parameters, and the results provide a theoretical reference for computer aided diagnosis. However, the model has some limitations. For example, angiogenesis and plaque cap formation are not considered, and the materials are actually diverse in the AS plaque development. Recent studies have shown that machine learning has a good effect on the classification of biological tissues [82, 83]. In future work we target to investigate the formation and development of fibrous cap, especially the impact of superficial calcification on plaque stability.
5 Conclusion
In this paper, combined with a full two-way coupled fluid–structure interaction model, the transport and deposition of major lipids on the porous blood vessel wall were investigated by solving the advection–reaction–diffusion kinetic equation with the finite-element method. Especially, the growth process of AS plaque, necrotic core, and stress in blood wall were studied. We get some main conclusions as follows: the plaque growth in the lesion area squeezed the walls of healthy areas. Low stress and high blood pressure contributed to the plaque formation and promoted the necrotic core growth. At the late growth stage, the stress of the plaque shoulder increased significantly, and the stress at the necrotic core was relatively large. In addition, the shear stress in the upstream shoulder of the plaque was larger than in the downstream. Plaque instability increased with the increase of the necrotic core volume within the plaque. This model may better predict formation process of AS plaque and the plaque instability in the process of AS development.
Data availability
All data generated or used during the study appear in the submitted article.
Abbreviations
- C :
-
Concentration
- D :
-
Diffusion coefficient
- ρ:
-
Blood density
- u w :
-
Convection coefficient of the conserved flux
- P :
-
Blood pressure
- μ :
-
Dynamic viscosity
- U :
-
Velocity of the blood
- t :
-
Time
- WSS:
-
Shear stress
- V :
-
Volume
- R :
-
The height of the necrotic core
- L :
-
Length of damage
- Kr:
-
Correction factor
- υ:
-
Poisson’s ratio
- \(\Omega\) :
-
Two-dimensional domain
- \(J\) :
-
Boundary flux
- \(\varepsilon_{p}\) :
-
porosity
- k :
-
Permeability
References
Zhou D, Li J, Liu D, Ji LY, Wang NQ, Jie D, Wang JC, Ye M, Zhao XH (2019) Irregular surface of carotid atherosclerotic plaque is associated with ischemic stroke: a magnetic resonance imaging study. J Geriatr Cardiol 16(12):872–879. https://doi.org/10.11909/j.issn.1671-5411.2019.12.002
Li J, Li D, Yang D, Hang HL, Wu YW, Yao R, Chen XY, Xu YL, Dai W, Zhou D, Zhao XH (2020) Irregularity of carotid plaque surface predicts subsequent vascular event: a MRI study. J Magn Reson Imaging 52(1):185–194. https://doi.org/10.1002/jmri.27038
Lei W, Hu J, Xie Y et al (2023) Mathematical modelling of the effects of statins on the growth of necrotic core in atherosclerotic plaque. Math Model Nat Phenom 18:11–28. https://doi.org/10.1051/mmnp/2023005
Thon MP, Hemmler A, Glinzer A, Mayr M, Widgruber M, Zernecke-Madsen A, Gee MW (2018) A multiphysics approach for modeling early atherosclerosis. Biomech Model Mechanobiol 17:617–644. https://doi.org/10.1007/s10237-017-0982-7
Basak S, Khare HA, Kempen PJ, Kamaly N, Almdal K (2022) Nanoconfined anti-oxidizing RAFT nitroxide radical polymer for reduction of low-density lipoprotein oxidation and foam cell formation. Nanoscale Adv. 4(3):742–753. https://doi.org/10.1039/D1NA00631B
Victoria-Montesinos D, Abellán Ruiz MS, Luque Rubia AJ, Martinez DG, Pérez-Piñero S, Sánchez Macarro M, García-Muñoz AM, García FC, Sánchez JC, López-Román FJ (2021) Effectiveness of consumption of a combination of citrus fruit flavonoids and olive leaf polyphenols to reduce oxidation of low-density lipoprotein in treatment-naive cardiovascular risk subjects: a randomized double-blind controlled study. Antioxidants 10(4):589–599. https://doi.org/10.3390/antiox10040589
Fok PW (2012) Growth of necrotic cores in atherosclerotic plaque. Math Med Biol A J Ima 29(4):301–327. https://doi.org/10.1093/imammb/dqr012
Newby AC, George SJ, Ismail Y, Johnson JL, Sala-Newby GB, Thomas AC (2009) Vulnerable atherosclerotic plaque metalloproteinases and foam cell phenotypes. Thromb Haemost 2009(101):1006–1011. https://doi.org/10.1160/TH08-07-0469
Kedem O, Katchalsky A (1958) Thermodynamic analysis of the permeability of biological membranes to non-electrolytes. Acta Biochim Biophys Sin 27:229–246. https://doi.org/10.1016/0006-3002(58)90330-5
Prosi M, Zunino P, Perktold K, Quarteroni A (2005) Mathematical and numerical models for transfer of low-density lipoproteins through the arterial walls: a new methodology for the model set up with applications to the study of disturbed lumenal flow. J Biomech 38(4):903–917. https://doi.org/10.1016/j.jbiomech.2004.04.024
Knight J, Olgac U, Saur SC, Poulikakos D, Marshall W Jr, Cattin PC, Alkadhi H, Kurtcuoglu V (2010) Choosing the optimal wall shear parameter for the prediction of plaque location—a patient-specific computational study in human right coronary arteries. Atherosclerosis 211(2):445–450. https://doi.org/10.1016/j.atherosclerosis.2010.03.001
Roustaei M, Nikmaneshi MR, Firoozabadi B (2018) Simulation of Low Density Lipoprotein (LDL) permeation into multilayer coronary arterial wall: Interactive effects of wall shear stress and fluid-structure interaction in hypertension. J Biomech 67:114–122. https://doi.org/10.1016/j.jbiomech.2017.11.029
Calvez V, Ebde A, Meunier N, Raoult A (2009) Mathematical modelling of the atherosclerotic plaque formation//Esaim: proceedings. EDP Sciences 28:1–12. https://doi.org/10.1051/proc/2009036
Wong KKL, Thavornpattanapong P, Cheung SCP, Sun ZH, Tu JY (2012) Effect of calcification on the mechanical stability of plaque based on a three-dimensional carotid bifurcation model. BMC Cardiovasc Disord 12:1–18. https://doi.org/10.1186/1471-2261-12-7
Pasqualino G (2019) Pattern formation in atherosclerotic plaques. http://hdl.handle.net/10222/76250. Accessed 26 Feb 2023
Mirzaei NM, Weintraub WS, Fok PW (2020) An integrated approach to simulating the vulnerable atherosclerotic plaque. Am J Physiol Heart Circ Physiol 319(4):H835–H846. https://doi.org/10.1152/ajpheart.00174.2020
Seneviratne AN, Edsfeldt A, Cole JE, Kassiteridi C, Swart M, Park I, Green P, Khoyratty T, Saliba D, Goddard ME, Sansom SN, Goncalves I, Krams R, Udalova IA, Monaco C (2017) Interferon regulatory factor 5 controls necrotic core formation in atherosclerotic lesions by impairing efferocytosis. Circulation 136(12):1140–1154. https://doi.org/10.1161/CIRCULATIONAHA.117.027844
Hao W, Friedman A (2014) The LDL-HDL profile determines the risk of atherosclerosis: a mathematical model. PLoS ONE 9(3):e90497. https://doi.org/10.1371/journal.pone.0090497
Rostam-Alilou AA, Jarrah HR, Zolfagharian A, Bodaghi M (2022) Fluid–structure interaction (FSI) simulation for studying the impact of atherosclerosis on hemodynamics, arterial tissue remodeling, and initiation risk of intracranial aneurysms. Biomech Model Mechanobiol 21:1393–1406. https://doi.org/10.1007/s10237-022-01597-y
Dirksen MT, van der Wal AC, van den Berg FM, van der Loos CM, Becker AE (1998) Distribution of inflammatory cells in atherosclerotic plaques relates to the direction of flow. Circulation 98(19):2000–2003. https://doi.org/10.1161/01.CIR.98.19.2000
Pedrigi RM, Mehta VV, Bovens SM, Mohri Z, Poulsen CB, Gsell W, Tremoleda JL, Towhidi L, Silva RD, Petretto E, Krams R (2016) Influence of shear stress magnitude and direction on atherosclerotic plaque composition. R Soc Open Sci. 3(10):160588. https://doi.org/10.1098/rsos.160588
Jager NA, de WallisVries BM, Hillebrands JL, Harlaar NJ, Tio RA, Slart RHJA, van Dam GM, Boersma HH, Zeebregts CJ, Westra J (2016) Distribution of matrix metalloproteinase in human atherosclerotic carotid plaques and their production by smooth muscle cells and macrophage subsets. Mol Imaging Biol 18:283Y291. https://doi.org/10.1007/s11307-015-0882-0
Morbiducci U, Kok AM, Kwak B, Stone PH, Steinman DA, Wentzel JJ (2016) Atherosclerosis at arterial bifurcations: evidence for the role of haemodynamics and geometry. Thromb Haemost 115(3):484–492. https://doi.org/10.1160/th15-07-0597
Virani SS, Alonso A, Benjamin EJ, Bittencourt MS, Callaway CW, Carson AP (2020) Heart disease and stroke statistics-2020 update: a report from the American Heart Association. Circulation 141:e139-596. https://doi.org/10.1161/CIR.0000000000000757
Liu Y, Luo X, Jia H and Yu B. The Effect of Blood Pressure Variability on Coronary Atherosclerosis Plaques. Front Cardiovasc Med. 2022; 9:803810. https://doi.org/10.3389/fcvm.2022.803810
Jarrah HR, Zolfagharian A, Bodaghi M (2022) Finite element modeling of shape memory polyurethane foams for treatment of cerebral aneurysms. Biomech Model Mechanobiol 21:383–399. https://doi.org/10.1007/s10237-021-01540-7
Sugiyama S, Niizuma K, Nakayama T, Shimizu H, Endo H, Inoue T, Fujimura M, Ohta M, Takahashi A, Tominaga T (2013) Relative residence time prolongation in intracranial aneurysms: a possible association with atherosclerosis. Neurosurgery 73(5):767–776. https://doi.org/10.1227/NEU.0000000000000096
He F, Hua L, Gao L (2017) Computational analysis of blood flow and wall mechanics in a model of early atherosclerotic artery. J Mech Sci Technol 31:1015–1020. https://doi.org/10.1007/s12206-017-0154-9
Ahmadpour-B M, Nooraeen A, Tafazzoli-Shadpour M, Taghizadeh H (2021) Contribution of atherosclerotic plaque location and severity to the near-wall hemodynamics of the carotid bifurcation: an experimental study and FSI modeling. Biomech Model Mechanobiol 20:1069–1085. https://doi.org/10.1007/s10237-021-01431-x
Wang H, Uhlmann K, Vedula V, Balzani D, Varnik F (2022) Fluid-structure interaction simulation of tissue degradation and its effects on intra-aneurysm hemodynamics. Biomech Model Mechanobiol 21(2):671–683. https://doi.org/10.1007/s10237-022-01556-7
Ebrahimi S, Fallah F (2022) Investigation of coronary artery tortuosity with atherosclerosis: a study on predicting plaque rupture and progression. Int J Mech Sci 223:107295. https://doi.org/10.1016/j.ijmecsci.2022.107295
Dhawan SS, Avati Nanjundappa RP, Branch JR, Taylor WR, Quyyumi AA, Jo H, McDaniel MC, Suo J, Giddens D, Samady H (2010) Shear stress and plaque development. Expert Rev Cardiovasc Ther 8(4):545–556. https://doi.org/10.1586/erc.10.28
Chalmers AD, Bursill CA, Myerscough MR (2017) Nonlinear dynamics of early atherosclerotic plaque formation may determine the efficacy of high-density lipoproteins (HDL) in plaque regression. PLoS ONE 12(11):e0187674. https://doi.org/10.1371/journal.pone.0187674
Linsel-Nitschke P, Tall AR (2005) HDL as a target in the treatment of atherosclerotic cardio vascular disease. Nat Rev Drug Discovery 4(3):193–205. https://doi.org/10.1038/nrd1658
Chalmers AD, Cohen A, Bursill CA, Myerscough MR (2015) Bifurcation and dynamics in a mathematical model of early atherosclerosis. J Math Biol 71:1451–1480. https://doi.org/10.1007/s00285-015-0864-5
Bulelzai MAK, Dubbeldam JLA (2012) Long time evolution of atherosclerotic plaques. J Theor Biol 297:1–10. https://doi.org/10.1016/j.jtbi.2011.11.023
Carvalho V, Carneiro F, Ferreira AC, Gama V, Teixeira JC, Teixeira S (2021) Numerical study of the unsteady flow in simplified and realistic iliac bifurcation models. Fluids 6(8):284–302. https://doi.org/10.3390/fluids6080284
Cilla M, Pena E, Martinez MA (2014) Mathematical modelling of atheroma plaque formation and development in coronary arteries. J R Soc Interface 11(90):20130866. https://doi.org/10.1098/rsif.2013.0866
Hariharan P, Nabili M, Guan A, Zderic V, Myers M (2017) Model for porosity changes occurring during ultrasound-enhanced transcorneal drug delivery. Ultrasound Med Biol 43(6):1223–1236. https://doi.org/10.1016/j.ultrasmedbio.2017.01.013
Cheema TA, Kim GM, Lee CY, Hong JG, Kwak MK, Park CW (2014) Characteristics of blood vessel wall deformation with porous wall conditions in an aortic arch. Appl Rheol 24(2):17–24. https://doi.org/10.3933/applrheol-24-24590
Palombo C, Kozakova M (2016) Arterial stiffness, atherosclerosis and cardiovascular risk: pathophysiologic mechanisms and emerging clinical indications. Vascul Pharmacol 77:1–7. https://doi.org/10.1016/j.vph.2015.11.083
Tang D, Yang C, Kobayashi S, Zheng J, Woodard PK, Teng ZZ, Billiar K, Bach R, Ku DN (2019) 3D MRI-based anisotropic FSI models with cyclic bending for human coronary atherosclerotic plaque mechanical analysis. J Biomech Eng 131(6):061010. https://doi.org/10.1115/1.3127253
Silva T, Jäger W, Neuss-Radu M, Sequeira A (2020) Modeling of the early stage of atherosclerosis with emphasis on the regulation of the endothelial permeability. J Theor Biol 496:496–515. https://doi.org/10.1016/j.jtbi.2020.110229
Chen C, Gu Y, Tu J, Guo X, Zhang D (2016) Microbubble oscillating in a microvessel filled with viscous fluid: a finite element modeling study. Ultrasonics 66:54–64. https://doi.org/10.1016/j.ultras.2015.11.010
Kirillova IV, Kossovich EL, Safonov RA, Chelnokova NO, Golyadkina AA; Shevtsova MS (2016) Finite Element Modeling of Atherosclerotic Plaque Evolution vol 3. 2016 3rd International Conference on Information Science and Control Engineering (ICISCE) IEEE. pp 973–977. https://doi.org/10.1109/ICISCE.2016.211
Ball RY, Stowers EC, Burton JH, Cary NRB, Skepper JN, Mitchinson MJ (1995) Evidence that the death of macrophage foam cells contributes to the necrotic core of atheroma. Atherosclerosis 114(1):45–54. https://doi.org/10.1016/0021-9150(94)05463-
Yuan Y, Li P, Ye J (2012) Lipid homeostasis and the formation of macrophage-derived foam cells in atherosclerosis. Protein Cell 3(3):173–181. https://doi.org/10.1007/s13238-012-2025-6
Lei W, Hu J, Liu Y, Liu W, Chen XK (2021) Numerical evaluation of high-intensity focused ultrasound-induced thermal lesions in atherosclerotic plaques. Math Biosci Eng 18:1154–1168. https://doi.org/10.3934/mbe.2021062
Esterbauer H, Striegl G, Puhl H, Rotheneder M (1989) Continuous monitoring of in vitro oxidation of human low density lipoprotein. Free Radical Res 6(1):67–75. https://doi.org/10.3109/10715768909073429
Schiesser WE (2018) PDE models for atherosclerosis computer implementation in R. J. synthesis lectures on biomedical engineering. Biomed Eng Lett 11:1–141. https://doi.org/10.2200/S00877ED1V01Y201810MAS022
Kruth HS, Huang W, Ishii I, Zhang WY (2002) Macrophage foam cell formation with native low-density lipoprotein. J Biol Chem 77(37):34573–34580. https://doi.org/10.1074/jbc.M205059200
Taylor BA, Panza G, Pescatello LS, Chipkin S, Gipe D, Shao WP, White CM, Thompson PD (2014) Serum PCSK9 levels distinguish individuals who do not respond to high-dose statin therapy with the expected reduction in LDL-C. J Lipids. 2014:140723. https://doi.org/10.1155/2014/140723
Akyildiz AC, Speelman L, Brummelen VH, Gutiérrez MA, Virmani R, Lugt AV, van der Steen FWA, Wentzel JJ, Gijsen F (2011) Effects of intima stiffness and plaque morphology on peak cap stress. Biomed Eng Online 10:1–13. https://doi.org/10.1186/1475-925X-10-25
Xie J, Zhou J, Fung YC (1995) Bending of blood vessel wall: stress-strain laws of the intima-media and adventitial layers. J Biomech Sci Eng 1(136):136–145. https://doi.org/10.1115/1.2792261
Khanafer K, Berguer R (2009) Fluid–structure interaction analysis of turbulent pulsatile flow within a layered aortic wall as related to aortic dissection. J biomech 42(16):2642–2648. https://doi.org/10.1016/j.jbiomech.2009.08.010
Chen XK, Hu XY, Jia P, Xie ZX, Liu J (2021) Tunable anisotropic thermal transport in porous carbon foams: The role of phonon coupling. Int J Mech Sci 306:106576. https://doi.org/10.1016/j.ijmecsci.2021.106576
Sun J, Balu N, Hippe DS, Xue YJ, Dong L, Zhao XH, Li FY, Xu DX, Hatsukami TS, Yuan C (2013) Subclinical carotid atherosclerosis: short-term natural history of lipid-rich necrotic core—a multicenter study with MR imaging. Radiology 268(1):61–68. https://doi.org/10.1148/radiol.13121702
Chang HJ, Lin FY, Lee SE et al (2018) Coronary atherosclerotic precursors of acute coronary syndromes. J Am Coll Cardiol 71(22):2511–2522. https://doi.org/10.1016/j.jacc.2018.02.079
Getz GS, Reardon CA (2012) Animal models of atherosclerosis. Prog Mol Biol Transl Sci 32(5):1–23. https://doi.org/10.1016/B978-0-12-394596-9.00001-9
Feuchtner G, Langer C, Barbieri F, Beyer C, Dichtl WG, Friedrich G, Schgoer W, Widmann G, Plank F (2021) The effect of omega-3 fatty acids on coronary atherosclerosis quantified by coronary computed tomography angiography. Clin Nutr 40(3):1123–1129. https://doi.org/10.1016/j.clnu.2020.07.016
Zhao X, Hippe DS, Li R, Canton GM, Sui BB, Song Y, Li FY, Xue YJ, Sun J, Yamada K, Hatsukami TS, Xu DX, Wang MX, Yuan C (2017) Prevalence and characteristics of carotid artery high-risk atherosclerotic plaques in Chinese patients with cerebrovascular symptoms: a Chinese atherosclerosis risk evaluation II study. J Am Heart Assoc 6(8):e005831. https://doi.org/10.1161/JAHA.117.005831
Virmani R, Kolodgie FD, Burke AP, Finn AV, Gold HK, Tulenko TN, Wrenn SP, Narula J (2005) Atherosclerotic plaque progression and vulnerability to rupture: angiogenesis as a source of intraplaque hemorrhage. Arterioscler Thromb Vasc Biol 25(10):2054–2061. https://doi.org/10.1161/01.ATV.0000178991.71605.18
Li AC, Glass CK (2002) The macrophage foam cell as a target for therapeutic intervention. Nat Med 8(11):1235–1242. https://doi.org/10.1038/nm1102-1235
Tash OA, Razavi SE (2012) Numerical investigation of pulsatile blood flow in a bifurcation model with a non-planar branch: the effect of different bifurcation angles and non-planar branch. Bioimpacts 2(4):195–205. https://doi.org/10.5681/bi.2012.023
Velican D, Velican C (1989) Coronary anatomy and microarchitecture as related to coronary atherosclerotic involvement. Med Interne 27(4):257–262. https://doi.org/10.1007/978-0-387-76852-6_4
Nishizawa A, Suemoto CK, Farias-Itao DS, Campos FM, Karen C, Silva S, Bittencourt MS, Grinberg LT, Leite REP, Ferretti-Rebustini REL, Farfel JM, Jacob-Filho W, Pasqualucci CA (2017) Morphometric measurements of systemic atherosclerosis and visceral fat: Evidence from an autopsy study. PLoS ONE 12(10):e0186630. https://doi.org/10.1371/journal.pone.0186630
Wang X, Ge J (2021) Haemodynamics of atherosclerosis: a matter of higher hydrostatic pressure or lower shear stress? Cardiovasc Res 117(4):e57–e59. https://doi.org/10.1093/cvr/cvab001
Meng H, Tutino VM, Xiang J, Siddiqui A (2014) High WSS or low WSS? Complex interactions of hemodynamics with intracranial aneurysm initiation, growth, and rupture: toward a unifying hypothesis. Am J Neuroradiol 35(7):1254–1262. https://doi.org/10.3174/ajnr.A3558
Xiong H, Liu X, Tian X, Pu L, Zhang HY, Lu MH, Huang WH, Zhang YT (2014) A numerical study of the effect of varied blood pressure on the stability of carotid atherosclerotic plaque. Biomed Eng Online 13(1):1–13. https://doi.org/10.1186/1475-925X-13-152
Manning-Tobin JJ, Moore KJ, Seimon TA, Bell SA, Sharuk M, Alvarez-Leite JI, Menno P, Winther JD, Tabas I, MasonFreeman W (2009) Loss of SR-A and CD36 activity reduces atherosclerotic lesion complexity without abrogating foam cell formation in hyperlipidemic mice. Arterioscler Thromb Vasc Biol 29(1):19–26. https://doi.org/10.1161/ATVBAHA.108.176644
Yang S, Wang Q, Shi W, Guo WC, Jiang ZI, Gong XB (2019) Numerical study of biomechanical characteristics of plaque rupture at stenosed carotid bifurcation: a stenosis mechanical property-specific guide for blood pressure control in daily activities. Acta Mech Sin 35:1279–1289. https://doi.org/10.1007/s10409-019-00883-w
Campbell IC, Weiss D, Suever JD, Virmani R, Veneziani A, Vito RP, Oshinski JN, Taylor WR (2013) Biomechanical modeling and morphology analysis indicates plaque rupture due to mechanical failure unlikely in atherosclerosis-prone mice. Am J Physiol Heart Circ Physiol 304(3):H473–H486. https://doi.org/10.1152/ajpheart.00620.2012
Pu L, Xiong H, Liu X (2014) Quantifying effect of blood pressure on stress distribution in atherosclerotic plaque. Int Conf Health Informaticsy 42(1):P216–P219. https://doi.org/10.1007/978-3-319-03005-0_55
Huang Y, Teng ZZ, Sadat U, Graves MJ, Bennett MR, Gillard JH (2014) The influence of computational strategy on prediction of mechanical stress in carotid atherosclerotic plaques: Comparison of 2D structure-only, 3D structure-only, one-way and fully coupled fluid-structure interaction analyses. J Biomech 47(6):1465–1471. https://doi.org/10.1016/j.jbiomech.2014.01.030
Manduteanu I, Simionescu M (2012) Inflammation in atherosclerosis: a cause or a result of vascular disorders? J Cell Mol Med 16(9):1978–1990. https://doi.org/10.1111/j.1582-4934.2012.01552.x
Fuchs FD, Whelton PK (2020) High blood pressure and cardiovascular disease. Hypertension 75(2):285–329. https://doi.org/10.1161/HYPERTENSIONAHA.119.14240
Eshtehardi P, Mcdaniel MC, Suo J, Dhawan SS, Timmins LH, Binongo JNG, Golub LJ, Corban MT, Finn AV, Oshinski JN (2012) Association of coronary wall shear stress with atherosclerotic plaque burden, composition, and distribution in patients with coronary artery disease. J Am Heart Assoc 1(4):e002543. https://doi.org/10.1161/JAHA.112.002543
Cecchi E, Giglioli C, Valente S, Lazzeri C, Gensini GF, Gensini R, Gensini L (2011) Role of hemodynamic shear stress in cardiovascular disease. Atherosclerosis 214(2):249–256. https://doi.org/10.1016/j.atherosclerosis.2010.09.008
Kim S, Giddens DP (2015) Thrombosis formation on atherosclerotic lesions and plaque rupture. J Biomech Sci Eng 137(4):0410071–04100711. https://doi.org/10.1111/joim.12296
Wang LM, Hu JW, Lei WR, Liu WY, Liu YT (2019) Mechanical stress analysis of defects in atherosclerotic plaque. J Anhui Normal Univ. 42(6):538–543. https://doi.org/10.14182/J.cnki.1001-2443.2019.06.006
Li ZY, Howarth S, Tang T, Martin G, Jean Marie UK, Jonathan G (2007) Does calcium deposition play a role in the stability of atheroma? Location may be the key. Cerebrovasc Dis 24(5):452–459. https://doi.org/10.1159/000108436
Theofilatos K, Stojkovic S, Hasman M, Baig F, Barallobre-Barreiro J, Schmidt L, Yin S, Yin X, Burnap S, Singh B (2022) A proteomic atlas of atherosclerosis: regional proteomic signatures for plaque inflammation and calcification. Cardiovasc Res. https://doi.org/10.1093/cvr/cvac066.204
Bajaj R, Eggermont J, Grainger SJ, Raber L, Parasa R, Khan AHA, Costa C, Erdogan E, Hendricks MJ, Chandrasekharan KH (2022) Machine learning for atherosclerotic tissue component classification in combined near-infrared spectroscopy intravascular ultrasound imaging: validation against histology. Atherosclerosis. https://doi.org/10.1016/j.atherosclerosis.2022.01.021
Acknowledgements
This study was supported by the National Nature Science Foundation of China (No.12274200、11774088) and Hengyang science and technology plan projects (No.202250045335).
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of Interest
The authors declared that no conflict of interest among all authors.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Lei, W., Qian, S., Zhu, X. et al. Haemodynamic Effects on the Development and Stability of Atherosclerotic Plaques in Arterial Blood Vessel. Interdiscip Sci Comput Life Sci 15, 616–632 (2023). https://doi.org/10.1007/s12539-023-00576-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12539-023-00576-w