1 Introduction

Arterial stenosis, as one of the most serious threats to cardiovascular health, has attracted more attention in recent years with improving living standards [1]. The correlations between physical activity and cardiovascular function and structural reforming have become an important topic in cardiovascular health management [2]. Many epidemiological studies have shown that moderate-intensity exercise reduces the risk of cardiovascular disease (CVD) [3]. However, exercise beyond a certain level induces increased oxidative stress of endothelial cells (ECs) [4], which may result in plaque rupture and severe cardiovascular accidents such as stroke or myocardial infarction [5]. For the benefit of CVD patients, an important question is how to ameliorate the risk of plaque rupture during exercise. To develop a dose–response relationship between physical activity and cardiovascular risk, it is necessary to quantify the influence of variations in blood pressure and flow rates during exercise on the mechanical environment around the plaque.

Mechanobiological studies have suggested that mechanical stimuli are closely associated with the pathological progression of atherosclerotic plaques. Elastic stress and viscous shear stress are key mechanical factors regulating the mechanotransduction of ECs and vascular smooth muscle cells (VSMCs), often being considered as decisive when studying plaque growth as well as rupture [6]. It has been demonstrated that low viscous shear stress caused by disturbed flow, especially at arterial bifurcations, contributes to local plaque buildup by upregulating the inflammatory responses of ECs [7]. Exercise-induced extra viscous stress enhances expression of endothelial nitric oxide synthase (eNOS) and proliferates production of nitric oxide (NO), which helps slow the progression of atherosclerosis [8]. Moderate exercise can also increase the mechanical stretch and maintain the physiological function of vascular cells [2]. However, stress beyond the normal range can result in pathological processes, for example, eroding the fibrous cap or weakening the plaque architecture [9, 10]. Clinical statistics and animal experiments have confirmed that plaque ulcers usually appear in the upstream region where the plaque experiences the highest viscous shear stress [11]. In addition, excessive mechanical stretch exerted by increased blood pressure causes VSMC migration and proliferation, which is related to development of atherosclerotic lesions [12, 13]. Analysis of the stress under different exercise conditions is valuable to quantify the mechanical environment around plaques, enabling the instability and vulnerability of a plaque to be described under various conditions, and thus the rupture risk to be further estimated.

It is well known that it is difficult to measure blood vessel stress in vivo using invasive procedures; thus numerical methods based on continuum mechanics are widely adopted for prediction of plaque stress responses [14]. Previous studies have shown that the oversimplified two-dimensional (2D) plaque model fails to provide accurate predictions of the high stress concentration location and peak stress value [15]. Although three-dimensional (3D) fluid–structure interaction (FSI) analysis is considered to be more accurate and reliable for quantifying plaque elastic stress and viscous shear stress [16], the large amount of calculations requires makes such analysis extremely computationally intensive. Besides, for FSI analysis with patient-specific requirements, the material constitutive properties are often abstruse, which limits the general accuracy of the in vivo stress prediction. Therefore, at the present stage, the most preferable method in practice is 3D structure-only analysis, which provides a balance between computational accuracy and efficiency [15]. To conduct patient-specific risk analysis, a general risk assessment tool for plaque rupture must first be developed, as presented herein. Based on critical stresses reported in literature, a risk stratification is also established to quantify the risk level of plaque rupture in daily activities.

Regarding the evaluation of in vivo stress distributions of stenosed vessels, it is well known that the influence of residual stress cannot be neglected [14]. Using the opening-angle technique, Cilla et al. [17] found that inclusion of the residual stress reduces the peak stress of an atherosclerotic plaque and affects the high stress distributions. A thermal expansion method was proposed by Yang et al. [18] as a relatively simple and convenient approach to construct the residual stress for stenosed vessels.

Herein, we use averaged clinical data and create a general stenosed human carotid bifurcation model to investigate the effects of plaque stiffness and stenosis on its local mechanical stress. To reduce the risk of plaque rupture during daily activities, a stenosis mechanical property-specific guide for blood pressure control is proposed. The remainder of this manuscript is organized as follows: In Sect. 2, an in vivo stress model for a stenosed carotid bifurcation is built based on the thermal expansion method [18], and the detailed stresses of the vessel are predicted numerically. In Sect. 3, the variations of the elastic shear stress and viscous shear stress under different exercise intensities are presented, and a risk index is proposed for quantitative risk assessment. Section 4 presents discussions on some key mechanical factors responsible for the significant increase in plaque stress and their association with plaque rupture.

2 Materials and methods

2.1 Geometries and constitutive relations

Based on continuum mechanics, we predict the in vivo stress of plaques in a carotid bifurcation under different exercise intensities. An ideal plaque on the lateral wall of the internal carotid artery (ICA) is constructed with an asymmetric stenosis [19], as shown in Fig. 1a. More details on the dimensions of the plaque are illustrated in Fig. 1b, showing that, by adjusting the parameters r2 and d2, different ICA stenoses (from 11% to 91%) can be obtained. The geometry of the vessel wall of the carotid bifurcation (Fig. 2) refers to the work of Delfino et al. [20], and the dimensions of the cross-sections marked from A to J are listed in Fig. 2b.

Fig. 1
figure 1

a 3D finite element model of stenosed human carotid bifurcation. b Dimensions of ICA stenosis. Section M–M is the cross-section of the narrowest lumen. The stenosis s is defined by the ratio of the section area of the plaque to the lumen area (\(\uppi d_{1}^{2} /4\)) on section M–M. The local diameter of the ICA lumen d1 = 6.6 mm. The radius of the plaque outline r1 = 6.0 mm

Full size image
Fig. 2
figure 2

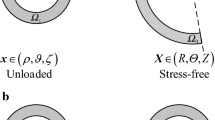
a Symmetric section view of stenosed human carotid bifurcation. b Cross-section dimensions of the vessel wall. Dashed lines denote cross-sections A–J, \(\varPhi_{ 0}\) denotes the opening angle in the stress-free configuration, \(\rho_{\text{i}}\) and \(\rho_{\text{o}}\) denote the inner and outer radii in the unloaded configuration

Full size image

Here, the vessel wall and plaque are regarded as isotropic and incompressible hyperelastic materials, referring to Demiray [21] and neo-Hookean [22] models. Table 1 presents the constitutive relations and material parameters of the stenosed carotid bifurcation, where a is a stress-like parameter and b is a dimensionless parameter. The shear modulus c is set to be 50, 100, and 200 kPa to represent different plaque stiffnesses. The blood is considered to be an incompressible Newtonian fluid [23], with density and viscosity parameters ρ and μ, respectively.

Table 1 Material properties of stenosed carotid bifurcation
Full size table

2.2 Stenosed wall model

In this work, the elastic stress distribution in the stenosed vessel with residual stress is obtained numerically by using the finite element method and thermal expansion method [18]. The commercial software ANSYS Mechanical APDL (Ver. 15.0, ANSYS, Inc., USA) is used to solve the stress–strain formulations of the stenosed wall model. To produce physiological loading in axial direction, 10% axial stretch is applied to the ends of the ICA and ECA, respectively [20]. According to measurements of the systolic pressure in CCA under different exercise intensities by Hellstrom et al. [24] as summarized in Table 2, uniform pressure in the range from 15.8 to 25.3 kPa is applied in the stenosed vessel lumen. The stenosed wall model is meshed with eight-node brick elements; the element number is summarized in Table 3.

Table 2 Blood pressure and flow rate in CCA measured under different exercise intensities [24]
Full size table
Table 3 Element numbers of stenosed wall model and fluid model
Full size table

2.3 Fluid model

Blood flow is calculated in the stenosed carotid lumen with a rigid wall and no-slip boundary condition. The blood flow at the CCA inlet is considered as Poiseuille flow with the flow rates listed in Table 2 for different conditions. The outlets of the ICA and ECA are set to be pressure free [25]. The fluid model is solved separately rather than coupled with the stenosed wall model. By solving the Navier–Stokes equations numerically with ANSYS Fluent (Ver. 15.0, ANSYS, Inc., USA), the hemodynamics in the stenosed carotid bifurcation is predicted. The SIMPLE algorithm is used to couple the pressure and velocity, and the residual error of convergence criterion is set to be less than 10−5. The fluid model is meshed with unstructured tetrahedral elements, with the boundary layer guaranteed to contain six elements along the normal direction of the wall. The element number is summarized in Table 3.

3 Results

3.1 Stress distributions

Figure 3 illustrates the elastic shear stress σrθ and viscous shear stress \(\tau_{\text{w}}\) of the plaque (c = 100 kPa) for the rest condition. Note that the direction of r and θ is defined in a cylindrical coordinate system with z-axis coinciding with the ICA axis. As shown by the arrow indicating the high-stress region, the elastic shear stress σrθ is always concentrated at the shoulder of the plaque. As the stenosis ratio is increased from 11% to 37%, the maximum elastic shear stress \(\sigma_{r\theta }^{\text{Max}}\) increases by 80% and reaches 139 kPa. For stenosis within the range of 50%–72%, \(\sigma_{r\theta }^{\text{Max}}\) exceeds 150 kPa and reaches a maximum value for a stenosis ratio of around 70%, but with further increase of the stenosis ratio from 72% to 91%, \(\sigma_{r\theta }^{\text{Max}}\) decreases slightly.

Fig. 3
figure 3

Contours of elastic shear stress \(\sigma_{r\theta }\) in the plaque and viscous shear stress \(\tau_{\text{w}}\) on the plaque surface for stenosis of a 11%, b 37%, c 50%, d 72%, and e 91%. The elastic shear stresses \(\sigma_{r\theta }\) shown in the 3D section views are the values of the volume elements. Stress concentration regions are marked by short arrows. As illustrated in e, the plane x′o′y′ is located on the narrowest cross-section. The z′-axis is parallel to the ICA axis. The viscous shear stress \(\tau_{\text{w}}\) is projected on the plane y′o′z′. The dashed lines denote the proximal and distal ends of the plaque and the narrowest location. Blood pressure and flow conditions \(P_{0}\) = 15.8 kPa, \(Q_{0}\) = 591 mL/min. Plaque stiffness c = 100 kPa

Full size image

The results also show that, for the viscous shear stress \(\tau_{\text{w}}\) with smaller stenosis ratio, i.e., 11%, lower \(\tau_{\text{w}}\) occurs at the upstream of the plaque center, and higher \(\tau_{\text{w}}\) occurs at the off-center region. For moderate stenosis ratios (37%–50%), both the shoulder and center of the upstream experience higher \(\tau_{\text{w}}\). For severe stenosis with ratio of 91%, the stress \(\tau_{\text{w}}\) is found to be concentrated at the upstream of the narrowest region.

Note that, for given stenosis ratio, the spatial distributions of both the elastic stress \(\sigma_{r\theta }\) and viscous stress \(\tau_{\text{w}}\) exhibit the same variations from the rest condition to highest exercise intensity.

3.2 Variations of maximum elastic shear stress

Figure 4a illustrates the variations of the maximum elastic shear stress \(\sigma_{r\theta }^{\text{Max}}\) with the stenosis ratio. Elevation of both the blood pressure and plaque stiffness results in an increase of \(\sigma_{r\theta }^{\text{Max}}\). With an increase of the stenosis ratio, a low-stiffness plaque (c = 50 kPa) experiences a substantial increase in \(\sigma_{r\theta }^{\text{Max}}\). Meanwhile, for a high stiffness plaque (c = 200 kPa), \(\sigma_{r\theta }^{\text{Max}}\) first increases then decreases, reaching a peak value of 317 kPa at the 50% stenosis ratio.

Fig. 4
figure 4

a Variations of maximum elastic shear stress \(\sigma_{r\theta }^{\text{Max}}\) in the plaque. The blood pressure varies from 15.8 kPa (\(P_{0}\)) to 25.3 kPa (\(P_{4}\)). b Ratios of \(\Delta \sigma_{r\theta }^{\text{Max}}\) to blood pressure increase \(\Delta P\). \(P_{0} \to P_{i}\) denotes blood pressure increase \(\Delta P\) from \(P_{0}\) to \(P_{i}\), in which \(\Delta P = P_{i} - P_{0}\), i = 1, 2, 3, 4. Plaque stiffness values of c = 50, 100, and 200 kPa are considered, respectively

Full size image

With an increase of the stenosis ratio, the variation of the increase ratio of \({{\Delta \sigma_{r\theta }^{\text{Max}} } \mathord{\left/ {\vphantom {{\Delta \sigma_{r\theta }^{\text{Max}} } {\Delta P}}} \right. \kern-0pt} {\Delta P}}\) as shown in Fig. 4b presents similar patterns to \(\sigma_{r\theta }^{\text{Max}}\) as shown in Fig. 4a. The data points with the same stenosis ratio show high consistency, indicating a linear relationship between the stress increase \(\Delta \sigma_{r\theta }^{\text{Max}}\) and blood pressure increase \(\Delta P\).

3.3 Variations of maximum viscous shear stress

As illustrated in Fig. 5a, the maximum viscous shear stress \(\tau_{\text{w}}^{{{\text{Max}}}}\) increases exponentially with the stenosis ratio. For low stenosis (< 37%), the stress magnitude is less than 7% of the maximum value (57 Pa), and no significant increase is observed during exercise. On the contrary, for high stenosis of 91%, increase of the exercise intensity from the rest to load4 condition induces a 60% increase of \(\tau_{\text{w}}^{\text{Max}}\).

Fig. 5
figure 5

a Variations of maximum viscous shear stress \(\tau_{\text{w}}^{\text{Max}}\) on the plaque surface. The blood flow at the CCA inlet varies from 591 mL/min (\(Q_{0}\)) to 839 mL/min (\(Q_{4}\)). b Ratios of \(\Delta \tau_{\text{w}}^{\text{Max}}\) to blood flow increase \(\Delta Q\). \(Q_{0} \to Q_{i}\) denotes blood flow increase \(\Delta Q\) from \(Q_{0}\) to \(Q_{i}\), in which \(\Delta Q = Q_{i} - Q_{0}\), i = 1, 2, 3, 4

Full size image

Figure 5b shows that the increase in the ratio \({{\Delta \tau_{\text{w}}^{\text{Max}} } \mathord{\left/ {\vphantom {{\Delta \tau_{\text{w}}^{\text{Max}} } {\Delta Q}}} \right. \kern-0pt} {\Delta Q}}\) changes exponentially as the stenosis ratio is increased. The overlap of the data points for different exercise intensities suggests a linear correlation between the stress increase \(\Delta \tau_{\text{w}}^{\text{Max}}\) and the blood flow increase \(\Delta Q\).

3.4 Comparison between maximum elastic shear stress and maximum viscous shear stress

Results in Figs. 4 and 5 show that the maximum elastic shear stress \(\sigma_{r\theta }^{\text{Max}}\) is about four orders of magnitude higher than the maximum viscous shear stress \(\tau_{\text{w}}^{\text{Max}}\). Both \(\sigma_{r\theta }^{\text{Max}}\) and \(\tau_{\text{w}}^{\text{Max}}\) exhibit a linear relationship with exercise intensity, and their relative magnitudes under the same exercise intensity are compared. As illustrated in Fig. 6a, we use the internal pressure \(P_{0}\) and the wall shear stress \(\tau_{\text{w}}^{\text{CCA}}\) at the CCA inlet as reference values to normalize \(\sigma_{r\theta }^{\text{Max}}\) and \(\tau_{\text{w}}^{\text{Max}}\), and the normalized stresses are expressed as \(\sigma_{\text{N}} = {{\sigma_{r\theta }^{\text{Max}} } \mathord{\left/ {\vphantom {{\sigma_{r\theta }^{\text{Max}} } {P_{0} }}} \right. \kern-0pt} {P_{0} }}\) and \(\tau_{\text{N}} = {{\tau_{\text{w}}^{\text{Max}} } \mathord{\left/ {\vphantom {{\tau_{\text{w}}^{\text{Max}} } {\tau_{\text{w}}^{\text{CCA}} }}} \right. \kern-0pt} {\tau_{\text{w}}^{\text{CCA}} }}\), respectively.

Fig. 6
figure 6

a Normalized stresses \({{\sigma_{r\theta }^{\text{Max}} } \mathord{\left/ {\vphantom {{\sigma_{r\theta }^{\text{Max}} } {P_{0} }}} \right. \kern-0pt} {P_{0} }}\) and \({{\tau_{\text{w}}^{\text{Max}} } \mathord{\left/ {\vphantom {{\tau_{\text{w}}^{\text{Max}} } {\tau_{\text{w}}^{\text{CCA}} }}} \right. \kern-0pt} {\tau_{\text{w}}^{\text{CCA}} }}\). b Degree of stress concentration \({{\sigma_{r\theta }^{\text{Max}} } \mathord{\left/ {\vphantom {{\sigma_{r\theta }^{\text{Max}} } {\sigma_{r\theta }^{\text{Mean}} }}} \right. \kern-0pt} {\sigma_{r\theta }^{\text{Mean}} }}\) and \({{\tau_{\text{w}}^{\text{Max}} } \mathord{\left/ {\vphantom {{\tau_{\text{w}}^{\text{Max}} } {\tau_{\text{w}}^{\text{Mean}} }}} \right. \kern-0pt} {\tau_{\text{w}}^{\text{Mean}} }}\). Plaque stiffness values of c = 50 kPa, 100 kPa, and 200 kPa are considered, respectively. \(P_{0}\) and \(\tau_{\text{w}}^{\text{CCA}}\) are adopted as reference values, in which \(\tau_{\text{w}}^{\text{CCA}}\) denotes the wall shear stress at the CCA inlet. \(\sigma_{r\theta }^{\text{Mean}}\) denotes the volume average of elastic shear stresses \(\sigma_{r\theta }\) in the plaque. \(\tau_{\text{w}}^{\text{Mean}}\) denotes the mean of viscous shear stresses \(\tau_{\text{w}}\) on the plaque surface. Blood pressure and flow conditions: \(P_{0}\) = 15.8 kPa, \(Q_{0}\) = 591 mL/min

Full size image

For 11%–37% stenosis, the maximum value of \(\sigma_{\text{N}}\) is up to 12.5, about ten times \(\tau_{\text{N}}\). The stress increase ratio with respect to the stenosis increase \(\Delta s\) is defined as \({{\Delta \sigma_{\text{N}} } \mathord{\left/ {\vphantom {{\Delta \sigma_{\text{N}} } {\Delta s}}} \right. \kern-0pt} {\Delta s}}\), with a magnitude of up to 17.8, which is four times \({{\Delta \tau_{\text{N}} } \mathord{\left/ {\vphantom {{\Delta \tau_{\text{N}} } {\Delta s}}} \right. \kern-0pt} {\Delta s}}\). For 37%–72% stenosis, \(\sigma_{\text{N}}\) exhibits no obvious increase, and it even decreases at c = 200 kPa. In contrast, a sharp increase of \(\tau_{\text{N}}\) is observed and the increase ratio \({{\Delta \tau_{\text{N}} } \mathord{\left/ {\vphantom {{\Delta \tau_{\text{N}} } {\Delta s}}} \right. \kern-0pt} {\Delta s}}\) is up to 30.5. The value of \(\tau_{\text{N}}\) catches up with \(\sigma_{\text{N}}\) at s = 72%. For stenosis s = 91%, \(\tau_{\text{N}}\) far exceeds \(\sigma_{\text{N}}\) with a magnitude of more than 24.0, and its increase ratio \({{\Delta \tau_{\text{N}} } \mathord{\left/ {\vphantom {{\Delta \tau_{\text{N}} } {\Delta s}}} \right. \kern-0pt} {\Delta s}}\) is up to 77.5.

Stress concentration is an important factor in plaque rupture. The degrees of stress concentration in Fig. 6b can be used to quantify the severity of stress concentration in the plaque, defined as \({{\sigma_{\text{C}} = \sigma_{r\theta }^{\text{Max}} } \mathord{\left/ {\vphantom {{\sigma_{\text{C}} = \sigma_{r\theta }^{\text{Max}} } {\sigma_{r\theta }^{\text{Mean}} }}} \right. \kern-0pt} {\sigma_{r\theta }^{\text{Mean}} }}\) and \(\tau_{\text{C}} = {{\tau_{\text{w}}^{\text{Max}} } \mathord{\left/ {\vphantom {{\tau_{\text{w}}^{\text{Max}} } {\tau_{\text{w}}^{\text{Mean}} }}} \right. \kern-0pt} {\tau_{\text{w}}^{\text{Mean}} }}\), respectively. It is found that \(\sigma_{\text{C}}\) is much larger than \(\tau_{\text{C}}\), and its magnitude can increase by more than 400% as the stenosis ratio is increased, which explains why local high elastic shear stress caused by severe stenosis serves as a key factor in plaque rupture. For 37%–72% stenosis, \(\sigma_{\text{C}}\) exhibits an increase with plaque stiffening. At 91% stenosis, the values of \(\sigma_{\text{C}}\) tend to be the same under different plaque stiffnesses, suggesting that, under high stenosis conditions, plaque stiffening has limited effects on plaque rupture.

3.5 Effects of stenosis variation on blood flow

In this study, the ratio of the blood flow rate in the ICA (\(Q_{\text{ICA}}\)) to the ECA (\(Q_{\text{ECA}}\)) is used to characterize the flow distribution (\({{Q_{\text{ICA}} } \mathord{\left/ {\vphantom {{Q_{\text{ICA}} } {Q_{\text{ECA}} }}} \right. \kern-0pt} {Q_{\text{ECA}} }}\)) at the carotid bifurcation. The results show that an increase of the exercise intensity has weak effects on the values of \({{Q_{\text{ICA}} } \mathord{\left/ {\vphantom {{Q_{\text{ICA}} } {Q_{\text{ECA}} }}} \right. \kern-0pt} {Q_{\text{ECA}} }}\), as shown in Fig. 7. For stenosis of less than 50%, \({{Q_{\text{ICA}} } \mathord{\left/ {\vphantom {{Q_{\text{ICA}} } {Q_{\text{ECA}} }}} \right. \kern-0pt} {Q_{\text{ECA}} }}\) presents small changes with a magnitude of around 1.3. For stenosis of more than 72%, a sharp decrease of \({{Q_{\text{ICA}} } \mathord{\left/ {\vphantom {{Q_{\text{ICA}} } {Q_{\text{ECA}} }}} \right. \kern-0pt} {Q_{\text{ECA}} }}\) from 1.1 to 0.3 is observed, which suggests that 70% ICA stenosis can substantially reduce the blood supply to brain tissue.

Fig. 7
figure 7

Variations of flow distribution \({{Q_{\text{ICA}} } \mathord{\left/ {\vphantom {{Q_{\text{ICA}} } {Q_{\text{ECA}} }}} \right. \kern-0pt} {Q_{\text{ECA}} }}\). The blood flow at the CCA inlet varies from 591 mL/min (\(Q_{0}\)) to 839 mL/min (\(Q_{4}\))

Full size image

3.6 Risk stratification for plaque rupture during exercise

Referring to former studies, \(\sigma_{\text{cri}} = 3 0 0\,{\text{kPa}}\) [6, 14] and \(\tau_{\text{cri}} = 30\,{\text{Pa}}\) [10] are widely used as critical values for high-risk plaques. In this work, we further define \({{\sigma_{r\theta }^{\text{Max}} } \mathord{\left/ {\vphantom {{\sigma_{r\theta }^{\text{Max}} } {\sigma_{\text{cri}} }}} \right. \kern-0pt} {\sigma_{\text{cri}} }}\) as a risk index for the maximum elastic shear stress \(\sigma_{r\theta }^{\text{Max}}\), and \({{\tau_{\text{w}}^{\text{Max}} } \mathord{\left/ {\vphantom {{\tau_{\text{w}}^{\text{Max}} } {\tau_{\text{cri}} }}} \right. \kern-0pt} {\tau_{\text{cri}} }}\) as a risk index for the maximum viscous shear stress \(\tau_{\text{w}}^{\text{Max}}\). The risk of plaque rupture for different ICA stenoses and exercise intensities can be divided into five stages using the risk index, viz. mild (0.0–0.25), moderate (0.25–0.50), significant (0.50–0.75), severe (0.75–1.0), and emergent (> 1.0) stages, as illustrated in Fig. 8.

Fig. 8
figure 8

Risk stratification for plaque rupture for different ICA stenoses and exercise intensities. a Risk index \({{\sigma_{r\theta }^{\text{Max}} } \mathord{\left/ {\vphantom {{\sigma_{r\theta }^{\text{Max}} } {\sigma_{\text{cri}} }}} \right. \kern-0pt} {\sigma_{\text{cri}} }}\), plaque stiffness c = 50 kPa; b risk index \({{\sigma_{r\theta }^{\text{Max}} } \mathord{\left/ {\vphantom {{\sigma_{r\theta }^{\text{Max}} } {\sigma_{\text{cri}} }}} \right. \kern-0pt} {\sigma_{\text{cri}} }}\), plaque stiffness c = 100 kPa; c risk index \({{\sigma_{r\theta }^{\text{Max}} } \mathord{\left/ {\vphantom {{\sigma_{r\theta }^{\text{Max}} } {\sigma_{\text{cri}} }}} \right. \kern-0pt} {\sigma_{\text{cri}} }}\), plaque stiffness c = 200 kPa; d risk index \({{\tau_{\text{w}}^{\text{Max}} } \mathord{\left/ {\vphantom {{\tau_{\text{w}}^{\text{Max}} } {\tau_{\text{cri}} }}} \right. \kern-0pt} {\tau_{\text{cri}} }}\). Referring to the different exercise intensities in Table 2, the blood pressure varies from 15.8 kPa (\(P_{0}\)) to 25.3 kPa (\(P_{4}\)), and the blood flow at the CCA inlet varies from 591 mL/min (\(Q_{0}\)) to 839 mL/min (\(Q_{4}\)). According to the risk index, the rupture risk is divided into five stages: mild (0.0–0.25), moderate (0.25–0.50), significant (0.50–0.75), severe (0.75–1.0), and emergent (> 1.0). The critical stresses are \(\sigma_{\text{cri}} = 3 0 0\,{\text{kPa}}\) [6, 14] and \(\tau_{\text{cri}} = 30\,{\text{Pa}}\) [10]

Full size image

Figure 8a shows that the risk for a low-stiffness plaque (c = 50 kPa) during exercise remains below significant unless the stenosis ratio is severe. The contour curves with a risk index of 0.25 and 0.50 are fit by blood pressure P and stenosis s (goodness of fit R2 > 0.99) as follows:

$$P = \left\{ {\begin{array}{ll} - 39.5s + 25.3, &\, s \in \left[ {11\% , \, 24\% } \right]\,{\text{for}}\,{\text{risk}}\,{\text{index is}}\, 0.25, \hfill \\ 60.8s^{2} - 100.7s + 61.2, &\, s \in \left[ {52\% , \, 91\% } \right]\,{\text{for}}\,{\text{risk}}\,{\text{index is}}\, 0.50. \hfill \\ \end{array} } \right. $$
(1)

The risk for a moderate-stiffness plaque (c = 100 kPa) in Fig. 8b varies from moderate to severe. The fit curves (R2 > 0.99) are expressed as follows:

$$P = \left\{ {\begin{array}{ll} 142.6s^{2} - 136.4s + 48.6, &\, s \in \left[ {22\% , \, 49\% } \right]\,{\text{for}}\,{\text{risk}}\,{\text{index\,is}}\, 0.50, \hfill \\ 4.4s + 12.4, &\, s \in \left[ {77\% , \, 91\% } \right]\,{\text{for}}\,{\text{risk}}\,{\text{index is}}\, 0.50, \hfill \\ - 11.6s + 31.5, &\, s \in \left[ {53\% , \, 72\% } \right]\,{\text{for}}\,{\text{risk}}\,{\text{index is}}\, 0.75, \hfill \\ 6.4s + 18.5, &\, s \in \left[ {72\% , \, 91\% } \right]\,{\text{for}}\,{\text{risk}}\,{\text{index is}}\, 0.75. \hfill \\ \end{array} } \right.$$
(2)

As illustrated in Fig. 8c, the maximum risk for a high-stiffness plaque (c = 200 kPa) could be emergent. The fit curves (R2 > 0.95) are expressed as follows:

$$P = \left\{ {\begin{array}{ll} - 57.0s + 27.0, &\, s \in \left[ {11\% , \, 20\% } \right]\,{\text{for}}\,{\text{risk}}\,{\text{index is}}\, 0.50 \hfill \\ 151.5s^{2} - 138.0s + 48.7, &\, s \in \left[ {22\% , \, 50\% } \right]\,{\text{for}}\,{\text{risk}}\,{\text{index is}}\, 0.75, \hfill \\ 17.2s^{2} - 14.7s + 20.4, &\, s \in \left[ {50\% , \, 91\% } \right]\,{\text{for}}\,{\text{risk}}\,{\text{index is}}\, 0.75, \hfill \\ - 13.1s + 30.3, &\, s \in \left[ {38\% , \, 50\% } \right]\,{\text{for}}\,{\text{risk}}\,{\text{index is}}\, 1.0, \hfill \\ 5.4s + 21.0, &\, s \in \left[ {50\% , \, 76\% } \right]\,{\text{for}}\,{\text{risk}}\,{\text{index is}}\,1.0. \hfill \\ \end{array} } \right.$$
(3)

Figure 8d shows the contour of the risk index \({{\tau_{\text{w}}^{{{\text{Max}}}} } \mathord{\left/ {\vphantom {{\tau_{\text{w}}^{{{\text{M}}ax}} } {\tau_{\text{cri}} }}} \right. \kern-0pt} {\tau_{\text{cri}} }}\). In terms of the flow rate Q at the CCA inlet and the stenosis s, the contour curves are fit (R2 > 0.99) as follows:

$$Q = \left\{ {\begin{array}{*{20}l} { - 2875s + 2248, \, s \in \left[ {49\% , \, 58\% } \right]\,{\text{for}}\,{\text{risk}}\,{\text{index is}} \, 0.25,} \hfill \\ { - 1823s + 1923, \, s \in \left[ {60\% , \, 73\% } \right]\,{\text{for}}\,{\text{risk}}\,{\text{index is}}\, 0.50,} \hfill \\ { - 2696s + 2733, \, s \in \left[ {70\% , \, 79\% } \right]\,{\text{for}}\,{\text{risk}}\,{\text{index is}}\, 0.75,} \hfill \\ { - 2323s + 2585, \, s \in \left[ {75\% , \, 86\% } \right]\,{\text{for}}\,{\text{risk}}\,{\text{index is}}\, 1.0. \, } \hfill \\ \end{array} } \right.$$
(4)

4 Discussion

As is well known, patients with arterial stenosis, especially older and sedentary individuals, are at risk of serious cardiovascular accidents caused by plaque rupture during high-intensity exercise. In this study, a stenosed carotid bifurcation model was developed based on averaged clinical data. By calculating the in vivo plaque stress under different exercise intensities, the biomechanical characteristics of plaque rupture were explored to help prevent severe cardiovascular events in daily activities.

4.1 Co-localization of high mechanical stresses

We found that high elastic shear stress often appears at the plaque shoulder (Fig. 3), which is consistent with numerical results in previous literature [18, 26]. Moreover, the concentration of viscous shear stress is also close to the plaque shoulder, which may upregulate expression of specific matrix metalloproteinases (MMPs) in this region and lead to erosive injury of fibrous cap [27]. The co-localization of high mechanical stresses around the plaque shoulder explains the high risk of eccentric plaque on the lateral ICA wall in a mechanical way.

4.2 Biomechanical characteristics associated with plaque rupture

Results in this paper show that both the stenosis ratio and plaque stiffness nonlinearly affect the maximum elastic shear stress \(\sigma_{r\theta }^{{{\text{Max}}}}\) of plaque during exercise (Fig. 4a). For a low-stiffness plaque (c = 50 kPa), an increase of the exercise intensity results in a 70% increase of \(\sigma_{r\theta }^{{{\text{Max}}}}\) at stenosis s > 90%, suggesting that low-stiffness plaques have relatively high risk under severe stenosis in daily activities. A high-stiffness plaque is more likely to rupture due to the larger magnitude of \(\sigma_{r\theta }^{{{\text{Max}}}}\). Therefore, patients with high-stiffness plaques should strictly monitor their daily blood pressure to reduce the rupture risk.

As the stenosis ratio is increased, the \(\sigma_{r\theta }^{{{\text{Max}}}}\) of a high-stiffness plaque is found first to increase then to decrease, suggesting the existence of a specific stenosis ratio for maximum rupture risk estimation (such as s = 72% for c = 100 kPa, and s = 50% for c = 200 kPa). From the mechanical point of view, a large-size plaque with high stiffness could act as a “stress shield” [6], bearing part of the mechanical stress in the vessel wall, which explains the stress decrease at high stenosis. In addition, the level of stress concentration for different plaque stiffnesses exhibits no obvious difference at s = 91% (Fig. 6b), suggesting that variation of the plaque stiffness has little influence on plaque rupture under high-stenosis conditions.

4.3 Contributions of elastic shear stress and viscous shear stress to plaque rupture

Comparison of the normalized stresses in Fig. 6a shows that the contributions of elastic shear stress and viscous shear stress to plaque rupture depend on the stenosis ratio. At low stenosis, the elastic shear stress is relatively higher, which may be the main mechanical stimulus increasing the rupture risk. In contrast, for severe stenosis (s > 90%), the dramatically increased viscous shear stress is likely to weaken the plaque architecture and make the plaque vulnerable. The normalized stresses at around 70% stenosis approximately equal each other, suggesting that tearing by the elastic shear stress and erosion by the viscous shear stress contribute equally to plaque rupture at this stenosis ratio.

4.4 Stenosis mechanical property-specific guide for blood pressure control

Based on the risk index defined in this study, a specific risk stratification is proposed in terms of exercise intensity. This stratification could serve as a guide to reduce plaque rupture risk by blood pressure control.

For a low-stiffness plaque (Fig. 8a), the rupture risk exceeds moderate under high-stenosis conditions. To avoid plaque rupture in daily activities, according to Eq. (1), the relationship between blood pressure P and stenosis s should satisfy

$$P < 60.8s^{2} - 100.7s + 61.2, \, s \in \left[ {52\% , \, 91\% } \right].$$
(5)

The maximum risk of a moderate-stiffness plaque can reach severe (Fig. 8b). To restrict the risk to below the significant stage, according to Eq. (2), the blood pressure P should satisfy

$$P < \left\{ {\begin{array}{ll} - 11.6s + 31.5, &\, s \in \left[ {53\% , \, 72\% } \right], \hfill \\ 6.4s + 18.5, &\, s \in \left[ {72\% , \, 91\% } \right]. \hfill \\ \end{array} } \right.$$
(6)

For a high-stiffness plaque (Fig. 8c), a critical stenosis (s = 50%) shows an extremely high risk during exercise. Referring to Eq. (3), the blood pressure P should satisfy

$$P < \left\{ {\begin{array}{ll} 151.5s^{2} - 138.0s + 48.7, &\, s \in \left[ {22\% , \, 50\% } \right], \hfill \\ 17.2s^{2} - 14.7s + 20.4, &\, s \in \left[ {50\% , \, 91\% } \right]. \hfill \\ \end{array} } \right.$$
(7)

The results in Fig. 8d show that it is high stenosis (s > 70%) rather than vigorous activity that causes high viscous shear stress and increases plaque vulnerability.

In addition, our results show a nonlinear relationship between the ratio of ICA stenosis and the perfusion of brain tissue (Fig. 7). It is found that increase of ICA stenosis below 50% has weak effects in terms of decreasing cerebral perfusion, while only high ICA stenosis above 70% significantly reduces the blood supply to brain tissue, in agreement with measurements in recent clinical experiments [28].

4.5 Limitations

The results of this study should be considered with some limitations. Plaques often contain different components such as fibrous cap, lipids, and intraplaque hemorrhage [29, 30], and the resulting discontinuities in material properties often cause a nonuniform stress distribution inside the plaque. The present study focuses rather on the effects of the plaque characteristics (such as stiffness, stenosis, and loading conditions) on the stress responses, and explores general rules for plaque rupture. For simplicity, the plaque is thus assumed to be homogeneous in this stress analysis. Although this study may not provide accurate results for the stress distributions and values, the trends in the stress variations and the relative magnitudes of the stress values in the results are still instructive. Moreover, the results show that the location of stress concentration is at the plaque shoulder, in good agreement with numerical results considering different plaque components [26, 31].

It is important to note that the presented methods could easily be applied to patient-specific cases by using proper medical images of stenosed vessels. In future work, more biomechanical parameters of the plaque will be introduced in the stress analysis, such as the location and morphology of the plaque and the material properties of different plaque components. This could help to establish a database of stress responses for different plaque types, and lay the foundation for further risk assessment of patient-specific plaques.

When the stenosis is high, intensive interactions between blood cells and the vessel wall will affect the local hydrodynamics around the stenosis dramatically. Generally, since the viscosity inside blood cells is higher than plasma, the velocity profiles of Casson flow instead of Poiseuille flow appear, which often increases the shear rate near vessel walls. On the other hand, for a given pressure drop over a stenosis, the larger apparent viscosity of blood flow for blood cell suspensions compared with plasma will reduce the mean flow velocity and decrease the shear rate near vessel walls. To address this non-Newtonian characteristic, further studies solving the fluid–membrane interactions in confined geometries are required.

5 Conclusions

Parametric analyses were performed under different exercise intensities to investigate the effects of plaque stiffness and stenosis on the in vivo stress of atherosclerotic plaques. The key mechanical factors associated with plaque rupture are discussed, and a risk stratification for vulnerable plaques is established. The results of this study reveal the effects of mechanical properties on various parameters and provide a solution for stenosis mechanical property-specific blood pressure control in cardiovascular health management. This will be of great importance to reduce cardiovascular risk in daily activities and improve the quality of life of CVD patients.