1 Introduction

Kidney cancer or renal cell carcinoma (RCC) has been ranked as the seventh leading cancer type among men in western communities. The incidence of RCC steadily rises by 2–4% each year [1]. RCC is a collection of various histological subtypes such as clear cell renal cell carcinomas (ccRCC), papillary renal cell carcinomas (pRCC), and chromophobe renal cell carcinomas (crRCC). Among them, ccRCC is the most common (70–85%) and lethal subtype [1]. Surgical and targeted therapies exist to treat the kidney cancer and they are also successful in improving the patient’s overall survival [2]. But most patients ultimately grow resistance toward these treatments and surrender to the disease.

Besides multiple discussions on cancer evolution and progression by various studies [3], cancer at its core is characterized by somatic copy number alterations and unique gene expression profiles. Therefore, there is a need to thoroughly understand the ccRCC disease for building reliable prognostic and therapeutic strategies by incorporating genomic data. Earlier research based on a single type of genomic data has reported a number of molecular alterations in ccRCC at the mRNA, miRNA, and DNA (copy number alterations) level. Most of the ccRCC cases have shown alterations in the short arm of chromosome 3 and 30–56% have the VHL (Von Hippel-Lindau) gene mutated [4]. However, these studies have not produced sufficient results as they lack in exploring the complex mechanism of multiple genomic processes in human diseases. Now, with emerging technologies for genome profiling, multiple genomic data types are available and analytic methods for integrating these data types provide a better understanding of cancer evolution and progression. This results in identification of targets and clinical prediction of cancer by incorporating the necessary interactions between the data types. Many recent studies have shown benefits of the integrated approach in ccRCC [5,6,7,8,9,10].

However, these analytical methods for multiple data types are facing two challenges: high dimensionality of data and the presence of complex correlations and interactions both within and between platform-specific features [11]. The proposed method is driven by the dataset from TCGA (The Cancer Genome Atlas) Pan-Cancer Survival Prediction Challenge project that contains different molecular types of KIRC (kidney renal cell carcinoma). In the proposed method, principal component analysis and its sparse version are the machine learning approaches used to overcome the first challenge of high dimensionality. The second challenge is handled through modeling the interactions by taking the product of principal component score vectors [12]. Additionally, it also finds important genomic variables that are linked to ccRCC progression.

To the best of our knowledge, very few studies of integrative analysis for ccRCC are available [5,6,7,8,9,10] and none of them have incorporated multi-level interaction effects, within and between the molecular data types when fitting the integrative model for RCC. So the proposed work contributes significantly in ccRCC research by providing a unique methodology that contains data type interaction effects at different levels. The method achieves better prediction with sparse principal components model by including latent feature interactions as compared to without including them.

2 Related Work

Earlier research on various types of cancer such as gene expression profiles in breast cancer [13], miRNA in lung cancer [14], copy number alterations in ovarian cancer [15], etc., was mainly focussed on single type of genomic data to derive biomarkers of prognostic significance or improve the clinical outcome of cancer. Although these studies helped in important discoveries, they were limited to one type of molecular data. However, a thorough and comprehensive understanding of cancer development and its biological mechanism requires the examination of the interplay between different layers of genomic data. This has motivated current research to integrate diverse types of genomic data. These studies have revealed many benefits of the integrated approach in different cancers [16, 17]. With the similar focus, various integrative studies in KIRC were conducted.

Dondeti et al. [5] identified potentially important targets in ccRCC by combining copy number and gene expression data. Two important chromosome 5q oncogenes are discovered whose overexpression play a sufficient role in promoting tumorigenesis in ccRCC. An integrated molecular analysis of ccRCC by Sato et al. [6] identified new mutated genes and pathways that are involved in the pathogenesis of ccRCC. Gene expression, DNA methylation, and copy number data for more than 100 ccRCC samples were analyzed using different sequencing techniques.

Multiple datasets of miRNA expression related to ccRCC were incorporated into an integrative framework by Chen et al. [7]. The study discovered 14 unique molecular pathways that have an important role in the production of ccRCC tumor. Integrative analysis for analyzing mRNA and miRNA interactions together was performed to build a predictive model for survival outcome by Chekouo et al. [8]. The Bayesian model proposed by them also identifies cancer biomarkers specific to KIRC progression.

A study by Butz et al. [9] integrated mRNA, microRNA, and protein expression data of ccRCC using pathway analysis. They identified three new potential biomarkers that are linked to kidney cancer. Similarly, the work by Bluyssen et al. [10] reviews the recent findings in the integrative studies of ccRCC. It discusses how significant technological advances led to the availability of different genomic data and helped in understanding the complex pathology of ccRCC and its molecular mechanism.

3 Dataset

In this study, the proposed method is tested using KIRC dataset [18] from TCGA Pan-Cancer Survival Prediction Challenge project [19]. The project home page can be accessed on Synapse (http://dx.doi.org/10.7303/syn1710282). The data available for each cancer type on the website contain core sample sets, comprising overall survival time, different types of molecular data, etc. The core tumor sample set is used in this study. The core data contain the survival time, gene expressions, micro-RNA expressions, and copy number alterations for tumor samples of patients diagnosed with KIRC. Survival data contain entries about overall survival time (to death) for each patient in days. Three genomic data types used in the study are as follows:

  1. 1.

    mRNA Expression: Messenger RNA or mRNA is the key molecule to enable gene expression for the production of proteins. For sequencing mRNA data, RNA sequencing (RNA-Seq) is used. Illumina HiSeq 2000 is the instrument used in RNA sequencing of the data used in this study.

  2. 2.

    microRNA (miRNA) Expression: miRNAs constitute a recently discovered class of short non-coding RNAs of around 22 nucleotides that have crucial roles in regulating the gene expression [20]. microRNA sequencing (miRNA-Seq) is used for sequencing miRNA data. It is a type of RNA-Seq, which is also known as small RNA sequencing as it constitutes small RNAs. Illumina Genome Analyzer/HiSeq 2000 is used as a tool or platform for performing small RNA sequencing for the miRNA data used in this study.

  3. 3.

    Somatic CNAs (Copy Number Alterations): Also referred as CNV (copy number variation), somatic CNA is a phenomenon in which parts of the genes are duplicated or deleted. An SNP array is a type of DNA microarray that is used to detect mutations in the genomic sequence. Chip-based methods for SNP arrays such as comparative genomic hybridization can detect genomic alterations leading to the loss of heterozygosity (LOH). Such a chip-based method or platform by Affymetrix, known as the Genome-Wide Human SNP Array 6.0 is used in this study for the detection of copy number variations.

The four types of data (three genomic types and survival time) were taken for 243 patients. Initially, predictors/features with zero variance from the three genomic data types were eliminated, leaving 795 features in miRNA, 20,203 in mRNA, and 69 alterations in sCNA. The dataset is summarized in Table 1.

Table 1 Dataset used in the study
Full size table

4 Proposed Method

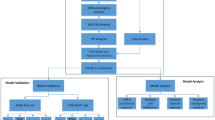
The proposed method initially analyzes data that are obtained from different data types by reducing the dimensionality using dimension reduction techniques. The resulting data are then integrated into a single statistical model by incorporating between and within interactions among data types, to predict clinical outcome and identify the clinically relevant genes. The diagram representing the proposed method is shown in Fig. 1.

Fig. 1
figure 1

High-dimensional data predictors from multiple genomic data like copy number and gene expression are converted into low-dimensional data predictors using dimensionality reduction techniques. Subsequently, within and between interactions of obtained predictors are used to perform predictive analysis using BMA for the required clinical outcome like survival time, and then variable selection procedure is performed

Full size image

Let X1,…, XK be the n × l1,…, n × lK matrices and Y be the n × 1 vector. These matrices represent the values of K groups (genomic data types) used in the present model with l1,…, lK genomic features along with the responses (clinical outcomes) vector taken from a random sample of n observations. The aim of the function is to predict the values in Y from the K groups of features and the interactions among them.

A conceptual model integrating the interactions within and between the groups of features can be written as

$$Y = t_{1} \left( {X_{1} } \right) + t_{2} \left( {X_{2} } \right) + \cdots + t_{\text{k}} \left( {X_{\text{k}} } \right)$$
(1)
$$+ \;s_{11} \left( {X_{1} \times X_{1} } \right) + s_{22} \left( {X_{2} \times X_{2} } \right) + \cdots + s_{KK} \left( {X_{\text{K}} \times X_{\text{K}} } \right)$$
(2)
$$+ s_{12} \left( {X_{1} \times X_{2} } \right) + s_{13} \left( {X_{1} \times X_{3} } \right) + \cdots + s_{{\left( {{\text{K}} - 1} \right){\text{K}}}} \left( {X_{{{\text{K}} - 1}} \times X_{\text{K}} } \right)$$
(3)
$$+ \;e,$$

where “A × B” is a matrix in which the ith row value corresponds to the Cartesian product of the values of the ith rows of A and B (i.e., the values of the interaction terms for observation i), and “A × A” is a matrix in which the ith row value corresponds to all pairwise products of the values in the ith row of A (so that there are no second-order terms in the model), for i = 1,…,n [11]. Here, consider {t(.), s(.)} be two functions of a data matrix X, which are defined below, and e is an n × 1 vector of error terms. The model terms are as follows:

  • Term (1) denotes data type-specific effects modeled as main effects for each data type.

  • Term (2) denotes within data type interaction effects and it represents interactions among the features from the similar data type.

  • Term (3) denotes between data type interaction effects and it represents interactions among the features from the different data types.

Now, to fit the above model, one needs to define the functions s(.) and t(.). The function tk(Xk) can be defined as a linear function Xkαk, i.e., tk(Xk) = Xkαk. The function skp(Xk × Xp) can be defined as a linear function (Xk × Xp)δkp, i.e., skp(Xk × Xp) = (Xk × Xp)δkp, where δkp is a vector of parameters having the identical length as (Xk × Xp) and αk is lK × 1, for k, p ∈ {1,…, K}. With these definitions, the model can be written as,

$$Y = \alpha_{o} + \mathop \sum \limits_{k} \mathop \sum \limits_{j = 1}^{{l_{\text{k}} }} \alpha_{\text{kj}} X_{kj} + \mathop \sum \limits_{k} \mathop \sum \limits_{{0 < i < j \le l_{k} }} \gamma_{\text{kji}} X_{\text{kj}} X_{\text{ki}} + \mathop \sum \limits_{k > p} \mathop \sum \limits_{j = 1}^{{l_{\text{k}} }} \mathop \sum \limits_{i = 1}^{{l_{\text{p}} }} \eta_{\text{kpji}} X_{\text{kj}} X_{\text{pi}} + e ,$$
(4)

where Xkj is the jth column of Xk, \(\alpha_{\text{o}}\) the intercept, \(\alpha_{\text{kj}}\)the member of αk, and \(\gamma_{\text{kji}}\) and \(\eta_{\text{kpji}}\) are members of δkp for k, p \(\in\) {1, …, K} [11]. Now if there are \(\bar{l} = l_{1} + l_{2} + \cdots + l_{\text{k}}\), then Eq. (4) will have \(\bar{l} + \bar{l}\left( {\bar{l} - 1} \right)/2\) values, which will even surpass the total observations n. In such a scenario, taking higher-order interactions will further increase the number of values polynomially, which may result in unstable model fitting. The KIRC dataset has data for n = 243 patients with \(\bar{l}\) = 21,607 predictors, that leads to (21,607)(21,606)/2 = 233,420,421 possible two-way interactions!

To simplify this, the dimensionality of input is reduced that will cover the maximum information in the data with lesser dimensions. If \(R\) is the dimension reduction technique that projects the higher dimensional features of data matrix Xk for k = 1,…, K into lower dimensional latent features matrix Hk (n × hk) containing latent feature scores, such that hk is less than lk, then \(R\) can be defined as follows:

$$R\left( {X_{\text{k1}} , \ldots , X_{{k_{{l_{k} }} }} } \right) \equiv \left\{ {H_{\text{k1}} , \ldots , H_{{{\text{k}}_{{{\text{h}}_{\text{k}} }} }} } \right\}$$

using \(R\), the new feature set is hk which is of far lower dimensions (tens) than lk (thousands). Therefore, the model equation can be rewritten with new functions constituting lower dimensional latent feature scores and their interactions, such as \(\bar{t}\)k(Hk) = Hkαk and \(\bar{s}\)kp(Hk × Hp) = (Hk × Hp)δkp, for k, p \(\in\) {1,…,K}.

With these definitions, the model can be rewritten as,

$$Y = \bar{\alpha }_{o} + \mathop \sum \limits_{k} \mathop \sum \limits_{j = 1}^{{l_{k} }} \bar{\alpha }_{\text{kj}} H_{\text{kj}} + \mathop \sum \limits_{k} \mathop \sum \limits_{ {0 < i < j \le l_{k} }} \bar{\gamma }_{\text{kji}} H_{\text{kj}} H_{\text{ki}} + \mathop \sum \limits_{k > p} \mathop \sum \limits_{j = 1}^{{l_{k} }} \mathop \sum \limits_{i = 1}^{{l_{p} }} \bar{\eta }_{\text{kpji}} H_{\text{kj}} H_{\text{pi}} + \bar{e},$$
(5)

where \(H_{\text{kj}}\) is the jth column of Hk, \(\bar{\alpha }_{\text{o}}\) the intercept, \(\bar{\alpha }_{\text{kj}}\) the main effect of the jth latent feature of the kth variable group, \(\bar{\gamma }_{\text{kji}}\) the interaction effect between the ith and the jth latent feature from the kth variable group, and \(\bar{\eta }_{\text{kpji}}\) is the interaction effect between the jth latent feature from the kth variable group and the ith latent feature for the pth variable group, for k, p \(\in\) {1, …, K} [11].

Therefore, for the fitting model (5), a dimensionality reduction approach \(R\) is needed which can be applied on each given data matrix Xk of actual features, resulting in an n × hk matrix Hk such that hk\(\le\)lk for k = 1,…, K and \(\bar{h} + \bar{h}\left( {\bar{h} - 1} \right)/2\) is less than \(n\). Therefore, H1,…, Hk will constitute of h1,…, hk latent scores for n units. If we compare the number of predictors and their interactions in this model from the model (4), there is a substantial reduction in the number of main effects and interaction effects, e.g., if h1 = 6, h2 = 5, h3 = 6, then model (5) would contain 17 main effects and 17(16)/2 = 136 interaction effects and overall 153 effects. This makes the model more scalable, interaction preserving and it also maintains the predictive accuracy.

Fitting the Model: After applying the above dimension reduction approach that maps the actual feature space from X to H space containing latent scores, next step is to perform model fitting (B) and variable selection procedure to evaluate the parameters in (5).

4.1 Dimensionality Reduction Techniques

For performing the function \(R\) in this work, principal component analysis (PCA) technique and its sparse version are used. PCA is a technique used to transform variables from higher dimensional space into lower dimensional space, where transformed variables are a linear combination of original variables. These new set of transformed variables is called principal components. In this case, new features will be of the form, Hkj = \(\rho_{\text{kj1}} X_{\text{k1}} + \cdots + \rho_{{{\text{kjl}}_{\text{k}} }} X_{{{\text{kl}}_{\text{k}} }}\) for j = 1,…,hk, which also helps in finding the dependencies in terms of the original features. Therefore, each principal component is a weighted average of all variables (e.g., genes) with a weight (called loading coefficient) assigned to each variable. The sparse version will take the loadings of variables that are ineffective in PCA as zero, which in turn helps in the variable selection process.

Various papers [21,22,23,24,25] demonstrate the use of dimensionality reduction techniques in case of datasets with large number of dimensions or features to reduce the number of computations and simplify the handling of data. One such technique is PCA, which is quite commonly used for dimensionality reduction in bioinformatics [12], and it can be implemented using singular value decomposition on matrix Xk for k = 1,…,K, where hk is the rank of the decomposition. It results in orthogonal components that are non-collinear and capture most of the information of original dataset. These principal components are ordered as per the maximum possible variance of the component, with the first having the maximum possible variance and so on. Different methods are available to specify the number of principal components to be retained [26]. In this work, we have used the method of “scree plot test”. The expected pattern in a scree plot includes a steep curve which is followed by a bend and ends with a horizontal line. Those components (or factors) are retained in the steep curve, which are before the first point that starts the flat line trend. The sparse version of PCA has indicated various advantages over traditional PCA in cancer research [27].

4.2 Model Fitting Using Bayesian Model Averaging

Here, the model Eq. (5) will be fitted with the obtained latent feature scores from the dimensionality reduction technique. Bayesian model averaging (BMA) procedure is selected as (B) to be used for the fitting model (5) on latent features. The typical model selection includes selecting a model from a class of models, and then continues as if the selected model had generated the data. But this leads to overconfident decisions and inferences. Compared to these regular modeling methods which overlook model uncertainty, BMA considers uncertainty and makes inferences by averaging over the posterior distributions of a range of possible models, weighted by their posterior model probabilities. This helps in selecting the most appropriate model for a given outcome variable as it has been shown that BMA gives a better predictive performance for new observations than fitting a single assumed to be the best model [28].

The BMA algorithm assigns a posterior probability to each model and for each variable included in a given model, the probability that the coefficient (or parameter value) for a given variable is non-zero is returned. Therefore, either the model with the highest posterior probability can be selected or a model that contains every variable for which the probability that the coefficient is non-zero is above some threshold can be selected. In this work, the model with the highest posterior probability is selected.

4.3 Selection of Significant Variables

Having obtained the model equation, the significant variables are selected from it. A list of significant variables is as follows. Dimensionality reduction technique \(R\) applied on Xk for each k = 1,…,K data type, generates a set of hk latent feature score vectors making Hk matrices, which are linear combinations of the original column vectors \(X_{\text{k1}} , \ldots , X_{{{\text{k}}_{{{\text{l}}_{\text{k}} }} }}\) such that Hkj = \(\rho_{\text{kj1}} X_{\text{k1}} + \cdots + \rho_{{{\text{kjl}}_{\text{k}} }} X_{{{\text{kl}}_{\text{k}} }}\) for j = 1,…,hk. Depending on the contribution of variables in the linear combination, \(R\) assigns higher or lower loading to that variable. The model selection process B results in a set of indices \({\mathcal{L}} \subset \left\{ {\left( {k,j} \right):j = 1, \ldots , h_{k} , k = 1, \ldots , K} \right\}\) such that the set of latent features \({\mathbb{N}} \equiv \left\{ {H_{\text{kj}} :\left( {k,j} \right) \in {\mathcal{L}} } \right\}\) is preserved in the model, where values of \({\mathbb{N}}\) can occur either as main effects or as part of an interaction. Now, the variables \(X_{\text{k1}} , \ldots , X_{{{\text{k}}_{{{\text{l}}_{\text{k}} }} }}\) are ordered as per their contributions. The maximum magnitude of the loadings that are assigned to each variable across all the latent features from group k retained by B is taken as a contribution.

Consider \(\left\{ {x_{\text{k1}}^{2} , \ldots , x_{{k_{{l_{k} }} }}^{2} } \right\}\) be the vector of maximum loading magnitudes arranged in non-increasing order. Now square all the components individually and divide each of them by the sum of these squared components resulting in \(y_{{{\text{k}}_{\text{j}} }} = x_{{{\text{k}}_{\text{j}} }}^{2} /\left( {x_{{{\text{k}}_{ 1} }}^{2} , + \cdots + , x_{{{\text{k}}_{{{\text{l}}_{\text{k}} }} }}^{ 2} } \right)\) for \(j = 1, \ldots , l_{\text{k}}\). Next, consider the variables associated with \(\left( {x_{{k_{1} }}^{2} , \ldots , x_{{{\text{k}}_{{{\text{l}}_{\text{z}} }} }}^{2} } \right)\) to be significant if \(z = \hbox{min} \left\{ {g :y_{{k_{1} }} + \cdots + y_{{k_{z} }} > {\daleth }} \right\},\) for some threshold \({\daleth } \in \left( {0,1} \right)\). If \({\daleth } = 0.8\), the procedure will select variables with squared maximum loading magnitude that constitutes minimum of 80% of the sum of squared maximum loading magnitudes for the variables in that group.

5 Results and Discussion

The present study is motivated by the challenges associated with analyzing the multi-genomic dataset for KIRC, available from TCGA Pan-Cancer Survival Prediction Challenge project. The focus of this study is on integrating gene expression and copy number data from the KIRC study. In this study, the outcome of interest is overall survival time acquired from n = 243 patient samples, where survival time is the time from initial diagnosis to death. The objective is to integrate the data from three genomic data types, such as mRNA, miRNA, and sCNA to predict the patient’s (log-transformed) survival time and to identify genes of biological significance in KIRC.

After removal of zero variance features, along with the survival time, the input data consists of feature matrices for three genomic data types as follows: \(l\)cnv = 69, \(l\)miRNA = 795, and \(l\)mRNA = 20,203, summing up to \(\bar{l}\) = 21,607 features. On application of principal components (PC) and sparse principal components (SPC) on these matrices, each technique selected to keep five sCNA features, six mRNA features, and five miRNA latent features, i.e., \(h\)cnv = 5, \(h\)mRNA = 6, and \(h\)miRNA = 5. Subsequently, these latent features and their interactions are used for fitting the model, wherein the best model is selected using the Bayesian model averaging procedure. The fitted linear regression model [29] is then used to predict the response variable, i.e., survival time for both with and without interaction effects. Thereafter, statistical results for linear regression model are calculated. To choose the best predictive model for latent features with and without the inclusion of interactions, a tenfold cross-validation procedure is used. The procedure splits the data into ten equal-sized parts (folds). Then one part is retained for predicting the response time and remaining nine parts are used for model fitting. This is repeated ten times for each part of the data and the resulting mean squared error of prediction (MSEP) is computed by taking an average of mean squared errors over all the parts. Further an alternative method is taken to test the prediction accuracy of the models. Here, an independent dataset test is performed where the data to be tested are never exposed during the model development process. The dataset is split according to 80/20 rule, i.e., 80% of dataset form the training set and 20% form the test set. The obtained models from BMA (with and without interactions) are first trained and then tested using the corresponding split datasets. Subsequently, the mean square error (MSE) is calculated for measuring the prediction error in the models.

Now, to perform the significant variable selection from the latent features that remain in the model, a threshold of eight is set, such that the energy retained is 80%. Finally, a list of genes obtained from the individual models for PC and SPC with the inclusion of interactions is prepared to check their biological roles.

Implementation of this work is performed in R language. PCA technique is implemented using the singular value decomposition (SVD) algorithm of the standard R package. SPC is implemented using the R language package ‘PMA’ [30], which executes the algorithm described in Witten et al. [30]. BMA is implemented using the R language package BMA [31].

5.1 Experimental Results

The Bayesian model averaging procedure selected regression with high posterior probability, which resulted in the selection of CNV and mRNA interaction as the variable in case of PC. In the case of SPC, CNV miRNA interaction and CNV mRNA interaction as the variables were selected. These equations are given in Table 2.

Table 2 Selected models by principal components and sparse principal components
Full size table

It can be observed that the model obtained from PC is a linear regression model with only one input variable whereas model from SPC is a multiple linear regression model with two input variables, one negatively correlated and one positively correlated. The linear regression statistics obtained for these two models are displayed in Table 3. Table 3 indicates that the standard residual error in PC model is somewhat higher than SPC model. Latent variables selected are also different in both cases. Moreover, higher adjusted R2, multiple R, and R2 values in SPC than in PC show a better model fitting in SPC.

Table 3 Linear regression statistics obtained from principal components and sparse principal components
Full size table

Low R2 values found in both the models indicate the inherent greater amount of unexplainable variation. Still the conclusion can be drawn that when multiple variables are included for a regression model, latent features with interactions have a reliable and statistically significant role in the models and, therefore, leads to better predictive and variable selection results. Additionally, Akaike Information Criterion (AIC) is used to compare both the models. AIC considers both the fitness of the model and the number of parameters used. We obtained AIC values 854 and 860 for SPC and PC models, respectively. A lower AIC value in case of SPC model that contains more parameters indicates a better fit.

The high probability fitted model and corresponding variable(s) selected by BMA for PC and SPC-based latent features are shown in Fig. 2. Each square displays a matrix, in which a variable is denoted by each row, and selected model in the BMA exploration is denoted by each column. The selected models are sorted in non-increasing order from left to right as per their posterior probabilities. The rectangle in the matrix is red if the variable is present in the model and white otherwise. The model’s posterior probability is relative to the thickness of each column. The plots make it easy to see the variables picked by the most probable models in BMA. The continuous horizontal bands show the consistency and convergence of model selection, representing that a variable appears regularly in the BMA exploration. It can be seen in Fig. 2 that under PC decomposition, only one interaction between CNV and mRNA represented by label CN.P3 × mR.P3 is selected and it is present consistently in the selected models, signifying that it is selected as a result of convergence. However, for SPC decomposition, two interactions, one between CNV and mRNA, and one between CNV and miRNA are selected, represented by labels CN.SP5 × mR.SP6 and CN.SP2 × miR.SP2, respectively. It can be noted that the first interaction is negatively associated while second is positively associated with the outcomes, and both appear consistently in the selected models. If only mRNA and CNV data types would have been considered for regression, then we would have 20,203 + 69 + 20,272(20,271)/2 = 205,497,264 independent variables in the regression model, which is computationally impractical. This makes the proposed method advantageous and efficient to deal with interactions.

Fig. 2
figure 2figure 2

a and b: Variables with continuous horizontal bands are selected for our models as these are included regularly in BMA exploration models, sorted in non-increasing order from left to right as per their posterior probabilities. Numbers following data type names (CN copy number, mR mRNA, miR = miRNA) list the latent features with interaction effects for principal components (PC) and sparse principal components (SPC)

Full size image

Figure 3 shows the boxplots indicating (with filled circles and in text) the MSEP achieved by tenfold cross validation, performed on PC and SPC models with and without the inclusion of interaction effects. It can be observed that in the case of PC model, when including the interaction terms MSEP was higher, as compared to PC model without interaction terms. However, MSEP is lower in the case of SPC model that includes interaction terms as compared to without interaction terms.

Fig. 3
figure 3

Boxplots of mean squared error prediction resulted from tenfold cross validation for the proposed method in case of SPC- and PC-based dimensionality reduction models with and without the inclusion of latent feature interactions. Obtained MSEP is shown above each box

Full size image

In the case of train/test split, datasets are split as per 80/20 rule. Out of total 243 observations, 194 were retained as training dataset and 49 as testing dataset. Table 4 shows the MSE values obtained from the PC and SPC models with and without interactions. Better fitting and prediction accuracy in PC models are observed.

Table 4 MSE values achieved in case of 80/20 split test for PC and SPC based models with and without interactions
Full size table

Plots of variable selection procedure conducted for the SPC model are shown in Fig. 4a–d. It illustrates sorted loading magnitudes for the 69 copy number alterations, 795 miRNA expression levels, and 20,203 mRNA expression levels, for the terms or components obtained from the selected linear model. Filled circles in blue correspond to the selected variables on the application of variable selection for each term at the threshold level of \({\daleth } =\) 0.8, while black ones are not selected.

Fig. 4
figure 4

Plots of variable selection conducted for SPC model

Full size image

The list of all the selected features obtained from PC and SPC model and the model equations for these models with and without the inclusion of interaction effects can be found in Supplementary file 1.

5.2 Biological Significance

From the variable selection process, a list of genes (for probes associated with expression and copy number) is prepared together with miRNAs for the PC and SPC models. This list is used to find the genes of biological significance by referring the published work. A majority of the selected variables are found to be associated with the KIRC cancer.

Inactivation of the Von Hippel-Lindau (VHL) tumor suppressor gene has been found to be responsible for the majority of ccRCC cases [32] and the proposed method has identified VHLL (Von Hippel-Lindau Tumor Suppressor Like) gene from the PC model. Additionally, the proposed method has identified significantly mutated genes from the models that are associated with the pathogenesis of ccRCC. It is evident from the findings of genes such as BAP1, SETD2, TCEB1, TET2 in mRNA variable analysis, which are reported in [6] as significant mutations in ccRCC.

Further, various new genes such as ACHANK, CUL7, MLL2 that are reported in [10] that have played a potential role in renal cell tumorigenesis, are identified by the models. The miRNAs variable selected by SPC model discovered miR-21 and miR-10b, which are stated in [18] to have strong regulatory interactions with ccRCC. Alterations of chromosomal regions in ccRCC have resulted in new candidate tumor suppressor genes (TSGs) and oncogenes. The proposed model identified copy number alteration (or CNV) at 1q24.1 that is reported in [32] as a potential risk factor for RCC. Other significant regions that were stated for ccRCC in [18] are at 3p25.3, 6q26, 9p23 for oncogenes VHL, QKI, and PTPRD, respectively. Supplementary file 2 lists all the significant markers based on the cited literature that are found from both the models.

5.3 Discussion

The present study is motivated by TCGA pan-cancer survival prediction project [19] that provides open access to well curated, computable datasets to analyze TCGA data for improving prognostic models. Unlike other such community-based project [33] that mainly deals with a specific type of cancer and data, the above project is chosen as it includes different types of cancer and their molecular data types from TCGA.

We have proposed a method for integrative analysis of different genomic data types available for KIRC dataset from the Pan-Cancer Survival Prediction project. The method incorporates interactions within and between these data types to build the model that predicts survival time of patients and identify significant tumor biomarkers. The model has the ability to simultaneously model all type of relations in the data in a single model and may be used for clinical diagnosis in future with further improvement in accuracy.

For a fair comparison with a work which employs similar predictive evaluation metric to measure the performance of linear regression-based survival model, we used the latent feature decomposition (LFD) study [11] applied on glioblastoma multiforme (GBM) dataset.

The LFD study integrated the data from four genomic platforms—mRNA, miRNA, DNA methylation, and CNV. It used several dimensionality reduction techniques to build the survival model and reported principal components and sparse principal components techniques to achieve the best results.

In case of both PC and SPC-based model in LFD, obtained mean squared error of prediction with interactions is 1.20. This seems to suggest that model fitting is better in LFD than the model used in this study. However, the proposed model brings new insights with reliable accuracy and variable selection into the integrative study based on KIRC.

Some of the limitations in the integrative study involve time intensive calculations for large-scale datasets while modeling interactions. Therefore, above discussion suggests that there is a plenty of room for methodological improvements in the study by incorporating more data types, other dimensionality reduction techniques and/or model selection criteria.

6 Conclusion and Future Work

In this paper, high-dimensional genomic (sCNAs) and transcriptomic (mRNA and miRNA) data from TCGA KIRC dataset are integrated, to predict survivals and identify significant genes whose expression levels affect the clinical outcome. Incorporating interactions among different genomic data types and using the dimensionality reduction techniques helps not only to reduce the large computations but also leads to an effective way of making predictions and identifying significant variables from the original featured dataset. The proposed method used two-dimension reduction techniques, PCA and SPCA to generate the latent features that were used to build the predictive models and carry out the variable selection. Among the methods, SPCA with a lower MSEP of 2.07 than MSEP of 2.11 with PCA performs better for the prediction on including interactions. However, both the models help in achieving improved and convenient model fitting in the BMA procedure with lesser computations and also included interaction effects for identifying potential markers in the integrative study of KIRC dataset. As future work, the proposed method can be extended to include more biological data types like DNA methylation and their interactions that may improve the predictive power of the model. In addition, we are planning to use other dimensionality reduction techniques that may lower the prediction error and lead to more sophisticated modeling for the proposed method.