An active set algorithm for robust combinatorial optimization based on separation oracles

Abstract

We address combinatorial optimization problems with uncertain coefficients varying over ellipsoidal uncertainty sets. The robust counterpart of such a problem can be rewritten as a second-oder cone program (SOCP) with integrality constraints. We propose a branch-and-bound algorithm where dual bounds are computed by means of an active set algorithm. The latter is applied to the Lagrangian dual of the continuous relaxation, where the feasible set of the combinatorial problem is supposed to be given by a separation oracle. The method benefits from the closed form solution of the active set subproblems and from a smart update of pseudo-inverse matrices. We present numerical experiments on randomly generated instances and on instances from different combinatorial problems, including the shortest path and the traveling salesman problem, showing that our new algorithm consistently outperforms the state-of-the art mixed-integer SOCP solver of Gurobi.

1 Introduction

We address combinatorial optimization problems given in the general form

$$\begin{aligned} \min _{x\in P\cap {\mathbb {Z}}^n}\; c^\top x \end{aligned}$$

(CP)

where $P\subseteq {\mathbb {R}}^n$ is a compact convex set, say $P\subseteq [l,u]$ with $l,u\in {\mathbb {R}}^n$, and the objective function vector $c\in {\mathbb {R}}^n$ is assumed to be uncertain. This setting appears in many applications where the feasible set is certain, but the objective function coefficients may have to be estimated or result from imprecise measurements. As an example, when searching for a shortest path in a road network, the topology of the network is usually considered fixed, but the travel times may vary depending on the traffic conditions.

A classical way of dealing with uncertain optimization problems is the strictly robust optimization approach, introduced in [3] for linear programming and in [2] for general convex programming; we also refer the reader to the book by Ben-Tal and Nemirovski [4]. In strictly robust optimization, we look for a worst-case solution, where the uncertain parameter c is assumed to belong to a bounded set $U\subseteq {\mathbb {R}}^{n}$, called the uncertainty set, and the goal of the robust counterpart is to compute the solution of the following min-max problem:

$$\begin{aligned} \min _{x\in P\cap {\mathbb {Z}}^n}\;\max _{c\in U}\; c^\top x \end{aligned}$$

(RP)

A natural choice in this approach are ellipsoidal uncertainty sets, defined as

$$\begin{aligned} U = \left\{ c\in {\mathbb {R}}^n \mid (c-{{\bar{c}}})^\top M (c-{{\bar{c}}})\le 1\right\} , \end{aligned}$$

where $M\in {\mathbb {R}}^{n\times n}$ is a symmetric positive definite matrix and ${{\bar{c}}}\in {\mathbb {R}}^n$ is the center of the ellipsoid. Assuming that the uncertain vector c in (CP), considered as a random variable, follows a normal distribution, we can interpret the ellipsoid U as a confidence set of c; in this case, M is the inverse covariance matrix of c and ${{\bar{c}}}$ is its expected value. Unfortunately, for ellipsoidal uncertainty sets, the robust counterpart (RP) is usually much harder to solve than the original problem (CP): it is known that Problem (RP) is NP-hard in this case for the shortest path problem, for the minimum spanning tree problem, and for the assignment problem [11] as well as for the unconstrained binary optimization problem [6].

Even in the case of a diagonal matrix M, i.e., when ignoring correlations and only taking variances into account, no polynomial time algorithm for the robust shortest path problem is known. There exists however an FPTAS for the diagonal case whenever the underlying problem (CP) admits an FPTAS [17], and polynomial time algorithms for the minimum spanning tree problem and the unconstrained binary problem have been devised for the diagonal case.

For general ellipsoids U, most exact solution approaches for (RP) are based on solving SOCPs. In fact, it is easy to see that the optimal objective value of the inner maximization problem

$$\begin{aligned} \max _{c\in U}\; c^\top x \end{aligned}$$

for fixed x is given by

$$\begin{aligned} {{{\bar{c}}}}^\top x + \sqrt{x^\top M^{-1} x}. \end{aligned}$$

Therefore, Problem (RP) is equivalent to the integer non-linear problem

$$\begin{aligned} \begin{array}{l l} \min &{} f (x) = c^{\top }x+\sqrt{x^{\top }Qx}\\ \text { s.t. }&{} x \in P\cap {\mathbb {Z}}^n \end{array} \end{aligned}$$

(P)

where $Q\in {\mathbb {R}}^{n\times n}$ is the symmetric and positive definite inverse of M and we replace ${\bar{c}}$ by c for ease of notation. Note that, when addressing so called value-at-risk models

$$\begin{aligned} \begin{array}{ll} \min &{} z \\ \text { s.t.} &{} \text {Pr}(c^\top x\ge z)\le \varepsilon \\ &{} x\in P\cap {\mathbb {Z}}^n, \end{array} \end{aligned}$$

we arrive at essentially the same formulation (P), assuming normally distributed coefficients again; see, e.g., [17].

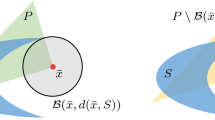
In the following, we assume that the convex set P is given by a separation algorithm, i.e., an algorithm that decides whether a given point ${\bar{x}}\in {\mathbb {R}}^n$ belongs to P or not, and, in the negative case, provides an inequality $a^\top x\le b$ valid for P but violated by ${\bar{x}}$. Even in cases where the underlying problem (CP) is tractable, the polytope ${\text {conv}}(P\cap {\mathbb {Z}}^n)$ may have an exponential number of facets, so that a full linear description cannot be used efficiently. This is true, e.g., for the standard formulation of the spanning tree problem. However, we do not require that a complete linear description of ${\text {conv}}(P\cap {\mathbb {Z}}^n)$ be known; it suffices to have an integer linear description, i.e., we allow $P\ne {\text {conv}}(P\cap {\mathbb {Z}}^n)$. In particular, our approach can also be applied when the underlying problem is NP-hard, e.g., when (CP) models the traveling salesman problem.

As soon as P is given explicitly by linear constraints $Ax\le b$ with $A\in {\mathbb {R}}^{m\times n}$ and $b\in {\mathbb {R}}^m$, the continuous relaxation of Problem (P) reduces to an SOCP of the form

$$\begin{aligned} \begin{array}{l l} \min &{} c^{\top }x+\sqrt{x^{\top }Qx}\\ \text { s.t. }&{} Ax \le b\\ &{} x\in {\mathbb {R}}^n. \end{array} \end{aligned}$$

(R2)

Such SOCPs can be solved efficiently using interior point algorithms [16] and popular solvers for SOCPs such as Gurobi [10], SeDuMi [19] or MOSEK [15] are based on interior point methods. However, in our branch-and-bound algorithm, we need to address a sequence of related SOCPs. Compared with interior point methods, active set methods have the advantage to allow warmstarts.

For this reason, in order to solve the SOCP relaxations of Problem (RP), we devised the active set algorithm EllAS. It is applied to the Lagrangian dual of (R2) and exploits the fact that the active set subproblems can be solved by closed form expressions. For this, the main ingredient is the pseudo-inverse of $AQ^{-\frac{1}{2}}$. Since the matrix A is updated in each iteration of the active set method, an incremental update of the pseudo-inverse is crucial for the running time of EllAS. Altogether, we can achieve a running time of $O(n^2)$ per iteration. Combined with an intelligent embedding into the branch-and-bound scheme, we obtain an algorithm that consistently outperforms the MISOCP solver of Gurobi 7.5.1, where the latter is either applied to a full linear description of P or, in case a compact linear description does not exist, uses the same separation oracle as EllAS.

The rest of the paper is organized as follows: the Lagrangian dual of (R2) is derived in Sect. 2. The closed-form solution of the resulting active set subproblems is developed in Sect. 3. The active set algorithm EllAS is detailed and analyzed in Sects. 4 and 5. In Sect. 6, we discuss how to embed EllAS into a branch-and-bound algorithm. Numerical results for random SOCP instances, random integer instances as well as instances of different combinatorial optimization problems are reported in Sect. 7. Section 8 concludes.

2 Dual problem

The algorithm we propose for solving Problem (RP) uses the Lagrangian dual of relaxations of the form (R2). Let $\mathscr {L}(x,\lambda ) : {\mathbb {R}}^n\times {\mathbb {R}}^m \rightarrow {\mathbb {R}}$ be the Lagrangian function associated to (R2):

$$\begin{aligned} \mathscr {L}(x,\lambda ) = c^\top x+\sqrt{x^{\top }Q x} + \lambda ^\top (Ax-b). \end{aligned}$$

The Lagrangian dual of Problem (R2) is then

$$\begin{aligned} \max _{\lambda \in {\mathbb {R}}^m_+} ~ \inf _{x\in {\mathbb {R}}^n} ~ \mathscr {L}(x,\lambda ). \end{aligned}$$

(1)

After applying the bijective transformation $z=Q^{\frac{1}{2}}x$, the inner minimization problem of (1) becomes

$$\begin{aligned} -b^\top \lambda + \inf _{z\in {\mathbb {R}}^n} \left( Q^{-\frac{1}{2}}\left( c+A^\top \lambda \right) \right) ^\top z + \Vert z\Vert \end{aligned}$$

for fixed $\lambda \in {\mathbb {R}}^m_+$. It is easy to see that

$$\begin{aligned} \inf _{z\in {\mathbb {R}}^n} \left( Q^{-\frac{1}{2}}\left( c+A^\top \lambda \right) \right) ^\top z + \Vert z\Vert = \min _{z\in {\mathbb {R}}^n} \left( Q^{-\frac{1}{2}}\left( c+A^\top \lambda \right) \right) ^\top z + \Vert z\Vert = 0 \end{aligned}$$

if $\Vert Q^{-\frac{1}{2}}(c + A^\top \lambda )\Vert \le 1$ and $-\infty$ otherwise. Therefore, Problem (1) reduces to

$$\begin{aligned} \begin{array}{l l} \max &{} -b^\top \lambda \\ \text { s.t. } &{} \left( c + A^\top \lambda \right) ^\top Q^{-1} \left( c+A^\top \lambda \right) \le 1\\ &{}\lambda \ge 0. \end{array} \end{aligned}$$

(D)

Theorem 1

For the primal-dual pair of optimization problems (R2) and (D), strong duality holds as soon as one of the two problems is feasible. Moreover, if one of the problems admits an optimal solution, the same holds for the other problem.

Proof

This follows from the convexity of (R2) and from the fact that all constraints in (R2) are affine linear. $\square$

In order to solve Problem (R2), we have devised the dual active set algorithm EllAS detailed in Sect. 4. Along its iterations, EllAS produces dual feasible solutions of Problem (D), converging to a KKT point of Problem (R2) and therefore producing also a primal optimal solution when terminating.

3 Solving the active set subproblem

At every iteration, the active set algorithm EllAS presented in the subsequent sections fixes certain dual variables to zero while leaving unconstrained the remaining variables. In the primal problem, this corresponds to choosing a set of valid linear constraints $Ax\le b$ for P and replacing inequalities by equations. We thus need to solve primal-dual pairs of problems of the following type:

$$\begin{aligned} \min ~~&f(x) = c^{\top }x+\sqrt{x^{\top }Qx}\\ \text {s.t.}~~&{\hat{A}}x = {\hat{b}}\\&x\in {\mathbb {R}}^n\; \end{aligned}$$

(P-AS)

$$\begin{aligned} \max ~&-{\hat{b}}^\top \lambda \\ \text {s.t.}~~&\left( c + {\hat{A}}^\top \lambda \right) ^\top Q^{-1} \left( c+{\hat{A}}^\top \lambda \right) \le 1\\&\lambda \in {\mathbb {R}}^{{\hat{m}}} \end{aligned}$$

(D-AS)

where ${\hat{A}}\in {\mathbb {R}}^{{\hat{m}}\times n}$, $b\in {\mathbb {R}}^{{\hat{m}}}$. For the efficiency of our algorithm, it is crucial that this pair of problems can be solved in closed form. For this, the pseudo-inverse $({\hat{A}}Q^{-\frac{1}{2}})^+$ of ${\hat{A}}Q^{-\frac{1}{2}}$ will play an important role. It can be used to compute orthogonal projections onto the kernel and onto the range of $Q^{-\frac{1}{2}}{\hat{A}}^\top$ as follows: we have

$$\begin{aligned} \text {proj}_{\mathrm{ker}\left( {Q^{-\frac{1}{2}}{\hat{A}}^\top }\right) }(y) = y-{\hat{A}}Q^{-\frac{1}{2}}\left( {\hat{A}}Q^{-\frac{1}{2}}\right) ^+y \end{aligned}$$

(2)

and

$$\begin{aligned} \text {proj}_{\mathrm{ran}\left( {Q^{-\frac{1}{2}}{\hat{A}}^\top }\right) }(y) = \left( {\hat{A}}Q^{-\frac{1}{2}}\right) ^+{\hat{A}}Q^{-\frac{1}{2}}y, \end{aligned}$$

(3)

see e.g. [13]. We later explain how to update the pseudo-inverse incrementally instead of computing it from scratch in every iteration, which would take $O(n^3)$ time; see Sect. 5.2.

In the following, we assume that the dual problem (D-AS) admits a feasible solution; this will be guaranteed in every iteration of our algorithm; see Lemma 1 below.

3.1 Dual unbounded case

If ${\hat{b}}\not \in {\text {ran}}({\hat{A}})$, or equivalently, if ${\hat{b}}$ is not orthogonal to ${\text {ker}}({\hat{A}}^\top )={\text {ker}}(Q^{-\frac{1}{2}}{\hat{A}}^\top )$, then the dual problem (D-AS) is unbounded, and the corresponding primal problem (P-AS) is infeasible. When this case occurs, EllAS uses an unbounded direction of (D-AS) to continue. The set of unbounded directions of (D-AS) is ${\text {ker}}(Q^{-\frac{1}{2}}{\hat{A}}^\top )$. Consequently, the unbounded direction with steepest ascent can be obtained by projecting the gradient of the objective function $-{\hat{b}}$ to ${\text {ker}}(Q^{-\frac{1}{2}}{\hat{A}}^\top )$. According to (2), this projection is

$$\begin{aligned} \text {proj}_{\mathrm{ker}\left( {Q^{-\frac{1}{2}}{\hat{A}}^\top }\right) }(-{\hat{b}}) = \left( {\hat{A}}Q^{-\frac{1}{2}}\right) \left( {\hat{A}}Q^{-\frac{1}{2}}\right) ^+{\hat{b}}-{\hat{b}}. \end{aligned}$$

3.2 Bounded case

If ${\hat{b}}\in {\text {ran}}({{\hat{A}}})$, we first consider the special case $\hat{b}=0$. As we assume (D-AS) to be feasible, its optimum value is thus 0. Therefore, the corresponding primal problem (P-AS) admits $x^* = 0$ as optimal solution. In the following, we may thus assume ${\hat{b}} \ne 0$. The feasible set of problem (D-AS) consists of all $\lambda \in {\mathbb {R}}^{{\hat{m}}}$ such that

$$\begin{aligned} \left\| Q^{-\frac{1}{2}} \left( c+{\hat{A}}^\top \lambda \right) \right\| \le 1, \end{aligned}$$

i.e., such that the image of $\lambda$ under $-Q^{-\frac{1}{2}}{\hat{A}}^\top$ belongs to the ball $B_1(Q^{-\frac{1}{2}}c)$. Consider the orthogonal projection of $Q^{-\frac{1}{2}}c$ to the subspace ${\text {ran}}(Q^{-\frac{1}{2}}{\hat{A}}^\top )$, which by (3) is

$$\begin{aligned} q:=\text {proj}_{\mathrm{ran}\left( {Q^{-\frac{1}{2}}{\hat{A}}^\top }\right) }\left( Q^{-\frac{1}{2}}c\right) =\left( Q^{-\frac{1}{2}}{\hat{A}}^\top \right) \left( Q^{-\frac{1}{2}}{\hat{A}}^\top \right) ^+ Q^{-\frac{1}{2}}c. \end{aligned}$$

If $||q-Q^{-\frac{1}{2}}c||>1$, then the intersection $B_1(Q^{-\frac{1}{2}}c)\cap {\text {ran}}(Q^{-\frac{1}{2}}{\hat{A}}^\top )$ is empty, so that Problem (D-AS) is infeasible, contradicting our assumption. Hence, we have that this intersection is a ball with center q and radius

$$\begin{aligned} r:=\sqrt{1-||q-Q^{-\frac{1}{2}}c||^2} \end{aligned}$$

and $\lambda \in {\mathbb {R}}^{{\hat{m}}}$ is feasible for (D-AS) if and only if $-Q^{-\frac{1}{2}}{\hat{A}}^\top \lambda \in B_r(q)$. Since ${\hat{b}}\in {\text {ran}}({\hat{A}}Q^{-\frac{1}{2}})$, we have $({\hat{A}}Q^{-\frac{1}{2}})({\hat{A}}Q^{-\frac{1}{2}})^+{\hat{b}}={\hat{b}}$. This allows us to rewrite the objective function $-{\hat{b}}^\top \lambda$ of (D-AS) in terms of $Q^{-\frac{1}{2}}{\hat{A}}^\top \lambda$ only, as

$$\begin{aligned} -\,{\hat{b}}^\top \lambda =-\,{\hat{b}}^\top \left( Q^{-\frac{1}{2}}{\hat{A}}^\top \right) ^+ \left( Q^{-\frac{1}{2}}{\hat{A}}^\top \right) \lambda . \end{aligned}$$

We can thus first compute the optimal solution $v^*\in {\text {ran}}(Q^{-\frac{1}{2}}{\hat{A}}^\top )$ of

$$\begin{aligned} \begin{array}{l l} \max &{} \; {\hat{b}}^\top \left( Q^{-\frac{1}{2}}{\hat{A}}^\top \right) ^+ v\\ \text { s.t.} &{} \; ||Q^{-\frac{1}{2}}c-v||\le 1, \end{array} \end{aligned}$$

which is unique since ${\hat{b}}\ne 0$, and then solve $v^*=-(Q^{-\frac{1}{2}}{\hat{A}}^\top )\lambda$. We obtain

$$\begin{aligned} v^*=q+\frac{r}{||\left( {\hat{A}}Q^{-\frac{1}{2}}\right) ^+{\hat{b}}||}\left( {\hat{A}}Q^{-\frac{1}{2}}\right) ^+{\hat{b}}, \end{aligned}$$

(4)

so that we can state the following

Proposition 1

Let ${\hat{b}}\in {\text {ran}}({\hat{A}}){\setminus }\{0\}$ and let $v^*$ be defined as in (4). Then, the unique optimal solution of (D-AS) with minimal norm is

$$\begin{aligned} \lambda ^*:=-\left( Q^{-\frac{1}{2}}{\hat{A}}^\top \right) ^+v^*. \end{aligned}$$

From $\lambda ^*$, it is possible to compute an optimal solution $x^*$ of the primal problem (P-AS) as explained in the following result.

Theorem 2

Let ${\hat{b}}\in {\text {ran}}({\hat{A}}){\setminus }\{0\}$. Let $\lambda ^*$ be an optimal solution of (D-AS) and $\bar{x}:=Q^{-1}(c+{\hat{A}}^\top \lambda ^*)$.

• (a) If ${\hat{b}}^\top \lambda ^*\ne 0$, then the unique optimal solution of (P-AS) is $x^*=\alpha {\bar{x}}$, with

  $$\begin{aligned} \alpha :=-\frac{{\hat{b}}^\top \lambda ^*}{c^\top {\bar{x}} -\sqrt{{\bar{x}}^\top Q{\bar{x}}}}. \end{aligned}$$

• (b) Otherwise, there exists a unique $\alpha < 0$ such that $\alpha {\hat{A}} {\bar{x}} = {\hat{b}}$. Then, $x^* = \alpha {\bar{x}}$ is the unique optimal solution of (P-AS).

Proof

Let $(x^*,\lambda ^*)$ be a primal-dual optimal pair for (P-AS) and (D-AS), which exists by the same reasoning as in the proof of Theorem 1. Since ${\hat{b}}\ne 0$ and ${\hat{A}} x^* = {\hat{b}}$, it follows that $x^*\ne 0$. The gradient equation yields

$$\begin{aligned} 0=\nabla _x \mathscr {L}(x^*,\lambda ^*) = c+\frac{2Qx^*}{2\sqrt{(x^*)^{\top }Q (x^*)}} +{\hat{A}}^\top \lambda ^* \end{aligned}$$

which is equivalent to

$$\begin{aligned} \frac{Q^{\frac{1}{2}}x^*}{\Vert Q^{\frac{1}{2}}x^*\Vert }=-Q^{-\frac{1}{2}}\left( c+{\hat{A}}^\top \lambda ^*\right) \end{aligned}$$

and hence to

$$\begin{aligned} x^*=\beta Q^{-1}\left( c+{\hat{A}}^\top \lambda ^*\right) =\beta {\bar{x}} \end{aligned}$$

for some $\beta \ne 0$. Since $\beta =-\Vert Q^{\frac{1}{2}}x^*\Vert$, we have $\beta <0$. By strong duality, we then obtain

$$\begin{aligned} -\,{\hat{b}}^\top \lambda ^*=c^\top x^*+\sqrt{(x^*)^\top Q(x^*)}=\beta c^\top {\bar{x}}+|\beta |\sqrt{{\bar{x}}^\top Q{\bar{x}}} =\beta \big (c^\top {\bar{x}}-\sqrt{{\bar{x}}^\top Q\bar{x}}\big ). \end{aligned}$$

Now if ${\hat{b}}^\top \lambda ^*\ne 0$, also the right hand side of this equation is non-zero, and we obtain $\beta$ as claimed. Otherwise, it still holds that there exists $\beta <0$ such that $\beta {\bar{x}}$ is optimal. In particular, $\beta {\bar{x}}$ is primal feasible and hence $\beta {\hat{A}} {\bar{x}} = {\hat{A}}(\beta {\bar{x}}) = {\hat{b}}$. As ${\hat{b}}\ne 0$, we derive ${\hat{A}} {\bar{x}} \ne 0$, as $\beta <0$. This in particular shows that $\beta$ is uniquely defined by $\beta {\hat{A}} {\bar{x}} = {\hat{b}}$. $\square$

Note that the proof (and hence the statement) for case (b) in Theorem 2 are formally applicable also in case (a). However, in the much more relevant case (a), we are able to derive a closed formula for $\beta$ in a more direct way.

4 The dual active set method EllAS

As all active set methods, our algorithm EllAS tries to forecast the set of constraints that are active at the optimal solution of the primal-dual pair (R2) and (D), adapting this forecast iteratively: starting from a subset of primal constraints $A^{(1)}x\le b^{(1)}$, where $A^{(1)}\in {\mathbb {R}}^{m^{(1)}\times n}$ and $b^{(1)}\in {\mathbb {R}}^{m^{(1)}}$, one constraint is removed or added per iteration by performing a dual or a primal step; see Algorithm 1. We assume that a corresponding dual feasible solutions $\lambda ^{(1)}\ge 0$ is given when starting the algorithm; we explain below how to obtain this initial solution.

At every iteration k, in order to decide whether to perform the primal or the dual step, the dual subproblem is addressed, namely Problem (D) where only the subset of active constraints is taken into account. This leads to the following problem:

$$\begin{aligned} \begin{array}{l l} \max &{} -{b^{(k)}}^\top \lambda \\ \text { s.t. } &{} \left( c + {A^{(k)}}^\top \lambda \right) ^\top Q^{-1} \left( c+{A^{(k)}}^\top \lambda \right) \le 1\\ &{} \lambda \in {\mathbb {R}}^{m^{(k)}}. \end{array} \end{aligned}$$

(D-ASk)

The solution of Problem (D-ASk) has been explained in Sect. 3. Note that formally Problem (D-ASk) is defined in a smaller space with respect to Problem (D), but its solutions can also be considered as elements of ${\mathbb {R}}^m$ by setting the remaining variables to zero.

In case the dual step is performed, the solution of Problem (D-ASk) gives an ascent direction $p^{(k)}$ along which we move in order to produce a new dual feasible point with better objective function value. We set

$$\begin{aligned} \lambda ^{(k)} = \lambda ^{(k-1)} + \alpha ^{(k)} p^{(k)}, \end{aligned}$$

where the steplength $\alpha ^{(k)}$ is chosen to be the largest value for which non-negativity is maintained at all entries. Note that the feasibility with respect to the ellipsoidal constraint in (D), i.e.,

$$\begin{aligned} \left( c + A^\top \lambda \right) ^\top Q^{-1} \left( c+A^\top \lambda \right) \le 1, \end{aligned}$$

is guaranteed from how $p^k$ is computed, using convexity. Therefore, $\alpha ^{(k)}$ can be derived by considering the negative entries of $p^{(k)}$. In order to maximize the increase of $-b^\top \lambda$, we ask $\alpha ^{(k)}$ to be as large as possible subject to maintaining non-negativity; see Steps 9–10 in Algorithm 2.

The constraint index j computed in Step 9 of Algorithm 2 corresponds to the primal constraint that needs to be released from the active set. The new iterate $\lambda ^{(k+1)}$ is then obtained from $\lambda ^{(k)}$, by dropping the jth entry.

Proposition 2

The set considered in Step 9 of Algorithm 2 is non-empty.

Proof

If Problem (D-ASk) is bounded, there is an index i such that ${\tilde{\lambda }}^{(k)}_i<0$, since ${\tilde{\lambda }}^{(k)}$ is dual infeasible. As $\lambda ^{(k-1)}\ge 0$, we derive $p^{(k)}_i = {\tilde{\lambda }}^{(k)}_i - \lambda ^{(k-1)}_i < 0$. If Problem (D-ASk) is unbounded, we explicitly check whether $p^{(k)}\ge 0$ and only continue otherwise. $\square$

The primal step is performed in case the solution of Problem (D-ASk) gives us a dual feasible solution. Starting from this dual feasible solution, we compute a corresponding primal solution $x^{(k)}$ according to the formula in Theorem 2. If $x^{(k)}$ belongs to P we are done: we have that $(x^{(k)}, \lambda ^{(k)})$ is a KKT point of Problem (R2) and, by convexity of Problem (R2), $x^{(k)}$ is its global optimum. Otherwise, we compute a cutting plane violated by $x^{(k)}$ that can be considered active and will be then taken into account in defining the dual subproblem (D-ASk) at the next iteration. The new iterate $\lambda ^{(k+1)}$ is obtained from $\lambda ^{(k)}$ by adding an entry to $\lambda ^{(k)}$ and setting this additional entry to zero.

Theorem 3

Whenever Algorithm EllAS terminates, the result is correct.

Proof

If Algorithm EllAS stops at the primal step, the optimality of the resulting primal-dual pair follows from the discussion in Sect. 3. If Algorithm EllAS stops at the dual step, it means that the ascent direction $p^{(k)}$ computed is a feasible unbounded direction for Problem (D), so that Problem (D) is unbounded and hence Problem (R2) is infeasible. $\square$

It remains to describe how to initialize EllAS. For this, we use the assumption of boundedness of P and construct $A^{(1)}$, $b^{(1)}$, and $\lambda ^{(1)}$ as follows: for each $i=1,\dots ,n$, we add the constraint $x_i\le u_i$ if $c_i<0$, with corresponding $\lambda _i:=-c_i$, and the constraint $-x_i\le -l_i$ otherwise, with $\lambda _i:=c_i$. These constraints are valid since we assumed $P\subseteq [l,u]$ and it is easy to check that $(A^{(1)})^\top \lambda ^{(1)}=-c$ by construction, so that $\lambda ^{(1)}$ is dual feasible for (D). Moreover, we can easily compute $(A^{(1)}Q^{-\frac{1}{2}})^+$ in this case, as $A^{(1)}$ is a diagonal matrix with $\pm 1$ entries: this implies $(A^{(1)}Q^{-\frac{1}{2}})^+=Q^{\frac{1}{2}}A^{(1)}$.

To conclude this section, we shortly discuss how to deal with linear equations in EllAS. While it is perfectly feasible to replace each equation by two linear inequalities and then apply the algorithm exactly as described above, its performance can be improved by dealing with equations directly. For an equation, the corresponding dual variable in (D) is not restricted to be non-negative any more. In particular, in Step 9 of Algorithm 2 we only need to take the minimum over those indices corresponding to bounded variables. In other words, dual variables corresponding to equations will never leave the active set again, so that the presence of equations does not significantly increase the number of active set iterations.

5 Analysis of the algorithm

In this section, we show that Algorithm EllAS converges in a finite number of steps if cycling is avoided. Moreover, we prove that the running time per iteration can be bounded by $O(n^2)$, if implemented properly.

5.1 Convergence analysis

Our convergence analysis follows similar arguments to those used in [18] for the analysis of primal active set methods for strictly convex quadratic programming problems. In particular, as in [18], we assume that we can always take a nonzero steplength along the ascent direction. Under this assumption we will show that Algorithm EllAS does not undergo cycling, or, in other words, this assumption prevents from having $\lambda ^{(k)} = \lambda ^{(l)}$ and $(A^{(k)}, b^{(k)}) = (A^{(l)}, b^{(l)})$ in two different iterations k and l. As for other active set methods, it is very unlikely in practice to encounter a zero steplength. However, there are techniques to avoid cycling even theoretically, such as perturbation or lexicographic pivoting rules in Step 9 of Algorithm 2.

Lemma 1

At every iteration k of Algorithm EllAS, Problem (D-ASk) admits a feasible solution.

Proof

It suffices to show that the ellipsoidal constraint

$$\begin{aligned} \left( c + {A^{(k)}}^\top \lambda ^{(k)}\right) ^\top Q^{-1} \left( c+{A^{(k)}}^\top \lambda ^{(k)}\right) \le 1 \end{aligned}$$

(5)

is satisfied for each k. For $k=1$, this is explicitely required for the input of Algorithm EllAS. Let $\lambda ^{(k)}$ be computed from $\lambda ^{(k-1)}$ by moving along the direction $p^{(k)}$. The feasibility of $\lambda ^{(k)}$ with respect to (5) then follows from the definition of $p^{(k)}$ and from the convexity of the ellipsoid, taking into account that $\alpha \le 1$, since otherwise we would not enter the dual step. $\square$

Proposition 3

At every iteration k of Algorithm EllAS, the vector $\lambda ^{(k)}$ is feasible for (D).

Proof

Taking into account the proof of Lemma 1, it remains to show nonnegativity of $\lambda ^{(k)}$, which is guaranteed by the choice of the steplength $\alpha ^{(k)}$. $\square$

Proposition 4

Assume that the steplength $\alpha ^k$ is always non-zero in the dual step. If Algorithm EllAS does not stop at iteration k, then one of the following holds:

• (i) $-{b^{(k+1)}}^\top \lambda ^{(k+1)}> -{b^{(k)}}^\top \lambda ^{(k)}$;

• (ii) $-{b^{(k+1)}}^\top \lambda ^{(k+1)}= -{b^{(k)}}^\top \lambda ^{(k)}$ and $\Vert \lambda ^{(k+1)}\Vert <\Vert \lambda ^{(k)}\Vert$.

Proof

In the primal step, suppose that ${\tilde{\lambda }}^{(k)}\ge 0$ solves Problem (D-ASk) and that the corresponding unique primal solution satisfies $x^{(k)}~\not \in ~P$. After adding a violated cutting plane, the optimal value of Problem (P-AS) strictly increases and the same is true for the optimal value of Problem (D-AS) by strong duality. Then,

$$\begin{aligned} p^{(k+1)} = \tilde{\lambda }^{(k+1)} - \lambda ^{(k)} = {\tilde{\lambda }}^{(k+1)} - \tilde{\lambda }^{(k)} \end{aligned}$$

is a strict ascent direction for $-b^\top \lambda$ and case (i) holds.

In the dual step, if $p^{(k+1)}$ is an unbounded direction, case (i) holds again. Otherwise, observe that $\lambda ^{(k)}\ne {\tilde{\lambda }}^{(k+1)}$, as ${\tilde{\lambda }}^{(k+1)}$ is not feasible with respect to the nonnegativity constraints. Then, since ${\tilde{\lambda }}^{(k+1)}$ is the unique optimal solution for Problem (D-ASk) with minimal norm, $p^{(k+1)} = {\tilde{\lambda }}^{(k+1)} - \lambda ^{(k)}$ is either a strict ascent direction for $-b^\top \lambda$, or $-b^\top p^{(k+1)} = 0$ and $p^{(k+1)}$ is a strict descent direction for $\Vert \lambda \Vert$, so that case (ii) holds. $\square$

Lemma 2

At every iteration k of Algorithm EllAS, we have $m^{(k)}\le n+1$. Furthermore, if Algorithm EllAS terminates at iteration k with an optimal primal-dual pair, then $m^{(k)}\le n$.

Proof

As only violated cuts are added, the primal constraints $A^{(k)}x=b^{(k)}$ either form an infeasible system or are linearly independent. If $m^{(k)} = n+1$, the primal problem is hence infeasible. Thus Problem (D-ASk) is unbounded, so that at iteration k a dual step is performed and a dependent row of $(A^{(k)}, b^{(k)})$ is deleted, leading to an independent set of constraints again. $\square$

Theorem 4

Assume that whenever a dual step is performed, Algorithm EllAS takes a non-zero steplength $\alpha ^k$. Moreover, assume that P is a polytope and that the separation oracle can produce at most m different inequalities. Then, after at most $n 2^{m}$ iterations, Algorithm EllAS terminates with a primal-dual pair of optimal solutions for (R2) and (D).

Proof

First note that, by Lemma 2, at most n dual steps can be performed in a row. Hence, it is enough to show that in any two iterations $k\ne l$ where a primal step is performed, we have $(A^{(k)}, b^{(k)})\ne (A^{(l)}, b^{(l)})$. Otherwise, assuming $(A^{(k)}, b^{(k)}) = (A^{(l)}, b^{(l)})$, we obtain ${\tilde{\lambda }}^{(k)}={\tilde{\lambda }}^{(l)}$ and hence $\lambda ^{(k)}=\lambda ^{(l)}$. This leads to a contradiction to Proposition 4. $\square$

5.2 Running time per iteration

After computing $Q^{-1}$ in the preprocessing, the running time in iteration k of EllAS is $O(n^2+m^{(k)}n)$ and hence linear in the size of the matrices Q and $A^{(k)}$, if implemented properly. The main work is to keep the pseudo-inverse $(A^{(k)}Q^{-\frac{1}{2}})^+$ up-to-date. Since $A^{(k)}Q^{-\frac{1}{2}}$ is only extended or shrunk by one row in each iteration, an update of $(A^{(k)}Q^{-\frac{1}{2}})^+$ is possible in $O(m^{(k)}n)$ time by a generalization of the Sherman–Morrison-formula [12]. Exploiting the fact that the matrix $A^{(k)}$ has full row rank in most iterations, we can proceed as follows. If $A^{(k+1)}$ is obtained from $A^{(k)}$ by adding a new row a, we first compute the row vectors

$$\begin{aligned} h:=aQ^{-\frac{1}{2}}\left( A^{(k)}Q^{-\frac{1}{2}}\right) ^+,\quad v:=aQ^{-\frac{1}{2}}-hA^{(k)}Q^{-\frac{1}{2}}. \end{aligned}$$

Now $v\ne 0$ if and only if $A^{(k+1)}$ has full row rank, and in the latter case

$$\begin{aligned} \left( A^{(k+1)}Q^{-\frac{1}{2}}\right) ^+=\left( (A^{(k)}Q^{-\frac{1}{2}})^+ \mid 0\right) -\tfrac{1}{||v||^2}v^\top (h \mid -1). \end{aligned}$$

Otherwise, if $v=0$, we are adding a linearly dependent row to $A^{(k)}$, making the primal problem (P-AS) infeasible. In this case, an unbounded direction of steepest ascent of (D-AS) is given by $(-h \mid 1)^\top$ and the next step will be a dual step, meaning that a row will be removed from $A^{(k+1)}$ and the resulting matrix $A^{(k+2)}$ will have full row rank again. We can thus update $(A^{(k)}Q^{-\frac{1}{2}})^+$ to $(A^{(k+2)}Q^{-\frac{1}{2}})^+$ by first removing and then adding a row, in both cases having full row rank.

It thus remains to deal with the case of deleting the rth row a of a matrix $A^{(k)}$ with full row rank. Here we obtain $(A^{(k+1)}Q^{-\frac{1}{2}})^+$ by deleting the rth column in

$$\begin{aligned} \left( A^{(k)}Q^{-\frac{1}{2}}\right) ^+-\tfrac{1}{||w||^2} ww^\top \left( A^{(k)}Q^{-\frac{1}{2}}\right) ^+, \end{aligned}$$

where w is the rth column of $(A^{(k)}Q^{-\frac{1}{2}})^+$.

Theorem 5

The running time per iteration of Algorithm EllAS is $O(n^2)$.

Proof

This follows directly from Lemma 2 and the discussion above. $\square$

Clearly, the incremental update of the pseudo-inverse $(A^{(k)}Q^{-\frac{1}{2}})^+$ may cause numerical errors. This can be avoided by recomputing it from scratch after a certain number of incremental updates. Instead of a fixed number of iterations, we recompute $(A^{(k)}Q^{-\frac{1}{2}})^+$ whenever the primal solution computed in a primal step is infeasible, i.e., violates the current constraints, where we allow a small tolerance.

In order to avoid wrong solutions even when pseudo-inverses are not precise, we make sure in our implementation that the dual solution $\lambda ^{(k)}$ remains feasible for (D-AS) in each iteration, no matter how big the error of $(A^{(k)}Q^{-\frac{1}{2}})^+$ is. For this, we slightly change the computation of ${\tilde{\lambda }}^{(k)}$: after computing ${\tilde{\lambda }}^{(k)}$ exactly as explained, we determine the largest $\delta \in {\mathbb {R}}$ such that $(1-\delta )\lambda ^{(k-1)}+\delta {\tilde{\lambda }}^{(k)}$ is dual feasible. Such $\delta$ must exist since $\lambda ^{(k-1)}$ is dual feasible, and it can easily be computed using the midnight formula. We then replace ${\tilde{\lambda }}^{(k)}$ by $(1-\delta )\lambda ^{(k-1)}+\delta {\tilde{\lambda }}^{(k)}$ and go on as before.

6 Branch-and-bound algorithm

For solving the integer Problem (RP), the method presented in the previous sections must be embedded into a branch-and-bound scheme. The dual bounds are computed by Algorithm EllAS and the branching is done by splitting up the domain $[l_i,u_i]$ of some variable $x_i$. Several properties of Algorithm EllAS can be exploited to improve the performance of such a branch-and-bound approach.

Warmstarts Clearly, as branching adds new constraints to the primal feasible region of the problem, while never extending it, all dual solutions remain feasible. In every node of the branch-and-bound-tree, the active set algorithm can thus be warm started with the optimal set of constraints of the parent node. As in [7, 8], this leads to a significant reduction of the number of iterations compared to a cold start. Moreover, the newly introduced bound constraint is always violated and can be directly added as a new active constraint, which avoids resolving the same dual problem and hence saves one more iteration per node. Finally, the data describing the problem can either be inherited without changes or updated quickly; this is particularly important for the pseudo-inverse $(AQ^{-\frac{1}{2}})^+$.

Early pruning Since we compute a valid dual bound for Problem (RP) in every iteration of Algorithm EllAS, we may prune a subproblem as soon as the current bound exceeds the value of the best known feasible solution.

Avoiding cycling or tailing off Last but not least, we may also stop Algorithm EllAS at every point without compromising the correctness of the branch-and-bound algorithm. In particular, as soon as an iteration of Algorithm EllAS does not give a strict (or a significant) improvement in the dual bound, the active set algorithm is stopped and we resort to branching. This excludes any potential cycling of the algorithm.

7 Numerical results

To test the performance of our algorithm EllAS, we considered convex SOCP instances (Sect. 7.1), random binary instances with up to one million constraints (Sect. 7.2), and combinatorial instances of Problem (RP), where the underlying problem is the Shortest Path problem (Sect. 7.3), the Assignment problem (Sect. 7.4), the Spanning Tree problem (Sect. 7.5), and the Traveling Salesman problem (Sect. 7.6). Concerning our approach, these combinatorial problems have different characteristics: while the first two problems have compact and complete linear formulations, the standard models for the latter problems use an exponential number of constraints that can be separated efficiently. In the case of the Spanning Tree problem, this exponential set of constraints again yields a complete linear formulation, while this is not the case for the NP-hard Traveling Salesman problem. In the latter case, however, we still have a complete integer programming formulation, which suffices for the correctness of our approach.

For all problems, we consider instances where the positive definite matrix $Q\in {\mathbb {R}}^{n\times n}$ is randomly generated. For this, we chose n eigenvalues $\lambda _i$ uniformly at random from [0, 1] and orthonormalized n random vectors $v_i$, each entry of which was chosen uniformly at random from $[-1,1]$. Setting ${\bar{Q}}=\sum _{i=1}^n\lambda _iv_iv_i^{\top }$, the entries of Q are given as $Q_{ij} = c_i c_j {\bar{Q}}_{ij}$, where c is the vector defining the linear term. For the random instances, the entries of c were chosen uniformly at random from $[-1,0]$, while for all remaining instances the entries of c were chosen uniformly at random from [0.5, 1.5]. In the (very few) cases where the smallest eigenvalue of Q turned out to be smaller than $10^{-8}$, we discarded the instance and produced a new one.

In the following, we present a comparison of BB-EllAS, an implementation of the branch-and-bound-algorithm based on EllAS in C++, with the MISOCP solver of Gurobi 7.5.1 [10]. According to the latest benchmark results of Hans D. Mittelmann [14], Gurobi is currently the fastest solver for SOCPs and MISOCPs. Furthermore, in order to analyze the performance of EllAS as an algorithm for convex SOCPs, we report in Sect. 7.1 a comparison between EllAS and the SOCP solver of Gurobi 7.5.1 [10].

For BB-EllAS, we use a simple home-made branch-and-bound framework using a straightforward depth first search. The most fractional variable is chosen for branching. We use an optimality tolerance of $10^{-4}$. The same tolerance is applied when deciding whether a constraint is violated in a separation procedure. For Gurobi, we use standard settings, except that we apply the same optimality tolerance as in BB-EllAS, setting the absolute optimality tolerance MIPGapAbs to $10^{-4}$. All other standard parameters are unchanged. In particular, Gurobi uses presolve techniques that decrease the solution times significantly. In case of the Spanning Tree problem and the Traveling Salesman problem, we apply dynamic separation algorithms using a callback adding lazy constraints. Again, constraints are added if the violation exceeds $10^{-4}$.

All our experiments were carried out on Intel Xeon processors running at 2.60 GHz. All running times were measured in CPU seconds (not including the time needed for instance generation) and the time-limit was set to one CPU hour for each individual instance. All tables presented in this section include the following data for the comparison between BB-EllAS and Gurobi: the number of instances solved within the time limit ($\#$ sol), the average running time, and the average number of branch-and-bound nodes where applicable. For BB-EllAS, we also report the average total number of active set iterations (iter) and the average number of times the pseudo-inverse $({A^{(k)}{Q^{-\frac{1}{2}}}})^+$ is recomputed from scratch, the latter in percentage with respect to the number of iterations ($\%$ ps). All averages are taken over the set of instances solved to optimality within the time limit. For all applications, we also present performance profiles, as proposed in [9]. Given our set of solvers $\mathcal {S}$ and a set of problems $\mathcal {P}$, we compare the performance of a solver $s \in \mathcal {S}$ on problem $p \in \mathcal {P}$ against the best performance obtained by any solver in $\mathcal {S}$ on the same problem. To this end we define the performance ratio $r_{p,s} = t_{p,s}/\min \{t_{p,s^\prime }: s^\prime \in \mathcal {S}\},$ where $t_{p,s}$ is the computational time, and we consider a cumulative distribution function $\rho _s(\tau ) = |\{p\in \mathcal {P}:\; r_{p,s}\le \tau \}| /|\mathcal {P}|$. The performance profile for $s \in S$ is the plot of the function $\rho _s$.

7.1 Random SOCP instances

We first consider continuous relaxations of Problem (P), where the vector $c\in {\mathbb {R}}^n$ and the positive definite matrix $Q\in {\mathbb {R}}^{n\times n}$ are randomly generated as described above. The objective function is of the form $c^\top x~+~\beta ~\sqrt{x^\top Q x}$, where we use $\beta = \sqrt{(1-\epsilon )/\epsilon }$ as proposed in [5]. In order to study the effect of changing the weight $\beta$ of the non-linear term, as done in [1], we consider instances with $\epsilon \in \{0.5, 0.2, 0.1, 0.05, 0.02, 0.01\}$, corresponding to values of $\beta$ between 1 and 7. The set P is explicitely given as $\{x\in [0,1]^n \mid Ax \le b\}$, where $A\in {\mathbb {R}}^{m\times n}$ and $b\in {\mathbb {R}}^m$ are also randomly generated: the entries of A were chosen uniformly at random from the integers in the range [0, 10] and we set $b_i=\lfloor 0.5~{\sum _{j=1}^na_{ij}}\rfloor$ for $i=1,\dots ,m$. Altogether, we generated 480 different instances: for each combination of $\epsilon$, $n\in \{25,50\}$, and $m\in \{10^3,10^4,10^5,10^6\}$, we generated 10 instances. Since the set P is explicitely given here, the linear constraints are separated by enumeration in BB-EllAS. More precisely, at Step 8 of Algorithm 3, we pick the linear constraint most violated by $x^{(k)}$.

In Table 1, we report the comparison between EllAS and the SOCP solver of Gurobi. Gurobi is not able to solve any instance with $n=50$ variables and $m = 10^6$ constraints within the time limit. On the other hand, EllAS is in general very fast, but there are some instances where it stops without reaching optimality (these instances are counted as unsolved). Our implementation of EllAS is in fact tuned to compute valid lower bounds for Problem (P) quickly: we stop our algorithm as soon as an iteration does not give us a strict (or significant) improvement in the dual bound. Nevertheless, EllAS is able to compute the optimum for 444 out of 480 instances and the average running time is below four CPU seconds for all instance types. In Fig. 1, we report the performance profiles for all the instances.

Table 1 Comparison on random SOCP instances

7.2 Random binary instances

We next consider instances of Problem (P) where the vector $c\in {\mathbb {R}}^n$ and the positive definite matrix $Q\in {\mathbb {R}}^{n\times n}$ as well as the polyhedron P are created exactly as described in the previous section, except that $b_i=\lfloor q \,{\sum _{j=1}^na_{ij}}\rfloor$ for $i=1,\dots ,m$, with $q \in \{0.1, 0.2, 0.5\}$. However, we now allow only binary solutions, i.e., we require $x\in P\cap \{0,1\}^n$. Altogether, we generated 1440 different problem instances for (P): for each combination of q, $\epsilon$, $n\in \{25,50\}$, and $m\in \{10^3,10^4,10^5,10^6\}$, we generated 10 instances.

In Tables 2, 3 and 4, we report the results for $q=0.5$, $q=0.2$, and $q=0.1$, respectively. Besides the results of BB-EllAS and Gurobi, we report the results obtained by BB-EllAS without using warmstarts (BB-EllAS NW) and by Gurobi where all constraints are defined as lazy constraints (Gurobi LC). The latter has been considered in order to improve Gurobi’s performance: from the results shown, it is clear that Gurobi benefits from the use of lazy constraints. It is also evident how the use of warmstarts improves the performance of BB-EllAS: the average number of iterations decreases up to a factor of 100. For BB-EllAS, smaller values of q lead to shorter running times in general. For Gurobi, instances with $q=0.2$ are the hardest to solve, while instances with $q=0.1$ are the easiest for both BB-EllAS and Gurobi. Note that the average number of branch-and-bound nodes enumerated by BB-EllAS is generally larger than the number of nodes needed by Gurobi, but always by less than a factor of 10 on average. On all instance classes, BB-EllAS is able to solve significantly more instances than Gurobi and Gurobi LC within the time limit, and in general has a faster running time. This is confirmed by the performance profiles presented in Fig. 2, where BB-EllAS clearly outperforms both Gurobi and the improved Gurobi LC.

Fig. 1

Performance profile with respect to running times for convex SOCP instances

Table 2 Comparison on random binary instances, $q = 0.5$

Table 3 Comparison on random binary instances, $q = 0.2$

Table 4 Comparison on random binary instances, $q = 0.1$

Fig. 2

Performance profiles with respect to running times for random binary instances

7.3 Shortest path problem

Given a directed graph $G =(V,E)$, where V is the set of vertices and E is the set of edges, and weights associated with each edge, the Shortest Path problem is the problem of finding a path between two vertices s and t such that the sum of the weights of its constituent edges is minimized. Our approach uses the following flow based formulation of the Robust Shortest Path problem:

$$\begin{aligned} \begin{array}{lllll} &{}\min &{}\, c^\top x+\sqrt{x^ \top Qx}&{}\\ &{}\text { s.t.} &{} \,\sum _{e \in \delta ^+ (i)}x_e - \sum _{e \in \delta ^- (i)}x_e = 0 &{}\quad \forall i \in V {\setminus } \{s,t\} \\ &{} &{} \,\sum _{e \in \delta ^+ (s)} x_e - \sum _{e \in \delta ^- (s)} x_e = 1 &{} \\ &{}&{} \,\sum _{e \in \delta ^+ (t)} x_e - \sum _{e \in \delta ^- (t)} x_e = -1 &{}\\ &{} &{}\, x \in \{0,1\}^{E}&{} \end{array} \end{aligned}$$

(6)

In our test set, we produced squared grid graphs with r rows and columns, where all edges point from left to right or from top to bottom. In this way, we produced graphs with $|V| = r^2$ vertices and $|E| = 2 r^2 -2r$ edges. In the IP model (6), we thus have $n:=2 r^2 -2r$ many variables, $|V|=r^2$ many equations, and $m:=2|E|=4r^2-4r$ many inequalities, all being box constraints. Since this number is polynomial in n, we can separate them by enumeration within EllAS, whereas we can pass the formulation (6) to Gurobi directly. Concerning the objective function of (6), we determined the expected lengths $c_i$ uniformly at random in [0.5, 1.5] and built the positive definite matrix Q as described above. Altogether, we generated 60 different problem instances for (6): for each $r\in \{10,\ldots ,15\}$ we generated 10 instances.

Table 5 Comparison on robust shortest path instances

In Table 5, we report the comparison between BB-EllAS and the MISOCP solver of Gurobi. The average number of branch-and-bound nodes enumerated by BB-EllAS is almost in the same order of magnitude of that needed by Gurobi. However, EllAS is able to process the nodes very quickly, leading to a branch-and-bound scheme that is faster than Gurobi in terms of computational time for the majority of the instances, as confirmed by the performance profiles shown in Fig. 3.

In terms of robustness, Gurobi outperforms BB-EllAS, being able to solve three instances more within the time limit. In fact, the running times of BB-EllAS exhibit a larger variance than those of Gurobi. This is mostly due to numerical issues: in instances without numerical difficulties, the incremental update of pseudo-inverses works very well and saves a lot of running time. However, in a few instances, we often have to recompute the pseudo-inverse from scratch to avoid numerical errors. E.g., when considering $r=10,11,12$ in Table 5, it can be observed that average running times for $r=11$ are larger than for $r=12$, even if the number of nodes enumerated is smaller. This is due to the larger number of pseudo-inverse recomputations (9.65 % of all iterations for $r=11$ vs. 1.71 % for $r=12$). Note that these percentages are significantly smaller for all other types of instances.

Fig. 3

Performance profile with respect to running times for shortest path instances

7.4 Assigment problem

Given an undirected, bipartite and weighted graph $G =(V,E)$ with bipartition $V=V_1\cup V_2$, the Assignment problem consists in finding a one-to-one assignment from the nodes in $V_1$ to the nodes in $V_2$ such that the sum of the weights of the edges used for the assignment is minimized. In other words, we search for a minimum-weight perfect matching in the bipartite graph G. Our approach uses the following standard formulation of the Assignment problem:

$$\begin{aligned} \begin{array}{lllll} &{}\min &{} \, c^\top x+\sqrt{x^ \top Qx}&{}\\ &{}\text { s.t.} &{} \,\sum _{e\in \delta (i)}x_e = 1 &{}\quad \forall i\in V \\ &{}&{}\, x \in \{0,1\}^{E}&{} \end{array} \end{aligned}$$

In the bipartite case, the above formulation yields a complete description of ${\text {conv}}(P\cap {\mathbb {Z}}^n)$, which is not true in the case of general graphs.

We consider complete bipartite graphs, so that the number of variables is $n=\tfrac{1}{4} |V|^2$. The number of equations is |V| while the number of inequalities is equal to n, since only box constraints of the type $x\ge 0$ need to be added; the remaining box constraints are then implied by the equations. In our instances, we use randomly generated expected weights $c_i\in [0.5, 1.5]$ again, while the non-linear part of the objective function is generated as before. Altogether, we generated 60 different problem instances: for each $|V|\in \{20,22,\ldots ,30\}$ we generated 10 different instances. Results are presented in Table 6 and Fig. 4. BB-EllAS is able to solve four instances more than Gurobi within the time limit and outperforms Gurobi in terms of computational time.

Table 6 Comparison on robust assignment instances

Fig. 4

Performance profile with respect to running times for assignment instances

7.5 Spanning tree problem

Given an undirected weighted graph $G =(V,E)$, a minimum spanning tree is a subset of edges that connects all vertices, without any cycles and with the minimum total edge weight. Our approach uses the following formulation of the Robust Spanning Tree problem:

$$\begin{aligned} \begin{array}{lll} &{}\min &{} \, c^\top x+\sqrt{x^ \top Qx}\\ &{}\text {s.t.} &{} \,\sum _{e\in E}x_e = |V|-1 \\ &{}&{}\, \sum _{e\subseteq X} x_e \le |X|-1 \forall \,\emptyset \ne X\subseteq V\\ &{}&{}\, x \in \{0,1\}^{E} \end{array} \end{aligned}$$

(7)

In the above model, the number of inequalities, taking into account also the non-negativity constraints, is $m=2^{|V|}-2+|E|$. Since this number is exponential in the input size, we also have to use a separation algorithm for Gurobi. For both BB-EllAS and Gurobi, we essentially use the same simple implementation based on the Ford–Fulkerson algorithm.

For our experiments, we considered both complete graphs and grid graphs, the latter being produced as for the Shortest Path Problem. In both cases, expected edge weights are randomly generated in [0.5, 1.5] again, while we built the positive definite matrix Q as above. Altogether, we generated 80 different problem instances: for each $|V|\in \{12,\ldots ,16\}$ we generated 10 different complete instances, while for each $r\in \{6,7,8\}$ we generated 10 different grid instances. As shown in Tables 7 and 8, BB-EllAS clearly outperforms the MISOCP solver of Gurobi on all the instances considered. For the performance profile, see Fig. 5.

Table 7 Comparison on robust minimum spanning tree instances (complete graphs)

Table 8 Comparison on robust minimum spanning tree instances (grid graphs)

Fig. 5

Performance profile with respect to running times for spanning tree instances

7.6 Traveling salesman problem

Given an undirected, complete and weighted graph $G =(V,E)$, the Traveling Salesman problem consists in finding a path starting and ending at a given vertex $v\in V$ such that all the vertices in the graph are visited exactly once and the sum of the weights of its constituent edges is minimized. Our approach uses the following formulation of the Traveling Salesman problem:

$$\begin{aligned} \begin{array}{lllll} &{}\min &{}\, c^\top x+\sqrt{x^ \top Qx}&{}\\ &{}\text {s.t.} &{}\, \sum _{e\in \delta (i)}x_e = 2 &{}\quad \forall i\in V \\ &{}&{}\, \sum _{e\in \delta (X)} x_e \ge 2 &{}\quad \forall \,\emptyset \ne X\subsetneq V\\ &{}&{}\, x \in \{0,1\}^{E}&{} \end{array} \end{aligned}$$

(8)

Again, we consider complete graphs. The number of inequalities including the bounds $x\in [0,1]^E$ is $m:=2^{|V|}-2+2|E|$ and hence again exponential. For both BB-EllAS and Gurobi, we basically use the same separation algorithm as for the Spanning Tree problem; see Sect. 7.5. Instances are identical to those generated for the Spanning Tree problem, but we can consider slightly larger graphs, namely graphs with $|V|\in \{14,\ldots ,18\}$. See Table 9 and Fig. 6 for the results.

Table 9 Comparison on robust traveling salesman instances

Fig. 6

Performance profile with respect to running times for traveling salesman instances

8 Conclusions

We presented a new branch-and-bound algorithm for robust combinatorial optimization problems under ellipsoidal uncertainty. We assume that the set of feasible solutions is given by a separation algorithm that decides whether a given point belongs to the convex hull of the feasible set or not, and, in the negative case, provides a valid but violated inequality. The branch-and-bound algorithm is based on the use of an active set method for the computation of dual bounds. Dealing with the Lagrangian dual of the continuous relaxation has the advantage of allowing an early pruning of the node. The closed form solution of the active set subproblems, the smart update of pseudo-inverse matrices, as well as the possibility of using warmstarts, leads to an algorithm that clearly outperforms the mixed-integer SOCP solver of Gurobi on most of the problem instances considered.