Abstract
This paper presents a set of new convex quadratic relaxations for nonlinear and mixed-integer nonlinear programs arising in power systems. The considered models are motivated by hybrid discrete/continuous applications where existing approximations do not provide optimality guarantees. The new relaxations offer computational efficiency along with minimal optimality gaps, providing an interesting alternative to state-of-the-art semidefinite programming relaxations. Three case studies in optimal power flow, optimal transmission switching and capacitor placement demonstrate the benefits of the new relaxations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Optimization technology is widely used in modern power systems [43] and has resulted in millions of dollars in savings annually [45]. Optimal power flow [31, 41], energy market calculations [44, 46], transmission switching [19, 23], distribution network configuration [1], capacitor placement [3, 17, 26], expansion planning [54, 60], vulnerability analysis [8, 9, 50, 51], and power systems restoration [16, 58] represent just a subset of power systems optimization problems. The core ingredient common to all such applications is the power flow equations, which model the steady-state power flow of Alternating Current (AC). These equations form a system of nonconvex nonlinear constraints, which constitute a challenge when embedded in optimization problems.
There is a rich literature on various approaches for handling these constraints ranging from metaheuristics [17, 26, 32] to linear approximations [15, 29, 61]. These methods offer no optimality guarantees or lead to infeasible solutions in the original AC model. Jabr [27] was the first to introduce a Second-Order Cone (SOC) relaxation of the power flow equations. Thereafter, Bai et al [5] presented a Semidefinite Programming (SDP) relaxation, that was used by Lavaei and Low [31] to provide tight optimality bounds on traditional test cases for the continuous optimal power flow problem.
This paper presents a further attempt to bridge the gap between approximate methods and global optimization for power systems. It introduces a novel convex quadratic relaxation of the AC power flow equations that is easily embedded in mixed-integer programming frameworks. As a side result, the paper shows that it is possible to strengthen the relaxation by exploiting redundancy. This idea extends the line of work introduced by Liberti in [33] and Ruiz and Grossmann in [49]. In the mixed-integer case, based on the work of Günlük and Linderoth in [21], and Hijazi et al. in [24, 25], perspective formulations of second-order cone and linear on/off constraints are presented.
The new relaxation is evaluated on three standard power systems problems: optimal power flow, optimal transmission switching and capacitor placement. To the best of our knowledge, this work constitutes the first attempt to provide global optimality guarantees on discrete optimization problems featuring the nonlinear power flow constraints on non-tree topologies. The experimental results show that the new relaxation provides an appealing tradeoff between accuracy and efficiency with computational time reductions up to two orders of magnitude when compared to the SDP relaxations [31]. In some test cases, the new relaxation provides stronger lower bounds than the SDP relaxation, which suggests that it captures a different convex structure of the power flow equations.
The rest of this paper is organized as follows. Section 2 reviews basic concepts defining the nonlinear power flow equations. Section 3 presents the prior art. Section 4 derives the new relaxation in the continuous space and Sect. 5 investigates the mixed-integer nonlinear extension with on/off constraints. Finally, case studies are developed in Sects. 6 and 7 concludes the paper.
2 A brief overview of AC power system optimization
2.1 AC power flow
A power network is composed of several types of components such as buses, lines, generators, and loads. The network can be interpreted as a graph \(\langle N,E \rangle \) where the set of buses N represents the nodes and the set of lines E represents the edges linking pairs of nodes. Every bus \(i \in N\) has two variables, a voltage magnitude \(v_i\), and a phase angle \(\theta _i\). Lines \((i,j) \in E\) have two constant electrical properties: the susceptance \({\varvec{b}_{ij}}\) and the conductance \({\varvec{g}_{ij}}\). All of the network components are governed by two fundamental physical laws: (1) Ohm’s Law,
where \(p_{ij}\) and \(q_{ij}\) respectively denote the active and reactive power flow on line \((i,j) \in E\). Note that AC power flow is asymmetric and typically \(p_{ij} \ne -p_{ji}\), \(q_{ij} \ne -q_{ji}\). And (2) Kirchhoff’s Current Law (i.e. flow conservation),
where \(p^g_{i}\) and \(q^g_{i}\) respectively denote the active and reactive power generation, \({\varvec{p}^d_i}\) and \({\varvec{q}^d_i}\) represent the predefined load at bus \(i \in N\). Observe that \(\sum \) over \((i,j)\in E\) collects the edges oriented in the from direction and \(\sum \) over \((j,i)\in E\) collects the edges oriented in the to direction around bus \(i\in N\); Thus capturing the asymmetry of AC power flow.
2.2 Network operation constraints
In addition to physical properties, power system optimization problems share a set of common operational constraints. The voltage magnitude \(v_{i}\) at every node \(i \in N\) should be maintained around a nominal value of 1.0. The acceptable deviations from this value (usually around \(\pm 20\,\%\)) are captured by the voltage bounds (\({\varvec{v}^l_i}, {\varvec{v}^u_i}\)). The network contains generators, which can produce active and reactive power respectively denoted \(p^g_i\) and \(q^g_i\) for bus \(i \in N\). The size and design of each generator enforces upper and lower bounds (\({ \varvec{p}^{gl}_i}, {\varvec{p}^{gu}_i}\)) and (\({\varvec{q}^{gl}_i}, { \varvec{q}^{gu}_i}\)) on the quantities they can output. A line \((i,j) \in E\) has two operational properties: A bound \(\varvec{\theta }^{u}_{ij}\) on the phase angle difference \(|\theta _{i} - \theta _{j}|\) and a thermal limit \({\varvec{t}}_{ij}\) on the line flow \(p^2_{ij} + q^2_{ij}\).
These operational constraints (5)–(9) combined with the power flow equations (1)–(4) form a common basis for all power network optimization problems.
2.3 Network operation objectives
Power network operations have traditionally focused on two natural objective functions: (1) power transmission loss minimization,
and (2) generator fuel cost minimization,
Observe that objective (10) is a special case of objective (11) where \(\varvec{c}_{2i}\!=\!0, \varvec{c}_{1i}\!=\!1, \varvec{c}_{0i}\!=\!0 \) for bus \(i \in N\) [55]. Hence, one can focus on objective (11) w.o.l.g.
3 State-of-the-art
Many approaches for handling the AC power flow equations have been devised. Broadly, they can be grouped into three categories: local methods, approximations, and relaxations.
Local methods attempt to solve the nonconvex AC power flows without offering any optimality guarantees. A comprehensive survey on different local nonlinear programming technologies for the Optimal Power Flow (OPF) problem is presented in [12]. When considering discrete variables, methods producing feasible solutions mainly rely on meta-heuristics and local search methods [17, 26, 32].
Several approximations of the AC power flow equations have been proposed [15, 29, 61]. These models have various tradeoffs in complexity, quality, and performance. Their key advantage is to produce a linear programming model that can be used as a building block in mixed-integer programs. Nevertheless, on a variety of applications, these approaches suffer from a lack of accuracy and may return solutions that are infeasible in the original AC model.
Convex relaxations of the AC equations are of great interest since they can be used for solving hybrid discrete/continuous optimization problems, offering optimality bounds for a global optimization approach and optimality measures for local methods.
Jabr [27] was the first to propose a SOC relaxation of the nonlinear power flow equations. More recently, Lavaei and Low [31] used the SDP relaxation of [5] to provide tight lower bounds for the OPF problem, and closing the optimality gap on a number of traditional instances. Sojoudi and Lavaei [52] were able to show how both relaxations are related, deriving the SOC model by further relaxing the SDP formulation. To the best of our knowledge, there has not been any relaxations directly handling the trigonometric functions defined in equations (1), (2). Although, there have been a number of problem-specific relaxations such as [47] or [54], that are not considered here. From a computational standpoint, SDP solvers are less mature than nonlinear solvers and their scalability remains an open question [40]. Furthermore, solvers integrating discrete variables on top of SDP models [34] are very recent and do not have the scientific maturity of convex mixed-integer nonlinear programming (MINLP) solvers [10].
The convex relaxations proposed here are tailored to scalable solving technology for continuous and mixed-integer programs, offer tight optimality gaps, and can be used in a variety of power systems applications.
4 The new quadratic convex (QC) relaxation
The new relaxation is based on exploiting convex envelopes of quadratic and trigonometric terms appearing in the AC power flow equations (1), (2). The approach is motivated by the narrow bounds observed on decision variables involved in power systems. All of the relaxations presented here are valid for a bound \(\varvec{\theta }^u \le \pi /2\). However, in practice, the design of the power network can make the acceptable phase angle difference as small as \(\pi /36\) [48].
To the best of our knowledge, the quadratic relaxation of the cosine function and the polyhedral relaxation of the sine function are novel contributions. While few global solvers handle trigonometric functions, the usual approach consists of using general-purpose linearization techniques.
Quadratic Relaxation of the Cosine Function. We first introduce
 , an approximation of the cosine function on the interval
\([-\varvec{\theta }^u ,\varvec{\theta }^u]\):
, an approximation of the cosine function on the interval
\([-\varvec{\theta }^u ,\varvec{\theta }^u]\):

This approximation over-estimates the original function.
Proposition 1

Proof
Based on the symmetry of both functions, one can only consider interval
\(\left[ 0, \varvec{\theta }^u\right] \). Observe that
 based on the trigonometric identity
based on the trigonometric identity
Indeed, observe that

We have
Finally, since both
 are concave strictly decreasing on the interval
\([0 , \varvec{\theta }^{u}]\) and intersect on the lower and upper bounds of this interval, and since
are concave strictly decreasing on the interval
\([0 , \varvec{\theta }^{u}]\) and intersect on the lower and upper bounds of this interval, and since
 , the property is true on the whole interval.
\(\square \)
, the property is true on the whole interval.
\(\square \)
Error Estimation. An upper bound on the maximum estimation error can be expressed in terms of \(\varvec{\theta }^{u}\).
Proposition 2

Proof
Consider the function \({\widehat{\cos }}(\theta ) = 1 - \frac{(\theta )^{2}}{2}\). First, it can be shown that

Based on the symmetry of both functions, this only needs to be proven on the interval \(\left[ 0, ~\theta ^u\right] \). Consider the function \(f : {\mathbb {R}}\rightarrow {\mathbb {R}},~ f(\theta ) = \cos (\theta ) - 1 + \frac{(\theta )^{2}}{2}\). Observe that \(f(0) = 0\) and \(\nabla f(\theta ) = \theta - \sin (\theta )\). Since \(\nabla f(\theta ) > 0,~ \forall \theta \in {\mathbb {R}}^+\), f is positive on this interval, and thus \(\cos (\theta )\ge {\widehat{\cos }}(\theta ) ,~\forall \theta \in \left[ -\varvec{\theta }^u,~ \varvec{\theta }^u \right] \).
Now, given the bounds
\(\left[ 0,~ \varvec{\theta }^u\right] \), the maximum difference between
 and
\({\widehat{\cos }}(\theta )\) can be obtained by solving the following optimization program:
and
\({\widehat{\cos }}(\theta )\) can be obtained by solving the following optimization program:
Since the objective function is strictly increasing, the optimal solution is attained at the upper bound \( \theta ^u\) with the corresponding optimal value \((\varvec{\theta }^{u})^{2}/2 + \cos (\varvec{\theta }^{u}) - 1\). \(\square \)
Based on Proposition 1, we define the quadratic relaxation of the cosine function as follows (Fig. 1a),

Polyhedral Relaxation of the Sine Function. A polyhedral relaxation of the sine function is defined based on the following inequalities (Fig. 1b):

Although the convex envelope for the sine function is polyhedral, its linear description involves solving a trigonometric equation and thus contains non-rational coefficients. The polytope defined here slightly overestimates this envelope.
Proposition 3

Proof
The proof will focus on \(\cos \left( {\varvec{\theta }^u}/{2}\right) \left( \theta -{\varvec{\theta }^u}/{2}\right) + \sin \left( {\varvec{\theta }^u}/{2}\right) \ge \sin (\theta )\), a similar reasoning applies for the right-hand side constraint. Observe that the left-hand side of the inequality represents the equation of the tangent line to the sine function at point \(\left( {\varvec{\theta }^u}/{2}, \sin \left( {\varvec{\theta }^u}/{2}\right) \right) \). This line intersects respectively with bounds \(-\varvec{\theta }^u\) and \(\varvec{\theta }^u\) at points \(\underline{\varvec{p}} = (-\varvec{\theta }^u, -({3}/{4})\cos \left( {\varvec{\theta }^u}/{2}\right) \varvec{\theta }^u + \sin \left( {\varvec{\theta }^u}/{2}\right) )\) and \(\overline{\varvec{p}} = (\varvec{\theta }^u, \cos \left( {\varvec{\theta }^u}/{2}\right) ({\varvec{\theta }^u}/2) + \sin \left( {\varvec{\theta }^u}/{2}\right) )\). One can show that both points are respectively above \(\underline{\varvec{p}}^* = (-\varvec{\theta }^u, \sin \left( -\varvec{\theta }^u\right) )\) and \(\overline{\varvec{p}}^* = (\varvec{\theta }^u, \sin \left( \varvec{\theta }^u\right) )\).
Letting \(g(\theta )-f(\theta ) = \sin (\theta ) + \sin (\theta /2) - (3/4)\cos (\theta /2)\theta = y_{\underline{\varvec{p}}} - y_{\underline{\varvec{p}}^*}\), one can prove that \(y_{\underline{\varvec{p}}} \ge y_{{\underline{\varvec{p}}}^*}\) by showing that \(g(\theta ) \ge f(\theta )\) \(\forall \theta \in \left[ 0,~ \pi /2\right] \).
On the one hand, consider the function \(f : {\mathbb {R}}\rightarrow {\mathbb {R}},~ f(\theta ) = ({3}/{4})\cos \left( {\theta }/{2}\right) \theta \), and observe that \(\nabla ^2 f(\theta ) = -({3}/{8})\left( {\theta }/{2}\cos \left( {\theta }/{2}\right) + 2\sin \left( {\theta }/{2}\right) \right) \).
Let \(h(\theta ) = -({3}/{8})\left( ({3}/{2})\cos \left( {\theta }/{2}\right) - {\theta }/{4}\sin \left( {\theta }/{2}\right) \right) \) denote the first derivative of \(\nabla ^2 f\). Note that both \(\cos (\theta )\) and \(-\sin (\theta )\) are strictly decreasing functions on the interval \(\left[ 0,~ \pi /2\right] \), and hence \(h(\theta )\) is strictly increasing on this interval. Since \(h(0) < 0\) and \(h(\pi /2) < 0\), it follows that \(h(\theta ) < 0,~ \forall \theta \in \left[ 0,~ \pi /2\right] \), and thus \(\nabla ^2 f(\theta )\) is strictly decreasing on the same interval. Finally, since \(\nabla ^2 f(0)=0\), this function is always negative on this interval and consequently f is concave. On the other hand, consider the function \(g : \mathbb R\rightarrow {\mathbb {R}},~ g(\theta ) = \sin (\theta ) + \sin (\theta /2)\). Observe that \(\nabla ^2 g(\theta ) = -\sin \left( \theta \right) - \sin \left( {\theta }/{2}\right) /4\). Since \(-\sin (\theta )\) is strictly decreasing on the interval \(\left[ 0,~ \pi /2\right] \) and \(\nabla ^2 g(0)=0\), this function is always negative over this interval and consequently g is concave over the same interval. Since \(f(0) = g(0) = 0\) and \(g(\pi /2)>f(\pi /2)\), because both functions are concave and strictly increasing on this interval, one can deduce that \(g(\theta )\ge f(\theta ),~ \forall \theta \in \left[ 0,~ \pi /2\right] \). A similar proof can be derived for the pair of points \((\overline{\varvec{p}}, \overline{\varvec{p}}^*)\). \(\square \)
Multilinear Terms. Multilinear expressions have been extensively studied in the literature and corresponding convex envelopes are well-defined in some cases. For bilinear expressions, convex envelopes were introduced by McCormick in [4, 37] (Fig. 2a, b) Multilinear terms such as \(v_iv_jv_k\) are relaxed using a sequential bilinear approach. The trilinear envelopes introduced by [38, 39] were also considered. Nevertheless, on all applications of interest, numerical experiments have shown that the sequential McCormick relaxation offers comparably tight bounds.
Quadratic Terms. Finally, quadratic terms \(v_i^{2}\) and \(v_j^{2}\) are relaxed into their convex envelopes as plotted in Fig. 3.
4.1 Power flow relaxation
The complete initial quadratic relaxation of the power flow equations is defined by the following set of convex constraints.

where

and

Corollary 1
The set of constraints (12)–(19) defines a relaxation of the feasible region corresponding to the AC power flow Eqs. (1), (2).
Proof
This is a direct result of Propositions 1, 2, and 3. \(\square \)
4.2 Relaxation strengthening
The idea of introducing redundancy to improve the relaxation of nonconvex programs was formalized by Liberti in [33] focusing on the particular case of bilinear expressions. Ruiz and Grossmann [49] present a class of “general reductions constraints” obtained by intersecting different formulations based on the physical interpretation of the problem. In the power modeling framework, we show that adding a relaxed version of the current magnitude constraints can lead to a substantially tighter relaxation.
4.2.1 The Current Magnitude Constraint
The seminal work [6] made a keen insight that the current magnitude, \(l_{ij}\), of an AC power line \((i,j) \in E\) is characterized by the nonconvex equation,
Observing that both v and l are positive, [18] utilized this redundant constraint to develop the following convex second-order cone constraint,

To realize the benefits of (21), l must be linked back to the other problem variables. The following line-loss equation was proposed by [18] to link l to the other model variables,
However, in the context of the variable space of the QC-core, we propose the following formulation,

On large test cases, numerical experiments show that constraints (23) lead to better solver convergence when compared to (22).
Proposition 4
[14] Constraint (23) is equivalent to (22).
We also introduce the following valid bounds on l,
Proposition 5
\(\varvec{l}^l_{ij} = 0, \varvec{l}^u_{ij} =\varvec{t}_{ij} / (\varvec{v}^l_{i})^2\) are valid bounds on \(l_{ij}\).
Proof
The lower bound follows from the fact that all of the terms in the current flow equation (20) are positive. The upper bound follows from reasoning about (20) along with the operational constraints (5) and (8). \(\square \)
Introducing auxiliary variables \(l_{ij} \in (\varvec{l}^l_{ij}, \varvec{l}^u_{ij})\), the strengthened QC relaxation is given by:
5 Extension to mixed-integer nonlinear programs
A natural extension for various problems in power systems is to allow topological change by means of opening line circuit breakers. The introduction of binary variables to model corresponding discrete variables leads to an additional level of complexity. Another major challenge is the modeling of on/off constraints appearing in these problems. This section leverages recent developments in disjunctive programming to derive strong formulations of power systems problems featuring line switching.
5.1 On/off constraints
An on/off constraint can be written as \(g(\mathbf {x}) \le 0 ~ \text {if} ~ z ~ = ~ 1\) where \(z \in \{0,1\}\) is the corresponding indicator binary variable. A standard reformulation consists in using big-M formulations, i.e., \(g(\mathbf {x}) \le (1-z)M\), where M represents a big constant. Unfortunately the continuous relaxations resulting from such models, although compact, often provide weak lower bounds. The on/off constraint can be reformulated as the union of two disjoint sets,
Given this approach, one can define the best convex relaxation of the on/off constraint to be the convex hull of the union \(conv \left( \varGamma _0 \cup \varGamma _1 \right) \). When the set \(\varGamma _0\) reduces to a single point (\(\mathbf {l}^0= \mathbf {u}^0 = 0\)), \(conv \left( \varGamma _0 \cup \varGamma _1 \right) \) can be formulated in the space of original variables [21]. The main result is the following
This result can be extended to the general case (\(\mathbf {l}^0 \ne \mathbf {u}^0\)) when functions g are monotonic [24]. Specifically, in the linear case where \(g(\mathbf {x}) = \varvec{a}^T \mathbf {x} - b\), the convex hull is defined in [25] as:
where m is the number of variables with nonzero coefficients in the linear constraint \(\varvec{a}^T \mathbf {x} - b\), and S any subset of \(\{1,\dots ,m\}\). Observe that for \(S =\emptyset \) one gets the big-M-like constraint
Note that (26) is not sufficient for defining the convex hull as shown in [25], therefore, one can strengthen the relaxation by introducing the remaining non-dominated constraints corresponding to non-empty sets S in (25).
5.2 On/off constraints in power systems
In power systems, a number of variables and constraints are affected by line switching. First, consider the phase angle variables \(\theta _i\), if a line (i, j) is switched off, the phase angle difference \(|\theta _i - \theta _j|\) becomes unconstrained. A valid upper bound is given by
Let \(z_{ij} \in \{0,1\}\) represent the line switching variable on line (i, j), then the power flow disjunctions are defined as follows.
5.2.1 Sine function disjunction
The sine function relaxation introduced in Sect. 4 can be written as a linear disjunction (indices are dropped for clarity purposes):

Based on results in [25], the convex envelope of each disjunction can be characterized in the space of original variables using (25).

5.2.2 Cosine function disjunction
The quadratic relaxation of the cosine function defined in (14) does not fit the hypothesis of (24). Its disjunctive version is given as follows,

Note that the existence of a compact representation for convex hulls of on/off constraints featuring non-monotonic functions is still an open question. Hence, we propose the following disjunctive formulation for this constraint:

Proposition 6
Proof
Since \(\varGamma ^*_{cs}\) is a convex set it is sufficient to show that \(\varGamma ^0_{cs} \subseteq \varGamma ^*_{cs}\) and \(\varGamma ^1_{cs} \subseteq \varGamma ^*_{cs}\). Intersecting \(\varGamma ^*_{cs}\) with \(\{z=0\}\) and \(\{z=1\}\) completes the proof. \(\square \)
5.2.3 Thermal limit disjunction
Let \({\varvec{t}}_{ij}\) denote the thermal limit on line (i, j), a similar formulation can be applied to the thermal limit constraints \(p_{ij}^2 + q_{ij}^2 \le {\varvec{t}_{ij}}\), with the following disjunction:
Based on (24) the convex-hull formulation is given by:
Observe the squaring of the binary variable, which conflicts with the natural intuition of multiplying the right-hand side with z. The squared formulation is naturally tighter in the continuous relaxation where z can take real values. Note that the linear constraints \( |p| \le z\varvec{t}\) and \(|q| \le z\varvec{t}\) are redundant compared to the second-order constraint, and thus are excluded from the relaxation.
5.2.4 Current magnitude disjunction
The disjunctive extension of (21) is given as follows,

Note that \(\varGamma ^0_l\) does not fit the hypothesis of (24). In order to follow these assumptions, we introduce a new redundant constraint:
This gives rise to a new disjunction defined as:
Based on (24), the convex-hull formulation is given by:
Following a similar argument using the upper bound of l instead of  , we observe another valid constraint,
, we observe another valid constraint,

5.2.5 Power flow disjunction
Finally, in the power flow constraints (12), (13), since \(\varvec{v}^l > 0\),  needs to account for the off-configuration of the line where \(p_{ij} = q_{ij} = 0\). This is accomplished by introducing auxiliary variables
needs to account for the off-configuration of the line where \(p_{ij} = q_{ij} = 0\). This is accomplished by introducing auxiliary variables  for \((i,j),(j,i) \in E\) and enforcing the following set of constraints:
for \((i,j),(j,i) \in E\) and enforcing the following set of constraints:



6 Case studies
With the theoretical foundation established, this section turns to empirical case studies to assess the value of the QC relaxation on classic power systems optimization problems. The results illustrate the following key points,
-
1.
The QC relaxation provides tighter bounds than the SOC relaxation [27], with similar runtime performance.
-
2.
The QC is significantly more scalable than the SDP relaxation [31] and, in some cases, the QC relaxation is stronger than the SDP relaxation.
-
3.
Utilizing the on/off formulations developed in Sect. 5, the QC relaxation is readily extended to power systems optimization problems with discrete decision variables.
The case studies are organized into three separate units, Optimal Power Flow, Optimal Transmission Switching, and Capacitor Placement, each of increasing model complexity. The value of the QC relaxation is discussed in depth for each problem before moving on to the next case study. Overall, the results show that the QC model combined with off-the-shelf industrial strength optimization technology strikes an appealing balance between strength, flexibility, and scalability.
Test Cases.
The QC relaxation is evaluated on 116 state-of-the-art AC transmission system test cases from the NESTA v0.6.0 archive [13]. These test cases range from as few as 3 buses to as many as 9000 and consist of over 35 different networks, which are grouped in three categories, typical operating condition (TYP), congested operating condition (API), and small angle difference condition (SAD).
It is important to note that these realistic power network datasets include additional operational parameters such as transformers, line charging, and bus shunts. For clarity purposes, these additional parameters have not been presented throughout the paper. A detailed discussion of how to extended all of the formulations presented herein can be found in the Appendix 1.
Implementation and Experimental Setting. All of the proposed models are implemented in AMPL [20]. IPOPT 3.12 [59] with linear solver ma27 [57] was used as the primary NLP solver, as suggested by [12]. Preliminary numerical experiments conducted on general-purpose global optimization solvers, such as Couenne [7] and SCIP [2], showed severe scalability issues on all of the nonconvex NLP and MINLP problems considered herein. The common outcome was that for cases over 10 buses, the average gap after 10 hours of computation was greater than 50 %, with many instances reporting a gap of 100 %. Hence, we adopt the strategy of using IPOPT 3.12 and Bonmin 1.8 [10] as heuristics for finding feasible solutions to the nonconvex NLPs and MINLPs respectively. The continuous QCQP relaxations are solved using IPOPT while the MIQCQP relaxations are solved using Gurobi 6.5.0 [22], to benefit from the industrial-strength branch-and-bound algorithm. The SDP relaxation is based on the state-of-the-art implementation [30] which uses a branch decomposition [35] for performance and scalability gains. The SDP solver SDPT3 4.0 [56] was used with the modifications suggested in [30]. An optimality tolerance of \(1.e^{-6}\) is used across all solvers.
The experiments are conducted on Dell PowerEdge R415 servers with Dual 3.1GHz AMD 6-Core Opteron 4334 CPUs and 64GB of memory. However, for a fair comparison with single threaded implementations (e.g. IPOPT), all of the algorithms are run on a single thread. A wall-clock time limit of 10 hours was used for all computations. The solver status messages are reported as follows: (bold) is used to indicate that a relaxation provided a feasible AC power flow solution; (inf.) indicates that the solver proved the model is infeasible; (—) is reported if no solution is available at solver termination; (tl.) indicates that the solver reached the time limit; and (ud.) appears when an optimality gap cannot be computed.
After both a feasible solution and a relaxation solution are computed, optimality gaps are used to compare the quality of various relaxations. The optimality gaps reported in the tables are computed using the ratio,
where \(\mathsf {primal}\) refers to the solution returned by the heuristic solvers on the nonconvex problem, and \(\mathsf {dual}\) refers to the lower bound produced by the various relaxations.
6.1 Optimal power flow
The Optimal Power Flow problem is a seminal power network optimization task [11]. An extensive literature view can be found in [41, 42]. The goal of this decision-support problem is to minimize generation costs (11) subject to power flow (1)–(4) and network operations constraints (5)–(9):
In this case study, five formulations related to the (AC-OPF) are considered:
-
1.
AC—the original nonconvex model
-
2.
QC-core—the initial QC relaxation
-
3.
QC—the strengthened QC relaxation
-
4.
SOCP—the relaxation introduced in [27]
-
5.
SDP—the relaxation introduced in [5] with the enhancements from [35]
The formulations for each of these models is discussed in detail in Appendices A and B and a comprehensive list of results can be viewed in Appendix D. A selected subset of the results are presented in Tables 1, 2. These selected cases illustrate the following key points.
Bounding strength. For around 50 % of the test cases considered, these relaxations exhibit an optimality gap of <1 %. This is to be expected in light of [31]. However, the remaining 50 % of cases show that all of the relaxations considered here can exhibit significant optimality gaps. It is interesting to note that the QC relaxation is stronger than the SDP model on the SAD instances, due to the tight phase angle bound constraints, which are well captured in the former. On the remaining instances, when the optimality gaps are significant, the SDP relaxation tends to dominate the QC and SOCP relaxations. Finally, the results highlight the fact that the QC relaxation is strictly better than the SOCP model.
Performance and scalability. A clear limitation of the SDP relaxation is scalability. It can take hours to converge on cases with a few thousand buses and runs out of memory on the largest case with over 9000 buses. In contrast, the QC and SOCP relaxations have no issues scaling to cases with several thousand buses. Furthermore, the QC relaxation has the best performance on the large 9000 bus test cases.
OPF summary. Overall, these results demonstrate that the QC relaxation strikes an appealing balance between the established SDP and SOCP relaxations on the (AC-OPF) problem. Building on these results, from this point forward, we focus on extending the QC relaxation to more challenging and interesting decision support problems featuring discrete decision variables.
6.2 Optimal transmission switching
The Optimal Transmission Switching (OTS) problem was originally introduced in [19] and has many interesting variations [23, 28]. It is a straight-forward extension of the OPF problem where lines can be disconnected from the network (i.e., “switched off”). Due to Ohm’s Law, removing lines in the network changes the flow of power and can reduce the generation costs [8]. In this OTS formulation, the binary variable \(z_{ij}\) indicates whether a line is included in the network or discarded. The AC-OTS problem can be formulated as the following nonconvex MINLP:
The (AC-OTS) problem is clearly an generalization of (AC-OPF), however the introduction of discrete variables naturally increases the complexity of the problem significantly.
In this case study, three formulations related to (AC-OTS) are considered:
-
1.
AC—the original nonconvex model
-
2.
QC-Weak—an on/off QC relaxation using a big-M formulation
-
3.
QC—an on/off QC relaxation using the tight formulations from Sect. 5
A detailed specification of these on/off QC relaxations can be found in Appendix 1. A selected subset of the results are presented in Table 3. The complete list of results can be viewed in Appendix 1. These selected cases illustrate the following key points.
Bounding strength. In a wide variety of test cases considered, the QC based OTS relaxations are able to prove the quality of the Bonmin-based heuristic is <1 %, which is a very encouraging result for studying AC-OTS. However, it is observed that the heuristic can fail to find a feasible solution on the larger test cases with 100–300 buses.
Performance and scalability. The results indicate that in many small test cases there is little difference between the two QC relaxations. As the size of the test cases increases, the tight QC formulation starts to bring some significant benefits over the big-M formulation. However, a very important observation is that both the primal heuristic and the relaxations struggle to solve test cases with 1000 buses or more. This Indicates that scalability of these methods is a key point for further investigation.
OTS summary. Overall, these results demonstrate that the QC relaxation with on/off constraints can be used to provide lower bounds to the (AC-OTS) problem for networks with up to 300 buses. Furthermore, in a variety of cases, the QC relaxation is able to demonstrate that when the Bonmin-based primal heuristic finds a feasible solution to (AC-OTS) those solutions are near global optimality.
6.3 Capacitor placement
The capacitor placement (CAP) problem is another well-studied power system network design problem with several variants [3, 17, 26]. The CAP problem is particularly challenging as reactive power and voltage play an essential role. Consequently, popular active-power-only approximations, such as the DC power flow model [53], cannot be applied to this problem. Informally speaking, the CAP problem consists of placing reactive power devices (i.e. capacitors and inductors) throughout a power network to improve the voltage profile. The version studied here aims at minimizing required investment in new capacitors and inductors, while satisfying a narrow voltage band \(({\varvec{v}^l}, {\varvec{v}^u})\) throughout the network. The integer variables \(c_i\),\(d_i\) represent the number of installed capacitors and inductors respectively on node \(i \in N\) and \(q^c_{i}, q^d_{i}\) represent the amount of reactive power injected by those devices. The capacity of each installed capacitor and inductor is given by \(\varvec{q}^{cu}, \varvec{q}^{du}\) respectively.
The AC-CAP model is then formulated as the following nonconvex MINLP:
In contrast to the (AC-OTS) problem, the on/off constraints in the (AC-CAP) problem are all linear, which allows us to use existing tight convex-hull formulations developed in [25].
In this case study, we only consider two formulations related to the (AC-CAP) problem:
-
1.
AC—the original nonconvex model
-
2.
QC—an extended QC relaxation with on/off constraints.
A detailed specification of this on/off QC relaxation can be found in Appendix 1. In our experiments, the following settings are used for the problem parameters,
A selected subset of the results are presented in Table 4. The complete list of results can be viewed in Appendix 1. These selected cases illustrate the following key points.
Bounding strength. On the majority of small test cases considered (i.e. \(|N| \le 30\)), the QC based CAP relaxation is able to prove that the quality of the Bonmin-based heuristic is optimal or only off by one. This is a very encouraging result for the quality of the heuristic. As the test case size increases, so does the number of installed devices but the optimality gap remains fairly consistent, ranging from 5 %–30 %. Additionally, the results on the SAD instances are particularly interesting as they illustrate how the QC relaxation can be used to effectively show there is no feasible solution to the nonconvex (AC-CAP) model.
Performance and scalability. In nearly all of the test cases considered, the QC relaxation is significantly faster at completing the branch-and-bound search than the nonconvex heuristic. This highlights the computational advantage of using a MIQP model over the more general MINLP model. This also suggests that the QC relaxation may be used in consort with a heuristic to search for high quality solutions. Similar to the OTS problem, it is observed that both the primal heuristic and the relaxations struggle to solve test cases with 1000 buses or more. This indicates that the scalability of these methods is a key point for future investigation.
CAP summary. On a variety of small cases, the QC relaxation is able to demonstrate that the feasible solutions produced by the Bonmin-based primal heuristic are globally optimal, or otherwise provides a tight optimality gap. However, on the more challenging test cases, the (AC-CAP) problem can present large optimality gaps. Overall, these results demonstrate that the QC relaxation with on/off constraints is an effective starting point for providing strong lower bounds to the (AC-CAP) problem for networks with up to 300 buses, but future work should further investigate ways to close large optimality gaps.
7 Conclusion
This work constitutes a significant step forward in the use of global optimization techniques for solving complex mixed-integer nonlinear problems arising in power systems. The new QC model incorporates original convex quadratic relaxations of various nonlinear functions and strikes an appealing tradeoff between flexibility, accuracy, and performance. These benefits were illustrated on three case studies: optimal power flow, optimal transmission switching, and capacitor placement. The declarative nature of the model represents a major advantage, making it an extensible and ready-to-use tool in different contexts. The NLP models had no difficulties scaling to the largest publicly available networks, with as many as 9000 nodes. However, the case studies revealed difficulties in scaling MINLP models to problems with over 500 nodes, identifying a key challenge for future work. From a general mathematical programming standpoint, reduction constraints based on exploiting redundancy in nonconvex programming constitute a promising perspective for broader research in global optimization.
Abbreviations
- N :
-
The set of nodes in a network
- E :
-
The set of edges in a network
- p, q :
-
Line active and reactive power flow
- \(v, \theta \) :
-
Voltage magnitude and angle
- \(p^g, q^g\) :
-
Generator active and reactive power output
- \(\varvec{p}^d, \varvec{q}^d\) :
-
Load active and reactive power demand
- \(\varvec{r}, \varvec{x}\) :
-
Line resistance and reactance
- \(\varvec{g}, \varvec{b}\) :
-
Line conductance and susceptance
- \(\varvec{t}, \varvec{\theta }^u\) :
-
Line thermal and angle difference limits
- \(\varvec{c}_0, \varvec{c}_1, \varvec{c}_2\) :
-
Generation cost coefficients
- \(\varvec{\theta }^M\) :
-
Big-M value for line angle differences
- \(x^u\) :
-
Upper bound of x
- \(x^l\) :
-
Lower bound of x
-
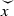 :
: -
Convex relaxation of x
- \(\varvec{x}\) :
-
A constant value
References
Borghetti, A., Paolone, M., C.A.N.: A mixed integer linear programming approach to the optimal configuration of electrical distribution networks with embedded generators. In: Proceedings of the 17th Power Systems Computation Conference (PSCC’11), Stockholm, Sweden (2011)
Achterberg, T.: SCIP: solving constraint integer programs. Math. Program. Comput. 1(1), 1–41 (2009). doi:10.1007/s12532-008-0001-1
Aguiar, R., Cuervo, P.: Capacitor placement in radial distribution networks through a linear deterministic optimization model. In: Proceedings of the 15th Power Systems Computation Conference (PSCC’05), Liege, Belgium (2005)
Al-Khayyal, F., Falk, J.: Jointly constrained biconvex programming. Math. Oper. Res. 8(2), 273–286 (1983)
Bai, X., Wei, H., Fujisawa, K., Wang, Y.: Semidefinite programming for optimal power flow problems. Int. J. Electr. Power Energy Syst. 30(6–7), 383–392 (2008). doi:10.1016/j.ijepes.2007.12.003
Baran, M., Wu, F.: Optimal capacitor placement on radial distribution systems. IEEE Trans. Power Deliv. 4(1), 725–734 (1989). doi:10.1109/61.19265
Belotti, P.: Couenne: User manual. Published online at https://projects.coin-or.org/Couenne/ (2009). Accessed 10 April 2015
Bienstock, D., Mattia, S.: Using mixed-integer programming to solve power grid blackout problems. Discret. Optim. 4(1), 115–141 (2007)
Bienstock, D., Verma, A.: The n-k problem in power grids: new models, formulations, and numerical experiments. SIAM J. Optim. 20(5), 2352–2380 (2010)
Bonami, P., Biegler, L.T., Conn, A.R., Cornuejols, G., Grossmann, I.E., Laird, C.D., Lee, J., Lodi, A., Margot, F., Sawaya, N., Wächter, A.: An algorithmic framework for convex mixed integer nonlinear programs. Discret. Optim. 5(2), 186–204 (2008)
Carpentier, M.J.: Contribution a letude du dispatching economique. Bulletin Society Francaise Electriciens (1962)
Castillo, A., O’Neill, R.P.: Computational performance of solution techniques applied to the acopf. Published online at http://www.ferc.gov/industries/electric/indus-act/market-planning/opf-papers/acopf-5-computational-testing.pdf (2013). Accessed 17 Dec 2014
Coffrin, C., Gordon, D., Scott, P.: NESTA, The Nicta Energy System Test Case Archive (2014). arXiv:1411.0359
Coffrin, C., Hijazi, H., Van Hentenryck, P.: DistFlow Extensions for AC Transmission Systems (2015) arXiv:1506.04773
Coffrin, C., Van Hentenryck, P.: A linear-programming approximation of ac power flows. INFORMS J Comput 26(4), 718–734 (2014). doi:10.1287/ijoc.2014.0594
Coffrin, C., Van Hentenryck, P., Bent, R.: Strategic stockpiling of power system supplies for disaster recovery. In: Proceedings of the 2011 IEEE Power and Energy Society General Meetings (PES) (2011)
Delfanti, M., Granelli, G., Marannino, P., Montagna, M.: Optimal capacitor placement using deterministic and genetic algorithms. IEEE Trans. Power Syst. 15(3), 1041–1046 (2000)
Farivar, M., Clarke, C., Low, S., Chandy, K.: Inverter var control for distribution systems with renewables. In: 2011 IEEE international conference on smart grid communications (SmartGridComm), pp. 457–462 (2011). doi:10.1109/SmartGridComm.2011.6102366
Fisher, E., O’Neill, R., Ferris, M.: Optimal transmission switching. IEEE Trans. Power Syst. 23(3), 1346–1355 (2008). doi:10.1109/TPWRS.2008.922256
Fourer, R., Gay, D.M., Kernighan, B.: AMPL: a mathematical programming language. In: Wallace, S.W. (ed.) Algorithms and Model Formulations in Mathematical Programming, pp. 150–151. Springer, New York (1989)
Günlük, O., Linderoth, J.: Perspective reformulations of mixed integer nonlinear programs with indicator variables. Math. Program. 124(1–2), 183–205 (2010)
Gurobi Optimization, Inc.: Gurobi optimizer reference manual. Published online at http://www.gurobi.com (2014)
Hedman, K., O’Neill, R., Fisher, E., Oren, S.: Optimal transmission switching with contingency analysis. IEEE Trans. Power Syst. 24(3), 1577–1586 (2009)
Hijazi, H., Bonami, P., Cornuéjols, G., Ouorou, A.: Mixed-integer nonlinear programs featuring “on/off” constraints. Comput. Optim. Appl. 52(2), 537–558 (2012)
Hijazi, H.L., Bonami, P., Ouorou, A.: A note on linear on/off constraints. Australian National University technical report (2014)
Huang, Y.C., Yang, H.T., Huang, C.L.: Solving the capacitor placement problem in a radial distribution system using tabu search approach. IEEE Trans. Power Syst. 11(4), 1868–1873 (1996)
Jabr, R.: Radial distribution load flow using conic programming. IEEE Trans. Power Syst. 21(3), 1458–1459 (2006)
Khodaei, A., Shahidehpour, M.: Transmission switching in security-constrained unit commitment. IEEE Trans. Power Syst. 25(4), 1937–1945 (2010)
Knight, U.G.: Power Systems Engineering and Mathematics, by U.G. Knight. Pergamon Press, Oxford (1972)
Lavaei, J.: OPF solver. Published online at http://ieor.berkeley.edu/~lavaei/Software.html (2014). Accessed 09 May 2016
Lavaei, J., Low, S.: Zero duality gap in optimal power flow problem. IEEE Trans. Power Syst. 27(1), 92–107 (2012). doi:10.1109/TPWRS.2011.2160974
Lee, K., Yang, F.: Optimal reactive power planning using evolutionary algorithms: a comparative study for evolutionary programming, evolutionary strategy, genetic algorithm, and linear programming. IEEE Trans. Power Syst. 13(1), 101–108 (1998)
Liberti, L.: Reduction constraints for the global optimization of NLPs. Int Trans Oper Res 11(1), 33–41 (2004). http://dx.doi.org/10.1111/j.1475-3995.2004.00438.x
Lofberg, J.: Yalmip : a toolbox for modeling and optimization in matlab. In: 2004 IEEE International Symposium on Computer Aided Control Systems Design, pp. 284 –289 (2004)
Madani, R., Ashraphijuo, M., Lavaei, J.: Promises of conic relaxation for contingency-constrained optimal power flow problem. IEEE Trans. Power Syst. (2015). doi:10.1109/TPWRS.2015.2411391
Madani, R., Sojoudi, S., Lavaei, J.: Convex relaxation for optimal power flow problem: mesh networks. IEEE Trans. Power Syst. 30(1), 199–211 (2015). doi:10.1109/TPWRS.2014.2322051
McCormick, G.: Computability of global solutions to factorable nonconvex programs: part i—convex underestimating problems. Math. Program. 10, 146–175 (1976)
Meyer, C.A., Floudas, C.A.: Trilinear monomials with positive or negative domains: facets of the convex and concave envelopes. In: Floudas, C.A., Pardalos, P.M. (eds.) Frontiers in Global Optimization, pp. 327–352. Springer, Boston (2004). doi:10.1007/978-1-4613-0251-3_18
Meyer, C.A., Floudas, C.A.: Trilinear monomials with mixed sign domains: facets of the convex and concave envelopes. J Glob. Optim. 29(2), 125–155 (2004)
Mittelmann, H.: Benchmarks for optimization software. http://plato.asu.edu/bench.html (2012). Accessed Feb 2014
Momoh, J., Adapa, R., El-Hawary, M.: A review of selected optimal power flow literature to 1993. I. nonlinear and quadratic programming approaches. IEEE Trans. Power Syst. 14(1), 96–104 (1999). doi:10.1109/59.744492
Momoh, J., El-Hawary, M., Adapa, R.: A review of selected optimal power flow literature to 1993. II. Newton, linear programming and interior point methods. IEEE Trans. Power Syst. 14(1), 105–111 (1999). doi:10.1109/59.744495
Momoh, J.A.: Electric Power System Applications of Optimization (Power Engineering (Willis)). CRC Press, Boca Raton (2001)
Munoz, J.R.A.: Analysis and application of optimization techniques to power system security and electricity markets. Ph.D. thesis, University of Waterloo (2008)
Ott, A.: Unit commitment in the pjm day-ahead and real-time markets. Published online at http://www.ferc.gov/eventcalendar/Files/20100601131610-Ott (2010). Accessed 22 April 2012
Overbye, T., Cheng, X., Sun, Y.: A comparison of the AC and DC power flow models for LMP calculations. In: Proceedings of the 37th Annual Hawaii International Conference on System Sciences, p. 9 (2004)
Phan, D.T.: Lagrangian duality and branch-and-bound algorithms for optimal power flow. Oper. Res. 60(2), 275–285 (2012)
Purchala, K., Meeus, L., Van Dommelen, D., Belmans, R.: Usefulness of DC power flow for active power flow analysis. Power Engineering Society General Meeting pp. 454–459 (2005)
Ruiz, J.P., Grossmann, I.E.: Using redundancy to strengthen the relaxation for the global optimization of MINLP problems. Comput. Chem. Eng. 35(12), 2729–2740 (2011)
Salmeron, J., Wood, K., Baldick, R.: Analysis of electric grid security under terrorist threat. IEEE Trans. Power Syst. 19(2), 905–912 (2004)
Salmeron, J., Wood, K., Baldick, R.: Worst-case interdiction analysis of large-scale electric power grids. IEEE Trans. Power Syst. 24(1), 96–104 (2009)
Sojoudi, S., Lavaei, J.: Physics of power networks makes hard optimization problems easy to solve. In: Power and Energy Society General Meeting, 2012 IEEE, pp. 1–8 (2012).doi:10.1109/PESGM.2012.6345272
Stott, B., Jardim, J., Alsac, O.: DC power flow revisited. IEEE Trans. Power Syst. 24(3), 1290–1300 (2009). doi:10.1109/TPWRS.2009.2021235
Taylor, J., Hover, F.: Linear relaxations for transmission system planning. IEEE Trans. Power Syst. 26(4), 2533–2538 (2011). doi:10.1109/TPWRS.2011.2145395
Taylor, J., Hover, F.: Convex models of distribution system reconfiguration. IEEE Trans. Power Syst. 27(3), 1407–1413 (2012). doi:10.1109/TPWRS.2012.2184307
Toh, K.C., Todd, M., Tutuncu, R.H.: Sdpt3—a matlab software package for semidefinite programming. Optim. Methods Softw. 11, 545–581 (1999)
U.K., R.C.: The HSL mathematical software library. Published online at http://www.hsl.rl.ac.uk/. Accessed 30 Oct 2014
Van Hentenryck, P., Coffrin, C., Bent, R.: Vehicle routing for the last mile of power system restoration. In: Proceedings of the 17th Power Systems Computation Conference (PSCC’11), Stockholm, Sweden (2011)
Wächter, A., Biegler, L.T.: On the implementation of a primal-dual interior point filter line search algorithm for large-scale nonlinear programming. Math. Program. 106(1), 25–57 (2006)
Wang, X., McDonald, J.: Modern Power System Planning. Mcgraw-Hill (Tx), Maidenheach (1994)
Zhuding, W., Du, P., Qishan, F., Haijun, L., David, C.Y.: A non-incremental model for optimal control of reactive power flow. Electr. Power Syst. Res. 39(2), 153–159 (1996)
Zimmerman, R., Murillo-Sandnchez, C., Thomas, R.: Matpower: Steady-state operations, planning, and analysis tools for power systems research and education. IEEE Trans. Power Syst. 26(1), 12–19 (2011). doi:10.1109/TPWRS.2010.2051168
Acknowledgments
The authors would like to thank Daniel K. Molzahn and Bernard C. Lesieutre for graciously providing a prerelease of their SDP based OPF solver, which was used in a earlier version of this manuscript. This work was conducted at NICTA and is funded by the Australian Government as represented by the Department of Broadband, Communications and the Digital Economy and the Australian Research Council through the ICT Centre of Excellence program.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: The QC formulations
This appendix describes a variety of extensions to the QC relaxation to key decision problems in power systems, including those featuring discrete variables.
1.1 A.1 Optimal power flow
The OPF problem is a simple extension of the QC relaxation. It only requires integration of the operational constraints and an appropriate objective function as follows,
1.2 A.2 Optimal transmission switching (OTS)
Before developing the QC-OTS formulations we first develop an on/off version of the McCormick envelopes from [37] to support the model. The on/off extension of the McCormick envelopes is given by the following disjunction:
Based on (24) the convex-hull formulation is given by:
We will use the notation \(\langle xy,z \rangle ^{M01}\) as the on/off extension of the McCormick relaxation \(\langle xy \rangle ^{M}\).
1.2.1 A.2.1 The QC-OTS formulations
In the OTS problem, discrete variables \(z_{ij} \in \{0,1\}\) for \((i,j) \in E\) are used to remove lines from the network. Let \(\varvec{\theta }^M\) be the largest possible phase angle difference between two disconnected buses, then a natural big-M extension of the (4.2) relaxation is as follows,

While a stronger formulation can be developed using the results from Sect. 5,

See Sect. 6.2 for an in depth study of these OTS relaxations.
1.3 A.3 Capacitor placement
All of the variable and network parameters of this model are defined in Sect. 6.3 and used in the (AC-CAP) formulation. The following model is a straight-forward relaxation of the CAP model using the QC constraints,
See Sect. 6.3 for an in depth experimental study of this CAP relaxation.
Appendix B: The SOCP and SDP power flow relaxations
In this section we review the formulations of two state-of-the-art power flow relaxations, the SOCP [27] and SDP [5] relaxations, which are used as points of comparison for this work. See Sect. 6.1 for a detailed study of these relaxations on the OPF problem.
SOCP. The SOCP relaxation is inspired by the following equivalence,
The validity of this equivalence is easily verified using the trigonometric identity \(\cos (x)^2 + \sin (x)^2 = 1\). The SOCP relaxation introduces the following W-space variables to replace the non-linear expressions,

In this lifted space, the valid equality (36) becomes,

And if relaxed to an inequality yields the following SOC constraint,

The SOCP relaxation is then given by lifting all of the power flow equations into the W-space and adding the valid SOC constraint as follows,
Extending this formulation to the OPF problem requires the following two insights on modeling the operational constraints in the W-space,


The equivalence of the first constraint is clear. For a derivation of the second constraint see [36]. Combining these derivations, a complete SOCP-based OPF formulation is given by,
SDP. Similar to the SOCP relaxation, the SDP relaxation begins by lifting the power flow problem into the W-space as specified above. It then defines the following matrix of complex numbers for \(1..n \in N\),

The key insight of the SDP relaxation is that W is positive-semidefinite, that is,
A derivation of this property can be found in [5, 52]. The core of the SDP relaxation is then given by,
Utilizing the operational constraints in the W-space, a complete SDP-based OPF formulation is given by,
A key limitation of the SDP relaxation is scalability. This is due to the current state-of-the-art in SDP solvers as well as the number of variables required by this formulation. Observe that the matrix W requires \(|N|^2\) new variables while the W-space from the SOCP relaxation only requires |E| variables. The sparsity of realistic power networks ensures that the number of variables needed in the SOCP relaxation is significantly less than the SDP relaxation. To increase the performance and scalability of the SDP relaxation [35] introduces a method where not all of the \(|N|^2\) variables are required. In this work we utilize this state-of-the-art SDP formulation.
Appendix C: Extensions for AC transmission system datasets
Typical power network datasets, such as those distributed with Matpower [62] include the following additional operational parameters: (1) multiple generators connected to the same bus; (2) multiple lines between buses; (3) bus shunts; (4) voltage transformers; and (5) line charging. In the rest of this section we review how the models in this paper can be extended to incorporate these parameters.
Power Flow Extensions. Let L be the set of lines in the network and let A be the set of triples (i, j, k) where \(k \in L\) is a unique identifier for each line in the network and \(i,j \in N\) define the two buses connected by this line. Note that the set L enables multiple lines to be connected between two buses. Let \(\varvec{b}^c_{k}\) be the line charging value for each line \(k \in L\). Let \(\varvec{tr}_k, \varvec{\theta }^s_k\) be the tap ratio and phase shifting transformer constants for each line \(k \in L\). While these values are typically given in polar coordinates, we transform them into rectangular coordinates as follows,
Combining these values with the line admittance parameters \(\varvec{g}_k, \varvec{b}_k\), we define the following constants for each line \(k \in L\),
The power flow equations are then extended as follows,
Observe that transformer parameters make the constants in these equations asymmetrical, a key difference to the simplified power flow Eqs. (1), (2).
Kirchhoff’s current law extensions. Let \(G_i\) be the set of generators at bus \(i \in N\) and let \(\varvec{g}^s_i, \varvec{b}^s_i\) be the active and reactive bus shunt values at that bus. Then the Kirchhoff’s Current Law constraints are extended as follows,
Extended optimal power flow. Combining these extensions, the extended optimal power flow problem is given by the following set of constraints,
Relaxation extensions. Observe that all of these model extensions result in simple modifications to the constants in front of the following key terms,
Because these terms remain unchanged by the extensions, nearly all of the constraints in the relaxations presented here can be adapted to these extensions simply by modifying various constant terms.
A notable exception is the current magnitude constraints (21)–(23) used in the QC model. Let \(A' \subseteq A\) contain one line for each pair of buses connected in A, then these two constraints are updated as follows \(\forall (i,j,k) \in A'\),


A derivation of these constraints can be found in [14].
Appendix D: Extended results
This appendix presents comprehensive results on all of the test cases in NESTA v0.6.0 [13]. In addition to the three categories of cases presented previously (i.e. TYP, API, and SAD), this section includes cases from the radial topologies (RAD), and nonconvex optimization (NCO) categories.
In the following result tables these annotations are used:
- ud.:
-
—undefined value
- bold :
-
—a relaxation provided a feasible AC power flow
- na.:
-
—the solver does not support all of the features of this test case
- —:
-
—no solution available at solver termination
- inf.:
-
—the solver proved the model is infeasible
- err.:
-
—the solver had an internal error
- oom.:
-
—the solver ran out of memory
- tl.:
-
—the solver reached the time limit
- \(\dagger \) :
-
—an annotation that the solver reached an internal iteration limit
- \(\star \) :
-
—an annotation that the solver reported numerical accuracy warnings
1.1 D.1 Optimal power flow
1.2 D.2 Optimal transmission switching
1.3 D.3 Capacitor placement
Rights and permissions
About this article
Cite this article
Hijazi, H., Coffrin, C. & Hentenryck, P.V. Convex quadratic relaxations for mixed-integer nonlinear programs in power systems. Math. Prog. Comp. 9, 321–367 (2017). https://doi.org/10.1007/s12532-016-0112-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12532-016-0112-z
Keywords
- Mixed-integer nonlinear programming
- Global optimization
- Convex relaxation
- Optimal power flow
- Optimal transmission switching
- Capacitor placement







 :
: