Fast approach for link prediction in complex networks based on graph decomposition

Abstract

Social networks such as Facebook, Twitter, etc. have dramatically increased in recent years. These databases are huge and their use is time consuming. In this work, we present an optimal calculation in graph mining for link prediction to reduce the runtime. For that purpose, we propose a novel approach that operates on the connected components of a network instead of the whole network. We show that thanks to this decomposition, the results of all link prediction algorithms using local and path-based similarity measure scan be achieved with much less amount of computations and hence within much shorter runtime. We show that this gain depends on the distribution of nodes in components and may be captured by the Gini and the variance measures. We propose a parallel architecture of the link prediction process based on the connected components decomposition. To validate this architecture, we have carried out an experimental study on a wide range of well-known datasets. The obtained results clearly confirm the efficiency of exploiting the decomposition of the network into connected components in link prediction.

1 Introduction

Interaction mining in complex networks has increasingly attracted the attention of several researchers and has become the subject of many branches of science. Various real-world systems can be modeled as networks in evolving interactions in the form of graphs (Newman 2003), such as computers, neural networks; chemical as well as online social networks (Zhou et al. 2009). In such networks, entities are represented by nodes or vertices, while edges between pairs of nodes describe interactions, associations, or relationships between nodes (Liao et al. 2015). Several efforts have been made to understand networks evolution (Albert and Barabasi 2002; Dorogovtsev and Mendes 2002), their relationships with both topologies and operation (Newman 2003; Boccaletti et al. 2006), as well as network characteristics (Costa et al. 2007).

Another important area of research in complex networks is interested in links between nodes and consists in studying the persistence of existing links or the prediction of new links when the networks evolves. Persistent links, also called durable links, stable links or permanent links, are links that exist in the past and will continue to exist in the future. On the other side, link prediction is related to detecting links that are missing in the past but that potentially will appear as new links in the future (Liben-Nowell and Kleinberg 2007).

Link prediction can be used in a variety of contexts: it has been used in bioinformatics to predict protein–protein interactions (PPI) (Yu et al. 2021). It is also used in security applications to identify hidden groups of terrorists and criminals (Hasan and Zaki 2011). It has been applied in healthcare to predict the spread of epidemic diseases (Kamath et al. 2001) and in the development of strategies to immunize potentially affected people to limit the spread of the epidemic. Link prediction has been used in the development of road networks to improve routes (Liu et al. 2011), in online connected community networks where future associations can be suggested as probable friendships, which can help the system to recommend new friends and thus increase their reliability towards the service (Dorogovtsev and Mendes 2002). Another example of practical use of link prediction is on Amazon, and Alibaba products, where recommended movies on Netflix and advertisements are displayed to users on Google AdWords and Facebook (Ibrahim and Chen 2015). Most link prediction algorithms that have been proposed are similarity-based algorithms, i.e., they are based on a similarity measure which assigns a score to each pair of vertices in order to quantify its probability of existence. Similarity based algorithms are widely used due to their prediction accuracy and their computational efficiency (Yang and Zhang 2016).Similarity-based algorithms can be classified into two types: Algorithms based on local information of nodes (nearest neighbor) and algorithms based on global path information (shortest path). However, since traditional link prediction algorithms try to evaluate all the absent links in a network, they generally cannot effectively handle large-scale complex networks. It is necessary to look for new techniques and approaches able to reduce the amount of computations during link prediction in such networks in order to ensure a reasonable consumption of time and memory space. The aim of the present paper is to address this problem and propose such a new approach based on the decomposition of the initial network into connected components. The idea is that in similarity-based algorithms for link prediction, the links between nodes belonging to different components do not matter. Our approach only focuses on the calculation of local links, i.e., links inside each component.

Moreover, from the observation that the components may be treated separately, in our approach again, we propose a parallel architecture for link prediction which distributes the set of components on several processors.

The main contributions of this paper can be summarized as follows.

• In the first part of our contribution, we show the importance of our approach and the gain we obtain by using the decomposition into connected components instead of working directly on the original graph. We formally analyze this gain in terms of the reduction of the number of calculated links. This gain is also illustrated experimentally in terms of runtime. Moreover, a comparison between the baseline approach, to which belong all previous works, and our approach has been done using the same databases.

• The second part of our contribution is based on the remark that the decomposition allows us to parallelize the calculations. So, we have derived four variants of our algorithm, according to: (1) the use or not of parallelism and/or (2) the inclusion or not of the decomposition step into the calculation process. The experimental study shows that parallelization allows us to save additional time.

The reminder of the paper is organized as follows. We present in Sect. 2 an overview of various measures based on local or neighborhood data as well as measures based on the shortest paths between nodes. Section 3 gives a formal description of the link prediction problem and highlights the potential difficulties due to the large size of networks for link prediction. Then, it discusses how the decomposition into connected components can be very useful in reducing the amount of computations. In Sect. 4 we present our proposed architecture for a link prediction system based on the decomposition of the network into its connected components. In particular, the proposed architecture exploits the decomposition to ensure a parallel treatment by distributing the components on several processors. In Sect. 5, we present the baseline algorithm which does not use decomposition and four variants of our proposed approach, based on decomposition, depending on whether the decomposition step is included in the scenario or not and whether the treatment is sequential or parallel. Section 6 is devoted to an experimental study for the validation of our proposal. Finally, in Sect. 7, we conclude our work and give some perspectives for future work.

2 Related work

In many link prediction methods, scores are derived from the class of immediate node neighborhoods. In other methods, scores calculation is based on paths between nodes (Wang et al. 2015; Lü and Zhou 2011). Several research works are based on the use of these measures either to compare the performance of new approaches (Li et al. 2020) or to modify them (Yang and Zhang 2016; Ahmad et al. 2020) and propose new extensions (Aziz et al. 2020). Among these measures which are still popularly used, we can quote the following measures categorized in two classes: those based on local information and those used in path methods.

2.1 Similarity indices based on local information

There are numerous local similarity measures. They are basically determined by the number of common neighbors shared by two nodes, say x and y. Let us denote by Γ(x) the set of x’s neighbors and by k(x) =|Γ(x)| the x’s degree. To each link (x, y) a score is assigned which is denoted by S_xy.

• Common neighbors (Liben-Nowell and Kleinberg 2007). This measure captures the common sense idea that two nodes are more likely to have a link if they have many common neighbors; this measure is defined as follows:

  $${{\varvec{S}}}_{{\varvec{x}}{\varvec{y}}}^{{\varvec{C}}{\varvec{N}}}=|\boldsymbol{\Gamma }({\varvec{x}})\cap \boldsymbol{\Gamma }({\varvec{y}})|$$

  (1)

• Jaccard index (Liben-Nowell and Kleinberg 2007). Jaccard index normalizes the size of common neighbors. This measure is defined by:

  $${{\varvec{S}}}_{{\varvec{x}}{\varvec{y}}}^{{\varvec{C}}{\varvec{N}}}=\frac{|\boldsymbol{\Gamma }({\varvec{x}})\cap \boldsymbol{\Gamma }({\varvec{y}})|}{|\boldsymbol{\Gamma }({\varvec{x}})\cup \boldsymbol{\Gamma }({\varvec{y}})|}$$

  (2)

• Adamic Adar index (Adamic and Adar 2003). This measure is calculated by adding weights to the nodes that are connected to both nodes x and y. It is defined by:

  $${{\varvec{S}}}_{{\varvec{x}}{\varvec{y}}}^{{\varvec{A}}{\varvec{A}}}=\sum_{{\varvec{Z}}\in \boldsymbol{\Gamma }({\varvec{x}})\cap \boldsymbol{\Gamma }({\varvec{y}})}\frac{1}{{\varvec{l}}{\varvec{o}}{\varvec{g}}{\varvec{k}}({\varvec{z}})}$$

  (3)

• Resource allocation index (Zhou et al. 2009). Considering a pair of nodes x and y that are not directly connected and assuming that the node x needs to give some resources to y with their common neighbors as transmitters, this measure is defined by:

  $${{\varvec{S}}}_{{\varvec{x}}{\varvec{y}}}^{{\varvec{R}}{\varvec{A}}}=\sum_{{\varvec{Z}}\in \boldsymbol{\Gamma }({\varvec{x}})\cap \boldsymbol{\Gamma }({\varvec{y}})}\frac{1}{{\varvec{k}}({\varvec{z}})}$$

  (4)

• Node and Link Clustering coefficient (NLC) (Wu et al. 2016a). This similarity method is based on the basic topological characteristic of a network called "Clustering Coefficient". Clustering coefficients of nodes and links are incorporated to calculate similarity score. This measure is defined as follows:

  $${{\varvec{S}}}_{{\varvec{x}}{\varvec{y}}}^{{\varvec{N}}{\varvec{L}}{\varvec{C}}}=\sum_{{\varvec{Z}}\in \boldsymbol{\Gamma }({\varvec{x}})\cap \boldsymbol{\Gamma }({\varvec{y}})}\frac{{{\varvec{S}}}_{{\varvec{x}}{\varvec{z}}}^{{\varvec{C}}{\varvec{N}}}}{{{\varvec{k}}}_{{\varvec{z}}}-1}\boldsymbol{*}{\varvec{C}}\left({\varvec{z}}\right)+\frac{{{\varvec{S}}}_{{\varvec{y}}{\varvec{z}}}^{{\varvec{C}}{\varvec{N}}}}{{{\varvec{k}}}_{{\varvec{z}}}-1}\boldsymbol{*}{\varvec{C}}\left({\varvec{z}}\right)$$

  (5)

• Clustering Coefficient for Link Prediction (Wu et al. 2016b). This method uses more information about the local link/triangle structure than the CAR index (Cannistraci et al. 2013), but costs less computation time. The key idea of the method is to exploit the value of links between other neighbors of common neighbors. It is defined as follows:

  $${{\varvec{S}}}_{{\varvec{x}}{\varvec{y}}}^{{\varvec{C}}{\varvec{C}}{\varvec{L}}{\varvec{P}}}=\sum_{{\varvec{Z}}\in \boldsymbol{\Gamma }({\varvec{x}})\cap \boldsymbol{\Gamma }({\varvec{y}})}\frac{{{\varvec{t}}}_{{\varvec{z}}}}{{\varvec{k}}\left({\varvec{z}}\right)({\varvec{k}}\left({\varvec{z}}\right)-1)/2}$$

  (6)

  such that: t_z is the number of triangles passing through node z.

• Common neighbor plus preferential attachment (CN + PA) index (Zeng 2016). This method is presented to estimate the probability of existence of a link between two nodes. Based on the combination of the two methods Common neighbor and preferential attachment (Mitzenmacher 2004). It is defined as follows:

  $${{\varvec{S}}}_{{\varvec{x}}{\varvec{y}}}^{\mathbf{C}\mathbf{N}+\mathbf{P}\mathbf{A}}=\left|\boldsymbol{\Gamma }\left({\varvec{x}}\right)\cap \boldsymbol{\Gamma }\left({\varvec{y}}\right)\right|+\boldsymbol{\alpha }\frac{\left|\boldsymbol{\Gamma }\left({\varvec{x}}\right)|\boldsymbol{*}|\boldsymbol{\Gamma }\left({\varvec{y}}\right)\right|}{\frac{\sum_{{\varvec{z}}\in {\varvec{V}}}|\boldsymbol{\Gamma }\left({\varvec{z}}\right)|}{|{\varvec{V}}|}}$$

  (7)

  where α is a parameter (e.g.: $\boldsymbol{\alpha }=0.01$ ) and $\frac{\sum_{{\varvec{z}}\in {\varvec{V}}}|\boldsymbol{\Gamma }\left({\varvec{z}}\right)|}{|{\varvec{V}}|}$ is equal to the mean degree⟨k⟩ of the network.

• Adaptive degree penalization for link prediction (ADP) (Martínez et al. 2016). The measure finds that the degree of penalization which better obtains the results of the link prediction can be estimated by considering the clustering coefficient of the network. The prediction technique automatically adapts to the network. It is defined as follows:

  $${{\varvec{S}}}_{{\varvec{x}}{\varvec{y}}}^{\mathbf{A}\mathbf{D}\mathbf{P}}=\sum_{{\varvec{Z}}\in \boldsymbol{\Gamma }({\varvec{x}})\cap \boldsymbol{\Gamma }({\varvec{y}})}{|\boldsymbol{\Gamma }\left({\varvec{z}}\right)|}^{-{\varvec{c}}{\varvec{\beta}}}$$

  (8)

  where c is the average clustering coefficient of the network and β is a constant (e.g. β = 2.5).

• Fuzzy modeling for link prediction (Tuan et al. 2019). Let µ_Γ(x) and µ_Γ(y)be the membership degrees of the sets of common neighbors Γ(x)and Γ(y)of the node x and y respectively, then:

  • The fuzzy common neighbor similarity score is defined as:

    $${{\varvec{S}}}_{{\varvec{x}}{\varvec{y}}}^{{\varvec{F}}{\varvec{C}}{\varvec{N}}}=\sum_{{\varvec{x}}\in \boldsymbol{\Gamma }\left({\varvec{x}}\right),{\varvec{y}}\in \boldsymbol{\Gamma }({\varvec{y}})}({{\varvec{\mu}}}_{\boldsymbol{\Gamma }({\varvec{x}})\boldsymbol{ }}{\cap{\varvec{\mu}}}_{\boldsymbol{\Gamma }({\varvec{x}})\boldsymbol{ }})$$

    (9)

  • The fuzzy Adamic–Adar Similarity Score is defined as:

    $${{\varvec{S}}}_{{\varvec{x}}{\varvec{y}}}^{{\varvec{F}}{\varvec{A}}{\varvec{A}}}=\sum_{{\varvec{Z}}\in \boldsymbol{\Gamma }({\varvec{x}})\cap \boldsymbol{\Gamma }({\varvec{y}})}\frac{1}{{\varvec{l}}{\varvec{o}}{\varvec{g}}(|{{\varvec{\mu}}}_{\boldsymbol{\Gamma }({\varvec{z}})\boldsymbol{ }}|)}$$

    (10)

    where the membership function is µ_Γ(z).

  • The fuzzy Jaccard Coefficient is given by:

    $${{\varvec{S}}}_{{\varvec{x}}{\varvec{y}}}^{\mathbf{F}\mathbf{J}\mathbf{C}}=\sum_{{\varvec{x}}\in \boldsymbol{\Gamma }\left({\varvec{x}}\right),{\varvec{y}}\in \boldsymbol{\Gamma }({\varvec{y}})}\frac{{{\varvec{\upmu}}}_{{\varvec{\Gamma}}(\mathbf{x})}{\cap {\varvec{\upmu}}}_{{\varvec{\Gamma}}(\mathbf{x})}}{{{\varvec{\upmu}}}_{{\varvec{\Gamma}}(\mathbf{x})}{\cup {\varvec{\upmu}}}_{{\varvec{\Gamma}}(\mathbf{x})}}$$

    (11)

• Triangle Structure Index (TRA) (Bai et al. 2018). This method offers us a new similarity index, by combining the aforementioned triangle structure and the idea of the RA index. It is defined as follows:

  $${{\varvec{S}}}_{{\varvec{x}}{\varvec{y}}}^{{\varvec{T}}{\varvec{R}}{\varvec{A}}}=\sum_{{\varvec{Z}}\in \boldsymbol{\Gamma }({\varvec{x}})\cap \boldsymbol{\Gamma }({\varvec{y}})}\frac{1+\Delta ({\varvec{x}},{\varvec{y}};{\varvec{z}})/2}{{\varvec{k}}\left({\varvec{z}}\right)}$$

  (12)

  where $\Delta$ is the number of triangles TRA formed by x, y and z, which is: $\Delta \left({\varvec{x}},{\varvec{y}};{\varvec{z}}\right)=\Delta \left({\varvec{x}},{\varvec{z}}\right)+\Delta \left({\varvec{y}},{\varvec{z}}\right).$

• Sam Similarity (Samad et al. 2019). This measure refers to the similarity of x to y as well as the similarity of y to x. It divides the similarity task computation into two parts. First, it determines how much x is similar to y. Second, it computes the similarity between y and x. Finally, the measure is defined by using both outcomes, as follows:

  $${{\varvec{S}}}_{{\varvec{x}}{\varvec{y}}}^{{\varvec{S}}{\varvec{a}}{\varvec{m}}}=\frac{\frac{\left|\boldsymbol{\Gamma }\left({\varvec{x}}\right)\cap \boldsymbol{\Gamma }\left({\varvec{y}}\right)\right|}{\boldsymbol{\Gamma }\left({\varvec{x}}\right)}+\frac{\left|\boldsymbol{\Gamma }\left({\varvec{x}}\right)\cap \boldsymbol{\Gamma }\left({\varvec{y}}\right)\right|}{\boldsymbol{\Gamma }\left({\varvec{y}}\right)}}{2}$$

  (13)

• Common Neighbor to Degree (CN2D) (Mumin et al. 2022). Consider two unconnected nodes a and b, and assuming that they have common neighbors between them. They are able to present and propagate some information through these neighbors in their interaction. The total resources allocated to the target node pair is estimated using the following equation:

  $${{\varvec{S}}}_{{\varvec{x}}{\varvec{y}}}^{\mathbf{C}\mathbf{N}2\mathbf{D}}=\left|\boldsymbol{\Gamma }\left({\varvec{x}}\right)\cap \boldsymbol{\Gamma }\left({\varvec{y}}\right)\right|+\upbeta \left(\frac{1}{{\varvec{m}}{\varvec{a}}{\varvec{x}}({{\varvec{k}}}_{{\varvec{x}},}{{\varvec{k}}}_{{\varvec{y}}})}\sum_{{\varvec{Z}}\in \boldsymbol{\Gamma }({\varvec{x}})\cap \boldsymbol{\Gamma }({\varvec{y}})}|\boldsymbol{\Gamma }\left({\varvec{z}}\right)|\right)$$

  (14)

  with a parameter β between 0 and 1, (e.g. β = 0.01).

2.2 Similarity indices based on path methods

Paths between two nodes can also be used to compute similarities between couples of nodes. Such methods are referred to as path-based metrics. The following are some of the most popular methods in this class:

• Common Neighbor and Distance index (Yang and Zhang 2016). This is an extension of common neighbors. It is based on two properties of a complex network, common neighbor and the distance between two nodes x and y.

  $${{\varvec{S}}}_{{\varvec{x}}{\varvec{y}}}^{{\varvec{C}}{\varvec{N}}{\varvec{D}}}=\left\{\begin{array}{c}\frac{{{\varvec{C}}{\varvec{N}}}_{{\varvec{x}}{\varvec{y}}}+1}{2}\Gamma \left({\varvec{x}}\right)\cap \Gamma \left({\varvec{y}}\right)\ne \varnothing \\ \frac{1}{{{\varvec{d}}}_{{\varvec{x}}{\varvec{y}}}}otherwise\end{array}\right.$$

  (15)

  where CN_xy is the number of common nodes between node x and y and d_xy is the distance between x and y.

• Newton’s Gravitational Law index (Ashraf et al. 2018). This measurement is inspired by Newton's law of universal gravitation, which states that the force exerted between two masses is proportional to the product of these masses, and inversely proportional to the square of the distance between their centers. It is defined as follows:

  $${{\varvec{S}}}_{{\varvec{x}}{\varvec{y}}}^{{\varvec{N}}{\varvec{G}}{\varvec{L}}{\varvec{I}}}=\frac{{{\varvec{C}}}_{{\varvec{D}}}\left({\varvec{x}}\right)\boldsymbol{*}{{\varvec{C}}}_{{\varvec{D}}}\left({\varvec{y}}\right)}{{\varvec{S}}{\varvec{P}}\left({\varvec{x}},{\varvec{y}}\right)}$$

  (16)

  where C_D denotes the degree of centrality, SP is the shortest path.

• Local major path degree(LMPD) (Yang et al. 2018). Local path between two nodes is equal to the sum of the degrees of the intermediate nodes. The local path designates the paths of two and three stages between two nodes, and this method is defined as follows:

  $${{\varvec{S}}}_{{\varvec{x}}{\varvec{y}}}^{{\varvec{R}}{\varvec{P}}}={\sum }_{{\varvec{\omega}}=1}^{{{\varvec{L}}}_{2}}\frac{1}{{({{\varvec{L}}{\varvec{P}}{\varvec{D}}}_{{\varvec{\omega}}})}^{\boldsymbol{\alpha }}}+{\sum }_{{\varvec{m}}=1}^{{{\varvec{L}}}_{3}}\frac{1}{{({{\varvec{L}}{\varvec{P}}{\varvec{D}}}_{{\varvec{m}}})}^{\boldsymbol{\alpha }}}$$

  (17)

  where ${LPD}_{i}={\sum }_{j=1}^{{n}_{i}}{k}_{j}$.

• Relative-path-based algorithm for link prediction (RP) (Li et al. 2020). This method assumes that paths between nodes and neighbors provide basic similarity characteristics. This method uses factorial information about paths between nodes and neighbors, in addition to paths between pairs of nodes, in the similarity calculation for link prediction. It is defined as follows:

  $${{\varvec{S}}}_{{\varvec{x}}{\varvec{y}}}^{{\varvec{R}}{\varvec{P}}}=\boldsymbol{\alpha }\frac{{{\varvec{S}}}_{{\varvec{x}},{\varvec{y}}}^{{{\varvec{D}}{\varvec{P}}}_{2}}}{\frac{1}{2}\left({{\varvec{S}}}_{{\varvec{x}}{,{\varvec{N}}}_{{\varvec{x}}}^{2}}^{{{\varvec{D}}{\varvec{P}}}_{2}}+{{\varvec{S}}}_{{\varvec{y}}{,{\varvec{N}}}_{{\varvec{y}}}^{2}}^{{{\varvec{D}}{\varvec{P}}}_{2}}\right)+1}+{\varvec{\beta}}\frac{{{\varvec{S}}}_{{\varvec{x}},{\varvec{y}}}^{{{\varvec{D}}{\varvec{P}}}_{3}}}{\frac{1}{2}\left({{\varvec{S}}}_{{\varvec{x}}{,{\varvec{N}}}_{{\varvec{x}}}^{3}}^{{{\varvec{D}}{\varvec{P}}}_{3}}+{{\varvec{S}}}_{{\varvec{y}}{,{\varvec{N}}}_{{\varvec{y}}}^{3}}^{{{\varvec{D}}{\varvec{P}}}_{3}}\right)+1}$$

  (18)

  where ${S}_{x,y}^{{DP}_{2}}=\sum_{{z}_{1},{z}_{2}\in {P}_{2}(x,y)}\frac{1}{{k}_{{z}_{1}}.{k}_{{z}_{2}}}$ et ${S}_{x,y}^{{DP}_{3}}=\sum_{{z}_{1},{z}_{2}\in {P}_{3}(x,y)}\frac{1}{{k}_{{z}_{1}}.{k}_{{z}_{2}}}$,P₂(x,y) et P₃(x,y)represent all intermediate nodes on paths of length 2 and 3 respectively between nodes x and y.

• Common neighbor centrality index (Ahmad et al. 2020). This measure is based on two vital properties of nodes, namely the number of common neighbors and their centrality. Common neighbor refers to the common nodes between two nodes. Centrality refers to the prestige that a node enjoys in a network, it is defined by:

  $${{\varvec{S}}}_{{\varvec{x}}{\varvec{y}}}^{{\varvec{C}}{\varvec{N}}{\varvec{C}}}=\boldsymbol{\alpha }(\left|\boldsymbol{\Gamma }\left({\varvec{x}}\right)\cap \boldsymbol{\Gamma }\left({\varvec{y}}\right)\right|)+(1-{\varvec{\upalpha}}).\frac{\mathbf{n}}{{\mathbf{d}}_{\mathbf{x}\mathbf{y}}}$$

  (19)

  where α is a parameter that varies in the interval [0, 1] and d_xy denotes the shortest distance between x and y.

3 Using decomposition to improve link prediction performance

The aim of this section is to formally define the problem of link prediction and study the impact of using as input the connected components of a network instead of the whole network on the amount of necessary computation and consequently on the runtime.

Definition 1

(Complex Network). A complex network is defined by a non-oriented graph G(V,E) where V is a set of nodes and E ⊆ V × V is a set of links between pairs of nodes.

We put n =|V| (number of nodes) and e =|E| (number of links) and we denote by E′ the set of absent links in the graph: E′ = {(x,y) ∈ V²|(x,y) ∉ E}.

Notice that if G is a complete graph (where there is a link between every pair of nodes), then the number of links is n.(n−1)/2.

In general, the size of E′ which represents the set of non-existing links in the network is n.(n−1)/2−e.

Existing link prediction algorithms based on local and path measure compute the scores for all the non-existing links belonging to E’ since they consider that any current non existing link may become an actual link in the future. Accordingly, for very large datasets, the number of potential links to evaluate may be very important. For example, in twitter-dataset (Reza and Huan 2009), we have 11.316.811 nodes and 85.331.846 links and then, the number of scores that should be calculated for non-existing links is more than 64 trillions!!

To overcome this problem, the solution we propose is based on the decomposition of our graph into its connected components. Indeed, as it will be shown later, for all approaches based on local and path measures, we only need to compute scores between nodes that both belong to the same component. This allows one to save runtime by reducing the number of required calculation operations. Moreover, the fact that connected components can be treated independently, allows one to perform parallel computation by affecting to each available processor a subset of components.

Definition 2

(Connected components). Let G = (V,E) be a graph representing a complex network.

A set C = {G₁ = (V₁,E₁),G₂ = (V₂,E₂),…,G_c = (V_c,E_c)} such that each G_i = (V_i,E_i) is a sub-graph of G defines a decomposition of G into its connected components if:

• $\bigcup_{i=1}^{c}{V}_{i}=V\, and\,\bigcup_{i=1}^{c}{E}_{i}=E$

• $\forall i\in \left\{1,\dots ,c\right\},\forall x,y\in {V}_{i} \,there\, is\, a\, path\, relating\, x \,and \,y$

• $\forall i, j\in \left\{1,\dots c\right\},\,such\, that\, i\ne j,{V}_{i}\cap {V}_{j}=\varnothing \,and\, {E}_{i}\cap {E}_{j}=\varnothing$

Suppose that Γ(x) denotes the set of neighbors of the node x, i.e., nodes having direct links with x, paths_x,y denotes the set of all paths of links relating x and y, and d_x,y denotes the distance between nodes x and y, i.e., the length of the shortest path between x and y. The following proposition states that nodes belonging to distinct components do not share any neighbors and are not related by any paths.

Proposition 1

Let C = {G₁ = (V₁,E₁),G₂  =(V₂,E₂),…,G_c  = (V_c,E_c)} be the set of connected components of a complex network G = (V,E). We have:

$$\forall i, j\in \{1,...,c\} s.t. i\ne j, \forall x\in Vi, \forall y\in Vj\left\{\begin{array}{c}\Gamma (x) \cap \Gamma (y) \ne 0\, (hence\, |\Gamma (x) \cap \Gamma (y)| = 0)\\ and\\ {paths}_{x,y} =\varnothing\, (hence\, {d}_{xy} = \infty )\end{array}\right.$$

(20)

Proof

For any x, y such that x ∈ V_i, y ∈ V_j and i $\ne$ j we have: Γ (x) ⊆ V_i and Γ(y) ⊆ V_j (all the neighbors of x (resp. y) are inside V_i (resp. V_j)). Then, since V_i ∩ V_j = $\mathrm{\varnothing }$. It follows that Γ(x) ∩ Γ(y) = $\mathrm{\varnothing }$. This immediately leads to the factthat |Γ(x) ∩ Γ(y)|= 0.

Now, if we suppose that there is a path relating x and y then there must be a path between some x′ and y′ such that x’ ∈ V_i and y’ ∈ V_j which is impossible since V_i ∩ V_j= $\mathrm{\varnothing }$ and E_i ∩ E_j = $\mathrm{\varnothing }$. Hence we obtain paths_x,y = $\mathrm{\varnothing }$. Since there is no path between x and y, then it follows immediately that d_xy = ∞..

Corollary 1

Given a local or a path-based similarity measure f we have:

$$\forall i, j\in \{1,...,c\} s.t. i\ne j, \forall x\in {V}_{i}, \forall y\in {V}_{j} : f(x,y) = 0$$

(21)

Proof

Follows immediately from Proposition 1 and the definitions of local and path-based similarity measures.

This corollary is important since it states that it suffices to only compute the similarity measure between couples of nodes belonging to the same component.

Now let Gain(G) be the gain obtained by using the decomposition of G into its connected components. Gain(G) is the number of couples of nodes (x,y) where x and y belong to two different components.

Proposition 2

Let C = {G₁ = (V₁,E₁),G₂ = (V₂,E₂),…,G_c = (V_c,E_c)} be the set of connected components of a social network G = (V,E). We put |V |= n, |V_i|= n_i for i ∈ {1,…,c} and |E|= e. We have:

$$Gain(G) =\sum_{i=1}^{c-1}\sum_{j=i+1}^{c}({n}_{i}*{n}_{j})$$

(22)

Proof

Let NEval(G) (resp. NEval′(G)) be the number of evaluated potential links by using decomposition (resp. without using decomposition). Then, Gain(G) = NEval′(G) − NEval(G).

$$ \begin{aligned} NEval\left( G \right) & = \mathop \sum \limits_{i = 1}^{c} \left( {\frac{{n_{i} \left( {n_{i} - 1} \right)}}{2} - e_{i} } \right) \\ & = \frac{1}{2}\mathop \sum \limits_{i = 1}^{c} n_{i} \left( {n_{i} - 1} \right) - \mathop \sum \limits_{i = 1}^{c} e_{i} \\ & = \frac{1}{2}\mathop \sum \limits_{i = 1}^{c} \left( {n_{i}^{2} - n_{i} } \right) - e \\ \end{aligned} $$

$$ \begin{aligned} NEval^{\prime}\left( G \right) & = \frac{{n\left( {n - 1} \right)}}{2} - e \\ & = \frac{1}{2}\left( {n^{2} - n} \right) - e \\ = \frac{1}{2}\left( {\left( {n_{1} + \cdots + n_{c} } \right)^{2} - \left( {n_{1} + \cdots + n_{c} } \right)} \right) - e \\ & = \frac{1}{2}\left( {\left( {n_{1}^{2} + n_{2}^{2} \cdots + n_{c}^{2} ) + 2(n_{1} n_{2} + \cdots n_{1} n_{c} + n_{2} n_{3} + \cdots + n_{c - 1} n_{c} } \right) - \left( {n_{1} + \cdots + n_{c} } \right)} \right) - e \\ & = \frac{1}{2}\left( {\mathop \sum \limits_{i = 1}^{c} n_{i}^{2} + 2\mathop \sum \limits_{i = 1}^{c - 1} \mathop \sum \limits_{j = i + 1}^{c} n_{i} n_{j} - \mathop \sum \limits_{i = 1}^{c} n_{i} } \right) - e \\ & = \frac{1}{2}\mathop \sum \limits_{i = 1}^{c} (n_{i}^{2} - n_{i} ) - e + \mathop \sum \limits_{i = 1}^{c - 1} \mathop \sum \limits_{j = i + 1}^{c} n_{i} n_{j} \\ & = NEval\left( G \right) + \mathop \sum \limits_{i = 1}^{c - 1} \mathop \sum \limits_{j = i + 1}^{c} n_{i} n_{j} \\ \end{aligned} $$

It follows that:

$$Gain(G) =\sum_{i=1}^{c-1}\sum_{j=i+1}^{c}({n}_{i}*{n}_{j})$$

Without using decomposition, all similarity indices based on local information and path methods calculate a score list (denoted scores′(G)) of all non-existent links in the graph:

$$score{s}^{^{\prime}}\left(G\right)= \left\{\left(x,y,{s}_{xy}^{method}\right)/x,y\in Vand (x,y)\notin E\right\}$$

(23)

The number of evaluated links is:

$$\left|{E}^{^{\prime}}\right|= Gain\,\left(G\right)+\sum_{i=1}^{c}\left|{E}_{i}^{^{\prime}}\right|=\sum_{i=1}^{c-1}\sum_{j=i+1}^{c}\left({n}_{i}*{n}_{j}\right)+\sum_{i=1}^{c}\left|{E}_{i}^{^{\prime}}\right|$$

(24)

After decomposition, this score list (denoted scores (G)) becomes:

$$scores\left(G\right)= \bigcup_{i=1}^{c}\left\{\left(x,y,{s}_{xy}^{method}\right)/x,y\in {V}_{i}and (x,y)\notin {E}_{i}\right\}$$

(25)

The number of evaluated links is:

$$\left|{E}^{^{\prime}}\right|-Gain\left(G\right)=\sum_{i=1}^{c}\left|{E}_{i}^{^{\prime}}\right|$$

(26)

For all the other non-existing links, the similarity measure is set to 0:

$$\forall i, js.t. i\ne j, \forall i\in {V}_{i}, \forall j\in {V}_{j}, {s}_{xy}^{method}=0$$

(27)

Let us consider some special cases:

• Case of one connected component (c = 1). In this case, the decomposition does not matter and Gain(G) = 0.

• Many components (c > 1). If there is more than one component, the gain is strictly positive. We can distinguish the two following particular cases:

  • Case where n₁≈ n₂≈ ··· ≈ n_c ≈ n_c.In this case the gain is maximal and it is given by:

    $$ \begin{aligned} Gain^{max} \left( G \right) & = \mathop \sum \limits_{i = 1}^{c - 1} \mathop \sum \limits_{j = i + 1}^{c} \left( \frac{n}{c} \right)^{2} \\ & = \frac{{{\text{c}}\left( {{\text{c}} - 1} \right)}}{2}\left( \frac{n}{c} \right)^{2} \\ & = \frac{{{\text{n}}^{2} \left( {{\text{c}} - 1} \right)}}{{2{\text{c}}}} \\ \end{aligned} $$

  • Case where n₁ = (n − c + 1),n₂ = n₃ = …n_c = 1. This case corresponds to the situation where each c − 1 components contains one node, and one component contains all the remaining n − c + 1 nodes. In this case the gain is minimal, and is given by:

    $$ \begin{aligned} Gain^{min} \left( G \right) & = \mathop \sum \limits_{i = 1}^{c - 1} \mathop \sum \limits_{j = i + 1}^{c} \left( {n_{i} n_{j} } \right) \\ & = \mathop \sum \limits_{j = 2}^{c} n_{1} *1 + \mathop \sum \limits_{i = 2}^{c - 1} \mathop \sum \limits_{j = i + 1}^{c} \left( {1*1} \right) \\ & = \mathop \sum \limits_{j = 2}^{c} \left( {n - c + 1} \right) + \mathop \sum \limits_{i = 2}^{c - 1} \mathop \sum \limits_{j = i + 1}^{c} \left( 1 \right) \\ & = \left( {{\text{c}} - 1} \right)\left( {n - c + 1} \right) + \frac{{\left( {c - 1} \right)\left( {c - 2} \right)}}{2} \\ & = \frac{{\left( {c - 1} \right)\left( {2n - c} \right)}}{2} \\ \end{aligned} $$

Example 1

Let us consider the graph G(V,E) depicted in Fig. 1a with |V|= n = 9 nodes and |E|= e = 8 edges. G contains c = 3 connected components. Without using decomposition, to predict future links, we need to calculate the score of all nonexistent links (28 links) as shown in Fig. 1b.

Fig. 1

The gain in terms of the number of calculated links by using decomposition illustrated on a simple undirected network

By using the decomposition of G into its connected components, instead of calculating the scores of the links that do not exist in the complete graph, we only calculate the scores of the links that do not exist inside the three components (c₁),(c₂) and (c₃) (see Fig. 1c). We have 0 links in (c₁), 0 links in (c₂) and 2 links in (c₃). The obtained gain is 26.

Example 2

We assume that G(V, E) is a training graph with |V|= n = 9 nodes. The number of connected components is c = 3. Table 1 illustrates the different possible cases of the nodes distribution on the components and the gain associated with each of these distributions.

Table 1 Various possible distributions of nodes on the components and their calculation results of Gain, Gini and Variance

We can notice that the gain clearly depends on the distribution of the nodes in the connected components: the more the distribution is homogeneous, i.e., where the nodes are more uniformly distributed over the components, the greater is the gain. By contrast, heterogeneous distributions lead to less important gains.

Now, we show that this idea may be captured by two further measures:

• The Gini coefficient is a measure that captures the inequality or the heterogeneity of a distribution. It used in different domains, namely in supervised learning for the construction of decision trees (Breiman et al. 1984; Daniya et al. 2020).For a decomposition C = {G₁ = (V₁,E₁), G₂ = (V₂,E₂),…,G_c = (V_c, E_c)} of a network G = (V,E), the Gini coefficient is defined by the following formula:

  $$Gini\left(G\right)=1-\sum_{i=1}^{c}{p}^{2}({n}_{i})$$

  (28)

  where P(n_i) is the proportion of nodes present in the component G_i(V_i,E_i) and it is determined as follows:

  $$p\left({n}_{i}\right)=\frac{\left|{V}_{i}\right|}{\left|\mathrm{V}\right|}=\frac{{n}_{i}}{\mathrm{n}}$$

  (29)

• The variance is a statistical measure of the dispersion of the values of a distribution. It is calculated as follows:

  $$Var\left(G\right)=\frac{\sum_{i=1}^{c}{|{n}_{i}-m|}^{2}}{\mathrm{c}}$$

  (30)

  where m is the mean value of the distribution, i.e., m = n/c.

The three measures (Gain, Gini and Variance) can be normalized to take their values in [0,1]. For that purpose, we use the following formula:

$${X}^{norm}=\frac{X-{X}^{min}}{{X}^{max}-{X}^{min}}\in \left[\mathrm{0,1}\right]$$

(31)

where X ∈ {Gain,Gini,Var}, X^norm(resp. X^max, X^min) is the normalized (resp. maximal, minimal) value of X. Namely, we can check that:

${Gini}^{max}\left(G\right)=1-\frac{1}{c}$ and ${Gini}^{min}\left(\mathrm{G}\right)=\frac{\left(c-1\right)(2n-c)}{{n}^{2}}$

${Var}^{max}\left(G\right)=\frac{\left(c-1\right){(n-c)}^{2}}{{c}^{2}}$ and ${Var}^{min}\left(\mathrm{G}\right)=0$

${Gain}^{max}\left(G\right)=\frac{{n}^{2}(c-1)}{2c}$ and ${Gain}^{min}\left(\mathrm{G}\right)=\frac{\left(c-1\right)(2n-c)}{2}$

Table 1 gives the directed and normalized values of the three measures (Gain, Gini and Variance) for the different possible distributions in our example. Figure 2 graphically depicts the obtained results.

Fig. 2

Gain, Gini and Variance rates according to the distribution of the nodes on the components

Interestingly enough, we can notice that the normalized gain and the normalized Gini coefficient coincide (Gain^norm(G) = Gini^norm(G)). In contrast, the normalized variance is inversely proportional to the normalized Gini and Gain, and more precisely: Var^norm(G) = 1 − Gain^norm(G).

4 The proposed architecture

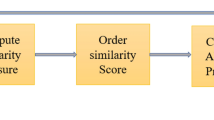
In this paper, we propose an architecture for the link prediction problem which is based on six main steps instead of four steps (Ying et al. 2014), namely: Data gathering, preprocessing, decomposition, parallelization, prediction and evaluation. Our architecture is depicted in Fig. 3.

Fig. 3

Parallel architecture for link prediction based on connected components decomposition

• Data gathering. This step consists of preparing the datasets corresponding to a network, into training and test subsets, the complete dataset is divided according to one of the two following cases:

  • The first principle relies on the evolution time of the dataset (Liben-Nowell and Kleinberg 2007). Since each interaction takes place in a particular instance, we define a training interval $\left[{t}_{0,}{t}_{0}^{^{\prime}}\right]$ which in turn defines the subgraphG^Tr = (V^Tr,E^Tr) containing all the interactions performed between the instants ${t}_{0,}$ and ${t}_{0}^{^{\prime}}$. Similarly, another test interval $\left[{t}_{1,}{t}_{1}^{^{\prime}}\right]$ defines a test sub-graph G^Ts = (V^Ts,E^Ts) containing all the interactions performed between the instants ${t}_{1,}$ and ${t}_{1}^{^{\prime}}$. This principle is used to predict the likelihood of future links (in dynamic networks (Kumar et al. 2020)).

  • Following the second principle, we randomly divide the set of links of the dataset into two subsets, namely, 90% (Lü and Zhou 2011; Xiao and Zhang 2015; Wang et al. 2017; Daminelli et al. 2015) [80% (Ahmad et al. 2020; Wu 2018), 70% (Sui et al. 2013)] of links in a training sub-graph G^Tr = (V ^Tr, E^Tr) and 10% (20%, 30%) of links in a test subset G^Ts = (V ^Ts, E^Ts) where E = E^Tr ∪ E^Ts and E^Tr ∩ E^Ts = ∅. This principle is used to find the missing links [in static networks (Kumar et al. 2020)].

• Preprocessing. This step consists of filtering some nodes of our network by:

  • Eliminating the isolated nodes (Lu et al. 2009) since it is difficult to predict anything about isolated nodes because one has no network-based information.

  • Discarding sometimes the low-degree nodes (Liben-Nowell and Kleinberg 2007; Lu et al. 2009; Scripps et al. 2009) because one has too little information about them.

  • Converting a directed network into an undirected one and subsequently, applying link prediction (Shibata et al. 2012).

  • Restricting the analysis to nodes that are common to the train and test networks (Lu et al. 2009) and eliminating the other nodes.

• Decomposition. In this step we decompose the training graph G = (V,E) into its connected components:

  $$ C\, = \,\{ G_{{1}} \, = \,\left( {V_{{1}} ,E_{{1}} } \right),G_{{2}} \, = \,\left( {V_{{2}} ,E_{{2}} } \right), \ldots ,Gc\, = \,\left( {Vc,Ec} \right)\} . $$

• Parallelization. The connected components are distributed through several processors. Each processor receives one or more components. We use the term local nodes to denote the nodes that each processor receives.

• Prediction. Each component is locally evaluated with its local nodes, and a partial score list is established. At this stage, only one similarity measure is used. In most cases, we want to predict only new links, i.e., links that are not present in the training component. At the end of this operation, all the local list scores are merged into a global list score

• Evaluation. Finally, it becomes possible to evaluate the performance of the prediction results by comparing them with the test subsets. We use different thresholds, parameters and performance measures.

5 Algorithms

In this section we present and compare, in terms of runtime, different scenarios that can be obtained by considering different choice criteria: whether we exploit or not the decomposition of the graph into connected component; whether the algorithm integrates the decomposition step, or directly receives as input the set of connected components, and whether the execution is sequential or parallel. This leads to five scenarios (Algo1-Algo5) explained in the following:

5.1 Without decomposition (Baseline method)

Algo 1. This algorithm corresponds to the baseline scenario, which corresponds to existing works, where the input is the whole graph, no decomposition is done, and of course the execution is sequential.

5.2 With decomposition (our approach)

In this part we propose four new variants of algorithms which exploit the decomposition (see Table 2): Algo2 is the basic algorithm of our approach which will be compared with the baseline algorithm (Algo1). The other algorithms (Algo3–Algo5) are improvements of our basic algorithm (Algo2). The proposed improvements are the following:

• Instead of considering the decomposition step inside the algorithm of link prediction, it suffices to perform it once and start the algorithm from the connected components. This avoids the useless repetitive execution of the same decomposition step in several executions.

• Since each component may be handled separately from the others, one can parallelize the algorithm instead of using a sequential treatment.

Table 2 The four variants of algorithms derived from our decomposition-based approach

Algo3 (resp. Algo4, Algo5) results from Algo2 by integrating the first improvement (resp. second improvement, both improvements).

Algo2. This algorithm includes the decomposition of the input graph into connected components. Then, the prediction task is sequentially executed on the set of connected components.

Algo3. This algorithm is similar to Algo2. but it does not include the decomposition step, but directly receives as input the set of connected components. The prediction task is then sequentially executed on the set of connected components too. Algo3. is obtained from Algo2. by modifying the input to be the set of connected components and by eliminating line 1.

Algo4. Now, this algorithm includes the decomposition of the input graph into connected components. Then, the prediction task is performed by a parallel execution on the set of connected components.

Algo5. This algorithm is similar to Algo4. but it does not include the decomposition step but directly receives as input the set of connected components. The prediction task is then executed in parallel on the m processors. Algo5. is obtained from Algo4. by modifying the input to be the set of connected components and by eliminating line 1.

6 Experimental results

6.1 Datasets

We have performed our experiments on several datasets representing different real-world complex networks from different sources and application domains. This collection covers a wide range of properties, sizes, average degrees, clustering coefficients and heterogeneity indices (see Table 3). This collection is freely downloadable from the address: http://noesis.ikor.org/datasets/linkprediction

• UPG, (Watts and Strogatz 1998) is a power distribution network.

• HPD, (Peri et al. 2003), YST, (Bu et al. 2003) and CEG, (Watts and Strogatz 1998) are biological networks.

• ERD, KNH, LDG, SMG, ZWL, CGS, (Batagelj and Mrvar 2006), HTC, CDM, (Newman 2001), NSC, (Newman 2006) and GRQ, (Leskovec et al. 2007) are co-authorship networks for different fields of study.

• HMT, (Kunegis 2013), FBK, (McAuley and Leskovec 2012), and ADV, (Massa et al. 2009) are social networks.

• UAL, (Massa et al. 2009) is an airport traffic network.

• EML, (Guimera et al. 2003) is a network of individuals who shared emails.

• PGP, (Boguña et al. 2004) is an interaction network of users of the Pretty Good Privacy algorithm.

• BUP, (Kunegis 2013) is a network of political blogs.

• Finally, INF, (Isella et al. 2011) is a network of face-to-face contacts in an exhibition.

Table 3 Illustration of properties of 22 real world networks

6.2 Results and discussion

To demonstrate the effectiveness of our idea on real-world datasets, we have randomly divided the existing links of each network into two sets: The training set and the test set representing 80% and 20% of the total links, respectively. We have used 22 different datasets in the experiments to evaluate the performance of the different methods proposed in this study.

All the calculations have been performed on a machine of type HP Z620Workstation with processor of model: Intel (R) Xeon (R) CPU E5-2620 v2 12cores of frequency 2.10 GHz and a memory size of 128 GB.

6.2.1 Impact of decomposition on the number of calculated links in different datasets

The first part of our experiments is devoted to evaluate the gain obtained for the different used datasets. Table 4 summarizes the obtained results. We notice that Gain₁ denotes the difference between the total number of links calculated without decomposition and those calculated by using decomposition. The gain is expressed in Table 4 both in terms of the number of treated links and in terms of their rate with respect to the total number of links in the train input graph. The corresponding value are put in bold font:

Table 4 Various possible distributions of nodes on the components and their calculation results of gain, Gini and variance

$${Gain}_{1}=\left|{E}_{Tr}^{^{\prime}}\right|-\sum_{i=1}^{c}\left|{E}_{i,Tr}^{^{\prime}}\right| $$

(32)

and

$${\mathrm{rate}}_{\mathrm{Gain}1}=\frac{\left|{E}_{Tr}^{^{\prime}}\right|-\sum_{i=1}^{c}\left|{E}_{i,Tr}^{^{\prime}}\right|}{\left|{E}_{Tr}^{^{\prime}}\right|}=\frac{{Gain}_{1}}{\left|{E}_{Tr}^{^{\prime}}\right|}$$

(33)

Gain₂ is the normalized gain contained in the interval [0,1]:

$${Gain}_{2}=\frac{{Gain}_{1}-{Gain}_{min}}{{Gain}_{max}-{Gain}_{min}}$$

(34)

Notice that Var and Gini in Table 4 denote the normalized values.

From Table 4, we can extract two graphs:

• In the first graph (see Fig. 4) we can observe that the value of the gain is zero for the first two datasets because they contain only one component and therefore the number of links calculated before and after the decomposition. Thereafter we have a gain progression which attains up to 94.19%of the number of links calculated without decomposition but ignored by using decomposition.

Fig. 4

Comparison between the calculated number of links with and without decomposition

Fig. 5

Comparison between the Gain, Variance and Gini values on several datasets

• The second graph (Fig. 5) illustrates the influence of the heterogeneity degree of nodes distribution through connected components on the obtained gain, captured equivalently by the Gini, the Variance or the direct gain normalized measures. We can notice that for the cases where there is only one component, the distribution has no meaning since all the measures (Gain, Gini and Variance) equal zero. When the number of components is greater than 1, The Figure confirms that the more (resp. less) the distribution is uniform the more (resp. less) important is the gain, i.e., the number of ignored links. This graph also confirms, on several real datasets, the relationships between normalized gain, Gini and variance measures already evoked in Sect. 3 on a small example.

To conclude this section, we can notice that the decomposition brings us for sure a gain as soon as the social network contains at least two connected components. This obtained gain is more important in the situations where the distribution of nodes through the components is more uniform which allows us to considerably save runtime, especially for large datasets. The following section focuses on the study of the impact of decomposition on runtime.

6.2.2 Impact of decomposition on runtime

The aim of this section is to show how the decomposition of the training graph helps one to substantially shorten runtime. Saving runtime is ensured thanks to decomposition by two means: First as discussed above, the decomposition allows one to reduce the very amount of necessary computations to perform (first experiment). In addition, the decomposition allows one to save additional runtime by paralleling the link prediction process on several processors (second experiment). Moreover, to have a global view, we give an overall comparison of all algorithms (the baseline algorithm and the different variants of our algorithms) by using four similarity measures and four datasets (third experiment).

• Experiment 1. Comparison between our basic algorithm and the baseline algorithm

In this first experiment, we use Jaccard index as a score measure. We execute all algorithms for 100 times on different synthetic datasets and we take the average runtime obtained for each synthetic dataset. We start from the BUP dataset (see Table 3) which contains one component and we generate new synthetic datasets by successively duplicating the initial one to obtain networks with 2 components, 3 components and so on until10 components. Notice that the obtained datasets are perfectly homogeneous since all the components are identical and accordingly, the obtained gain is optimal (see Table 5 and 6). In Table 5, the number of links treated by Algo2 (after decomposition) as well as its run time are put in bold font to highlight the fact that these results obtained by Algo2 are always better than those obtained by Algo1. In Table 6, the best obtained results in terms of runtime appear in bold font.

Table 5 Results obtained by Algo1 (basic algorithm) and our algorithm Algo2 (with decomposition) on different synthetic datasets with Jaccard index

Table 6 Results obtained by our four algorithms with decomposition on connected components on different synthetic datasets with Jaccard index

We compare our basic proposed algorithm which uses decomposition and performs in sequential way (Algo2) with the baseline algorithm without decomposition which corresponds to the existing approaches (Algo1). The aim of this comparison is to show the impact of exploiting decomposition into connected components on shortening runtime in link prediction.

Table 5 illustrates the results obtained from the first experiment. From Table 5, we can extract the graph depicted in Fig. 6.

Fig. 6

Comparison between the basic algorithm (Algo2) and our proposed algorithm (Algo2) in terms of runtime on synthetic datasets.

From the graph depicted in Fig. 6 we can notice that our algorithm using decomposition (Algo2) clearly outperforms the basic algorithm which does not use decomposition (Algo1) with a very important gap, especially in the case of large graphs with an important number of components, so it is better to decompose the graph before the calculations.

• Experiment 2. Comparison between the variants of our proposed approach

We have demonstrated in Sect. 6.2.1 and Experiment 1 above the necessity of decomposition to minimize the number of links and the runtime. In this second experiment, we limit the comparison to the four variants of our proposed approach (Algo2–Algo5). Recall that the four variants are based on decomposition and they vary according to: (1) the use or not of parallelism and/or (2) the inclusion or not of the decomposition step into the calculation process. Notice that in this experiment we use the same settings and follow the same steps as in Experiment 1.

Table 6 illustrates the results obtained from the second experiment. From Table 6, we can extract the graph depicted in Fig. 7.

Figure 7

Comparison between the four ours algorithms (Algo2–Algo5) using decomposition in terms of runtime on synthetic datasets

On the one hand, we can observe that the necessary time to decompose the graph into connected components is almost negligible. Indeed we can see that the curve for the sequential (resp. parallel) algorithm Algo2 (resp. Algo4) including the decomposition step is very close to that of the sequential (resp. parallel) algorithm Algo3 (resp. Algo5) which directly receives as input the decomposed graph. On the other hand, we can observe that the parallel algorithms Algo4 and Algo5 are much faster than the sequential algorithms Algo2 and Algo3.

In summary, we can confirm the efficiency of using decomposition prior to link prediction. Indeed, this considerably reduces the amount of required computations and consequently leads to a remarkable decrease in runtime.

Moreover, the parallelization of the link prediction process, made possible thanks to the use of connected components instead of a whole network as input, provides us with an additional gain in terms of runtime. The more the network is large, i.e. has a larger number of components and the distribution of nodes through the components is more homogeneous, the more important is the effect of parallelization in reducing the runtime.

• Experiment 3. Overall Comparison between all the algorithms

In the third experiment we have applied the five algorithms (Algo1-Algo5) on four real datasets: NSC, CGS, HTC, and GRQ. In addition, we have used for each dataset four score measures: Jaccard index, Common Neighbor (CN),Adamic Adar index (AA) and Resource allocation index (RA). The implementation of these measures can be found in the networkx library.¹]

The results are shown in the graphs of Fig. 8. According to these graphs:

• We can notice that the four variants of our proposed approach using decomposition (Algo2-Algo4) clearly outperform the baseline algorithm which does not use decomposition (Algo1) with significant gap, especially in the case of large graphs with an important number of components.

• It is also worth noting that the gain rate in terms of calculation time between the baseline algorithm Algo1 and the other proposed algorithms varies according to the change in the variance (resp. Gini) rate: the lower (resp. higher) is the variance (resp. Gini) rate, the higher is the gain rate and vice versa.

Fig. 8

Comparison between all five algorithms on four datasets and using four similarity measures

7 Conclusion

In this paper, we presented an efficient approach for link prediction in large social networks which starts from the set of connected components of a network instead of the whole network itself. The key idea of our proposal is that in all algorithms based on local and path-based measures, it suffices to evaluate links relating nodes of the same component. We have shown that this enables us to considerably save runtime by reducing the number of necessary calculations.

We have formally studied the gain obtained thanks to decomposition and shown both theoretically and experimentally that this gain is more important when the distribution of nodes on the components of the considered network is homogeneous.

Moreover, we have also shown that using decomposition makes possible the parallelization of the link prediction process by distributing the components on several processors. This may provide us with additional gain in terms of runtime, especially for large networks, having a large number of components and where the distribution of nodes on components is homogeneous.

As future work, we plan to develop a fast link prediction library based on our idea of network decomposition and including all local information-based and path-based similarity indices. We plan also to develop a method for combining local and global information for the evaluation of inter-components links that are completely neglected in local and path-based methods, but may make sense in some practical contexts.