1 Introduction

The common problem of estimating the global minimum of a multi-dimensional function is given as

$$\begin{aligned} x^{*}=\text{ arg }\min _{x\in S}f(x) \end{aligned}$$
(1)

where \(S\subset R^{n}\) is defined by:

$$\begin{aligned} S=\left[ a_{1},b_{1}\right] \otimes \left[ a_{2},b_{2}\right] \otimes \ldots \left[ a_{n},b_{n}\right] \end{aligned}$$
(2)

This problem appears in many scientific areas such as Yapo et al. (1998), Duan et al. (1992), chemistry Wales and Scheraga (1999), Pardalos et al. (1994), economics Gaing (2003) etc. During the past years many methods have been proposed in the relevant literature to tackle the global optimization problem. These methods usually are divided into two main categories: deterministic and stochastic. The first category includes techniques such as interval methods Lin and Stadtherr (2004), the TRUST method Barhen et al. (1997), fuzzy optimization methods Angelov (1994) etc. Typically, the deterministic methods are more hard to implement than stochastic methods and in some cases they require a—priory knowledge of the objective function. On the other hand, the stochastic methods are more easy to implement and hence there are a great variety of stochastic optimization methods such as: Simulated Annealing Kirkpatrick et al. (1983), Controlled Random Search Price (1977), Genetic Algorithms Goldberg (1989), Michaelewizc (1996) and Particle Swarm Optimization Kennedy and Eberhart (1999). The Particle Swarm Optimization method (PSO) is a , population-based method. The method creates a population of candidate solutions (swarm of particles) that are evolved simulating the movement of actual particles. For that purpose, each particle maintains its current position \(\overrightarrow{x}\) and a corresponding velocity \(\overrightarrow{u}\). The PSO method has been applied with success in a wide area of problems such as problems from physics de Moura Meneses et al. (2009), Shaw and Srivastava (2007), medicine Wachowiak et al. (2004), Marinakis (2008), economics Park et al. (2010), electronics Hosseini et al. (2019) etc. During the recent years, many modifications of the original PSO method have been suggested such as hybrid techniques Liu et al. (2005), Shi et al. (2005), methods to improve the calculation of the parameters of the method (such as inertia, velocity) Tang and Fang (2015), Yasuda and Iwasaki (2004), Shahzad et al. (2009), methods that adapt the control parameters of the PSO in order to learn only feasible solutions Isiet and Gadala (2019), chaotic quantum-behaved particle swarm optimization techniques Mariani et al. (2012), Araujo and Coelho (2008) etc.

Hybrid methods tends to locate more accurately the global minimum but usually the required an additional amount of function calls. On the other hand, methods that used modified versions of the velocity tends to avoid the explosion problem of the PSO technique but in some cases they are trapped to a local minimum instead of locating the global one.

This article proposes a new stopping rule specifically designed for PSO methods and a technique to bound the velocity avoiding calculation of the objective function outside of the domain definition S (Eq. 2). Various experiments were conducted on a series of well-known test functions from the relevant literature in order to demonstrated the efficiency of the proposed modifications and the results are listed.

The rest of this article is organized as follows: in Sect. 2 the general description of the PSO method is provided as well as the proposed modifications, in Sect. 3 the test functions are described with the conducted experiments and finally in Sect. 4 some conclusions are derived.

2 Method description

The general scheme of the PSO method is listed in Algorithm 1. The algorithm has m particles and each particle has n elements where n is the dimension of the objective function. Each of the m particles is associated with two vectors: the position \(x_{i}\) of the particle and the velocity \(u_{i}\) of the particle. At every iteration a new position \(x_{i}\) is calculated as a combination of the old position \(x_{i}\), the associated velocity \(u_{i}\), the previous best location of the particle \(p_{i}\) and the best location of all particle \(p_{\text{ best }}\). The new point \(x_{i}\) is updated using

$$\begin{aligned} x_{i}=x_{i}+u_{i} \end{aligned}$$
(3)

In most cases the following scheme is used to update the j element of the velocity \(u_{i}\)

$$\begin{aligned} u_{ij}=\omega u_{ij}+r_{1}c_{1}\left( p_{ij}-x_{ij}\right) +r_{2}c_{2}\left( p_{\text{ best },j}-x_{ij}\right) \end{aligned}$$
(4)

where

  1. 1.

    The variables \(r_{1},\ r_{2}\) are random numbers in the range [0,1].

  2. 2.

    The parameters \(c_{1},\ c_{2}\) are constant numbers usually in the range [1,2].

  3. 3.

    The variable \(\omega\) is called inertia and typically is in the range [0,1]. This article uses an update mechanism for the inertia proposed in Shi and Eberhart (1998) and it is given below:

    $$\begin{aligned} \omega =\omega _{\text{ max }}-\frac{k}{k_{\text{ max }}}\left( \omega _{\text{ max }}-\omega _{\text{ min }}\right) \end{aligned}$$
    (5)

    where k is the current number of iterations and \(k_{\text{ max }}\) the maximum number of allowed iterations. Also, \(\omega _{min},\ \omega _{max}\) are user defined and for this article \(\omega _{\text{ min }}=0.4,\ \omega _{\text{ max }}=0.9.\)

Nevertheless, it is clear that Eq. 3 can produce elements that are not belong to set S. This article proposes in Sect. 2.3 a technique that can prevent such cases.

The PSO algorithm terminates when the termination criteria are hold. In these article two stopping criteria are used: a termination check based on the variance of the best discovered minimum that was also proposed in the previous work Tsoulos (2008) and a new termination check based on the changes of the best located positions. The first procedure is defined in Sect. 2.1 and the second in Sect. 2.2.

figure a

2.1 Termination rule based on variance

At every iteration k the variance of \(f\left( p_{\text{ best }}\right)\) is measured. Denote this variance with \(\sigma ^{(k)}\). If there is no any new minimum found for a number of generations, then it is highly possible that the algorithm has found the global minimum and hence it should terminate. The algorithm terminates when

$$\begin{aligned} \sigma ^{(k)}\le \frac{\sigma ^{(\text{ klast })}}{2} \end{aligned}$$
(7)

where \(\text{ klast }\) is the last iteration where a new minimum was found. As an example consider the function Rastrigin defined as

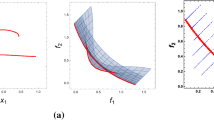
$$\begin{aligned} f(x)=x_{1}^{2}+x_{2}^{2}-\cos \left( 18x_{1}\right) -\cos \left( 18x_{2}\right) \end{aligned}$$

The global minimum in the range \([-\,1,1]^{2}\) is the value − 2.0 Now consider a PSO with 100 particles and let the algorithm terminates when the current number of iterations \(k\ge 200\). The progress of minimization for the Rastrigin function is outlined in Fig. 1. The algorithm located the global minimum at the early stages of the run and before iteration 20. Now consider the plot of the variance of best located value at Fig. 2. The variance decreases very smoothly and hence it can be used as a criterion to terminate the algorithm and preventing unnecessary function calls.

Fig. 1
figure 1

Plot of the progress of minimization for the Rastrigin function

Full size image
Fig. 2
figure 2

The plot of the variance of the Rastrigin function

Full size image

2.2 Termination rule based on similarity

Let us denote with \(p^{(k)}\) the table with the best locations of each particle at iteration k. Also set \(E=0\) at the beginning of the algorithm. At every iteration \(k>1\) we measure the quantity

$$\begin{aligned} g=\left\| p^{(k)}-p^{(k-1)}\right\| \end{aligned}$$
(8)

If \(g<e\), where e a small positive number, then \(E=E+1\). In other words the similarity between the best location between two successive iterations is measured. The algorithm terminates when \(E\ge E_{\text{ max }}\), where \(E_{\text{ max }}\) a small positive integer number. To outline the efficiency of this stopping rule consider again the Rastrigin problem and the same test run with 100 particles and \(K_{max}=200\) as in Sect. 2.1 In Fig. 3 the graph of the quantity g is plotted against the number of iterations. As it can be noticed the value of g very soon tends to zero and hence this quantity can be used as a stopping rule.

Fig. 3
figure 3

Similarity check plot for the Rastrigin function

Full size image

2.3 Velocity bound technique

A common problem of the PSO method is the production of points that are outside of the domain range of the objective function. This problem produced when the changes in the velocity performed without control and it is usually called explosion. The velocity bound technique suggested here is used to prevent this effect with some changes in the basic PSO algorithm.

The first change is performed when the velocities are initialized. The new procedure for velocity initialization is shown in Algorithm 2.3. This procedure ensures that at least for the first iteration of the PSO method every point \(x_{i}\in S\). The second change is to alter the Eq. 4 in order to ensure that every \(x_{i}\in S\). The proposed change for the update of the velocities is listed in algorithm 2.3. This algorithm does not perform any changes in the velocity that will responsible for producing points \(x_{i}\) outside of the domain range.

figure b
figure c

3 Experiments

In order to measure the efficiency of the proposed modifications a series of test functions provided in Ali et al. (2005) were used. These problems are listed in Table 1.

Table 1 Test functions used in the experiments
Full size table

The proposed modifications have been evaluated in terms of number of function calls and successful discover of global minimum using four different experiments:

  1. 1.

    With the variance stopping rule only. In this test only the stopping rule that is based on variance was used. This test is denoted as VARIANCE in the experiments.

  2. 2.

    With the similarity stopping rule only, where only the stopping rule based on similarity was used. This test is denoted as SIMILARITY in the experiments.

  3. 3.

    A test that combines the variance stopping rule and the new bounding technique of velocities. This test is named as VBOUND in the experiments.

  4. 4.

    A test that combines both the similarity stopping rule and the new bounding technique. This test is named SBOUND in the experiments.

The parameters of the PSO method used in the relevant experiments are listed in Table 2. The results for the previous four experiments are listed in Table 3. The column FUNCTION represents the objective function. The numbers in cells stand for the average number of function calls from 30 independent runs using different seeds for the random generator each time. The numbers in parentheses denote the fraction of runs where the global minimum was located. If this number is missing then the global minimum was discovered in every independent run (100% success). The last row of the table contains the total number of function calls for all experiments as well as the average number of success rate. At the end of every run the local search optimization method BFGS of Powell Powell (1989) was applied.

Also, the original pso method using the similarity stopping rule and the new bounding technique has been compared with Quantum behaved PSO method Sun et al. (2006) for the above test functions. The results from this comparison are listed in Table 4. The proposed stopping rule of similarity has been applied successfully in Quantum Pso method and as a consequence the method terminated successfully in the majority of cases. The Quantum PSO method requires less number of function calls for a series of optimization problems in two dimensions but for problems of higher dimension the proposed technique performs better.

From the conducted experiments it is clear that the SIMILARITY rule outperforms VARIANCE stopping rule in almost any test function in terms of function calls and success rate. Also, the new bounding technique for the velocity reduces dramatically (in most cases) the number of required function calls for both stopping rules.

Table 2 Parameters of the PSO method
Full size table
Table 3 Experiments with the two stopping rules and the bound technique
Full size table
Table 4 The proposed method compared against Quantum PSO using the similarity stopping rule
Full size table

4 Conclusions

Two modifications for the general PSO method have been proposed in this article: a stopping rule and a bounding technique for the velocity of the particles. Both modifications are general enough and they can be incorporated in any PSO variant. These modifications does not require any additional information from the objective function and they do not affect the speed of the algorithm since they have small overhead in the computation time. The experimental results indicates that the new stopping rule outperforms another statistical based stopping rule used in the past years and also the conjunction of the new stopping rule with the bounding technique reduces the number of function evaluations needed to discover the global minimum.