1 Introduction

The fuzzy neural networks (FNN) are hybrid models based on the incorporation of fuzzy systems, which are capable of generating interpretability to the results, with the generalist capacity of artificial neural networks, which have several training techniques to solve problems that normally humans act. These structures have been applied in several contexts in the area of artificial intelligence, such as binary patterns classification (de Campos Souza et al. 2018; de Campos Souza and de Oliveira 2018; Lughofer et al. 2018; Lughofer 2012), regression (Juang et al. 2010), time series forecasting (Han et al. 2018; Bordignon and Gomide 2014; Rosa et al. 2013; de Campos Souza and Torres 2018), rainfall (Sharifian et al. 2018), financial market (Rosa et al. 2014), software effort estimation (Souza et al. 2018), failures prediction in some engineering contexts (Song et al. 2018; Tang et al. 2017; de Jesús Rubio 2018, 2017) and so on.

The architecture of fuzzy neural networks have layers that can perform various tasks. Generally, the first layer is responsible for partitioning the input data according to the chosen fuzzy technique. Fuzzy neurons are constructed according to training data and may generate fuzzy rules for the construction of expert systems (Buckley and Hayashi 1994). In the second layer, the updating of the parameters involved may involve techniques such as backpropagation, gradient descent (Amari 1993) and extreme learning machine (Huang et al. 2006), which consists in determining parameters of the hidden layers of the networks at random and calculate the final weights using least squares concepts. The second layer may contain artificial neurons or neural logic neurons. These neurons enable the transformation of model elements into if/else fuzzy rules. The neurons and, orPedrycz and Gomide (2007), unineurons, Pedrycz (2006) and nullneuron, Hell et al. (2008) are highlighted as neurons with this capacity. Evolutionary and genetic approaches are also used. Finally, these models use a neural network of aggregation with artificial neurons to carry out their responses. In general, neurons use activation functions commonly known to obtain the final network output.

When verifying that fuzzy neural networks suffer from problems related to the number of neurons, regularization techniques were incorporated into the models, allowing the less significant neurons to be discarded from the model. In particular techniques such as the regression ridge (Tikhonov et al. 2013), LARS (Hansen 1982) and the bootstrap lasso (Bach 2008) are employed to define the architecture of fuzzy neural networks. This paper presents a new training model in fuzzy neural networks where the first layer of the model has its fuzzy neurons with the synaptic weights and bias defined by wavelet transform functions (Daubechies 1990). The Gaussian membership functions of the fuzzy neurons in the first layer are defined by an algorithm fully data-driven called SODA (Self-Organized Direction Aware) (Gu et al. 2018). This algorithm applies the concept of a directional component based on extra cosine similarity to work in conjunction with a traditional distance metric. In summary, SODA uses nonparametric Empirical Data Analysis (EDA) (Angelov et al. 2017) operators to automatically identify the critical modes of the data pattern from the empirically observed training samples and uses them as focal points to form data clouds. The second layer of the model is composed of unineurons that perform the aggregation of the fuzzy neurons of the first layer. In order to eliminate unnecessary neurons to the model, the algorithm bolasso Bach (2008) to eliminate neurons using the lasso method according to a decision consensus and some bootstraps. Finally, the artificial neural network is present in the third layer of the model, but different from the model of de Campos Souza et al. (2018), where linear activation functions are used, the concepts of rectified linear units (ReLU) are used (Maas et al. 2013).

This type of approach using logical neurons that aggregate neurons formed by cloud techniques allows a more significant number of input data to be worked by the model in a time less than exponential approaches proposed by models that have fuzzification processes based on the model Anfis (Jang 1993).

To verify the capacity of the new model, binary pattern classification tests will be performed in order to evaluate aspects of model accuracy. The paper is organized as follows: Sect. 2 presents the main concepts that guide the research, such as the definitions of fuzzy neural networks, wavelets, regularization and activation functions. Section 3 will present the steps and concepts related to the methodology proposed to generate the first layer weights of the FNN based on the wavelet transform, and the concepts of SODA to construct the first layer neurons, in addition to the artificial neurons based on the activation functions of type ReLU to perform the of binary patterns classification in the output of the model. Section 4 will present the methodology used in the tests, including the bases, and the algorithms used to perform the binary pattern classification. Finally, in Sect. 5 the conclusions of the work will be presented.

2 Literature review

2.1 Fuzzy neural network

Over the last few decades, fuzzy systems and their hybrid derivations have been shown to be able to simulate the typical human reasoning ability in a computationally efficient way. An important area of current research is the development of such systems with a high level of flexibility and autonomy to evolve their structures and knowledge based on changes in the environment, being able to handle modeling, control, prediction and classification of patterns in a situation not stationary, susceptible to constant changes. Fuzzy neural networks are characterized by neural networks composed of fuzzy neurons (Pedrycz and Gomide 2007). The motivation for the development of these networks lies in its easy interpretability, being possible to extract knowledge from its topology. These networks are formed by a synergistic collaboration between fuzzy set theory and neural networks allowing a wide range of learning abilities, thus providing models that integrate the uncertain information handling provided by the fuzzy systems and the learning ability granted by the neural networks (Pedrycz 1991). Thus a Fuzzy neural network can be defined as a fuzzy system that is trained by an algorithm provided by a neural network. Given this analogy, the union of the neural network with the fuzzy logic comes with the intention of softening the deficiency of each of these systems, making us have a more efficient, robust and easy to understand a system.

2.2 Fuzzy neural networks models

FNNs are composed of logical neurons, which are functional units that add relevant aspects of processing with learning capacity. They can be seen as multivariate nonlinear transformations between unit hypercubes (Pedrycz 1991). Studies propose the generalization of logical neurons and and or that are constructed through extensions of t-norms and s-norms. One of the most important features of these neurons, called unineurons, Pedrycz (2006) and nullneurons, Hell et al. (2008), are their ability to vary smoothly from a neuron or to and and vice versa, depending on the need for the problem to be solved. This causes the final structure of the network to be determined by the training process, making this structure more general than fuzzy neural networks formed only by classical logical neurons.

These intelligent models have an architecture based on multilayer networks, where each one of them has different functions for the activities carried out. The layers of a fuzzy neural network can act as fuzzification, transforming numerical data into representations of fuzzy sets, other layers can perform with the defuzzification making the inverse process (convert fuzzy sets into numerical values). Some layers have with fuzzy rules, where they are usually called of fuzzy inference systems and layers representing neural aggregation networks. Each model has layers and different training techniques to solve problems. As examples of three-layers architectures, the proposals of Souza 2018, de Campos Souza and Torres (2018), Guimarães et al. (2018), de Campos Souza et al. (2018) and Guimaraes et al. (2018). Already the models that have four and five layers in its structure, we can highlight the models of Lin et al. (2018) and Kasabov (2001) respectively. In most models, the first layer is the one that partitions the input data, transforming them into fuzzy logical neurons. Algorithms common to these approaches are fuzzy c-means (Bezdek et al. 1984), clouds (Koutrika et al. 2009) and functions based on ANFIS techniques (Jang 1993). The fuzzy neural networks may also present training characteristics based on recurring functions (Yen et al. 2018; Ballini and Gomide 2002), evolving concepts (Silva et al. 2014; Rosa et al. 2013, 2014) and contours-correlated functions (Ebadzadeh and Salimi-Badr 2018).

In this paper, the highlight will be the extreme learning machine (Huang et al. 2006) in conjunction with fuzzy data processing techniques in the first layers. These approaches have already been used in models such as (Souza 2018; de Campos Souza and Torres 2018; Lemos et al. 2012; Rong et al. 2009), differing from the model proposed in this paper by the type of algorithm used for the fuzzification process.

The main difference will be between the change of the ANFIS model (Jang 1993) that uses equally spaced membership functions to a cloud approach. The nature of the input data of the model will have greater significance for the construction of the neurons than an exponential relationship of grid division proposed by models that are based on the techniques of the division of the sample space. This will allow the fuzzification technique used in the fuzzy neural network to create the number of neurons in the first layer much lower when compared to the approaches that use the ANFIS. In techniques that the main fuzzification parameters are based on structures of pertinence functions, many neurons may represent empty or inexpressive spaces for the problem. The SODA technique works with the representativeness of the data, allowing only representative neurons to be created according to the density of the data in the sample space. The fuzzification approach in the input sets defines the number of neurons that will make up the network. Therefore the cloud fuzzification technique leaves the fuzzy neural network more optimized, without losing its ability to solve problems.

Another difference in the approach proposed in this work is how the parameters of the neurons of the first layer (weight and bias) are defined according to the wavelet transform (Daubechies 1990), thus allowing a relationship between the input data of the model and its initial parameters. For this, the concept of the discrete wavelet transform is used through the application of filter banks. This technique can process data at different scales or resolutions and, regardless of whether the function of interest is an image, a curve or a surface, wavelets offer an excellent technique in representing the detail levels present in the data, thus allowing the values recovered are derived from the representation of the input data. In this case, the values obtained by the techniques to be assigned to the weights and bias of the neurons of the first layer will have a representation on the data that will operate, different from the traditional approach that determines these values in a random way and without a meaning of relation with the of the problem.

The unineuron proposed by Lemos et al. (2010) is used to facilitate the actuation of the model, being able to act in different moments like type AND and type OR. This approach allows greater flexibility of the rules of the fuzzy inference system. Unlike the FNN algorithms explained in this topic, the model proposed in this paper intends to use a data cloud technique to create the first layer neurons. Also, in the neuron of the neural aggregation network, we want to insert an activation function that does not activate all fuzzy rules of the problem at the same time. This means only a few features are taken into account in the problem, making the neural network sparse, efficient and easy to process.

2.3 Evolving hybrid models

Intelligent evolving systems are based on online machine learning methods for intelligent hybrid models. These systems are characterized by their ability to extract knowledge from data and adapt their structure and parameters to better adapt to changes in the environment (Kasabov and Filev 2006). They are formed by an evolutionary set of locally valid subsystems that represent different situations or points of operation. The concepts of this learning methodology make it possible to develop unsupervised clustering algorithms capable of adapting to changes in the environment as the current knowledge is not sufficient to describe such changes (Angelov et al. 2008).

The term “evolving” should not be confused with “evolutionary.” Genetic algorithms (Goldberg and Holland 1988) and genetic programming, are based on the evolutionary process that occurs in populations of individuals and use operators based on the concepts of selection, crossing, and mutation of chromosomes as adaptive mechanisms. Also evolving fuzzy systems are based on the process of evolution of individuals throughout their life; specifically the process of human learning, based on the generation and adaptation of knowledge from experiences (Angelov and Zhou 2008).

The evolving models and evolutionary algorithms, which alter parameters as they update new training inputs (Angelov et al. 2010), can be exemplified by the hybrid models proposed by Angelov et al. (2008), Zhang et al. (2006), Aliev et al. (2009), Liao and Tsao (2004), Kasabov (2001), Wang and Li (2003), Yu and Zhang (2005), Hell et al. (2014), Kasabov and Song (1999), Fei and Lu (2018), Maciel et al. (2012), Yu et al. (2018), Pratama et al. (2017), Rong et al. (2009), Lughofer (2011), Angelov and Filev (2004), Subramanian and Suresh (2012), Rong et al. (2006), Rong et al. (2011), Kasabov and Song (2002), de Campos Souza et al. (2019), Angelov and Kasabov (2005), Angelov et al. (2004), Baruah and Angelov (2012), Angelov and Kasabov (2006), Perova and Bodyanskiy (2017).

2.4 Self-organized direction aware data partitioning algorithm- SODA

The process by which fuzzy models treat data can determine how hybrid models can have the interpretability of their results closer to their real world. Models that are fully data-driven are the targets of recent research and have achieved satisfactory results in a cloud data cluster. This clustering concept focused on data is called Empirical Data Analytics (EDA) (Angelov et al. 2017). This concept brings together the data without statistical or traditional probability approaches, based entirely on the empirical observation of the input data of the model, without the need for any previous assumptions and parameters (Gu et al. 2018).

SODA is a data partitioning algorithm capable of identifying peaks/modes of data distribution and uses them as focal points to associate other points to data clouds that resemble Voronoi tessellation. Data clouds can be understood as a particular type of clusters, but with a much different variety. They are non-parametric, but their shape is not predefined and predetermined by the type of distance metric used. Data clouds directly represent the properties of the local set of observed data samples (Gu et al. 2018). The approach employs a magnitude component based on a traditional distance metric and a directional/angular component based on the cosine similarity.

The main EDA operators are described in Angelov et al. (2017), which are also suitable for streaming data processing. The EDA operators include the Cumulative Proximity, Local Density, and Global Density. The local density \(D_n\) is defined as the inverse of the normalized cumulative proximity and directly indicates the main pattern of observed data Angelov et al. (2017), where D for the training input \(x_i\)= (1, 2,...,N); \(N_u\) > 1 is defined as follow Gu et al. (2018):

$$\begin{aligned} D_n(x_i)=\frac{\sum _{j=1}^{n} \pi _n (x_j)}{2n\pi _n(x_j)} \end{aligned}$$
(1)

Global density is defined for unique data samples together with their corresponding numbers of repeats in the dataset/stream, and of a particular unique data sample, \(u_i\) (i=1, 2, ...\(n_u\); \(n_u\) \(\ge\) 1) is expressed as the product of its local density and its number of repeats considered as a weighting factor Angelov et al. (2017) as follows:

$$\begin{aligned} D^G_n(u_i)=f_i D_n (u_i) \end{aligned}$$
(2)

As the main EDA operators (cumulative proximity, local density (D) and global density (\(D^G\))) can be updated recursively, the SODA algorithm can be suitable for online processing of streaming data, causing the updating of density groups of data in an evolving process. The algorithm is performed used in this paper utilizing the following steps (Gu et al. 2018):

Stage 1- Preparation: we calculate the average values between every pair of input data, \(x_1, x_2, \ldots , x_n\) for both, the square angular components, \(d_A\) and square Euclidean components, \(d_M\).

Stage 2- DA Plane Projection: The DA projection operation works with the unique data sample that has the most significant global density, namely \(u^*\) \(_1\). It is initially set to be the first reference, \(\mu _1\) \(\leftarrow\) \(u_1\), which is also the origin point of the first DA plane, denoted by P1 (\(L_c\) \(\leftarrow\) 1, \(L_c\) is the number of existing DA planes in the data space).

Stage 3: Identifying the Focal Points: for each DA plane, expressed as \(P_e\), find the adjacent DA planes.

Stage 4: Forming Data Clouds: After all the DA planes reaching for the modes/peaks of the data density are identified, we consider their origin points, denoted by \(\mu _o\), as the focal points and use them to form data clouds according to as a Voronoi tessellation (Okabe et al. 2009). It is worth to stress that the theory of data clouds is quite similar to the idea of clusters, but differs in the following characters:

  1. (i)

    data clouds are nonparametric;

  2. (ii)

    data clouds do not have a specific shape;

  3. (iii)

    data clouds represent the real data distribution. Figure 1 shows an example of the SODA definition and the center of cloud grouping defined by the algorithm. The data submitted to the SODA model are normalized.

Fig. 1
figure 1

SODA algorithm

Full size image

2.5 Wavelets

Wavelet is a function capable of decomposing and representing another function described in the time domain so that we can investigate this other function in different frequency and time orders. In Fourier analysis, can only identify information about the frequency domain, but we can not know when these repetitions that we study happen. Meantime, in wavelet analysis, we can also extract information from the function in the time domain. The detailing of the frequency domain analysis decreases as time resolution increases, and it is impossible to increase the detail in one domain without decreasing it in the other. Using wavelet analysis, you can choose the best combination of details for an established goal. Adapting this concept to the fuzzy neural networks, the use of wavelet functions can allow the values destined for the bias and the weights of the neurons to be determined according to their nature and no longer in a random way (Daubechies 1990). In this paper, the discrete wavelet will be adopted. This type of methodology is much used in data compression.

In order to calculate the discrete wavelet transforms, it is through the filter bank application where the filter determined by the coefficients \(\textit{h}=\{h_n\}_{n\in {\mathbb {Z}}}\) corresponds to a high pass filter and the filter \(\textit{g}=\{g_n\}_{n\in {\mathbb {Z}}}\) to a low pass filter. Each of these coefficients in the discrete wavelet transform is tabulated. Emphasis is given to the use of the operator \((\downarrow 2)\) is the sub-sampling operator. This operator applied to a discrete function (a sequence) reduces its number of elements in half, recovering only the components in even positions, allowing the procedure to be faster and more precise (Daubechies 1990). The filters h and g are linear operators, which can be employed to the input x as a convolution:

$$\begin{aligned} c(n)= & {} \sum _{k} g(k)x(n-k) = g*x \end{aligned}$$
(3)
$$\begin{aligned} d(n)= & {} \sum _{k} h(k)x(n-k) = h*x \end{aligned}$$
(4)

The decomposition with the filter decays the signal into only two frequency bands. The chaining of a series of filter banks can be accomplished using sub-sampling operation to provide the division of the sampling frequency by 2 to each new filter bank threaded (Daubechies 1990). Figure 2 shows a schematic of the two filters.

Fig. 2
figure 2

Filter decomposition signal of input. Avaliable: https://zh.wikipedia.org/wiki/File:Wavelets-Filter_Bank.png

Full size image

2.6 Rectified linear activation—ReLU

The activation functions allow the introduction of a nonlinear component in the intelligent models, especially those neurons that use logical representations of the human artificial neuron. This characteristic allows intelligent models, such as fuzzy neural networks, to learn more than linear relationships between dependent and independent variables (Karlik and Olgac 2011). Therefore, understanding the functioning of the activation function and in which contexts it can best be applied are preponderant foundations for the success of the model in performing activities that simulate human behavior. They are essential to provide a representative capability for fuzzy neural networks by introducing a nonlinearity component. On the other hand, with this power, some difficulties arise, mainly due to the diversified nature of activation functions, that can vary the effectiveness of their actions according to specific characteristics of the database to which the model is being submitted. In general, by introducing non-linear activation, the cost surface of the neuron is no longer convex, making optimization more complicated. In problems that use parameterization by descent gradients, non-linearity makes it more identifiable which elements need adjustment (Karlik and Olgac 2011). In models of fuzzy neural networks, the main functions of activation are those that use the hyperbolic tangent, Gaussian and linear. Other functions can be highlighted for convolutional and big data problems such as the ReLU (2011), Elu (2015) and Leaky Relu (2013) functions.

A model that has been used to solve various problems is Rectified Linear Activation (ReLU). It a the nonlinear activation function more usually applied to compose neural networks to solve image detection problems. His proposes that if the input is no important to the model, the ReLU function will apply its value to zero and the feature will not be activated. This proposes that at the same moment, only several features are activated, creating the sparse neuron, efficient and straightforward for computing. In these circumstances, the inputs and combinations of a more representative characteristic can act dynamically and efficiently to improve the accuracy of the model (Karlik and Olgac 2011).

Artificial neural networks with the ReLU function are secure to optimize since the ReLU is hugely similar to the identity function. The only difference is that ReLU produces zero in half of its domain. As a consequence, the derivatives stay large while the unit is active (Goodfellow et al. 2016).

3 SODA wavelets regularized fuzzy neural network and ReLU activation function

3.1 Network architecture

The fuzzy neural network described in this chapter follows most of the structure defined in de Campos Souza et al. (2018). However, modifications were made in the first layer (fuzzification) and the third layer (the neural network of aggregation). Unineuron is used to construct fuzzy neural networks in the second layer to solve pattern recognition problems and bring interpretability to the model.

The first layer is composed of neurons whose activation functions are membership functions of fuzzy sets defined for the input variables. For each input variable \(x_{ij}\), \(L_c\) clouds are defined \(A_{lcj}\), \(l_c\) = 1 ...\(L_c\) whose membership functions are the activation functions of the corresponding neurons. Thus, the outputs of the first layer are the membership degrees associated with the input values, i.e., \(a_{jlc} = \mu ^A_{lc}\) for j = 1 ...N and \(l_c\) = 1 ...\(L_c\), where N is the number of inputs and \(L_c\) is the number of fuzzy sets for each input results by SODA.

The second layer is composed by \(L_c\) fuzzy unineuron. Each neuron performs a weighted aggregation of all of the first layer outputs. This aggregation is performed using the weights \(w_{ilc}\) (for i = 1 ...N and \(l_c\) = 1 ...\(L_c\)). For each input variable j, only one first layer output \(a_{jlc}\) is defined as input of the \(l_c\)-th neuron. So that w is sparse, each neuron of the second layer is associated with an input variable. Finally, the output layer is composed of one neuron whose activation functions (f) are ReLU Maas et al. (2013). The output of the model is:

$$\begin{aligned} \mathbf{y }= sign \sum _{j=0}^{l_c} f(z_lv_l) \end{aligned}$$
(5)

where \(z_0\) = 1, \(v_0\) is the bias, and \(z_j\) and \(v_j\), j = 1, ..., \(l_c\) are the output of each fuzzy neuron of the second layer and their corresponding weight, f is the activation function and sign is an operator that transforms the output of the neuron to 1 if it is greater than zero and -1 if it is less than zero, respectively. Figure 3 presents an example of FNN architecture proposed in this paper.

Fig. 3
figure 3

FNN architecture

Full size image

3.2 A proposition to update first layer weights and bias using wavelets

For the first layer of the FNN, training will be performed with each output of the filters of each level of the wavelet transform, thus allowing to update the weights, which by the original definition in de Campos Souza et al. (2018) should be randomly assigned, assigning them the corresponding values of the output of the wavelet filters. Thus, the training of the fuzzy neural network can happen in a parallel way. In addition to allowing better representation of the problems for the weights and bias of the fuzzy neuron.

The algorithm below presents the necessary information about the steps performed to carry out the training and present in Algorithm 1.

In the first layer of this architecture, the initial vector has \(l_c\) values. After the application of the wavelet transform, the resulting vector still with \(l_c\) elements but part of this vector is responsible for the high frequencies (detail), and the other part is responsible for the low frequencies (approximation).

Initially, the wavelet transform is applied to the input data resulting in a vector \(\psi _1\). This vector is then passed to a detail removal function that matches the size of the obtained vector to the size of the output of the current layer so that training can be done resulting in a vector \(\phi _1\). In other words, if the first hidden layer of the FNN has seven neurons, only the first seven values of the vector \(\psi _1\) will be used for the attribution of the weights, the others will be discarded.

Consider that for the FNN example, the initial vector has nine elements. After applying the Wavelet transform, the resulting vector continues with nine elements but part of this vector is responsible for the high frequencies (detail), and the other part is responsible for the low frequencies (approximation). When operating \(RemoveDetails(\psi _1)\) only the first seven elements of the vector are used. In this way, we have two vectors: a vector of 9 items (input of the first layer) and another vector of 7 features (output of the first layer). From this vector of 7 elements, the values responsible for the approximation are assigned to the bias and the detail value to the weights of the neurons in the first layer.

The high filter values will be assigned to the neuron weights, and the low filter values will be allocated to the bias. This procedure ensures that the same amount of weights and bias that would be randomly assigned are provided based on the wavelet transform, allowing these two parameters to be based on the characteristics of the database submitted to the model.

Figure 4 shows that with the input data of the fuzzy neural network model the low and high pass filter functions generate approximation and detail vectors with the input data. In this case, each of these vectors will be assigned to the bias (low) and the weights (high) of the neurons of the first layer. This assignment was made arbitrarily because in preliminary tests it did not matter if it was otherwise.

figure a
Fig. 4
figure 4

Value assignment wavelet for the weights of the neuron and the bias

Full size image

3.3 Training fuzzy neural network

The membership functions in the first layer of the FNN are adopted in this paper as Gaussian, constructed through the centers (\(\beta\)) obtained by the method of granularization of the input space (SODA) and by the randomly defined sigma (\(\sigma\)). Another difference in the first layer is the definition of the fuzzy neuron weights using the wavelet transform. The number of neurons \(L_c\) in the first layer is defined according to the input data, and by the number of partitions (\(\rho\)) defined parametrically. This approach partitions the input space, following the definition logic of creating data nodes. The centers of these created clouds make up the Gaussian activation functions of the fuzzy neurons. These changes will allow the adaptation of the data according to the basis submitted to the model, allowing a more independent and data-centered approach. The second layer performs the aggregation of the \(L_c\) neurons from the first layer through the unineurons proposed by Lemos et al. (2010). These neurons use the concept of uninorm Yager and Rybalov (1996), which extends t-norm and s-norm, allowing the values of the identity element (o) to change between 0 and 1. Therefore, the identity element allows the change of the calculation in the fuzzy neuron in a simple way by alternating the aggregation of elements between an s-norm (if o = 0) and an t-norm (if o = 1). Thus the value of the identity element allows the uninorm Yager and Rybalov (1996) to have the freedom to transform the unineurons into andneurons or in orneurons, within the resolution of the problem. In this paper, the uninorm (U) is expressed as follows:

$$U(x,y) = \left\{ {\begin{array}{*{20}l} {oT(\frac{x}{o},\frac{y}{o}),} \hfill & {if\;y \in [0,o]} \hfill \\ {o + (1 - o)S(\frac{{x - o}}{{1 - o}},\frac{{y - o}}{{1 - o}}),} \hfill & {if\;y \in [o,1]} \hfill \\ {max\;(x,y)\;or\;min\;(x,y),} \hfill & {otherside} \hfill \\ \end{array} } \right.$$
(6)

where T are t-norms, S is a s-norms and o is the identity element. In this paper, we considered the t-norm operator the product and as s-norm operator the probabilistic sum.

The unineuron proposed in Lemos et al. (2010) performs the following operations to compute its output:

  1. 1

    each pair (\(a_i\), \(w_i\)) is transformed into a single value \(b_i\) = h (\(a_i\), \(w_i\));

  2. 2

    calculate the unified aggregation of the transformed values with uninorm U (\(b_1, b_2 \ldots b_n\)), where n is the number of inputs.

The function p (relevancy transformation) is responsible for transforming the inputs and corresponding weights into individual transformed values. This function fulfills the requirement of monotonicity in value which means if the input value increases the transformed value must also increase. Finally, the function p can bring consistency of effect of \(w_i\). A formulation for the p function can be described as Lemos et al. (2010):

$$\begin{aligned} p(w,a)= wa+wo \end{aligned}$$
(7)

using the weighted aggregation reported above the unineuron can be written as Lemos et al. (2010):

$$\begin{aligned} \mathbf{z }=UNI (w;x;a)=U^n_{i=1} p(w_i, a_i) \end{aligned}$$
(8)

The fuzzy rules can be extracted from the network topology and are presented in Eq. 9.

$$\begin{aligned} \begin{aligned} Rule_1: \ If \ x_{i1} \ is \ A_1^1 \ with \ certainty \ w_{11} \ldots \\ and/or \ x_{i2} \ is \ A_1^2 \ with \ certainty \ w_{21} \ldots \\ Then \ y_1 \ is \ v_1\\ Rule_2: \ If \ x_{i1} \ is \ A_2^1 \ with \ certainty \ w_{12} \ldots \\ and/or \ x_{i2} \ is \ A_2^2\ with \ certainty \ w_{22} \ldots \\ Then \ y_2 \ is \ v_2\\ Rule_3: \ If \ x_{il} \ is \ A_3^1 \ with \ certainty \ w_{13} \ldots \\ Then\ y_3\ is \ v_3\\ Rule_4: \ If \ x_{i2} \ is \ A_3^2 \ with \ certainty \ w_{23} \ldots \\ Then \ y_4 \ is \ v_4 \end{aligned} \end{aligned}$$
(9)

After the construction of the \(L_c\) unineuron, the bolasso algorithm (Alg. 2) Bach (2008) is executed to select LARS using the most significant neurons (called \(L_\rho\)). The final network architecture is defined through a feature extraction technique based on l1 regularization and resampling. The learning algorithm assumes that the output hidden layer composed of the candidate neurons can be written as de Campos Souza et al. (2018):

$$\begin{aligned} f(x_i)=\sum _{i=o}^{L_\rho } v_iz_i(x_i)=z(x_i)v \end{aligned}$$
(10)

where v = [\(v_0, v_1, v_2, \ldots , v_{L\rho }\)] is the weight vector of the output layer and z (\(x_i\)) = [\(z_0, z_1 (x_i), z_2 (x_i) \ldots z{L\rho } (x_i\))] the output vector of the second layer, for \(z_0\) = 1. In this context, z (\(x_i\)) is considered as the non-linear mapping of the input space for a space of fuzzy characteristics of dimension \(L_\rho\) (de Campos Souza et al. 2018).

Subsequently, following the determination of the network topology, the predictions of the evaluation of the vector of weights’ output layer are performed. In this paper, this vector is considered by the Moore-Penrose pseudo Inverse de Campos Souza et al. (2018):

$$\begin{aligned} \mathbf{v }= \mathbf{Z }^+\mathbf{y } \end{aligned}$$
(11)

where \(Z^+\) is pseudo-inverse of Moore-Penrose of z which is the minimum norm of the least squares solution for the weights of the output layer and y is the vector of expected output in supervised training.

3.4 Model consistent Lasso estimation through the bootstrap—Bolasso

A universal algorithm used for estimating the parameters of a regression model and selecting relevant characteristics is the Least Angle Regression (LARS) Efron et al. (2004). LARS is a regression algorithm for high-dimensional data that is capable of estimating not only regression coefficients but also a subset of candidate regressors to be included in the final model. LARS is used in the de Jesús Rubio et al. (2018) and de Jesus Rubio et al. (2018) models to perform operator hand movements learning in a manipulator. A modification of the LARS allows the creation of the lasso using the ordinary least squares, a restriction of the sum of the regression coefficients (Efron et al. 2004). Consider a set of n distinct samples (\(x_i\), \(y_i\)), where \(x_i\) = [\(x_{i1}\), \(x_{i2}\), ..., \(x_{iN}\)] \(\varepsilon\) \({\mathbb {R}}^N\) and \(y_i\) \(\varepsilon\) \({\mathbb {R}}\) for i = 1, ..., N, the cost function of Lasso algorithm can be defined as:

$$\begin{aligned} \sum _{i=1}^{N} \Vert z(x_i)\mathbf{v } -y_i \left\| _2 +\lambda \Vert \mathbf{v } \right\| _1 \end{aligned}$$
(12)

where \(\lambda\) is a regularization parameter, commonly estimated by cross-validation.

The first term of (12) corresponds to the sum of the squares of the residues (RSS). This term decreases as the training error decreases. The second term is an \(\ L_1\) regularization term. Generally, this term is added, since it improves the generalization of the model, avoiding the super adjustment and can generate sparse models (Efron et al. 2004).

The LARS algorithm can be used to perform the model selection since for a given value of \(\lambda\) only a fraction (or none) of the regressors have corresponding nonzero weights. If \(\lambda\) = 0, the problem becomes unrestricted regression, and all weights are nonzero. As \(\lambda _{max}\) increases from 0 to a given value \(\lambda _{max}\), the number of nonzero weights decreases to zero. For the problem considered in this paper, the \(z_{L\rho }\) regressors are the outputs of the significant neurons. Thus, the LARS algorithm can be used to select an optimal subset of the significant neurons that minimize (12) for a given value of \(\lambda\).

Bolasso can be seen as a regime of consensus combinations where the most significant subset of variables on which all regressors agree when the aspect is the selection of variables is maintained (Bach 2008). Bolasso uses the decision threshold system (\(\gamma\)) that represents the choice of model regularization, that is, when the value of \(\gamma\) is indicated, it defines the percentage involved in choosing the best regressors. For example, if \(\gamma\) = 0.5 means that if the neuron is at least 50% of resampling as a relevant neuron, it will be chosen for the final model.

Bolasso procedure is summarized in Algorithm 2.

figure b

3.5 Use of activation functions of type rectified linear activation (ReLU) in the neural network aggregation

In sequence to classify higher efficient functions to act as activation functions the paper (Karlik and Olgac 2011) determined the rectified linear activation (ReLU). This function is defined by:

$$\begin{aligned} f_{ReLU}(z_{L\rho })=max \ (0,z_{L\rho }). \end{aligned}$$
(13)

In Eq. (5) the function f is replaced by the function \(f_{ReLU}\).

The learning method can be synthesized as demonstrated in Algorithm 3. It has three parameters:

  1. 1

    the number of grid size, \(\rho\);

  2. 2

    the number of bootstrap replications, bt;

  3. 3

    the consensus threshold, \(\gamma\).

figure c

4 Test of binary patterns classification

4.1 Assumptions and initial test configurations

In this section, the assumptions of the classification tests for the model proposed in this paper are presented. To perform the tests, real and synthetic bases were chosen, seeking to verify if the accuracy of the proposed model surpasses the traditional FNN techniques of pattern classification. The following tables present information about the tests, presenting factors such as the percentage of samples destined for the training and testing of fuzzy neural networks. All the tests with the involved algorithms were done randomly, avoiding tendencies that could interfere in the evaluations of the results. The model proposed in this paper, called SODA-FNN, was compared to fuzzy neural network classifiers using fuzzy c-means (FCM-FNN) (Lemos et al. 2012) and genfis1 (GN-FNN) (de Campos Souza et al. 2018) in the fuzzification process.

In the last two models, the weights and bias were used in the first and second layers randomly, already in the approach proposed in this paper, the weights and bias in the first layer are defined by the wavelets. The number of primary neurons of each model is defined according to the number of centers (FCM-FNN), membership functions (GN-FNN) and grid size (SODA-FNN). For uniformity of the tests, the values involved in the first layers of the models, which end up defining the number of \(L_c\) neurons, were arbitrated in the range of [3–5], where the best results were defined using cross-validation. In the three models, the unineuron is adopted as logical neuron of the second layer. The activation functions of the neurons used in artificial neural networks were ReLU (SODA-FNN), sigmoid (FCM-FNN) and a linear function (GN-FNN). A total of 30 experiments were performed with the three models submitted to all test bases.

In all tests and all models, the samples were shuffled in each test to demonstrate the actual capacity of the models. Percentage values for the classification tests are presented in the results tables, accompanied by the standard deviation found in the 30 replicates. The outputs of the model were normalized to 0 and 1 to aid the correct calculations. The factors evaluated in this paper are as follows:

$$\begin{aligned} accuracy=\frac{TP+TN}{TP+FN+TN+FP} \end{aligned}$$
(14)
$$\begin{aligned} AUC=\frac{1}{2}(sensitivity+specificity) \end{aligned}$$
(15)

where the sensitivity and specificity are calculated using the following equations:

$$\begin{aligned} sensitivity=\frac{TP}{TP+FN} \end{aligned}$$
(16)
$$\begin{aligned} specificity=\frac{TN}{TN+TP} \end{aligned}$$
(17)

where, \(TP =\) true positive, \(TN=\) true negative, \(FN =\) false negative and \(FP=\) false positive. All weights of the output layer were obtained using ELM methods in all models.

4.2 Database used in the tests

The following tables identify the settings applied in the tests. In Table 1, the information of the synthetic bases used in the binary pattern classification tests. In Table 2 the real bases extracted from Bache and Lichman (2013) for classification problems.

Table 1 Synthetic dataset used in the experiments
Full size table
Table 2 Real dataset used in the experiments
Full size table

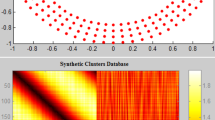
Figure 5 shows the characteristics of the synthetic bases used in the tests.

Fig. 5
figure 5

Synthetic dataset

Full size image

4.3 Binary pattern classification tests

Tables 3 and 4 present the accuracy and AUC results respectively of the tests with the synthetic bases.

Table 3 Acurracy of the model in the tests performed
Full size table
Table 4 AUC of the model in the tests performed
Full size table

After carrying out the tests with synthetic bases, it was confirmed that the proposed model presented smaller accuracy results in the spiral base, which has greater complexity in its composition. The other bases had an equivalent precision within the standard deviation found in the experiments. We highlight the precision of the proposed model and the one that uses a sigmoid activation function, which had a high success rate in all experiments. Figure 6 presents the result of SODA and Fig. 7 the model decision space and Fig. 8 decision 3d plot.

The decision space present in Fig. 7 demonstrates that the technique can act as an excellent pattern classification. Decision spaces are suitable for separating the main samples intended for testing.

Fig. 6
figure 6

Synthetic dataset—SODA result

Full size image
Fig. 7
figure 7

Synthetic Dataset- FNN decision

Full size image
Fig. 8
figure 8

Synthetic Dataset- FNN decision -3d

Full size image

In the next test of pattern classification using real databases will be compared in each one of the models the accuracy of model (Table 5), AUC (Table 6), execution time (Table 7) and the number of fuzzy rules (Table 8) used to obtain the results. Tests performed on a desktop machine with Intel Core i5-3470 processor 3.20GHz and 4.00GB Memory.

Table 5 Accuracy of the model in the tests performed
Full size table
Table 6 AUC of the model in the tests performed
Full size table

In the execution of real tests, it was verified that the model proposed in this paper obtained superior results of accuracy in six of the nine datasets proposed in the test. In the datasets that the model did not take the best test results, it obtained results close to the models evaluated in the test.

From the lower results of the model, the values of the test with the heart dataset are highlighted. The model proposed in this paper obtained a significant difference for the other models in the analysis. Another factor that can also be considered as non-positive was the high standard deviation for the result of the ionosphere base. Although the model obtained the best average results, it showed much instability in solving the problem. On the other hand, in the tests of mammography, transfusion and German credit, the model was very stable in the results. This factor may have happened because the nature of the data is greatly varying in the problems that it presented high standard deviation and remained more stable (or the issues have this nature) during the patterns classification tests.

Table 7 Algorithm execution time for pattern classification (in seconds)
Full size table

The results of Table 7 of the tests prove that the model presents a shorter execution time of binary pattern classification when compared to the other FNN in the test. This enables the proposal acts with less time due to the techniques used to carry out the correct identification of the patterns.

Table 8 Number of fuzzy rules used by the model
Full size table

Another relevant factor about the model is that in addition to presenting a smaller number of fuzzy rules (Table 8), it also presented a much shorter execution time (Table 7) than techniques that use grouping or the model of equally spaced membership functions. If the differences in time and complexity of the fuzzy neural network were much smaller with a limited number of samples, this difference should appear more evident when the model solves problems with many features and also a high number of samples. Therefore, because it has achieved the majority of the best results in the tests of classification of patterns with real databases using less time and a smaller number of neurons/rules, the viability of the model in the resolution of these problems is verified.

An architecture with a smaller number of neurons facilitates the reading of the most relevant fuzzy rules. As the SODA technique works with the data according to their complex nature, problems become more representative directly affecting the constructed fuzzy rules, allowing them to be more representative of the nature of the problem.

It should be noted that FNN now becomes a model to work with a high number of samples or problems with many features, such factor was very complicated when using the ANFIS process in the fuzzification of the model. Extracting knowledge from large volumes of data is a current and fundamental problem for many corporations.

5 Conclusion

The fuzzy neural network proposed in this paper obtained better results than other models that use the extreme learning machine and fuzzy logic neurons. The use of the wavelet transforms allowed the model to use the training data to define the values of the weights and bias in the first layer, thus allowing the parameters of the model to be more coherent with the data submitted to the model. The use of unineuron facilitates the transition of the use of the AND and OR neurons, allowing the interpretation of the fuzzy rules to be closer to the real one. Finally, the use of the SODA technique maintained the interpretability capacity of the FNN model and significantly reduced the execution time when compared to the other FNN models that use logical neurons and fuzzy grouping techniques. Finally, the use of the ReLU activation function helped to improve the responses obtained by the FNN model when compared to the models that use linear and sigmoidal activation functions in real datasets.

The patterns classification tests with less number of fuzzy rules and the use of faster activation functions allow the model proposed in this paper to be identified as a model that maintained the accuracy of pattern classification and at the same time significantly decreased the response time to carry out the activities. This approach accredits the model to work with large-scale databases (big data).

The tests performed verified that the definition of weights and bias using wavelets, the use of a cloud data group and the use of the ReLU activation function is satisfactory for the classification of binary patterns executed by fuzzy neural networks. Basing the parameters to represent the characteristics of the base, we find essential variations in the results of precision found. This approach brings more representativeness to the results of the FNN that can elaborate more fuzzy rules with the input data.

For future work can be checked the impact on the model output and the processing time of your actions using other types of membership functions. Because data clouds theory allows the use of any existing membership function, there may be improvements in the classification of patterns by changing the type of function used.

Other approaches can be performed to optimize parameters related to Grid size, the number of bootstrap repetitions and consensus threshold. Despite finding suitable results, cross-validation spends a high computational time to perform the combinations defined in the tests and determine the models. With advanced optimization techniques, genetic algorithms and other existing intelligent approaches, the best model parameters can be found more dynamically and efficiently. Also in extensions of this work can be applied problems of linear regression, prediction of time series to verify if the model maintains its capacity of universal approximation. Other training approaches can also be evaluated to identify the impacts ELM can generate on parameter setting. Finally, the application of this intelligent model is stimulated for problems with larger dimensions than those that were initially submitted to the test. The SODA technique lowers the complexity of the network structure, so for problems of high dimensionality and Big Data, the model may be suitable to deal with such kind of problems. Testing real problems with large volumes of data is a strongly encouraged approach to examining the model.