1 Introduction

One of the main concerns in control and analysis of the behavior of the nonlinear systems is the knowledge of their exact model. To unravel this problem, different identification methods have been presented to estimate the dynamics of these systems in recent years. Various analytical techniques exist for linear systems such as the recursive least square method (Godfrey and Jones 1986), recursive prediction error technique (Billings et al. 1991), maximum-likelihood method (Bresler and Macovski 1986), and orthogonal least square estimation technique (Chen et al. 1989). Despite the desirable performance of these methods, due to dependency of these structures on some assumptions such as unimodal performance landscapes, differentiability of the performance function, and trapping in local minima, the range of their proficiency is limited (Ursem and Vadstrup 2004).

Due to the complexity of nonlinear systems, however, researchers take some parameters as constant when they want to identify system parameters using analytical methods (Ishaque et al. 2011). They may even ignore some parameters for simplicity (Babu and Gurjar 2014; Hejri et al. 2014; Malekzadeh et al. 2018a, b). This is while such simplifications might have severe impact on system modeling.

Many practical systems do not satisfy these assumptions and as a result, these methods are not usable for them. To get rid of these restrictions, researchers proposed stochastic optimization algorithms such as genetic and particle swarm optimization (PSO) (Malekzadeh et al. 2012, 2016; Azami et al. 2012; Salahshour et al. 2018a, b; Costa et al. 2013; Angelov et al. 2008; Sadeghi-Tehran et al. 2012). The chaotic-based optimization algorithm is another example that attracts researcher attentions in different fields in recent years.

Bounded unstable dynamic behavior with sensitivity to initial conditions and semi-stochastic properties are the main reasons to employ this method in optimization problems (Salahshour et al. 2018a, b; Tavazoei and Haeri 2007; Acharjee and Goswami 2010; Mendel et al. 2011; Li and Yin 2014; Angelov and Yager 2013; Zhou and Angelov 2007; Angelov et al. 2013).

A combination of PSO and neural networks with nonlinear autoregressive with exogenous input in order to identify realistic distillation column has been presented in Jaleel and Aparna (2018). In Zheng and Liao (2016), authors proposed an improved PSO algorithm called SEPSO. They tested their method on a two-link robot. A brief overview of previous researches also reveal that solar panel has attracted many in the community as a remarkable case study in identification process. In Xiong et al. (2018), the authors used improved whale optimization algorithm, in order to identify photo-voltaic parameters. Other methods such as Improved Shuffled Complex Evolution Algorithm (Gao et al. 2018), Adaptive Differential Evolution Algorithm (Chellaswamy and Ramesh 2016), Repaired Adaptive Differential Algorithm (Gong and Cai 2013), Hybrid Flower Pollination Algorithm (Xu and Wang 2017), Simplified Teaching Based Optimization (STBLO) (Niu et al. 2014) have been used for solar panel parameter identification. Another case study attracted attention in parameter identification is chaotic system. Chaos theory is a branch of mathematics focusing on the behavior of dynamical systems that are highly sensitive to initial conditions. Chaotic systems can be used in random-based optimization algorithms instead of random processes. Nowadays, this behavior has been applied in different case studies such as chaotic neural networks (Zhou and Chen 2000) and combination of chaos sequences with evolutionary optimization algorithms in order to search the global optimum (Chatterjee et al. 2011). A new type of chaotic optimization algorithms (COA) is emerged which uses the chaotic sequence in all steps of optimization, namely “global and local optimization”. This paper presents an improved Lozi map-based chaotic optimization algorithm (ILCOA) with such features as higher stability, better escaping the local minima, and improved performance with respect to the regular Lozi map-based chaotic optimization algorithm (LCOA). Also, a new selection strategy for step size λ, namely Semi-Exponentially Step Size (SESS) is proposed which focuses more on small λ and leads to better exploitation for refining the results. The rest of this paper is organized as follows.

Section 2 presents a general form of parameter identification of nonlinear systems. The proposed optimization algorithm is illustrated in Sect. 3. Section 4 demonstrates the simulation results of ILCOA in parameter identification and the conclusion of this study is rendered in Sect. 5.

2 Problem Statement

Different kinds of general nonlinear models have been presented in the literature. The dynamics of most engineering systems and industrial processes can be defined by some of these nonlinear models. This reduces the problem of dynamic identification to just parameter estimation. To illustrate the parameter identification method that is proposed in this study, consider the following nonlinear system definition:

$$\dot {X}=F(X,{X_0},\varphi )$$
(1)

where \(X={[{x_1},{x_2}, \ldots ,{x_n}]^T} \in {R^n}\)is the state vector, \({X_0}\) implies the initial states and \(\varphi \in {R^m}\) is the unknown parameter vector. Also, \(F\) is a given nonlinear vector function. According to (1), the estimated model is defined as follows:

$$\dot {\hat {X}}=F(\hat {X},{X_0},\hat {\varphi })$$
(2)

where \(\hat {X}={[{\hat {x}_1},{\hat {x}_2}, \ldots ,{\hat {x}_n}]^T} \in {R^n}\) is the estimated state vector and \(\hat {\varphi } \in {R^m}\) is the estimated parameter vector.

In order to realize parameter identification, the proposed optimization algorithm is employed to minimize the mean square errors (MSEs) between real and estimated responses for a number of given samples. As we know MSE is considered as a measure of fitness for the estimation of the model parameters. Therefore, the cost function is considered as follows:

$$J=Mse=\frac{1}{N}{\sum\limits_{{k=1}}^{N} {\left[ {X(k) - \hat {X}(k)} \right]} ^2}$$
(3)

where \(N\) is the number of samples.

3 Proposed optimization algorithm (ILCOA)

3.1 Lozi map based chaotic optimization algorithm (LCOA)

Lozi map-based chaotic optimization algorithm has recently been propounded by Coelho (dos Santos Coelho 2009).

The Lozi map can be represented by

$${y_1}\left( k \right)=1 - a.\left| {{y_1}\left( {k - 1} \right)} \right|+y\left( {k - 1} \right)$$
(4)
$$y\left( k \right)=b \cdot {y_1}\left( {k - 1} \right)$$
(5)
$$z\left( k \right)=\frac{{y\left( k \right) - \alpha }}{{\beta - \alpha }}$$
(6)

where k denotes the iteration number. In this work, we normalize the values of y in the range [0,1] to each decision variable in the n-dimensional space of optimization problem. Thus y \(\in\) [− 0.6418, 0.6716] and [α, β] =(− 0.6418, 0.6716). This work uses parameters a = 1.7 and b = 0.5 (Farahani et al. 2012). The following equation provides a functional optimization problem which is used to formulate many unconstrained optimization problems:

$${\text{Find }}X{\text{ to minimize }}f(X),X = [x_{1} ,x_{2} , \ldots ,x_{n} ],$$

where f is the objective function and X is the decision solution vector including n variables which are limited by lower (Li) and upper bounds (Ui). The chaotic search procedure based on the Lozi map can be illustrated as follows (dos Santos Coelho 2009; Farahani et al. 2012);

Step 1 Initialization of variables and initial conditions: Set k = 1, y1(0), y(0), a = 1.7 and b = 0.5 for the Lozi map. Set the initial best objective function f *.

Step 2 Algorithm of chaotic global search:

figure a

where Mg and ML denote maximum number of iterations in the chaotic global and local searches, respectively; f* and X* are the best objective function and the best solution from the current run of the chaotic search, respectively. The effect of the current best solution on the process of generating a new trial solution is controlled by the step size λ. A small λ leads to exploitation which improves results of the local search while a large one leads to a global exploration of search space.

3.2 Improved Lozi map-based chaotic optimization algorithm (ILCOA)

A simplified version of He´non map, Lozi map, is conventionally employed by the LCOA as choatic map in order to replace conventional methods of generating random numbers in both global and local optimization procedure, resulting in a fast converging algorithm capable of searching the search space in a more precise way. The global and local searching capacities and computational efficiency of LCOA has deep roots in the ability of chaotic map to seek the whole search space since the whole optimization procedure is carried out based on chaotic sequences.

An example of evolution of Lozi map is shown in Fig. 1a in which darker areas represent areas with high density where most generated numbers are focused at, while light areas depict areas with lower densities;

Fig. 1
figure 1

Example of evolution (20,000 samples) of a Lozi map. b Modified Lozi map (C1 = 0.4, C2 = 0.8)

Full size image

It can vividly be seen from Fig. 1a that numbers generated by Lozi map suffer from an unfair and unevenly distribution. As it is visible from the figure, we have a very low and low densities respectively at around the bottom, and upside of the interval while a high percentage of generated numbers concentrated in upper half of the interval, in other words, almost 60% of the density is focused in 40% of the area. Furthermore, almost only 25% of the density belongs to the upper half of the interval (0, 0.4) which constitutes 40% of the total area. The remaining density (15%) is focused in (0.8, 1) or 20% of the area. As the Lozi map based generated numbers are not proportionately distributed in the search space, numerous searches are close to the upper half of the interval. As a result the searching capacity, especially around the bottom of the interval, is very weak and unpromising and obviously not beneficial, especially for chaotic global search.

In optimization processes, we usually deal with complex problems with several local minima while we are unaware of the presumptive position of global minimum. Therefore, we are compelled to choose a sufficiently large search space to avoid the trap of local minima. Our problem of having unproportionally distributed numbers, however, would be aggravated this way. Because, the larger the search space, the more parts of it will be out of reach. The size of search space, however, is not the only factor that can adversely affect our problem; the problem can also become more complicated in cases where we are dealing with high-dimensional optimization problems in which the individuals have truly a faint chance to simultaneously reach both the bottom and top areas of the interval. Thus, the algorithm becomes unstable and the optimization result may become very different in each run. The ILCOA algorithm is proposed to combat this problem.

In our proposed ILCOA, we propound to divide the chaotic variable interval to three distinct areas in order to meet the challenge; A1 = [0, C1], A2 = [C1, C2], and A3=[C2, 1], in which 0 < C1 < 0.5, and 0.5 < C2 < 1 are adjustable parameters. During the global search subroutine of ILCOA, when an individual zi is generated, it would be checked to see if it is fallen into area A2. If it belongs to the area A2, it will be passed to the next step at which its cost will be calculated. For the cases of falling into either area A1 or A3, however, it must be regenerated. Lower (Li) and upper limits (Ui) of solution variables must be reformed, as well. Thus, for chaotic global search subroutine of ILCOA, Ui and Li must be replaced by Uinew and Linew, respectively.

where:

$$U_{i}^{{new}}=\left[ {\left( {1 - {C_1}} \right)/\left( {{C_2} - {C_1}} \right)} \right]{U_i}+\left[ {\left( {1 - {C_2}} \right)/\left( {{C_2} - {C_1}} \right)} \right]{L_i}$$
(7)
$$L_{i}^{{new}}=\left[ { - {C_1}/\left( {{C_2} - {C_1}} \right)} \right]{U_i}+\left[ {{C_2}/\left( {{C_2} - {C_1}} \right)} \right]{L_i}$$
(8)

From Fig. 1b, showing distribution of generated numbers by modified lozi map, uniformly distributed density can distinctly be deduced. Analogous modifications are required to be applied to local search subroutine. Thus, in chaotic local search subroutine, we propose the following mapping to be applied to the modified Lozi map:

$$z_{{_{i}}}^{{new}}=\left( {1/\left( {{C_2} - {C_1}} \right)} \right) \times \left( {{z_i} - {C_1}} \right)$$
(9)

where similar to chaotic global search subroutine, C1 \(\leq\) zi \(\leq\) C2; therefore: 0 \(\leq\) zinew \(\leq\) 1.

Another important parameter affecting convergence behavior of optimization method, i.e. step size λ, needs to be modified as well. Selection of the step size λ has a proximate effect on the process of generating a new trial solution. The balance between the global and local exploration abilities is provided by an appropriate value of λ. In this work, we introduce a new selection strategy for step size λ namely; semi-exponentially step size (SESS), which focuses more on smaller values of λ and adds to a better exploitation for refining the results:

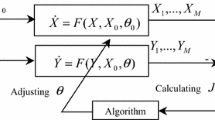
$$\left\{ \begin{gathered} \lambda ={\lambda _{\hbox{max} }} - \frac{{{\lambda _{\hbox{max} }} - {\lambda _{mid}}}}{{{\text{ite}}{{\text{r}}^{\text{1}}}_{{{\text{max}}}}}} \times {\text{iteration}},{\text{ 1}} \leq {\text{iteration}} \leq {\text{ite}}{{\text{r}}^{\text{1}}}_{{{\text{max}}}}{\text{ }} \hfill \\ \lambda =\left[ {{\lambda _{\hbox{max} }} - \left( {{\lambda _{\hbox{max} }} - {\lambda _{mid}}} \right)} \right] \times \exp \left( {\frac{{{\text{ite}}{{\text{r}}^{\text{1}}}_{{{\text{max}}}} - {\text{iteration}}}}{k}} \right),{\text{ ite}}{{\text{r}}^{\text{1}}}_{{{\text{max}}}} \leq {\text{iteration}} \leq {\text{ite}}{{\text{r}}^{\text{2}}}_{{{\text{max}}}} \hfill \\ \end{gathered} \right.$$
(10)

where λmax is the initial step size, λmid is the step size of linear section ending, itermax2 is the total searching generations in local search subroutine (itermax2 = ML), itermax1 is the used generations the step size of which is linearly reduced. Different ending values of λ can be achieved through adjusting k. It is evident from (10) that, at the initial searching stage λ will be linearly reduced, so that a better global exploration of search space would be possible. Furthermore, around the global optimum, it is possible to concentrate most iterations at small λ by using the exponential term of (10), and achieve more precision. Flowchart of the proposed ILCOA is provided by Fig. 2.

Fig. 2
figure 2

Flowchart of the proposed ILCOA

Full size image

4 Simulation results

To evaluate the performance of the proposed algorithm, we implemented it on 3 systems: Lu system, Lorenz system and the permanent magnet synchronous motor. Lu and Lorenz systems are benchmark systems, on which the algorithms are implemented for testing their performance and having a fair comparison with other existing algorithms. The synchronous permanent magnet motor system formulate the physical dynamics of a motor model. This system is included along with the two benchmark systems as an example of a practical system, with which we deal very much in the industry.

In this section, GA, PSO, DE, ABC, DE/ABC and WOA algorithms are implemented on each system and compared with the proposed algorithm. The purpose of these algorithms is to identify the system parameters so that the cost function (3) tends to zero. The number of iterations was constant in all algorithms and set to 200 to have a correct comparison between the algorithms. Population size was considered to be 30 for each algorithm. Each algorithm was separately run for 30 times. Moreover, the sampling rate was considered to be 0.001 for all systems. The simulation has been implemented in a 64-bit version of MATLAB 2016a and run on Windows 10, CORE i7 Intel, 8 GB Ram.

4.1 Chen system

In the first example, Chen system (1999), whose equations are given below, is investigated:

$$\begin{gathered} \dot {x}=a(y - x) \hfill \\ \dot {y}=(c - a)x - xz+cy \hfill \\ \dot {z}=xy - bz \hfill \\ \end{gathered}$$
(11)

where \(x,y\,\,{\text{and}}\,\,z\) the state variables, and \(a,b\) and \(c\) are system parameters that are equal to 35, 3 and 28, respectively. The initial values of the state variables are [x(0) y(0) z(0)] = [0 2 10].

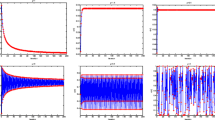
Table 1 contains the best value of the cost function and the identified values after 30 runs of the algorithms. We can clearly see from this table that the proposed algorithm can able to identify parameters better than other algorithms, and the best performance after it, is related to the DE/ABC algorithm followed by the LCOA algorithm. Figures 3, 4 and 5 show the relative estimation error obtained from each run, where the relative estimation error of the parameter \(\theta\) is obtained from the relation \((\tilde\theta-\theta)/\theta\), in which \(\tilde\theta\) is the estimated parameter and \(\theta\) is the original parameter. As stated above, the best case is when the algorithm has the least error in identifying the parameters and when the value of the cost function tends to zero. Therefore, it can be concluded from Figs. 3, 4 and 5 that the ILCOA algorithm has a better performance than other algorithms. Figure 6 shows the best value obtained for the cost function through the 200 iterations among the 30 runs. It can also be easily seen in this figure that the ILCOA algorithm has a better performance than other algorithms and has been able to bring the cost function well towards zero. It can be seen in Figs. 7, 8 and 9 how the parameters converge to their original value. It can be seen that the ILCOA algorithm has been able to converge towards the parameter’s original value with good speed and precision and shows a good performance among other algorithms.

Table 1 Statistical results from the seven algorithms on the Chen system
Full size table
Fig. 3
figure 3

The mean error value of the identified parameter \(a\) in the Chen system

Full size image
Fig. 4
figure 4

The mean error value of the identified parameter in the Chen system

Full size image
Fig. 5
figure 5

The mean error value of the identified parameter \(c\) in the Chen system

Full size image
Fig. 6
figure 6

Convergence of the cost function’s value in the Chen system

Full size image
Fig. 7
figure 7

Convergence of the identified parameter \(a\) to the original value of the parameter \(a\) in the Chen system

Full size image
Fig. 8
figure 8

Convergence of the identified parameter \(b\) to the original value of the parameter in the Chen system

Full size image
Fig. 9
figure 9

Convergence of the identified parameter \(c\) to the original value of the parameter \(c\) in the Chen system

Full size image

In Table 2, in order to compare ILOCA and LOCA, the values of their corresponding cost functions in 10 separate runs have been shown. Going through the results one can see that the ILOCA algorithm is more stable. Moreover, its cost function reaches a lower value.

Table 2 The results of cost function for ILCOA and LCOA on the Chen system
Full size table

4.2 Lorenz system

In the second example, we investigate the Lorenz system (Lorenz 1963), whose equations are given below.

$$\begin{gathered} \dot {x}=a(y - x) \hfill \\ \dot {y}=(b - z)x - y \hfill \\ \dot {z}=xy - cz \hfill \\ \end{gathered}$$
(12)

where \(x,y\), and \(z\) are the state variables, \(a,b\), and \(c\) are system parameters that are equal to 10, 28, and 8.3 respectively. The initial values of the state variables are [x(0) y(0) z(0)] = [2 1 1].

Table 3 shows that the ILCOA algorithm has been able to perform better than other algorithms over 30 runs, and after it, the DE/ABC and LCOA algorithms have the best performance. The famous and powerful PSO algorithm failed to appear as it should and did not have an appropriate performance. Figures 10, 11 and 12 show the relative error of identifying the parameters. In this figure, the relative error of identifying the parameters over 30 runs is measured and put along with each other for comparison. Figure 13 shows the convergence of the cost function to zero, in which it can be easily seen that the algorithm that has been able to achieve a lower cost function is the ILCOA algorithm. Figures 14, 15 and 16 show the convergence of the identified parameters towards the original value of the parameters. It can be seen that the proposed algorithm has been able to quickly identify the original value of the parameter. With paying a little attention to the figures, the strength and accuracy of the proposed algorithm can be seen.

Table 3 Statistical results from the seven algorithms on the Lorenz system
Full size table
Fig. 10
figure 10

The mean error value of the identified parameter in the Lorenz system

Full size image
Fig. 11
figure 11

The mean error value of the identified parameter in the Lorenz system

Full size image
Fig. 12
figure 12

The mean error value of the identified parameter in the Lorenz system

Full size image
Fig. 13
figure 13

Convergence of the cost function’s value in the Lorenz system

Full size image
Fig. 14
figure 14

Convergence of the identified parameter to the original value of the parameter in the Lorenz system

Full size image
Fig. 15
figure 15

Convergence of the identified parameter to the original value of the parameter in the Lorenz system

Full size image
Fig. 16
figure 16

Convergence of the identified parameter to the original value of the parameter in the Lorenz system

Full size image

In Table 4, in order to compare ILOCA and LOCA the values of their corresponding cost functions in 10 separate runs have been shown. Going through the results one can see that the ILOCA algorithm is more stable. Moreover, its cost function reaches a lower value.

Table 4 The results of cost function for ILCOA and LCOA on the Lorenz system
Full size table

4.3 The permanent magnet synchronous motor system

In the last example, the permanent magnet synchronous motor system (Wang et al. 2014), whose equations are given below, is investigated.

$$\begin{gathered} \dot {x}= - x+yz \hfill \\ \dot {y}= - y - xz+az \hfill \\ \dot {z}=z+b(y - z) \hfill \\ \end{gathered}$$
(13)

where \(x,y\), and \(z\) are the state variables, and \(a,b\) are the system parameters, which are 20 and 5.46, respectively. The initial values of the state variables are [x(0) y(0) z(0)] = [5 1 − 1].

Table 5, similar to Tables 1 and 3, shows the best value for the cost function over 30 runs, as well as the values of the identified parameters. It can be seen that the ILCOA algorithm identifies the parameters with a value of the cost function less than the other algorithms. The DE/ABC algorithm has shown a good performance. Figures 17 and 18 show the relative error of the identified parameters \((a,b)\) obtained from the relations, respectively. The ILCOA algorithm has the lowest relative error over 30 runs compared to the other algorithms. From the performance of the algorithms based on the convergence of the cost function to zero, it can be seen in Fig. 19 that the ILCOA algorithm has been able to perform better than other algorithms. In Figs. 20 and 21 that show the convergence of identified parameters to the original value of the parameters, it can be well seen that the proposed algorithm has been able to identify the parameters well in a timely manner. It can be clearly concluded from all the figures that the proposed algorithm has a very good performance compared to other algorithms.

Table 5 Statistical results from the seven algorithms on the permanent magnet synchronous motor system
Full size table
Fig. 17
figure 17

The mean error value of the identified parameter in the permanent magnet synchronous motor system

Full size image
Fig. 18
figure 18

The mean error value of the identified parameter in the permanent magnet synchronous motor system

Full size image
Fig. 19
figure 19

Convergence of the cost function’s value in the permanent magnet synchronous motor system

Full size image
Fig. 20
figure 20

Convergence of the identified parameter to the original value of the parameter in the permanent magnet synchronous motor system

Full size image
Fig. 21
figure 21

Convergence of the identified parameter to the original value of the parameter in the permanent magnet synchronous motor system

Full size image

In Table 6, in order to compare ILOCA and LOCA the values of their corresponding cost functions in 10 separate runs have been shown. Going through the results one can see that the ILOCA algorithm is more stable. Moreover, its cost function reaches a lower value.

Table 6 The results of cost function for ILCOA and LCOA on the permanent magnet synchronous motor system
Full size table

5 Conclusion

In this paper, the ILCOA algorithm has been presented to identify the parameters of nonlinear systems. The ILCOA algorithm has been a good choice for evaluating the unknown parameters of the nonlinear dynamic system due to its high performance, short and desirable run time in finding global minima and avoiding local minima. This algorithm has been used along with other algorithms to identify two chaotic systems of Chen and Lorenz as well as a permanent magnet synchronous motor system. Simulation results ascertain the very good performance and high speed of this algorithm in identifying these systems in comparison with other algorithms.