1 Introduction

Successful transmission of power over a particular area or tremendous district which is ensured by the electrical system is an interconnection of various fundamental parts. To ensure compelling operation and solidness of the interconnected power system (Naidu et al. 2014) honest to goodness collaboration between the transmitting, generating, and distributing components of the power system is basic. Dynamic power balance and constant frequency are required Mosaad and Salem (2014) to ensure strength of the power system. Some certified outcomes to power plants and safe operation of systems, and furthermore clients is passed on when in doubt by repeat vacillations, for instance, from working condition it builds the generator sets and assistant power machines go off to some faraway place, finally impacts the entire fiscal operation of power grid (Sun et al. 2016) diminishing the mechanical productivity and influences power plant operation to go out of order from money related proficiency.

In power systems under load varieties Mosaad and Salem (2014) frequency control is a key soundness measure. Basic level and optional level are the two fundamental levels where frequency is controlled. Totally started inside 10–30 s after the unevenness the essential level is a decentralized speed control of the attracted age units. At the mandatory time of 10–20 min (Rerkpreedapong et al. 2003) the optional level, i.e., load frequency control (LFC), is then sent inside. Since the errand is to limit the variety between the zone frequency and the TLP interchange the idea of load frequency control (LFC) is specifically identified with the previously mentioned factors. At invalid position (Sahu et al. 2015; Parmar et al. 2014; Shivaie et al. 2015; Sekhar et al. 2016) the key thing is to keep up the consistent state. In conventional to build load frequency controller (Khezri et al. 2016; Pan and Das 2015) unique controllers have been connected. However in view of established and experimentation approaches the current LFC systems in the useful power systems utilize the pi sort controllers that are tuned on the web. To upgrade the LFC of the multi-region system many control approaches likewise included that have been used for instance, load–frequency controller (Selvakumaran et al. 2012), non-linear sliding mode controller (SOC), Optimal Load Frequency Control (OLFC) (Shayeghi et al. 2009; Yu et al. 2004), load frequency control (Jiang et al. 2012), Polar Fuzzy Controller (PFC) (Chaturvedi et al. 2015) and Load Frequency Control (LFC), field programmable gate array (FPGA) implementation of reversible watermarking (RW) algorithm (Yang et al. 2018; Parmar 2014; Zribi 2005). On the off chance that the idea of the aggravation fluctuates, they may not execute not surprisingly as these control approaches are intended for a particular unsettling influence. Additionally for vast systems like power systems with nonlinearities and not characterized parameters since they are show based controllers that are needy to a particular model, and are not usable, and after that thus, for LFC issue in deregulated conditions (Mi et al. 2016; Qian et al. 2015) a versatile and adaptable controller are more appropriate.

This paper introduces the Load Frequency Control (LFC) of three area power system using a technique called enhanced linear quadratic regulator (ELQR) based state feedback gain controller. The three area power system contains the combination of reheat thermal generator, wind generator and hydro power system. The proposed new intelligent controller is called as enhanced linear quadratic regulator (ELQR) which is the joined execution of both the Kalman filter (KF) and LQR. Here, a KF is designed to assessment the required state variables at the expense of slight performance degradation. KF uses the state space matrices Q and R, and the initial values for the calculation of gain values to assessment the real signal value. As per the non-linear frequency variation of the three area system, the ELQR predicts the optimal state feedback gain parameters of the controller. This procedure guarantees the system frequency control under the load disturbance influence by minimizing the automatic control error (ACE) and the tie line power variation. The proposed technique is clearly described in detail. The remainder of this article is organized as follows, the recent research work and the background of the research work is discussed in Sect. 2: the proposed technique thorough explanation is explained in Sects. 3 and 4. The suggested technique achievement results and the related discussions are given in Sect. 5 and the paper is concluded in Sect. 6.

2 Recent research works: a brief review

Every once in a while finished most recent couple of decades keeping in mind the end goal to show better unique reactions the LFC issue of an interconnected power system arrange is extended by a few researches. In the literature a couple of control strategies are talked about here to solve LFC issue.

To outline a control law, which viably worked out the issue on the most ideal approach to adequately using the aggregate tie-line power flow in the interconnected power systems Cai et al. (2017) have proposed another methodology which associated the structure and vitality properties of multi territory LFC system. With PI and supplementary ADP control, Dong et al. (2017) have presented a novel occasion activated approach for LFC system. The trivial event’s transmission was turned away by using their proposed outline. To handle LFC issue for an interconnected power system arrange Guha et al. (2018) have shown the utilization of BSA as new optimization algorithm that gives a broad examination of its tuning displays. To restrain wellness work using their proposed methodology, ITSE are considered. In perspective of a blend of a novel heuristic calculation, named MHSA, M. Khooban et al. (2017) have presented a novel clever versatile PI controller, and to deal with the issue of load frequency control plan in islanded small scale networks the general sort II fuzzy logic is utilized.

To control the frequency in load of an interconnected power system that fuses a breeze cultivate Liu et al. (2017) have inspected another sorted out DMPC. The LFC structure is reproduced to offer a wind-speed dependent optimization mode since the dynamic model for the WTG is exceptionally not exactly the same as the standard power plant. With a particular ultimate objective to deal with the LFC issue of a two-area interconnected multi-source power system, Sahu et al. (2016) have proposed a half and half LUS– TLBO evaluation is utilized to upgrade the additions of the proposed fuzzy and conventional PID controller. Finally, for wide assortment in parameters of power system, it was shown that the proposed LUS-TLBO algorithm optimized fuzzy-PID controller makes the AGC structure more overwhelming and stable. As following control issues of vast scale system in proximity of both external agitating impacts and constraints, Ma et al. (2014) have figured the LFC issue of the deregulated multi-zone interconnected power system which addresses the necessities on rate of generator and load set reference point inside breaking points.

2.1 Background of the research work

A load frequency controller (LFC) is generally used to guarantee a decent nature of the power systems through controlling the deviations. The audit of the current research work exhibits that, while keeping the frequency variances inside pre-determines limits, the LFC constitutes an imperative capacity of power system operation where to manage the yield power of every generator at recommended levels is the principle objective. In a multi-zone interconnected power system to protect zero unfaltering state blames and to finish the demanded dispatch conditions in addition to it must be incredible against unidentified outside aggravations and system model and parameter vulnerabilities are the destinations of the LFC. To work out the LFC issue in present day power system systems a few examines are in the advancement. PID controller, dynamical fuzzy network (DFN), dynamic wavelet network (DWN), two-level structure, decentralized adaptive control scheme, robust analysis, fuzzy logic controller (FLC), DE optimized parallel 2-DOF PID controller, dual mode controllers, output feedback controller, Fuzzy C-Means clustering technique, Neural network model predictive control (NN-MPC), Genetic Algorithm (GA), Particle Swarm Optimization (PSO) algorithm etc are few of the strategies for working out the LFC. The control activity of this controller is relying upon the tuning gains however normally the PID sort controllers are connected. In managing the nonlinear characteristics of the power system, they have their own issues the artificial intelligence (AI) systems like FLC, NN and so forth techniques are viable. Be that as it may, it experiences choosing number of layers and to get the productive signals requires hard work, the long training time, needs fine tuning and simulation before operation. The pondering in the field of controller parameter optimization, the global optimization techniques like GA, PSO and DE has bothered. Inferable from the thought of their administrators, the computational trouble of this populace based calculation is raised. Subsequently, to make beyond any doubt the predetermined issue, the optimal solution convergence time is raised. Viable control topologies are required to beat these issues. To take care of this issue not very many works are exhibited in writing and the introduced works are inadequate. To do this exploration work, these disadvantages have provoked.

3 Interconnection of multi area power system

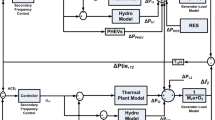
An interconnected multi area power system comprises of multiple areas in control which are interconnected by means of tie lines power. In every control area the generators of the power system are expected to form a coherent group. The power system few areas are assumed to have a load disruption of various magnitudes. The power system investigated here is assumed to have three control areas, for example, thermal unit, hydro unit and wind power unit which are shown in Fig. 1. Each of these areas supplies its power to the user pool and the tie-line power enables the electric power to flow between the associated areas. In this way, the load distribution in one area influences the power flow on tie-lines and also the output frequencies of different areas. Along these lines, each area of the control system needs information to convey the local frequency to its steady state value from the transient situation of the corresponding area. While the frequency is the information about each area and the disturbance of TLP flow is the information about the other area. The modeling of the three area power system is clarified in the subsection.

Fig. 1
figure 1

Schematic diagram of power system with three areas

Full size image

3.1 Modeling of three area power system

The mathematical relation of the three area power system model is developed to be linear by making certain assumptions and approximations. The interconnection of the three area system utilizing MATLAB/Simulink has been shown in Fig. 2.

Fig. 2
figure 2

Block diagram of an AGC for thermal-wind-hydro power system

Full size image

The modeling depends on the transfer function approach and the state space modeling of system has been done to investigate the execution of the integral action based controller and LQR-PID controller. The Laplace domain function state space equations is spoken to as,

$$\Delta {f^i}(s)=\,\frac{{K_{p}^{i}}}{{1+sT_{p}^{i}}}\left[ {\Delta P_{g}^{i}(s) - \Delta P_{d}^{i}(s) - \Delta P_{{tie}}^{i}(s)} \right]$$
(1)
$$\Delta P_{r}^{i}(s)=\,\frac{1}{{1+sT_{t}^{i}}}\Delta X_{e}^{i}(s)$$
(2)
$$\Delta P_{g}^{i}(s)=\,\left[ {\frac{{1+sK_{r}^{i}T_{r}^{i}}}{{1+sT_{r}^{i}}} - } \right]\Delta P_{r}^{i}(s)$$
(3)
$$\Delta P_{{ref}}^{i}(s)=\, - \frac{{K_{I}^{i}}}{s}\left[ {\frac{{{B^i}}}{{2\pi }}\Delta {f^i}(s)+\Delta {P^i}(s)} \right]$$
(4)
$$\Delta X_{e}^{i}(s)=\frac{1}{{1+sT_{g}^{i}}}\left[ {\,\Delta P_{{ref}}^{i}(s) - \frac{1}{{2\pi {R^i}}}\Delta {f^i}(s)} \right]$$
(5)

Where, \((i=1,\,2,\,3)\) represents the each area of the thermal, wind and hydro units in the power system. \(\Delta {f^i}\) is the frequency incremental change of the \({i^{th}}\) area, \(k_{p}^{i}\), \(k_{I}^{i}\) and \(k_{r}^{i}\) are the gain constant of generator, integral controller and reheat thermal unit of the \({i^{th}}\) area, \(T_{p}^{i}\), \(T_{g}^{i}\) and \(T_{r}^{i}\) are the time constant of the power system, generator and reheat unit of \({i^{th}}\) area. \(\Delta X_{e}^{i}\) is the governor valve position of the \({i^{th}}\) area, \(\Delta P_{g}^{i}\), \(\Delta P_{d}^{i}\) and \(\Delta P_{r}^{i}\) are the power area of the generator, demand and regeneration and \(\Delta P_{{tie}}^{i}\) is the tie-line power. For each area, the state space equation identified with the variables is different depending upon the system design. The deviation of tie line power in the power system is expressed as follows,

$$\Delta P_{{tie}}^{{12}}(s)=\,\frac{{{T_{12}}}}{{2\pi s}}\left[ {\Delta {f^1}(s)+\Delta {f^2}(s)} \right]$$
(6)
$$\Delta P_{{tie}}^{{23}}(s)=\,\frac{{{T_{23}}}}{{2\pi s}}\left[ {\Delta {f^2}(s)+\Delta {f^3}(s)} \right]$$
(7)
$$\Delta P_{{tie}}^{{31}}(s)=\,\frac{{{T_{31}}}}{{2\pi s}}\,\left[ {\Delta {f^3}(s)+\Delta {f^1}(s)} \right]$$
(8)

The term \(\Delta P_{{}}^{i}\)\((i=1,\,2,\,3)\) variables in the state equation is clarified as far as tie line power deviations regarding the corresponding area and it is represented as,

$$\Delta P_{{}}^{1}(k)=\,\Delta P_{{tie}}^{{12}}(k)+{a_{31}}\Delta P_{{tie}}^{{31}}(k)\,\,\,\,$$
(9)
$$\Delta P_{{}}^{2}(k)=\,\Delta P_{{tie}}^{{23}}(k)+{a_{12}}\Delta P_{{tie}}^{{12}}(k)$$
(10)
$$\Delta P_{{}}^{3}(k)=\,\Delta P_{{tie}}^{{31}}(k)+{a_{23}}\Delta P_{{tie}}^{{23}}(k)\,$$
(11)

where, \({a_{12}}\), \({a_{23}}\) and \({a_{31}}\) are represented as − 1 since here it is assumed as the rated power of each area is equal and \(k\) represents the sampling index. The power errors in the tie line is calculated from the below expression as,

$$\Delta P_{{err}}^{i}=\,\Delta P_{{act}}^{i}+\Delta P_{{tie}}^{i}\,\,\,\,$$
(12)

In the steady state condition, the ACE signal is generated from the error signal. To eliminate the frequency error in all areas is the main goal of the LFC is not yet to keep up the tie-line power. In each area by diminishing the ACE signal to zero, the frequency deviation alongside the error in the tie-line power is additionally limited. The ACE error signal is expressed as,

$$ACE_{{}}^{i}=\sum\limits_{{i=1}}^{N} {\Delta P_{{tie}}^{i}} \,+\,\,{B^i}\Delta f_{{}}^{i}$$
(13)

where, \(AC{E^i}\) is the actuating control error signal of the \({i^{th}}\) area, \(\Delta P_{{tie}}^{i}\) is the deviation of power interchange between the associated areas, \(\Delta {f^i}\) is the deviation in frequency and \(N\) is the number of areas interconnected with area \(i\). \({B^i}\) is the frequency bias factor of area\(i\) which is given by,

$${B^i}=\frac{1}{{{R^i}}}+{D^i}$$
(14)

The actuating error signal activates the changes in the frequency set point of area \(i\), the deviation of tie-line power and the frequency deviation is zero when the steady state condition is reached. The steady state form in the three area power system in Laplace domain function is expressed as below,

$$X^{\prime}\;(s)=A^{\prime}\;{X^T}(s)+B^{\prime}\;{U^T}(s)$$
(15)

where, \(X\) is the state vector and the demand vector is \(U\). The state variables and input for the three area power system utilizing conventional integral controller is expressed as,

$${X^T}={\left\{ {\Delta {f^i},\,\Delta P_{r}^{i},\Delta P_{g}^{i},\,\Delta P_{{ref}}^{i},\Delta X_{e}^{i}\,,\,\Delta P_{{tie}}^{i}} \right\}^T},\,\,\,\,\,i=1,2,3$$
(16)
$${U^T}={\left\{ {\Delta P_{d}^{1},\Delta P_{d}^{2},\Delta P_{d}^{3}\,} \right\}^T}$$
(17)

where, \(\Delta {f^i}\)is the frequencies incremental change of the\({i^{th}}\)area, \(\Delta X_{e}^{i}\) is the governor valve position of the \({i^{th}}\) area, \(\Delta P_{g}^{i}\), \(\Delta P_{d}^{i}\) and \(\Delta P_{r}^{i}\) are the power area of the generator, demand and regeneration and \(\Delta P_{{tie}}^{i}\) is the tie-line power. Also, to extend the physical constraints, the generation limits are assumed to be 0.1 pu for thermal areas and for the hydro area, 4.5% per second is assumed. The frequency bias and speed drop control has been applied for the wind plant. Additionally the damping ratio and natural frequency for proper modeling of the wind plant has been chosen precisely. To keep up the stability, the active power of each area must be controlled. The range for the gain parameters is changed in accordance to keep up the stability of the system and the controllers are effortlessly feasible to design with the optimized values. The performance index for Kalman based state feedback gain controller is chosen as an integral square error (ISE) which is expressed as,

$$ISE=\int {\left\{ {{{(\Delta {f^i})}^2}+{{(\Delta P_{{tie}}^{i})}^2}} \right\}} dt$$
(18)
$$LQR=\frac{1}{2}\int {\left\{ {{X^T}QX+{U^T}RU} \right\}}$$
(19)

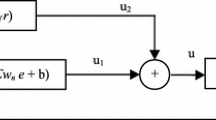
where, \(Q\) and \(R\) are the state weighting matrix and control weighting matrix. The weight matrices \(Q\) and\(R\) of the LQR controller is ideally chosen for the proper designing of LQ regulator and for the stability of the system. The optimal design of regulator is accomplished by changing the diagonal elements of \(Q\) and without changing the element matrix of \(R\). The weight matrices of the LQ regulator are selected by means of Kalman filter and the desired response of the system. For the enhanced LQR controller, the Kalman filter enhances the initial value of \(Q\) and \(R\) for both the diagonal matrices with a specific end goal to minimize the complexity of the system.

4 ELQR based control design for LFC

In this segment, the gain parameters of the PID controller are resolved utilizing the ELQR based approach for the automatic frequency regulation of the interconnected three area power system. Here, the proposed technique for the controller is called as the enhanced linear quadratic regulator (ELQR) is the joined execution of both the Kalman filter (KF) and the LQR. In the proposed technique, the weight matrices of the LQR are adjusted with assistance of KF technique in light of the frequency deviation between the three area systems. As per the non-linear frequency variation of the three area system, the ELQR is recognized the optimal state feedback gain parameters of the controller.

The non linear power system of a state space model is observed to be in linearized form for the utilization of the LQR. The state space equation of system for the analysis of LFC is represented as (Rubio et al. 2017),

$$U= - {K_{lqr}}X$$
(20)

So as to decide the optimal control inputs, while optimizing the state factors at the same time, the quadratic objective function which has to be minimized is shown by (18). The feedback gain matrix \(K\) which is dictated by utilizing the MATLAB command is given by (Pan et al. 2016a, b),

$${K_{lqr}}=LQR\left[ {A,\,B,\,Q,\,R} \right]$$
(21)

where, \(A\) and \(B\) are the system and the input matrixes respectively, the gain matrix \(K\) is acquired by solving the algebraic Riccati equation as (Rubio et al. 2018b),

$${K_{lqr}}={R^{ - 1}}{B^T}P$$
(22)

In light of the above equation, the optimal control pulse of (20) becomes (Pan et al. 2016a, b),

$$U={R^{ - 1}}{B^T}PX$$
(23)

The matrix \(P\) can be evaluated by the following Eq. (24) then the system is said to be in stable condition (Rubio 2018),

$$P={A^T}P(A - B{K_{lqr}})+Q$$
(24)

The weighting matrix \(Q\) is symmetric positive definite and the weighting factor \(R\) is positive constant. In general, the weighting matrix \(Q\) is varied, keeping \(R\) fixed to obtain the optimal control signal from the LQR. The corresponding state feedback gain matrix is given as,

$${K_{lqr}}={R^{ - 1}}{B^T}P={R^{ - 1}}\left( {\begin{array}{*{20}{c}} 0&0&{{K_{lqr}}} \end{array}} \right)\,\left[ {\begin{array}{*{20}{c}} {{P_{11}}}&{{P_{12}}}&{{P_{13}}} \\ {{P_{12}}}&{{P_{22}}}&{{P_{23}}} \\ {{P_{13}}}&{{P_{23}}}&{{P_{33}}} \end{array}} \right]$$
(25)
$${K_{lqr}}={R^{ - 1}}K\left( {\begin{array}{*{20}{c}} {{P_{13}}}&{{P_{23}}}&{{P_{33}}} \end{array}} \right)= - \left( {\begin{array}{*{20}{c}} {{K_p}}&{{K_i}}&{{K_d}} \end{array}} \right)$$
(26)

The corresponding expression for the control signal is,

$$U= - {K_{lqr}}X= - \left( {\begin{array}{*{20}{c}} {{K_p}}&{{K_i}}&{{K_d}} \end{array}} \right)\left[ {\begin{array}{*{20}{c}} {X1} \\ {X2} \\ {X3} \end{array}} \right]={K_i}\int {e(t)dt+{K_p}} e(t)+{K_d}\frac{d}{{dt}}e(t)$$
(27)

Under some condition, to locate the optimal gain matrix, without changing the control and state matrices, the LQR controller can be laid utilizing the Ricatti condition. The optimal filter can also be considered in situations where some unknown states are available. For this kind of system without an integrator, the decided matrices of \(A\) and \(B\) together with the control and weight matrices \(Q\) and \(R\) are utilized to locate the optimal gain matrix \({K_{lqr}}\). The effective matrix utilized in the LQR controller are given below,

$$Q=\left[ {\begin{array}{*{20}{c}} {Q_{{11}}^{1}}& \ldots &{Q_{{1n}}^{n}} \\ \vdots & \vdots & \vdots \\ {Q_{{n1}}^{n}}& \ldots &{Q_{{nn}}^{n}} \end{array}} \right]$$
(28)
$$R=\left[ {\begin{array}{*{20}{c}} {R_{{11}}^{1}}& \ldots &{R_{{1n}}^{n}} \\ \vdots & \vdots & \vdots \\ {R_{{n1}}^{n}}& \ldots &{R_{{nn}}^{n}} \end{array}} \right]$$
(29)

According to the requirements, the results of state variables can be varied by changing \(Q\). As for the pole placement, the LQ optimal state feedback \(U= - {K_{lqr}}X\) is not implemented without the full measurement. However, we derive a state estimate such that \(U= - {K_{lqr}}X\) remains optimal for the output feedback problem. This state assessment is created by the Kalman filter which described in the following section.

5 State estimation of LQR using Kalman filter

In the interconnected system, not all the states are measurable; in order to overcome the limitation Kalman filter is utilized. In this paper, a Kalman filter is designed to assessment the required state variables at the expense of slight performance degradation. The Kalman filter uses the state space matrices \(Q\) and \(R\), and the initial values for the calculation of gain values to assessment the real signal value. The structure of the proposed controller using estimates obtained from the Kalman filter is shown in Fig. 3.

Fig. 3
figure 3

Closed loop structure of ELQR Controller

Full size image

Using the linear discrete state and measurement equation the designing of Kalman filter is explained in the following steps.

The state equation is represented as,

$$x\;(k+1)=A\; \times \;x(k)+B\; \times \;u(k)+G\; \times \;w(k)$$
(30)

The measurement equation is represented as,

$$y(k)=C\; \times \;x(k)+v\; \times \;(k)$$
(31)

where, \(x(k)\) represents the state vector of the system, \(A\) is the transition matrix in system, \(B\) is the control distribution matrix and \(G\) is the transition matrix of system noise. \(u(k)\) is the input vector and \(w(k)\) is the zero mean in random Gaussian noise vector and named as covariance structure. In the measurement equation, \(y(k)\) is the measurement vector, \(C\) is the measurement matrix, and \(v(k)\) is the zero mean measurement noise vector and named as the covariance structure. Since there is no correlation between the system noise \(w(k)\) and the measurement noise \(v(k)\), the covariance matrix of \(w(k)\) and \(v(k)\) vector is given by,

$$E\left( {\begin{array}{*{20}{c}} {w(k)}&{{w^T}(j)} \end{array}} \right)=Q(k)\; \times \;\delta (kj)$$
(32)
$$E\left( {\begin{array}{*{20}{c}} {v(k)}&{{v^T}(j)} \end{array}} \right)=R(k)\; \times \;\delta (kj)$$
(33)

where, E is the expected value operator, \(\delta (kj)\) is the kronecker symbol, the optimum linear Kalman filter that estimates the state vector of the system is described with the following recursive equations,

The equation of extrapolation value is,

$${X_e}\left( {{k \mathord{\left/ {\vphantom {k {k - 1}}} \right. \kern-0pt} {k - 1}}} \right)=A{X_e}({{k - 1} \mathord{\left/ {\vphantom {{k - 1} {k - 1}}} \right. \kern-0pt} {k - 1}})+B{K_{lqr}}(k - 1)\;\left[ {{X_d} - {X_e}({{k - 1} \mathord{\left/ {\vphantom {{k - 1} {k - 1}}} \right. \kern-0pt} {k - 1}})} \right]$$
(34)

The innovation sequence,

$$\Delta (k)=Z(k) - C{X_e}(k/k - 1)$$
(35)

Equation of the estimation value,

$${X_e}\left( {{k \mathord{\left/ {\vphantom {k k}} \right. \kern-0pt} k}} \right)={X_e}({k \mathord{\left/ {\vphantom {k {k - 1}}} \right. \kern-0pt} {k - 1}})+K(k)\Delta (k)$$
(36)

The gain matrix of the optimum linear Kalman filter is (Jesús Rubio et al. 2018; Páramo-Carranza et al. 2017; Rubio et al. 2017, 2018a),

$$K(k)=P({k \mathord{\left/ {\vphantom {k k}} \right. \kern-0pt} k} - 1){C^T}\left[ {CP({k \mathord{\left/ {\vphantom {k {k - 1}}} \right. \kern-0pt} {k - 1}})} \right]{C^T}+{R^{ - 1}}(k)$$
(37)

The filtering error of the covariance matrix is,

$$P({k \mathord{\left/ {\vphantom {k k}} \right. \kern-0pt} k})=\left[ {I - K(k)C} \right]P({k \mathord{\left/ {\vphantom {k k}} \right. \kern-0pt} k} - 1)$$
(38)

The extrapolation error of the covariance matrix is (Páramo-Carranza et al. 2017; Rubio et al. 2017, 2018a),

$$P({k \mathord{\left/ {\vphantom {k {k - 1}}} \right. \kern-0pt} {k - 1}})=AP({{k - 1} \mathord{\left/ {\vphantom {{k - 1} k}} \right. \kern-0pt} k} - 1){A^T}+B{D_m}(k - 1){B^T}+GQ(k - 1){G^T}$$
(39)

where, \({X_d}\) is the desired vector and \(I\) is the identity matrix. Kalman filter tries to estimate the real signal from the deviated signal using the Expressed steps and between the two signals the value is minimized.

6 Results and discussion

The simulation results of three area power system model were studied in this section and the linear quadrature regulator (LQR) controller optimized with the Kalman filter. Initially, the impact of composed LQR controller is analyzed on the LFC performance of examined power system model demonstrates. The objective function is minimized for the design of ELQR controller and the estimation of matrix Q and R are also obtained. Also, the feedback gain matrix is obtained by using MATLAB/Simulink platform. Then the efficacy of the proposed technique in obtaining the optimal gains of the installed conventional controller in the studied power system for the best performance of the LFC is examined. Each controller are obtained and contrasted with the different existing techniques by the dynamic performances corresponding to the optimized controller gains for. The performance of the adaptive technique in the controller is analyzed by two different cases as discussed below.

6.1 Case 1: analysis under normal load condition

In this case, the optimal gain parameters obtained by the proposed control technique of the controller is examined. The area control error (ACE) maximum value in input to the controllers of respective areas is observed. The dynamic responses corresponding to the area control error (ACE) for three area power system is compared with the different techniques as shown in Fig. 4. On examining the responses in Fig. 4, it is plainly observed that the settling time, peak deviations and the magnitude of oscillations of the proposed are less when compared with the existing techniques in all the three areas of the system. From the figure, it is clear that ACE with the proposed technique settles quicker and having less overshoot than the existing procedure. Hence from the perspective of settling time, peak overshoot and the magnitude of oscillations the better dynamic responses of the system utilizing PID controller in nearness of the proposed technique. In presence of proposed technique the tie line power flow signal with PID controller is contrasted with algorithms like PSO, BFO and LQR-PSO. For this the gain of PID controllers are optimized by these algorithms separately.

Fig. 4
figure 4

The dynamic response of ACE for three area system is compared under normal load condition of a area-1, b area-2 and c area-3

Full size image

The dynamic reactions of the system relating to the frequency deviation of the three area system are contrasted with other algorithm such as PSO, BFO and LQR-PSO as shown in Fig. 5. In this way it is likewise observed from the figure that the proposed technique has fast settling time, peak overshoot and the magnitude of oscillations when compared with the existing techniques in all the three areas of the power system. The dynamic response corresponding to the tie line power flows for three areas system is contrasted with the distinctive techniques as shown in Fig. 6. On examining the responses in Fig. 6, it is plainly observed that the settling time, peak deviations and the magnitude of oscillations of the proposed are less contrasted when with the existing techniques in all the three areas of the system. In presence of proposed technique the tie line power flow signal with PID controller is contrasted with algorithms like PSO, BFO and LQR-PSO. For this the gain of PID controllers are optimized by these algorithms separately.

Fig. 5
figure 5

Comparison of Frequency deviation of three area system under normal load condition of a area-1, b area-2 and c area-3

Full size image
Fig. 6
figure 6

Contrasted of dynamic response of Tie Line Power flow of three area system under normal load condition of a area-1, b area-2 and c area-3

Full size image

6.2 Case 2: analysis under variation of load by 1%

The system under study has been subjected to the load change of 1% at a time in all the three areas of the network. The ACE, the tie line power flow and frequency response has also been observed in all the three cases. The controllers of separate areas are observed by the most extreme estimation value of Area Control Error (ACE) contribution. The dynamic responses corresponding to the Area Control Error (ACE) for three area system is compared with the different techniques as shown in Fig. 7. On examining the responses in Fig. 6, it is obviously observed that the settling time, peak deviations and the magnitude of oscillations of the proposed are less when contrasted with the existing techniques in all the three areas of the system. These PSO, BFO and LQR-PSO algorithms is contrasted in the ACE signal with PID controller in presence of proposed technique.

Fig. 7
figure 7

The dynamic response of ACE is contrast with the three area system under 1% load variation of a area-1, b area-2 and c area-3

Full size image

The dynamic responses of the power system corresponding to the deviation of frequency in the three area system are compared with other algorithm such as PSO, BFO and LQR-PSO as shown in Fig. 8. In the responses, the frequency deviation of power system for 1% load deviation in all the three areas. When the same load variations are made in other areas the frequency changes but it is settled with properly tuned controller. Thus from the figure it can been seen that the proposed technique has peak deviations, fast settling time, and the magnitude of oscillations when compared with the existing techniques in all the three areas of the power system.

Fig. 8
figure 8

Comparison of frequency deviation of three area system under 1% load variation of a area-1, b area-2 and c area-3

Full size image

Table 1 shows the settling time of ΔF, ΔPtie and ACE in all the three areas of the power system. The settling time of the ΔF1 ΔF2 ΔF3 ΔPtie1 ΔPtie2 ΔPtie3 ACE1 ACE2 and ACE3 of the power system values are listed here. The proposed technique is tabulated with under normal and 1% load variation. It is observed from the Table 1 the proposed techniques gives better results than the other techniques such as GA, PSO, FPA, LQR and LQR-KF. Several works have suggested various version of Kalman filter such as Discrete-time Kalman filter for Takagi–Sugeno fuzzy models, Stable Kalman filter and neural network for the chaotic systems identification and so on. The proposed approach provides a significantly smaller processing time than the processing time of the other algorithms while the ACE is also reduced. To the non linear field of the three area system, the proposed ELQR predicts the optimal state feedback gain parameters of the controller. This procedure guarantees the system frequency control under the load disturbance.

Table 1 Settling Time of ΔF, ΔPtie and ACE in all the three areas of the power system
Full size table

The dynamic responses corresponding to the tie line power flows for three areas system is compared with the different techniques as shown in Fig. 9. On examining the responses in Fig. 9, it is clearly seen that the settling time, peak overshoot and the magnitude of oscillations of the proposed are less when compared with the existing techniques in all the three areas of the system. The tie line power flow signal with PID controller in presence of proposed technique is contrast for algorithms like PSO, BFO, and LQR-PSO. It is observed that the peak overshoot and undershoot of the response decrease significantly with the proposed technique.

Fig. 9
figure 9

Comparison of dynamic response of Tie line power flow of three area system under 1% load variation of a Area 1, b Area 2 and c Area 3

Full size image

7 Conclusion

In this paper, a new intelligent technique of enhanced linear quadratic regulator (ELQR) based state feedback gain controller is proposed for LFC in a three area connected power system. The three area thermal-wind-hydro interconnected power systems are considered for the dynamic execution scrutiny. In the proposed methodology, the weight matrices of the LQR are anticipated with the assistance of KF technique in light of the frequency deviation between the three area systems. As per the non-linear frequency variation of the three area system, the ELQR is distinguished the optimal state feedback gain parameters of the controller. This procedure is guarantees the system frequency control under the load disturbance influence by limiting the Automatic Control Error (ACE) and Tie Line Power (TLP) variation. The proposed methodology is executed in MATLAB/Simulink working stage and the presentations are evaluated by using the correlation examination with the current systems of PSO, BFO and LQR-PSO techniques. The outcomes reveal that ELQR based controllers gives better execution as far as lesser oscillations, frequency deviation and quick settling time. In the future research work we will work on the advanced learning control methods such as composite learning. With different combinations of turbines the controller can further be implemented on four area system. Similarly, via trial and error method the state space and robust controllers were also tuned which was quite time consuming.