Introduction

Precipitation is the main source of soil moisture and drinking water in semiarid areas. Precipitation observations are crucial for hydrology, meteorology, geology, climatology and environmental monitoring and analysis. However, it is almost impossible to have stations (measuring precipitation, temperature, wind, etc.) that cover the whole area of interest, particularly in areas with no human activity. Meteorological stations have limited, localized and dispersed point distributions. Spatial interpolation of weather parameters is considered to be an important aspect for most hydrological studies (Lam et al. 2015; Xu et al. 2015). Spatial interpolation is a technique that is used to estimate values for any distributed variable where none exists; develop a surface representing elevation, precipitation, temperature, pollution or other environment layers; or approximate values for any geographic location using known specific points. Meteorological stations are used as known locations, and their values are used to estimate (or predict) the values of a data surface in locations where no point data exist, as represented in raster grid format.

Spatial interpolation techniques can be divided into deterministic interpolation models (e.g. IDW, trend surface analysis or least square regression, radial basis function, and global polynomial interpolation) and geostatistical models (e.g. OK, SK, and UK) (Johnston et al. 2001; Wang et al. 2014). Deterministic models based on the assumption that the interpolated surface is more influenced by nearby points and less by distant points and depend on particular mathematical formulas that control the smoothness of the interpolated surface. Geostatistical models based on statistical models which include statistical relationship between the points (i.e. Autocorrelation) and rely on the assumptions that data come from stationary stochastic process. Spatial interpolation models can also be classified into three classes based on the method and scale of the interpolation application: models considered as simple interpolative, models use ancillary data, and models using complex models (Yang et al. 2015).

The desired time scale, spatial resolution (Frazier et al. 2016), the density of the station network, and the topographic complexity (Hofstra et al. 2008) are the leading factors of determining the complexity of the suitable spatial interpolation method and making the spatial pattern. Spatial variance varies especially for precipitation as the time scale varies mainly for annual means (Frazier et al. 2016; Nalder and Wein 1998; Tveito et al. 2008; WMO 2008). The uncertainties related to the predictions increase noticeably as the time integration and station density decrease. This leads to the need of more complex models (Tveito et al. 2008; Frazier et al. 2016).

A number of spatial interpolation models have been created and applied in several fields of spatial interpolation (Frazier et al. 2016; Hofstra et al. 2008; Brunetti et al. 2014; Goovaerts 2000; Hutchinson 1998; Lloyd 2005; Wang et al. 2014; Xu et al. 2015). A number of studies has been conducted in using interpolation methods with a small number of stations. For example, Dirks et al. (1998) conducted a comparative study applying four spatial interpolation methods for 13 precipitation stations, Keblouti et al. (2012) compared three methods using 10 stations, and Wang et al. (2014) compared six interpolation methods using 12 meteorological stations. These studies used several common methods among them such as IDW and some of uncommon methods such as local polynomial interpolation (LPI) and Spline without applying several parameters and models. Dirks et al. (1998) and Keblouti et al. (2012) said IDW while Wang et al. (2014) said LPI outperformed the other methods.

The objective of this study is to compare the ability of 8 different spatial interpolation methods in modelling precipitation and temperature with different integration periods, i.e. daily, monthly, and annual total precipitation; monthly and annual average precipitation; and daily, monthly, and annual average temperature, in a local scale with a small number of stations i.e. 17 stations, using different parameters and models for each method.

The methods used are: inverse distance weighting (IDW), Thiessen polygons (TP), thin plate spline (TPS), trend surface analysis (TSA), local polynomial interpolation (LPI), ordinary Kriging (OK), universal Kriging (UK) (sometimes called Kriging with External Drift KED), and simple Kriging (SK).

Study Area and Data Collection

This study aims to conduct a thorough comparison of several interpolation methods and identify the best method for generating precipitation and temperature maps. In the scope of this study, the word best refers to the model with the lowest values of errors (i.e. RMSE, and MSRE) and highest agreement (i.e. r2 and CE) and the worst, on the contrast, refers to the model with the highest values of errors and lowest agreement.

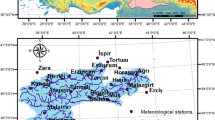
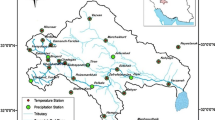
Maps are to be generated for three sub-basins called (coded) 1822, 1801, and 1805, as seen in Fig. 1. These three sub-basins are part of the Seyhan Basin located in southwest Turkey. To include all of the influencing stations (i.e. having spatial correlation) in the area inside the basin borders, stations were chosen inside and outside the borders. The area includes parts of four of Turkey’s provinces: Adana, Kayseri, Kahramanmaras, and Sivas. During the study period, the sub-basins are: rural, agricultural, not hydrologically disturbed, and having no water storage structure. The annual average temperature of the study area is 9.1 °C, the maximum temperature 29.8 °C observed in July, and the minimum temperature − 6.8 °C observed in January.

Fig. 1
figure 1

The distribution of the meteorological stations and the topographic map of the study area which is located in Seyhan Basin, Turkey and covers parts of Kayseri, Adana, K. Maras, and Sivas provinces

Full size image

Observations of 17 stations were collected from DMI (Devlet Meteoroloji Isleri), the Turkish General Directory of Meteorology. The stations density is one station per 3000 km2. The data were collected for the period from 1/1/1987 to 31/12/1994. For every station, the collected data included total daily precipitation and average daily temperature. In some stations, some missing (non-recorded) observations were filled using the arithmetic average; they had no effect on the result due to the low amount of such instances. A simple statistical table for the collected data for all of the stations are summarized in Tables 1 and 2.

Table 1 Statistics of the observed daily total precipitation (in mm) of 17 stations for the period of 1987–1994
Full size table
Table 2 Statistics of the observed daily average temperature (°C) of 17 stations for the period 1987–1994
Full size table

Methods

In this study, 8 interpolation methods were used with different parameters for deterministic methods and different models for geostatistical methods. Each method with different parameters and models was applied to every integration period. The integration periods used are: daily, monthly, and annual total precipitation; and daily, monthly, and annual average temperature.

The main steps of this study are (1) convert the daily (i.e. average for temperature and total for precipitation) observations for all stations to monthly and annual values; (2) apply each method considered in this study with a variety of parameters; and (3) implement cross-validation to assess the accuracy of the method using the root mean squared error (RMSE), mean squared relative error (MSRE), coefficient of determination (r2), and coefficient of efficiency (CE). All of the steps and methods were implemented using the statistics language R with the exception of exporting several maps to ArcGIS. A brief description of each method is introduced in the next section.

Inverse Distance Weighting (IDW)

IDW is a direct deterministic interpolation method that is broadly applied in spatial interpolation applications. It was developed based on the assumption that the interpolated points are the most affected by the nearest points and the least affected by the most distant points (Wang et al. 2014; Borges et al. 2016). IDW is a local, exact, and deterministic method.

The general equation of IDW is as follows:

$$ \hat{Z}\left( {s_{0} } \right) = \mathop \sum \limits_{i = 0}^{N} \lambda_{i} Z(s_{i} ) , $$
(1)

where \( {\hat{\text{Z}}}\left( {{\text{s}}_{0} } \right) \) is the estimated values at location \( {\text{s}}_{0} \), \( {\text{N}} \) is the number of points located around the point to be estimated used in the calculation, \( Z\left( {{\text{s}}_{\text{i}} } \right) \) is the value of the known points measured at \( {\text{s}}_{\text{i}} \), and \( \uplambda_{\text{i}} \) is the weight corresponding to each known point, which is inversely proportional to the distance between the known points and the estimated point. The weights are calculated as follows:

$$ \lambda_{i} = \frac{{d_{i0}^{ - p} }}{{\mathop \sum \nolimits_{i = 1}^{N} d_{i0}^{ - p} }} , $$
(2)

where \( p \) is the power, which controls the influence of the distance between the points on the estimation value; \( {\text{N}} \) is the number of points used in the estimation; and \( d_{i} \) is the distance between the point to be estimated \( {\text{s}}_{0} \) and the known point \( {\text{s}}_{\text{i}} \) (Isaaks and Srivastava 1989; Nalder and Wein 1998; Borges et al. 2016). IDW was applied with three power \( p \) values: 1, 2, and 3 for all of the integration periods for precipitation and temperature.

Thiessen Polygons/Nearest Neighbor (TP)

Thiessen polygons, which are named according for its developer, Thiessen (1911), are considered to be a special case of the IDW method because only one point, i.e. the nearest point, is used in the interpolation. A Thiessen polygon consists of all of the points in a polygon that lie nearer to the point used for constructing that polygon than to any another point (Goovaerts 2000). TP is a local, exact, and deterministic method (Shope and Maharjan 2015).

Thin Plate Spline (TPS)

Thin plate spline was described in detail by (Wahba 1990). For a bivariate thin plate spline (i.e. one type of TPS) estimations of \( {\text{Z}}\left( {{\text{s}}_{\text{i}} } \right) \) for measured points \( {\text{i}} = 1 \ldots {\text{N}} \), is calculated as follows:

$$ Z\left( {s_{i} } \right)\, = \,f\left( {s_{i} } \right)\, + \, \in \left( {s_{i} } \right), $$
(3)

whereas \( \in \left( {{\text{s}}_{\text{i}} } \right) \) represents random errors, which are assumed to be uncorrelated random errors and independent with a zero mean and variance \( \upsigma^{2} \), and \( {\text{f}}\left( {{\text{s}}_{\text{i}} } \right) \) represents an unknown deterministic smooth function, which can be estimated by the minimization of the following:

$$ \mathop \sum \limits_{i = 1}^{N} \left[ {Z\left( {s_{i} } \right) - f\left( {s_{i} } \right)} \right]^{2} + \lambda J_{m}^{d} \left( f \right) $$
(4)

where \( {\text{f}}\left( {{\text{s}}_{\text{i}} } \right) \) is the fitted function values at the ith data point; \( \lambda \) is the so-called regularizer or smoothing parameter, which controls the trade-off between fitting the data as close as possible without losing the smoothness (i.e. if \( \uplambda = 0 \) the function models the points exactly with zero noise, whereas if \( \uplambda \) is very large, the function will be a hyperplane); and \( J_{m}^{d} \) is a measure of the smoothness of function \( f \). The form \( J_{m}^{d} \) depends on two parameters: the number of independent variables \( d \) and the order of the partial derivatives \( m \).

Trend Surface Analysis/Global Polynomial Interpolation (TSA)

TSA fits a smooth surface to measure points using a mathematical function. Over the area to be estimated, the surface of TSA changes gradually from one region to an adjacent region, and it has the ability to obtain a global trend in data. TSA utilizes all of the measured points to interpolate the surface in contrast to several other methods, such as IDW and LPI (i.e. briefed in the next section), which use a specific subset of measured points (Wang et al. 2014). TSA/GPI is considered to be a global, inexact, deterministic method.

The principle of TSA/GPI is that the entire study area is presented by a formula that estimates the value \( {\hat{\text{Z}}}\left( {{\text{s}}_{i} } \right) \) at any location based on the \( {\text{X}}_{\text{i}} , {\text{Y}}_{\text{i}} \) coordinates of that location. The general function is described as follows:

$$ \hat{Z}\left( {s_{i} } \right) = f \left( {X_{i} , Y_{i} } \right) $$
(5)

The main objective in TSA/GPI is to use all of the measured points of the study area to obtain a formula that best describes that area. Many formulas exist, but the simplest one that can describe a surface is the first order bilinear surface:

$$ f \left( {X, Y} \right) = b_{0} + b_{1} x + b_{2} y + \varepsilon $$
(6)

A second order trend surface can be represented by the following:

$$ f \left( {X, Y} \right) = b_{0} + b_{1} x + b_{2} y + b_{3} x^{2} + b_{4} xy + b_{5} y^{2} + \varepsilon $$
(7)

In Eq. (7), not only are the individual variables with their parameters present, but so too is the cross product (i.e. \( {\text{b}}_{4} {\text{xy}} \)). Higher order trend surfaces include more cross product terms, not only higher powers of \( {\text{x}} \) and \( {\text{y}} \) (Huisman and By 1999). Regardless of using first, second, or even third order trend surfaces, the parameters of the used formula are obtained using a regression technique utilizing all of the measured points of the area of interest.

Local Polynomial Interpolation (LPI)

Global interpolation is based on the assumption that the entire study area can be represented by a general formula. However, in many cases, representing the study area by the same mathematical surface misrepresents the real surface. This representation prevents variations within the natural geographic field. LPI was developed to override this shortcoming.

LPI has the same mathematical representation and fitting procedure as TSA/GPI, except LPI fits a local formula by utilizing measured points within a specified area, unlike TSA/GPI, which uses all of the measured point. The specified areas can overlap, and the estimated surface value at the center of that area is the predicted value (Huisman and By 1999; Wang et al. 2014). LPI is a local, inexact, deterministic method.

Ordinary Kriging (OK)

Kriging is a local interpolation method that was initially developed by a mining engineer called D. G. Krige and a geostatistician called Georges Matheron. The Kriging method uses a subset of geostatistical interpolation methods with the assumption that closer points are more likely to be similar, whereas farther points are more likely to be different. To evaluate the dissimilarity between points, Kriging uses a semivariogram. The experimental semivariogram \( {\hat{\gamma }}\left( {\text{h}} \right) \) is calculated using the following equation:

$$ \hat{\gamma }\left( h \right) = \frac{1}{N\left( h \right)}\mathop \sum \limits_{i = 1}^{N\left( h \right)} \left[ {Z\left( {s_{i} } \right) - Z\left( {s_{i} + h} \right) } \right]^{2} $$
(8)

where \( {\text{h}} \) is the lag, \( {\text{Z}}\left( {{\text{s}}_{\text{i}} } \right) \) is a set of data points, and N is the number of pairs of data points separated by \( {\text{h}} \). A model is used to fit the experimental variogram. In this study, three models are used to compare the results: spherical, Gaussian, and linear. To save space, only the equation of the spherical model is mentioned. The spherical model is the most used model because it generally provides the best fit to the data. The spherical model is represented by the following:

$$ \gamma \left( h \right) = \left\{ {\begin{array}{*{20}l} {\theta_{0} + \theta_{s} \cdot \left[ {\frac{3h}{2a} - \frac{1}{2}\left( {\frac{h}{a}} \right)^{3} } \right]} \hfill & {for\quad h \le a} \hfill \\ {\theta_{s} } \hfill & {for \quad h > a} \hfill \\ \end{array} } \right., $$
(9)

where \( {\text{a}} \) is the range, \( \uptheta_{\text{s}} \) is the partial sill, and \( \uptheta_{0} \) is the nugget (Frazier et al. 2016; Webster and Oliver 2007). The lag \( {\text{h}} \) is considered to be the average distance between neighboring points, and the nugget \( \uptheta_{0} \) effect is attributed to the measurement errors for distances smaller than the data intervals (Borges et al. 2016).

Several types of Kriging methods have been widely used in different applications. Ordinary Kriging OK is the most used type. It is, in general, used as a base method to be compared with other methods (Goovaerts 2000; Mair and Fares 2011; Frazier et al. 2016; Sanchez-Moreno et al. 2013). OK assumes that the mean is constant, but its emphases on the spatial mechanisms are unknown (Isaaks and Srivastava 1989; Cressie 1990; Borges et al. 2016). The representation of OK for a spatial process \( Z\left( s \right) \) is as follows:

$$ Z\left( s \right) = \mu + \delta \left( s \right) $$
(10)

where \( \upmu \) is an unknown expected value of a random process and \( \updelta\left( {\text{s}} \right) \) is a zero mean naturally from a stationary random process with an existing semivariogram.

The OK estimator is described exactly as Eq. (1) (i.e. the same equation of IDW) with the exception of weights, which are calculated based on the model fitting on the variogram differently from IDW, which is calculated according to the inverse distance. Kriging is an unbiased and optimal estimator, which means that the weights \( \uplambda_{\text{i}} \) in all Kriging methods are summed to 1. The weights \( \uplambda_{\text{i}} :i = 1, \ldots ,N \) are calculated under the uniform unbiased condition as follows:

$$ E\left( {\hat{Z}\left( {s_{0} } \right)} \right) = E\left( {Z\left( {s_{0} } \right)} \right) \quad \mathop \sum \limits_{i = 1}^{N} \lambda_{i} = 1, $$
(11)

under the restriction of the minimization of the prediction error variance \( \upsigma\left( {{\text{s}}_{0} } \right) \),

$$ \sigma \left( {s_{0} } \right) = E\left( {Z\left( {s_{0} } \right) - \hat{Z}\left( {s_{0} } \right)} \right)^{2} . $$
(12)

OK is a local, exact, and stochastic method.

Universal Kriging (UK)

The main assumption of UK is that the data have a significant spatial trend, which makes it different from OK, which assumes no trend (Wang et al. 2014). A secondary variable is used by UK in the form of external drift or a trend (such as elevation or temperature), which gives UK the ability to account for nonstationarity in the data throughout the study area because there is a linear relationship between the interpolated variable and the used external drift, which is assessed locally (Goovaerts 2000; Frazier et al. 2016). Therefore, UK is sometimes called Kriging with external drift (KED). The trend or drift has continuous spatial variation, but is too irregular to be modelled by a simple mathematical functions. UK uses stochastic and deterministic components to incorporate the external variable into the Kriging system to overcome the irregularity (Webster and Oliver 2007). Taking into account the two constraints on the weights, UK uses \( N + 2 \) equations to solve for the weights. The estimator of UK or KED is described as follows:

$$ \hat{Z}_{UK} \left( {s_{0} } \right) = \mathop \sum \limits_{i = 1}^{N} \lambda_{i}^{UK} z\left( {s_{i} } \right) $$
(13)

In this method, elevation extracted from the ASTER DEM (NASA 2016) was used as the external drift with the three models. Elevation used considering that it has high influence in the variation of the spatial pattern as it varies between 16 and 3764 m (see Fig. 1).

Simple Kriging (SK)

Sometimes the mean of the random variable can be assumed according to the nature of the problem. This knowledge should be used to improve the estimation, and this can be done by using simple Kriging (SK). SK uses \( N \) equations to solve for \( N \) unknowns, and the estimator is described as follows:

$$ \hat{Z}_{SK} \left( {s_{0} } \right) = \mathop \sum \limits_{i = 1}^{N} \lambda_{i} z\left( {s_{i} } \right) + \left\{ {1 - \mathop \sum \limits_{i = 1}^{N} \lambda_{i} } \right\}\mu $$
(14)

The weights \( \uplambda_{\text{i}} \) are no longer constrained to the summation of 1, and unbiasedness is guaranteed by addition of the second part of Eq. (14). For the reason that weights are not summed to 1, covariances, \( {\text{C}} \), must be used instead of semivariances, \( \gamma \) (Webster and Oliver 2007). Comparing simple Kriging to ordinary Kriging, simple Kriging is supposed to produce smaller variance by having the mean estimated from the observed data.

Validation

The assessment of accuracy can be performed using a technique called cross-validation that is the most applied technique in climate studies. Cross-validation helps in making decisions about which model is best at estimating the surface using the measured points (Tveito et al. 2008; Borges et al. 2016). One of the cross-validation methods is leave one out cross-validation (LOOC). In this method, one point is left out of sample data, whereas the other points are used to estimate the value of the left point. This procedure continues until a value for each of the original data points is estimated (Isaaks and Srivastava 1989).

One of the shortcomings of using cross-validation is that the interpolation model is defined using all of the sample data, which implies that the validation can be considered to be not completely independent (Tveito et al. 2008; Borges et al. 2016). Therefore, different techniques were considered in this study, including separating the precipitation station data into 15 stations for interpolation and 2 stations for validation.

Four different measures used in validating interpolation methods (Borges et al. 2016; Brunetti et al. 2014; Frazier et al. 2016; Robinson and Metternicht 2006; Seo et al. 2015) were applied in all of the methods for each integration period and used for comparing the interpolating methods: The root mean square error (RMSE), The mean squared relative error (MSRE), The coefficient of determination (\( r^{2} \)), The coefficient of efficiency (\( CE \)).

Results and Discussion

The applied 8 interpolation methods are used to provide an interpolation map for the whole study area utilizing several measured points. Therefore, a number of maps were generated. To save space, as examples, maps of every method for the monthly total precipitation and monthly average temperature for 1 month (i.e. June 1989) are shown in Figs. 2 and 3.

Fig. 2
figure 2

Examples of interpolated maps of monthly total precipitation (in mm) for each of the 8 interpolation methods. The month chosen as an example is June 1989

Full size image
Fig. 3
figure 3

Examples of interpolated maps of monthly average temperature (in  °C) for each of the 8 interpolation methods. The month chosen as an example is June 1989

Full size image

By examining these figures, the differences among the used methods and their theoretical nature can be clearly seen. The IDW interpolation map constructs circles or ellipsoids around the points used for the interpolation, and every one of these shapes represents a value. These shape values decrease, going further from the center, which highlights the theoretical background, as represented by Eqs. (1) and (2). The Thiessen polygon interpolation map shows that every known point is represented by a polygon, which gives it a district nature. The LPI map is different from the TSA map in that the former has local shapes separated from the entire area and has internal discontinuities due to the local nature of the method. TSA uses one formula to model the whole area, whereas LPI uses many formulas in several parts of the area. The three maps of the Kriging methods (i.e. OK, UK, and SK) look similar, with slight differences in the values in some parts of the study area. For example, for the precipitation monthly maps shown in Fig. 2, OK has slightly higher values in the upper middle part of the study area, whereas SK has slightly lower values in the center of the study area. In the temperature maps shown in Fig. 3, UK has slightly lower values in the right part of the study area than in SK and UK.

After obtaining the results of the interpolation of each method, cross-validation measurements were obtained to make comparisons and identify the capability of these methods to spatially interpolate each weather parameter in several integration periods with a small number of stations. The obtained measurements are summarized in Tables 3 and 4. r2 and normalized CE (CE was normalized in the figures to have comparable values) are shown in Figs. 4, 5, 6 and 7 to provide a better visual comparison.

Table 3 Validation measurements: RMSE, MSRE, r2, and CE of daily, monthly, and annual total precipitation (in mm) interpolations
Full size table
Table 4 Validation measurements: RMSE, MSRE, r2, and CE of daily, monthly, and annual average temperature (in  °C) interpolations
Full size table
Fig. 4
figure 4

Coefficient of determination r2 values for the 8 methods with various parameter for 3 integration times (i.e. daily, monthly, and annual totals) of Precipitation

Full size image
Fig. 5
figure 5

Normalized coefficient of efficiency CE values for the 8 methods with various parameter for 3 integration times (i.e. daily, monthly, and annual totals) of Precipitation

Full size image
Fig. 6
figure 6

Coefficient of determination r2 values for the 8 methods with various parameter for 3 integration times (i.e. averages) of Temperature

Full size image
Fig. 7
figure 7

Normalized coefficient of efficiency CE values for the 8 methods with various parameter for 3 integration times (i.e. averages) of Temperature

Full size image

According to the Figs. 4, 5, 6 and 7, TP has the lowest values of r2 and CE for both precipitation and temperature, which may be due to the district nature of this method. Looking at Tables 3 and 4, TP has the highest values of RMSE and MSRE, which means that this method performed the worst. Similarly, the OK method with a spherical model has a poor performance for both precipitation and temperature in all of the integration periods. Notwithstanding the high r2 values for the average temperature in all the integration periods, it has low values of CE and high values of MSRE and RMSE.

IDW with a power of three is identified as the best at modelling precipitation. This finding is not consistent with: (Apaydin et al. 2004), who found that in 19 studies, IDW was not recommended (i.e. mentioned in his research) for interpolating precipitation, except in one, and (Wang et al. 2014) who found LPI outperformed IDW. On the contrast, this finding agrees with (Dirks et al. 1998; Keblouti et al. 2012). IDW was also found to be the best method for interpolating temperature, with the highest (high r2 and CE and low RMSE and MSRE) validations.

TPS can also be considered to be a well-behaving model because it has high values for all of the integration periods, except CE values for the temperature, which are slightly low. Among the Kriging methods, OK, UK, and SK all with the Gaussian model performed better by having less error and higher agreement in modeling precipitation for the various integration periods, which indicates that the Gaussian model better models the precipitation data than the two other models used. However, OK with the linear model, UK with the Gaussian model, and SK with the linear model have higher results in modeling the temperature, which gives preference, in general, to the linear model for the temperature data.

Even though, the elevation was used as an external drift with hope of improving the result, as in (Goovaerts 2000; Moges et al. 2007), UK with the three models has shown no advantage, similar to the findings of (Frazier et al. 2016; Wang et al. 2014; Mair and Fares 2011), in comparison with OK and SK.

In terms of integration periods, the annual cross validation results have shown instability in the interpolation methods unlike the daily and monthly results, which changed together in most of the methods. Monthly average temperature have the highest r2 values, whereas monthly total precipitation and monthly average temperature have the highest CE. In precipitation, the best interpolated integration period is the monthly total, whereas the monthly average of temperature is the best in most of the used methods with the various parameters.

Specifically, the values of the cross-validation measurements slightly change from method to method and from one integration period to another. In one method, considering a specific measurement can be found as having the lowest error while in another measurement having the highest in comparison with other methods, so there is no clear evidence that one method is superior to another at modeling an area with small number of stations and highly changing elevation, with the exception of the TP, IDW and LPI methods. The obvious worst modeling is achieved using TP, and the best modeling is achieved using the other two methods.

Conclusion

Eight deterministic and geostatistical spatial interpolation techniques were used in this study, and 4 cross-validation measurements were obtained to compare the capability of the methods and identify the best modeling method of precipitation and temperature for several integration periods for the study area. Generally, no method is superior to the others from one integration period to another. Comparing the four validation measurements, IDW with a power of three is identified as the best modeling of precipitation and temperature. Not surprisingly, TP had the worst performance for all of the integration periods and for the two weather parameters. All the methods are capable of modeling the different integration periods for both precipitation and temperature.

All of the methods are better at interpolating the temperature in the different integration periods, due to the smoothness in the variation of the temperature through the area. In contrast, precipitation is worse due to the coarse variation throughout the area.

The used period is limited to 8 years. Therefore, using longer time series data for both precipitation and temperature is recommended to examine the annual interpolation in more detail.

UK with elevation as external drift has no advantage in comparison with SK and OK even though the elevation which has high range is thought as an influencing factor in such scale and station network density. Therefore, the use of other factors, such as the distance to rivers, slope, and aspect, is recommended.