Introduction

Each core or tool belonging to a lithic assemblage has its own life history. It begins when a specific piece of raw material is selected from a sourcing location and ends when the object is discarded for the last time (Leroi-Gourhan 1993; Odell 2001; Schiffer 1987; Sellet 1993; Shott 2003). This implies that each archaeological object has an inherent value related to the amount of work and time invested in its elaboration and its replacement possibilities, a real time of use, and a theoretical potential amount of use related to the degree of maintenance and re-use until its exhaustion. This makes the concepts of procurement and manufacture, use-life (Schiffer 1987), and curation (Shott 1996) key concepts for the understanding of lithic technology.

The amount of work invested in a lithic tool until it is abandoned is represented by knapping, either through the detachment of flakes in cores or by retouching in tools. Given the reductive and unidirectional nature of lithic knapping, one way to objectively evaluate the amount of work invested is through the quantification of reduction intensity—that is, the measurement of the amount of mass or volume removed from the original blank until the core or tool is discarded. In this paper, we will refer to “volume” as a measuring unit when talking about reduction, but mass can similarly be calculated throughout the process.

The management of lithic tools through reduction can be affected by multiple factors such as raw material quality, size or accessibility, group mobility and transport patterns, occupation type and duration, and the function among others (Andrefsky 1994; Blades 2003; Carr and Bradbury 2011; Kuhn 1990; Morales 2016; Nelson 1991; Rolland and Dibble 1990; Schiffer 1987). Given that there is a connection between reduction as a physical process and curation as a behavioral one (Shott and Weedman 2007), the quantification of reduction intensity can help us better understand behavioral patterns, technological and economic organization strategies, and ultimately, cognitive capabilities such as planning and adaptation.

One way to quantify the intensity of reduction would be to calculate the percentage of removed or remaining volume in relation to the volume of the original blank. However, without complete refits, the exact amount of material that has been removed from each core cannot be determined. In this situation, several indexes and equations have been developed to estimate the size of the original blanks in the case of retouched tools (Morales et al. 2015), or through different parameters as an indirect reflection of this reduction (Clarkson 2013; Douglass et al. 2018; Li et al. 2015).

Regarding cores, there is the case of the Cortex Ratio, which uses geometric solid formulas to estimate the surface area of the original blank (Dibble et al. 2005; Douglass et al. 2008; Holdaway et al. 2008; Lin et al. 2010, 2015). In these studies, the quantity of cortex expected to be represented in an archaeological assemblage if all the elements were present is calculated using geometric volume formulas. The total assemblage volume is used to calculate the total cortical surface area. To do this, the volume of the assemblage is divided by the number of cores, and the result is subsequently used to calculate the surface value from the volume value, using either the sphere (Dibble et al. 2005) or ellipsoid formulas (Douglass et al. 2008; Lin et al. 2010). This result is then multiplied by the number of cores present in the assemblage. Finally, this resulting value is compared to the observed quantity of cortex documented in the same archaeological assemblage to quantify the over- or underrepresentation of cortical surfaces (Douglass et al. 2008). Recently, these kinds of geometric reconstructions have been used to obtain the volume ratio instead of the Cortex Ratio (Ditchfield 2016a; Ditchfield et al. 2014; Phillipps and Holdaway 2016), since it has the advantage of being applicable to assemblages produced from nodules that are not completely cortical in origin (Ditchfield 2016a).

These approaches have been applied to several archaeological assemblages and are considered a robust method for measuring the transport of artifacts and, ultimately, the degree of mobility of past human groups (Ditchfield 2016a; Ditchfield et al. 2014; Douglass et al. 2008; Holdaway et al. 2008; Phillipps and Holdaway 2016). The Cortex Ratio has been interpreted as a reduction intensity proxy based on the premise that a more reduced assemblage will present a smaller proportion of cortical surfaces (Dibble et al. 2005).

Although they can be useful tools for measuring the overall reduction of an assemblage, these approaches are not aimed at quantifying the reduction of each core individually. Therefore, it is not possible to analyze the internal distribution of the reduction degrees within each assemblage. This problem is also present in other proxies used as references for reduction intensity, such as the flakes-cores ratio or the noncortical flakes-cortical flakes ratio (Ditchfield 2016a).

Some authors have highlighted the importance of analyzing the distribution of reduction degrees through the individual characterization of each tool, since “the mean is a measure of central tendency that is strictly valid only for normal distributions” (Shott and Sillitoe 2005, p. 659). Furthermore, under the same central tendency, different distributions that may represent different discard patterns can be hidden (i.e., an assemblage in which some cores are exhaustively reduced and others are only tested will have a similar mean to another assemblage in which all cores are reduced at an intermediate level) (Shott and Sillitoe 2004). For these reasons, an analysis of the distribution of the individual values in each assemblage allows for a more effective evaluation of the assemblage’s formation processes through, for example, survival analysis (Douglass et al. 2018; Morales 2016; Shott 2002; Shott and Seeman 2015; Shott and Sillitoe 2005, 2004).

This kind of analysis has been applied mainly to retouched artifacts, including unifacial lateral scrapers (Eren et al. 2005; Kuhn 1990) or distally retouched end-scrapers (Eren et al. 2005; Morales et al. 2015; Shott and Weedman 2007), as well as Aterian tanged tools (Iovita 2011) or bifacial tools (Clarkson 2002). In certain cases, it has been used to reconstruct the original volume of flakes from different attributes of the preserved platform (Shott et al. 2000), such as the exterior platform angle (EPA) or platform depth (Dibble and Rezek 2009), or through the flake’s surface such as the Initial-/Terminal-Mass Comparison (ITMC) (Clarkson and Hiscock 2011) or its dimensions (Dibble and Rezek 2009).

Similarly, different reduction measures for blades have been used, either using the original thickness of each blade to estimate its original surface (Blades 2003) or adapting the ITMC for unretouched (Muller and Clarkson 2014) and retouched blades (Muller et al. 2018). Various methods have also been developed using the cross-sectional geometry of retouched tools to reconstruct the original size of the flakes prior to retouching, such as the Geometric Index of Unifacial Stone Reduction (GIUR) (Kuhn 1990), the Estimated Reduction Percentage (ERP) (Eren et al. 2005; Morales et al. 2015), or indexes combining the height of retouch with the length of the retouched edge to estimate the volume lost (Bustos-Pérez and Baena 2019).

Regarding cores, morpho-technical parameters have been used to indirectly reflect their reduction: the Flake Scar Density (Shipton 2011) or Scar Density Index (SDI), which is based on the relationship between the number of scars on a core’s surface (Clarkson 2013), the percentage of non-cortical surface (Li et al. 2015), the number of scars present on each core (Bradbury and Carr 1999; Shott 1996), the number of exploitation and/or percussion surfaces, the number of convergences of exploitation surfaces, the angle of the platform, or the combination of several of these attributes (Douglass et al. 2018).

However, many of these parameters can be affected by both the size of the original blank and the strategy used in the reduction process, especially when comparing archaeological assemblages with different characteristics (e.g., unifacial and bifacial reduction strategies, or different raw materials). In addition, some parameters are the result of the reduction strategy employed more than the by-product of the intensity of reduction (Lombao et al. 2019).

Additionally, the indexes obtained through some of these methods (i.e., SDI) generate relative measurement units, being therefore impossible to qualitatively assess the results they produce individually. On the contrary, they require the comparison of the reduction degree on more than one assemblage (different archaeological sites, levels, raw materials, or reduction strategies), in order to obtain interpretable results.

Conversely, the expression of the reduction intensity in terms of the relationship between the volume of the original blank and the volume of the discarded core has multiple advantages: first, by being a real and tangible unit of measure, it facilitates the individual characterization of the reduction intensity of each core. Second, it estimates the size of the original blank, thus providing information regarding raw material selection. Third, linking the intensity of reduction to the size of the selected original blank can lead to better inferences about the raw material economy and transport strategies. Finally, the intensity of reduction expressed both in absolute and relative common scales allows for the exploration of the possible correspondence between knapping strategies and stages of reduction, providing highly relevant information in studies of technological variability.

For these reasons, this paper presents a new methodological proposal to estimate the volume size of original blanks and quantify the degree of reduction in cores in terms of percentage of remaining or removed volume the Volumetric Reconstruction Method (VRM), together with the results of an experimental program carried out to evaluate its reliability to estimate an original blank’s size and intensity of reduction.

Methods

The Volumetric Reconstruction Method

The VRM was designed with the goal of reconstructing an original blank before it was knapped. We used geometric formulas that require the data of the dimensions, or more specifically the semi-axes, of each core or tool in order for the formulas to be appropriately calculated. However, during the knapping process, each removal modifies the shape and size of the core or tool (from now on, for a matter of readability, we will refer to “cores” when dealing with both cores and tools on cobble). This modification eventually affects one or more of the three dimensions of the core, depending on the relative position of each removal. Thus, it is necessary to consider the need for a “correction” of the core’s dimensions. Otherwise, we would be calculating an unrealistic volume, closer to the core’s final stage since it would be defined by the dimensions of the discarded stage. As such, in order to estimate the real original volume, it is necessary to reconstruct the three dimensions of each blank in their pre-knapping stage, and then apply the appropriate geometric volume formula to them.

Therefore, we face two challenges: first, finding this “correction unit” for the maximal dimensions once the core has been discarded, and second, calculating the necessary number of corrections required for each one of the core dimensions.

Regarding the first issue, our proposal is based on the utilization of some of the dimensional attributes of the flakes belonging to the same assemblage as the analyzed cores/tools. Since flakes are the “positive” products of the removals from the core’s surface, we can assume that some of the flakes’ dimensions reflect the dimensional modifications produced on the core. Specifically, for the application of the VRM, we have used two correction measures: median flake platform thickness and median flake thickness.

We used the assemblage’s median flake platform thickness in order to correct the length and width of each core. For example, in any bifacial knapping process we can observe how the length and width of the core are progressively reduced. This reduction corresponds to the thickness of the obtained flakes’ platforms, as the flake platform resulting from a removal in the core’s surface A corresponds with the flake surface in the core’s surface B, and vice versa (Fig. 1). In the absence of other variables, we use the median thickness of the flakes to correct the maximum thickness of the core when needed (when thickness’ limits do not correspond to cortical surfaces).

Fig. 1
figure 1

3D refit that shows how the maximum length of the core is reduced by the platform thickness of the flake

Full size image

The resulting variation in the dimensions of flakes found in an archaeological assemblage might be high. Considering this, we used the median flake thickness and the median flake platform thickness as correction units (Fig. 2), without considering the specific knapping method through which the flakes were produced. We did this because it is sometimes impossible to identify which knapping method has been used to obtain each flake by analyzing the flake’s attributes (especially in the first stages of any reduction sequence). Furthermore, in order to avoid the possibility that a hypothetical excess of debris in the assemblage would affect these correction units, we only used flakes larger than 20 mm, an arbitrary threshold based on the assumption that larger products are large enough to generate large-scale changes in core dimensions. This threshold, however, can be adapted to every assemblage by analyzing size distribution patterns. In this sense, it is important to verify the size distribution pattern in each assemblage, in order to check whether the mean or the median is more appropriate to use for the flake and platform thicknesses. For an assemblage with raw material variability, correction units must be specifically determined for each one of them.

Fig. 2
figure 2

Flake measurements used as “Correction Units”

Full size image

Regarding the second challenge, finding the specific number of required correction units to apply to each dimension, we performed a diacritical analysis of each core, attending not only to the location and direction of the removals but also to the number of generations of removals in each maximum dimension. Therefore, each generation identified in each sector of the core corresponds to a correction unit (Fig. 3).

Fig. 3
figure 3

Measurements of blanks and identification of scar generations for the application of the VRM. L length, W width, T thickness. Red scars: number of scars for the correction of maximum length. Blue scars: number of scars for the correction of maximum width

Full size image

In unifacial knapping strategies (e.g., unifacial unipolar), it is only necessary to quantify the number of generations that have occurred, which are the correction units needed per knapped surface. Conversely, in bifacial knapping strategies (e.g., discoid), it is necessary to calculate the number of generations that correspond to the core’s maximum axis on both of the surfaces. Furthermore, in multifacial knapping strategies (e.g., polyhedrons), it is necessary to quantify the number of generations in those surfaces that correspond to the maximal dimensions of the core. Finally, it is not necessary to apply any correction unit to the maximal dimensions of cortical surfaces (Fig. 3).

After the required number of correction units has been established, it has to be multiplied (1) by the median of the flakes platform thickness, to obtain the core’s length and width; and (2) by the median of the flakes’ thickness, to obtain the core’s thickness. The resulting values are then added to the length, width, and thickness of the core, respectively. These new “corrected” dimensions can be used to calculate the estimated original volume of the blank by introducing them into the ellipsoid formula:

$$ \mathrm{Ellipsoid}\ \mathrm{volume}=\pi \times \frac{4}{3} \times \mathrm{a}\times \mathrm{b}\times \mathrm{c} $$

where

$$ a=\frac{\mathrm{Length}+\left(\mathrm{Median}\ \mathrm{platform}\ \mathrm{thickness}\times \mathrm{Number}\ \mathrm{of}\ \mathrm{corrections}\ \mathrm{for}\ \mathrm{length}\right)}{2} $$
$$ b=\frac{\mathrm{Width}+\left(\mathrm{Median}\ \mathrm{platform}\ \mathrm{thickness}\times \mathrm{Number}\ \mathrm{of}\ \mathrm{corrections}\ \mathrm{for}\ \mathrm{width}\right)}{2} $$
$$ c=\frac{\mathrm{Thickness}+\left(\mathrm{Median}\ \mathrm{flake}\ \mathrm{thickness}\times \mathrm{Number}\ \mathrm{of}\ \mathrm{corrections}\ \mathrm{for}\ \mathrm{thickness}\right)}{2} $$

Finally, the volume of the discarded core should be divided by the volume obtained through the ellipsoid formula (Fig. 4). The result is then multiplied by 100, thereby obtaining the estimated percentage of remaining volume for each core.

Fig. 4
figure 4

Semi-axis used in the volume formula of the ellipsoid

Full size image

In summary, the required steps to apply the VRM are the following:

  1. 1.

    Calculate the mean or median of the flakes’ platform thickness and the flakes’ mean or median thickness from the archaeological assemblage.

  2. 2.

    Measure the three morphological dimensions of each core based on its minimum bounding box and obtain the core’s volume through 3D models.

  3. 3.

    Diacritical analysis of the cores: the number of generations of scars must be identified and quantified for each morphological axis, because the position of the scars on the core may affect none, one, two, or all three maximal axes (length, width, and thickness).

  4. 4.

    Multiply the number of required correction units by the median flake platform thickness (core length and width) and by the median flake thickness (core thickness).

  5. 5.

    Add these values to the dimensions of the core.

  6. 6.

    Apply the ellipsoid volume formula using the corrected dimensions to obtain the estimated original volume.

  7. 7.

    Finally, divide the volume of the analyzed core by the estimated original volume of the blank prior to knapping, and multiply the result by 100 to obtain the percentage of the remaining volume on the core.

To convert the value of the estimated original volume into mass, it is necessary to know the density of each core. To do this, the mass is divided by the volume of the core in its final form to obtain the density value for each core. In this way, the estimated original mass of one core is obtained by multiplying the value of its density by its estimated original volume obtained in step 6.

Experimental design

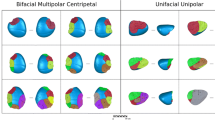
To verify the performance of the VRM, we designed and carried out an experimental program. A total of 64 cobbles of quartzite, quartzarenite, and sandstone from Olmos de Atapuerca and the terraces of the Arlanzón River (Burgos), weighing between 381 and 4424 g, were used for knapping. There was no deliberate selection of morphology or size, but variation was sought in both aspects. Four knappers (two women and two men) with different degrees of experience participated in the experiment. Each knapper worked on 16 cobbles, divided into four groups, each associated with a different knapping strategy: unifacial unipolar, bifacial multipolar centripetal, multifacial multipolar, and handaxe production. Although strict guidelines were not provided on how to carry out each type of reduction, they can be defined in general terms as follows:

  • Bifacial multipolar centripetal: two opposite faces of the blank separated by a plane of horizontal intersection were reduced. Flakes were removed following a perimetral scheme along the edge of the core. This reduction could have been done following the alternating method, the alternate method, or a combination of both (Fig. 5a).

  • Unifacial unipolar: removals were performed on a single surface, striking on a single unprepared percussion surface. No restrictions on the perimetral development of the knapping sequence were imposed, but flakes had to be produced unidirectionally on the same axis of the blank (Fig. 5b).

  • Multifacial multipolar: removals were carried out by taking advantage of the faces of the core as either percussion platform or exploitation surfaces, depending on which was appropriate for each removal. In this way, the core was constantly turned without following a defined or organized scheme (Fig. 5c).

  • Handaxes: these blanks were flaked on two opposites faces—separated by a plane of horizontal intersection—following a perimetral scheme to configure a tip at the distal part of the blank and a more rounded shape in the opposite end. Each knapper configured each handaxe according to his/her own criteria, without generating a specific shape or morphology (Fig. 5d).

Fig. 5
figure 5

Type of core reduction used in the experiment. a Bifacial multipolar centripetal, b unifacial unipolar, c multifacial multipolar, and d handaxe

Full size image

Knappers freely choose their cobbles and the hammerstones. They were also free to apply the reduction strategy that they considered optimal for each blank, and to decide to what degree they reduced them. The only requirement was for them to generate reduction variability, as we were interested in how the VRM performs at different stages/phases/degrees of reduction. The experiment produced a sample of 16 cores from each group, with random internal variability in terms of degree of reduction.

Each blank was scanned in 3D, measured, and weighed before and after the experiment, to obtain the volume (mm3), surface (mm2), dimensions (mm), and weight (g) of each initial and final blank. The cores and blanks were 3D scanned using a Breuckmann SmartSCAN3D-HE Scanner with a 250-mm field of view (Breuckmann Optocat 2012 R2-2206 software). From the 3D models, the dimensions, surface, and volume of each object were calculated using Meshlab software. These models are available for scientific and/or academic purposes at https://doi.org/10.5281/zenodo.3368659 (Lombao 2019).

Regarding flakes, 1629 flakes larger than 20 mm were obtained. Morphological and technical measures (especially the thickness and the platform thickness), and weight, were taken (see histograms in Supplementary Fig. S1). The complete sample of cores and flakes and the attributes measured for this experiment are available for further method implementation or new research proposals in Supplementary Databases 1 and 2.

Statistical procedures

First, we compared how the VRM operates using the ellipsoid volume formula and four other geometric volume formulas: cube, sphere, cylinder, and prism, to evaluate which geometric formula is more accurate. Due to the non-parametric distribution of the data (Shapiro-Wilk (p) < 0.05), both Pearson’s r and Spearman’s Rho were used. In similar experiments, the coefficient of determination (r2) has been used to evaluate the inferential power of these methods (Clarkson 2013; Eren et al. 2005; Hiscock and Tabrett 2010; Morales et al. 2015).

Since the VRM is expressed in standard units of measurement for the estimation of the volume of the original blank, these estimations can be compared to actual values to verify their accuracy and check if biases occur by means of under- or overestimation of the results. To do this, we calculated the average error (AE), which expresses the average of the difference between each estimated value and its actual one. However, it must be noted that “non-biased” is not equivalent to “precise,” (e.g., negative values in errors can compensate for positive values in other errors), so it is possible for a model to have a very low bias and be inaccurate at the same time. Therefore, the mean absolute error (MAE) and the root mean squared error (RMSE) were calculated to check the accuracy of the VRM.

Using the average of the original real volume as a reference, it is possible to obtain the percentage of average error (%AE), the percentage of mean absolute error (%MAE), and the percentage of the root mean squared error (%RMSE), which allows us to directly compare the accuracy of the different geometric volume formulas.

We also compared the medians (Mann-Whitney test) and the distributions (Kolmogorov-Smirnov test) of the values between the real and the estimated original volume.

Second, to evaluate the effects of the reduction strategy on the estimation of reduction intensity, we performed ANOVA analyses to compare the means between the real and estimated percentages of remaining volume for each type of reduction strategy. We also used a Kolmogorov-Smirnov test to compare the distributions of the values. Furthermore, we performed Pearson correlation (r) tests and compared the regression function of each reduction strategy through ANOVA tests.

Finally, in order to assess whether the size of the cores affects the reconstructions performed with the VRM, we compared the relationship between the final weight of the core and the original weight estimated using the VRM.

Resamples

Assemblages recovered from archaeological sites mostly present different kinds of biases, either due to anthropic processes prior to the burial of the assemblage, post-depositional processes that can alter their integrity, or/and limitations derived from the excavation process (e.g., excavation extension). In addition, the formation of time-averaged layers because of re-occupation events creates palimpsests where the identification of discrete occupation-related assemblages is not always easy.

As the VRM is based on both the analysis of cores and the measurement of flakes from the same assemblage, it is necessary to verify how different kinds of bias affect the VRM estimation. To do this, we carried out two resampling experiments to simulate different possible scenarios:

  • First, we performed 1000 random resamplings to select the 20% of the flakes from the experimental assemblage, obtaining 1000 different values for average flake and platform thickness. In this case, we use the means of both the flake’s thickness and the platform instead of the median, as the mean generates an assemblage with higher internal variability (see Supplementary Fig. S2 for the resampling results using medians). Then, we calculated the VRM for each case, obtaining the range of variability in the calculation of the remaining volume percentage for each core depending on random sampling biases. Finally, we calculated the difference between the remaining volume percentage obtained with 100% of the flakes and the remaining volume percentage obtained in each random resampling for each core.

  • To evaluate another possible scenario, in which there would be a differential transport of material, we performed two more resamplings. After weighing each flake, we ranked all flakes by weight and selected the top 20% of largest flakes (“Largest Flake Subset” [LFS]) and the bottom 20% of the smallest flakes (“Smallest Flake Subset” [SFS]) of the entire sample to generate two different size bias scenarios and compare the performance of the VRM in non-randomly biased assemblages.

  • Finally, with the goal of measuring how the number of generations influences the estimations obtained through the VRM, we have modified the number of generations, creating several different scenarios and simulating potential inter-analyst variability:

    • Scenarios A and B have been created by increasing + 1 and + 2 generations respectively for each of the core’s dimensions, which implies a + 3 increase in the identified generations per core in scenario A, and a + 6 increase in the identified generations per core in scenario B.

    • Scenarios C and D have been created by diminishing − 1 and − 2 generations respectively for each of the core’s dimensions and keeping a 0 value for those dimensions in which no generation has been identified.

    • To observe the influence of small changes in the number of identified generations derived from an expectable inter-observer error, we have generated two final scenarios. Scenario E adds one generation only to one of the core’s dimensions, while scenario F extracts one generation only to one of the core’s dimensions.

The entire process of obtaining volumes with different geometric formulas, as well as the different resampling processes (both random and size) and the statistical treatment of the data, was carried out on R (R Core Team 2013). All scripts and the steps that were followed are described in the Supplementary Material.

Results

Geometric formulas

Table 1 shows the results of the tests for the volumetric reconstruction of the blanks for each geometric volume formula. Pearson’s r values, the coefficient of determination (r2), and Spearman’s Rho are remarkably high for both the shape of the ellipsoid and the prism, indicating that there is a strong linear correlation between the estimated values and the original ones (Table 1). The fact that these coefficients are the same for the prism and the ellipsoid can be explained by the fact that their respective formulas use the same dimensions (with the same corrections) to obtain the estimated volume. The difference between the two formulas is that in the ellipsoid, it is applied to the semi-axes of the length, width, and thickness, while in the prism, the entirety of the axes is used, causing an overestimation of the original volume. This overestimation also occurs when using the sphere and cube formulas, which overestimate the results by using the semi-major axis to define the radius in the case of the sphere and the major axis in the case of the cube.

Table 1 Results for each type of geometric formula when comparing the real and estimated original volume of the blanks
Full size table

Regarding the average error (AE), the results obtained using the ellipsoid formula are the least biased, since it does not over- or underestimate the data, while the other geometric formulas systematically overestimated the volumes (Table 2).

Table 2 Results of average error (AE), mean absolute error (MAE), root mean squared error (RMSE), and their percentages (%) for each geometric formula used
Full size table

This can be seen in Fig. 6, which shows how the errors in the ellipsoid reconstruction follow a normal distribution, with a mean very close to zero. In addition, it presents the narrower distribution curve of error values compared to other geometric formulas, which indicates that there is no bias in the estimations and that errors are smaller than in the other geometric formulas.

Fig. 6
figure 6

Histograms showing the distribution of the errors (i.e., differences between real and estimated values) for each geometric formula

Full size image

Furthermore, the ellipsoid is the most accurate formula because it has a much lower mean absolute error (MAE) compared to that obtained through other geometric formulas. The average deviation ratio between the estimated and real values (%MAE), 17.88%, is substantially lower than the percentages obtained using the other geometric formulas.

Regarding root mean squared error (RMSE), the ellipsoid is again the best geometric formula, providing more precise estimations of the original volumes, since it has a lower RMSE and %RMSE, indicating that the maximal errors are lower in the ellipsoid than other geometric formulas.

When comparing real and estimated values by applying the ellipsoid volume formula, there are no statistically significant differences between them, either in the medians (Mann-Whitney (p) = 0.38), or in the distribution of the values (Kolmogorov-Smirnov (p) = 0.55), contrary to results obtained using other geometric formulas (see Supplementary Table S1).

The overestimation detected in the reconstructions of the original volumes using the VRM with different geometric formulas turns into an overestimation of the reduction degree and an underestimation of the percentage of remaining volume. In this way, the use of the cube, sphere, cylinder, and prism formulas results in percentage values of remaining volume that are significantly lower than the real ones (see Supplementary Table S1). Indeed, the estimations of the remaining percentage obtained by the ellipsoid formula are very similar to the real ones, and there are no significant differences between them, either in the average values (Student’s t test (p) = 0.83) or in the distribution of the values (K-S (p) = 0.84).

Similarly, the Pearson r values (r = 0.85, p = 6.01 e−19) and the coefficient of determination (r2 = 0.72) between the estimated remaining volume percentages through the ellipsoid formula and the real percentages indicate that there is a strong correlation between them (Fig. 7a).

Fig. 7
figure 7

Correlation plot a showing the relationship between real and estimated percentages of volume; b showing the relationship between real and estimated percentages of volume by reduction strategy

Full size image

When comparing the differences between predicted and actual percentage of remaining volume across the reduction intensity, the obtained regression coefficient is r = − 0.29, p = 0.01. Therefore, there is a slight tendency to overestimate the percentage of remaining volume on the initial phases of reduction and to underestimate it on more advanced phases. Nevertheless, a more detailed evaluation classifying the results in different intervals of reduction intensity (100–60%, 60–30%, and 30–0% of remaining volume) displayed no significant differences across them (Kruskal-Wallis test (chi-squared = 2.26, df = 2, p = 0.32)).

Reduction strategy and size

Results from the ANOVA comparing the regression function of each reduction strategy show that there are significant differences between them (ANOVA df = 3; F = 6.9, p = 0.0001). A further analysis indicates that these differences are between bifacial (handaxes and bifacial multipolar centripetal) and unifacial (unifacial unipolar) strategies, and between bifacial multipolar centripetal and multifacial multipolar cores (see supplementary Table S2). Although the slopes are very similar in the regression lines of the four reduction strategies (Fig. 7b), their intercepts are different. This indicates that throughout the reduction sequence, the VRM behaves similarly in each of the four reduction strategies.

Although there is a tendency toward underestimation in the case of unifacial unipolar cores, when comparing each type of reduction strategy individually, there were no statistically significant differences between the estimated and real percentages of reduction, either in the mean or in the distribution of the values (see Table 3). Thus, Pearson’s r values and the coefficient of determination (r2) are high for all the types of core reduction and are slightly lower in the case of multifacial multipolar cores. This indicates that the type of reduction strategy does not affect the estimations obtained with the VRM.

Table 3 Results for each group of reduction strategies when comparing the real and estimated percentages of remaining volume
Full size table

It should be noted that in five cases, there was a deviation above ± 16% of the remaining volume percentage with respect to the original. One of these cases was a broken handaxe, which accounts for its high deviation. The other four cases were in multifacial multipolar cores. Therefore, we have confirmed that less systematic reduction strategies may produce a greater deviation in the estimates. Regardless, even within multifacial multipolar cores, this high deviation only affects 25% of them.

To assess whether the size of the blanks can affect the reconstructions performed with the VRM, we compared the relationship between the final volume of the core and the original volume estimated through the VRM (Fig. 8). Thus, we obtained a Pearson correlation (r = 0.74, r2 = 0.55, p = 1.87 e−12) very similar to the correlation between the volume of the final core and the original volume of each blank (r = 0.66, r2 = 0.44, p = 1.58 e−09). This indicates that the estimation of the original sizes by means of the VRM is not affected by the final size of the cores. Furthermore, a t test comparing the regression function of both regression lines shows that there are no statistical differences between both (Student’s t test (p) = 0.72).

Fig. 8
figure 8

Correlation plot showing the relationship between the final volume of cores and the real and estimated volumes of the original blanks

Full size image

Resampling (randomly biased record)

As mentioned above, to observe how the VRM is affected in cases of biased archaeological assemblages, we performed 1000 random simulations by resampling 20% of the flakes from the experimental assemblage. We calculated the difference between the remaining volume percentage of each core obtained from the entire assemblage and the remaining volume percentage of each core obtained in each of the 1000 random biased resamples.

The results of the 1000 resamplings show a mean absolute difference of − 2.20 ± 0.67 with respect to the estimated remaining volume percentage of the cores using the entire assemblage, where the maximal differences range between − 6.04% and + 0.15% (Fig. 9). This indicates a low incidence of the correction factors—that is, the mean of the flake thickness and platform thickness—in randomly (non-size) biased assemblages.

Fig. 9
figure 9

a Histogram showing the distribution error for 1000 resamples (percentage of remaining volume (100% of flakes) − percentage of remaining volume (20% of flakes)) for each reduction strategy. b Boxplot and jitter plot showing the distribution error for the 1000 resamples (percentage of remaining volume (100% of flakes) − percentage of remaining volume (20% of flakes) for each core

Full size image

Resampling (size bias)

In the case of SFS resampling, there is an average overestimation of the remaining volume percentage of 9.93 ± 2.36, compared with the unbiased sample, with deviations ranging from 3.90 to 13.88% of the remaining volume. When we analyzed the LFS resampling, there was an average underestimation of − 11.36 ± 2.23% of the remaining volume, ranging between − 15.85 and − 5.92%.

Although these differences are considerable, it should be noted that the correction factors for both subsets have very different values and represent extreme cases of a partial, biased record. Thus, (1) for 100% of the flakes median flake thickness is 11 mm, and median platform thickness is 10 mm; (2) with 20% of smaller flakes, the median thickness and platform thickness is 6 mm; and finally, (3) with 20% of the largest flakes, the medians are 21 mm and 17 mm, respectively, which is more than three times the values of the small ones.

This implies that although clear differences exist in the estimation of the reduction degree in cases of large differences in the flakes’ thicknesses, they are not as marked as we expected a priori. In addition, when comparing two archaeological assemblages, we must consider the different values of the correction factors for each archaeological assemblage, and qualitatively assess whether the differences in the values of the degree of reduction obtained are due to the size of the flakes or to any processes (natural or cultural) that may have resulted in a dimensional selection of the flakes in the archaeological site.

Measuring the effect of number of generations

Scenario A (+ 1 generations in each core’s dimensions) underestimates the original results in a − 12.07% ± 4.99% of the remaining volume. In scenario B (+ 2 generations in each core’s dimensions), the underestimation increases to an average of − 20.05% ± 8.09%.

Scenario C (− 1 generations in each core’s dimensions) overestimates the remaining volume in 8.98% ± 4.36%, increasing to 17.96% ± 7.24% in scenario D (− 2 generations in each core’s dimensions).

Last, in scenario E (+ 1 generations just in one of each core’s three dimensions), we observe an average underestimation of − 2.92% ± 1.41% with a maximum deviation of − 6.63% and a minimum deviation of − 1%. On the contrary, scenario F (− 1 generations just in one of each core’s three dimensions) produced an average overestimation of 2.54% ± 1.66%, with a maximum deviation of 7.90%.

Therefore, the increase or decrease in the identification of the generations of removals in each core determines the estimation of the percentage of the remaining volume obtained though the VRM. Logically, in those scenarios where big increases or decreases are produced (A, B, C, and D), the results show significant variation in comparison with the result obtained without subsequent modifications. Despite these differences, it is necessary to point out that these scenarios simulate a considerable error (an increment of six generations in total for each one of the cores) and, the same way that happened with the large variation in the flake’s thicknesses, these differences are not as remarkable as we expected.

On the contrary, scenarios E and F simulate more realistic changes that may occur by inter-observer variability. These scenarios show how the increase or decrease of identified generations in just one dimension for each core causes a descent or increase of the percentage of the remaining volume of approximately 2%, which does not generate statistically significant differences between them and the obtained result without modifications (Student’s t test (p) = 0.32, Student’s t test (p) = 0.41, respectively).

Discussion and conclusions

Hiscock and Tabrett (2010) proposed a set of seven characteristics that a reduction index should have in order to be universally applicable. Although these characteristics were formerly oriented to methodologies and indexes for retouched tools, it is also possible to apply them to cores as well. These characteristics are as follows: (1) high inferential capacity; (2) unidirectional relationship between index and reduction; (3) utility—that is, the index must be useful along the reduction process; (4) sensitivity to small variations in the degree of reduction; (5) versatility in its adaptability to differentiate patterns of retouching (in the case of cores, to different reduction strategies); (6) capacity to operate with varied blanks; and (7) scale independence.

To measure the inferential capacity of the methods for estimating lithic reduction, researchers have often used the Pearson (r) and the coefficient of determination (r2) to evaluate the relationship between these parameters and the amount of volume removed. In this sense, the VRM has fairly strong inferential power (characteristic 1), as shown by the values of the coefficient of determination, very close to the boundary of 0.8 established as very strong by Hiscock and Tabrett (2010).

These statistical tests are useful because they measure the strength of the response of a dependent variable (the estimated index of reduction). However, when there are changes in the independent variable (the degree of reduction), the exclusive use of the coefficient of determination for evaluating the inferential capacity of one method has several risks: though extreme values may cause higher linear correlations, some biases may be hidden in the form of under- or overestimation under a high coefficient of determination. Therefore, it is necessary to compare slopes and intercepts of the regressions to improve the accuracy of each reduction index.

For these reasons, we have not only used the Pearson and coefficient of determination, but also compared the central trends and the distributions of both the estimated and real values, and note that there are no statistically significant differences between them. In addition, the fact that VRM provides reduction values as a percentage of the volume removed confirms that this method and the formula of the ellipsoid volume can be used to obtain non-biased and accurate values.

Indirectly, these correlation values indicate that the VRM is unidirectional in nature (characteristic 2), since the more the degree of reduction increases, the more the percentage of estimated removed volume increases as well. This has been confirmed through a non-sequential and non-directed knapping experiment, in which random variability of reduction degrees has been generated. Therefore, a sequential experiment could be a means by which this unidirectional characteristic can be verified.

Likewise, the VRM can be used to accurately estimate reduction intensity throughout the reduction process, rather than in only some initial and final stages (characteristic 3). Cores produced in our experiment show different degrees/percentages of reduction, and results obtained with the VRM are remarkably similar to the real ones, independent of reduction stage. The results show a slight tendency to underestimate the percentage of reduction in the most exhausted cores, but there are no statistically significant differences in the errors among the different reduction intervals.

Furthermore, using the VRM, a single removal on the surface of the core will be detected in the percentage of estimated remaining or removed volume, because the core dimensions are corrected according to the position and sequencing of scars. Simulating changes in the identification of removals show how slight modifications due to inter-observer errors create an average variation of ~ 3% of the remaining volume. This confirms the sensitivity of VRM when it comes to detecting small modifications that may be produced through reduction intensity (characteristic 4).

In this sense, one advantage of using 3D models is that measurements are generated automatically and are therefore more reliable than ones made by hand (Dibble and Bernard 1980; Morales et al. 2015). However, when applying VRM, it is important to quantify the scars and the generations of removals on the same axis where the maximum length, width, and thickness have been measured, in order to make the appropriate corrections.

Nevertheless, to evaluate these two last characteristics, it is essential to consider the overlapping effect of removals, because it may cause underestimation on the reconstructions under certain circumstances. This mainly occurs in cores which have been extremely reduced by means of unifacial strategies, opening the door for results of estimated reduction being lower than the real ones at these final stages of knapping (Lombao et al. 2019).

Despite the slight differences in the operation of the VRM depending on knapping strategies, the method adapts well to each core’s characteristics, which allows reduction intensity to be estimated over a wide range of knapping strategies (unifacial, bifacial, and multifacial strategies) with sufficient accuracy. The estimations of percentage of the volume removed obtained through different knapping strategies are statistically similar to the real ones, which supports the versatility of the method (characteristic 5). Furthermore, the application of VRM can be extended to estimate the reduction intensity in some types of tools, such as handaxes made on cobbles. It is likely to correctly estimate reduction intensity in other tools, such as choppers and chopping tools, due to their similarity to some of the reduction strategies tested in our experiment.

Our results show that the VRM reliably estimates the sizes of initial blanks, regardless of the shape and/or size of the original cobble (characteristic 6). Unlike other methods, the VRM is not affected by the size of the original blank (Lombao et al. 2019), meaning assemblages with different initial dimensions can be compared.

The VRM has not been tested yet in non-fluvial blanks (e.g., flint nodules) and cores on flakes, so experiments checking its reliability in these types of blanks should be carried out in the future. However, in many cases, flint nodules also present ellipsoid shapes, such as kidney-shaped flints. Furthermore, other studies point to the ellipsoid as the geometric shape that better predicts the cortical surface of flint nodules (Douglass et al. 2008; Lin et al. 2010), so, presumably, the VRM should also fit in these cases. In addition, an advantage of this method is that it is possible to adapt the geometric formula to obtain the shape’s volume that better fits the blank format. For example, if we know that the available formats in an archaeological site are tabular blanks, then we can choose other formulas, such as those for a cube or a prism, in order to obtain more accurate estimations of the original sizes of the archaeological cores. In this sense, instead of the type of raw material used, the main obstacle to the archaeological application of the VRM would appear in those cases where we cannot know the shape of the original blanks due to their high morphological variability, such as irregular flint blocks.

Regarding scale-independence (characteristic 7), the VRM can be used to quantify the reduction degree both in absolute and relative terms, since it is possible to estimate the amount of material removed (in mm3 or grams, for example), as well as both the percentage of removed and remaining material. This can be used to compare different assemblages and/or cores regardless of their size, using as a reference to the degree of reduction in terms of percentage of the removed/remaining volume. It can also be used to obtain information on size selection strategies for the initial blanks of the cores found in an archaeological site, and can help elucidate relevant prehistoric matters, such as the role of raw material size in (1) lithic assemblage variability, (2) reduction intensity, and (3) raw material transport (Andrefsky 2008; Ditchfield 2016b). In addition, the VRM may be used to complement the analysis of the cortical ratio (Dibble et al. 2005), as it is possible to estimate the amount of material (in mass and volume) that should remain in a complete assemblage and check whether it corresponds to the mass or volume remaining in the archaeological assemblage.

Furthermore, random resamplings prove that it is not necessary to have a complete record to estimate the VRM; it is possible to use this method in archaeological sites excavated in extension, or excavated in pits and trenches. However, we must highlight some limitations of the method: for example, resamplings with the 20% largest flakes and the 20% smallest flakes proved that the VRM is sensitive to extreme changes in flake size. Therefore, in order to compare two archaeological assemblages, we must assess whether there is or not a pattern of selection/differential preservation of the flakes; however, this pattern would need to be extreme to markedly affect the results.

In addition, it is frequent that archaeological contexts are formed by the accumulation different occupations and/or episodes of transport of raw material, thus not all the flakes of the assemblage would match with the cores. Even though we have not performed tests on how the VRM would be affected by the presence of “intrusive” flakes in the experimental assemblage, the resampling results for the flakes show that the presence of these type of items coming from different reduction sequences would just affect the results if their size is radically different from the rest of the flakes of the assemblage. In this case, the influence of these outliers can be limited by using the median of the flake’s platform thickness and the median of the flake’s thickness, instead of the mean.

Likewise, it is necessary to test the efficacy of the VRM in more standardized industries (e.g., Levallois, laminar cores), where knapping strategies likely need similar adjustments, and so estimations of remaining percentages will be almost equal. Finally, the applicability of VRM to cores on flakes should be explored with a new experiment designed to evaluate how this method works under these conditions, and to determine whether it is more useful to apply a geometric formula different from the ellipsoid volume to reconstruct the original volume of the flake-blanks.