Introduction 

Internal instability in granular soils occurs when its finer particles erode through the pore spaces, resulting in mutation of geo-hydraulic characteristics such as shear strength and permeability (Imre 1995; Vaughan and Soares 1982; Kenney and Lau 1985; Scheuermann and Kiefer 2010; Israr et al. 2016). The internal instability of a soil is closely related to its particle size distribution (PSD) that occurs when its skeleton of coarser particles cannot protect the finer particles from erosion to result marked changes in its original particle size distribution (Kenney and Lau 1985; Lőrincz et al. 2015) . Occurrence of internal instability results in significant reduction in geotechnical characteristics of soils such as shear strength and permeability (Imre et al. 2012; McDougall et al. 2013). Thus far, numerous empirical and semi-empirical methods to examine the potential of internal instability based on PSD curves have been proposed. Reportedly, more than 46% of all hydraulic structure failures worldwide are somehow associated with the seepage-induced internal instability failures including piping, suffusion, lateral pumping, flood-induced breaches of riverbanks, and sinkholes at the downstream of earthen dams, (Richards and Reddy 2007; Foster et al. 2000). The probability or likelihood of a soil to exhibit internal instability is governed by geometrical constraints such as its particles and constriction size distributions, whereas the development and progression of internal instability would be controlled by hydromechanical constraints such as specific combinations of larger hydraulic flows and gradients, and lower effective stresses and shear strength of soils (Smith and Bhatia 2010; Zhang et al. 2021). This study purports to evaluate the former aspect of ascertaining the potential of internal instability of soils using controlled laboratory hydraulic test results corroborated with rigorous analysis of geometrical constraints based on fractal entropy of particle size distribution of soils.

Various methods have been proposed thus far based on the particle size distribution (PSD) of soils to evaluate their potential of internal instability. USACE (1953) investigated the inherent (internal) stability of a filter soil mixed with sand and gravel to evaluate its ability to refrain from particle segregation, and then proposed guidelines for selecting the stable and effective filter. Istomina (1957) evaluated the coefficients of uniformity (Cu) of granular soils and suggested an internal stability criterion based on Terzaghi (1939) filter design method. Likewise, Kezdi (1979) and Sherard (1979) independently proposed criteria similar to Istomina (1957) that divided the PSD curve into finer (erodible fine particles) and coarser (stable coarse particles) fractions. Assuming the former to be a base soil and the latter to be a filter, they applied Terzaghi’s (1939) filter rule to determine whether the filter could retain the base fraction for a given soil to be characterized as internally stable. Kenney and Lau (1985) introduced a new stability ratio (H/F)min from the PSD curve to quantify the internal instability of granular soils, where F is the mass fraction finer than particle size d and H is the mass fraction between particle size d and 4d. Later on, Chapius (1992) showed that these criteria from Kenney and Lau (1985), Kezdi (1979), and Sherard (1979) are similar and could be expressed in terms of the secant slope of the PSD curve.

Burenkova (1993) followed by Wan and Fell (2008) proposed identical methods to examine the internal stability of broadly graded soils (e.g., sand-gravel with silty and clayey fines) based on particle sizes from the PSD curve such as \({D}_{5}\), \({D}_{15}\), \({D}_{20}\), \({D}_{60}\), and \({D}_{90}\), but none of the above criteria was sensitive to the level of compaction of soils. Indraratna et al. (2018) then combined the PSD-based criterion of Kenney and Lau (1985) with the constriction size distribution (CSD)-based filter design method of Indraratna et al. (2015) and proposed a new geometrical method for assessing internal stability as a function of the relative density (\({R}_{d}\)) of soils. This CSD-based method could accurately assess the correct potential of instability for a large experimental database of 92 test results (\(\approx 99\mathrm{\%}\) success). However, from practical perspective, the PSD-based methods are still preferred for prompt evaluations of internal instability potential, because the CSD-based methods require computer aid to perform complex discretization and computations to demarcate between base and filter fractions, as well as to obtain the PSD of base and CSD of filter for assessing the internal stability.

Based on relative proportioning of particle sizes in a PSD curve, Full et al. (1983) pioneered the use of entropy to define the aggregate properties of select granular soils. According to Lőrincz et al. (2015), a simple particle size distribution curve could be idealized into discrete size fractions, and its structural or internal stability against the inception of geo-hydraulic failures could be expressed as a function of these fractions. Jaynes (1957) established that the probability of occurrence of internal instability may be associated to the curves with highest intact uncertainty or the maximum grading entropy. This study deeply examines the combined role of both particle size distribution curve and its associated fractal grading entropy, now on called as grading entropy, in correctly quantifying potential of internal instability. In the following sections of this paper, the internal stability of 10 different granular soils with known PSD curves and maximum entropy has been experimentally evaluated. Furthermore, it is also examined how the shape of the PSD curves, the percentage of erodible fractions, and the relative distribution of particle sizes in a soil (i.e., grading entropy) would affect its internal stability.

Laboratory program

Test material and geometrical assessments

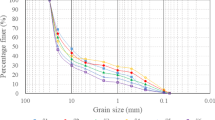
In this study, twenty (20) long-term hydraulic tests were carried out on ten granular soils with \({C}_{u}\) ranging between 1 and 40. As Fig. 1 shows, these soils contain sand and sand-gravel mixtures that conform to the typical selection ranges for designing filters to protect railway substructures and hydraulic structures (Selig and Waters 1994; Israr and Indraratna 2017). All the test specimens were prepared by compacting at almost 50% relative density to obtain repeatable results for valid comparisons. Ten (10) tests were carried out with a hydraulic flow applied from the bottom to the top of the test samples, and 10 where the flow was applied from the top of the test samples to the bottom. This approach would enable one to examine whether or not the internal instability potential of soils would be influenced by a change in the direction of flow and the repeatability of tests carried out in this study.

Fig. 1
figure 1

Particle size distributions tested in this study (shaded area represents the typical ranges of subballast and downstream protective filters; the vertical dashed lines represent the abstract fraction system for discretizing PSD in several fractions)

Full size image

Table 1 summarizes the geometrical assessments of internal instability potential through some of the well-accepted PSD-based criteria. For instance, Kezdi (1979)’s method assessed soils 1–7 as internally stable, and soils 8–10 as unstable; Kenney and Lau (1985) assessed soils 7–8 to be unstable, whereas Sherard (1979) only assessed soils 9–10 as being unstable. The criteria from Burenkova (1993) and Wan and Fell (2008) classified all the soils as stable, while Indraratna et al. (2018) assessed soils 5–8 as unstable. All these soils have been re-examined experimentally in the following sections of this paper.

Table 1 Summary of physical soil properties and laboratory test results for current study
Full size table

Test setup and apparatus

As Fig. 2 shows, the hydraulic test chamber is a smooth wall Perspex cell with an internal diameter of 150 mm and a height of 250 mm that could accommodate a 200-mm-long soil specimen. To avoid the boundary effects and development of preferential flow paths, most previous filtration testing used equipment with a size ratio R (= Dcell/d100) ranging between 6 and 8, where Dcell and d100 represent the cell diameter and particle size at 100% finer by mass, respectively. For instance, some studies reported that these values helped to avoid the effects of boundary wall friction, the development of preferential flow paths and excessive frictional resistance to the erosion of fines, and consistent and repeatable results (Fannin and Moffat 2006; Xiao and Shwiyhat 2012; Zou et al. 2013). An electro-pneumatic automated hydraulic pump applied inflow to the test specimens at a predetermined pressure, while a pressure transducer connected downstream from the test specimen could monitor outflow pressure during the hydraulic tests. Flow through the test specimens incurred a significant loss of hydraulic head that varied from soil to soil. An outlet valve helped to control the differential pressure applied to the test specimens, and it could be deduced from the difference between the inflow and outflow pressures. Fine particles that eroded with the flow could be captured in a downstream sedimentation tank for post-test forensic analysis.

Fig. 2
figure 2

Illustration of (a) test apparatus and (b) its schematic view

Full size image

Sampling, saturation, and test repeatability

The test specimens were prepared by mixing a predetermined weight of dry soil and then compacting it into five distinct and uniform layers within the test chamber to achieve a length of 200 mm. To obtain the target relative density (≈ 50%), the limiting void ratios \({e}_{\mathrm{max}}\) and \({e}_{\mathrm{min}}\) for each soil were determined using the standard test procedures ASTM D- 4253 (2006a) and ASTM D-4254 (2006b), respectively. The sample preparation method of Indraratna et al. (2018) was found to be effective in obtaining an \({R}_{d}\approx 50\mathrm{\%}\), so the soil was placed in discrete layers and then compacted by a 750 gm, 300 mm long by 20-mm diameter steel rod. According to the procedure outlined by Scott et al. (2012), the compaction energy (\({E}_{c}\)) needed to prepare specimens with Rd≈ 50% was estimated to be around 270 \(\mathrm{kJ}/{\mathrm{m}}^{3}\).

The test specimen was saturated by de-airing it under a back pressure of 120 kPa for 3 h, after which the de-aired and filtered water was circulated for at least 24 h under a constant hydraulic head of 50 mm. The complete saturation of a specimen was achieved to a satisfactory extent by obtaining Skempton’s B value above 0.95, and this was completed in multiple pressure ramps with a low-pressure difference of 10 kPa between the cell and back pressures (Zhang and Israr 2021). Specimen uniformity with respect to particle size distribution and compaction was ensured by preparing additional test specimens using the above procedure. For instance, uniformity with respect to particle size distribution was examined by comparing pre- and post-test PSD curves (see Table 1). Here, less significant changes in the pre-test and post-test PSD curves and the coefficients of uniformity (\({C}_{u} = {D}_{60}/{D}_{10}\)) for the middle layer (80 to 120 mm length) of an internally stable soil was enough to prove uniformity with respect to particle distribution. Whereas the erosion would be partially represented by the loss of finer fractions that would markedly alter the post-test \({C}_{u}\) compared to the initial sample; for example, the \({C}_{u}\) for soil-5 decreased from 20 to 5 due to erosion of fines at the particle size \({d}_{10}\)-level. Similarly, uniformity with regards to compaction could be examined by comparing the overall dry density (\({\gamma }_{d}\)) of each specimen with small samples cored within different layers of the same specimen. A soil specimen was assumed to be uniform and free of any layering effects when its local and overall dry densities were the same, and with less than 6% standard deviation (Israr et al. 2016).

Test procedure and rationale

The test procedure consisted of subjecting the fully saturated specimen to a hydraulic flow under predetermined pressures to keep the hydraulic gradients within certain limits. For example, with a geometrically assessed internally stable soil, increments of \(i\) were held between 0.04 and 0.05, and between 0.02 and 0.025 for an unstable soil (Skempton and Brogan 1994). Based on the author’s previous experience, these increments of \(i\) were enough to avoid potential disturbance to the test specimens and to obtain accurate critical hydraulic gradients \({i}_{cr}\) for internal instability (Israr et al. 2016). Hydraulic tests at a certain hydraulic gradient i continued (i.e., for 60 to 90 min each stage) until a steady state flow condition was reached and then another increment of i was applied for the subsequent test stage. The effluent flow rate could be deduced by repeatedly collecting a prerequisite volume of effluent and the time of flow during the tests. The flow curves were obtained by plotting the effluent flow velocity versus the applied hydraulic gradient, while the saturated hydraulic conductivities (k) of the soils could be determined from the slope of the flow curves by assuming linear Darcy’s law (Skempton and Brogan 1994).

In this study, the seepage-induced internal instability occurred in the non-Darcy regime of flow where its inception was characterized by a marked rise in the slope of the flow curves and a significant increase in effluent turbidity (≫ 60 NTU), where NTU stands for nephelometric turbidity unit. The current tests were continued for 2 to 3 h after the inception of instability or seepage failure while the corresponding \({i}_{a}\)-values were assumed to be critical hydraulic gradient (\({i}_{cr}\)); this would also correspond to the signs of visual instability in the test samples such as heave, piping, or suffusion. The tested specimens were retrieved from three to five distinct soil layers for post-test sieve analysis, and the results were then compared to the pre-test original PSD curves; soil with an unaltered PSD in the middle layer (80 to 120 mm) would be considered as internally stable.

Results and discussion

Table 1 summarizes test conditions such as the direction of flow and the physical properties of tested soils such as the coefficient of uniformity (\({C}_{u}\)) and relative density (\({R}_{d}\)). It also tabulates observations from the hydraulic tests of this study such as the percentile erosion (%), the critical hydraulic gradients (\({i}_{cr}\)), and the types of seepage failure (i.e., heave or suffusion).

Figure 3a, b, and c show the results of the hydraulic tests, including the effluent flow and variations in turbidity against the hydraulic gradients (\(i\)) applied for select tests (i.e., soil-4U, soil-5U, and soil-8U, respectively). The flow curve for the internally stable soil-4 abided by Darcy’s law to an appreciable length, such that an \(i\)-values up to 0.20 were plotted linearly against the effluent flow velocity (\(v\)). The increase in \(i\)-values from 0.20 to 0.60 caused a slight increase in the flow velocity, and the relationship between \(i\mathrm{ and }v\) became non-linear, while a further increase in \(i\) up to 0.80 rearranged the fine particles at the upper and lower boundaries of the test samples. The hydraulic gradients \(i\) approaching 1.0 generated the localized horizontal and inclined channels, and at \(i\ge 1.0\), these channels joined together to induce heave failure in soils 1–4 and soils 9–10 that were subjected to upward hydraulic flow. These observations are consistent with those reported by Skempton and Brogan (1994), where small differences in specimen responses and magnitudes of critical hydraulic gradients may be attributed to a relatively higher compaction of current test samples. For the tests under downward flow, seepage failure in the samples was recognized by a sudden drop in hydraulic gradient and axial bulging (hydraulic dilation) of specimen with limited erosion (\(\ll 2\mathrm{\%}\)), because no visible heave developments could be recorded. For instance, the original height of the test sample increased markedly when the hydraulic gradients approached unity (\(i\approx 1.0\)).

Fig. 3
figure 3

Effluent flow velocity and turbidity plotted against applied hydraulic gradient. (a) Soil-4U. (b) Soil-5U. (c) Soil-8U

Full size image

Not surprisingly, internally unstable soils 5–8 suffered from excessive erosion of their finer fraction (i.e., suffusion) at much smaller hydraulic gradients (\(i\ll 1.0\)), regardless of the flow direction. For instance, soils 5 and 8 showed excessive suffusion at \({i}_{cr,a}\approx 0.56\mathrm{ and }0.30\), respectively (see Fig. 3b, c and Table 1) that could be identified by the excessive erosion of finer fractions and a slight reduction in specimen volume under both upward and downward flows. For example, soil-8U and soil-8D had a total erosion of 12.75% and 16.8%, respectively. However, the hydraulic response of soils remains unchanged in the upward and downward flow, although the former would require a higher \({i}_{cr}\) and more time to induce same amount of erosion as the latter. A probable explanation of this discrepancy could be the effect of gravity such that the upward flow would require more effort to dislodge finer particles and erode them through the soil. In essence, downward flow would represent a worst-case scenario because particle erosion would be assisted by gravity, as shown by the effluent turbidity variations in Fig. 3.

Figure 4 shows a comparison between the average critical hydraulic gradients (\({i}_{cr,a}\)) from the tests under upward flow and those under downward flow where the data points plot along the line of equality, thus showing acceptable repeatability of current tests. The data points plot slightly below the line of equality because the \({i}_{cr,a}\)-values for downward flow were smaller than those for upward flow, which indicates that downward flow was assisted by gravity.

Fig. 4
figure 4

Comparison between upward and downward critical hydraulic gradients of this study (note: filled and hollow symbols represent stable and unstable samples, respectively)

Full size image

Figure 5a and b show comparisons between pre- and post-test PSD curves for the middle layers (i.e., 80 to 120 mm) retrieved from samples 3U and 3D, respectively. Here the internally stable soil experienced very small variations in its PSD curve in the middle layer, for example, there were no significant changes in the pre- and post-test gradations of soils 1–4 and 9–10 or their \({C}_{u}\)-values because there was a negligible erosion of fines (Table 1).

Fig. 5
figure 5

Pre-test and post-test PSD analyses for the select stable samples. (a) Soil-3U. (b) Soil-3D

Full size image

Similarly, the pre- and post-test PSD analyses of the middle layer of soils 5 and 8 in upward and downward flow tests are shown in Fig. 6; here, Fig. 6a shows that soil 5U experienced erosion of its fines that resulted in marked changes in its original PSD curve that characterized soil-5 as being internally unstable. However, under a downward flow (i.e., soil-5D), the same sample soil-5 experienced 23.6% more erosion for the same flow time, albeit at a slightly smaller \({i}_{cr,a}\) (Fig. 6b). Moreover, Fig. 6c shows that the internally unstable soil-8U exhibited up to 23.9% internal erosion from its middle layer, and that increased to 28.6% under downward flow (Fig. 6d). However, this increase in internal erosion and thus the internal instability was found proportionally related to the broadness and relative percentage of the erodible fraction of a soil gradation. For example, all the current soils had a similar range of different particle sizes ranging between 0.07 and 20 mm, and soils 1–4 and 9–10 with narrow and non-linear gradations with almost the same sized particles were more stable than the non-uniform soils (e.g., soils 5–8). This means the unstable non-uniform soils tended to be uniform and internally stable when subjected to seepage-induced erosion of their finer fractions, and therefore the internal stability of a PSD curve would depend on (1) the width of PSD curves and (2) relative proportioning of finer and coarser fractions in a soil. This is explained further using grading entropy theory in the following sections, while basic concepts related to grading entropy are presented in Appendix-I.

Fig. 6
figure 6

Pre-test and post-test PSD analyses for the select unstable samples. (a) Soil-5U. (b) Soil-5D. (c) Soil-8U. (d) Soil-8D

Full size image

Table 2 summarizes the entropy parameters for current experimental data. Figure 7a and b schematically illustrate how to discretize a PSD curve and calculate entropy parameters for soil-8U before and after the hydraulic test. Comparison of Fig. 7a with b shows that more than 20% erosion of fines resulted in the complete loss of particle classes C1 and C2 and a significant reduction in the original Cu from 40 to 9.0, thus yielding a completely new and internally stable PSD curve. In essence, the entropy increment (\(\Delta H\)) was found to be an effective and consistent measure of internal instability potential when compared to the existing criteria.

Table 2 Assessing the internal stability of current test data using the proposed grading entropy-based method
Full size table
Fig. 7
figure 7

Discretization of PSD curves for soil-8U in abstract fractions. (a) Pre-test. (b) Post-test

Full size image

Figure 8a shows the relationships between the entropy increment (\(\Delta H\)) and average critical hydraulic gradient (\({i}_{cr,a}\)) for the experimental data in this current study. The soils could be consistently characterized into stable and unstable samples using the stability boundary proposed by Indraratna et al. (2018) based on \({i}_{cr,a}\)-values. Similarly, Fig. 8b plots \(\Delta H\) against the overall erosion (\(f\)), so the same dataset could be successfully classified as stable or unstable using the existing erosion-based criteria (Kenney and Lau 1985; Israr and Israr 2018).

Fig. 8
figure 8

Correlation between ∆H and (a) icr,a and (b) f

Full size image

Maximum fractal entropy principal

A given set of PSD curves may possess a variety of grading entropies; however, only PSD with maximum entropy would exhibit a unique optimal distribution, which may be pertinent to determining the risk of instability. In this section, three maximum entropy cases based on the above entropy parameters, H, \(\Delta H\), and the normalized entropy increment \(\Delta h\), are analyzed.

According to the principle of maximum entropy, the maximum entropy (H) can be achieved using Lagrange multipliers as follows (Singh 2014):

$${L}_{\mathrm{max }H}=-{\sum}_{i=1}^{N}{C}_{i}\frac{{p}_{i}}{{C}_{i}}{\mathrm{log}}_{2}\frac{{p}_{i}}{{C}_{i}}+\lambda {\sum}_{i=1}^{N}({p}_{i}-1)$$
(1)

where \({L}_{\mathrm{Max }S}\) is the Lagrange function of maximum entropy, while \({p}_{i}\) is the frequency of ith fraction, \(\lambda\) is the Lagrange multiplier of the corresponding constraint (\(\sum_{i=1}^{N}({p}_{i}-1)\)). By differentiating the Lagrange function with respect to the relative frequencies \({p}_{i}\), and equating the derivative to zero, Eq. (1) takes the following form:

$$\frac{{\partial L}_{\max H}}{\partial p_i}=-\log_2\frac{p_i}{C_i}-\frac1{\ln\;2}+\lambda=0$$
(2)

where \({C}_{i}\) represents the number of imaginary elementary cells in the ith fraction divided by dmin (i.e., minimum particle size). Simplifying Eq. (2) further to obtain:

$$\frac{p_i}{C_i}=2^{\lambda-\frac1{\ln\;2}}=\mathrm{constant}$$
(3)

Following the same procedure as maximum H, the maximum \(\Delta H\) can be obtained from the following steps (Lorincz et al. 2005):

$${L}_{\mathrm{max }\Delta H}=-{\sum}_{i=1}^{N}{p}_{i}{\mathrm{log}}_{2}{p}_{i}+\lambda {\sum}_{i=1}^{N}({p}_{i}-1)$$
(4)
$${p}_{1}={p}_{2}={p}_{3}=\dots ={p}_{N}=1/N$$
(5)

where N represents the numbers of discretization of a PSD curve using the abstract fraction system (AFS), \({L}_{\mathrm{max }\Delta S}\) is the Lagrange function of maximum \(\Delta H\). Thus, the maximum normalized entropy increment (\(\Delta h\)) can be obtained from the same procedure as following:

$$L_{\Delta h}=-\frac1{\ln\;N}\sum\nolimits_{i=1}^Np_i\log_2p_i+\lambda_1\sum\nolimits_{i=1}^N\left(p_i-1\right)+\lambda_2\left[\sum\nolimits_{i=1}^Np_i\left(i-1\right)-A(N-1)\right]$$
(6)

where \(A\) represents normalized base entropy, while \({L}_{\Delta h}\) is the Lagrange function of maximum \(\Delta h\).

Notably, these entropy parameters \(H\), \(\Delta H\), and \(\Delta h\) would reach their maximum values at specific conditions. For instance, the fractal entropy \(H\) would become \({H}_{\mathrm{ max}}\) should the following condition meets (Lorincz 1990):

$$\frac{p_1}{C_1}=\frac{p_2}{C_2}=\dots=\frac{p_i}{C_i}=\dots=\frac{p_N}{C_N}=C;\;C=\mathrm{constant}$$
(7)

Similarly, the fractal entropy increment \(\Delta H\) would be maximum (i.e., \(\Delta {H}_{\mathrm{max}}\)) when condition in Eq. 8 would satisfy:

$${p}_{1}={p}_{2}={p}_{3}=\dots ={p}_{N}=1/N$$
(8)

whereas the normalized fractal entropy increment \(\Delta h\) would approach its peak value (i.e., \({\Delta h}_{\mathrm{max}}\)) at the following condition (Eq. 9):

$${p}_{i}={a}^{i-1}{p}_{1}, i=\mathrm{1,2},\dots ,N$$
(9)

where the sequence \({p}_{1},{p}_{2},{\dots ,p}_{i},\dots ,{p}_{N}\) is a geometric progression with a multiplier of a (\(a>0)\) and \({p}_{1}=\frac{1-a}{1-{a}^{N}}\), a is also a function of Lagrange multipliers calculated based on the principle of maximum entropy.

From Eqs. 7–9, there are three series of grading curves according to the above three cases, especially, when a = 0.5, 2, and 1. Notably, both cases of Eqs. 7 and 8 may be derived from the third case of Eq. 3 that means \({H}_{\mathrm{max}}\) and \(\Delta {H}_{\mathrm{max}}\) are special cases of\({\Delta h}_{\mathrm{max}}\). This may be the reason why one is always interested in \({\Delta h}_{\mathrm{max}}\) line (Singh 2014). Furthermore, Eq. 7 suggests that the PSD curves with maximum H (i.e.,\({H}_{\mathrm{ max}}\)) can be plotted as straight lines in the common particle size d versus percentile finer by mass F plane (i.e., \(d-F\) plane), and thus curves with concave upward in a semi-logarithmic \(\mathrm{log}d-F\) plane, while their slopes of PSD curves decrease with the increasing N-values (Israr and Zhang 2021). Similarly, previous Eq. 2 shows that the PSD curves with maximum \(\Delta H\) (i.e.,\({\Delta H}_{\mathrm{max}}\)) are uniformly distributed among all fractions, and plot log-linearly in the semi-logarithmic \(\mathrm{log}d-F\) plane, while their slopes of PSD curves decrease with the increasing N-values (Lőrincz et al. 2015).

Internal instability potential of PSD curve in maximum entropy conditions

The normalized base entropy \(A\) and entropy increment \(\Delta H\) are computed for the tested soils and the results are plotted in Fig. 9. As shown, all the tested soils have optimal PSD curves as their \(\Delta H\) values close to \({\Delta h}_{\mathrm{max}}\) with the results sorted distinctly along the boundary of \({\Delta h}_{\mathrm{max}}\) line, despite there being no clear distinction between the internally stable and unstable soils (given by solid and hollow symbols, respectively). Notably, optimal PSD curve (\({\Delta h}_{\mathrm{max}}\) line in \(A\)-\(\Delta h\) plane) shows potential of internal instability, except those close to the vertex of \({\Delta h}_{\mathrm{max}}\) line (\(A\) close to 0.5). Figure 9 shows that soils 3–8 plotted near the vertex of \({\Delta h}_{\mathrm{max}}\) line ambiguously show both stable and unstable from test result (soils 3–4 are stable, soils 5–8 are unstable). Furthermore, in order to assess the potential of instability of optimal PSD curves plotted near the vertex of \({\Delta h}_{\mathrm{max}}\) line, the case of \(\Delta {H}_{\mathrm{max}}\) can be considered, as it is mentioned above that \(\Delta {H}_{\mathrm{max}}\) is the vertex of \({\Delta h}_{\mathrm{max}}\) line, and PSD curves with \(\Delta {H}_{\mathrm{max}}\) are the global optimal grading distributions. Considering the PSD curves are straight lines at \(\Delta {H}_{\mathrm{max}}\), coefficient of uniformity (\({C}_{u}\)) can be used to distinguish between internally stabile and unstable PSD curves.

Fig. 9
figure 9

Correlation between normalized base entropy parameter \(\mathrm{A}\) and entropy increment \(\Delta H\) (note: filled and hollow symbols represent stable and unstable samples, respectively)

Full size image

As Fig. 10 shows, \(\mathrm{log}{C}_{u}\) is plotted in \(\mathrm{log}d-F\) plane, where \(\mathrm{log}{C}_{u}\) increases with increase in N and decrease in slope of log-linear PSD curves (\(\Delta {H}_{\mathrm{max}}\)). Not surprisingly, soils become unstable with the increasing logCu and N, which implies that the internal stability of optimal PSD curve is a function of \({C}_{u}\) and N.

Fig. 10
figure 10

Effects of uniformity coefficient (Cu) and fractal number (N) on internal instability potential of soil-4 and soil-7

Full size image

As Fig. 11 depicts, \({\Delta h}_{\mathrm{max}}\) is linearly correlated with logN for different values of \(A\), while their corresponding \({R}^{2}\)-values remain well above 99%. Given that the fractal number N directly represents the breadth of a PSD curve that would significantly affect soil’s potential of internal instability. Therefore, this study adopts the linear correlation observed between \({\Delta h}_{\mathrm{max}}\), and \(\log\;N\) as a factor to evaluate the potential of internal instability of soils. Not surprisingly, the current experimental and assessment results agree closely with this hypothesis, whereby optimal PSDs in the conditions of \(\Delta {H}_{\mathrm{max}}\) are internally stable, while those in the condition of \({\Delta h}_{\mathrm{max}}\) possess significant potential of internal instability. In essence, there exists a clear boundary in the \(A\)-\(\Delta h\) plane to differentiate between internally stable and unstable PSDs. Accordingly, the line connecting the vertex of the ellipse with its boundaries at 0 and 1 on the abscissa may be regarded as a conservative boundary for promptly assessing the internal instability potential of a given soil. For instance, both Tables 1 and 2 show there exists a clear distinction between internally stable and unstable gradations for the current experimental data, whereby all the stable soils possessed a relatively higher grading entropy. Apparently, there exists a unique relationship between \({h}_{0}\) and \(\Delta h\) for the unstable soil samples that is elaborated in the following section.

Fig. 11
figure 11

Correlations between \(\Delta h\) and N for the condition of \({\Delta h}_{\mathrm{max}}\)

Full size image

Criterion and verification

Based on the analysis, it may be anticipated that the PSD curves in \({\Delta h}_{\mathrm{max}}\)-state would be internally stable except those plotted closer to the vertex vicinity, which is a function of values of both \({C}_{u}\) and \(N\). Therefore, a novel criterion based on grading entropy is proposed here to evaluate internal instability potential of soils. For completeness, the entropy parameters (i.e., \(\Delta h\), \({C}_{u}\), and \(N\)) may be deduced by discretising the PSD curves using AFS introduced in Appendix-I. Subsequently, the corrected normalized entropy increment given by \(B\) would read:

$$B=\Delta h\times {\mathrm{log}}_{N}^{{C}_{u}}$$
(10)

In essence, the boundary demarcating between internally stable and unstable soils can be obtained in the plane \(A-B\) by linearly joining the origin (0, 0) with the peak point (i.e., vertex of \(A-B\) curve) through a straight line and then joining the vertex with the point (1, 0) on the abscissa (\(A\)-axis) through another straight line to draw a clear boundary, as depicted in Fig. 12. Mathematically, Eq. 11(a) would govern the ascending limit for \(0\le A<0.5\), as follows:

Fig. 12
figure 12

Graphical representation of proposed criterion, i.e., correlation between normalized base entropy parameter \(A\) and corrected normalized entropy increment \(B\)

Full size image
$$B=\frac{2A}{\mathrm{ln}\left(2\right)}$$
(11)

While for the descending limit from the vertex, i.e.,\(, 0.5\le {h}_{0}\le 1\), \(B\)-value would read:

$$B=\frac{2}{\mathrm{ln}\left(2\right)}-\frac{2A}{\mathrm{ln}\left(2\right)}$$
(12)

Thus, a soil plotted anywhere outside the triangular area may be characterized as internally stable.

As Table 2 shows, the current experimental data in the previous Table 1 has been re-evaluated using the above technique, and then the results have been compared with those obtained from five of the well-accepted PSD-based methods of Kezdi (1979), Sherard (1979), Kenney and Lau (1985), Burenkova (1993), and Wan and Fell (2008). For reference, all the existing criteria adopted for comparison with the proposed entropy approach have been summarized in Table 3 with their relevant mathematical models. Not surprisingly, the proposed method yielded only two inconsistent but conservative predictions compared to eight unsafe predictions from Burenkova (1993) and Wan and Fell (2008), 12 inconsistent predictions from Sherard (1979) that include eight unsafe and four conservative, 10 predictions from Kezdi (1979) that include six unsafe and four conservative, and four unsafe predictions from Kenney and Lau (1985). In essence, the criteria of Kezdi (1979) and Kenney and Lau (1985) had much higher success rates and the least unsafe predictions than the others. However, none of them had an acceptable degree of accuracy and safety in delineating the correct potential of internal instability that would be consistent with the experimental results of this study.

Table 3 Brief summaries of existing criteria for assessing internal stability of soils
Full size table

To demonstrate implications of current proposition, an additional dataset of dozens of laboratory tests on broadly graded, gap-graded, uniform, and non-uniform soils with uniformity coefficients ranging between 1 and 7831 have been collected from the existing literature (e.g., Åberg 1993; Fannin and Moffat 2006; Indraratna et al. 2015; Israr and Indraratna 2017; Kenney and Lau 1985; Lafleur et al. 1989; Li 2008; Nguyen et al. 2013; Wan and Fell 2008; and Skempton and Brogan 1994). For brevity, assessments of internal instability potential from the proposed method have been compared with those from two well-accepted existing methods of Kezdi (1979) and Kenney and Lau (1985), and the results are summarized in Table 4.

Table 4 Verification of proposed method with the published data
Full size table

Not surprisingly, both existing methods show large errors in correctly delineating the collected dataset with 18 and 26 inaccurate assessments from Kezdi (1979) and Kenney and Lau (1985), respectively. Where in contrast, the current method yields only 10 incorrect but conservative assessments (i.e., 5 of Wan and Fell, 2 of Åberg, and 1 each of Li, Lafleur, and Indraratna et al.). It is noteworthy that 5 out of the 11 incorrect predictions of current method consist of soils with Cu exceeding 700 and particle sizes ranging between 0.001 and 26.4 mm (i.e., clay-silt-sand-gravel mixtures). Similarly, both methods of Kezd and Kenney and Lau could not assess accurately the results from Wan and Fell, while all three methods conservatively assessed sample G of Åberg and M6 of Lafleur et al. as internally unstable. In summary, the current fractal entropy-based criterion has proven to be more realistic and conservative with 87% success than the existing methods of Kezdi and Kenney and Lau yielding 78% and 68% success, respectively.

Limitations of this study

The 1D vertical flow created using the laboratory equipment will be different to the non-vertical seepage paths in full-scale earth structures in terms of actual hydraulic gradients, seepage forces and energy losses occurring in practice. The influence of scale effects is inevitable in this study as in most civil engineering testing processes. The author has not applied any dimensional analysis to their current physical modelling to transform the laboratory data to be more realistic to real-life situations. Given that the proposed method is predominantly based on particle fractal entropy (i.e., PSD curve), the relative density (\({R}_{d}\)) and loading conditions may still have some influence on the hydraulic response of the tested soils, albeit the proposed model being more reliable than the other existing PSD-based criteria when considering many published data points. In view of the above, future studies may incorporate the role of compaction on the grading entropy to extend the scope to real-life filtration scenarios in various earth structures under complex cyclic loading and corresponding non-vertical flow paths.

Conclusions

The results from an experimental program of 20 hydraulic tests on 10 sand-gravel mixtures with different optimal PSD curves for the condition of maximum entropy increment (\({\Delta h}_{\mathrm{max}}\)) subjected to upward and downward hydraulic flow to examine their internal stability were reported. The ensuing analysis facilitated the proposal of a new internal stability criterion based on the grading entropy, and the principle of maximum entropy that could evaluate a large body of published data more promptly and accurately than a number of existing PSD-based approaches. The specific findings from this study are summarized as follows:

Soils with \({C}_{u}>10\) exhibited suffusion at \({i}_{cr}\) which is well below that for a quick condition in internally stable sands, and heave in gravels and sand-gravel mixtures (i.e. \(\approx 1.0\)). These soils suffered from excessive internal erosion (\(f\gg 4\mathrm{\%}\)), which caused permanent changes in their original PSD curves and an up to 80% reduction in \({C}_{u}\)-values. Nevertheless, downward flow caused a greater extent of erosion (> 20%) due to the additional effect of gravity forces when compared to upward flow.

Although the post-test PSD curves for unstable soils were internally stable, they represented a new soil gradation with a different hydraulic conductivity and higher stability than the original soil. For instance, broadly graded soils will erode to form quasi-uniform gradations over time. The uncertainty or the tendency of change in a PSD curve during flow could be analyzed to quantify the potential instability of a tested soil; the proposed grading entropy-based criterion could effectively serve this purpose in greater confidence than other existing criteria.

Contrary to several well-accepted criteria based on specific particle sizes such as d85 and D15, the proposed criterion could realize a given particle size distribution into various size fractions to apply the grading entropy concept. Subsequently, the information extracted from these pre-determined fractions could be represented by a unique set of maximum entropy and entropy increment to accurately delineate the potential of internal instability of soil. For brevity, the instability potentials of select soils have been evaluated in this study for maximum entropy condition that showed that the soils with increasing coefficient of uniformity (Cu) and fractal numbers (N) tend to become internally unstable when the \(\Delta h\)-value plots in the vicinity of the vertex of maximum \(\Delta h\)-line.

Appendix I. Basic entropy principles

To compute grading entropy from a PSD curve, the range of particle sizes should be divided into a series of size fractions to determine the relative frequency of each fraction, and different size fractions can maximize the amount of information extracted from PSD curve. For instance, Lőrincz et al. (2015) discretized the PSD curve into various size fractions to obtain an abstract fraction system (AFS) and the information of all the fractions were obtained by means of statistical distribution. In this study, AFS is defined in terms of a geometric progression with a multiplier of 2 that would discretize a PSD curve into several fractions for enhanced accuracy (e.g., d = 0.0625, 0.125, 0.5, 1, 2 mm), as shown by the dashed lines in previous Fig. 7. This current AFS distribution is based on actual sieve sizes that would express the information of particles sizes in a PSD curve more practically. During grading entropy calculations, for the purpose of reducing the error from different size fractions, each fraction is discretized further based on a minimum grain diameter (dmin) to obtain a virtual elementary cell system. The relative frequency of jth imaginary cell within the ith fraction would be as follows:

$${\mu }_{ij}=\frac{{p}_{i}}{{C}_{i}}, j=\mathrm{1,2},\dots ,{C}_{i}$$
(13)

where \({p}_{i}={M}_{i}/M\) (such that \(\sum_{i={i}_{1}}^{N}{p}_{i}=1\)) is the relative frequency of ith fraction, N is the number of fractions of a PSD curve, M is the total weight of the soil sample, \({M}_{i}\) is the weight corresponding to the ith fraction, and \({C}_{i}\) is the number of the imaginary elementary cells divided by dmin within ith fraction.

Based on statistical entropy theory, generalizing Eq. 12 gives the grading entropy of the soil:

$$H=-{\sum}_{i=1}^{N}{\sum}_{j=1}^{{C}_{i}}{\mu }_{ij}\mathrm{log}{\mu }_{ij}=-{\sum}_{i=1}^{N}{p}_{i}{\mathrm{log}}_{2}{x}_{i}+{\sum}_{i=1}^{N}{p}_{i}{\mathrm{log}}_{2}{C}_{i}$$
(14)

Equation 14 can be split into two parts:

$$H={H}_{0}+\Delta H$$
(15)

where \({H}_{0}(=\sum_{i=1}^{N}{p}_{i}{\mathrm{log}}_{2}{C}_{i})\) and \(\Delta H(=-\sum_{i=1}^Np_i\log_2\;p_i)\) are the entropy parameters, while \({H}_{0}\) and \(\Delta H\) represent entropy increment and base entropy, respectively. Two normalized entropy parameters can be given by (Imre et al. 2022):

$$A=\frac{{H}_{0}-{H}_{0\mathrm{min}}}{{H}_{0\mathrm{max}}-{H}_{0\mathrm{min}}}=\frac{\sum_{i=1}^{N}{p}_{i}(i-1)}{N-1}$$
(16)
$$\Delta h=\frac{\Delta H}{\mathrm{ln}N}$$
(17)

where \(A\) and \(\Delta h\) are the normalized base entropy and normalized entropy increment, respectively, and \({H}_{0\mathrm{min}}\) and \({H}_{0\mathrm{max}}\) express the eigen-entropy of the smallest and largest fractions in the soil, respectively.