Introduction

A sunspot has an intense magnetic field and cool temperature, and the center temperature of a sunspot is 6400 °F. Galileo made drawings of sunspots in 1612 (TJO News 2006). Sunspots are associated with active regions, which are areas of locally increased magnetic flux of the sun (Kevin et al. 2014). A maximum number of sunspots are known as solar maximum. Sunspots often appear near 30–35° north and south of the sun’s hemisphere with higher latitudes. The solar activity or sunspot is generated due to geomagnetic disturbances. Two types of magnetic lines are associated with sunspots. One is open whereas, the other is closed. Open lines extend out to long distances from the sun. The closed lines form loops and return back to the sun (Enfield et al. 1991).

Sunspots consist of cycles, and each cycle has a different duration. The average duration of sunspot cycles is slightly greater than 11 years. In each cycle, the number of sunspots varies from a maximum to minimum and again back to maximum. Cycle 1 consists of 11.3 years, cycle 2 has 9 years, cycle 3 (9.3 years), cycle 4 (13.7 years), cycle 5 (12.6 years), cycle 6 (12.4 years), cycle 7 (10.5 years), cycle 8 (9.8 years), cycle 9 (12.4 years), cycle 10 (11.3 years), cycle 11 (11.8 years), cycle 12 (11.3 years), cycle 13 (11.9 years), cycle 14 (11.5 years), cycle 15 (10 years), cycle 16 (10.1 years), cycle 17 (10.4 years), cycle 18 (10.2 years), cycle 19 (10.5 years), cycle 20 (11.7 years), cycle 21 (10.3 years), cycle 22 (9.7 years), cycle 23 (11.7 years) and cycle 24 is proceeding which is started in January 2008 and will last until 2018.

As for the fractal dimensions are concerned, two basic types of fractals exist. One of the self-similar and the other is self-affine. In the self-similar type, the geometric object is composed into a union of rescaled copies of itself with uniform in all directions or rescaling isotropic. Whereas in the self-affine type, the geometric object is described as the union of rescaled copies of itself depending on the direction or rescaling anisotropic. The self-similarity and self-affinity both are linear transformations.

A commonly used method to calculate the fractal dimension is the Hausdorff-Besicovich method. Alternative methods such as a box counting method, rescaled range analysis, and Higuchi’s method are also frequently used. Box dimension or box counting method is more appropriate than the methods mentioned above (Michael 1988). Fractal dimension describes the roughness and smoothness of the data. In the case of the sun, it is used to determine the correlation between solar cycles (Gayathri and Selvaraj 2010). Fractal geometry plays an active role in the study of topography and spatial analysis. The fractal concept plays an essential role in the scaling symmetry. Scaling symmetry is defined as the geometric object size reduced or expanded, whereas the new object is the same as that of the original object characteristics. The fractal analysis is a common approach for self-affine structures. The fractal parameters are evaluated by using three methods that include scaling analysis, spatial correlation analysis, and spectral analysis (Chen 2010). In spectral analysis, the energy spectrum and correlation function are able to convert into another Fourier transform (Chen 2009). The relations among different fractal parameters are calculated by using spectral analysis, which is based on correlation functions.

n this paper, we intend to explore the relationship between two methods of fractal dimension: one is the self-similar (FDS) which is calculated by the box counting method, and another is the self-affine (FDA) which is calculated by rescaled range analysis of sunspot cycles. The second part consists of the wave-spectrum scaling equations for calculating fractal dimensions of sunspot which are presented. The third section pertains to the discussion regarding the fractal geometry parameters of sunspot cycles and the fourth section is a conclusion.

Mathematical models and fractal dimension relations

In this section, brief information about certain qualities of universal scaling laws is explored.

Spatial correlation dimensions

Fractal dimension can be measured with a characteristic scale. Three basic concepts regarding the fractal dimension of sunspots can be described as follows.

The plane of sunspots has Euclidean dimension d = 2. The smallest unit of the sunspot is considered as a point, so the topological dimension of sunspots is considered to be dt = 0. So the fractal dimension of sunspots ranges from dt = 0 to d = 2. Fractal analysis of sunspot time series presented here is based upon the existence of correlation among sunspot cycles. Therefore, this study is associates fractal analysis with correlation analysis. In this sense, the generalized fractal dimension is often called the correlation dimension (Chen and Jiang 2010; Grassberger and Procaccia, 1983). Fractal dimension can be used to study time series data using the relationship between fractal dimension and Hurst exponent:

$$ {\mathrm{FD}}_{\mathrm{S}}=2-{\mathrm{HE}}_{\mathrm{S}} $$
(2.1)

FD equal to 1.5 indicates that the events are unpredictable and no correlation exists between two successive events. The process becomes more and more predictable as the value of the fractal dimension approaches to 1. Fractal dimension ranging from 1 to 1.5 indicates that the process is persistent. A rise in the value of the fractal dimension above 1.5 means that the process is anti-persistent. The value of FD = 1.5 indicates that the data is random, whereas FD = 1 reveals that the time series data is purely deterministic (Shaikh et al. 2008).

The length of each sunspot cycle and FDS is related by the following equation:

$$ \updelta (C)={\updelta}_1{C}^{\mathrm{FDs}-d}={\updelta}_1{C}^{\hbox{--} \beta } $$
(2.2)

where δ1 is the proportionality coefficient and β = d − FDS is the scaling exponent. Note that FDS < d (Frankhauser 1998). If the value of FDS lies between 1 and 2, then scaling exponents range forms 0 to 1. If FDS < 1 or FDS > 2, then the value of β > 1 or β < 0, respectively. For the solar cycle, the fractal dimension FDS can be considered as a one-point correlation dimension which indicates a zero-order correlation dimension. A correlation of zero order indicates that no relationship exists between cycles.

The wave-spectrum relation of sunspots

This section stresses upon the calculation of spectral exponent and spatial autocorrelation coefficient (spatial scaling). These two play an important role to study the spatial behavior of data. The data under consideration comprises 23 sunspot cycles. To perform spatial scaling, the correlation function associated with data is changed into an energy spectrum using Fourier transform (Chen 2009). In addition to other methods, Fourier transform can also be used to study similarity. In this method, relations of fractal parameters are determined by calculating spectral exponents. For this purpose, the following scaling law is used:

$$ f\ \left(\lambda \rho \right)={\lambda}^{\beta }f\ \left(\lambda \right) $$
(2.3)

Where λ denotes the scaling factor, β describes the scaling exponent (β = d − FDS), and ρ is called the length variable of each cycle.

Applying Fourier transform to 2.3, the following scaling relation is obtained:

$$ F\ \left(\uplambda \upgamma \right)=\mathrm{F}\ \left[f\ \left(\lambda \rho \right)\right]={\lambda}^{-\left(1-\beta \right)}\ F\ \left[f\ \left(\rho \right)\right]={\lambda}^{-\left(1-\beta \right)}\ F\ \left(\upgamma \right) $$
(2.4)

where F is known as the Fourier operator and γ denotes the wave number, whereas F (γ) is the image function of f (λ). Equation 2.4 finally gives the following wave-spectrum relation:

$$ S\ \left(\upgamma \right)\propto {\upgamma}^{-2\left(1-\beta \right)} $$
(2.5)

Relation 2.5 provides a numerical relation between fractal dimension and the spectral exponents by taking β = d – FDS (Eq. 2.2), thus:

$$ \mathrm{S}\ \left(\upgamma \right)\propto {\upgamma}^{-2\left(1-\mathrm{d}+\mathrm{FDs}\right)}={\upgamma}^{-2\left(\mathrm{FDs}-1\right)}={\upgamma}^{\hbox{--} \alpha } $$
(2.6)

Here,

$$ \alpha =2\ \left({\mathrm{FD}}_{\mathrm{S}}-1\right) $$
(2.7)

where α is the spectral exponent and considered to be a constant. When the range of fractal dimension is 1 < FD < 2, then the spectral exponent correlation dimension is said to be a point-point correlation dimension. This means that there exists a spatial correlation between two adjacent points of each cycle. Spatial correlation describes the correlation between a spot’s spatial direction and the average receiving spot again. Equation 2.7 gives the required relation between FD and α. FD and α possess one-point correlation dimension and the point-point correlation dimension, respectively. The one-point correlation shows the spatial correlation between the given spot and other spots of the cycle. The relation between the fractal dimension (FD) and spectral exponent (α) was introduced by Higuchi (1988) and is described by the following relation:

$$ \mathrm{FD}=\left(5-\alpha \right)/2 $$
(2.8)

The relation among fractal dimension (FD), spectral exponent α, and Hurst exponent HE is given by Burlaga (Burlaga and Klein 1986; Turcotte 1992) as given by Eq. 2.9.

$$ \alpha =5-2\mathrm{FD}=2\mathrm{HE}+1 $$
(2.9)

α = 0 describes a white noise-like system. It means that the system is uncorrelated and the power spectrum is independent of the frequency. α = 1 is known as flicker or 1/f noise system which indicates a moderate correlation. α = 2 is called a Brownian noise-like system, which shows a strong correlation. In general, the fractal dimension FD lies in the range (0 < FD < 2), but the fractal dimension in the range (1 < FD < 2) indicates that the state under consideration is highly random and irregular. In such case, spectral exponents range as (1 < α < 3) (Mandelbort and Van Ness 1968).

The parameters to determine the fractal dimension can be calculated by using two methods: self-similarity and self-affinity; consequently, two different fractal dimensions are obtained viz. Self-similar fractal dimension (FDS) and Self-affine fractal dimension (FDA). Here, the wave-spectrum scaling is performed by calculating both the fractal dimensions, viz. FDS and FDA. Earlier, this sort of analysis was performed by Liu and Liu (1992) and Mandelbrot (1999) using FDA. The Hurst exponent (HEA) can be calculated by the method of rescaled range analysis (Hurst et al. 1965); H is described by the power function R(τ)/S(τ) = (τ/2)H (Feder 1988). The Hurst exponent (HES) can be calculated by the method of box counting technique. The relationship between FDS and FDA can be described from Eq, 2.7 and 2.9 giving 2.10:

$$ {\mathrm{FD}}_{\mathrm{S}}=\frac{7}{2}-{\mathrm{FD}}_{\mathrm{A}} $$
(2.10)

The situation can be expressed logically by the following flowchart (Figure 1).

Fig. 1
figure 1

A sketch map among the relationship of different fractal parameters

Full size image

The spatial activity of sunspots is supposed to be expressed as a fractal Brownian motion (fBm); thus, the value of FD of each cycle of sunspots lies between 1 and 2.

The relation between spatial autocorrelation coefficient (C∇) and HE based on fBm can be given as follows:

$$ \mathrm{C}\nabla ={2}^{2\mathrm{HE}-1}-1 $$
(2.11)

where C∇ represents the spatial autocorrelation coefficient, which is based on the multiple-lag 1-dimension spatial autocorrelation. Spatial autocorrelation is used to measure the correlation of spots with itself through the active region. It should be noted that the value of HE = ½ means that C∇ = 0 which is considered to be the Brownian motion. If HE > ½, then C∇ > 0 representing that positive spatial autocorrelation exists. HE < ½ implies that C∇ < 0 which indicates that the spatial autocorrelation is negative.

The numerical relationship between different fractal parameters like FDS, FDA, HES, HEA, αS, αA, CA∇, and CS∇ can be computed by using Eqs. 2.9, 2.10, and 2.11. The results described in Table 1 shows that all values are within a significant scale. FDS ranging from 1 to 1.5 shows that the number of spots is correlated to each other and has linear behavior. The Hurst exponents (HE) ranging from 0.5 to 1 indicate the persistence of sunspot cycles. Relation 2.10 is theoretically valid when the fractal dimension FDS values range from 1.5 to 2.

Results and discussions

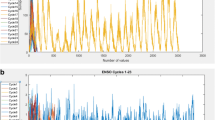
This study attempts to evaluate the fractal dimensions of sunspot data using scaling analysis and spectral analysis. Also, the cycle-wise spatial data correlation is determined. It is found that the correlation function is 1-dimensional (linear relation). Fractal parameters are calculated in a significant range using self-similar fractal dimension (FDS) and self-affine fractal dimension (FDA). Table 1 indicates that the values of FDS and FDA in each cycle exist in a range from 1 to 1.5 which indicate that cycle is persistent, correlated, and predictable. The value of FDA was found to be greater than FDs in all cycles. Similarly, both self-similar Hurst exponent HES and self-affine Hurst exponent HEA values range from 0.5 to 1 which reveals that each cycle is persistent. HES are found to be greater than HEA. Since the fractal dimension lies between 1 and 2, the scaling exponent β ranges from 0 to 1. This range for β confirms its validity. The value of β shows that the data has a 1-point correlation dimension and the dynamical behavior of the data is linear. Table 1 describes the numerical relation between the spectral exponent (α) and autocorrelation coefficient (C∇) which are calculated by using both the self-similar fractal dimension and the self-affine fractal dimension. If 1 < DF < 2, then the spectral exponent α has a range from 1 to 3. α = 0 indicates a white noise-like system which describes uncorrelated behavior. α = 1 is called a flicker which represents a moderately correlated behavior. α = 2 is called a Brownian noise-like system and shows a strong correlation. Self-similar spectral exponent (αS) and self-affine spectral exponent (αA) are calculated by using relation 2.8. Values of αS and αA reveal that the cycles behave like a Brownian noise. If 1 < FDS < 2, then the spectral exponent α describes a point-point correlation. It is to mention that there exists a relationship between one-point correlation dimension FDS and the point-point correlation dimension (α). The autocorrelation coefficient (C∇) describes the multiple-lag 1-dimension spatial autocorrelation of sunspot cycles. The autocorrelation coefficient (C∇) is calculated by relation 2.11. C∇ = 0 if HE = ½ which indicates a Brownian motion. If HE > ½, then C∇ > 0 which indicates a positive spatial autocorrelation. If HE < ½, then C∇ < 0 which represents the negative spatial autocorrelation. The autocorrelation coefficients (CS∇and CA∇) show positive spatial autocorrelation except in case of CA∇ in cycle 3 and cycle 17 where the negative correlation appears. Figure 1 indicates a sketch map of the relationship of different fractal parameters. Figure 2 represents the combined behavior of each solar cycle in one diagram. Figure 3 describes the compression between the self-similar fractal dimensions and self-affine fractal dimensions in each cycle.

Table 1 The numerical relationship between different fractal dimensions, Hurst exponent, autocorrelation coefficient and spectral exponents can be express as
Full size table
Fig. 2
figure 2

Comparative studies of wave-spectrum scaling parameter of self-similar and self-affine of each sunspot cycles

Full size image
Fig. 3
figure 3

Compression of self-similar and self-affine fractal dimension of sunspots cycles

Full size image

Conclusion

This study investigates the relationship between self-similar fractal dimensions (FDS ) and self-affine fractal dimensions (FDA). FDS is calculated by using a box counting method, and FDA is calculated by rescale range analysis method. Hurst exponents are calculated by self-similar Hurts exponent (HES) and self-affine Hurts exponent (HEA). Spectral exponents are calculated using relation 2.8. Respective values of αS and αA are compared using Eq. 2.9. For the calculation of autocorrelation coefficient, Eq. 2.11 is used. Table 1 exhibits the numerical values of Hurst exponents, spectral exponent, and autocorrelation coefficient using self-similar and self-affine techniques. Sunspot cycles are overall persistent and correlated. HES values are greater than HEA. All values of the spectral exponent (αS and αA) of each sunspot cycles behave like a Brownian noise. The autocorrelation coefficient in both cases lies in a valid range. Self-similar fractal dimensions (FDS) and self-affine fractal dimensions (FDA) obtained by using relation 2.10 failed to give a well-defined relationship. This is because the method is useful only in case the fractal dimension ranges between 1.5 and 2. Here, the fractal dimensions of sunspot cycles are less than 1.5.