Introduction

Recently, the extension of existing geodetic control networks using traditional terrestrial techniques has become impractical over time. Therefore, it is a mandatory mission to combine satellite and terrestrial networks to grasp the benefit from modern technology measurements. The global positioning system (GPS) networks are related to world geodetic system 1984 (WGS84) datum, while terrestrial geodetic networks are related to national, local, or regional geodetic datums (Rabah et al. 2015; Abou-Beih and Al-Garni 1996). To fully utilize the system, therefore, countries using different datums for their own coordinate bases have to either make a datum transformation platform between their datum and the global geodetic datum or change the datum to the global one (Kwon et al. 2005; Jones 2002). For this reason, datum transformation determination has become a major practice to transform the coordinates from the global geodetic datum to local datum.

Geodetic datum transformation is the determination of a mathematical relationship that is to be used in transforming a set of coordinates from one geodetic datum to another (Dawod and Dalal 2000; Rabah et al. 2016). Two different types of mathematical models can be considered for transformation between any two coordinate systems. The first is the conventional techniques, which can be considered as a mathematical model that addresses the problem with geometrical explanations that are under consideration. For example, the Hotine Krakiwsky, Thomson, Ten Parameters, Helmert, Molodensky, Affine, Five Parameters, and Three Parameters Models are considered as conventional ones (Herrault et al. 2013; Ziggah et al. 2013; Vandenberg 1999; Mataija et al. 2014). The second is the numerical techniques that address the problem by taking the mathematical model and its properties into consideration to obtain the best result that satisfies the accuracy that is required (Herrault et al. 2013). The numerical models include multiple regression equation, least squares collocations (LSC), artificial neural networks (ANN), and minimum curvature surface (MCS) (El-Shambaky 2004; Tierra et al. 2008). Herein, the distortion is discovered in the old geodetic network rather than the geometrical explanation through the transformation process. In this study, we will use the available data in Egypt to compare the two techniques and estimate the better one that can be applied in our case.

Herein, many studies proposed and evaluated the datum transformation in one, two, and three directions (1D, 2D, and 3D) using the conventional and numerical techniques (Tierra et al. 2008; Ardalan et al. 2002; Fazilova 2017; Mataija et al. 2014; Lwangasi 1993; Khazraei et al. 2017; Akyilmaz et al. 2009). The following is the literature review for the datum transformation techniques and applications: Fang (2014) utilized the total least squares method to adjust the datum transformation in 2 and 3Ds, and he applied the method to transform the datum transformation. He found that the proposed method can be applied to translation in-between two datums at millimeter-level accuracy. Yang (1999) compared the least squares and robust estimator to transform the datum area in China, and he found that when the coordinates contaminated by outliers, the two methods can be given reasonable results. Abou-Beih and Al-Garni (1996) utilized the polynomial technique to transform the Saudi-Arabian area, and they found that the shift of the x, y, and z directions are 5.11, 5.46, and 6.73 cm, respectively. Ardalan et al. (2002) applied the Molodensky technique to transform the geoid datum of the east Germany, and they observed that the geoid height transformed in-between two geoid models with accuracy of 3.89 cm. Civicioglu (2012) proposed and compared a different method for the geocentric datum transformation and he found that the computational intelligence algorithms are good tools that can be used to transform the datums. Kinneen and Featherstone (2004) evaluated the regression, Molodensky, Helmert, and 3D similarity based on the Intergovernmental Committee on Surveying and Mapping (ICSM) parameters which is transformation datum models over Australia network; and they found that the 3D similarity-ICSM model accuracy is the best conformal transformation for Australia. The Helmert model is adjusted using least square to transform the France datum and found that the local system coordinates (x,y) are well defined (Mataija et al. 2014). In addition, the ANN was utilized to transform the 1, 2, and 3Ds of the datum transformation and was found to be a good numerical tool that can be used to fit and transform the coordinate systems (Tierra and Romero 2014; Srivastava et al. 2014; Tierra et al. 2008; Akyilmaz et al. 2009; Erol and Erol 2012, 2013). For example, Ziggah et al. (2016) evaluated the datum transformation in-between two coordinate systems using ANN, and they found that the ANN with nonlinear function solution is highly accurate than the linear one. Liao et al. (2012) utilized the ANN to predict the orientation parameters of the earth, and they observed that the significance is improved between the ANN model prediction results and measurements. Moreover, the ANN model is used to transform 2D coordinate system and found that the model is optimum to transform the datums with high accuracy (Konakoglu et al. 2016).

In Egypt, the datum transformation are studied and evaluated previously; the following are the problems and summary for the datum transformation in Egypt. The datum transformation problems can be concluded that the old local geodetic network was inaccurate, limited, and inconsistent (Shaker et al. 2007), and some of the data set used in the transformation process were missing, such as height information (Elmaghraby et al. 2005; Zaki 2015). Therefore, Egyptian studies approached the transformation into two ways: the first approach was to readjust the old Egyptian geodetic network as an entire block to obtain a modified old Egyptian Geodetic Datum 1930 (EGD30) to make the transformation step between datums using conventional techniques. The trails included all of the available missing data they could obtain such as the precision of control points and geoid undulation; these trials summarized in Shaker et al. (2007). The second way is to accept old EGD30 coordinates as they are and make the transformation process directly between EGD30 and WGS84. The conventional and numerical transformation models are used and applied in this case; the trials for that case can be found in Abd-Elmotaal (1994), El-Tokhey et al. (2015), Dawod and Dalal (2000), Dawod and Abdel-Aziz (2003) and Shaker et al. (2007). From these studies, it can be concluded that the conventional transformation models reveal inconsistency in the precision along the whole network as the permanent reason that it is not easy to obtain a precise transformation set over the Egyptian area. Therefore, there is an opinion to adopt a regional transformation solution strategy, which means to model WGS84/EGD30 transformation and existing EGD30 network distortions; each regional geodetic can produce a coordinate shift for each Egyptian governorate. Moreover, it can be noted that the numerical models can be applied over the Egyptian territory without a need for a transformation parameter set. In addition, the datum transformation can be applied in three directions. Moreover, the numerical models can address the EGD30 coordinates accompanied with their inconsistency, and finally, when those models use distortion as a verification tool; and the average distortion of these models in the 3D is observed within 60 cm and within 1.20 m in space (El-Shambaky 2004). Herein, it should be mention that the numerical studies for the 3D datum transformation in Egypt are limited in the polynomial and MCS models (El-Shambaky 2004; Abd-Elmotaal 1994; Dawod et al. 2010).

However, the aims of this study are to design and evaluate the ANN, for the first time in Egypt, as a novel model to transform the geocentric datum transformation WGS84/EGD30 in a 3D based on the available data of the Egyptian networks. To achieve this, the previous conventional and numerical models were applied and compared with ANN design model over the Egypt area.

Egyptian geodetic network

In Egypt, the geodetic network can be divided into networks I and II (El-Shambaky 2004; Shaker et al. 2007). Network I started in the year 1907 and was finished in 1945; Network II was constructed and observed from 1955 and was finished in 1968 (Dawod and Abdel-Aziz 2003; Shaker et al. 2007). The geodetic observations of networks I and II were taken while the geoid in Egypt was unknown. Thus, the gravimetric reductions on the collected observations were neglected. Network I was adjusted section by section, not as one block; moreover, it had good observations and some defects in the processing and adjustments were found (El-Shambaky 2004). Thus, its precision is not the same everywhere and could be more or less than 1:100,000 (El-Shambaky 2004; Shaker et al. 2007). The coordinates of network II stations were computed from the collected observations without gravimetric reductions and without any type of adjustment; the precision of network II is less than that of network I and could be more or less than 1:50,000 (Shaker et al. 2007; Saad and Elsayed 2007).

In 1992, the Egyptian Survey Authority (ESA) steering committee developed a plan for the creation of a new datum for Egypt (Rabah et al. 2015). The ESA decided to replace the EGD30 and the associated projection system, Egyptian Transverse Mercator (ETM), with the WGS84 and the associated projection system, Universal Transverse Mercator (UTM). In addition, the ESA proposed a new projection system called the Modified Transverse Mercator (MTM) that is related to the WGS84 (El-Tokhey et al. 2015). In 1995, the ESA announced the new datum for EGD30 geodetic first-order control points of Egypt entitled “High Accuracy Reference Network (HARN)”; this network was tied to the international geodetic network (IGS) and the GPS data were processed using the precise ephemeris (Mina 2006). The HARN network is divided into two sub-networks: HARN order-A and HARN order-B. The HARN order-A network consists of 30 stations covering the Egyptian territory with an average spacing of approximately 200 km. Its relative accuracy estimate is 1:10,000,000 or 0.10 part per million (ppm) (Rabah et al. 2015, 2016). Few stations from the old Egyptian first-order triangulation network have been utilized as GPS stations in this network. HARN order-B network, also called the National Agricultural Cadastral Network (NACN), consists of 140 stations. The NACN covers the Nile valley and delta with a spacing of approximately 30–40 km (Rabah et al. 2015). The relative accuracy estimate of this network is 1:1,000,000 or 1 ppm (Dawod and Abdel-Aziz 2003). The results of analyzing both networks were defined in International Terrestrial Reference Frame 1994 (ITRF1994) epoch 1996; more review for the HARN and NACN network can be found in Rabah et al. (2015); Abd-Elmotaal (1994); and Dawod (2009).

In this study, the available first-order control points (14 points) are used as common points. These points belong to HARN order-A and EGD30 networks and 11 check points are utilized to validate the transformation datum model; these points belong to HARN order-B and EGD30 networks. Figure 1 shows the distribution of common and check points. From Fig. 1, it can be seen that the model design cannot be considered for the whole area of Egypt, while the west area is not covered.

Fig. 1
figure 1

Distribution the available of common and check points

Full size image

Methods

As mentioned above, the transformation models can be divided into conventional and numerical transformation models; therefore, in this study, we utilized the common methods that are applied in Egypt to compare it with a novel model design, the ANN model.

Previous common models

The following is the summary of the effectively utilized methods for the three directions’ datum transformation in Egypt. For conventional transformation, two transformation models are widely used to transform the datums from collocated coordinates, which are the Bursa–Wolf similarity and Molodensky models.

In the well-known Bursa–Wolf similarity 3D, seven parameter transformation (Helmert) model can be presented as follows (Deakin 2006; Závoti and Kalmár 2016):

$$ {S}_{\mathrm{i}}=T+ kR{P}_i $$
(1)

where S i and P i (i = 1, . . . n) are two column vector sets of collocated 3D coordinates in two different systems, n represents the number of points used, T = (∆X, ∆Y, ∆Z)T denotes three translation parameters, k refers the scale parameter, and the 3 × 3 rotation matrix R contains three rotation parameters (Abd-Elmotaal 1994). Obviously, to determine the seven parameters, the number of collocated coordinates S i , and P i should be greater than or equal to three (Shen et al. 2006).

The Molodensky model describes the relationship between any two different 3D coordinate systems by seven unknown parameters, and it is given by Deakin (2006):

$$ {S}_i=T+{P}_{\mathrm{o}}+\mathrm{kR}\Delta {P}_{\mathrm{o}\mathrm{i}} $$
(2)

where Po defines the position vector of the initial point of the network. In this case, the rotations and the scale are only applied on the vector ∆Poi between any terrain point (Pi) and the initial point (Po) (El-Shambaky 2004).

For numerical transformation, two transformation models are utilized in this study, which found a high performance for the datum transformation in Egypt; these are the second-degree regression and MCS models (Abd-Elmotaal 1994; El-Shambaky 2004; Dawod et al. 2010).

The coordinate shift of datum components (Xo, Yo, Zo) for the x, y, and z directions, respectively, of n stations in the polynomials of degree k, in this study, where the second degree is applied, can be calculated as follows (Abd-Elmotaal 1994; El-Shambaky 2004):

$$ {X}_{\mathrm{o}}={\sum}_{\mathrm{i}=0}^{\mathrm{k}}{\sum}_{\mathrm{j}=0}^{\mathrm{i}}{a}_{\mathrm{i}\mathrm{j}}{\lambda}^{\mathrm{i}-\mathrm{j}}{\phi}^{\mathrm{j}} $$
(3)

where ϕ and λ are the geodetic latitude and longitude in radians, respectively. The aij is the regression coefficients and it can be estimated by a least squares fitting technique. Similar can be calculated for the shift components Yo and Zo (Abd-Elmotaal 1994).

The MCS is an old and ever-popular approach for constructing a smooth surface from irregularly spaced data (El-Shambaky 2004). This model is approved to be used as a tool for datum transformation in 1 and 3D in Egypt (El-Shambaky 2004). The surface can be interpolated by MCS with bi-harmonic splines or can be gridded with an iterative finite difference scheme. The mathematical formula for MCS looks for a 2D surface f(x, y) in region D, corresponding to the minimum of the Laplacian power (El-Shambaky 2004):

$$ \underset{\mathrm{D}}{\iint }{\left|{\nabla}^2f\left(x,y\right)\right|}^2 dxdy $$
(4)

where ∇2 denotes the Laplacian operator. Alternatively, seeking f(x, y) as the solution of the biharmonic differential equation(∇2)2f(x, y) = 0, the solution of this differential equation can be solved using Taylor’s theorem to linearize the nonlinear biharmonic differential equation to have a simple mathematical form in one variable as in Eq. (5) and Fig. 2.

$$ {\left(\frac{\partial^2\phi }{\partial {\mathrm{x}}^2}\right)}_0=\frac{1}{{\mathrm{h}}^2}\left[{\phi}_1+{\upphi}_3-2{\phi}_0\right] $$
$$ {\left(\frac{\partial^2\phi }{\partial {\mathrm{y}}^2}\right)}_0=\frac{1}{{\mathrm{k}}^2}\left[{\phi}_2+{\phi}_4-2{\phi}_0\right] $$
(5)

where ϕ0 is the known observed value, and {ϕ1, ϕ2, ϕ3, ϕ4} represent the unknown values in two directions (x and y) in a grid system as shown in (Fig. 2). The distance between the observed value and the unknown values on the grid is indicated by the arm of grid length h and k. All of the details about how Eq. 4 is used to solve the Egyptian datum transformation problem can be found in El-Shambaky (2004).

Fig. 2
figure 2

Unit of a grid system used in the MCS solution

Full size image

Artificial neural network design transformation model

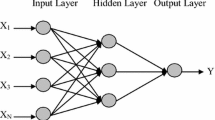
Recently, an artificial neural network (ANN) has been used in transformation between Cartesian coordinates, geodetic coordinates, or plane coordinate systems related to two different systems (Tierra and Romero 2014; Tierra et al. 2008). When the ANN is properly designed and trained, it can be used for spatial datum transformation as an alternative tool in datum transformation for geographic information system (GIS) applications; it is practically applicable. More accurate spatial datum transformation based on ANNs can be expected with large and high-quality spatial data and with improved geographical coverage (Ziggah et al. 2016; Tierra and Romero 2014). The following is the ANN model design. Three layers are the component of the ANN; these are input, hidden, and output layers; each layer contains one or more neurons (Ziggah et al. 2016; Haykin 1994; Hagan et al. 1995), as presented in Fig. 3. An ANN structure can be modeled as in Eq. 6 (Ziggah et al. 2016).

$$ {S}_{\mathrm{k}}^{\mathrm{l}}={\sum}_{\mathrm{i}=1}^{\mathrm{n}}{X}_{\mathrm{i}}{W}_{\mathrm{i}}^{\mathrm{l}}+{b}_{\mathrm{o}}^{\mathrm{l}} $$
(6)

where Xi is a vector contains the input data, Wi represents the connection weight vector from the previous layer of neurons, bo is the bias weight that corresponds to an additional independent input, n is the number of input data, l is the number of hidden layers, and k is the number of destination neuron of ANN. The result from Eq. 6 is applied in a transfer function f(S) that gives an output according to Eq. 7.

$$ {a}_{\mathrm{k}}^{\mathrm{l}}=f\left({\mathrm{S}}_{\mathrm{k}}^{\mathrm{l}}\right) $$
(7)

where \( f\left({\mathrm{S}}_{\mathrm{k}}^{\mathrm{l}}\right) \) represents the transfer function, and \( {a}_{\mathrm{k}}^{\mathrm{l}} \) is the output of the transfer function. The activation function determines the amplitude of the data coming from the previous layers of the neuron; this is the same function that is responsible for activating or deactivating the data that is being issued to subsequent layers of the network. Although many different functions could be a successful transfer function, usually a differentiable and bounded function is used (Haykin 1994; Hagan et al. 1995). This study uses an ANN based on sigmoid and linear functions to represent the shift in the three directions between common points at the two datums EGD30/ WGS84 according to Eq. 8.

$$ P{\left(\phi, \lambda \right)}_{\mathrm{EGD}30}=P{\left(\phi, \lambda \right)}_{\mathrm{WGS}84}+T $$
(8)

where P(ϕ, λ)EGD30 and P(ϕ, λ)WGS84 are the curvilinear coordinates of the common point on EGD30 and WGS84, respectively, and T is a vector of the true target shift in the three directions (Δx,Δy,Δz) where every component represents the difference between Cartesian coordinates at the common points. A multilayer neural network has been used to simulate the relationship between the curvilinear coordinates of the common point on EGD30 and every shift component of the vector T separately. The designed network that is used is a two-layer feed-forward network with a sigmoid transfer function in the hidden layer and a linear transfer function in the output layer. The network structure is presented in Fig. 3.

Fig. 3
figure 3

Typical designed four hidden layer neural network

Full size image

This network is used in two stages; the first stage is used to train the network, and the training process is an iterative procedure. This iterative process defines the parameters, calculates the error, and updates the parameters by propagating back the effect of the error to each parameter. The training process continues until the network error reaches an acceptable value or has a stable state of estimated unknown parameters (Haykin 1994; Hagan et al. 1995).

The steps in the first training stage process can be summarized as follows. First, the input vectors contain curvilinear coordinates of the common points based EGD30 P(ϕ, λ)EGD30, and the target response vector contains the true shift in Cartesian coordinates T = Δx, or Δy, or Δz. Therefore, the network is solved for every true target shift component separately. In the second step, the neural algorithm will use initial values of the unknown weights and biases as mentioned in Eq. 6. The results will be transferred to the second hidden layer according Eq. 7 and using the sigmoid function as a transfer function that is depicted in Eq. 9. In the third step, the neural algorithm will again add the initial values of the unknown weights and biases belonging to the hidden layer no. 2 to the outputs from hidden layer no. 1 as shown in Fig. 3. Then, the resultant will be transferred to the output layer using the linear transfer function as shown in Eq. 10 to estimate the shift transformation values.

$$ {f}_1\left({\mathrm{S}}_{\mathrm{k}}^{\mathrm{l}}\right)=\frac{e^{{\mathrm{S}}_{\mathrm{k}}^{\mathrm{l}}}-{e}^{-{\mathrm{S}}_{\mathrm{k}}^{\mathrm{l}}}}{e^{{\mathrm{S}}_{\mathrm{k}}^{\mathrm{l}}}+{e}^{-{\mathrm{S}}_{\mathrm{k}}^{\mathrm{l}}}} $$
(9)
$$ \hat{\mathrm{T}}={f}_2\left({\mathrm{S}}_{\mathrm{k}}^{\mathrm{l}}\right)={\mathrm{S}}_{\mathrm{k}}^2 $$
(10)

The neural algorithm will calculate the residuals between the target response value and the estimated response. Then, the Levenberg–Marquardt algorithm adaptively varies the unknown parameters (weights and biases) between the gradient descent update and the Gauss–Newton update according to Eq. 11 (MathWorks Inc. 2015), until the algorithm reaches a stable state, which means that there is no significant change in the estimated unknown parameters. At this point, the algorithm adopts the latest estimated parameters (weights and biases) of the model.

$$ \Delta {R}_{\mathrm{k}}=-{\left[{J}^{\mathrm{T}}J+{\mu}_{\mathrm{k}}I\right]}^{-1}{J}^{\mathrm{T}}\left(T-\hat{T}\right) $$
(11)

where ΔRk is the theoretical difference between successive estimations of the same unknown parameter; it is also called a performance index. JTis the transpose Jacobian matrix with respect to the unknown parameters \( {\left[\frac{\mathrm{\partial R}}{\mathrm{\partial W}},\frac{\mathrm{\partial R}}{\mathrm{\partial W}}\right]}^{\mathrm{T}} \), μk is a scalar value used to help the Hessian matrix (JTJ) to be invertible, I is an identity matrix with dimensions equal to the number of unknown parameters, and T and \( \hat{\mathrm{T}} \) represent the target and output response data. From the solution of the network for a specific shift component, it is easy to obtain both connected and bias weights as mentioned in Eq. 6. In the second stage, the same network with previous calculated weights and biases can be used to simulate the shift transformation of the check points. Figure 4 illustrates the x direction process to estimate the datum shift in this direction; in addition, the parameters used and estimated are presented in the figure.

Fig. 4
figure 4

Flowchart to simulate the check points in the x direction

Full size image

From the estimated shift vector, the distortion between the true shift and the estimated shift can be calculated (D = [δx δy δz]), while D is the distortion vector in three directions, and δx δy δz are the vectors of distortion for the x, y, and z directions, respectively. The average resultant distortion in the space is used to evaluate the model design, which can be calculated as follows:

$$ {D}_{\mathrm{ave}}=\frac{1}{n}{\sum}_{\mathrm{i}=1}^n\sqrt{\updelta_{{\mathrm{x}}_{\mathrm{i}}}^2+{\updelta}_{{\mathrm{y}}_{\mathrm{i}}}^2+{\updelta}_{{\mathrm{z}}_{\mathrm{i}}}^2} $$
(12)

Herein, it should be mentioned that to study the impact of the data errors on the ANN model, the assuming errors will be studied, while the Egyptian data errors are not available as presented previously. Meanwhile, the input data errors on the neural network model are investigated through error propagation rules; to show that impact, Eq. 9 can be reformed as follows:

$$ {f}_l\left({S}_k^l\right)=\tanh \left({S}_k^l\right) $$
(13)

where \( \tanh \left({S}_k^l\right) \) is the hyperbolic tangent function of \( {S}_k^l \) , substitute from Eq. 6 in Eq. 13 to get Eq. 14, as follows:

$$ {f}_l\left({S}_k^l\right)=\tanh \left({\sum}_1^n{X}_i{W}_i^l+{b}_o^1\right) $$
(14)

Substituting Eq. 14 in the Eq. 6, the estimated shift can be formed in a linear form as in Eq. 15, as follows:

$$ \hat{\mathbf{T}}={\sum}_i^m\left\{{W}_i^k\right({\sum}_1^n\tanh \left({X}_i{W}_i^l+{b}_o^1\right)+{b}_o^k\Big\} $$
(15)

where m represents the number of first hidden layer’s output neurons, and k represents the output layer index. After that, applying Eq. 16 to estimate the error propagation for Eq. 15 provided that we will consider the estimated weights and biases as constants and geodetic coordinates (ϕ,λ) as independent observations in radian units, and there is no correlation between them (Mikhail 1976).

$$ {\sigma}_{\hat{T}}^2=J{\Sigma}_{xx}{J}^T $$
(16)

where \( {\sigma}_{\hat{T}}^2 \) represents the variance of the estimated shift, Jis the Jacobian matrix relative to the geodetic coordinates, and Σ xx represents the variance–covariance matrix for observations. The elements of the Jacobian matrix can be calculated based on Eqs. 17 and 18, as follows:

$$ \frac{\partial \hat{\mathbf{T}}}{\partial \varphi }={\sum}_i^m\left\{{W}_i^k\bullet {W}_{i\left(\varphi \right)}^l{\sum}_1^n\left[{I}_{\left(m,1\right)}-{\tanh}^2\left({X}_i{W}_i^l+{b}_o^1\right)\right]+{b}_o^k\right\} $$
(17)
$$ \frac{\partial \hat{\mathbf{T}}}{\partial \lambda }={\sum}_i^m\left\{{W}_i^k\bullet {W}_{i\left(\lambda \right)}^l\right({\sum}_1^n\left[{I}_{\left(m,1\right)}-{\tanh}^2\left({X}_i{W}_i^l+{b}_o^1\right)\right]+{b}_o^k\Big\} $$
(18)

where subscript i(ϕ), i(λ) means the weight vector associated to geodetic coordinates (ϕ,λ), respectively, and I represents an identity vector with dimension (m,1) .

The model evaluation and assessment

To assess the performance of the previous and design models, the following statistical evaluation are utilized. A linear regression model between both true and estimated transformed coordinates of the points is used according to the following equation in the three directions.

$$ \hat{\mathrm{y}}=\alpha y+\beta $$
(19)

where \( \hat{\mathrm{y}} \) and y are estimated and true coordinates on EGD30, and (α, β) represent the regression factors. A value closer to (1,0) means that the estimated transformed coordinates have a strong correlation with the true coordinates, and the transformation model has the ability to map the original coordinates in the new geodetic datum perfectly without residuals. Additionally, to determine the strength of the correlation, three statistics will be calculated. These statistics are the sum of squares due to errors or residuals (SSE); this statistic measures the total deviation of the transformed coordinates against the true coordinates and can be calculated as follows:

$$ \mathrm{SSE}={\sum \limits}_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{y}}_{\mathrm{i}}-{\hat{\mathrm{y}}}_{\mathrm{i}}\right)}^2 $$
(20)

A value of SSE closer to 0 indicates that the transformation model has a smaller random error component and that the fit will be more useful for prediction. The second statistic is R2; this statistic measures how successful the transformation model explains the variation of the data, and it can be calculated by:

$$ {R}^2=1-\frac{\mathrm{SSE}}{\mathrm{SST}} $$
(21)

where SST represents the sum of squares about the mean (\( SST=\sum \limits_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{y}}_{\mathrm{i}}-\overline{\mathrm{y}}\right)}^2 \)), where \( \overline{\mathrm{y}} \) is the mean of the true coordinates. This statistic can take a value between 0 and 1, with a value closer to 1 indicating that a greater proportion of variances for the model. The last statistic is the root-mean-square error (RMSE); a RMSE value closer to 0 indicates a fit that is more useful for prediction.

Results and discussions

Development of the ANN model design

In this study, the standard multilayer feedforward network with a sigmoid transfer function in the hidden layer and a linear transfer function in the output layer is used because of its ability to approximate any measurable function to any desired degree of accuracy provided sufficiently many hidden units; in other word, it is a universal mapping tool (Hornik et al. 1989; Hagan et al. 1995). The model is designed using two input parameters and one output. Therefore, the neuron number in the hidden layer is the main factor for the model design. However, the first stage in the design of the ANN model is designing the number of neurons. It is important to determine a suitable number of neurons and layers. As more neurons and more layers lead to more unknown weights and biases to be estimated. To solve this issue, the growing method is used, which means growing the number of neurons to obtain proper performance (Haykin 2001). Table 1 illustrates the average distortion in the three directions and the average resultant distortion (Dave) in the space for various numbers of neurons based on the check points. From Table 1, it is obvious that the minimum average resultant distortion in space resulted from using four neurons in the designed neural network. The second indicator is the range of distortion that is shown smaller with four neurons. Using four neurons with almost close values in the three direction results is shown for the datum distortion (range within 16 cm), while with other numbers of neurons, this value ranges from 35 to 125 cm.

Table 1. Average distortion in check points with different numbers of neurons (unit in m)
Full size table

In addition, Tables 2 and 3 illustrate the RMSE for the three directions’ distortion of check and common points, respectively. From Table 2, it can be seen that the number of neurons 3 and 4 has shown a lower distortion than neurons 1, 2, and 5. The calculated RMSE for both trails are found that the RMSE of X, Y, and Z are 0.616, 0.751, and 0.317 m, respectively, for the three neurons, while the RMSE with four neurons are found as 0.406, 0.300, and 0.311 m for the X, Y, and Z directions, respectively.

Table 2 RMSE of distortion in Check points with different numbers of neurons (unit in m)
Full size table
Table 3 Residuals RMSE for the common points with different number of neurons (unit in m)
Full size table

From Table 3, it is clear that, with increasing the number of neurons, the precision of the models increases while the number of weights and biases are increased; therefore, the residual estimate for the common points decrease. On the other side, the increase of neurons results in over-fitting problem. Meanwhile, the existence of multiple non-linear hidden layers will make the designed neural network a very expressive model that can learn very complicated relationships between the inputs and outputs. With limited training data, however, as in our case in Egypt, many of these complicated relationships will be the result of sampling noise, so they will exist in the training set but not in real test data even if it is drawn from the same distribution. This leads to an over-fitting problem (Srivastava et al. 2014). Thus, it is important to have a balance state between the ability of the neural model to represent the common points used in the training stage and the ability of the model to predict optimum outputs based on the check points. According to the previous concept, the minimum number of neurons has been chosen to avoid the over-fitting problem based on common points, and to have minimum distortion with high precision based on check points. Thus, the solution with four neurons gives an optimum and consistent solution for all three directions. Therefore, the ANN model 2-4-1 is a better model that can be used in our case.

In addition, to show the impact of error propagation on the precision of the design neural network model (ANN 2-4-1) through the boundary of Egypt, Table 4 depicts the statistical assessment of the estimated shift’s standard deviation in the three directions based on the errors in the geodetic coordinates with different amount of errors ranging from 1 to 60 s. From Table 4, it is clear that the most affected output is shift-y components, while both shift-x and shift-z have a small error reached to 1 mm at 60 s level of error in geodetic position. This is because the available distortion data in y direction is higher than those in the other directions (El-Shambaky 2004; Shaker et al. 2007; Rabah et al. 2015). Moreover, it can be seen that shift-y is very sensitive to the errors in the geodetic coordinates, as at 1 s level the average error in the shift component will reach 9 mm. Unfortunately, the error in the EGD30’s observations was not available. Table 4 can be used to predict the level of errors that can be adopted through the transformation process in advance. Generally, from Table 4, it is obvious that neural network model can accommodate the impact of errors in the observed data in both x and z directions, while it is sensitive for the distortion of the available data in y direction.

Table 4 Impact of data errors on the estimated shift’s precision (unit mm)
Full size table

Development model validation and assessment

After the design process of a suitable neural network, a comparison study between the designed neural model and previously mentioned transformation models will be described as follows to assess the accuracy of this model and choose a suitable transformation technique over Egypt area: In the beginning of this comparison, three main indicators will be selected. The first is the amount of average residuals (AR) and the degree of correlation between common points’ coordinates and their estimated transformed coordinates generated by various transformation models as mentioned before in “The model evaluation and assessment.” The second indicator is the ability of transformation models to predict transformed coordinates using a new set of validation points (check points) associated with its precision to show vision about the uncertainty of the those models, and the last one shows some desirable advantages of the transformation models when used with a map projection process such as conformity. To show the first indicator, the residuals of common points related to every transformation model in each direction are calculated. The average of residuals in every direction is listed in Table 5. Additionally, Fig. 5 shows the space model residuals based on every common point; it represents the space resultant of residuals in every direction.

Table 5 Statistical analysis results for transformation models based on common points
Full size table
Fig. 5
figure 5

Space model residuals over the common points

Full size image

From Table 5 and Fig. 5, it can be noticed that the amount of average residuals (AR) in the x direction when using a neural network model is near to zero while it ranges from 40 to 80 cm in other transformation models. In the y direction, the AR is equal to 5 cm, but in the other models, it ranges from 164 to 211 cm. Finally, in the z direction, the value of AR from the neural network is near to zero, and in the other transformation models, it ranges from 63 to 147 cm. To explain the zero average values that appear in Table 5, a linear regression model between both true coordinates and estimated transformed coordinates of the common points is used according to Eq. 19 in the three directions. Moreover, the statistical evaluation for the models is presented in Table 5. It can be seen that the neural model is the only model that reaches or is close to the value of 1.0 in all directions for the α parameter of the correlation regression; in addition, the smallest values for the β parameter are shown also with neural model. Obviously, the model can explain nearly 100% of the total variation in the true coordinates about the average. Moreover, according to the RMSE statistic, the closest value to zero in all directions is achieved by the neural model, indicating that the neural model has the ability to predict transformed coordinates more precisely than the other transformation models. In addition, it can be seen that the ANN model is more effective for the coordinate’s transformation fitting with the available data distortion errors in y direction than other models. As well as, the R2 and SSE are shown equal one and close to zero, respectively, for the neural model. From a previous comparison, it can be concluded that the neural network model is more suitable to represent the inconsistent common points that existed in the old EGD30 datum because it has a high degree of correlation between the model used and the existing common points. Additionally, the neural network model keeps the original common point coordinates without changes according to the ESA records.

Moreover, for the second indicator, transformation models are used to predict the coordinates of the check points; the average distortions and their precision based on standard deviation (σ) at check points are listed in Table 6. The distortion vector in space (Dave), as mentioned in Eq. 12, and its space precision are included in Table 6.

Table 6 Distortions of transformation models over check points (unit m)
Full size table

Additionally, Fig. 6 represents the space model distortion over the check points. From Table 6 and Fig. 6, it can be noticed that the distortions resulting from the neural network in all directions are less than 50 cm. The average (δx) in the neural network is the smallest distortion in this direction; the improvement of distortion relative to other models ranges from 0.4 to 70%. In the average (δy), the improvement value ranges from 33 to 80%. Moreover, in the average (δz), the range of improvement is 43 to 78%.

Fig. 6
figure 6

Space model distortion over check points

Full size image

Finally, the average distortion in space (Dave) has improved values ranging from 37 to 72%. Moreover, the prediction ability precision of ANN has an improvement values ranging from 17.5 to 64%. According to the second comparison, it is clear that the neural network can more precisely predict the transformed coordinates and better than the other models used in Egypt previously. It is also important to note that the previous transformation models used in Egypt need to know the priori precision of common points as a first step in the least squares solution, but this information is not available in EGD30 common points (El-Shambaky 2004; Abd-Elmotaal 1994; Abou-Beih and Al-Garni 1996). In contrast, the neural network model did not need a priori knowledge of common points’ precision to begin its solution.

For the last indicator, the conformity property according to the accuracy testing was studied. This test has two levels; the first level compares actual and transformed projected positions using UTM projection for both common and check points. The test involves only horizontal accuracy once the coordinate values have been determined; the resultant residual distance ΔR (\( \Delta R=\sqrt{{\Delta E}^2+{\Delta N}^2} \)) for each point should be computed; where ΔE and ΔN are the residuals (actual minus transformed) in the east and north directions, respectively. Table 7 illustrates the comparison between transformation models with respect to resultant residual distances (ΔR) for both common points and check points.

Table 7 Comparison UTM projection models according to resultant residuals
Full size table

From Table 7, it is clear that in common points, the neural transformation model gives the minimum resultant residuals of 5.10 cm with an accuracy of 9.68 cm. This result indicates an improvement of resultant residuals of at least 97% with an improvement in accuracy of 92%. At check points, it is obvious that the neural model can predict the projected coordinates with minimum resultant residuals of 29.32 cm with an accuracy of 20.16 cm; these results indicate an improvement of resultant residuals of at least 51%, with a 45% improvement in accuracy.

The second level test depends on the geometrical interpretation of the neural transformation model. It is known that, the UTM projection belongs to a conformal projection type (Srivastava et al. 2014). Additionally, the transformation from one grid to another can be done by two models: conformal and affine transformation. The difference between the two models is the scale in the east and north directions. In the first model, the scale is equal in both directions, while in the second model, the scales in both directions are not equal (Richard 2009). According to previous information, both common points and check points transformed by a neural model are projected on the UTM system as first datum observations, and their actual projected coordinates on the UTM system are used as the second datum using the classical method of least squares adjustment with conditions to estimate the affine model’s parameters according to Eq. 22.

$$ \left.\begin{array}{l}{E}^{\prime }={s}_xE\cos \left(\theta \right)-{s}_yN\sin \left(\theta \right)+{x}_o\\ {}{N}^{\prime }={s}_xE\sin \left(\theta \right)+{s}_yN\cos \left(\theta \right)+{y}_o\end{array}\right\} $$
(22)

where (E′, N′) represent the actual projected coordinates, (E, N) are the transformed projected coordinates, (s x ,s y ) are the scales in both directions, (θ) is the rotation angle, and (x o ,y o ) are the shift parameters in both directions. The parameter values and their standard deviations are shown in Table 8; from this table, it can be observed that the scales in both directions are equal, indicating that the affine model changed to a conformal model that keeps the internal angles between projected points unchanged. Additionally, the scale value deviation has a small value of 0.0001, indicating that the neural transformation model produces conformal projected coordinates suitable with a large scale map. According to a previous comparison, the main conclusion is that the neural network model is the most suitable to predict transformed coordinates among other models in two and three directions.

Table 8 Estimated parameters of affine model
Full size table

Conclusions

From the previous study, it is obvious that Egyptian datum transformation is not an easy process because of the inaccuracy and inconsistency in the old local geodetic network in Egypt. A neural network with two neurons in the input layer, four neurons in two hidden layers, and one neuron in the output layer is selected as a suitable datum transformation model according to three indicators: first, the minimum space distortion; second, the consistency between individual distortions, and finally, avoiding the over-fitting problem. In addition, the uncertainty of datum transformation and impact of the data errors are evaluated for the design model. The assessment of the selection model is shown that the developed ANN model is significant to correct and solve the coordinate transformation problem in Egypt.

The results of the comparison between the designed neural network and the other transformation models, which are the Helmert, Molodensky, regression, and minimum curvature surface, used in Egypt show that the neural network model gives the minimum residuals attached to common points, indicating that the neural network has a high degree of correlation between the model and the existing common points, which leads the neural model to keep the original common point coordinates without changes according to the ESA records. Second, the neural network model gives the most minimum space and individual average distortions among other transformation models, and it improves the average space distortion by a range of 37 to 72%. Moreover, the prediction ability precision of ANN has an improvement values ranging from 17.5 to 64% in three directions for the Cartesian coordinates. In the individual directions, the neural model improves the distortion by 0.4 to 80% in all directions; the neural model improves the residual distances in the map projection by 51 to 97%, with 45 to 92% of improvement in accuracy while keeping the conformity property advantage during the projection process. Thus, the neural network can precisely estimate the transformed coordinates better than other models used in Egypt.

Finally, the neural network model did not need a priori knowledge of common points’ precision to begin its solution; in contrast, the other transformation models need this information as a first step in the solution although this information is not available in the old EGD30 common points. For all of these reasons, the final conclusion can be summarized as follows: applying the neural network technique is the most suitable method for use as a tool to solve the datum transformation problem in Egypt, and the high advanced soft computing techniques are suitable to estimate the shift of datum’s; herein, it mentions that the future work should be compared a development model with a high advanced one.