A state-of-the-art realization of cyclic railway timetable computation

Abstract

We describe the periodic event scheduling problem (PESP) based on periodic event networks and extend it by symmetry constraints. The modeling power of the PESP is discussed for automatic calculation of feasible periodic railway timetables. Including the described extensions, complete modeling of integrated regular-interval timetables is possible. Encoding the PESP to propositional logic enables the usage of efficient SAT solvers for solving the PESP. However, optimizing timetables by linear programming is possible, too. As almost all real-world timetable problems are heavily overconstrained, methods for automatic resolving of conflicts are described. Since there is still a lack of efficient conflict resolving algorithms for large-scale intermeshed railway networks, we introduce several strategies for efficiently resolving conflicts and intelligently decomposing timetable problems and discuss the trade-off between computation time and reduction of the solution space. These strategies allow quick adaption to small changes as well. The described methods are implemented in the software system TAKT. We apply the enhanced TAKT to a timetabling study and present some key figures and results.

1 Introduction

Today, planning and disposition of railway transport in Germany is often manual labor—computers only hold, manage and visualize data. These labor-intensive processes lead to mostly evolutionary timetabling, such that every year only the necessary changes are done to fit the timetable to changed infrastructure or a changed network. Using state-of-the-art techniques, it is nearly impossible to build only one fully optimized railway timetable from scratch for large and intermeshed railway networks like the German one. As this obviously does not tap the railway’s full potential, diverse high-quality timetable variants have also a key role in design of tomorrow’s railway infrastructure and in reliable stability and capacity analysis leading to efficient and sound railway networks.

Since railways are a quite long-standing business, they have grown large bundles of complicated operational rules and versatile constraints. Hence, a model is needed which covers a wide range of possible constraints.

At the Chair of Traffic Flow Sciences at TU Dresden, the software system TAKT has been developed for several years in close collaboration with DB Netz AG. It tackles exactly these kinds of issues and solves them by state-of-the-art operations research techniques. The connection and interaction between the different approaches will be subject of this work. The specific use case TAKT was developed for is long-term timetabling studies. The scope of these studies is to evaluate both different operational concepts (different routes, stopping patterns, vehicles and so on) and different infrastructure states. Even at this long-ranging sight, infrastructure operators, transport companies, regional and national authorities impose many requirements resulting in a high number of constraints. Therefore, conflict resolution plays a major role. Timetable optimization based on predicted passenger demand is a possible post process following conflict resolution.

In Sect. 2 we give the preliminaries for periodic event scheduling. After showing the possibilities for solving timetabling instances in Sect. 3, we introduce in Sect. 4 the state-of-the-art conflict resolving of infeasible instances. After presenting our computational results in Sect. 5, we conclude the work in Sect. 6 and give a further scientific outlook.

2 Periodic event scheduling problem

In the last 15 years, the periodic event scheduling problem (PESP) has been established as one of the most suitable problem formulations for periodic timetabling. It is introduced by Serafini and Ukovich (1989). The related periodic event network (PEN) permits flexible representation of almost all periodic timetable’s constraints. For instance, the PESP and its application to railway timetabling are discussed in detail by Nachtigall (1998) and Opitz (2009).

The train network, which is the base of the timetabling problem, contains periodic trains $\fancyscript{L}$ running on a railway network with stations $\fancyscript{S}$. Each train $L \in \fancyscript{L}$ serves a specified sequence of Stations $S \in \fancyscript{S}$. All constraints are modeled into a PEN. Its nodes $v \in \fancyscript{V}$ represent arrival events $(L, { arr }, S) \in \fancyscript{V}$ and departure events $(L, { dep }, S) \in \fancyscript{V}$. The timetable $\mathbf {T} \in \mathbb {Z}^{|\fancyscript{V}|}$ assigns to every event $v \in \fancyscript{V}$ a potential $T_v \in \mathbb {Z}$, $0 \le T_v < t_T$. In a periodic timetable with period $t_T \in \mathbb {N}^+$ the event happens periodically at all times $T_v + zt_T$, $z \in \mathbb {Z}$.

The network’s arcs $a \in \fancyscript{A} :i \rightarrow j$ are basically time consuming processes. All arcs’ processing times are constrained by lower bounds $t_{min,a}$ and upper bounds $t_{max,a}$. This range is also written as $[t_{min,a}, t_{max,a}]_{t_T}$. A timetable $\mathbf {T}$ is considered valid if and only if

$$\begin{aligned} \forall a \in \fancyscript{A} :\exists z_a \in \mathbb {Z} :t_{min,a} \le T_j - T_i - z_a t_T \le t_{max,a}. \end{aligned}$$

(1)

The lower slack $y_a$ is the deviance of the actual processing time from the lower bound such that

$$\begin{aligned} 0 \le y_a = T_j - T_i - z_a t_T - t_{min,a} < t_T. \end{aligned}$$

(2)

The PESP is the decision problem, whether there exists any valid timetable for a given PEN $\fancyscript{N} = (\fancyscript{V}, \fancyscript{A}, t_T)$. For feasible problems, a timetable can be calculated.

This universal problem allows the modeling of running times, dwell times, headways and transfer times. For instance, trains are encoded as alternating sequences of running activities $(L, dep , S) \rightarrow (L, arr , S')$ and stops $(L, arr , S) \rightarrow (L, dep , S)$. Headways between different trains include both safe headways representing the permitted minimum headway and also evenly distributed intervals between different trains running partly on the same railway line. Transfer times include several of different requirements: vehicle transfers, staff transfers and passenger transfers.

Fig. 1

An event network of two trains on a single track line with stations A, B and C

Likewise, symmetry is a common requirement in periodic timetabling (Stähli 1970). A train and its associated returning train are considered to be symmetric, if their arrival and departure times are aligned symmetrically along symmetry axis in time (see Eq. (3)), which is called symmetry minute s and is equal in the whole network. Hence, the trains meet each other at point of time s. The symmetric timetables’ advantage is the satisfied symmetric property of transfers. Thus, all transfers automatically are fulfilled in both directions. Previous works like Liebchen (2006) and Opitz (2009) only consider ideal symmetry without any deviation. In practical applications, this is hardly ever accomplishable as even running times are often asymmetric due to slopes or direction dependent maximum speeds. So we introduce a symmetry deviation to model this requirement.

This constraint is special, as it cannot be modeled by Eq. (1) (even without symmetry deviation) as it was proven by Liebchen (2006). Subsequently, the problem has to be extended by additional constraints $a \in \fancyscript{A}_S :i \rightarrow j$, where i is the arrival event of one train and j the departure event of the associated returning train. A certain maximum absolute deviation from symmetry $d_a \in \mathbb {N}$ is permitted. The actual symmetry deviation is denoted as symmetry slack $y_a \in \mathbb {Z}$. Applying the permitted slack (5) to formulation of symmetry axis (3) results in an inequation (6) quite similar to (1).

$$\begin{aligned} T_j - (s + y_a) -z_a t_T&= (s + y_a) - T_i \end{aligned}$$

(3)

$$\begin{aligned} T_i + T_j - z_a t_T&= 2s + 2y_a \end{aligned}$$

(4)

$$\begin{aligned} -d_a \le y_a&\le d_a \end{aligned}$$

(5)

$$\begin{aligned} 2s - 2d_a \le T_i + T_j - z_a t_T&\le 2s + 2d_a \end{aligned}$$

(6)

Thus, in extension of requirement (1) a timetable is only considered valid if it holds as well:

$$\begin{aligned} \forall a \in \fancyscript{A}_S :\exists z_a \in \mathbb {Z} :2s - 2d_a \le T_i + T_j - z_a t_T \le 2s + 2d_a \end{aligned}$$

(7)

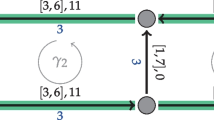
The PESP extended by symmetry constraints allows fully modeling Integrated regular-interval timetables (IRIT) (Opitz 2009). IRIT is a ideal concept of timetabling (refer to Lichtenegger 1990) established in Germany and several other European countries. Figure 1 shows a simple exemplifying PESP network with symmetry constraints.

3 Solving the PESP in TAKT

The PESP is proven to be NP-complete (Serafini and Ukovich 1989). Hence, solving real-world PESP instances is a challenging task (Opitz 2009). The currently most efficient approach for solving the PESP is conducted by using state-of-the-art SAT solvers (Großmann 2011). SAT is the boolean satisfiability problem determining if there exists any interpretation satisfying a given propositional formula. SAT is likewise NP-complete (Cook 1971), yet, for SAT very efficient solvers exist (Manthey and Saptawijaya 2010). It was shown that SAT solvers outperform all previously known approaches for solving the PESP despite the additional time needed for encoding and decoding SAT instances (Großmann et al. 2012).

Propositional logic uses boolean variables $q \in \fancyscript{R}$. Literals L are either variables q or their negation $\lnot q$. Clauses are disjunctions of literals $c = \bigvee _i L_i$. Propositional formulas in conjunctive normal form (CNF) are conjunctions of clauses $\fancyscript{F} = \bigwedge _j c_j$. An interpretation J assigns to every variable either the value true or false, denoted as t or f, respectively. A formula $\fancyscript{F}$ is satisfiable ($\fancyscript{F}^J = t$) if and only if there exists a J such that all clauses contain at least one literal assigned to t under J. An interpretation J is called model (denoted $J \models \fancyscript{F}$), if and only if $\fancyscript{F}^J = t$.

The PEN’s constraints are encoded to propositional formulas using order encoding which is introduced for general finite ordered domains (Tanjo et al. 2011). All potentials $T_v$ are encoded to $t_T - 1$ boolean variables $q_{n,i}$, whereas $q_{v,i} = t$ represents $T_v \le i$ and thus, $q_{v,i} = f$ represents $T_v > i$. The function $enc$ maps the set of events $\fancyscript{V}$ to a propositional formula in CNF, such that this ordering holds:

$$\begin{aligned} enc (v)=(\lnot q_{v,-1} \wedge q_{v,t_T-1})\bigwedge _{i\in [0,t_T-1]}(\lnot q_{v,i-1}\vee q_{v,i}) \end{aligned}$$

(8)

This encoding for variables of finite ordered domains is discussed in details by Tanjo et al. (2011). In order to encode all events’ potentials, which will be the decoded schedule afterwards, we define

$$\begin{aligned} \Omega _\fancyscript{N}:= \bigwedge _{v\in \fancyscript{V}} enc (v). \end{aligned}$$

(9)

After a model $J$ has been found for this formula, extracting the value of the event v by $J$ is done by the function $\xi _v(J)$, where $\xi _v(J)= k$ such that $J\not \models q_{v,k-1}$, $J\models q_{v,k}$ and $k\in [0,t_T-1]$. $\xi _n$ is well-defined and ensures extracting exactly one value due to the following lemma. For detailed proofs we refer to the literature (Großmann 2011; Großmann et al. 2012).

Lemma 1

Let $\fancyscript{N} = (\fancyscript{V}, \fancyscript{A}, t_T)$ be a PEN, $n\in \fancyscript{V}$ be an event and $J$ an interpretation. Then

$$\begin{aligned} \text {(i)}\quad &J\models enc (v) \Leftrightarrow \exists ! k\in [0,t_T-1]:\forall i\in [-1,k-1]: J\not \models q_{v,i},\\ \text {(ii)}\quad &\forall j\in [k,t_T-1]:J\models q_{v,j}. \end{aligned}$$

Proof

(sketch) “$\Rightarrow$”: Let $J\models enc (n)$. To show:

$$\begin{aligned}&\exists k\in [l,u]:\forall i\in [l,k-1]:J\not \models q_{v,i},\forall j\in [k,u-1]:J\models q_{v,j}\quad \wedge \end{aligned}$$

(10)

$$\begin{aligned}&\not \exists h\in [l,u],h\ne k:\forall i\in [l,h-1]:J\not \models q_{n,i},\forall j\in [h,u-1]:I\models q_{v,j} \end{aligned}$$

(11)

Equation (10) is simply shown with mathematical induction. Equation (11) is simply shown without loss of generality $h>k$ implies $q_{v,k}^J=f$, which is in contradiction to (10). “$\Leftarrow$”: can be simply shown with mathematical induction as in “$\Rightarrow$”. $\square$

Extracting the schedule $\mathbf {T}$ can be done on a per-element basis from a model $J$ with

$$\begin{aligned} \forall v\in \fancyscript{V}:T_v=\xi _{n}(J). \end{aligned}$$

(12)

Fig. 2

Feasible (striped) and infeasible (white) regions for constraint $[3,5]_{10}$ between events $i\in \fancyscript{V}$ and $j\in \fancyscript{V}$. The gridded square shows an infeasible rectangle

Subsequently, all constraints can easily be encoded to clauses by excluding for each constraint all invalid combinations of values $(T_i, T_j)$. Excluding each single pair would result in a quadratic number of clauses such that each constraint is encoded soundly (Großmann 2011). Hence, it would be more efficient to encode not just a single pair but a larger set of pairs which will be rectangles. This approach is described in the following. Figure 2 shows the feasible and infeasible regions for the constraint $[3,5]_{10}$ and all pairs of a particular rectangle, that shall be excluded for event $i\in \fancyscript{V}$ and $j\in \fancyscript{V}$. We can exclude all infeasible pairs of a rectangle $[i_1,i_2]\times [j_1,j_2]$ that is a subset of the infeasible region by a single clause:

$$\begin{aligned} enc \_rec ([i_1,i_2]\times [j_1,j_2])=\lnot q_{i,i_2}\vee q_{i,i_1-1}\vee \lnot q_{j,j_2}\vee q_{j,j_1-1} \end{aligned}$$

(13)

The following lemma ensures that each pair of the encoded rectangle is not satisfiable with respect to the encoded formula and thus, not part of a feasible schedule.

Lemma 2

Let $r=([i_1,i_2]\times [j_1,j_2])$ be a rectangle in the infeasible region of the constraint $(i,j)\in \fancyscript{A}$. Then

$$\begin{aligned} J\models enc \_rec (r) \Leftrightarrow (\xi _i(J),\xi _j(J))\notin r \end{aligned}$$

with $J$ being an interpretation.

Proof

“$\Rightarrow$”:

$$\begin{aligned} J\models enc \_rec (r)\Rightarrow (\lnot q_{i,i_2}\vee q_{i,i_1-1}\vee \lnot q_{j,j_2}\vee q_{j,j_1-1})^J=t \end{aligned}$$

(14)

Proof by contradiction: assume $(\xi _i(J),\xi _j(J))\in r=([i_1,i_2]\times [j_1,j_2])$. Then

$$\begin{aligned} i_1\le \xi _i(J)\wedge i_2\ge \xi _i(J)\wedge j_1\le \xi _j(J)\wedge j_2\ge \xi _j(J) \end{aligned}$$

which results in

$$\begin{aligned}&q_{i,i_2}^J=t\wedge q_{i,i_1-1}^J=f\wedge \lnot q_{j,j_2}^J=t\wedge q_{j,j_1-1}^J=f\\&\quad \Rightarrow (\lnot q_{i,i_2}\vee q_{i,i_1-1}\vee \lnot q_{j,j_2}\vee q_{j,j_1-1})^J=f\end{aligned}$$

This is a contradiction to (14). Hence,

$$\begin{aligned} (\xi _i(J),\xi _j(J))\notin r \end{aligned}$$

“$\Leftarrow$”: analogous to “$\Rightarrow$”. $\square$

Excluding all infeasible rectangles of a given constraint a with the given encoding $enc \_rec$ as of (13) results in the complete and sound encoding for a. Applying this to all constraints in the set of edges $\fancyscript{A}$ and connecting this with the encoded nodes $\Omega _\fancyscript{N}$ conjunctively results in the to be encoded propositional formula in CNF. Lemma 1 ensures that we can extract exactly one point in time for each event. Extrapolating Lemma 2 to each constraint ensures the sound and complete encoding for a PEN.

This results in the equivalence of searching for an interpretation J satisfying $\fancyscript{F}$ and searching for a valid timetable $\mathbf {T}$ for PEN $\fancyscript{N}$. For further reading on encoding PESP to SAT we refer to the literature (Großmann et al. 2012).

An interpretation J satisfying $\fancyscript{F}$ can be easily decoded to a timetable $\mathbf {T}$ by reversing the described encoding. Solving the PESP by this approach results in one valid timetable, since it is a decision problem. Global timetable optimization can be achieved by minimizing the weighted sum of slacks using integer linear programming (ILP). Lots of different objectives can be modeled by weighting factors, for example sum of journey time for all passengers or the number of needed train sets (Liebchen 2006; Opitz 2009). Yet most implementations of passenger flow based timetable optimization lack proper assignment of passenger flows as described in Kümmling (2013): large and complex railway networks require sophisticated traffic assignment methods to achieve a reliable prognosis of traffic streams within the network on the one hand. On the other hand, traffic assignment and timetable optimization are heavily interdependent. This is especially a problem in regional and long-distance train networks with large intervals (120 min) between trains. Yet no methods are known to conduct timetable optimization and a sound traffic assignment simultaneously. For a comprehensive survey on further methods for timetable optimization and a wide variety of problem formulations and objectives we refer to Cacchiani and Toth (2012) and Törnquist (2006).

4 Resolving conflicts

Although, solving the PESP is a challenging task, usually only solving the initially formulated timetable problem is not the scope of work as almost all real timetable problems initially are not satisfiable. This is reasoned by the fact that at first the constraints are arranged idealistically tight, for example dwell times are set to the minimum possible dwell time as this would result in minimal journey times if satisfiable. Therefore, the real task is the identification and resolving of conflicts resulting in a minimally relaxed yet valid timetable.

Let $\fancyscript{N} = (\fancyscript{V}, \fancyscript{A}, t_T)$ be a PEN. A conflict $\fancyscript{C} = (\fancyscript{V}, \fancyscript{Z}, \mathbf {T})$ with $\fancyscript{Z} \subseteq \fancyscript{A}$ is called local conflict for $\fancyscript{N}$ if and only if $\fancyscript{C}$ is infeasible and $\fancyscript{C}$ gets feasible by removing any constraint in $\fancyscript{Z}$. A simple example conflict is outlined in Fig. 3. As the event network’s constraints are encoded to separate clauses, local conflicts have a counterpart in SAT: A formula $\fancyscript{M}$ in CNF is called minimally unsatisfiable subformula (MUS) if and only if $\fancyscript{M}$ is unsatisfiable and $\fancyscript{M}$ becomes satisfiable by removing any clause $c \in \fancyscript{M}$. Likewise, there are highly efficient extractors for finding MUS (Ryvchin and Strichman 2011). Once a MUS is found, it can be decoded back to local conflicts (Großmann 2012).

Fig. 3

Local conflict within a quite small sample event network

Constraints in $\fancyscript{Z}$ are relaxed by increasing the upper bound $t_{max,a}$ ($a\in \fancyscript{Z}$), whereas symmetry constraints are relaxed by increasing maximum symmetry deviation $d_a$. Several constraints, especially safety headway constraints, but also other constraints by user’s request, are prohibited to be relaxed at all. In real world railway PEN, the majority of constraints are unrelaxable headway constraints. Consequently, every conflict at first has to be checked on whether any relaxation of the relaxable arcs could solve the conflict. This is done by removing all relaxable arcs from the network and solving the remaining network. Remaining conflicts are intrinsic conflicts of the railway network’s infrastructure and its operating program and thus, have to be manually resolved by modifying the operating program or the infrastructure. The extraction of local conflicts offers a detailed analysis of the bottlenecks (Opitz 2009).

Resolving conflicts involves two steps: firstly, the network is resolved by a quick heuristic, resulting in far too high relaxations. The simplest heuristic relaxes evenly all relaxable constraints by the same slack until the network is feasible. Afterwards, the relaxations are minimized under preservation of the network’s feasibility. Minimization is done by either iterative usage of SAT solvers or direct usage of ILP solvers. The iterative process does not achieve the global minimum, but features much lower calculation times, whereas ILP solvers enable the use of more advanced objective functions.

Despite the impressive speedup achieved by using SAT solvers (Großmann et al. 2012), a lot of timetabling problems are still too vast to be resolved directly in one piece in reasonable time. Therefore, strategies for an intelligent decomposition of the timetabling problem is a necessity. We present two approaches for this problem.

On the one hand, in hierarchical planning, the train network is sub-classified in several levels, for instance long-distance trains, local trains and freight trains as shown in Fig. 4. The trains of the highest level are scheduled first and then are left fixed, then the next level is scheduled which is iteratively proceeded. This approach represents the current manual timetabling processes well and easily fits to established paradigms. It reduces calculation time vastly, but it also cuts down the solution space remarkably.

Fig. 4

Example for hierarchical planning

On the other hand, a new method does not influence the solution space and also results in a considerable reduction of computation time: Some infeasible parts of the timetable network are extracted and resolved separately. Afterwards, all found out relaxations are adopted into the full network, which is then resolved again. Two automatic algorithms for determination of such network parts were developed: local conflict search, as described above and corridor analysis. Corridor analysis extracts the nodes and arcs of a train and its returning train and adds a defined amount of neighboring nodes and arcs. Far more sophisticated algorithms and combined strategies are currently under intensive research. Manual extraction of few heavily crowded and closely intertwined urban networks out of regional or national networks deliver effective results as well.

Both methods allow an intelligent and quick way of incremental scheduling, as they enable to fit small changes into existing timetables easily. Whereas solving whole networks takes hours, it is only a matter of minutes to include changes and to generate valid timetables again. Furthermore, it is possible to evaluate different operating programs and infrastructural states quickly.

5 Application and results

As described in the beginning, the presented algorithms are implemented in the modular timetabling software system TAKT of the Chair of Traffic Flow Science at TU Dresden. The PEN is generated automatically from given input data. This is necessary, as large timetabling problems can consist of up to one million arcs and ten thousands of nodes, which cannot be calculated manually. The program assigns the optimal route on the track layout for each train automatically and calculates the running times within seconds. All minimum headways are calculated individually based on microscopic infrastructure data and the previously calculated running times.

After running time calculation, all running times are considered constant. This is a requirement because the minimum safe headways depend linearly but discontinuously on running times (Kümmling 2014) and the PESP does not allow for dependencies between different arcs. This enables us to reduce PEN size as well by removing arrival arcs and uniting stopping arcs with neighboring arcs (condensation, see Opitz 2009). For calculating headways we use commonly established methods. We refer to Müller (1934) for a comprehensive overview and to Nachtigall (1998) for application in PESP.

This PEN is the universal interface to different PESP solvers, allowing the usage of different solvers like the presented SAT-based approach, but also for instance LP-based solvers. The SAT-based PESP solver uses external SAT solvers. So far, the best overall performance was reached with the Glucose SAT solver (Audemard and Simon 2013).

Fig. 5

Example of hierarchical planning sequence

The presented methods are applied to a case study of the German long-distance passenger railway network and the regional trains within the German region south-east (Saxony, Thuringia and Saxony-Anhalt). Firstly, the two networks were solved separately. As the network of regional trains is denser, a particular complex part (Leipzig region) was extracted and the relaxations needed for this part were calculated beforehand. Table 1 shows key figures of these instances. Fig. 5 outlines the sequence of timetabling steps.

Table 1 Key figures of sample instance

Calculating a completely conflict-free timetable for the long-distance network takes about 2.5 h. Determining a valid timetable for the regional trains in the described two iterations took approximately 2 h each. In the joint network of both long-distance and regional trains, the long-distance trains were fixed to the determined timetable, whereas the regional trains were not fixed, but the relaxations computed before adopted to the event network. Solving the joint network took about 30 min. Providing fully correct input data, the program does not need any assistance to calculate applicable timetables. Having large amounts of input data, flaws like wrong train routes, missing stops, bogus connections are common. Thanks to the relaxation handling described before, the flaws can be detected and removed iteratively without calculating the timetable from scratch over and over again. The computations were conducted on an Intel Xeon CPU X5450 based server with 16 GB RAM, but used not more than one core and 500 MB RAM. The SAT instances are solved by the SAT solver Glucose version 2.3.¹

Based on the PESP a more advanced model for completely automatic calculation of freight train paths along corridors is developed, that allows dynamic track allocations and dynamic selection of suitable speed profiles for freight trains. It outperforms the work of experienced experts even on highly crowded lines by far—the same number of or even more train paths with a better quality are achieved in much lower time (Opitz 2009; Weiß et al. 2014).

Fig. 6

Screenshot of timetable visualization in TAKT

Additionally, TAKT features several visualization tools for evaluation of the resulting timetables, one example is displayed in Fig. 6.

6 Conclusion

As it was shown in this work, SAT-based PESP solving and local conflict search provide a powerful base for fully automatic timetabling. The usage of SAT allows solving larger networks which could not be solved before. Intelligent problem reduction and partition algorithms allow further increments in network size and reductions in calculation time respectively. These improvements permit additional extensions to the PESP model as well. For instance, dynamic track allocation for passenger trains will rise the flexibility of PESP in practical applications further.

The described management of relaxations offers an easy and efficient way for evolving timetables from scratch, which was successfully field-tested on large-scale railway networks. The possibility of fast rescheduling and the variety of realizable constraints opens periodic event scheduling for new fields like capacity research of several infrastructure states or railway traffic management in a completely new manner.