Exact and heuristic approaches to the robust periodic event scheduling problem

Abstract

In the periodic event scheduling problem, periodically reoccurring events need to be scheduled, subject to constraints on the resulting time differences. A typical application for this type of problem relates to train schedules, which have to repeat every hour for passenger convenience. As external disruptions may occur, robustness considerations need to be included in the scheduling process. In this work, we present a recovery approach for instances where integer programming methods can be applied, and a bi-criteria local search algorithm for large-scale instances. In computational experiments, we compare solutions calculated using the recovery approach to risk-averse and to risk-oblivious solutions. Our results suggest that the solutions generated by our approach have a favorable trade-off between cost and robustness. Furthermore, we compare the local search algorithm to a simplified approach that includes the desired robustness level as a hard constraint. The experiments show that our algorithm finds an improved set of non-dominated solutions within equal computation times.

1 Introduction

In the Periodic Event Scheduling Problem (PESP) as introduced in Serafini and Ukovich (1989), periodically reoccurring events need to be scheduled according to given feasible time spans. The most prominent example for this type of problem are train schedules, in which train arrivals and departures repeat, e.g., every 15, 30, 60, or 120 minutes for passenger convenience, see Liebchen and Möhring (2007); Odijk (1996); Nachtigall (1998); Peeters (2003). Successful applications of this model include the optimized timetable for the underground railway of Berlin [see Liebchen (2008)], and the timetable for the largest Dutch railway contractor, the Nederlandse Spoorwegen, see Kroon et al. (2009).

Methods to solve PESP instances most commonly include mixed-integer programming techniques, see Liebchen et al. (2008); but also constraint programming techniques are frequently used, see, e.g., Kroon et al. (2009); Oliveira (2001); Isaai and Singh (2000); Goerigk and Schöbel (2013). Recently, local search heuristics like the modulo network simplex method (Nachtigall and Opitz 2008; Goerigk and Schöbel 2013) have become a valuable alternative due to their ability to tackle larger instances, as it is usually the case in real-world problems.

As delays create considerable passenger inconvenience as well as operational costs and should not be neglected when designing a periodic timetable fit for practice, several attempts have been made to find robust timetables, i.e., timetables that behave “well” in a to-be-specified sense under the existence of delays.

The case of aperiodic robust timetabling—in a problem variant that is solvable in polynomial time—has been intensively studied, see, e.g., Liebchen et al. (2009); Fischetti and Monaci (2009). For a survey on this field, see Goerigk and Schöbel (2010), where an experimental comparison between several robustness models has been made. Note that other problem variants for the aperiodic case may be NP-hard, see, e.g., Caprara et al. (2002); Cacchiani et al. (2010a, b).

In the case of periodic robust timetabling, already the nominal problem is strongly NP-hard and computationally difficult to solve. Thus, complex robustness models are not a practical option for large instances. A survey on robust timetabling (considering both periodic and aperiodic models) can be found in Cacchiani and Toth (2012). In Fischetti and Monaci et al. (2009), a linear robustness objective is proposed for the aperiodic case, based on statistical evidence [see also Kroon et al. (2007)]. The resulting model is then solved by a commercial mixed-integer programming solver. In Cacchiani et al. (2012), a Lagrangian optimization method is adapted to take robustness into account, and the resulting optimization scheme is applied to a variant of the timetabling problem. In the recent work of Caimi et al. (2011), an extension of the PESP, the flexible periodic event scheduling problem is introduced, in which intervals are used instead of fixed event times. The added flexibility can be understood as a measure of robustness, which increases the chances of finding a feasible timetable on a microscopic level. Similar to this work, they also consider a bi-objective approach, considering both travel time and robustness simultaneously.

Contributions: We consider robust periodic timetabling models under a long-term planning horizon, where it is possible to adjust the timetable once the realized scenario becomes known. Ideally, the adjusted timetable performs well in this scenario (i.e., passenger have short travel times), while it is at the same time not too different from the originally planned schedule. Such an approach is covered by the recently introduced concept of RecOpt from Goerigk and Schöbel (2014).

However, as the periodic event scheduling problem is already notoriously difficult to solve in its nominal, non-robust variant, it is beyond hope to solve the robust model for anything but small instances. We therefore consider a heuristic approach for medium-sized instances.

For the largest (and possibly also most realistic) instances, even this heuristic approach is not applicable, as it involves the solution of several nominal subproblems. We suggest to use a local search heuristic instead, which aims at minimizing travel times for a given desired amount of robustness. Thus, as an example for the value of the algorithm engineering paradigm in robust optimization, see Goerigk and Schöbel (2013), we highlight the advantage of explicitly including the size of instances in the choice of the “right” robustness approach.

For each robustness approach, we present numerical results, showing that (a) the resulting solutions are a reasonable compromise between risk-averse and risk-oblivious solutions, (b) this also holds if simulated delays are considered, and c) the non-dominated solutions generated by the bi-criteria local search algorithm are better than the non-dominated solutions found when robustness is the desired robustness level as a hard constraint.

Overview: In Sect. 2, we introduce the nominal periodic event scheduling problem with its application to periodic timetabling. The first approach to robustness, which is suitable for instances up to medium size and based on a recovery strategy, is presented in Sect. 3. We then discuss the bi-criteria approach for large-scale problems in Sect. 4. After presenting numerical results for both approaches in Sect. 5, we conclude this work in Sect. 6.

2 PESP and periodic timetabling

A periodic event $i$ is a countably infinite set of events $i_p$, $p\in \mathbb {Z}$, with occurrence times

$$\begin{aligned} t(i_p)=t(i)+p \cdot T \end{aligned}$$

for a given period $T$ Serafini and Ukovich (1989). A span constraint consists of an interval $[l_{ij},u_{ij}]\subset \mathbb {R}$ for a pair of events $(i,j)$. The span constraint is satisfied if

$$\begin{aligned} (t(j) - t(i)) \text { mod }\, T \in [l_{ij},u_{ij}], \end{aligned}$$

where $x\, \text { mod } T := \text {argmin}\{z\in \mathbb {R}_+ : \exists d\in \mathbb {Z}\text { s.t. } x = z + dT\}$. Note that possible multiple span constraints between two events can be rewritten as a single span constraint. The PESP problem is given as follows: For a given finite set of events with a period $T$ and a finite set of span constraints, find a time $t(i)$ for each periodic event $i$ such that all span constraints are satisfied. It is shown by Serafini and Ukovich (1989) that PESP is NP-hard by transformation from the Hamiltonian Circuit Problem.

As pointed out in Sect. 1, the most prominent application of the PESP is train timetabling. Therefore, we will use the terminology of train timetabling in the following; however, applications to other transportation systems are possible. Based on the PESP, the periodic timetabling problem can be formulated by introducing Event-Activity-Networks (EAN) to model the time-dependent behavior of the various vehicles considered [see Odijk (1996)]. EANs are directed graphs $G = (\mathcal {E},\mathcal {A})$ with nodes $\mathcal {E}= \mathcal {E}_{arr} \cup \mathcal {E}_{dep}$ that represent arrival and departure events of every train line at every station, and edges $\mathcal {A}= \mathcal {A}_{drive} \cup \mathcal {A}_{wait} \cup \mathcal {A}_{change}$ representing a type of activity:

• 1. Driving activities $\mathcal {A}_{drive}\subseteq \mathcal {E}_{dep} \times \mathcal {E}_{arr}$ that model the time a train needs to travel from one station to the other

• 2. Waiting activities $\mathcal {A}_{wait}\subseteq \mathcal {E}_{arr} \times \mathcal {E}_{dep}$ that model the time a train spends idle at a station, waiting for passengers to board and deboard

• 3. Changing activities $\mathcal {A}_{change}\subseteq \mathcal {E}_{arr} \times \mathcal {E}_{dep}$ that model the time a passenger needs to transfer from one train to another at the same station.

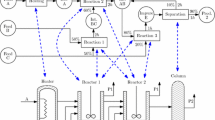
Other types of activities that are frequently used include headway activities that model the security distance between two trains using the same infrastructure; such additional activities can be easily included throughout the remainder of the paper. The events are periodic since all arrivals and departures are repeated in every period, and for each of the activities a span constraint is given which contains the minimal and the maximal duration of the activity. The minimal duration guarantees a certain level of robustness while the maximal duration controls the quality of the timetable. Figure 1 gives an example for the general structure of such a network. In station A, passengers would like to change from a train of line 1 into a train of line 2 and vice versa. In station B, there are passengers who change from line 2 to line 3.

Fig. 1

Detail of an event-activity-network

The goal is to find a timetable assigning a time $\pi _i:=t(i) \mod T \in \mathbb {R}$ to each of the events $i \in \mathcal {E}$ for a given period $T$ such that the span constraints are satisfied, i.e., $(\pi _j - \pi _i) \text { mod } T \in [l_{ij},u_{ij}]$ for each activity $(i,j)\in \mathcal {A}$. The objective in the timetabling problem we consider here is to minimize the total passenger traveling time given as

$$\begin{aligned} \sum _{(i,j) \in \mathcal {A}} \omega _{ij} \left[ \left( \pi _j - \pi _i\right) \text { mod }\,{\it T} \right] , \end{aligned}$$

where $\omega _{ij}$ is the number of passengers that would like to use activity $(i,j)\in \mathcal {A}$; typically, this number needs to be estimated in real-world applications. Note that other objective functions are possible, as, e.g., the ratio of waiting times to journey times, see Isaai and Singh (2000).

Instead of the event times $\pi _i, i \in \mathcal {E},$ one can equivalently determine the duration $x_{ij}=\pi _j-\pi _i+zT$ for any edge $(i,j) \in \mathcal {A}$, where $z$ is the smallest integer value such that $x_{ij} \ge l_{ij}$. Using this concept, an alternative formulation (used by the modulo network simplex) has been suggested in Nachtigall (1998). Let $\mathcal {T}= (\mathcal {E},\mathcal {A}_\mathcal {T})$ be a spanning tree with its corresponding fundamental cycle matrix $\Gamma$, then the periodic timetabling problem can be formulated as follows:

$$\begin{aligned} \text {(PTT)}\qquad \min&\sum _{(i,j)\in \mathcal {A}} \omega _{ij} x_{ij} = TravelTime(x)\\ \text {s.t}\quad&(x,z) \in \mathcal {F}(l) \end{aligned}$$

where

denotes the set of feasible solutions and $x = (x_{ij})_{(i,j)\in \mathcal {A}}$ and $l = (l_{ij})_{(i,j)\in \mathcal {A}}$. For details and correctness we refer to Nachtigall (1998). As the variables $z_{ij}$ model the periodic character of the problem, they will be referred to as modulo parameters.

Constraint (1a) ensures that the activity durations $x$ yield a potential $\pi$ that is uniquely determined up to the modulo operator, while Constraint (1b) ensures that the lower and upper activity bounds are fulfilled.

Note that the modulo parameters are the reason why this problem is NP-hard. For fixed variables $z_{ij}$ the timetabling problem is the dual of a minimum cost flow problem that can be solved efficiently using the network simplex method. On the other hand, the variables $z$ are easily obtained for a given feasible duration vector $x$.

3 Recovery to optimality

The problem formulation (PTT) does not take disruptions into account, which inevitably occur during operation of a periodic schedule. Causes of these disruptions are manifold: Bad weather conditions like snow, rain or storm, construction sites, accidents and many more uncontrollable effects impair the operability of a timetable.

Instead of considering the nominal problem formulation (PTT), in which we assume that all problem parameters are known in advance, we now consider an uncertain problem version (PTT($l$), $l\in \mathcal {U}$), in which the lower activity bounds are not given exactly, but known to come from a finite uncertainty set $\mathcal {U}=\{l^1,\ldots ,l^N\}$. The set $\mathcal {U}$ therefore captures possible disruptions of the schedule like bad weather conditions, technical failures or accidents. We will refer to the elements of $\mathcal {U}$ as scenarios. Note that to model delay scenarios, we do not need to assume uncertain upper bounds on activities; however, the operator might decide to relax the upper bounds in case of delays. In the following, we will assume that upper bounds are large enough to allow a feasible solution to exist in every considered scenario, and ignore uncertainty in the upper bounds.

The reformulation of the parameterized problem family back to a single problem is called robust counterpart, and various proposals how to do this have been made in the recent literature [(e.g., Ben-Tal and Nemirovski (1998); Fischetti and Monaci (2009)].

We will denote the set of feasible solutions in scenario $\xi \in \mathcal {U}$ as $\mathcal {F}(\xi )$. In many applications, there exists a so-called nominal scenario $\hat{\xi }\in \mathcal {U}$ that corresponds to an undisturbed setting. For the periodic timetabling problem, the nominal scenario is $\hat{\xi }=\hat{l}$.

Following Ben-Tal and Nemirovski (1998), a simple approach to find the robust counterpart is by requiring feasibility in all scenarios, which is also called the strictly robust counterpart. For (PTT), this amounts to solving

$$\begin{aligned} \text {(SR)}\qquad \min Travel Time(x)\\ \text {s.t}\quad&(x,z) \in \mathcal {F}(l^i) \ \forall l^i \in \mathcal {U}\end{aligned}$$

Note that $\bigcap _{i=1}^N \mathcal {F}(l^i) = \mathcal {F}(l^{wc})$, where $l^{wc}_j = \max _{l^i\in \mathcal {U}} l^i_j$ denotes the activity-wise worst-case. Therefore, (SR) can be transformed to a problem of type (PTT) again. However, this approach might be too restrictive for real-world timetabling problems: Solving (SR) means finding a timetable that can be used without any change for all possible scenarios, e.g., a schedule has enough buffer times to be used during a snowstorm as well as during nice summer weather.

A step towards practical applicability has been made with the concept of recovery robustness by Liebchen et al. (2009), where it is allowed to update a solution once the scenario becomes known. In this section, we draw upon the related concept of recovery-to-optimality as introduced in Goerigk and Schöbel (2014) to find periodic timetables that can be updated to an optimal timetable in every scenario with minimal recovery costs.

We assume that the costs to modify one periodic schedule $x^1$ to another one $x^2$ is given by a function $d(x^1,x^2)$ that does not depend on the modulo parameters $z$. This represents the fact that the modulo parameters are variables introduced for the integer programming formulation, but are not perceivable during operation. Instead, the most obvious instrument to change a timetable from the practitioner’s point of view is to modify the driving and waiting durations $x$.

The recovery-to-optimality counterpart [(RecOpt) for short] for of an uncertain optimization problem is given as follows: Find a solution that minimizes the maximum distance to an optimal solution in any scenario (or, alternatively, the sum of distances to optimal solutions). While the former problem can also be interpreted as a center location problem, the latter corresponds to a median problem. In the case of (PTT), we can formulate the center version of (RecOpt) the following way:

$$\begin{array}{lll} \text {(RecOpt-PTT)}& {\min}&\max _{i=1}^N d(x,x^i)\\ &\text {s.t.}&(x,z)\in \mathcal {F}(\hat{l})\\ &&(x^i,z^i) \in \mathcal {F}(l^i) \ \forall l^i\in \mathcal {U}\\&&TravelTime(x^i) = opt(l^i)\ \forall l^i\in \mathcal {U}, \end{array}$$

where $opt(l)$ denotes the optimal objective value for the periodic timetabling problem with respect to the lower bounds $l$, which needs to be computed in a preprocessing step.

Note that $d$ should reflect the possible recovery actions the operator can use. In a setting where it is prohibited to prepone an event with respect to a published schedule, a non-symmetric function $d$ should be used. Otherwise, a metric can be applied.

For metrics $d$ induced by polyhedral norms, we can directly rewrite (RecOpt-PTT) to a mixed-integer program. As an example, using

$$\begin{aligned} d^\infty (x^1,x^2)=\max _{a\in \mathcal {A}} |x^1_a - x^2_a| \end{aligned}$$

and considering the center problem, we have the following mixed-integer linear program:

The variable $c$ represents the maximum $d^\infty$ distance of the robust solution $x$ to the solutions $x^i$ of the respective scenarios. To determine this distance, the Constraints (3) are used. Constraint (8) ensures that the solutions $x^i$ are optimal for their respective scenario.

Obviously, (RecOpt) significantly increases the problem size – in this case, for a nominal problem with $n$ variables and $m$ constraints, the (RecOpt-PTT-$d^\infty$) counterpart consists of $(|\mathcal {U}|+1)(n+1)$ variables and $(|\mathcal {U}|+1)(n+1) + |\mathcal {U}|$ constraints. For a problem that is already computationally challenging on its own, this is highly undesirable.

We can simplify (RecOpt) by precomputing an optimal solution for every scenario, and minimizing the recovery distance to these fixed points in the solution space.

Algorithm 1

• 1. Given: An uncertain periodic timetabling problem (PTT($l$), $l\in \mathcal {U}$), and a function $d$.

• 2. Solve the instances PTT($l$) for all $l\in \mathcal {U}$. Let $x^l$ be the resulting solutions.

• 3. Solve the problem $\min \{ \max _{l=1,\ldots ,N} d(x,x^l) : (x,z)\in \mathcal {F}(\hat{l}) \}$. Let $(x^*,z^*)$ be the resulting solution.

• 4. Return: A heuristic solution $(x^*,z^*)$.

This heuristic approach can be applied when the instance size is too large to be solved by the above IP formulation, and is motivated by the following considerations: It is exact, if there is a unique optimal solution to every scenario. Furthermore, we show that we may neglect nominal feasibility when calculating the robust solution in Step 3, if (a) no headway activities are used, and (b) the recovery distance does not depend on the changing activities, i.e., upper bounds of changing activities are sufficiently large to not affect feasibility, and the recovery difference between two schedules does not take differences in changing times into account (see the appendix for more details). The advantage is that we are able to reuse any algorithm that solves the nominal (non-robust) periodic timetabling problem, and one of the standard algorithms from location theory, to solve (RecOpt-PTT) in this setting.

4 Local search for robustness

We now consider problem instances that are too large to be solved exactly. Assuming a robustness function $Robustness: \mathbb {R}^{|\mathcal {A}|} \rightarrow \mathbb {R}$ is given, which evaluates how capable a timetable is to handle delays, we would like to solve the bi-criteria robust periodic timetabling problem:

$$\begin{aligned} \text {(RPTT)}\qquad&{\left\{ \begin{array}{ll} \min &{} TravelTime(x)\\ \max &{} Robustness(x) \end{array}\right. }\\ \text {s.t}\quad&(x,z) \in \mathcal {F}(\hat{l}) \end{aligned}$$

There are many possibilities of how to design such a robustness function, apart from the distance to an optimal solution as in the previous section. One is to generate a large number of random delays, and to measure their impact under a given disposition rule, e.g., postponing every event as far as necessary to become feasible again. However, even though this approach would represent the robustness of a timetable very adequately, it is computationally too difficult to be included in the optimization process.

We will therefore assume that $Robustness(x) = r^t x$ is a linear function, and the weights $r_e$ represent the benefit of buffering edge $e\in \mathcal {A}$. For the following considerations, we use a robustness function that is motivated by the work of Fischetti and Monaci et al. (2009) and Kroon et al. (2007) – see also Cacchiani et al. (2012). Let $pos(e)$ denote the position of a driving or waiting activity $e$ within its corresponding trip $trip(e)$, i.e., the path of the train serving the respective activity within the EAN. We then define the robustness weight $r_e$ of a driving or waiting activity $e\in \mathcal {A}_{drive} \cup \mathcal {A}_{wait}$ as

$$\begin{aligned} r_e&:= \frac{ \max _{e'\in \mathcal {A}_{drive} \cup \mathcal {A}_{wait}} \{\tilde{r}_{e'}\} - \tilde{r}_e}{|\mathcal {A}|\cdot \max _{e'\in \mathcal {A}_{drive} \cup \mathcal {A}_{wait}} \{\tilde{r}_{e'}\} - \sum _{e'}\tilde{r}_{e'}}\\ \text {where } \, {\tilde{r}}_e&= (1-e^{-\lambda \cdot pos(e)}) \cdot \left( |trip(e)| - pos(e)\right) \\ \end{aligned}$$

and the overall robustness of a timetable as

$$\begin{aligned} Robustness(x) := \sum _{e\in \mathcal {A}_{drive} \cup \mathcal {A}_{wait}} r_e (x_e - l_e) \end{aligned}$$

We modify the modulo simplex algorithm in order to find Pareto optimal solutions using the $\varepsilon$-constraint method. Note that also other algorithms from multi-criteria optimization would be applicable, as, e.g., the weighted sum approach. However, operators would typically prefer direct control of the robustness of a solution over indirect control; i.e., using a budget on the robustness is a natural choice. An example for direct robustness control used in practice is applying the same relative buffer to all driving activities.

The original modulo simplex algorithm consists of two phases: A local search phase in the spanning tree structures, and a search for an improving cut [see Goerigk and Schöbel (2013) for details]. In the local search phase, a spanning tree structure is iteratively improved by exchanging tree- and non-tree-edges, similar to the classic network simplex method. Contrary to the latter, a local optimum is not necessarily global, which is why further methods to overcome such an optimum need to be applied. This is done in the second phase: A connected cut is greedily found, that is, the current solution is modified along the edges induced by a graph cut. As this is not a move within the local neighborhood of the spanning tree structure, a new structure has to be generated. This is done by fixing the modulo parameters of the current solution, and solving the dual of the resulting problem. As this dual is a min-cost flow problem, the classic network simplex method can be applied, which yields a new spanning tree structure.

Let $R$ be the minimal required robustness of a solution. In order to find a timetable with robustness of at least $R$, we impose the following two rules on the local search phase:

Rule 1.1: If the current robustness is greater or equal to $R$, choose a neighbor with robustness greater or equal to $R$ that minimizes the travel time.

Rule 1.2: If the current robustness is smaller than $R$, choose a neighbor that maximizes the robustness.

Rule 1.1 makes sure that the local search does not violate the robustness constraint, while Rule 1.2 forces the algorithm to try to satisfy the constraint again, should it be violated. Therefore, the only possibility for the robustness constraint to be violated is by means of phase 2.

For phase 2, the following rules hold:

Rule 2.1: If the current robustness is greater or equal to $R$, minimize the travel time when rebuilding the spanning tree structure from the current modulo parameters.

Rule 2.2: If the current robustness is smaller than $R$, maximize the robustness when rebuilding the spanning tree structure from the current modulo parameters.

Note that Rule 2.2 can be applied as the robustness objective robustness is a linear function, and thus can be used in the classic network simplex algorithm. All other modifications can still be used for non-linear robustness objectives. A schematic view on the algorithm is given in Fig. 2. As the algorithm does not necessarily converge, but can endlessly switch between regions with too less and regions with satisfactory robustness, an iteration limit is imposed. When this limit is reached, the best solution found is returned.

Fig. 2

Schematic overview of the algorithm

We present an example in Fig. 3, where we plot the travel time and robustness for a single run of the algorithm. The minimal required robustness $R$ is 14. When a local minimum with respect to travel time is found in iteration 476, a connected cut is applied that reduces travel time (Rule 2.1). The algorithm now strives to increase the robustness to a feasible level (Rule 1.2). After failing to do so by getting stuck in a local maximum with respect to robustness, a connected cut is applied that maximizes the robustness again (Rule 2.2.). This continues until the iteration limit of 2,000 is reached. The best feasible solution is saved and the algorithm ends.

Fig. 3

An example for the proposed algorithm

5 Experiments

Trying to compare the recovery approach from Sect. 3 to the algorithm from Sect. 4 may seem a natural experimental approach. However, we argue that both approaches to robustness do not only differ in the problem size they are designed for, but also in their definition of robustness, and should better be compared to competitors from their own domain. Therefore, we evaluate the recovery approach in Experiment 1 compared to strict robustness and the nominal problem, and compare the Pareto solutions of the local search algorithm to solutions generated using fixed buffer times in Experiment 2. More details can be found in Sects. 5.1 and 5.2, respectively. Note that while the first experiment compares concepts, the second experiment compares algorithms.

Environment: All experiments were conducted on a PC running Ubuntu 11.10 with 24 GB main memory and an Intel Xeon E5520 processor, running with 4 cores at 2.26 GHz and 8MB cache. Only one core was used and a fraction of the memory was used. All code is written in C++ and has been compiled with g++ 4.4.3 and optimization flag -O3.

5.1 Experiment 1: Small and medium sized instances

Test instances: We randomly generated two sets of instances: Denote by an instance of size $n$ an instance with $n$ lines of length $n$, and $1.5n$ change activities. The lower bound $l_{ij}$ for a driving or waiting activity $(i,j)$ is randomly chosen from the interval $[1,30]$, while the upper bound is chosen from $[2l_{ij},2l_{ij}+40]$. The period $T$ is 60, and change activities have durations from the interval $[3,62]$. Line frequencies are set to 1 (which is relevant for constructing event-activity networks, see Siebert and Goerigk (2013)). The first set of generated instances consists of instances of size from 5 to 11, 10 each, totalling to 70 instances. The second set consists of instances of size from 20 to 30, 1 each, totalling to 11 instances.

The uncertainty set for each instance consists of $\mathcal {A}/10$ scenarios. In each scenario, $\mathcal {A}/5$ random activities $a$ are assigned increased lower bounds $(1.1 + \alpha )l_a$, where $\alpha$ is a random number from the interval $[0,0.9]$. Per instance, 5 uncertainty sets were generated, and results averaged.

Setup: In this experiment, we try to compare both the direct MIP formulation (RecOpt-PTT-$d^\infty$) and the approach based on Algorithm 1 to the strictly robust and the nominal solution. For the smaller dataset we solved (RecOpt-PTT), (SR) and (PTT) using the MIP-solver Gurobi 5.0 by Gurobi Optimization Inc (2012). For the larger dataset exact MIP solutions could not be produced in reasonable time (runtimes $>$ 1 h), and the modulo simplex heuristic by Goerigk and Schöbel (2013) was used instead. We solved the strictly robust and the nominal problem, and all scenarios separately. We then calculated the $d_2^2$ median with respect to driving and waiting activities for all scenarios, fixed these durations, and postoptimized the change durations using Gurobi again, resulting in a heuristic (RecOpt-PTT) solution. It is unreasonable to apply the local search heuristic to this problem size, where the preferrable RecOpt approach is applicable.

Results: Calculation times were in the order of seconds. The results on both datasets are presented in Fig. 4. While the solid lines represent the value of TravelTime, the dashed lines give the recovery distance. As expected, the travel time of the (RecOpt-PTT) solution is in between the travel time of the strictly robust and the nominal solution. For increasing instance size, the strictly robust solution becomes unattractively expensive, while the travel time of (RecOpt-PTT) keeps close to the nominal objective.

Fig. 4

Results for experiment 1. Solid lines denote travel time, and dashed lines recovery distance

Concerning the recovery distance, (RecOpt-PTT) yields the smallest costs, as expected. Note that the distance is bounded by $T=60$ for the smaller instances, as we used the $d^\infty$ center, while the $d_2^2$ median distance is not bounded. While both the strictly robust and the nominal solution are expensive to recover in the case of the small instances, this is different for the larger instances, where the nominal solution shows a recovery distance that is only slightly larger than the recovery distance of the heuristic (RecOpt-PTT) solution. The large recovery costs of the strictly robust solution for these instances can be explained by the increasing number of scenarios (which depends on the number of activities), which forces the strictly robust approach to use larger buffer times.

The results show that both presented approaches to (RecOpt-PTT) are easily applicable for instances of size up to 30, and suggest that solutions yield a good trade-off between travel time and robustness in terms of recovery distance. Testing the heuristic approach we used for the medium-sized instances also for the small-sized instances, we found that optimal recovery distances were achieved in nearly all cases; thus confirming the quality of the heuristic solutions.

To better evaluate the differences between the three types of timetables, we also evaluate their performance under delays. In order to do so, we expand the periodic networks and timetables for the smaller dataset over a finite time horizon, generate random delays, and propagate the delays through the network using an always-wait policy for changing activities. This way, built-in buffer times help avoiding the spread of delays to subsequent events. The time horizon used was 4 h, and for every timetable 10 times 25 delays were generated, that may increase the duration of a driving or waiting activity by a factor up to 2. Note that, even though 25 source delays were generated, the number of delayed activities will be higher, as these delays propagate through the network. We measure the average delay over all events. Results are shown in Fig. 5.

Fig. 5

Average delay of events for randomly generated delays

Results belonging to the same class of instance size are connected via a black line. In the strictly robust solutions, we find the smallest delay of events, while the nominal solution shows the largest delay and the (RecOpt-PTT)-solution lies in between. Note that the average delay decreases for increasing network size, as a constant number of delays was used. We find that (RecOpt-PTT) solutions not only show a good performance with respect to the recovery distance (which they do by design), but are also a compromise between strict and nominal solutions when no recovery is possible.

5.2 Experiment 2: large instances

Test instance and starting solution: The high-speed railway instance R1L1 from the LinTim-toolbox [see Goerigk et al. (2013, 2014)] was used, which consists of 3664 events and 6381 activities, of which are 2827 change-, and 3554 waiting- or driving-activities¹. The network consists of 250 stations and 55 trains, and is based on real-world data modelling the intercity rail transport in Germany (for comparison, the instance considered in Caimi et al. (2011) has 212 events and 647 activities). We intended the starting solution to maximize robustness, therefore we chose the maximum allowed slack for every driving and waiting activity, and minimized the resulting weighted changing times, as this does not decrease the robustness.

Setup: Note that it is hopeless to apply the RecOpt heuristic to instances of this size, as even solving a single PESP instance is notoriously difficult. Also, a weighted sum approach to solve (RPTT) is inapplicable in practice, where the planner needs direct control over the guaranteed value of robustness of a solution.

We proceed as follows: As the robustness of the starting solution, i.e., the optimal solution of (RPTT) with respect to Robustness, is approximately 15.238, we run the robust local search algorithm with $R\in \{0,1,\ldots ,15\}$, where R is the minimal required robustness, and an iteration limit of 2000. The maximal value of $15$ for $R$ was determined by calculating $Robustness(u)$. In order to evaluate the efficient solutions found this way, we compare the proposed heuristic to a different approach: We calculate solutions using the original modulo network simplex method on modified instances, where the robustness level is implemented as a hard constraint on the lower activity bounds. Specifically, we distribute a total slack of $S\in \{0,A,2A,\ldots ,7A\}$ according to the distribution as described in Section 4, where $A=|\mathcal {A}_{drive}\cup \mathcal {A}_{wait}|$. It is not possible to use more slack than $7A$ this way without violating the upper bounds on the activities. Again, 2000 iterations are used, and the efficient solutions determined.

Results: In Fig. 6a, we present the efficient solutions as found by the robust local search. Due to the iteration limit of 2000, robustness levels smaller than 7 did not impose a restriction on the search process. Therefore, all of these runs yield approximately the same solutions, differing only by the randomized connected cuts.

Fig. 6

Pareto front of solutions

For the efficient solutions, there seems to be a linear relationship between robustness and travel time, with slope of approximately 1, meaning that, in order to double the robustness, also passengers need to travel twice as long. Furthermore, the gap between the travel time of the most robust solution, and the travel time of the solution with a robustness level of 15 is larger than would be expected in a linear relationship. This is partially due to the algorithm design, which makes it possible to explore more solutions when the robustness constraint is not tight.

The efficient solutions calculated by ensuring robustness by modifying the lower bounds on the activities are compared to the robust local search solutions of the same robustness level in Fig. 6b. Out of 8 solutions, 6 are dominated, while on the other hand, none of the efficient solutions of the robust algorithm is dominated. The least squares fit lines are clearly separated. Table 1 shows the respective objective values. We may thus conclude that the proposed heuristic generates better solutions than the simple approach of ensuring robustness as hard constraints.

The computation time was approximately $1.5$ s per iteration in all cases, leading to total runtime of 3,000 seconds for every parameter setting.

Table 1 Objective values of efficient solutions

6 Conclusion

We considered different approaches to include robustness in the periodic event scheduling problem, proposing to choose the robustness model depending on the problem size and thus available computational resources.

Based upon our computational experience, we classified three types of instances using the number of lines involved: Small instances with up to 11 lines, medium instances with up to 30 lines, and large instances with more than 30 lines. For small instances where mixed-integer programming can be applied, we presented a model that minimizes the recovery distance to an optimal solution in every scenario. We showed that this problem can be separated depending on the recovery measure, and used this approach to solve medium instances heuristically. For larger instances, we described a local search algorithm to find periodic timetables with a prescribed robustness level.

In an experimental evaluation, we compared both approaches to competitors for the respective problem size.

Appendix: Decomposition of RecOpt-PTT

The following lemma is given in Goerigk and Schöbel (2014).

Lemma 1

Let $x^1, \ldots , x^N\in \mathbb {R}^n$ be optimal solutions to the scenarios $\xi ^1,\ldots ,\xi ^N$ and let $x^*$ be the solution of a location problem (Loc) that is of one of the following forms:

• 1. $loc(x)= \sum _{i=1}^N d^2(x^i,x)$, where $d^2$ is the squared Euclidean distance.

• 2. $loc(x)= \sum _{i=1}^N d(x^i,x)$, where $d$ is linear equivalent to the Euclidean distance.

• 3. $loc(x)= \max _{i=1}^N d(x^i,x)$, where $d$ is linear equivalent to the Euclidean distance.

• 4. $loc(x)= \sum _{i=1}^N d(x^i,x)$, where $d$ is any $l_p$-norm for $1 < p < \infty$ and $n=2$.

Let $Q(x^i) \le \delta$, $i=1,\ldots ,N$, for some convex function $Q:\mathbb {R}^n \rightarrow \mathbb {R}$, $\delta \in \mathbb {R}$. Then

$$\begin{aligned} Q(x^*) \le \delta . \end{aligned}$$

Definition 1

Let $P$ be an optimization problem, and let $(\mathcal {X}_1,\mathcal {X}_2)$ be a partition of the problem variables. Let $\mathcal {F}$ be the set of feasible solutions for $P$. We call $P$ combinable with respect to the variables $\mathcal {X}_1$, if

$$\begin{aligned} x_1 \in Pr_{\mathcal {X}_1} (\mathcal {F}) \end{aligned}$$

for all $x_1 \in \mathrm{conv} \{x^1_1, \ldots , x^N_1\}$ and every set of feasible solutions $\{(x^1_1,x^1_2), \ldots ,(x^N_1,x^N_2)\}$ to $P$.

Theorem 1

Let $(P(\xi ),\xi \in \mathcal {U})$ be an uncertain optimization problem with finite uncertainty, and let $P(\hat{\xi })$ be combinable with respect to the variables $\mathcal {X}_1$. Let $\mathcal {F}(\xi ) \subseteq \mathcal {F}(\hat{\xi })$ for all $\xi \in \mathcal {U}$. Let $d$ be a metric of any of the types from Lemma 1 that only depends on the variables $\mathcal {X}_1$. Then there is a solution to (RecOpt) that is feasible for the nominal scenario.

Proof

Let $\{x^1,\ldots ,x^N\}$ be optimal solutions to the scenarios $\{\xi ^1,\ldots ,\xi ^N\}$, respectively. Let $(x_1^*, x_2^*)\in \mathcal {X}_1\times \mathcal {X}_2$ be an optimal solution to the location problem (Loc). Due to Lemma 1, we have $x_1^* \in \mathrm{conv}\{x^1_1, \ldots , x^N_1\}$.

As $P$ is combinable, there is an $x_2'$ such that $(x_1^*,x_2')$ is feasible for the nominal problem. As $d$ does not depend on the variables in $\mathcal {X}_1$, $(x_1^*,x_2')$ has the same objective value for (Loc) as $(x_1^*, x_2^*)$, which completes the proof.

We conclude that in the case of periodic timetabling, we can separately solve every scenario, solve an unconstrained location problem, and find an optimal solution to (RecOpt-PTT):

Corollary 1

If there is a unique optimal solution to every scenario, (RecOpt-PTT) with respect to a metric equivalent to $l_2$, or $l_2^2$ considering only activities from $\mathcal {A}_{drive} \cup \mathcal {A}_{wait}$ can be solved to optimality by solving $N$ periodic timetabling problems, and one unconstrained location problem.