Hierarchical Human Machine Interaction Learning for a Lower Extremity Augmentation Device

Abstract

For several years considerable effort has been devoted to the study of human augmentation robots. Traditionally, the focus of exoskeleton system has always been on model-based control framework. It seeks to model the dynamic system from prior knowledge of the robot as well as the pilot. However, in lower extremity exoskeleton, the control method depends on not only the modelling accuracy but also the physical human–machine interaction changed from personal physical conditions. To address this problem, in this paper, we present a model-free incremental human–machine interaction learning methodology. In a higher level, the methodology can plan the motion of exoskeleton with the sequence of rhythmic movement primitives. In the lower level, the gain scheming is updated from the dynamic system based on a novel proposed learning algorithm efficient $PI^2$-CMA-ES. Compared with $PI^{BB}$, a particular feature is that it directly operates on the Cholesky decomposition of the covariance matrix, reducing the computational effort from $O(n^3)$ to $O(n^2)$. To evaluate our proposed methodology, we not only demonstrate its applications on the single leg exoskeleton platform but also test on our lower extremity augmentation device. Experimental results show that the proposed methodology can minimize the interaction between the pilot and the exoskeleton compared with the traditional model-based control strategy.

1 Introduction

Quite recently, considerable attention has been paid to the powered exoskeleton, both for the lower and upper extremities [1,2,3,4,5]. In the related application, the lower extremity exoskeleton has been shown great potential, ranging from human strength augmentation to medical assistance as well as motor rehabilitation. In all those cases, the principal characteristics are designed to mimic human movement primitives. To follow the human intention precisely, the exoskeleton should be able to detect human motion intention with little interaction between the exoskeleton and the pilot. In order to address this crucial issue, current research on motion capture is focused on two types controllers, i.e. model-based controller and sensor-based controller.

The core idea of sensor-based controllers is that the input to the controller is collected from the sensor system. Besides, by applying many variations of control strategies, such as impedance control and master-slave control [6], the robotic system can follow the real-time human intention. For instance, with impedance control, the Hybrid Assistive Limb (HAL) exoskeleton is driven by Electro-Myo-Graphical (EMG) sensors data [7]. In their experiments, the pilot’s intention is recognized from different reference patterns through measurement from the EMG sensors directly. Additionally, fuzzy impedance control [8] and active impedance control [9] are designed for adaptation to the changing of the interaction dynamics, measured by the force sensor mounted between the human and the exoskeleton. The main advantage of this type of controllers is that it does not depend on the model, which may bring some benefits for control system design. However, the obvious limit is that the robotic control quality relies heavily on the complicated sensors system.

An alternative is based on the human–robot coupling dynamic model. One of this kind of solution is proposed in [10], and the control method is so-called Sensitivity Amplification Control (SAC) which is applied in Berkeley Lower Extremity Exoskeleton (BLEEX) [11]. As for the control scheme, the sensitivity factor is utilized to make the system more sensitive to the interaction. Thus the interaction force is naturally minimized. Without the need of the sensors to directly measuring the interaction force, the SAC control strategy simplifies the sensors system. Although the complexity of the sensor system is reduced, this methodology has a strong dependence on the accuracy of the dynamic models. Since the dynamic model is quite complicated, the identification process for the model parameters is never an easy task [12]. Furthermore, in [13], Mitrovic et al. analysis a strong case for the limitations of dynamic models. However, SAC has high sensitivity to the human motion, but also to the environment. Therefore if the undesired disturbance acts on the device, the exoskeleton will response the undesired motion intention.

Most of the control methodology mentioned above is characterized by the negative error feedback control with high gain, just like the traditional robotics control strategy. However, when pilot interacts with an exoskeleton, a high gain may lead to unsafety and energy consuming. Thus, the concept of adaptive impedance with the time-varying derivative and proportional gains can be considered as an alternative. However, “the selection of good impedance parameters [...] is not an easy task” [14].

To address this issue, one possible solution is the optimal control [15, 16], where its gain scheduling is automatically selected via many optimal algorithms. However, it still relies on the model-based derivations. Thus, in the complex environment where the prior model’s knowledge is not clear enough, such algorithms are not applicable. Closely related to optimal control is Reinforcement Learning (RL) [17]. The main idea of RL is that, through error and trial, the learning algorithm updates the parameters with minimizing reward function. As the main advantage, the algorithm explores the environment without prior knowledge. Nevertheless, RL suffers high-dimensional curse in continuous state control.

Fig. 1

The proposed hierarchical human–machine interaction learning methodology for a lower augmentation device control

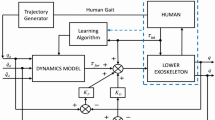
From the point view of biological movements, we hope that the exoskeleton acts as human, in another, the exoskeleton should ensure the safe interaction with a human, which implies that the impedance control strategy should be time-varying and compliant. Consequently, we consider the exoskeleton control as a biological motor system, which has some advantages over the other control strategies regarding robustness, performance, and versatility. Thus, for exploring the possibility of inheriting the merits of sensor-based and model-based controller together, a novel Human Machine Incremental Learning strategy is proposed, which is introduced in Fig. 1. A novel designed exoskeleton so-called lower extremity augmentation device (LEAD) is applied to addressed these crucial issues in this paper, as shown in Fig. 2. The strategy is free of dynamic model and does not depend on the complicated sensor system. On the other hand, the methodology seeks to implement a low time-varying impedance gain scheduling.

Fig. 2

Lower extremity augmentation device (LEAD) and pilot. From the point view of biomechanical consideration, exoskeleton can be seen as an anthropomorphic device which is parallel with the human body. In the design of exoskeleton, the comfortable locomotion is achieved by designing the number of DOF to be close to humans. Thus, our exoskeleton is designed as follows: the knee joint is actuated by a DC motorized ball screw; the hip joint in the sagittal plane is also an active joint, which is driven by a disk-type motor; the other joints are passive with elastic components due to the simplification of the control system and the consideration of total mass

Not akin to the excellent work in [18, 19], the essential difference is that we aim to learn the human motion primitives in real-time with rhythmic movement primitives, which is more natural since the normal human locomotion is also periodic. Moreover, the Q reinforcement learning algorithm is easily suffered from the curse of dimensionality and mainly for the discrete system. In this paper, we aim to provide an online learning algorithm based on the Monte Carlo sampling methods and address the issues in the continuous region of interest.

The main contributions of this paper are given as follows:

• 1. The hierarchical learning framework consists of high-level motion planning and low-level impedance controller is introduced in this paper.

• 2. We propose a human locomotion model with RMPs as well as sparse pseudo-input Gaussian process regression.

• 3. A novel model-free reinforcement learning methodology, so-called Efficient $PI^2$ CMA-ES, is presented in this paper for the purpose of learning the motion trajectory online.

• 4. Finally, we demonstrate that with the proposed learning algorithm, the compliance between the exoskeleton and human can be adapted and simultaneously, the desired trajectory can be followed.

The remainder of this paper is organized into five sections, after the introduction, Sect. 2 outlines related works of Human–Machine Interaction and reinforcement learning based on stochastic optimal control. Section 3 is devoted to discussing the human–machine coupling model as well as Rhythmic Movement Primitives (RMPs). The main routine of the novel reinforcement learning algorithm, so-called Efficient $PI^2$-CMA-ES is presented in Sect. 4. Section 5 compares the proposed learning methodology with several state-of-the-art algorithms and summarizes the results of our simulation work.

2 Related Works and Background

2.1 Human Machine Interaction and Impedance Control

With the aim to maintain safe physical interaction and achieve robustness towards disturbance, exoskeleton should adapt impedance with biomechanical system [20] and improve user’s motion agility [9].

In tradition robotics system, the control methodology is often with constant high gain parameters, as well as negative feedback control loop. Thus, to achieve high accuracy trajectory tracking leads to massive energy consumption. Especially for industrial robots, the safety of staffs is guaranteed with cages built near the robots. As for autonomous mobile robots, energy consumption is a standard criterion that quantitively evaluates the ability of robots.

We consider exoskeleton as an autonomous mobile legged robot that is driven by human intention or human movement primitives. The safety of the pilot is the first factor that be carefully considered by the designer. Furthermore, most of the exoskeletons are required to work in the environment with limited resource. Especially for military applications, the pilot is asked for long hiking and executing the task in a rugged environment.

A distinctive characteristic is that the interaction is not only defined as an input to the controller, but also a factor that we want to get close to its minimal. A direct and proper choice dealing with it is applying impedance control methodology [21, 22], which maps the force according to the difference between desired state and real state. A typical formulation with stiffness K, damping D, mass M as follows

$$\begin{aligned} F = M(\ddot{x} - \ddot{x}_d) + D(\dot{x} - \dot{x}_d) +K(x - x_d). \end{aligned}$$

(1)

For two decades, impedance control has been combined with other control methods especially in feedback loop [23, 24]. However establishing a perfect dynamic model is not an easy task, since mechanical friction, system disturbance, and signal noise exist all the time. Moreover, deriving a good impedance controller requires knowledge of both the environment, robot and also well understanding of the system parameters.

2.2 Reinforcement Learning in High Dimensions

In recent years, reinforcement learning (RL) has shown great potential in autonomy, adaptivity as well as the flexibility of robots regarding specific tasks. Furthermore, RL can be derived from various aspects, such as stochastic optimal control, dynamic programming, probability exploration and policy gradient improvement. With the purpose of generating more scalable algorithms with fewer variable and higher efficiency, RL trends towards combining traditional techniques from dynamic programming and optimal control with current learning algorithms from statistic estimation.

In terms of finite horizon optimal control problems, Differential Dynamic Programming (DDP) [25] is one of the most popular algorithms, which combines model-based RL and optimal control. In DDP, detectability and stabilizability are of great importance for local dynamics approximation concerning convergence. The control policy consists of closed-loop gains and open feedforward loop parameters. Nevertheless, the space state trajectory is optimized locally. As a result, the DDP cannot cope both with planning and gain scheduling. A computation improvement is suggested in [26]. However, this algorithm can only be used in low-dimensional problems.

In [27], the author proposes a min-max Differential Game Theory approach with robotics application. In essence, the approach is a combination of $H_\infty$ control and Differential Game Theory. Although the feedback control is robust to model and dynamics uncertainty, it might result in over conservative control policies. As for the linear system, the robustness of the algorithm is feasible with $\beta$-iteration, while for the nonlinear system, the robustness is not guaranteed.

An alternative algorithm so-called Receding Horizon DDP is provided in [28] with rather an efficient way of solving the local optimal control problem. However, the optimal trajectories and control computing is off-line. The work on LOR-trees is a variation of DDP, which is based on state space approximation. The model-based approach, so-called iterative Linear Quadratic Regulator (iLQR) [29] can improve sampling using control funnels. Despite the improvement in sampling, a key limitation is that the high dimensional dynamical problem is not addressed.

The work by Todorov [30,31,32] on stochastic optimal control presents that the Bellman equation can be defined as the Kullback-Leibler divergence for the discrete optimal control problems. The most interesting aspects are that this kind of problems is equivalent to dealing with continuous state dynamics with quadratic value function and under Gaussian noise. In [30], the stochastic optimal control problem is investigated in discrete state dynamics, and thus it is defined as a Markov Decision Process.

The learning methodology proposed in this paper so-called Efficient $PI^2$-CMA-ES, is based on $PI^2$ algorithm and CMA-ES framework. The $PI^2$ can explore in continuous state space and perform policy improvement concerning the quality of the solution and convergence speed, such as REINFORCE [33] and Natural Actor-Critics [34]. The advantage of $PI^2$ over the others is that not like the DDP, it does not suffer from the curse of dimensions and is totally model-free. An improvement of $PI^2$ is introduced in [35], so-called $PI^{BB}$. The original $PI^2$ is constrained with the $\sigma = \lambda R^{-1}$, where R is the cost matrix, and $\lambda$ is a constant proportional to 1 / h. Thus, based on the Monte Carlo roll-outs, the exploration noise is sampled from a constant covariance matrix. However, the $PI^{BB}$ is black-box optimization algorithm, which can be seen as a “Covariance Matrix Adaptation - Evolutionary Strategy”.

2.3 Dynamical Movement Primitives with Central Pattern Generators

Modelling a nonlinear system is rather complicated due to complex state transitions in response to parameter updates, difficulty in coping with prediction and analysis of long-term behaviour. Thus from the traditional view, coming up with a robust control solution for agility exoskeleton system [11, 36] is not an easy task, since the human biological motor system and human–machine interaction add a strong nonlinearity to our control system.

For periodic human locomotion, neural and phase oscillators are widely applied regarding a set of Degrees of Freedom (DOF). Central Pattern Generators (CPGs) are typical effective alternative solution to rhythmic movement [37, 38]. The main advantage of CPGs is that it is not necessarily taking the system’s dynamics and control dimensionality into account. Besides the robustness of the system and smooth rhythmic motion patterns can be easily gained from sensor data [39, 40].

However, the necessary proper parametrization of CPGs is difficult, since the state-space designing process is strenuous. Also note that, although by applying biomechanics and reduction of the active DOFs, the dimensionality can be simplified. Nevertheless, the prior of tuning process knowledge is still required.

The Rhythmic Movement Primitives (RMPs) are nonlinear dynamical systems that generate rhythmic movements by limit cycle attractor as well as means of points [41]. By using attractor dynamics, RMPs are able to design complicated parameterized trajectories which are robust against external disturbance and easily modulated. Thus, it has been used for trajectories generating, obstacle avoiding. However, when dealing with high-dimension state space, the learning process of RMPs weights is still complex [42].

To address this issue, we seek to combine RMP and CPG together, in which we use RMP’s design rule to hand-tuned CPGs. Thus, a canonical system is employed to generate asynchronous convergence state space. Moreover, a transformation system integrates the reference trajectories, and a function approximator forms a smooth desired trajectory. Furthermore, the force term of the approximator modifies the attractor landscape of control strategy and forms a CPG trajectory. To sum up, the proposed solution is independent of initial condition and adapts to new situation which can be designed online.

3 Locomotion of Exoskeleton

In this section, the dynamic learning model is established based on variable impedance control and RMPs, which is an extended work of [43]. Firstly, we focus on the HMI modelling that obeys rigid body dynamics. Secondly, A sequence movement primitives with human–exoskeleton locomotion are planned by phase resetting and frequency adaptation.

3.1 Dynamical Model Representation

Without loss of generality, the exoskeleton dynamic is represented in a general formulation given as

$$\begin{aligned} \varvec{M(q)\ddot{q} + C(q, \dot{q}) \dot{q} + P(q) = \tau }, \end{aligned}$$

(2)

where $\varvec{M(q)}$ is defined as a symmetric inertial matrix; $\varvec{C(q, \dot{q})}$ consists of the Centrifugal and Coriolis matrix; $\varvec{P(q)}$ is the gravitational matrix and $\varvec{\tau }$ is defined as the actuated torque.

As there exists difficulty in dealing with exoskeleton dynamics in the above formula, we transform the equations into state space

$$\begin{aligned} \varvec{\dot{q}^v}&= \varvec{M (q_p)^{-1}(-C(q_p, q_v) - P(q_p) + \tau )} \end{aligned}$$

(3)

$$\begin{aligned} \varvec{\dot{q}^p}&= \varvec{q^v}, \end{aligned}$$

(4)

The torque term can be written as follows

$$\begin{aligned} \tau _i = K_{P,i}(q_{d,i}^P - q_i^P) + K_{D,i} (q_{d,i}^v - q_i^v) + u_{com,i}, \end{aligned}$$

(5)

where $K_{P,i}$ and $K_{D,i}$ are positive-definite variable, which represents as stiffness variable and damping variable, respectively. With the computed torque method, a feedforward term $u_{com,i}$ is added to the control input in order to eliminate the nonlinearity in the dynamics. Based on Lagrange algorithm, $u_{com,i}$ only compensates the forces due to Coriolis acceleration, gravity and inertia terms, but not the interaction force between pilot and exoskeleton. Thus the learning interaction force is independent of $u_{com,i}$.

Based on the principle of impedance control [21], in [43] the connection between the damping and stiffness parameters is defined as $K_{D,i} = \xi \sqrt{K_{P,i}}$, where $\xi$ is a positive constant.

Note that, although our proposed learning methodology is model-free, the system controller does require a model of an exoskeleton. It is well explained in [44], “If the movement would involve both the compensation of the task dynamics and arm dynamics this generalization would not be possible”. Also, note that the human reduces the effect of dynamics of their arm by using feed-forward control [45] since the exoskeleton’s performance should not depend on the specific human subject with different inverse dynamic model.

In brief, the impedance is parameterized by the gain scheme, i.e. stiffness $K_P$ and damping $K_D$. The main idea of interaction control is to define $K_P$ as a function of implemented movement.

3.2 Interaction Model Representation

Since RMPs are employed to follow human joint trajectories, the exoskeleton device should provide the necessary information about human movement primitives. However, as suggested by [11], the movement intention of the pilot should not be acquired from sensors mounted on the skin such as sEMG sensors. That kind of sensors has a strong dependence on the location of the skin. Moreover, it is not convenient for the pilot to wear the sEMGs sensors whenever he or she wants to use the exoskeleton device. Therefore, we propose a nonlinear regression model to provide the required information for exoskeleton locomotion by applying sparse Pseudo-input gaussian processes (SPGPs) [46]. This model can be interpreted as a mapping from the interaction force to the joint angles in real time.

In our setting, when learning the regression model, the input of N training sets is defined as $\varvec{X} = \{ \varvec{q}_{k-1}, \varvec{F} \}$, with $\varvec{q}_{k-1}$ and $\varvec{F}$ donating joints angles and interaction force respectively at time $k-1$. While the corresponding output is given as $\varvec{y} = \{\varvec{q}_k \}$. Assuming the mapping function $f(\varvec{x})$ corrupted by Gaussian noise $\mathcal {N}(0, \beta ^{-1})$, the generative model is given below

$$\begin{aligned} \varvec{f}(\varvec{X}) \sim GP (0, k(\varvec{X},\varvec{X})),\ \ \varvec{y} \sim \mathcal {N}(\varvec{f}, \beta ^{-1}I) . \end{aligned}$$

(6)

Since the function $\varvec{f}$ should be marginalized out to find the marginal likelihood and predictive distribution, the computation expense related to an inversion $n \times n$ matrix requires $O(n^3)$ time complexity.

Fig. 3

General schematic of CPG locomotion

To address this issue, we employ a computationally tractable regression method, so-called SPGPs mentioned above. The SPGPs aims to construct the regression function with a set of m ($m < N$) input-output pairs $\overline{\varvec{X}} = \{ \overline{x}_m \}_{m = 1}^{M}$ and $\varvec{\overline{f}} = \{ \overline{f}_m \}_{m=1}^{M}$, which can be interpreted as “inducing points”. Consequently, these assumption leads to the data points likelihood as follows

$$\begin{aligned} p(\varvec{y} | \varvec{x}, \varvec{\overline{X}}, \varvec{\overline{f}}) = \mathcal {N}(\varvec{y} | \varvec{K}_{NM}\varvec{K}_{M}^{-1}\varvec{\overline{f}}, \varvec{\varLambda } + \sigma ^2 \varvec{I}), \end{aligned}$$

(7)

Placing a Gaussian prior on the inducing targets $p(\varvec{\overline{f}} | \varvec{\overline{X}}) = \mathcal {N}(\varvec{\overline{f}} | 0, \varvec{K}_M)$, we obtain the posterior distribution over the inducing targets

$$\begin{aligned} p(\varvec{\overline{f}} | D, \varvec{\overline{X}}) = \mathcal {N}(\varvec{\overline{f}} | \varvec{K}_M \varvec{Q}_M^{-1}(\varLambda + \sigma ^2 \varvec{I})^{-1}\varvec{y}, \varvec{K}_M \varvec{Q}_M^{-1} \varvec{K}_M), \end{aligned}$$

(8)

with $\varvec{Q}_M = \varvec{K}_M + \varvec{K}_{MN} (\varLambda + \sigma ^2 \varvec{I})^{-1} \varvec{K}_{NM}$.

Thus, the predictions is given by marginalising out the inducing targets, which is a typical operation in Gaussian process. More specifically, Given a new data point, by integrating the likelihood Eq. (7) with the posterior Eq. (8), we have the distribution over the prediction

$$\begin{aligned} {\begin{matrix} p(y_{*} | x_{*}, D, \overline{\varvec{X}}) &{}= \int p(y_* | x_*, \overline{\varvec{X}}, \overline{\varvec{f}}) p(\overline{\varvec{f}} | D, \overline{\varvec{X}}) d \overline{\varvec{f}} \\ {} &{}= \mathcal {N}(y_* | \mu _*, \sigma _*^2) , \end{matrix}} \end{aligned}$$

(9)

with the mean and covariance of prediction distribution given as

$$\begin{aligned} \mu _*&= \varvec{k}_*^T \varvec{Q}_M^{-1} \varvec{K}_{MN} (\varLambda + \sigma ^2 \varvec{I})^{-1}\varvec{y} \end{aligned}$$

(10)

$$\begin{aligned} \sigma _*^2&= K_{**} - \varvec{k}_*^T(\varvec{K}_M^{-1} - \varvec{Q}_M^{-1}) \varvec{k}_* + \sigma ^2, \end{aligned}$$

(11)

with $K_{**}$ donating the covariance between new input points, also likewise for the other indexes. The inferring of the posterior distribution over the targets correspond to learn the regression model. In addition, with the assumption of connection of the inducing target and training data, the sparse Gaussian process can achieve effective learning with the computational complexity of $O(NM^2)$.

3.3 Rhythmic Movement as a CPG

Without feedback of the sensor data, Central Pattern Generators (CPGs) are defined as the neural circuits in the spinal cord of vertebrates. In this paper, the motion of each leg is address by each CPG. Each unit generator is driven by a nonlinear function, which consists of a pattern generator defined by a rhythmic generator.

From Fig. 3, each leg is composed of 2 active DOFs, i.e. hip joint and knee joint both in the sagittal plane. The others are passive joint as mentioned before. Besides, we describe the walking movement sequence by employing RMP. Each locomotion period starts with a new initial phase and maybe a different frequency. To regulate the desired phases of each exoskeleton leg, we couple among the neural oscillators. This motivation is driven by biological conception, which is naturally used in human locomotion and gait transition. The hypothesis assumes that dealing with neural oscillators is of great importance in desired phased coordinates [47].

The period locomotion is implemented by a phase oscillator, and is also as a timer which can generate rhythmic movement for a single leg. The coupling terms of the oscillator i is introduced as follows

$$\begin{aligned} \dot{\phi }(t) = \omega + \kappa \sum _{i = 1}^{n} C_{ij} sin(\phi _j(t) - \phi _i(t) - \phi _{bias}), \end{aligned}$$

(12)

where $C_{ij}$ is a $n \times n$ matrix, which presents the connection between the other oscillators, and $\kappa$ is a positive coupling strength. Besides, $\phi _i(t)$ and $\phi _j(t)$ are reference trajectories, and $\phi _{bias}$ is the phase bias between two reference phase trajectory.

Fig. 4

Foot switch location. In order to maximize the sensitivity of the contact, the foot switches are mounted underneath ridges in the position of toe and heel respectively

Fig. 5

Rhythmic movement primitives (RMPs). RMPs aim to generate arbitrary smooth continuous periodic movement primitives with a simple linear dynamical system as well as a nonlinear component $g_k \theta$. The nonlinear component is comprised of now von Mises basis functions, multiplied with a learning weight vector $\theta$. The canonical system elements, amplitude $r_t$ and phase $s_t$ are presented in polar coordinates, essentially representing a periodic behaviour. The rhythmic movement has a period of 1 second with a reaching goal the end of one cycle. Although the proportional gain schedules $K_p$ are not transformation system, we would rather define as a approximator $K_{p,t} = g_k \theta$

Note that, the motivation behind this oscillator is that along with the rising of time keeping clock, the period phase monotonically increases with the rate $\omega$. The rhythmic signal of oscillator acts as a timer for the implementation of the rhythmic primitives. To be more specific, the formulation is applied to coordinate the desired phase connection. Among the canonical oscillators, we design the desired phase difference such that the joints in the same leg with zero phase difference, and the joints in the different leg with an opposite phase ($\pi$ phase difference). More specifically, we define $\phi _1$, $\phi _2$ as a joint phase of knee and hip in the left leg $S_{left}$, and $\phi _3$, $\phi _4$ as a joint phase of knee and hip in the right leg $S_{right}$. Besides , the following condition is also required, $\phi _1 - \phi _2 = 0$, $\phi _3 - \phi _4 = 0$, $\phi _1 - \phi _3 = \pi$ and $\phi _2- \phi _4 = \pi$. Therefore, the element of relationship matrix C is written as below

$$\begin{aligned} C_{ij} = {\left\{ \begin{array}{ll} 0 &{} \text {if } i = j; \\ 1 &{} \text {if } i,j \in S_{left}\ or\ S_{right}; \\ -1 &{} \text {else}. \end{array}\right. } \end{aligned}$$

(13)

We employ the phase resetting to avoid the discontinuity of the motion planning. Figure 4 gives the design conception of exoskeleton shoes. The phase resetting is driven by the specific event

$$\begin{aligned} \dot{\phi }_{ref}&= \hat{\omega }_{ref}^n + \delta (t-t_{heel})(\phi _{heel} - \phi _{ref}) \end{aligned}$$

(14)

$$\begin{aligned} \hat{\omega }_{ref}^{n+1}&= \hat{\omega }_{ref}^n + K(\omega _{measured}^n - \hat{\omega }_{ref}^n). \end{aligned}$$

(15)

As soon as the heel of left leg strikes at the ground, the phase of the left leg $\phi$ is defined as $\phi _{heel} = 0$, on the contrary, the phase of the right leg is defined as $\phi _{heel} = \pi$ naturally. n is the steps’ counter and $\delta$ is known as Dirac delta function.

3.4 Motion Planning with Rhythmic Dynamical Movement Primitives

The desired state $\dot{q}_{d,j}^p$,$\dot{q}_{d,j}^v$ are acquired by employing Rhythmic Movement Primitives (RMPs). Every RMP forms its trajectory, which means the following description hold for every DOF.

Two actuated joints (hip joints and knees joints) in each leg are equipped by a RMP. For the convenience, we define the indexes as follows: $i =1$ , $i = 2$ for $R_{hip}$ and $R_{knee}$ respectively, and $i =3$ , $i = 4$ for $L_{hip}$ and $L_{knee}$ separately. In this paper, we only present the necessary formulation, and we leave the more specific information to [41, 48]. The one-DOF RMP is written as a state space model

$$\begin{aligned} \begin{bmatrix} \dot{q}_{d,j}^v \\ \dot{q}_{d,j}^p \\ \end{bmatrix} = \frac{1}{\tau }\begin{bmatrix} \alpha \beta&\alpha \\ 0&1 \\ \end{bmatrix}\begin{bmatrix} g - q_{d,j}^p \\ - q_{d,j}^v \\ \end{bmatrix} + \frac{1}{\tau } \begin{bmatrix} \varvec{g^j\theta _{ref}^j} \\ 0 \\ \end{bmatrix}, \end{aligned}$$

(16)

where $\alpha$ and $\beta$ are positive constants and $\tau$ is a time constant. $\phi$ and r represents phase and amplitude respectively. g is defined as a goal. The second term $\varvec{g^j\theta _{ref}^j}$ is a nonlinear force term which is chosen to be periodic. The shape of movement is defined by the parameter $\varvec{\theta _{ref}^j}$, which is a learning parameter. The normal weight $\varvec{g^j}$ is given by

$$\begin{aligned} g_k^j = \dfrac{w_k(s_t)}{\sum _{k=1}^{N} w_k(s_t)}r_j, \end{aligned}$$

(17)

where $w_k(s_t)$ is a non von Mise basis function, satisfying Eq. (18)

$$\begin{aligned} w_k(s_t) = \exp (h_k(\cos (\phi _j - c_k)- 1)). \end{aligned}$$

(18)

However, the RMP system does not simultaneously converge to the goal. In order to couple with multiple DOFs exoskeleton locomotion in one dynamic system, a first-order linear dynamics so-called canonical system is presented in Eq. (19) as well as Eq. (20)

$$\begin{aligned} \tau \dot{r}_i&= - \mu (r_i - r_{i,0}) \end{aligned}$$

(19)

$$\begin{aligned} \dot{\phi }_i&= \alpha _{\phi }, \end{aligned}$$

(20)

where the canonical system is functioned with amplitude $r_i$ and period phase $\phi$. Since the dependency of the explicit time is avoided, the dynamic system is an autonomous system.

Fig. 6

Upper right graph: the updated distributions of CMA-ES. Lower left graph: mapping from costs of sample points to probability. Note that the updated distributions do not consist of all the sample points, only the points with high probability are considered as eliteness

As follows from Fig. 5, the core idea of RMPs is to generate a desired variables represented as position, velocity, and acceleration for the controller, then the controller transfers these variables to motor commands.

4 Incremental Human Machine Interaction Learning

Human walking locomotion consists of period movement sequences. Each sequence might differ with the others regarding time period, walking speed and locomotion profile. Therefore, it is difficult to propose a learning algorithm with one step of parameters updating that can perfectly describe walking sequences. In this subsection, we present an incremental reinforcement learning method and extend the sequence primitives to RMPs.

Our proposed learning methodology hinges on two contributions, i.e. subsection parameter updating of sequence primitives; subsection learning routine of Efficient $PI^2$-CMA-ES.

4.1 Efficient $PI^{2}$-CMA-ES

The $PI^2$ algorithm is a reinforcement learning method, which is derived from the first principle of optimal control. Its name comes from the Feynman–Kac lemma, which can be transformed from the Hamilton–Jacobi–Bellman lemma. It seeks to use parameterized policies from the point view of the probability-weighted averaging. Consequently, with the conclusion of the path integral stochastic optimal, the path cost for the specific RMPs case is given as

$$\begin{aligned} {\begin{matrix} C(k, i) &{}= \phi _{t_N,k} + \sum _{j = i}^{N-1} q_{t_j,k} \\ &{} \qquad +\frac{1}{2}\sum _{j = i+1}^{N-1}(\varvec{\theta } + M_{t_j,k} \epsilon _{t_j,k})^T R (\varvec{\theta } + M_{t_j,k} \epsilon _{t_j,k}), \end{matrix}} \end{aligned}$$

(21)

where $\phi _{t_N,k}$, $q_{t_j,k}$ are the terminal cost and immediate cost respectively, and $\epsilon _{t_j,k}$ is written as the samples from normal distribution. Besides, $M_{t_j,k}$ is a projection matrix of the range space $\varvec{g_{t_i}}$, written as follows

$$\begin{aligned} M_{t_j,k} = \frac{R^{-1}g_{t_j,k}g_{t_j,k}^T}{g_{t_j,k}R^{-1}g_{t_j,k}^T}. \end{aligned}$$

(22)

Furthermore, compared with the traditional reinforcement learning, the core idea is that the curse of the dimensionality associated with state action pairs can be simply avoided. By applying the constraints $\varSigma = \lambda R^{-1}$, $PI^2$ keeps a fixed update covariance. However this constraint is not necessary, since 1) positive-semid, the $PI^2$ applies the finite constraint matrix can be seen as a vice versa and covariance matrix 2) a positive-semidefinite matrix with positive weight-average is also a positive-semidefinite matrix [49].

Rather than using a constant covariance matrix, we focus on a variant $PI^2$ with an adaptation covariance matrix. The Covariance Matrix Adaptation Evolution Strategy (CMA-ES) [50] is developed for solving ill-conditioned problems by accelerating the convergence rate. Besides, CMA-ES can generate offspring candidates from parents and explore to the prevailing narrow valley. To be specific, the main difference of update rule is shown as in Fig. 6.

The main properties of CMA-ES used in this paper are introduced as follows:

• 1. The probabilities can be defined by the user and the default setting is fully explained by [50].

• 2. Samples are acquired from the Gaussian distribution $N(\theta , \sigma ^2 \varSigma )$. Note that the covariance matrix is governed by the step size $\sigma$ and shape $\varSigma$, and are updated respectively.

• 3. The covariance matrix and step-size are maintained in the ‘evolution path’, which seeks to update the parameters iteratively. The convergence speed is significantly improved since the correlations of the consecutive step is exploited incrementally.

The Efficient $PI^2$-CMA-ES proposed in this paper, is a novel variant of $PI^2$ and CMA-ES, as presented in Algorithm 1. The interesting property is that it reduces the computing cost by Cholesky decomposition from $O(n^3)$ to $O(n^2)$ [51]. The main algorithm is introduced in three routines in pseudo-code and the default parameters are presented in Table 1. In the core part, the new candidate is selected from the normal distribution with the mean from a $PI^2$ update rule and the covariance depending on the CMA-ES principle.

Table 1 Default parameters for CMA evolution strategy

Fig. 7

The generic loop of parameters updating. The policy improvement of gains and trajectory are updated separately, although they share the same cost functions

The indicator function is used to test the candidate elitism. Thus the value is one if the last mutation succeeds and otherwise zero.

The step size is updated relying on the learning rate $c_p$ by a target default rate $p_{succ}^{target}$, as presented in Algorithm 2. The motivation is that the step size should be amplified if the success rate is a high value, from the point of heuristics, and the step size should be lessened since the success rate is low. Note that, the default parameters are rooted according to [52].

As described in Algorithm 3, instead of operation in covariance matrix, it can be directly implemented on the Cholesky components and their inverse. Thus, the update of the covariance matrix is never calculated explicitly.

4.2 Parameters Updating

In our proposed learning framework, the movement primitives and variable impedance gain are simultaneously updated, as shown in Fig. 7. Thus, we rewrite the Eq. (16) and add a function approximator to $K_{P,i}$

$$\begin{aligned} \dfrac{1}{\tau } \dot{q}_{d,j}^v&= \alpha (\beta ((g_j + \epsilon ^g) - q_{d,j}^p) - q_{d,j}^v) + \varvec{g_{i}^{i,T}(\theta _{ref}^i + \epsilon ^i) } \end{aligned}$$

(23)

$$\begin{aligned} K_{i}&= \varvec{g_{t,K}^{i,T} (\theta _K^i + \epsilon _K^i) }. \end{aligned}$$

(24)

Before implementing a roll-out, the shape exploration noise $\epsilon ^i$ and the gain exploration noise $\epsilon _K^i$ are generated by the sampling from each Normal distribution respectively with mean $\theta$ and covariance $\varSigma$.

Then by these ‘noisy’ the RMP can generate a bunch of movement primitives $[\dot{q}_{d,j}^p, \dot{q}_{d,j}^v]$ with a slight difference. Thus each trajectory leads to different penalties. According to these penalties, the parameters are updated by applying the proposed Efficient $PI^2$-CMA-ES. The most crucial part of this update rule is explained in the next subsection.

In Dynamic Movement Primitive (DMP) the g is written as a goal which leads the attractor to approximate the target, while in RMP the g is defined as a baseline. Considering the difference between each human walking cycle, the exoskeleton should adapt to the changeable movement primitives as long as the pilot’s path pattern varies. Thus the direct feedback derived from sensor observation data is the interaction force, which is changing during the human locomotion. An alternative explanation is that the trajectory does not fit for the pilot, and it should be adapted to the movement primitives. From intuition, we would rather have a changeable attracting goal than a fixed baseline. Besides, in order not to lose the advantage of the limit cycle attractor, the incremental goal learning is a good option.

Inspired by [53], we seek to update the goal and shape simultaneously. Note that, as for sequence primitives learning, the goal potentially influences not only the current trajectory penalty but also the whole sequence trajectories. When the learning of shape parameter is implemented, the goal should be kept constant so as not to avoid updating the shape of trajectory. Thus, there is no temporal dependency effect of goal on the cost.

To update the goal, the whole learning strategy remains the same. The main difference is that we update the goal using the total trajectory cost, not a cost of single sequence movement. This means that the probability is only computed at the first start moment of the learning. Besides, in order to shape a smooth trajectory, we add another equation

$$\begin{aligned} \tau \dot{g} = \alpha _g (g_0 - g). \end{aligned}$$

(25)

Accordingly, the goal parameters are updated on the basis of total trajectory cost, while the variable impedance parameters and shape parameters are updated according to every single sequence. Note that, each sequence is divided by walking resetting and the whole trajectory update consists of every sub-trajectory updates. The motivation behinds this is that the smoothness and continuity are considered with a simultaneous update of goal and trajectory parameters in order to avoid a jerk or stroke primitive.

Fig. 8

One DOF (knee joint) experiment. To illustrate our proposed learning scheme, the experiment is implemented on a single DOF exoskeleton platform. All active joint motors are turned off except the right knee to simulate as one DOF experiment platform. Also, through the connection cuff, the interaction between the pilot and the exoskeleton is compliantly connected and also the pilot’s shoes are attached to the exoskeleton shoes. With the assistance torque from the DC motorized ball screw actuator, the pilot is asked to periodically sway his leg, which can be seen as a typical rhythmic movement primitive. From the a–g shown above, the periodic movements are recorded according to the simulation timer

5 Experiment Evaluation and Discussion

In this section, we conduct two experiments to evaluate the proposed methodology. The goal of the first experiment is to compare the learning performance of the proposed Efficient $PI^2$-CMA-ES with $PI^2$ [48] and $PI^{BB}$ [35]. Secondly, we compare the Efficient $PI^2$-CMA-ES with the Sensitivity Amplification Control (SAC) algorithm which is considered as a start-of-the-art control scheme typically for the exoskeleton [54].

5.1 Experiments on Single Joint Exoskeleton System

In order to evaluate the proposed learning algorithm, we apply $PI^2$, $PI^{BB}$ and our methodology on a single joint exoskeleton platform. In the experiment, the pilot’s whole leg is attached with the exoskeleton, which makes the swing primitives possible only with the knee joint in the sagittal plane.

The $PI^{BB}$ is a black-box optimization (BBO) algorithm, also derived from $PI^2$. The motivation behind choosing these two algorithms is that RL and BBO are two typical approaches to performing the optimization from action perturbation as well as parameter perturbation respectively. The policy improvement of BBO is focused on reward weighted averaging. However, the parameters updating is based on the gradient estimation. Thus, these two typical algorithms are the concrete implementation of the state-of-the-art RL and BBO.

For the following experiments, we define the learning task with the following immediate reward function, which is an implementation of a specific task according to [55]

$$\begin{aligned} r_t = W_{gain}\sum _{j}K_{P,t}^t + W_{acc}\ddot{x} + W_{via} f_{error}, \end{aligned}$$

(26)

where $\sum _{j}K_{P,t}^t$ is the sum of the control proportional gain over time. It seeks to improve desired performance such as energy saving, less wear and tear and the compliant interaction which leads to the behaviour of safety and robustness. The acceleration term $\ddot{x}$ is to penalize the cost of high jerk of human motion. This regularization term corresponds to finding the trade-off between the generality of optimization as well as the fit to the learning trajectory. The term via-point $f_{error}$ consists of several tracking errors and is written as follows

$$\begin{aligned} f_{error} = \sum _k \beta (q^d_k - q_k)^2, \end{aligned}$$

(27)

where $q_k$ is the joint angle planned by RMP, while $q^d_k$ is the desired joint predicted with the SPGPs. Therefore, we do not need to mount sensors on the body of the pilot, such as sEMGs or IMU (inertial measurement units). Note that we choose several points from the trajectory to function the tracking error penalty, not all of the trajectory. The motivation behind this is that we would rather plan the movement primitives rather than follow the fixed trajectory.

As shown in Fig. 8, the platform is driven by a DC motor, which provides extra strength for the pilot’s knee joint. The encoder is mounted on the knee joint as well as the hip joint to measure the actual joint angle. The reference joint angle is provided with an inclinometer, which is attached to the pilot. In addition, the interaction between the pilot and the exoskeleton is compliant through a connection cuff. The pilot’s shoes are attached to the exoskeleton shoes. Therefore, the pilot can interact with the exoskeleton flexibly and driven the exoskeleton easily with imposed force. Since the human locomotion is focused on the period walking pattern, the primitive of the knee joint is also designed as a periodic movement. The pilot is asked to sway his leg periodically, which is well interpreted in Fig. 8.

Fig. 9

Learning costs with different initial exploration magnitudes. We compare Efficient $PI^2$-CMA-ES, $PI^{BB}$ and original $PI^2$ with three different magnitudes ($\lambda = 1, 10, 50$)

Fig. 10

The exploration magnitudes during learning process. Note that both $PI^{BB}$ and Efficient $PI^2$-CMA-ES update an adaptation covariance. However, $PI^2$ keeps a fix covariance during learning procedure

As can be seen from Figs. 9 and 10, the Efficient $PI^2$-CMA-ES outperforms better convergence behavior than $PI^{BB}$ and $PI^2$. For $PI^{BB}$ and Efficient $PI^2$-CMA-ES, the exploration magnitudes are varying over time with the update of covariance matrices. While for $PI^2$, the covariance matrices maintain the same during learning, since the covariance matrices are not updated. For $\lambda = 20$, both $PI^{BB}$ and Efficient $PI^2$-CMA-ES have a nice convergence behaviour, while $PI^2$ also shows a good behaviour in convergence, but “vibrates” with a high cost. Consequently, this kind of behaviour also appears when magnitude $\lambda = 50$, as $PI^2$ has a larger penalty value. However, when $\lambda = 1$ the convergence of $PI^2$ is much slower, but performs better in convergence cost. Moreover, the Efficient $PI^2$-CMA-ES converges at 18th step, barely influenced by the initial magnitude, while $PI^{BB}$ converges at 30th step. The interesting property presented in these two figures is that a larger exploration magnitude does not always have a positive effect on learning speed. To be more specific, as shown in Fig. 9, for $\lambda = 50$, both $PI^{BB}$ and $PI^2$ present a poor behaviour in terms of convergence speed from step round 8th to step 18th, While $PI^2$-CMA-ES works better, converged at step 18th nearly. It can be explained that although the larger magnitude is good for exploration, it can not work for the whole learning procedure. Besides, the variant covariance matrix is updated from the penalty which already exists.

Fig. 11

Left graph: flat walking experiment with LEAD system. Right upper graph: initial and final gain scheduling for hip joint of left leg. Right lower graph: initial and final gain scheduling for knee joint of left leg

From those results we have three conclusions for our proposed learning methodology: (1) The convergence speed of Efficient $PI^2$-CMA-ES does not rely on the initial value too much. However, for $PI^2$ and $PI^{BB}$, a good initial magnitude start may have nice effect on learning speed. (2) The Efficient $PI^2$-CMA-ES increases exploration magnitude when the cost results in a high value. (3) The Efficient $PI^2$-CMA-ES automatically decreases exploration magnitude when the task has been fulfilled.

5.2 Experiments on the LEAD System

The develop LEAD control architecture mainly consists of the sensing system, the CAN (Controller Area Network) bus communication system and the embedded controller. The CAN bus communication system can achieve a high rate of 1Mbit per second real-time performance. The embedded coral controller is designed on dual-core processor Freescale and ARM-Cortex-A9 in an Ubuntu 12.04. The processing and fusion of sensor data, as well as the control command, is processed in this embedded board. The communication between the high-level controller and low-level driven system is connected to the first channel of the CAN, while the second channel is used to communicate with the sensor system. The sensor system is basically composed of the force switches, the force sensors, the optical encoders and incline angle system which is used to demonstrate the simulation of our proposed methodology.

Fig. 12

Upper graph: right upper graph: the HMI comparison of right leg between SAC and efficient $PI^2$-CMA-ES. Lower graph: the HMI comparison of left leg between SAC and efficient $PI^2$-CMA-ES

For evaluating the control performance of our proposed learning methodology, we test our learning algorithm and SAC control framework on the LEAD robotics system with a flat walking pattern, as shown in the left graph of Fig. 11. The SAC control algorithm is mainly designed to detect the human motion intention with the interaction between the exoskeleton and the pilot.

After the online learning in RMPs, the LEAD system shows a good performance in coping with the flat walking pattern. The gain self-tuning is presented in the right graph of the Fig. 11, which shows a learning procedure in a gait period. For gain scheduling, the initial gain for each joint is set to be 50, and also a lower bound is written as 10 according to experimental experience; After 40 learning loops, the gain scheduling is shown as the solid blue curve in the right graph of the Fig. 11. Besides, the Fig. 12 illustrates the control performance of the SAC algorithm and Efficient $PI^2$-CMA-ES methodology respectively. As shown in Fig. 12, comparing with the HMI force of SAC algorithm, the interaction force of Efficient $PI^2$-CMA-ES is much smaller in both right leg and right leg. Besides, the tracking error of the flat walking is shown in Fig. 14. The exoskeleton can follow the pilot’s motion with little tracking error in flat walking, which illustrates that the HMI between the device and the pilot can be significantly reduced. Besides, since the movement primitives vary during the locomotion, through online learning of parameters the exoskeleton can adapt to different walking primitives.

Fig. 13

Left graph: the pilot with exoskeleton goes downstairs. Right graph: the pilot with exoskeleton goes upstairs. We extend the experiments to going upstairs and downstairs

Fig. 14

Upper graph: tracking errors of hip joints of three different walking patterns (flat walking, upstairs, downstairs). Lower graph: tracking errors of knee joints of three different walking patterns (flat walking, upstairs, downstairs)

Furthermore, we extend experiments to going upstairs and downstairs, as shown in Fig. 13. The experimental results in Fig. 14 indicate that through incremental HMI learning the LEAD is also able to follow the more complex human motion and show a good control performance. Also, note that an interesting property in three walking patterns is that comparing the range of hip joint angle in three different walking pattern, we find that the range of hip motion in an upstairs case is larger than in flat walking. Moreover, when in downstairs case, the pilot lifts hip lower than in flat walking. From our intuition, we also feel more tired going upstairs the flat walking and downstairs.

6 Conclusion

In this paper, we propose a learning control methodology so-called Incremental Human–Machine Interaction Learning for our Lower Extremity Augmentation Device. The reinforcement learning algorithm based on Efficient $PI^2$-CMA-ES can simultaneously learn rhythmic movement primitives and gain scheduling. Through incremental goal updating, the exoskeleton can adapt to different walking patterns by on-line trajectory updating.

Furthermore, in order to evaluate the performance and feasibility of our proposed learning methodology, we experiment on the single leg exoskeleton platform as well as the LEAD system. The results show a satisfying speed of learning convergence, compared with several state-of-the-art model-free reinforcement learning algorithms. Also, the HMI force between the pilot and the exoskeleton can be significantly reduced compared with the SAC control framework. Although the work done in this paper is mainly focused on the learning from human motion trajectory, the original design of this device is to enhance human endurance or augment human ability, such as weightlifting or hiking. However, if the user is a health human subject, the proposed algorithm in this paper may be a feasible solution since the human movement primitives is normal.

The future work will be focused on the learning of more complex movement primitives in more complicated constraint environment. The daily human life consists of many kinds of discrete and periodic motions. In addition, the environment is usually more unpredictable and stochastic than the flat ground or upstairs. Finally, understanding with limit sensor information is also a crucial task for human–machine coupling control.